Как найти вакуум формула

Абсолютным давлением р
называется
гидростатическое давление, определяемое
по формуле (64).

Из этой
формулы следует, что абсолютное давление
слагается
из двух составляющих: внешнего давления
,
передаваемого
жидкостью по закону Паскаля, и давления,
определяемого
величиной γh.
Последнее
называют относительным или, если
на свободной поверхности жидкости
действует атмосферное давление,
избыточным
давлением. Исходя
из принятой формулировки
формулу (64) можно переписать в следующем
виде:

(65)

где
избыточное давление

(66)

Из
последнего равенства следует, что
избыточное давление изменяется
с глубиной по линейному закону

(67)

и в
координатах р/у
и
h
изобразится
в виде биссектрисы координатного угла
[1].

Абсолютное
давление не может быть отрицательным,
так как
жидкость не сопротивляется растяжению.
Избыточное давление
как разность
может быть и
больше, и меньше нуля, т. е.
отрицательное
избыточное давление называют
вакуумметрическим
давлением,
т.е.

(здесь
hвак
называется вакуумметрической
высотой). Можно
написать

;

тогда
вакуумметрическая высота выразится
формулой

.(68)

Вакуумметрическая
высота
h_вак
возрастает по величине с уменьшением
абсолютного давления и в пределе, когда
р_абс
= 0
(отрицательным
абсолютное давление быть не может),
достигает максимума
,
т. е. величины атмосферного давления.

3.6. Давление жидкости на плоские стенки. Центрдавления

Определение силы давления.
Предположим, что плоская стенка,
ограждающая некоторую массу неподвижной
жидкости, наклонена к горизонту под
углом α. Определим силу Р, с которой
жидкость действует на выбранную в
пределах этой стенкиплощадку
(рис. 10).

В каждой точке на этой
площади гидростатическое давление
равно р и
отвечает формуле р
=
, где dP
— элементарная сила,
аdω -элементарная
площадка.

Следовательно,
сила, с которой жидкость действует на
элементарную
площадку dω,
будет равна dP
=
pdω.
Эта сила направлена
по нормали к плоскости стенки. Аналогично
будет определяться
сила давления жидкости на любую другую
элементарную
площадку dω.
Поэтому
искомую силу Р, с которой покоящаяся
жидкость действует
на площадь
,
можно найти
как равнодействующую системы
параллельных сил dP,
равную
их алгебраической сумме.

Рис. 10 – К определению силы давления на
плоскую стенку

Итак,
искомая сила

.

Но в
любой точке гидростатическое
давление ,откуда

(69)

Ориентируем
данную площадь относительно соответственно
расположенных координат осей. Примем
за ось 0x
линию
пересечения
свободной поверхности воды с плоскостью
стенки и
направим
координатную ось
0z’*
вниз
вдоль стенки (рис. 10).

В этой
координатной системе все точки
определяются координатами
x́́’
и
ź’,
поэтому глубину h
выразим
через ź’,
а именно:
h=z‘
sin
.

Итак, силу Р
можно определить по
формуле

,

или

(70)

Для
определения интеграла
обратим внимание на то,что
подынтегральное выражение можно
рассматривать как статический
момент площадки dω
относительно координатной оси 0х
(или
оси 0х’).
Тогда
этот интеграл представит собой сумму
статических моментов элементов площади
ω, т. е. статический момент
самой площади
относительно той же оси 0х.

Известно,
что статический момент площади
относительно любой оси, лежащей в той
же плоскости, равен произведению этой
площади на расстояние от центра ее
тяжести до оси моментов.

Таким образом,

,

где z’_c
– расстояние от точки с
(центра
тяжести площади ω) до
оси 0х́
(оси
моментов).

Делая
соответствующие подстановки в формулу
(70), получим

P. (71)

Здесь первое слагаемое
р₀ω
представляет собой атмосферное давление
на свободную поверхность, передаваемое
жидкостью по
закону Паскаля, а второе — давление,
оказываемое на
стенку уже самой жидкостью (можно сказать
— избыточное давление).

Перепишем
формулу (71) в более удобном для практических
расчетов виде. Заметим, что произведение
z‘_c
sin
α равно глубине
погружения центра тяжести площади ω
под уровень свободной
поверхности h_с,
поэтому

, (72)

или, за вычетом атмосферного давления,

. (73)

Произведение
h_сω

представляет собой объем цилиндра с
площадью
основания, равной
,
и высотой, равнойh_c,
с учетом чего формулу (73) можно прочитать
так: сила,
с которой жидкость действует
на плоскую стенку, равна весу жидкости
в объеме цилиндра
с основанием, равным площади данной
стенки, и высотой,
равной глубине погружения центра тяжести
этой площади
под уровень свободной поверхности.

Формулу (73) можно еще упростить.

Так как
γh_c
представляет
собой гидростатическое давление в
центре тяжести площади
,
то справедливо равенство

Р = р_с
ω. (74)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ВАКУУМ, разреженное состояние газа. При обычных условиях (760 мм давления ртутного столба и температуре = 0°) в 1 см³ газа находится Зх10¹⁹ молекул. В лучшем, достижимом современными средствами вакууме давление газа достигает 10^-8—10^-9 мм ртутного столба, или около 10^-11 Atm. Так как число молекул пропорционально давлению, то оно при этих условиях равно Зх10¹⁹х10^-11=3×10⁸, т. е. в лучшем вакууме имеется все-таки огромное число молекул (100 млн. на 1 см³). Однако разного рода физические явления в газе определяются не столько числом молекул, сколько средней свободной длиной пути λ, т. е. тем средним путем, который каждая молекула пролетает между двумя соседними столкновениями. Величина эта при атмосферном давлении для разных газов разная, но в общем имеет значение около 10^-5 см. При уменьшении давления газа р величина λ меняется обратно пропорционально р, так что при давлении в 10^-11 Atm она имеет значение 10⁶ см, т. е. 10 км. При наличии такого вакуума в сосуде с линейными размерами в 20—30 см, молекулы, в нем находящиеся, практически никогда не будут сталкиваться между собой, но будут лишь ударяться о стенки прибора. В соответствии с этим все свойства вакуума резко отличаются от свойств плотных газов. В физике принято называть вакуумом именно такие разрежения, когда λ имеет величину большую, чем размеры прибора, т. е. >10—30 см, что отвечает давлениям р < 10^-3—10^-4 мм ртутного столба.

Для уяснения дальнейшего необходимо остановиться на характеристике некоторых свойств вакуума. Внутреннее трение газа, как известно, обусловлено передачей количества движения молекулами быстрых слоев молекулам, двигающимся более медленно. Коэффициент внутреннего трения η = v∙ϱ∙λ/3, где ϱ – плотность газа, а λ – свободная длина пути; т. к. ϱ пропорционально, а λ обратно пропорционально давлению газа, то η не зависит от давления. В вакууме условия совершенно меняются: молекулы между собой более не сталкиваются, и трение обусловливается передачей количества движения непосредственно стенке; трение, так сказать, перестает быть внутренним и становится внешним. При этом трение разреженного газа, конечно, делается пропорциональным числу ударов молекул о стенку, т. е. падает при уменьшении давления. То же относится к теплопроводности. Если между двумя параллельными плоскостями с разными температурами Т₁ и Т₂ находится плотный газ, то внутри газа происходит прямолинейное падение температуры вследствие того, что передача тепла идет через столкновения между молекулами. В вакууме, где столкновений между молекулами нет, передача тепла идет так: молекула, сталкиваясь с горячей стенкой, приобретает энергию молекулы стенки; отразившись, она ударяется о холодную стенку, передает ей избыток энергии и, отражаясь снова, имеет уже энергию, отвечающую молекулам холодной стенки. Т. о. здесь нельзя говорить о градиенте температуры внутри газа. Теплопроводность плотного газа, как и внутреннее трение, не зависит от давления; теплопроводность же вакуума, конечно, пропорциональна давлению. Для характеристики различия в свойствах вакуума и плотных газов можно привести еще пример: в сосуде, разделенном на две части перегородкой с отверстием (причем температура стенок одной части будет Т₁, а другой – Т₂), в случае плотных газов давление газа в обеих частях одинаково. Трактовать вакуум как сжимаемую жидкость нельзя: стационарное состояние здесь определится из условия, что числа молекул, пролетающих через отверстие в ту и другую сторону за единицу времени, д. б. равны друг другу. Число молекул, летящих из более горячей части в холодную (Т₁>Т₂), будет пропорционально n₁u₁, где n₁ – число молекул в единице объема первой части сосуда, а u₁ – их скорость. Соответственно в другую сторону будет лететь n₂u₂ молекул. Условие равновесия: n₁u₁ = n₂u₂, а так как n пропорционально плотности газа, а плотность пропорциональна давлению р, деленному на абсолютную температуру Т, то

Скорости молекул, как известно, пропорциональны √T, отсюда имеем

Таково условие равновесия в вакууме вместо условия р₁ = р₂ в плотных газах.

Эти особые свойства вакуума позволяют сконструировать ряд манометров, которыми можно измерять давление газа в вакууме. Из них основным прибором для измерения давления является манометр Мак-Лауда.

Прибор (фиг. 1) состоит из закрытого капилляра К₁, соединенного с баллоном. Действие его заключается в следующем. Из прибора, давление в котором необходимо измерить, газ поступает через трубку а в объем Н. Поднятием груши с ртутью пространство Н выключается от остальной установки, и газ в ней дальнейшим поднятием ртути сжимается до того, что весь вгоняется в капилляр К₁. Если разность уровней ртути в капилляре К₁ и капилляре К₂, соединенном всегда с прибором, равна h, то давление в приборе легко м. б. вычислено по закону Бойля-Мариотта р = h∙v/V где v – объем сжатого воздуха в капилляре К₁, а V – первоначальный объем воздуха, т. е. объем сосуда Н. Этим очень простым способом легко измерить давления до 10^-5 мм. Недостатком его является то, что он не измеряет упругости насыщенных паров, которые могут иметься в установке. Кроме того, если нужен вакуум меньше 10^-4 мм, между этим манометром и прибором приходится ставить ловушку с жидким воздухом для того, чтобы не дать пройти в прибор парам ртути.

Из манометров, основанных на изменении трения с уменьшением давления в вакууме, известен манометр Габера. Он представляет собой кварцевый стерженек, конец которого оттянут в виде тонкой нити длиной около 10 см, а диаметром в несколько сотых или десятых мм. Тем или иным способом кварцевый стерженек закрепляется в вертикальном положении в стеклянном сосуде, присоединенном к тому прибору, где требуется измерить вакуум. Ударяя пальцем по прибору, приводят нить в колебательное состояние и наблюдают амплитуду в микроскоп, через фокус которого проходит свободный конец нити. Вследствие трения амплитуда постепенно уменьшается, т. к. молекулы, налетающие на нить, берут на себя часть ее количества движения. Простое уравнение позволяет связать время t, в течение которого амплитуда нити убывает вдвое, и давление р газа в вакууме:

где М – молекулярный вес газа, b и а — некоторые постоянные, определяемые размерами и материалом нити (b также пропорционально абсолютной температуре Т°). При р = 0 b/t₀ = а, или b/a = t₀, т. е. отношение констант b/a определяет время t₀ собственного затухания нити вследствие трения внутри кварца при его упругих колебаниях (величина очень малая). Этот способ особенно пригоден, когда измерения производятся в парах химически активных элементов (йод, хлор и т. п.), когда нельзя иметь никаких металлических частей. Кроме того, если измерить р отдельно каким-либо другим методом, то применение манометра Габера позволяет определить молекулярный вес М газа, находящегося в вакууме. Этим манометром в его простой форме можно измерить давление от 10^-2 до 10^-5 мм ртутного столба. При некоторых усовершенствованиях область давлений может быть расширена от 10^-6 до 10^-1 мм ртутного столба.

Метод измерения вакуума, основанный на изменении теплопроводности в зависимости от давления, дан Пирани. Метод заключается в том, что платиновая или вольфрамовая проволока, длиной в 20—50 см и диаметром в несколько сотых мм, закрепляется помощью стеклянных ножек в вакууме (наподобие закрепления волосков электрических лампочек). По проволоке пускается ток в несколько десятков mА, чтобы нагреть ее приблизительно до 200°. Количество тепла, выделяющееся в нити, определяется формулой Джоуля W = i²R, где i – сила тока, a R – сопротивление нити. Так как сопротивление платины R по определенному закону меняется с температурой ее, то, измеряя R мостиком Уитстона, можно определить температуру Т нити. Зная количество тепла и температуру, можно определить коэффициент теплоотдачи. Обычно поступают так: изменяя ток i, а, следовательно, и W, держат R, а, следовательно, и Т, постоянным. Тогда, чем больше теплоотдача, тем больше нужно взять i; градуируя прибор с помощью манометра Мак-Лауда, можно найти зависимость между i и давлением р. Схема установок изображена на фигуре 2. Интервал давления, которое измеряется этим манометром, – от 4,5х10^-2 до 7х10^-6 мм ртутного столба.

Электрические свойства вакуума дали ему главнейшее техническое значение. Если увеличивать электрическое напряжение между двумя электродами в б. или м. плотном газе, то сначала ток практически равен 0 (т. к. газы при малых напряжениях очень хорошие изоляторы), затем возникает небольшой ток, увеличивающийся с увеличением напряжения, причем появляется видимое свечение газа; наконец, если плотность газа большая, то происходит явление искрового разряда, при сравнительно же малых давлениях (< 10—15 мм) – явление гейслерового разряда. Явление это объясняется следующим образом. В газе всегда имеется некоторое число электронов. Под действием электрического поля скорости электронов возрастают на протяжении одного свободного пути λ между соседними столкновениями с молекулами. При каждом столкновении электроны отдают свою избыточную энергию молекулам газа. Эта энергия, очевидно, равна произведению заряда электрона е на разность потенциалов на концах пройденного электроном пути λ. W = е∙х∙λ, где х – напряжение поля. Если энергия W электрона достаточно велика для того, чтобы разбить молекулу (при ударе о нее электрона) на ион и электрон, то в газе появляется новая пара ионов, которые, в свою очередь, являются ионизаторами новых молекул (процесс нарастает лавинообразно), – сила тока увеличивается. В вакууме, где свободная длина пути во много раз превышает размеры прибора, этого явления быть не может, чем и объясняется роль вакуума в электротехнике. Помещая в вакуум испускатель электронов в виде накаленной вольфрамовой проволоки, получают чисто электронный ток, определяющийся исключительно конструкцией прибора и накалом испускателя. Можно применить какие угодно напряжения между электродами без появления в газе положительных ионов. Т. о., например, прикладывая между испускателем и анодом очень большую разность потенциалов V, позволяем электронам скопить огромную энергию, равную eV (при этом она уже не тратится на ионизацию, так как встреч электрона с молекулами практически не происходит). Ударяясь с такой энергией о катод, электроны испускают рентгеновы лучи. Если источника электронов нет, а имеются в вакууме два холодных электрода, из которых тщательно удалены окклюдированные газы, то разряд пройти не может.

Поэтому вакуум может сделаться лучшим изолирующим материалом, который, как было выяснено на основании исследований в Ленинградской физико-технической лаборатории, со временем может послужить для устройства мощных высоковольтных генераторов, работающих по типу электростатических машин. Между прочим, на этих электрических свойствах вакуума основан прибор, позволяющий измерять давление газов в вакууме до крайне малых значений. Этот прибор (фиг. 3) в сущности представляет собой обычную усилительную лампу.

Между испускателем и сеткой приложена очень небольшая разность потенциалов, препятствующая попаданию электронов на сетку, но позволяющая все же части электронов проникать сквозь ячейки ее в пространство между анодом и сеткой; анод же имеет очень большой положительный потенциал (несколько сот V) относительно испускателя. Электроны, проходя сквозь сетку до анода, встречают изредка на своем пути молекулы; вероятность этого процесса пропорциональна давлению остатков газа. Появляющиеся в результате этого положительные ионы попадают на сетку и создают ток между анодами и сеткой. Отношение этого тока сетки к току анода, конечно, очень мало, но естественно возрастает с увеличением давления. На фиг. 4 приведены графики, связывающие изменение давления в приборе и отношение токов сетки и анода.

Этот метод позволяет измерить давление в пределах от 10^-1 до 10^-8 мм ртутного столба.

Для уяснения устройства насосов и методов откачки необходимо дать несколько определений и выяснить роль проводки от насоса к выкачиваемому сосуду. Мощностью насоса S называется тот объем газа, который он ежесекундно удаляет из откачиваемого сосуда при том давлении р, которое в это время имеет место в приборе, т. е. если объем откачиваемого сосуда V, то где dр есть изменение давления в сосуде. Так как насос соединяется не непосредственно с откачиваемым сосудом, но с помощью трубок той или иной длины, то мощность S откачки не равна мощности S₀ насоса, но меньше ее. Если х есть давление в сосуде, а р – в насосе, то объем ежесекундно проходящего через проводку (соединяющую насос с прибором) газа равен где W – сопротивление проводки. Величина W для плотных газов, согласно закону Пуазейля, равна где L – длина трубки, R – радиус ее сечения, η – коэффициент внутреннего трения. Так как трение в вакууме совсем иное, то для вакуума W имеет величину меньшую. Вместо формулы Пуазейля имеем для вакуума формулу Кнудсена:

где ϱ – плотность газа. При мощности насоса S₀ объем ежесекундно удаляемого им из самого себя газа равен причем V₂ – объем при давлении р в насосе. Если S есть скорость удаления газа из откачиваемого сосуда, то где V₁ – объем газа, взятый при давлении х в сосуде. Так как из сосуда удаляется то же самое весовое количество газа (сколько проходит через трубки, столько же удаляется насосом), то S_X= S₀∙p = (x-p)/W. Отсюда мощность, с которой удаляется газ из откачиваемого прибора:

Мощность S₀ изучена для разного типа насосов; она непостоянна и зависит от давления. Величины S₀ будут даны ниже. На фиг. 5 приведена диаграмма, позволяющая простым способом количественно оценить роль различной проводки на основе формул (2) и (3): на оси ординат отложены S₀, на оси абсцисс – S.

Вся таблица относится к воздуху и к L = 1 м. Поясним пользование таблицей на примерах.

1) Определить максимальную (при S0 = ∞) скорость откачки в случае проводки, состоящей из трубки длиной 2,25 м и ø = 4 мм. Кривая ø = 4 мм при S₀ = ∞ имеет значение 27, т. е. насос бесконечной мощности дает скорость откачки 27 см³/сек при длине проводки в 1 м. Так как скорость откачки обратно пропорциональна длине, то при длине проводки в 2,25 м скорость

2) Имеется насос Лангмюра S₀ = 1000 см³. Проводка состоит из трубки длиной 1 м и диаметром 16 мм. Тогда, находя пересечения прямой S₀ = 1000 с кривой ø = 16 мм, имеем: S = 340 см³/сек.

3) При трубке длиной 1 м и ø = 16 мм и насосе, для которого S₀ = 1200 см³/сек, S составляет 25% от S₀. (Действительно, S₀ = 1200; S = 300.)

Форвакуумные насосы. Большое разрежение получается в две стадии. Сначала необходимо получить предварительное разрежение, так называемый форвакуум. Насосы, употребляемые для этого, называются форвакуумными. Затем другие насосы, вакуумные, откачивают дальше. В качестве форвакуумных насосов в настоящее время употребляются гл. образом вращающиеся масляные насосы. Уплотнение насоса достигается тем, что все трущиеся части тщательно пришлифованы и обильно смазаны маслом. Некоторые конструкции насосов устроены так, что они прямо погружены в масло. Наиболее употребительными являются насосы, выпускаемые фирмами Лейбольд и Пфейфер. Конструкция насоса фирмы Лейбольд (насос Геде) изображена на фиг. 6.

На валу В сидит цилиндр А со стальными планками S, которые прижимаются пружиной к стенкам латунной станины G. С передней стороны все это закрыто хорошо пришлифованной латунной плитой Р. В коробку О наливается масло до уровня m. Стеклянное окошко F служит для контроля над количеством масла. Вал выводится наружу через сальник b. При вращении цилиндра А в направлении против часовой стрелки воздух всасывается через С и выталкивается через клапан D и канал k в коробку О. Скорость откачки таких насосов пропорциональна числу оборотов. Для этого типа насосов скорость откачки равна ~27 см³/сек. Предельное давление 0,1—0,05 мм. Насосы, которые выпускаются фирмой Пфейфер, отличаются от насосов Лейбольда устройством клапана и тем, что в них весь корпус насоса погружен в масло. Скорость откачки этих насосов достигает 1600 см³/сек, их предельное давление 0,1—0,001 мм. Фирма Пфейфер выпускает также комбинированные насосы, двойные и тройные, которые обладают или еще большей скоростью откачки или меньшим предельным давлением (до 10^-4 мм). Насосы Пфейфер и аналогично им устроенные насосы фирмы Сименс-Шуккерт обладают тем недостатком, что при их остановке масло из насосов всасывается, если не принять мер, в установку. Насосы Геде свободны от этого недостатка. В последние годы фирма Лейбольд выпустила новую дешевую модель форвакуумных насосов. По устройству они представляют среднее между старыми насосами Геде и насосами Пфейфер. Корпус их сделан из железа и весь погружен в масло. Скорость откачки очень невелика, предельное давление 0,1—0,05 мм. Недавно форвакуумные насосы разных типов начали изготовлять в СССР. Почти все форвакуумные насосы при вращении в противоположную сторону могут служить нагнетающими насосами. В этих условиях форвакуумые насосы дают от 1,5 до 3 Atm.

Вакуумные насосы. Для получения высокого вакуума употребляются два типа насосов: 1) ртутные диффузионно-конденсационные и 2) вращающиеся молекулярные.

1) Диффузионно-конденсационные насосы (фиг. 7). Струя ртутного пара течет по трубе А в направлении, указанном стрелкой. Внутрь А вставлена труба D₁—D₂, в которой имеется кольцевой разрыв е; С – труба, ведущая к откачиваемому пространству, наполненному каким-нибудь газом.

Через Е пропускается вода для охлаждения стенок трубы А. Из щели е атомы ртути разлетаются в направлении, указанном стрелками. Чем ближе к щели е, тем плотность ртутных паров больше. В струе ртутного пара в А парциальное давление газа равно нулю, и вследствие разности парциальных давлений, газ диффундирует из трубы С в А. Если плотность вблизи самой щели е настолько велика, что диффундирующие молекулы сталкиваются с атомами ртути, не доходя до края щели е, откачки происходить не будет. Если плотность атомов ртути в струе такова, что столкновения с ними происходят редко, молекулы газа попадают из трубы С в В и уносятся струей ртутного пара. Насос будет работать тем лучше, чем больше скорость струи ртутного пара. Большая скорость в некоторых насосах достигается особой формой сопла, в других насосах – интенсивным охлаждением. Расчет показывает, что щель должна быть порядка длины свободного пути. Когда скорость ртутного пара равна или более тепловой скорости атомов, то ртутные атомы, несмотря на наличие щели, к стенкам трубки А лететь почти не будут и поэтому не будут мешать диффузии газа из С в А; в этом случае размеры щели не имеют большого значения. Скоростью ртутного пара определяется также и форвакуумное давление (давление в А). Если форвакуумное давление больше определенной величины, то газ из А начинает проходить в С, и там происходит повышение давления. Так как скорость диффузии не зависит от абсолютной величины давления, то эти насосы теоретически могут дать бесконечное разрежение. Ниже приводится описание самых употребительных насосов, основанных на указанном принципе. а) Насос Лангмюра (фиг. 8).

В баллон А наливают ртуть, которая подогревается электрической печью. Ртутный пар конденсируется на стенках трубы С, охлаждаемых водой, протекающей через К и J. Откачиваемый газ засасывается через зазор Е и трубу F из прибора. G – ловушка, которая охлаждается жидким воздухом и предохраняет прибор от ртутного пара. Форвакуумный насос присоединяется к N. Скорость откачки этого насоса около 1500—4000 см³/сек, требуемый форвакуум 5х10^-2—10^-3 мм. б) Металлический насос Лангмюра (фиг. 9).

Ртуть в D нагревается, проходит через сопло F, под крышкой Е меняет направление и конденсируется на охлаждаемых водой стенках J. Переменой направления струи достигается то, что ртутный пар совсем не попадает в вакуумную часть. Откачиваемый прибор присоединяется к С, форвакуумный насос присоединяется к В. Скорость откачки такого насоса около 4000 см³/сек, требуемый форвакуум около 0,5 мм. в) К-насос Фольмера (фиг. 10).

Пары идут из а через b, при прохождении через с меняют направление и конденсируются на охладителе е; насос через трубку V соединяется с форвакуумным насосом, а через Н – с откачиваемым прибором. Скорость откачки и форвакуумное давление такие, как у других стеклянных насосов. Большинство описанных до сих пор насосов требуют форвакуумного давления порядка 10^-2 мм. Для его получения приходится применять вращающиеся масляные насосы, которые довольно дороги, а иногда бывают неудобны (когда нужно избежать попадания в вакуум следов углеводородов).

Поэтому чрезвычайно полезными являются ртутно-конденсационные насосы, дающие возможность работать с форвакуумом от водоструйного насоса. Эти насосы отличаются очень узкой щелью или соплом, что дает им возможность выдержать большее давление в форвакууме. Но это же обстоятельство очень сильно снижает скорость откачки. Для получения высокого вакуума нужно, кроме них, употреблять еще какой-нибудь насос из ранее описанных. Наиболее употребительными конструкциями форвакуумных ртутно-конденсационных насосов являются насос Фольмера (фиг. 11) и насос, изображенный на фиг. 12. Они дают разрежение до 10^-3 мм и требуют форвакуума в 15—20 мм. Скорость откачки около 200 см³/сек.

Форвакуумный ртутно-конденсационный насос часто соединяют с вакуумным в один двухступенчатый насос, который дает те же результаты, что и два насоса, соединенные последовательно, но обладает многими преимуществами: одно подогревающее и охлаждающее устройство, компактность и т. д. Внешний вид одного из таких насосов – двухступенчатого насоса Фольмера – дан на фиг. 13; форвакуумное давление – 15 мм; скорость откачки очень велика: около 5000 см³/сек.

Недавно фирмой Лейбольд выпущен трехступенчатый насос Геде, который по своим качествам оставляет далеко позади все описанные насосы. Он сделан весь из стали. Верхнее сопло служит вакуумным насосом и устроено, как в насосах Лангмюра (фиг. 9). Среднее сопло имеет коническую насадку и работает, как вакуумный насос Крофорда. Нижнее сопло также коническое. Скорость струи в нем очень велика, зазор очень мал; этим достигается возможность работы с форвакуумом в 20 мм. Скорость откачки верхнего сопла около 40000 см³/сек. Недостатком этого насоса является большое количество отдельных частей, соединенных винтами. Легко может случиться, что где-нибудь уплотнение окажется недостаточным, и в насос будет натекать воздух. Кроме того, этот насос легко может быть испорчен химически активными газами.

Вращающиеся молекулярные насосы. Когда молекулы газа отражаются от быстро движущейся поверхности, они приобретают составляющую скорость в направлении ее движения. Если цилиндр А быстро вращается в направлении стрелки (фиг. 14), то ударяющиеся о него в пункте n молекулы приобретут скорость в направлении вращения, и давление в точке mбудет выше, чем в n.

Эта разность давлений не сможет выравняться, если зазор между А и В будет достаточно мал. Таким именно образом устроен вращающийся молекулярный насос Гольвега. В корпусе с геликоидальными вырезами вращается полый барабан из дюралюминия со скоростью 4000 об/мин.; зазор между ним и корпусом равен 0,05 мм. Воздух засасывается в трубу, которая подведена к середине корпуса, и направляется в геликоидальные вырезы, глубина которых уменьшается от середины к концам. Эти вырезы открываются в форвакуумное пространство, с которым соединен форвакуумный насос. Ротор электромотора сидит на одном валу с барабаном насоса и находится в пространстве, где давление равно форвакуумному. Противоположный конец вала выведен под крышку, где давление также равно форвакуумному. Этим достигается хорошее уплотнение выводов вала. При форвакууме в 0,1 мм окончательное давление около 10^-7 мм; скорость откачки 2300 см³/сек.

Откачка. Наиболее существенной частью процесса откачки является удаление газа, абсорбированного и адсорбированного стеклянными и металлическими частями прибора. По своему химическому составу газ этот представляет смесь паров воды, СО₂, СО, N₂ и т. п. Для удаления газов из стекла необходимо прогревать его в вакууме под непрерывно работающими насосами при температуре, близкой к 450°. После 2—3-часового прогрева главные массы газа и водяных паров можно считать удаленными; чем выше температура прогрева, тем лучшие будут достигнуты результаты. Для стекла пирекс эта температура м. б. доведена до 700°; для нормального типа стекла она не должна превышать 500°. Значительно более сложной задачей является удаление газов из металла, так как металлические части ряда вакуумных приборов подвергаются иногда в процессе работы значительному нагреванию (антикатоды рентгеновских трубок, аноды генераторных ламп и кенотронов и прочих). Для достижения сколько-нибудь удовлетворительных результатов необходимо прогревать металлические части при возможно более высоких температурах, близких к температуре плавления. Из этих соображений материалом для конструирования различного рода вакуумных приборов могут служить металлы с достаточно высокими температурами плавления: вольфрам, молибден, тантал, никель, железо и некоторые другие. Медь и алюминий могут употребляться лишь в местах, не подвергающихся сколько-нибудь значительному нагреванию. Перед помещением металлических частей в вакуум их следует прокалить в атмосфере водорода для восстановления имеющегося на них слоя окиси. Прогрев металлических частей в вакууме для удаления из них газов производится токами Фуко высокой частоты или электронной бомбардировкой. Тренировка электронной бомбардировкой генераторной лампы средней мощности производится следующим образом. После 2—3-часового прогрева баллона лампы под непрерывно работающими насосами можно приступить к тренировке электродов. Для этого соединяют накоротко сетку и анод и подают между ними и накаливающейся нитью лампы разность потенциалов, несколько превышающую нормальную рабочую. Нужно следить, чтобы в момент подачи напряжения в баллоне не вспыхивало лиловатое свечение, обусловленное ионизацией остатков газа в лампе. Если такого свечения нет, доводят анод до желто-белого свечения, выключая напряжение немедленно по появлении объемного свечения, указывающего на выделение газа. После нескольких операций выделение газа из анода прекращается; при этом прибор, измеряющий силу тока в цепи анод-нить, дает постоянные показания. Если больших колебаний анодного тока нет, тренировка считается законченной, и лампу отпаивают. В течение всего процесса откачки в специальной ловушке между насосами и откачиваемой лампой должен находиться жидкий воздух, служащий для вымораживания ртутных паров, проникающих из насосов. Употребление в вакуумной части проводки кранов и шлифов нежелательно, так как это влечет за собой попадание в вакуум паров замазки. Для предохранения форвакуумного насоса от попадания в него из установки паров воды рекомендуется ставить между ними сушилки с хлористым кальцием.

Детали вакуумных приборов. а) Впаи. При заводском изготовлении разного рода вакуумных приборов: рентгеновских трубок, генераторных ламп, кенотронов и т. п., рассчитанных на длительную работу, особое внимание следует обращать на места выводов внутренних электродов. При впаивании металла в стекло приходится подбирать коэффициенты расширения близкими друг к другу, т. к. в противном случае по затвердевании стекла оно или отстает от металла или же дает трещины. Наиболее удобным материалом для впаев является платина, имеющая коэффициент расширения, близкий к свинцовому (α = 9х10^-6) и обыкновенному стеклу (α = 8,5х10^-6). В последнее время из-за дороговизны платины употребляют в качестве материала для впаев специальный сплав никеля с железом — инвар (36% Ni), а также обыкновенную красную медь. При впаивании меди ее следует сначала прогреть в окисляющем пламени горелки до получения на ней слоя черной окиси меди. После этого ее опускают в насыщенный раствор буры и повторяют эту операцию до тех пор, пока ее поверхность не приобретет ярко-красного оттенка. К меди, обработанной т. о., стекло прилипает и (при не слишком большой толщине впая) почти совершенно от него не отстает. Для впаев в ножки ламп накаливания и катодных ламп употребляется инвар с 40% содержанием Ni, покрытый снаружи слоем меди, составляющим в сечении около 20% площади впая. Общий коэффициент расширения таких проволок близок к коэффициенту расширения стекла. Наличие же внешней медной рубашки уменьшает слишком большое электрическое сопротивление инварного впая. На заводах Филлипса употребляется в качестве материала для впаев сплав из 85% железа и 15% хрома, также обладающий близким к стеклу коэффициентом расширения. б) Краны, шлифы и замазки. В лабораторной практике, где приборы б. ч. от насосов не отпаиваются, большое применение имеют краны, шлифы и замазки. В вакуумной части установки могут употребляться краны лишь с очень большими отверстиями (не менее 4—5 мм) и с очень тщательной пришлифовкой. Хороший вакуумный кран почти не дает течи при смазке его специальной замазкой (Vakuumhahnfett). К кранам в форвакуумной части проводки не следует предъявлять особенно высоких требований, т. к. течь в ней менее опасна. В лабораторной практике употребляются шлифы диаметром до 60—70 мм. Шлифы больших диаметров недостаточно механически прочны, и употребление их нежелательно. Смазку шлифов следует производить замазкой для кранов, а также специальными мягкими сортами замазок. Необходимо помнить, что проворачивать шлиф диаметром более 50 мм под вакуумом опасно; проворачивать вообще можно только шлифы, смазанные замазкой для кранов, причем их следует всегда несколько прогревать. Для соединения между собой частей приборов, для вывода электродов, вмазки янтарей и т. п. очень удобно употребление различных легкоплавких замазок (менделеевской, пицеина, сургуча и т. п.). Замазку следует наносить в полужидком состоянии и только на прогретые части прибора. После придания ей нужной формы следует оплавить ее поверхность небольшим пламенем, чтобы таким образом сделать ее совершенно гладкой. Хорошо замазанный впай ничем в смысле течи не отличается от впая в стекло.

Вспомогательные методы откачки. а) Абсорбция углем. При низких температурах некоторые специально приготовленные сорта угля (уголь кожуры кокосового ореха, кожуры абрикосовых косточек) обладают способностью поглощать большое количество газа. Этим явлением пользуются часто в вакуумной технике, когда в сравнительно короткое время нужно достичь больших степеней разрежения. Предварительно активированный прогревом до 800—900° уголь помещают в цилиндрический сосуд из тугоплавкого стекла, припаивают к прибору и под непрерывной откачкой прогревают при 400—500° в течение 2—3 ч. После прогрева прибор отъединяют от насосов и баллон погружают в сосуд Дьюара с жидким воздухом. Получаемое т. о. разрежение в приборе в короткий промежуток времени достигает 10^-8 мм ртутного столба. б) Абсорбция распылением металла. Явлением абсорбции газа распыленным металлом пользуются в заводских условиях при откачке микроламп. При монтировке лампы на ее анод помещают небольшой кусочек магния, который после откачки и отпайки лампы возгоняется на стенки баллона. Возгонка производится прогревом всех металлических частей лампы токами Фуко высокой частоты. Весь процесс такой химической откачки продолжается всего лишь несколько секунд. Предварительно электронной бомбардировкой металлические части микролампы не тренируются, т. к. их нить, покрытая торием, не выносит сколько-нибудь длительных перекалов. в) Откачка возгонкой фосфора. На современных заводах, изготовляющих лампы накаливания, в большом употреблении следующий метод их откачки. На нить лампы перед запайкой нити в баллон наносится коллоидный раствор красного фосфора в спирту. После откачки лампы простым масляным насосом до давления в 0,01—0,001 мм ртутного столба она отпаивается, и нанесенный на нее красный фосфор прогревом нити испаряется, переходя при этом в активную модификацию. Химическое действие активной модификации фосфора и происходящая при возгонке его ионизация связывают остатки газа, заключенного в баллоне.

Источник: Мартенс. Техническая энциклопедия. Том 3 – 1928 г.

В самых разнообразных областях техники и науки, в самых разных технических приборах и сооружениях
требуется проводить измерения давления жидкостей или газов. В зависимости от назначения
инженеры должны иметь возможность проводить измерения давления и использовать
соответствующие единицы для точного отображения этих показаний, а также уметь правильно или
оперировать.

Единицы измерения давления

Гидростатическое
давление, как и
напряжение, в системе СГС измеряется в дин/см², в
системе МКГСС — кгс/м², в
системе СИ — Па. Кроме того, гидростатическое давление измеряется в кгс/см², высотой
столба жидкости (в м вод. ст., мм рт.ст. и т. д.) и, наконец, в атмосферах физических (атм) и
технических (ат) (в гидравлике пока еще
преимущественно пользуются последней единицей). Для перевода одних единиц измерения давления в
другие Вы можете воспользоваться
нашим конвертером
давлений.
В ней есть возможность перевести бар, Psi. ат в Па, МПа в м.вод. столба или ртутного столба и
т.д.

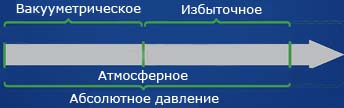
Абсолютное значение

Абсолютное давление ─ это истинное давление жидкостей, паров или газов, которое отсчитывается от
абсолютного
нуля давления (абсолютного вакуума).

Избыточное давление

Разность между абсолютным давлением p и атмосферным давлением p_а называется избыточным
давлением и обозначается р_изб:

р_изб = p – p_а

или

р_изб/γ = (p – p_а)/γ = h_п

h_п в этом случае называется пьезометрической высотой, которая является мерой
избыточного давления.

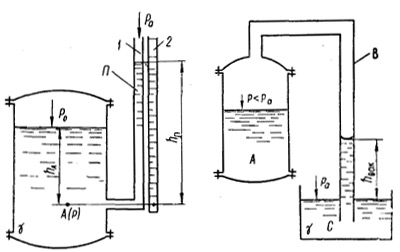
На рисунке показан закрытый резервуар с жидкостью, на поверхности которой давление p_0.
Подключенный к резервуару пьезометр П (см. рис. ниже) определяет избыточное
давление в точке А.

Абсолютное и избыточное давления, выраженные в атмосферах, обозначаются соответственно ата и
ати.

Вакууметрическое давление

Вакуумметрическое давление, или вакуум, — недостаток давления до атмосферного
(дефицит давления), т. е. разность между атмосферным или барометрическим и абсолютным давлением:

р_вак = p_а – p

или

р_вак/γ = (p_а – p)/γ =
h_вак

где h_вак — вакуумметрическая высота, т. е. показание вакуумметра В,
подключенного к резервуару, показанному на рисунке ниже. Вакуум выражается в тех же единицах,
что и давление, а также в долях или процентах атмосферы.

Из выражений последних двух выражений следует, что вакуум может изменяться от нуля до
атмосферного давления; максимальное значение h_вак при нормальном атмосферном давлении
(760 мм рт. ст.) равно 10,33 м вод. ст.

Unit Converter