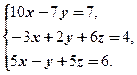Как найти ведущий элемент

Единственное ограничение,
которое было нами введено при разработке
алгоритма Гаусса, – это требование того,
чтобы ведущий элемент

не равнялся нулю. Если же окажется, что

,
то можно произвести в матрице

перестановку строк или столбцов, которая
не изменит решения системы. Алгоритм,
реализующий такую стратегию, называется
выбором ведущего элемента.

Выбор максимального
по модулю ведущего элемента позволяет
к тому же уменьшить вычислительные
погрешности, возникающие в силу того,
что компьютер работает с числами
ограниченной разрядности. Действительно,
объединив формулы (4) и (5) и опустив
верхние индексы, получим общую формулу
преобразований прямого хода

(1.15)

Выражение,
выделенное в скобках, называется
множителем. Выбирая максимальный по
модулю ведущий элемент

,
получим, что множитель будет меньше
единицы, т.е. «новое» значение коэффициента

получается из «старого» путем вычитания
небольшой поправки, которая не будет
вносить значительных искажений.

Можно реализовать
несколько путей поиска максимального
по модулю элемента. Если этот процесс
осуществлять по всем коэффициентам,
участвующим в дальнейшем исключении

(1.16)

для

то говорят о методе исключения с полным
упорядочением. Такой алгоритм достаточно
сложен и по трудоемкости сравним с
прямым ходом, а поэтому используется
редко.

Большую
популярность имеют стратегии частичного
упорядочения по строкам (или столбцам)

(1.17)

Ищется номер строки m,
в которой находится максимальный по
модулю элемент и осуществляется обмен
строками.

Выбор ведущего
элемента с частичным упорядочением
приводит к появлению еще одного вложенного
цикла, т.е. выполнению

операций дополнительно.

Модернизируем процедуру
решения СЛАУ, вставив в неё фрагмент
с частичным выбором ведущего элемента:

………….

eps:=1.0e-6;

for
k:=1 to n do { прямой ход}

begin
s:=a[k,k]; m:=k;

for i:=k+1 to n do

begin t:=a[i,k];

if
abs(t) >
abs(s) {
поиск максимального элемента в к-ом
столбце}

then
begin s:=t; m:=i end

end;

if
abs(s)< eps
{система плохо обусловлена; ее решение
требует специальных приемов}

then
begin writeln (‘Error 01’); Exit end;

if m<>k

then
for j:=k to n+1 do Swap (a[k,j],a[m,j]); {обмен
строками}

for
j:=k+1 to
n+1 do {
нормировка на единицу диагонального
элемента

}

a[k,j]:=a[k,j]/s;

……………

Здесь Swap
(a[k,j],a[m,j])
– процедура обмена двух элементов.

Проведите тестирование
подпрограмм, осуществляющих решение
систем линейных уравнений методом
Гаусса, вычисление определителя и
обратной матрицы.

В приведенной выше тестовой
матрице последовательно будем уменьшать
на порядок диагональные элементы,
выбирая их равными 0,4; 0,04; 0,004;…Сравнить
результаты, полученные с выбором и без
выбора ведущего элемента. Определить,
в каком разряде после запятой наблюдаются
отклонения.

Уменьшая на порядки величину
диагональных элементов, необходимо
провести расчеты для матриц разной
размерности, например, n=10,
100, 500. Сравнить результаты расчетов с
выбором и без выбора ведущего элемента.

Провести расчеты с матрицей,
размером 10х10, в которой диагональные
элементы, последовательно изменяясь
на порядок величины, отличаются на
десять порядков. Сравнить результаты
расчетов с выбором и без выбора ведущего
элемента.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пример 5.1. Решить следующую задачу линейного программирования симплекс-методом:

Решение:

I итерация:

1 этап: формирование исходной симплекс-таблицы.

Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.

В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:

Приведем целевую функцию к следующему виду:

На основе полученной задачи сформируем исходную симплекс-таблицу:

Таблица 5.3

Исходная симплекс-таблица

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

3 этап: проверка совместности системы ограничений ЗЛП.

На данной итерации (в таблице 5.3) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).

4 этап: проверка ограниченности целевой функции.

На данной итерации (в таблице 5.3) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с отрицательным элементом в строке целевой функции (кроме колонки свободных чисел), в которой не было бы хотя бы одного положительного элемента).

5 этап: проверка допустимости найденного базисного решения.

Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.

6 этап: проверка оптимальности.

Найденное базисное решение не является оптимальным, так как согласно признаку оптимальности (признак 4) в строке целевой функции не должно быть отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, согласно алгоритму симплекс-метода переходим к 8 этапу.

8 этап: определение разрешающего элемента.

8.1. Определение разрешающей колонки.

Так как найденное базисное решение допустимое, то поиск разрешающей колонки будем производить по следующей схеме: определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.3, таких колонок две: колонка «х1» и колонка «х2». Из таких колонок выбирается та, которая содержит наименьший элемент в строке целевой функции. Она и будет разрешающей. Колонка «х2» содержит наименьший элемент (–3) в сравнении с колонкой «х1». Следовательно, ее принимаем в качестве разрешенной.

8.2. Определение разрешающей строки.

Для определения разрешающей строки находим положительные оценочные отношения свободных чисел к элементам разрешающей колонки, строка, которой соответствует наименьшее положительное оценочное отношение, принимается в качестве разрешенной.

Таблица 5.4

Исходная симплекс-таблица

В таблице 5.4 наименьшее положительное оценочное отношение соответствует строке «х5», следовательно, она будет разрешающей.

Элемент, расположенный на пересечение разрешающей колонки и разрешающей строки, принимается в качестве разрешающего. В нашем примере – это элемент , который расположен на пересечении строки «х5» и колонки «х2».

9 этап: преобразование симплекс-таблицы.

Разрешающий элемент показывает одну базисную и одну свободную переменные, которые необходимо поменять местами в симплекс-таблице, для перехода к новому «улучшенному» базисному решению. В данном случае это переменные х5 и х2, в новой симплекс-таблице (таблице 5.5) их меняем местами.

9.1. Преобразование разрешающего элемента.

Разрешающий элемент таблицы 5.4 преобразовывается следующим образом:

Полученный результат вписываем в аналогичную клетку таблицы 5.5.

9.2. Преобразование разрешающей строки.

Элементы разрешающей строки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей строки приведены в таблице 5.5.

9.3. Преобразование разрешающей колонки.

Элементы разрешающей колонки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, а результат берется с обратным знаком. Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.

9.4. Преобразование остальных элементов симплекс-таблицы.

Преобразование остальных элементов симплекс-таблицы (т.е. элементов не расположенных в разрешающей строке и разрешающей колонке) осуществляется по правилу «прямоугольника».

К примеру, рассмотрим преобразование элемента, расположенного на пересечении строки «х3» и колонки «», условно обозначим его «х3». В таблице 5.4 мысленно вычерчиваем прямоугольник, одна вершина которого располагается в клетке, значение которой преобразуем (т.е. в клетке «х3»), а другая (диагональная вершина) – в клетке с разрешающим элементом. Две другие вершины (второй диагонали) определяются однозначно. Тогда преобразованное значение клетки «х3» будет равно прежнему значению данной клетки минус дробь, в знаменателе которой разрешающий элемент (из таблицы 5.4), а в числителе произведение двух других неиспользованных вершин, т.е.:

«х3»: .

Аналогично преобразуются значения других клеток:

«х3 х1»: ;

«х4»: ;

«х4 х1»: ;

«х6»: ;

«х6 х1»: ;

« »: ;

« х1»: .

В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5).

II итерация:

1 этап: составление симплекс-таблицы.

По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

Таблица 5.5

Симплекс-таблица II итерации

2 этап: определение базисного решения.

В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.5):

.

Как видно, при данном базисном решении значение целевой функции =15, что больше чем при предыдущем базисном решении.

3 этап: проверка совместности системы ограничений.

Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.5 не выявлена.

4 этап: проверка ограниченности целевой функции.

Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.5 не выявлена.

5 этап: проверка допустимости найденного базисного решения.

Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.5) содержится отрицательный элемент: –2 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.

8 этап: определение разрешающего элемента.

8.1. Определение разрешающей колонки.

Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.5, такой колонкой является только одна колонка: «х1». Следовательно, ее принимаем в качестве разрешенной.

8.2. Определение разрешающей строки.

Согласно полученным значениям положительных оценочных отношений в таблице 5.6, минимальным является отношение, соответствующее строке «х3». Следовательно, ее принимаем в качестве разрешенной.

Таблица 5.6

Симплекс-таблица II итерации

9 этап: преобразование симплекс-таблицы.

Преобразования симплекс-таблицы (таблицы 5.6) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.7.

III итерация

1 этап: построение новой симплекс-таблицы.

По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

Таблица 5.7

Симплекс-таблица III итерации

2 этап: определение базисного решения.

В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.7):

.

3 этап: проверка совместности системы ограничений.

Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.7 не выявлена.

4 этап: проверка ограниченности целевой функции.

Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.7 не выявлена.

5 этап: проверка допустимости найденного базисного решения.

Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.7) содержится отрицательный элемент: –3 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.

8 этап: определение разрешающего элемента.

8.1. Определение разрешающей колонки.

Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.7, такой колонкой является только одна колонка: «х5». Следовательно, ее принимаем в качестве разрешенной.

8.2. Определение разрешающей строки.

Согласно полученным значениям положительных оценочных отношений в таблице 5.8, минимальным является отношение, соответствующее строке «х4». Следовательно, ее принимаем в качестве разрешенной.

Таблица 5.8

Симплекс-таблица III итерации

9 этап: преобразование симплекс-таблицы.

Преобразования симплекс-таблицы (таблицы 5.8) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.9.

IV итерация

1 этап: построение новой симплекс-таблицы.

По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

Таблица 5.9

Симплекс-таблица IV итерации

2 этап: определение базисного решения.

В результате проведенных симплекс-преобразований получили новое базисное решение, согласно таблице 5.9 решение следующее:

.

3 этап: проверка совместности системы ограничений.

Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.9 не выявлена.

4 этап: проверка ограниченности целевой функции.

Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.9 не выявлена.

5 этап: проверка допустимости найденного базисного решения.

Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.9) нет отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

7 этап: проверка альтернативности решения.

Найденное решение является единственным, так как в строке целевой функции (таблица 5.9) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

Ответ: оптимальное значение целевой функции рассматриваемой задачи =24, которое достигается при .

Пример 5.2. Решить вышеприведенную задачу линейного программирования при условии, что целевая функция минимизируется:

Решение:

I итерация:

1 этап: формирование исходной симплекс-таблицы.

Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.

В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:

Приведем целевую функцию к следующему виду:

На основе полученной задачи сформируем исходную симплекс-таблицу:

Таблица 5.10

Исходная симплекс-таблица

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

3 этап: проверка совместности системы ограничений ЗЛП.

На данной итерации (в таблице 5.10) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).

4 этап: проверка ограниченности целевой функции.

На данной итерации (в таблице 5.10) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с положительным элементом в строке целевой функции (колонка свободных чисел не рассматривается), в которой не было бы хотя бы одного положительного элемента).

5 этап: проверка допустимости найденного базисного решения.

Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.10) нет положительных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

7 этап: проверка альтернативности решения.

Найденное решение является единственным, так как в строке целевой функции (таблица 5.10) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

Ответ: оптимальное значение целевой функции рассматриваемой задачи =0, которое достигается при .

Пример 5.3. Решить следующую задачу линейного программирования симплекс-методом:

Решение:

I итерация

1 этап: составление исходной симплекс-таблицы.

Задача линейного программирования задана в каноническом виде. Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные. Примем в качестве базисных – переменные х1 и х2.

Умножим (поэлементно) первую строку на –3 и сложим со второй:

.

Умножим вторую строку на :

.

Сложим вторую с первой строкой:

.

В результате система ограничений примет следующий вид:

Выразим базисные переменные через свободные:

Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:

.

Запишем целевую функцию в следующем виде:

.

Составим исходную симплекс-таблицу:

Таблица 5.11

Исходная симплекс-таблица

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

Найденное базисное решение является вырожденным, т.к. имеется базисная переменная х2, равная нулю.

3 этап: проверка совместности системы ограничений ЗЛП.

Так как в таблице 5.11 имеется строка с отрицательным свободным числом (–1), в которой нет ни одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной), то согласно признаку несовместности (признак 1) система ограничений данной задачи не совместна (строка целевой функции при рассмотрении данного признака не учитывается). Следовательно, рассматриваемая задача линейного программирования не имеет решения.

Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности ее системы ограничений.

Симплекс-метод решения задач линейного программирования.
Для упрощения процесса решения исходные данные задачи линейного
программирования при решении ее симплекс методом записываются в специальные
симплекс-таблицы. Поэтому одна из модификаций симплекс метода получила название
табличный симплекс метод. Задача линейного программирования в каноническом виде:
F=a0,1×1+a0,2×2+…a0,nxn+b0→ max
a1,1×1+a1,2×2+…a1,nxn+ xn+1=b1
a2,1×1+a2,2×2+…a2,nxn+xn+2=b2
…………………………………
am,1×1+am,2×2+…am,nxn+xn+m=bm
Исходная таблица для задачи имеет следующий вид:
Таблица 1 – Симплекс-таблица
Базис
b
x1
x2
…
xn-1
xn
xn+1
xn+2
…
xn+m
F
b1
b2
…
bm
-b0
a1,1
a2,1
…
am,1
-a0,1
a1,2
a2,2
…
am,2
-a0,2
…
…
…
…
…
a1,n-1
a2,n-1
…
am,n-1
-a0,n-1
a1,n
a2,n
…
am,n
-a0,n
Оценочное
выражение
–
x1, x2, xn – исходные переменные, xn+1, xn+2, xn+m – дополнительные переменные. Все
дополнительные переменные мы приняли как базисные, а исходные переменные
как небазисные (дополнительные записаны в первый столбец симплекс-таблицы а
исходные в первую строку). При каждой итерации элементы симплекс-таблицы
пересчитывают по определенным правилам.
Подготовительный этап
Приводим задачу линейного программирования к каноническому виду
F=a0,1×1+a0,2×2+…a0,nxn +b0 → max
a1,1×1+a1,2×2+…a1,nxn+xn+1=b1
a2,1×1+a2,2×2+…a2,nxn+xn+2=b2
…………………………………
am,1×1+am,2×2+…am,nxn+xn+m=bm
В случае если в исходной задаче необходимо найти минимум – знаки
коэффициентов целевой функции F меняются на противоположные a0,n=-a0,n. Знаки
коэффициентов ограничивающих условий со знаком “≥” так же меняются на
противоположные. В случае если условие содержит знак “≤” – коэффициенты запишутся
без изменений.
Шаг 0. Составляем симплексную таблицу, соответствующую исходной задаче
Таблица 2 – Симплекс-таблица, соответствующая исходной задаче
Базис
b
x1
x2
…
xn-1
xn
xn+1
xn+2
…
xn+m
b1
b2
…
bm
a1,1
a2,1
…
am,1
a1,2
a2,2
…
am,2
…
…
…
…
a1,n-1
a2,n-1
…
am,n-
a1,n
a2,n
…
am,n
Оценочное
выражение
–
F
b0
-a0,1
-a0,2
…
-a0,n
–
1
-a0,n1
Шаг 1. Проверка на допустимость.
Проверяем на положительность элементы столбца b (свободные члены), если среди
них нет отрицательных, то найдено допустимое решение (решение, соответствующее
одной из вершин многогранника условий) и мы переходим к шагу 2. Если в столбце
свободных членов имеются отрицательные элементы, то выбираем среди них
максимальный по модулю – он задает ведущую строку k. В этой строке так же находим
максимальный по модулю отрицательный элемент ak,l – он задает ведущий столбец – l и
является ведущим элементом. Переменная, соответствующая ведущей строке
исключается из базиса, переменная соответствующая ведущему столбцу включается в
базис. Пересчитываем симплекс-таблицу согласно правилам.
Если же среди свободных членов есть отрицательные элементы – а в
соответствующей строке – нет то условия задачи несовместны и решений у нее нет.
Если после перерасчета в столбце свободных членов остались отрицательные
элементы, то переходим к первому шагу, если таких нет, то ко второму.
Шаг 2. Проверка на оптимальность.
На предыдущем этапе найдено допустимое решение. Проверим его на
оптимальность
Если среди элементов симплексной таблицы, находящихся в строке F (не беря в
расчет элемент b0 – текущее значение целевой функции) нет отрицательных, то найдено
оптимальное решение.
Если в строке F есть отрицательные элементы, то решение требует улучшения.
Выбираем среди отрицательных элементов строки F максимальный по модулю (исключая
значение функции b0)
a0,l=min{a0,i }
l – столбец в котором он находится, будет ведущим. Для того, чтобы найти
ведущую строку, находим отношение соответствующего свободного члена и элемента из
ведущего столбца, при условии, что они неотрицательны.
bk/ak,l =min {bi/ai,l } при ai,l>0, bi>0
k – cтрока, для которой это отношение минимально – ведущая. Элемент ak,l ведущий (разрешающий). Переменная, соответствующая ведущей строке (xk) исключается
из базиса, переменная соответствующая ведущему столбцу (xl) включается в базис.
Пересчитываем симплекс-таблицу по формулам. Если в новой таблице после
перерасчета в строке F остались отрицательные элементы переходим к шагу 2
Если невозможно найти ведущую строку, так как нет положительных элементов в
ведущем столбце, то функция в области допустимых решений задачи не ограничена алгоритм завершает работу.
Если в строке F и в столбце свободных членов все элементы положительные, то
найдено оптимальное решение.
Правила преобразований симплексной таблицы.
При составлении новой симплекс-таблицы в ней происходят следующие
изменения:

Вместо базисной переменной xk записываем xl; вместо небазисной
переменной xl записываем xk.

ведущий элемент заменяется на обратную величину ak,l’= 1/ak,l

все элементы ведущего столбца (кроме ak,l) умножаются на -1/ak,l

все элементы ведущей строки (кроме ak,l) умножаются на 1/ak,l

оставшиеся элементы симплекс-таблицы преобразуются по формуле ai,j’=
ai,j- ai,lx ak,j/ ak,l
Схему преобразования элементов симплекс-таблицы (кроме ведущей строки и
ведущего столбца) называют схемой «прямоугольника».
Рис. 7 – Правило «прямоугольника»
Пример решения задачи линейного программирования симплекс-методом.
Преобразуемый элемент ai,j и соответствующие ему три сомножителя как раз и
являются вершинами «прямоугольника».
Решим прямую задачу линейного программирования симплексным методом, с
использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 7x 1 + 5×2 при
следующих условиях-ограничений.
2×1 + 3×2≤19
2×1 + x2≤13
3×2≤15
3×1≤18
Для построения первого опорного плана систему неравенств приведем к системе
уравнений путем введения дополнительных переменных (переход к канонической форме).
2×1 + 3×2 + 1×3 + 0x4 + 0x5 + 0x6 = 19
2×1 + 1×2 + 0x3 + 1×4 + 0x5 + 0x6 = 13
0x1 + 3×2 + 0x3 + 0x4 + 1×5 + 0x6 = 15
3×1 + 0x2 + 0x3 + 0x4 + 0x5 + 1×6 = 18
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
22 31 10 01 00 00 
A = 0 3 0 0 1 0 
3 0 0 0 0 1 
Решим систему уравнений относительно базисных переменных:
x3, x4, x5, x6,
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,19,13,15,18)
Таблица 3 – I симплекс-таблица, соответствующая исходной задаче
Базис
B
x1
x2
x3
x4
x5
x6
x3
19
2
3
1
x4
13
2
1
1
x5
15
3
1
x6
18
3
1
F(X0)
-7
-5
Переходим к основному алгоритму симплекс-метода.
Итерация №0.
Текущий опорный план неоптимален, так как в индексной строке находятся
отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как
это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее:
Следовательно, 4-ая строка является ведущей.
Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и
ведущей строки.
Таблица 4 – I симплекс-таблица, соответствующая исходной задаче, содержащая
оценочный столбец
Базис B
x1
x2
x3
x4
x5
x6
min
x3
19
2
3
1
91/2
x4
13
2
1
1
61/2
x5
15
3
1
x6
18
1
3
6
F(X1) 0
-5
-7
Получаем новую симплекс-таблицу:
Таблица 5 – II симплекс-таблица, соответствующая исходной задаче
Базис
B
x1
x2
x3
x4
x5
x6
-2
x3
7
3
1
/3
-2
x4
1
1
1
/3
x5
15
3
1
1
x1
6
1
/3
F(X1)
42
-5
21/3
Итерация №1.
Текущий опорный план неоптимален, так как в индексной строке находятся
отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как
это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления: bi / ai2
и из них выберем наименьшее:
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (1) и находится на пересечении ведущего столбца и
ведущей строки.
Таблица 6 – II симплекс-таблица, соответствующая исходной задаче, содержащая
оценочный столбец
Базис
B
x1
x2
x3
x4
x5
x6
min
-2
x3
7
3
1
/3 21/3
-2
x4
1
1
/3 1
1
x5
15 0
3
1
5
1
x1
6
1
/3 F(X2)
42 0
21/3 0
-5
Получаем новую симплекс-таблицу:
Базис
x3
x2
x5
x1
F(X2)
Таблица 7 – III симплекс-таблица, соответствующая исходной задаче
B
x1
x2
x3
x4
x5
x6
4
1
-3
11/3
-2
1
1
1
/3
12
-3
1
2
1
6
1
/3
47
5
-1
Итерация №2.
Текущий опорный план неоптимален, так как в индексной строке находятся
отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x6, так как
это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления: bi / ai6
и из них выберем наименьшее:
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (11/3) и находится на пересечении ведущего столбца и
ведущей строки.
Таблица 8 – III симплекс-таблица, соответствующая исходной задаче, содержащая
оценочный столбец
Базис
B
x1
x2
x3
x4
x5
x6
min
1
x3
4
1
-3
1 /3 3
-2
x2
1
1
1
/3
x5
12 0
-3
1
2
6
1
x1
6
1
/3
18
F(X3)
47 0
5
-1
Получаем новую симплекс-таблицу:
Таблица 9 – IV симплекс-таблица, соответствующая исходной задаче
B
x1
x2
x3
x4
x5
x6
3
1
3
/4 -2 /4 0
1
1
3
1
/2 -1/2
1
1
6
-1 /2 1 /2
1
-1
5
1
/4 3/4
3
3
50
/4 2 /4
Конец итераций: индексная строка не содержит отрицательных элементов – найден
оптимальный план
Окончательный вариант симплекс-таблицы:
Таблица 10 – Симплекс-таблица, соответствующая конечной итерации
Базис
B
x1
x2
x3
x4
x5
x6
3
1
x6
3
/4
-2 /4
1
1
-1
x2
3
1
/2
/2
1
1
x5
6
-1 /2
1 /2
1
-1
3
x1
5
1
/4
/4
3
3
F(X4)
50
/4
2 /4
Оптимальный план можно записать так:
x2 = 3
x1 = 5
F(X) = 5•3 + 7•5 = 50
Базис
x6
x2
x5
x1
F(X3)

1. На первом шаге прямого хода метода Гаусса выбирается максимальный по модулю элемент в первом столбце. Этот элемент является ведущим. Если он равен нулю, то detA = 0. Если ведущий элемент не является элементом , то перестановкой строк помещаем его в  . При этом соответственно переставляются элементы вектора b. Затем применяются формулы метода Гаусса.

2. На -м шаге прямого хода метода Гаусса непреобразованный столбец – это часть столбца i, начиная с элемента , то есть . Находим максимальный по модулю элемент  в непреобразованном столбце. Этот элемент является ведущим. Если он равен нулю, то detA = 0. Если ведущий элемент не является элементом , то перестановкой строк помещаем его в  . При этом соответственно переставляются элементы вектора b. Затем применяются формулы метода Гаусса.

3. После (n-1)-го шага получаем верхнюю треугольную матрицу U и преобразованный вектор правой части.  Выполняем обратную подстановку.

Метод Гаусса с частичным выбором ведущего элемента в отсутствие ошибок округления для невырожденных матриц позволяет получить точное решение, а для вырожденных матриц – сообщение о том, что матрица вырождена.

Пример

Решить систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента.

Решение

Рассмотрим ту же систему линейных уравнений, что и в предыдущих примерах.

Прямой ход метода Гаусса

Прежде всего, выбираем максимальный по модулю элемент в первом непреобразованном столбце:

,   , следовательно,  ведущим элементом является 10.

Ведущим  элементом является элемент , поэтому перестановка строк не нужна. Умножим первое уравнение на 0.3 и прибавим ко второму. Умножим первое уравнение на -0.5 и прибавим к третьему. Получим:

 

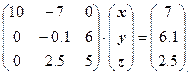
Рассмотрим следующий непреобразованный столбец:

,              , следовательно, ведущим элементом является 2.5, а не  -0.1, как в методе Гаусса без выбора ведущего элемента. Но ведущий элемент не является элементом    (при ) , поэтому  необходимо переставить строки матрицы А, чтобы элемент 2.5 стал элементом .

При перестановке строк необходимо одновременно поменять местами элементы вектора правой части . Получим:

.

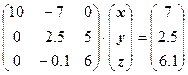
Умножим второе уравнение на 0.4 и прибавим к третьему. Получим:

.

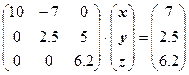
Мы получили систему линейных уравнений с верхней треугольной матрицей.

Обратная подстановка

,        следовательно, ;

,                       ;

,              

Ведущими элементами являются числа: 10, 2.5, 6.2,  все они по модулю больше 1, следовательно,  алгоритм является вычислительно устойчивым.

В методе Гаусса с частичным выбором ведущего элемента, в отличие от метода Гаусса без выбора ведущего элемента, в случае необходимости меняются местами уравнения системы линейных уравнений. За счет этого не возникает проблем, если у невырожденной матрицы какой-либо из главных миноров равен нулю.

Рассмотрим метод Гаусса с частичным выбором ведущего элемента с точки зрения операций над матрицами.

Теорема

Произвольная невырожденная матрица перестановкой строк (столбцов) может быть приведена к матрице с главными минорами, отличными от нуля (, где P – матрица перестановок).

Матрица Р получается из единичной матрицы перестановкой строк (столбцов).

Сложность метода Гаусса с частичным выбором ведущего элемента

Число арифметических действий, необходимых для его реализации: , где n – число уравнений. Оценим сложность по памяти: требуется память для хранения n² элементов матрицы, вектора b (n элементов) и вектора x (n элементов), в результате, .

Метод Гаусса с частичным выбором ведущего элемента является устойчивым, если все ведущие элементы по модулю больше единицы.

Следует отметить, что метод Гаусса с частичным выбором ведущего элемента – это основной алгоритм вычислительной математики линейной алгебры.

Метод Гаусса с полным выбором ведущего элемента отличается от метода Гаусса с частичным выбором ведущего элемента тем, что на каждом шаге прямого хода ведущий элемент ищется в непреобразованной части матрицы. Непреобразованная часть матрицы – это квадратная матрица размерности n-i+1, получаемая вычеркиванием первых   i – 1  строк и первых   i – 1  столбцов. В методе Гаусса с полным выбором ведущего элемента возможна не только перестановка строк матрицы и соответствующих элементов правой части, но и перестановка столбцов матрицы и, соответственно, изменение порядка следования неизвестных.