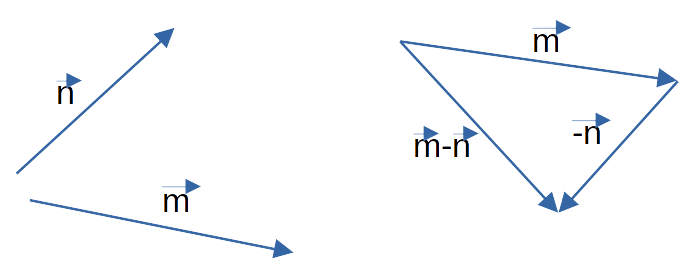
В статье Сумма векторов мы научились складывать векторы, здесь мы научимся их вычитать. На самом деле, все предельно просто. Пусть у нас есть два вектора a⃗vec{a} и b⃗vec{b}, как найти вектор a⃗−b⃗vec{a}-vec{b}, то есть, разность векторов a⃗vec{a} и b⃗vec{b}? Мы можем написать так:
a⃗−b⃗=a⃗+(−1)⋅b⃗vec{a}-vec{b}=vec{a}+(-1)cdotvec{b}
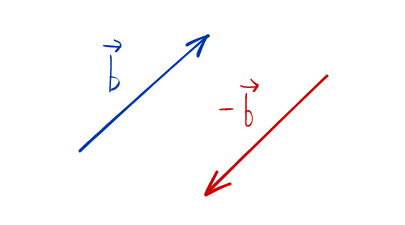
Смотрите, мы от разности векторов перешли к сумме векторов. Нам нужно сложить векторы a⃗vec{a} и (−1)⋅b⃗(-1)cdotvec{b}. Ну с первым то все понятно, а что такое (−1)b⃗(-1)vec{b}? Это просто вектор b⃗vec{b}, умноженный на минус единицу, это вектор −b⃗-vec{b}.
При умножении любого вектора на (−1)(-1) его длина остается той же, а направление меняется на противоположное.
Итак, у нас есть векторы a⃗vec{a} и b⃗vec{b}:
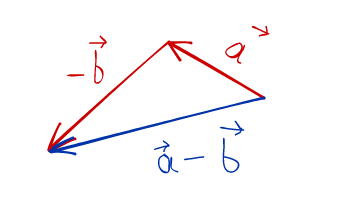
Найдем их разность. Для этого перейдем от этих векторов к векторам a⃗vec{a} и −b⃗-vec{b} и сложим их. Складывать векторы мы уже умеем, для этого можно воспользоваться или правилом треугольника или правилом параллелограмма:
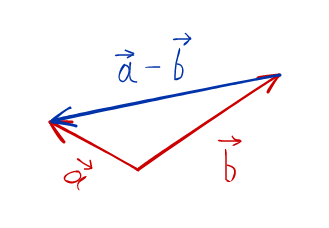
Теперь забудем о векторе −b⃗-vec{b}, у нас ведь вначале были только a⃗vec{a} и b⃗vec{b}:
Как видите, вычитать векторы ничуть не сложнее, чем их складывать. В какой-то мере вычитать ещё проще.
Чтобы найти разность векторов a⃗vec{a} и b⃗vec{b} нужно совместить начала этих векторов, а потом провести вектор из конца вектора b⃗vec{b} в конец вектора a⃗vec{a}.
На практике вам может помочь следующие рассуждения. Подумайте, какой вектор нужно добавить к вектору b⃗vec{b} чтобы получить вектор a⃗vec{a}. Этот вектор и будет a⃗−b⃗vec{a}-vec{b}.
Если у нас есть несколько векторов a⃗,b⃗,c⃗,d⃗vec{a}, vec{b}, vec{c}, vec{d} и нам нужно, например найти разность a⃗−b⃗−c⃗−d⃗vec{a}-vec{b}-vec{c}-vec{d} то нужно действовать поочередно. Сначала находим разность a⃗−b⃗vec{a}-vec{b}, потом от получившегося вектора отнимаем c⃗vec{c}, потом отнимаем d⃗vec{d}.
Тест по теме «Разность векторов»
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Определение
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
Определение
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
Разность векторов
Определение
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
- Постройте сумму, т. е. соедините начало первого отрезка и конец второго.
Нет времени решать самому?
Наши эксперты помогут!
Примеры вычисления разности векторов
Примеры
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
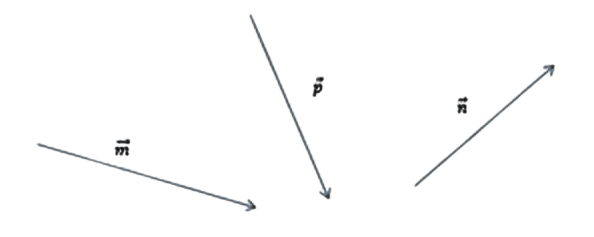
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
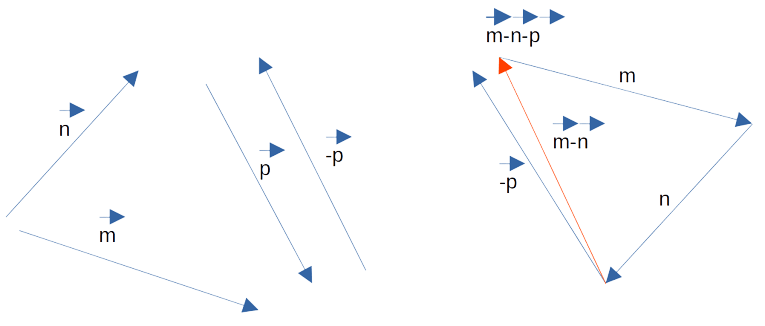
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
-
Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
-
Разность векторов
-
Формула вычитания векторов
-
Формула вычитания векторов
- Примеры задач
Сумма векторов
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c, начало которого совпадает с началом a, а конец – с концом b. При этом конец вектора a должен совпадать с началом вектора b.
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c, совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
ci = ai + bi
Элементы вектора c равняются попарной сумме соответствующих элементов a и b.
| Для плоских задач | a + b = {ax + bx; ay + by} |
| Для трехмерных задач | a + b = {ax + bx; ay + by; az + bz} |
| Для n-мерных векторов | a + b = {a1 + b1; a2 + b2; … an + bn} |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: (a + b) + c = a + (b + c)
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (-a) = 0
Примечание: Вектор –a коллинеарен и равен по длине a, но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
Для вычитания векторов также применяется правило треугольника.
Если из вектора a вычесть b, то получится c, причем должно соблюдаться условие: b + c = a
Формула вычитания векторов
ci = ai – bi
Элементы вектора c равны попарной разности соответствующих элементов a и b.
| Для плоских задач | a – b = {ax – bx; ay – by} |
| Для трехмерных задач | a – b = {ax – bx; ay – by; az – bz} |
| Для n-мерных векторов | a – b = {a1 – b1; a2 – b2; … an – bn} |
Примеры задач
Задание 1
Вычислим сумму векторов a = {3; 5} и b = {2; 7}.
Решение:
a + b = {3 + 2; 5 + 7} = {5; 12}.
Задание 2
Найдем разность векторов a = {4; 8; -2} и b = {-1; 9; 5}.
Решение:
a – b = {4 – (-1); 8 – 9; -2 – 5} = {5; -1; -7}.
Векторы на ЕГЭ по математике. Действия над векторами
-
Сложение векторов
-
Вычитание векторов
-
Умножение вектора на число
-
Скалярное произведение векторов
-
Онлайн-курс «Математика 10+11 100 баллов»
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения 
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
Автомобиль движется из A в B. Конечный результат — его перемещение из точки A в точку B, то есть перемещение на вектор 
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: 

До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1. Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y, абсцисса и ордината.
Вектор также задается двумя координатами: 
Здесь в скобках записаны координаты вектора 
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
к оглавлению ▴
Сложение векторов
Для сложения векторов есть два способа.
1. Правило параллелограмма. Чтобы сложить векторы 


Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 



По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В, из В в С, из С в D, затем в Е и в F. Конечный результат этих действий — перемещение из А в F.
При сложении векторов 



к оглавлению ▴
Вычитание векторов
Вектор 



Теперь понятно, что такое вычитание векторов. Разность векторов 



к оглавлению ▴
Умножение вектора на число
При умножении вектора 



к оглавлению ▴
Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 


Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе вуза.
к оглавлению ▴
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
ПОДРОБНЕЕ
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Векторы наu0026nbsp;ЕГЭ поu0026nbsp;математике. Действия над векторами» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Откладывание вектора от данной точки
Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
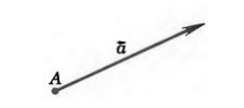
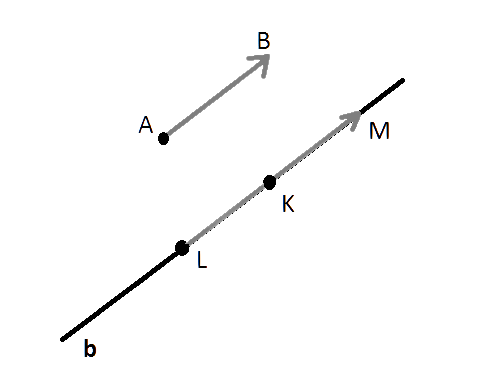
Определение 1
Если точка $A$ начала какого-либо вектора $overrightarrow{a}$, то говорят, что вектор $overrightarrow{a}$ отложен от точки $A$ (рис. 1).
Рисунок 1. $overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
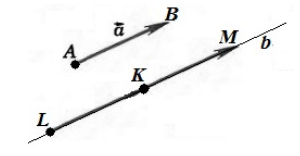
От любой точки $K$ можно отложить вектор $overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
-
Вектор $overrightarrow{a}$ – нулевой.
В этом случае, очевидно, что искомый вектор — вектор $overrightarrow{KK}$.
-
Вектор $overrightarrow{a}$ — ненулевой.
Обозначим точкой $A$ — начало вектора $overrightarrow{a}$, а точкой $B$ – конец вектора $overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $overrightarrow{a}$. Отложим на этой прямой отрезки $left|KLright|=|AB|$ и $left|KMright|=|AB|$. Рассмотрим векторы $overrightarrow{KL}$ и $overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $overrightarrow{a}$ (рис. 2)
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Вычитание векторов. Правило первое
Пусть нам даны векторы $overrightarrow{a}$ и $overrightarrow{b}$.
Определение 2
Разностью двух векторов $overrightarrow{a}$ и $overrightarrow{b}$ называется такой вектор $overrightarrow{c}$, который при сложении с вектором $overrightarrow{b}$ дает вектор $overrightarrow{a}$, то есть
[overrightarrow{b}+overrightarrow{c}=overrightarrow{a}]
Обозначение: $overrightarrow{a}-overrightarrow{b}=overrightarrow{c}$.
«Вычитание векторов. Как найти разность векторов» 👇
Построение разности двух векторов рассмотрим с помощью задачи.
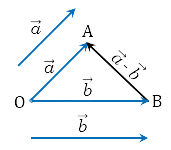
Пример 1
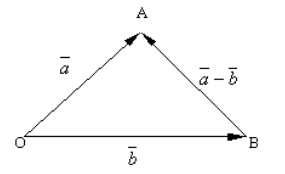
Пусть даны векторы $overrightarrow{a}$ и $overrightarrow{b}$. Построить вектор $overrightarrow{a}-overrightarrow{b}$.
Решение.
Построим произвольную точку $O$ и отложим от нее векторы $overrightarrow{OA}=overrightarrow{a}$ и $overrightarrow{OB}=overrightarrow{b}$. Соединив точку $B$ с точкой $A$, получим вектор $overrightarrow{BA}$ (рис. 3).
Рисунок 3. Разность двух векторов
По правилу треугольника для построения суммы двух векторов видим, что
[overrightarrow{OB}+overrightarrow{BA}=overrightarrow{OA}]
То есть
[overrightarrow{b}+overrightarrow{BA}=overrightarrow{a}]
Из определения 2, получаем, что
[overrightarrow{a}-overrightarrow{b}=overrightarrow{BA}]
Ответ: $overrightarrow{a}-overrightarrow{b}=overrightarrow{BA}$.
Из этой задачи получаем следующее правило для нахождения разности двух векторов. Чтобы найти разность $overrightarrow{a}-overrightarrow{b}$ нужно от произвольной точки $O$ отложить векторы $overrightarrow{OA}=overrightarrow{a}$ и $overrightarrow{OB}=overrightarrow{b}$ и соединить конец второго вектор с концом первого вектора.
Вычитание векторов. Правило второе
Вспомним следующее необходимое нам понятие.
Определение 3
Вектор $overrightarrow{a_1}$ называется произвольным для вектора $overrightarrow{a}$, если эти векторы противоположно направлены и имеют равную длину.
Обозначение: Вектор $(-overrightarrow{a})$ противоположный для вектора $overrightarrow{a}$.
Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.
Теорема 2
Для любых двух векторов $overrightarrow{a}$ и $overrightarrow{b}$ справедливо следующее равенство:
[overrightarrow{a}-overrightarrow{b}=overrightarrow{a}+(-overrightarrow{b})]
Доказательство.
По определению 2, имеем
Прибавим к обеим частям вектор $left(-overrightarrow{b}right)$, получим
Так как векторы $overrightarrow{b}$ и $left(-overrightarrow{b}right)$ противоположны, то $overrightarrow{b}+left(-overrightarrow{b}right)=overrightarrow{0}$. Имеем
Теорема доказана.
Из этой теоремы получаем следующее правило для разности двух векторов: Чтобы найти разность $overrightarrow{a}-overrightarrow{b}$ нужно от произвольной точки $O$ отложить вектор $overrightarrow{OA}=overrightarrow{a}$, затем от полученной точки $A$ отложить вектор $overrightarrow{AB}=-overrightarrow{b}$ и соединить начало первого вектора с концом второго вектора.
Пример задачи на понятие разности векторов
Пример 2
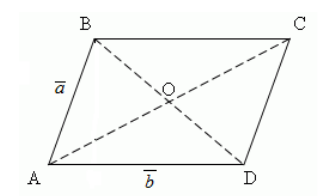
Пусть дан параллелограмм $ADCD$, диагонали которого пересекаются в точке $O$. $overrightarrow{AB}=overrightarrow{a}$, $overrightarrow{AD}=overrightarrow{b}$ (рис. 4). Выразить через векторы $overrightarrow{a}$ и $overrightarrow{b}$ следующие векторы:
а) $overrightarrow{DC}+overrightarrow{CB}$
б) $overrightarrow{BO}-overrightarrow{OC}$
Рисунок 4. Параллелограмм
Решение.
а) Произведем сложение по правилу треугольника, получим
[overrightarrow{DC}+overrightarrow{CB}=overrightarrow{DB}]
Из первого правила разности двух векторов, получаем
[overrightarrow{DB}=overrightarrow{a}-overrightarrow{b}]
б) Так как $overrightarrow{OC}=overrightarrow{AO}$, получим
[overrightarrow{BO}-overrightarrow{OC}=overrightarrow{BO}-overrightarrow{AO}]
По теореме 2, имеем
[overrightarrow{BO}-overrightarrow{AO}=overrightarrow{BO}+left(-overrightarrow{AO}right)=overrightarrow{BO}+overrightarrow{OA}]
Используя правило треугольника, окончательно имеем
[overrightarrow{BO}+overrightarrow{OA}=overrightarrow{BA}=-overrightarrow{AB}=-overrightarrow{a}]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
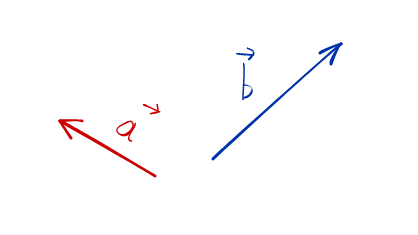
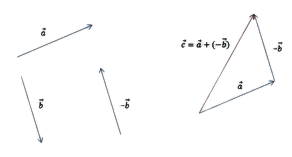

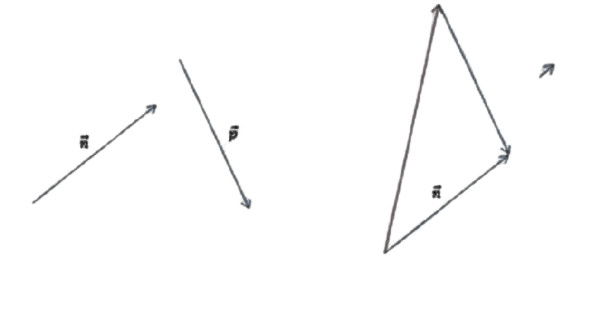














 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»