Как найти вектор через его середину - Сайт, где вы сможете решить свои вопросы

Нахождение координат середины отрезка: примеры, решения

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.

Середина отрезка на координатной прямой

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B : необходимо определить координату x C .

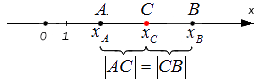
Поскольку точка C является серединой отрезка А В , верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C – x A = x B – x C

Тогда возможно два равенства: x C – x A = x B – x C и x C – x A = – ( x B – x C )

Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных – несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A ( x A ) и B ( x B ):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Середина отрезка на плоскости

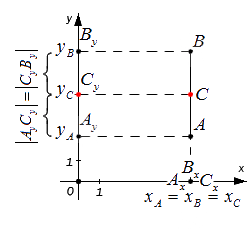
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y – проекции точек A , B и C на оси координат (прямые О х и О y ).

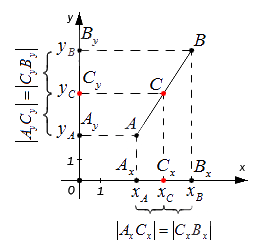
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

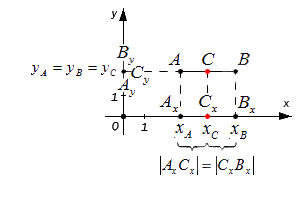
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A ( x A , y A ) и B ( x B , y B ) определяются как:

( x A + x B 2 , y A + y B 2 )

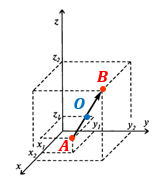
Середина отрезка в пространстве

Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z – проекции всех заданных точек на оси системы координат.

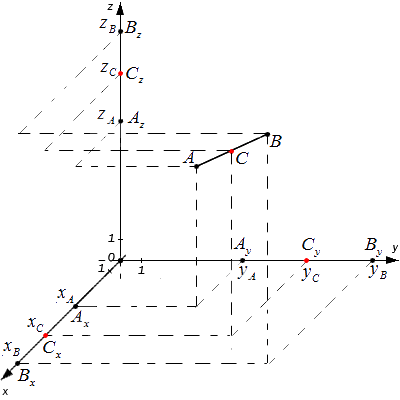
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A ( x A , y A ) и B ( x B , x B ) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) , O B → = ( x B , y B ) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C ( x A + x B 2 , y A + y B 2 , z A + z B 2 )

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.

Исходные данные: на плоскости – точки с заданными координатами А ( – 7 , 3 ) и В ( 2 , 4 ) . Необходимо найти координаты середины отрезка А В .

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = – 7 + 2 2 = – 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ: координаты середины отрезка А В – 5 2 , 7 2 .

Исходные данные: известны координаты треугольника А В С : А ( – 1 , 0 ) , В ( 3 , 2 ) , С ( 9 , – 8 ) . Необходимо найти длину медианы А М .

Решение

По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M :

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + ( – 8 ) 2 = – 3

Поскольку теперь нам известны координаты обоих концов медианы (точки A и М ), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М :

A M = ( 6 – ( – 1 ) ) 2 + ( – 3 – 0 ) 2 = 58

Ответ: 58

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 ( 1 , 1 , 0 ) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M ( 4 , 2 , – 4 ) . Необходимо рассчитать координаты точки А .

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А : x M = x A + x C 1 2 ⇒ x A = 2 · x M – x C 1 = 2 · 4 – 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M – y C 1 = 2 · 2 – 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M – z C 1 = 2 · ( – 4 ) – 0 = – 8

Ответ: координаты точки А ( 7 , 3 , – 8 ) .

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Прямоугольная система координат

В планиметрии мы уже рассматривали прямоугольную систему координат. Ее образовывали 2 перпендикулярные друг другу оси – Ох и Оу. С ее помощью можно было определить положение любой точки на координатной плоскости, просто указав две ее координаты – абсциссу х и ординату у.

В стереометрии необходимо определять положение точки уже не на плоскости, а в пространстве. Для этого добавляется третья ось Оz, которую ещё называют осью апликат. Каждые пара осей образует свою отдельную координатную плоскость, всего получается три таких плос-ти: Оху, Охz и Oуz.

Точка О именуется началом координат. Она делит каждую ось на два луча, один из которых – это положительная полуось, а второй – отрицательная полуось.

Для каждой точки в пространстве можно указать три координаты, однозначно определяющие ее положение в пространстве. Пусть в пространстве есть некоторая точка М. Опустим из нее перпендикуляры на координатные плоскости. В свою очередь из этих проекций точки М опустим перпендикуляры уже на координатные оси. В результате будет построен прямоугольный параллелепипед. Измерения этого параллелепипеда и будут координатами точки М:

Если точка M находится в одной из координатных плоскостей, то одна из ее координат будет нулевой. Например, если М принадлежит плоскости Охz, то нулю будет равна координата у. Если же точка располагается на одной из координатных осей, то у нее уже две координаты будут нулевыми. Так, если точка находится на оси Ох, то только координата х может быть ненулевой, а у и z окажутся нулевыми координатами.

На показанном рисунке ребра параллелепипеда лежат на положительных полуосях, поэтому все координаты положительны. Если же какие-то ребра будут лежать на отрицательных полуосях, то и соответствующие координаты будут отрицательными.

Координаты вектора

Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.

Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:

где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а<3; – 2; – 4>.

Задание. Разложите на орты вектор

Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.

Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.

Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.

Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:

Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:

Задание. Найдите сначала сумму, а потом разность векторов а <3; 7; 5>и b<2; 4; 6>.

Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это х_а, у_а и z_а. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:

Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:

Задание. Вычислите коорд-ты вектора р, зная, что:

Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:

Получается, что вектор p имеет координаты <0; – 2; 3>.

Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:

Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:

Координаты радиус-векторов будут совпадать с координатами их концов:

Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).

Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:

Задание. От точки K(10; 6; 13) отложен вектор m<3; 2; 5>, конец совпал в точку H. Найдите коорд-ты точки H.

Решение. Коорд-ты вектора m и его концов связаны формулами:

Координаты середины отрезка

Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:

Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:

Аналогично можно получить аналогичные формулы для коорд-т у и z:

Рассмотрим несколько задач на координаты точек.

Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).

Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:

Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.

Решение. Сначала запишем формулу для коорд-ты х:

Вычисление длины векторов и расстояния между точками

Рассмотрим радиус-вектор ОМ с коорд-тами . Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:

Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:

Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.

Задание. Найдите длину вектора m<– 2; 9; 6>.

Решение. Просто используем формулу:

Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:

Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).

Решение. Просто подставляем коорд-ты точек в формулу:

Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).

Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:

Коллинеарность векторов

Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что

Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:

Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть

В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами <0; 0; 0>. Он условно признается коллинеарным любому вектору.

Задание. Выясните, какие из этих пар векторов коллинеарны:

Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:

Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.

Повторяем эти действия в задании б):

На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.

В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.

В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:

Коэффициент k получился одинаковым, поэтому вектора коллинеарны.

В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.

Ответ: а) да; б) нет; в) нет; г) да; д) да.

Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).

Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.

Сначала вычислим коорд-ты векторов АВ и ВС:

Теперь проверяем, коллинеарны ли эти вектора:

Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.

Определение компланарности векторов

Пусть у нас есть три вектора с известными коорд-тами:

Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:

где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:

Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.

Задание. Определите, компланарны ли вектора

Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:

Значит, рассмотренная тройка векторов компланарна.

Задание. Располагаются ли в одной плос-ти вектора:

Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:

Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.

Скалярное произведение векторов

В 9 классе мы уже изучали скалярное произведение векторов.

Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.

Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.

Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:

Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:

Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов аа; у_а> и b<х_b; y_b> можно было рассчитать так:

Задание. Вычислите скалярное произведение векторов:

На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.

Задание. Вычислите угол между векторами:

Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:

Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).

Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:

Далее рассчитываем скалярное произведение векторов:

Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:

Задание. В прямоугольном параллелепипеде АВСDA₁B₁C₁D₁ ребра имеют длину:

Рассчитайте угол между векторами DB₁ и BC₁.

Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:

При этом построении граничные точки векторов будут иметь следующие коорд-ты:

Находим коорд-ты векторов, а также их длины:

Рассчитываем скалярное произведение DB₁ и BC₁:

Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.

Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.

[spoiler title=”источники:”]

http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/

http://100urokov.ru/predmety/koordinaty-v-stereometrii

[/spoiler]

Источник

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

$vec{a}(x_{a};: y_{a};: z_{a})$

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

$vec{a}=vec{AB}(x_{B}-x_{A};: y_{B}-y_{A};: z_{B}-z_{A})$

Длина вектора vec{AB} в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:

$|vec{a}|=sqrt{x^{2}_{a}+y^{2}_{a}+z^{2}_{a}}=sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}$ Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

$x_{M}=frac{x_{A}+x_{B}}{2};: : y_{M}=frac{y_{A}+y_{B}}{2};: : z_{M}=frac{z_{A}+z_{B}}{2}$

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов:

$vec{a}+vec{b}=vec{c}(x_{a}+x_{b};: y_{a}+y_{b};: z_{a}+z_{b})$

Разность векторов:

$vec{a}-vec{b}=vec{d}(x_{a}-x_{b};: y_{a}-y_{b};: z_{a}-z_{b})$

Произведение вектора на число:

$lambda cdot vec{a}=vec{p}(lambda x_{a};: lambda y_{a};:lambda z_{a} )$

Скалярное произведение векторов:

$vec{a}cdot vec{b}=|vec{a}|cdot |vec{b}|cdot cosvarphi =x_{a}cdot x_{b}+y_{a}cdot y_{b}+z_{a}cdot z_{b}$

Косинус угла между векторами:

$cosvarphi =frac{vec{a}cdot vec{b}}{|vec{a}|cdot vec{|b|}}=frac{x_{a}cdot x_{b}+y_{a}cdot y_{b}+z_{a}cdot z_{b}}{sqrt{x^{2}_{a}+y^{2}_{a}+z^{2}_{a}}cdot sqrt{x^{2}_{b}+y^{2}_{b}+z^{2}_{b}}}$

Прямые AE и BK — скрещиваются. Найдем угол между векторами vec{AE} и vec{BK} . Для этого нужны их координаты.

$, \ A(0;0;0)\ B(1;0;0)\ E(frac{1}{2};0;1)\ K(1;frac{1}{2};1)$

Запишем координаты векторов:

$vec{AE}left (frac{1}{2};0;1 right )$

$vec{BK}left (0;frac{1}{2};1 right )$

и найдем косинус угла между векторами vec{AE} и vec{BK} :

Координаты точек A, B и C найти легко:

$Aleft ( frac{1}{2};-frac{1}{2};0 right )$

$Bleft ( frac{1}{2};frac{1}{2};0 right )$

$Cleft ( -frac{1}{2};frac{1}{2};0 right )$

Из прямоугольного треугольника AOS найдем $OS=frac{sqrt{2}}{2}.$

Координаты вершины пирамиды: $Sleft ( 0;0;frac{sqrt{2}}{2} right ).$

$Eleft ( frac{1}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

$Kleft ( -frac{1}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

Найдем координаты векторов и :

$overrightarrow{AE}left ( -frac{1}{4};frac{3}{4};frac{sqrt{2}}{4} right )$

$overrightarrow{BK}left ( -frac{3}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

и угол между ними:

$cosvarphi =frac{overrightarrow{AE}cdot overrightarrow{BK}}{left |overrightarrow{AE} right |cdot left |overrightarrow{BK} right |}=frac{1}{6}$

Покажем теперь, как вписать систему координат в треугольную призму.

Запишем координаты точек:

$A_{1}(0;0;1)$

$B(frac{1}{2};frac{sqrt{3}}{2};0)$

$B_{1}(frac{1}{2};frac{sqrt{3}}{2};1)$

$C_{1}(-frac{1}{2};frac{sqrt{3}}{2};1)$

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

$D(frac{1}{4};frac{sqrt{3}}{4};1)$

Найдем координаты векторов и $overrightarrow{BC}_{1}$ , а затем угол между ними:

$overrightarrow{AD}(frac{1}{4};frac{sqrt{3}}{4};1)$

$overrightarrow{BC_{1}}(-1;0;1)$

$cosvarphi =frac{overrightarrow{AD}cdot overrightarrow{BC_{1}}}{left |overrightarrow{AD} right |cdot left |overrightarrow{BC_{1}} right |}=frac{3}{2sqrt{10}}$

Плоскость в пространстве задается уравнением:

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

$left{begin{matrix} A+C+D=0\ 2A-2B+D=0\ 4A+B+2C+D=0 end{matrix}right.$ .

Пусть, например, D = −2. Тогда:

$left{begin{matrix} A+C-2=0\ 2A-2B-2=0\ 4A+B+2C-2=0 end{matrix}right.$ ;

$left{begin{matrix} A+C=2\ A-B=1\ 4A+B+2C=2 end{matrix}right.$ .

Выразим C и B через A и подставим в третье уравнение:

$left{begin{matrix} C=2-A\ B=A-1\ 4A+A-1+4-2A=2 end{matrix}right.$ .

Решив систему, получим:

$, \ A=-frac{1}{3}\ , \ B=-frac{4}{3}\ , \ C=frac{7}{3}$

Уравнение плоскости MNK имеет вид:

$-frac{1}{3}x-frac{4}{3}y+frac{7}{3}z-2=0.$

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку $M(x_{0}, y_{0}, z_{0}),$ имеет вид:

$A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0.$

Угол между плоскостями равен углу между нормалями к этим плоскостям:

$cosvarphi =frac{left |vec{n}_{1}cdot vec{n}_{2} right |}{|vec{n}_{1}|cdot |vec{n}_{2}|}$

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Итак, первый вектор нормали у нас уже есть: $vec{n}_{1}=overrightarrow{AC}(1;1;0).$

Напишем уравнение плоскости AEF.

$, \ A(0;0;0)\ E(frac{1}{2};0;1)\ , \ F(0;frac{1}{2};1)$

$left.begin{matrix} A\ , \ E\ , \ F end{matrix}right|$ $, \ 0cdot A+0cdot B+0cdot C+D=0\ , \ frac{1}{2}cdot A+0cdot B+1cdot C+D=0\ , \ 0cdot A+frac{1}{2}cdot B+1cdot C+D=0$

Упростим систему:

$left{begin{matrix} D=0\ frac{1}{2}A+C=0\ , \ frac{1}{2}B+C=0 end{matrix}right.$ .

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

$cosvarphi =frac{|2+2|}{sqrt{2}cdot sqrt{9}}=frac{4}{sqrt{2}cdot 3}=frac{4}{sqrt{2}cdot 3}=frac{2sqrt{2}}{3}$

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

Итак, AA₁ = √3

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор $vec{n_{1}}(1;0;0)$ .

$B_{1}left ( 5;, 0;, sqrt{3} right )$

Координаты вектора $overrightarrow{B_{1}D}$ — тоже:

$overrightarrow{B_{1}D}left ( -5;, sqrt{33};, -sqrt{3} right )=overrightarrow{n}_{2}$

Находим угол между плоскостями, равный углу между нормалями к ним:

$cos, varphi =frac{5}{sqrt{25+33+3}}=frac{5}{sqrt{61}}$

Зная косинус угла, находим его тангенс по формуле

$1+tg^{2}varphi =frac{1}{cos^{2}varphi }$

Получим:
$tg, varphi =frac{6}{5}.$

Ответ: $frac{6}{5}.$

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

$sin, varphi =frac{left | overrightarrow{n}cdotoverrightarrow{a} right |}{left | overrightarrow{n} right |cdot |overrightarrow{a}|}$

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

$Eleft ( 1;, frac{1}{2};, 1 right )$

Находим координаты вектора $overrightarrow{AE}left ( 0;, frac{1}{2};, 1 right )$ .

Найдем угол между прямой и плоскостью:

$sin, varphi =frac{left | overrightarrow{AC}cdot overrightarrow{AE} right |}{|overrightarrow{AC}|cdot|overrightarrow{AE}|}=frac{2}{2cdot sqrt{2}cdot sqrt{5}}=frac{1}{sqrt{10}}$

Ответ: $frac{1}{sqrt{10}}.$

$h=frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{sqrt{A^{2}+B^{2}+C^{2}}}$

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = $frac{6}{sqrt{5}}$ . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

$A_{1}left ( 0, ;0;, frac{6}{sqrt{5}} right )$

$left.begin{matrix} A_{1}\ B\ D end{matrix}right|$ $begin{matrix} frac{6}{sqrt{5}}C+D=0\ sqrt{10}A+D=0\ 3sqrt{10}B+D=0 end{matrix}$

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

$h=frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{sqrt{A^{2}+B^{2}+C^{2}}}=frac{6sqrt{10}}{sqrt{50+36+4}}=frac{6sqrt{10}}{sqrt{90}}=2.$

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Середина вектора

Формула

Чтобы найти середину вектора по координатам нужно вычислить сумму координат начала и конца вектора и разделить на два.

Например, пусть на плоскости заданы точки $ A(x_1;y_1) $ и $ B(x_2;y_2) $ вектора $ overline{AB} $. Тогда его середина находится по формуле: $$ O (x;y) = O bigg(frac{x_1+x_2}{2};frac{y_2+y_2}{2}bigg) $$

Если вектор задан в пространстве трёмя координатами $ A (x_1;y_1;z_1),B (x_2;y_2;z_2) $, то середину можно найти по аналогичной формуле: $$ O (x;y,z) = O bigg(frac{x_1+x_2}{2};frac{y_1+y_2}{2}; frac{z_1+z_2}{2} bigg) $$

Откуда выведена формула? Если вектор спроецировать на координатную ось $ Ox $, то можно будет применить формулу для нахождения середины отрезка к самому вектору. По сути вектор это направленный отрезок, который имеет начало и конец.

Примеры решений

Пример

Пусть вектор $ overline{AB} $ задан в пространстве трёмя точками $ A(1,3,5) $ и $ B(3,7,1) $. Найти середину вектора.

Решение

Итак, как найти середину вектора? По правилу мы должны сложить соответствующие координаты точек начала и конца вектора и разделить пополам:

$$ O = bigg (frac{1+3}{2};frac{3+7}{2};frac{5+1}{2} bigg) = (2;5;3) $$

Точка $ O (2;5;3) $ – является серединой вектора $ overline{AB} $

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ O (2;5;3) $$

Источник

ОСИ КООРДИНАТ:

Для понимания темы «вектор», надо сначала разобраться с понятием «декартовы координаты».

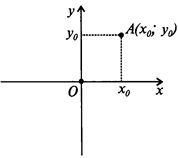
ось x — ось абсцисс;
ось y — ось ординат,
точка О — начало координат.

Любой точке плоскости сопоставляются два числа:

абсцисса x₀,
ордината y_0.

Эти числа называются декартовыми координатами данной точки.

ВЕКТОР:

Вектор — направленный отрезок прямой. То есть это отрезок, для которого указано, какая из его точек является началом, а какая — концом.

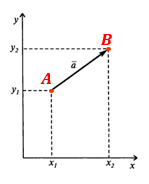
Пусть имеются две точки:

A с координатами $(x_1;,y_1)$
B с координатами $(x_2;,y_2)$.

Тогда мы имеем вектор $,overline {!AB,}$, который обозначим за $overline a.$

На примере вектора рассмотрим основные понятия, связанные с векторами.

Во-первых, для каждого вектора можно найти его координаты и модуль.

КООРДИНАТЫ ВЕКТОРА И МОДУЛЬ ВЕКТОРА:

Координаты вектора — разности координат конца и начала вектора. На примере вектора $overline a$ его координатами будут: $(a_x;,a_y).$ Свойства координат вектора:

Координаты вектора не изменяются при параллельном переносе.
У равных векторов соответствующие координаты равны.

Нахождение координат вектора:

Координаты вектора $overline a;(a_x;,a_y)colon$

$begin{aligned}&a_x=x_2-x_1\&a_y=y_2-y_1end{aligned}$

То есть, координаты вектора $overline acolon (x_2-x_1;,y_2-y_1;,z_2-z_1).$

Модуль вектора — длина вектора (обозначается ). Находится как квадратный корень из суммы квадратов координат вектора.

$|overline a|=sqrt{(a_x)^2+(a_y)^2vphantom{bigl(}}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2vphantom{bigl(}}$

Если рассмотреть пространственный вектор, то в эти формулы добавляется третья координата — z.

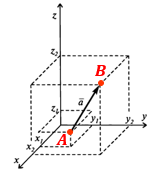
Координаты вектора $overline a;(a_x;,a_y;,a_z)$:

$begin{aligned}&a_x = x_2-x_1 \ &a_y = y_2-y_1 \ &a_z = z_2 – z_1end{aligned}$

То есть, координаты вектора $overline acolon (x_2-x_1;,y_2-y_1;,z_2-z_1).$

Модуль вектора $overline acolon$

$|overline a|=sqrt{(a_x)^2+(a_y)^2+(a_z)^2vphantom{bigl(}}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2vphantom{bigl(}}$

СЕРЕДИНА ВЕКТОРА:

Чтобы найти середину вектора по координатам нужно:

1. Вычислить сумму координат начала и конца вектора.

2. Разделить на два.

НА ПЛОСКОСТИ	В ПРОСТРАНСТВЕ
O — середина вектора $,overline {!AB,}$

$begin{aligned}&A,(x_1;,y_1), B,(x_2;,y_2) \[3pt] &O(x;y)=left(frac{x_1+x_2}{2};,frac{y_1+y_2}{2}right)end{aligned}$	$begin{aligned}&A,(x_1;,y_1;,z_1), B,(x_2;, y_2;, z_2) \[3pt] &O(x;y;z)=left(frac{x_1+x_2}{2};,frac{y_1+y_2}{2};,frac{z_1+z_2}{2}right)end{aligned}$

ВИДЫ ВЕКТОРОВ:

Единичный вектор — вектор, длина которого равна 1.

Нулевой вектор — отдельные точки плоскости. У такого вектора конец и начало совпадают, а его длина (его модуль) равен нулю.

Коллинеарные и компланарные векторы

Коллинеарные векторы — векторы, которые параллельны одной прямой или которые лежат на одной прямой.

Два коллинеарных вектора $|overline a| и |b|$ называются сонаправленными только тогда, когда их направления соответствуют друг другу:

$|overline a|{small uparrowuparrow}|overline b|$

Компланарные векторы — векторы, которые параллельны одной плоскости или которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельная двум любым векторам, поэтому два произвольных вектора являются компланарными.

АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД ВЕКТОРАМИ:

	НА ПЛОСКОСТИ	В ПРОСТРАНСТВЕ
Координаты вектора $overline {c,}$	Сложение векторов: $overline {c,}=overline a + overline b$
$x$	$c_x = a_x + b_x$	$c_x = a_x + b_x$
$y$	$c_y = a_y + b_y$	$c_y = a_y + b_y$
$z$	—	$c_z = a_z + b_z$
Координаты вектора $overline {c,}$	Вычитание векторов: $overline {c,}=overline a – overline b$
$x$	$c_x = a_x – b_x$	$c_x = a_x – b_x$
$y$	$c_y = a_y – b_y$	$c_y = a_y – b_y$
$z$	—	$c_z = a_z – b_z$
Координаты вектора $overline {b}$	Умножение вектора на число: $overline b = lambdaoverline a$
$x$	$overline b_x = lambda a_x$	$overline b_x = lambda a_x$
$y$	$overline b_y = lambda a_y$	$overline b_y = lambda a_y$
$z$	—	$overline b_z = lambda a_z$
Значение числа $s$	Скалярное умножение векторов: $s = overline acdotoverline b$
$s=a_x!cdot b_x + a_y!cdot b_y$	$s=a_x!cdot b_x + a_y!cdot b_y + a_z!cdot b_z$

ГЕОМЕТРИЧЕСКОЕ СЛОЖЕНИЕ И ГЕОМЕТРИЧЕСКАЯ РАЗНОСТЬ ВЕКТОРОВ:

СЛОЖЕНИЕ

Сумма двух векторов находится с помощью правила треугольника или правила параллелограмма: $overline {c,} = overline a + overline b$.

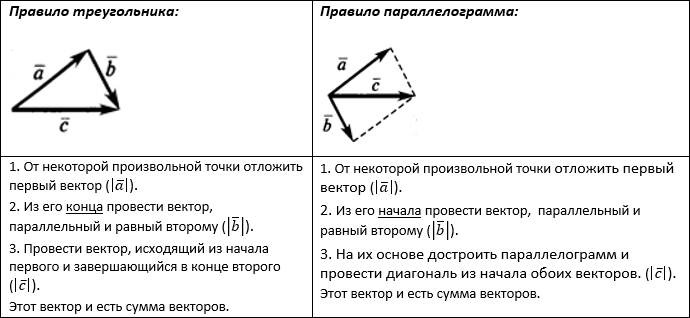
${mathbf {Теоремаcolon}}\ Для любых трёх точек A,,B,,C справедливо соотношениеcolon overline{!AB,}+,overline{!BC,}=,overline{!AC,}!.$

${mathbf {РАЗНОСТЬ}}\Разность двух векторов overline a и overline b;— это вектор overline {c,}, который в сумме с вектором overline b даёт вектор overline a \ overline b + overline{c,} = overline aquadRightarrowquadoverline{c,} = overline a – overline b$

$Вектор overline {c,} можно найти также, складывая с вектором overline a вектор bigl(-overline bbigr), противоположный вектору overline bcolon \ overline {c,} = overline a + bigl(-overline bbigr)$

Источник

Вспомним для начала основные понятия и формулы.

Р10

Пусть даны две точки: А(x1; x2) и B(y1; y2). Рассмотрим отрезок AB.

Длина отрезка АВ – это расстояние между точками A и B, его величина вычисляется по следующей формуле:

Рассмотрим теперь вектор AB. Напомню, что вектор – это направленный отрезок, то есть для него указано, какая из двух точек A и B является началом, а какая – концом. На рисунке ниже слева изображен отрезок AB, а справа – вектор AB с началом в точке A и концом в точке B.

Координаты вектора AB вычисляются следующим образом: из соответствующих координат конца вектора вычитаются соответствующие координаты начала вектора. Например, для нашего вектора AB это будет выглядеть так: AB(x2 – x1; y2 – y1).

Замечу, что модулем вектора AB называется длина отрезка AB.

Вспомним как найти координаты середины отрезка AB. Для этого есть простая формула:

x = (x1 + x2)/2, y = (y1 + y2)/2.

До этого момента мы рассматривали координаты на плоскости, а что, если речь пойдет о пространстве? Тут, оказывается, тоже все просто.

Пусть даны две точки A(x1; x2; x3) и B(y1; y2; y3).

Формула для вычисления длины отрезка AB, расположенного в пространстве будет выглядеть так:

А координаты середины отрезка AB найдем по формуле

x = (x1 + x2)/2, y = (y1 + y2)/2, z = (z1 + z2)/2.

И еще одна полезная формула: если вектор задан своими координатами, например, MN(x1; x2; x3), то его модуль вычисляется по формуле:

Чтобы сложить два или более векторов, нужно сложить их соответствующие координаты, например,

(x1; x2; x3) + (y1; y2; y3) = (x1 + y1; x2 + y2; x3 + y3).

Чтобы умножить вектор на число, нужно умножить каждую его координату на это число, например,

5 · (x1; x2; x3) = (5 · x1; 5 · x2; 5 · x3).

Скалярным произведением двух векторов а и b называется число

a · b = |a”b| · сos (a, b),

Чтобы вычислить скалярное произведение векторов, заданных координатами, например, MN(x1; x2; x3) и PK(y1; y2; y3), можно воспользоваться следующей формулой:

MN · PK = x1 · y1 + x2 · y2 + x3 · y3.

Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

На практике коллинеарность векторов (x1; x2) и (y1; y2) проще всего проверить, используя следующее свойство: коллинеарные векторы имеют пропорциональные координаты, то есть существует число p, такое, что (x1; x2) = p · (y1; y2).

Существуют также такие понятия, как сонаправленные векторы и противоположно направленные векторы. Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону, соответственно, противоположно направленные векторы – это коллинеарные векторы, которые направлены в разные стороны.

Теперь давайте рассмотрим несколько задач на эту тему.

Задача 1.

Доказать, что треугольник с вершинами A(6; -4; 2), B(3; 2; 3) и C(3; -5; -1) прямоугольный.

Решение.

Вполне очевидно, что для доказательства этой задачи достаточно показать, что один из углов треугольника ABC равен 90 градусов. Вспомним формулу для вычисления скалярного произведения через модули соответствующих векторов и косинус угла между ними, преобразуем ее и воспользуемся для нахождения угла.

сos (a, b) = a · b/|a”b|.

Для начала нам понадобятся координаты всех векторов, задающих стороны треугольника, их модули и всевозможные скалярные произведения. Вычисляем их.

Координаты векторов:

AB(3 – 6; 2 – (-4); 3 – 2) = AB(-3; 6; 1);

BC(3 – 3; -5 – 2; -1 – 3) = BC(0; -7; -4);

CA(6 – 3; -4 – (-5); 2 – (-1)) = CA(3; 1; 3).

Модули:

|AB| =

|BC| =

|CA| =

Скалярные произведения:

AB · BC = (-3) · 0 + 6 · (-7) + 1 · (-4) = 0 – 42 – 4 = -46;

BC · CA = 0 · 3 + (-7) · 1 + (-4) · 3 = 0 – 7 – 12 = -19;

AB · CA = (-3) · 3 + 6 · 1 + 1 · 3 = -9 + 6 + 3 = 0.

Теперь легко заметить, что угол между векторами AB и CA равен 90 градусов, так как

сos (AB, CA) = AB · CA / |AB”CA| = 0.

А, значит, угол А треугольника ABC равен 90 градусов, то есть треугольник ABC – прямоугольный, что и требовалось доказать.

Задача 2.

Даны точки А(0; 1; 2), B(1; 2; 4), C(-1; -1; 3) и D(1; 0; 0). Точки M и N – середины отрезков AC и BD. Найдите вектор MN и его модуль.

Решение.

Для начала найдем координаты точек M и N.

M((0 – 1)/2; (1 – 1)/2; (2 + 3)/2) = M(-1/2; 0; 5/2);

N((1 + 1)/2; (2 + 0)/2; (4 + 0)/2) = N(1; 1; 2).

Теперь найдем координаты вектора MN:

MN(1 – (-1/2); 1 – 0; 2 – 5/2) = MN(3/2; 1; -1/2).

Осталось найти модуль вектора MN.

|MN| =

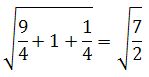
Задача 3.

При каких значениях x векторы (x³– 1)a и 2xa сонаправлены, где a – вектор, не равный нулевому вектору?

Решение.

Для того чтобы данные векторы были сонаправлены, необходимо, чтобы коэффициенты (x³– 1) и 2x имели одинаковый знак, а значит, чтобы выполнялось следующее неравенство: (x³ – 1) · 2x > 0. Решим его методом интервалов и найдем соответствующие x.

Получим x € (-∞; 0) U (1; +∞).

Если бы в задаче требовалось узнать, при каких x данные векторы будут противоположно направлены, мы бы потребовали, чтобы у коэффициентов (x³ – 1) и 2x были различные знаки.

Задача 4.

Даны координаты вершин четырехугольника: A(2; -2), B(-3; 1), C(7; 7) и D(7; 1). Доказать, что ABCD – трапеция.

Решение.

Так как трапеция – это четырехугольник, у которого одна пара противолежащих сторон параллельна, то для доказательства нам достаточно показать, что векторы BC и AD – коллинеарны, то есть лежат на параллельных прямых. Найдем для начала их координаты.

BC(7 – (-3); 7 – 1) = BC(10; 6);

AD(7 – 2; 1 – (-2)) = AD(5; 3).

Заметим, что координаты векторов пропорциональны: (10; 6) = 2 · (5; 3). Это и указывает на то, что данные векторы коллинеарны, а, значит, ABCD – трапеция.

Остались вопросы? Не знаете, как выполнять действия над векторами?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Источник

Нахождение координат середины отрезка: примеры, решения

Середина отрезка на координатной прямой

Середина отрезка на плоскости

Середина отрезка в пространстве

Определение координат середины отрезка через координаты радиус-векторов его концов

Примеры решения задач на нахождение координат середины отрезка

Векторы в пространстве и метод координат

Система координат в пространстве

Плоскость в пространстве задается уравнением:

Геометрия

Прямоугольная система координат

Координаты вектора

Координаты середины отрезка

Вычисление длины векторов и расстояния между точками

Коллинеарность векторов

Определение компланарности векторов

Скалярное произведение векторов

Векторы в пространстве и метод координат

Система координат в пространстве

Плоскость в пространстве задается уравнением:

Середина вектора

Формула

Примеры решений

Вам также может понравиться

Как найти главное дело

Как составить расписку с продавца

Треснул фундамент дома как исправить

Добавить комментарий Отменить ответ