Решение задач методом Гаусса
Содержание:
Решение задач методом Гаусса. Применение метода Гаусса к задачам линейной зависимости систем векторов
Мы уже говорили о том, что одной из важных задач линейной алгебры является выяснение факта – линейно зависима или независима в пространстве  система векторов
система векторов  . Метод Гаусса играет здесь решающую роль.
. Метод Гаусса играет здесь решающую роль.
Определение 1. Линейное уравнение называется однородным, если свободный член уравнения равен нулю. Система, состоящая из однородных уравнений, сама называется однородной.
Однородная система  линейных уравнений с
линейных уравнений с  неизвестными имеет вид:
неизвестными имеет вид:
 (1)
(1)
Однородная система всегда совместна, т.к. одним из ее решений является  .
.
Это решение называют нулевым. Важно знать имеет ли конкретная однородная система ненулевые решения.
Теорема 1. Однородная линейная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Заметим, что система (1) может быть записана в векторном виде
 . (2)
. (2)
В этой записи участвуют  векторов:
векторов:

Т.о., неизвестные  являются коэффициентами линейной комбинации векторов
являются коэффициентами линейной комбинации векторов  . Поэтому, решая методом Гаусса систему (1.3), мы ищем коэффициенты .
. Поэтому, решая методом Гаусса систему (1.3), мы ищем коэффициенты . . Если окажется, что решение единственное (т.е. нулевое), то система векторов
. Если окажется, что решение единственное (т.е. нулевое), то система векторов  линейно независима. В противном случае она линейно зависима.
линейно независима. В противном случае она линейно зависима.
Пример №19
Дана система из четырех векторов, принадлежащих  :
:
 (3)
(3)
Является ли эта система линейно зависимой в  ?
?
Решение:
Запишем уравнение  , которое в координатной записи представляет собой однородную линейную систему
, которое в координатной записи представляет собой однородную линейную систему

Если система уравнений (4) имеет только нулевое решение, то система векторов (3) линейно независима в  . Если же имеются и ненулевые решения, то система векторов (3) линейно зависима.
. Если же имеются и ненулевые решения, то система векторов (3) линейно зависима.
Применим к системе уравнений (4) метод Гаусса:

Получилась система уравнений с базисными неизвестными  и свободным неизвестным
и свободным неизвестным  . Наличие свободного неизвестного означает, что решений бесконечное множество. Следовательно, система векторов (3) линейно зависима в
. Наличие свободного неизвестного означает, что решений бесконечное множество. Следовательно, система векторов (3) линейно зависима в  .
.
Индекс цен и индекс инфляции. Ортогональные векторы
Одним из способов определения индекса цен и уровня инфляции является расчет стоимости «потребительской корзины», состоящей из основных видов товаров и услуг, получаемых потребителями. Обычно это 300 необходимых видов товаров и услуг. В табл. 1 приведен условный пример, отражающий изменение стоимости потребительской корзины по трем товарам.
Табл. 1. Изменение стоимости товаров, входящих в потребительскую корзину


Индекс цен р и индекс инфляции i рассчитываются следующим образом:
р =  • 100% = 106,3%, i= р -100 = 6,3%.
• 100% = 106,3%, i= р -100 = 6,3%.
Т.к. i > 0, то это инфляция – повышение общего (среднего) уровня цен в экономике страны. Заметим, что при i
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
16.1. Применение элементов линейной алгебры в экономике. Использование алгебры матриц. Матричные вычисления
Использование элементов алгебры матриц является одним из основных методов решения многих экономических задач. Особенно этот вопрос стал актуальным при разработке и использовании баз данных: при работе с ними почти вся информация хранится и обрабатывается в матричной форме.
Рассмотрим типичные задачи, использующие понятие вектора и его свойства.
1. Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в табл. 16.1.
Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р Выпускаемой продуции предприятия.

Решение. По данным табл. 16.1 составим четыре вектора, характеризующие весь производственный цикл:
 = (20, 50, 30,40) — вектор ассортимента,
= (20, 50, 30,40) — вектор ассортимента,
 = (5, 2, 7, 4) — вектор расхода сырья,
= (5, 2, 7, 4) — вектор расхода сырья,
 = (10, 5, 15, 8) — вектор затраты рабочего времени,
= (10, 5, 15, 8) — вектор затраты рабочего времени,
 = (30, 15, 45, 20) — ценовой вектор.
= (30, 15, 45, 20) — ценовой вектор.
Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента  На три других вектора, т. е.
На три других вектора, т. е.

2. Предприятие выпускает 4 вида изделий с использованием 4-х видов сырья. Нормы расхода сырья даны как элементы матрицы А:

Требуется найти затраты сырья на каждый вид изделия при заданном плане их выпуска: соответственно 60, 50, 35 и 40 ед.
Решение. Составим вектор-план выпуска продукции

Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду; этот вектор затрат вычисляется как произведение вектора  на матрицу А:
на матрицу А:

3. Пусть затраты 4-х видов сырья на выпуск 4-х видов продукции характеризуются матрицей А, приведенной в предыдущей задаче. Требуется найти: а) общие затраты на сырье для каждого вида продукции и его перевозку; б) общие затраты на сырье и его транспортировку при условии заданного вектора-плана предыдущей задачи, если известны себестоимости каждого вида сырья и его доставки (соответственно 4, 6, 5, 8 и 2, 1, 3, 2 ден. ед.).
Решение. Составим матрицу себестоимостей сырья и его доставки (соответственно 1-я и 2-я строки):

Тогда ответ на первый вопрос задачи дается в виде произведения матрицы А на транспонированную матрицу CT:

Суммарные затраты на сырье и его доставку (в денежных единицах) при векторе-плане выпуска продукции  = (60, 50, 35, 40) определяются произведением вектора
= (60, 50, 35, 40) определяются произведением вектора  на матрицу АСT:
на матрицу АСT:

4. В табл. 16.2 приведены данные о дневной производительности 5 предприятий, выпускающих 4 вида продукции с потреблением 3-х видов сырья, а также продолжительность работы каждого предприятия в году и цена каждого вида сырья.

1) годовую производительность каждого предприятия по каждому виду изделий;
2) годовую потребность каждого предприятия по каждому виду сырья;
3) годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска продукции указанных видов и количеств.
Решение. Нужно составить матрицы, характеризующие весь интересующий нас экономический спектр производства, а затем при помощи соответствующих операций над ними получить решение данной задачи. Прежде всего приведем матрицу производительности предприятий по всем видам продукции:

Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду продукции. Следовательно, годовая производительность J-Го предприятия по каждому виду продукции получается умножением J–Гo столбца матрицы А на количество рабочих дней в году для этого предприятия (J = 1, 2, 3, 4, 5). Таким образом, годовая производительность каждого предприятия по каждому из изделий описывается матрицей

Матрица затрат сырья на единицу изделия (эти показатели по условию одинаковы для всех предприятий) имеет вид

Дневной расход по типам сырья на предприятиях описывается произведением матрицы В на матрицу А:

Где I-я строка соответствует номеру типа сырья, а J-Й столбец — номеру предприятия согласно табл. 16.2 (I = 1, 2, 3; J = 1, 2, 3, 4, 5). Ответ на второй вопрос задачи получим по аналогии с матрицей АГод умножением столбцов матрицы ВА На соответствующие количества рабочих дней в году для предприятий — это годовая потребность каждого предприятия в каждом виде сырья:

Введем вектор стоимости сырья

Тогда стоимость общего годового запаса сырья для каждого предприятия получается умножением вектора  на матрицу ВAГод:
на матрицу ВAГод:

Следовательно, суммы кредитования предприятий для закупки сырья определяются соответствующими компонентами вектора  .
.
5. Отрасль состоит из П предприятий, выпускающих по одному виду продуции каждое; обозначим объем продукции I-го предприятия через Xi. Каждое из предприятий отрасли для обеспечения своего производства потребляет часть продукции, выпускаемой им самим и другими предприятиями. Например, в отрасли электротехнического оборудования часть продукции предприятий, выпускающих электродвигатели, силовые кабели, электрокары и т. д., употребляется практически всей отраслью. Пусть Aij — доля продукции I-го предприятия, потребляемая J-М предприятием для обеспечения выпуска своей продукции объема Xj. Возникает естественный вопрос о величине Yi — количестве продукции I-го предприятия, предназначенной для реализации вне данной отрасли (объем конечного продукта). Эта величина легко может быть подсчитана по формуле

Введем в рассмотрение матрицу порядка N, описывающую внутреннее потребление отрасли:

Тогда вектор конечного продукта является решением матричного уравнения

Или с использованием единичной матрицы Е получаем

Рассмотрим конкретный пример при П = 3. Пусть вектор выпуска продукции отрасли и матрица внутреннего потребления имеют соответственно вид

Используя формулу (16.1) и правило сложения матриц, получаем вектор объемов конечного продукта, предназначенного для реализации вне отрасли, состоящей из 3-х предприятий:
Модель равновесных цен
Рассмотрим теперь балансовую модель, двойственную к модели Леонтьева, так называемую модель равновесных цен. Пусть, как и прежде, А — матрица прямых затрат, х — вектор валового выпуска. Обозначим через р = (ри . р„) > 0 вектор цен (где р, — цена единицы продукции /-Й отрасли), тогда, например, первая отрасль получит доход, равныйрХх. Часть своего дохода эта отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции ей необходима продукция первой отрасли в объеме ап, второй отрасли в объеме а2, и-й отрасли в объеме апХ. На покупку этой продукции ею будет затрачена сумма, равная апрх + а2х р2 +. + йп1рп. Следовательно, для выпуска продукции в объеме хг первой отрасли необходимо потратить на закупку продукции других отраслей сумму, равную Xi(aup+a2iP2 + . + о„1 р„). Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим через К, (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции). Таким образом, имеется следующее равенство:
Разделив это равенство на Х, получаем
где vt = V/x — норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции). Подобным же образом получаем для остальных отраслей:
Найденные равенства, как нетрудно видеть, могут быть записаны в матричной форме следующим образом:
где v = (vi, V2. v„) — вектор норм добавленной стоимости.
Как мы видим, полученные уравнения очень похожи на уравнения модели Леонтьева, с той лишь разницей, что х заменен нар, у — на v, А — на А Т .
Модель равновесных цен позволяет при известных величинах норм добавленной стоимости прогнозировать цены на продукцию отраслей, а также изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.
Замечание 2Л6. Если умножить уравнение Леонтьева (2.34) слева на вектор равновесных цен р т , то с учетом (2.35) получим
В левой части этого равенства находится суммарная стоимость, выпускаемой отраслями продукции. В правой части первое слагаемое представляет собой суммарную добавленную стоимость всех отраслей, а второе слагаемое — стоимость конечного спроса.
Пример 2.7. Рассмотрим экономическую систему, состоящую из трех условных отраслей — топливно-энергетической промышленности и сельского хозяйства. Пусть
— транспонированная матрица прямых затрат, v = (4, 10, 4) — вектор норм добавленной стоимости. Определим равновесные цены. Для этого, как и в модели Леонтьева, воспользуемся формулой
где S T = <(Е – А)1 ) — транспонированная матрица полных затрат.
[spoiler title=”источники:”]
http://matica.org.ua/metodichki-i-knigi-po-matematike/osnovy-matematiki-i-ee-prilozheniia-v-ekonomicheskom-obrazovanii-krass-m-s-chuprynov-b-p/16-1-primenenie-elementov-lineinoi-algebry-v-ekonomike-ispolzovanie-algebry-matritc-matrichnye-vychisleniia
http://bstudy.net/682725/ekonomika/model_ravnovesnyh
[/spoiler]
Модель равновесных цен
Рассмотрим теперь балансовую модель, двойственную к модели Леонтьева, так называемую модель равновесных цен. Пусть, как и прежде, А — матрица прямых затрат, х — вектор валового выпуска. Обозначим через р = (ри . р„) > 0 вектор цен (где р, — цена единицы продукции /-Й отрасли), тогда, например, первая отрасль получит доход, равныйрХх. Часть своего дохода эта отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции ей необходима продукция первой отрасли в объеме ап, второй отрасли в объеме а2, и-й отрасли в объеме апХ. На покупку этой продукции ею будет затрачена сумма, равная апрх + а2х р2 +. + йп1рп. Следовательно, для выпуска продукции в объеме хг первой отрасли необходимо потратить на закупку продукции других отраслей сумму, равную Xi(aup+a2iP2 + . + о„1 р„). Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим через К, (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции). Таким образом, имеется следующее равенство:
Разделив это равенство на Х, получаем
где vt = V/x — норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции). Подобным же образом получаем для остальных отраслей:
Найденные равенства, как нетрудно видеть, могут быть записаны в матричной форме следующим образом:
где v = (vi, V2. v„) — вектор норм добавленной стоимости.
Как мы видим, полученные уравнения очень похожи на уравнения модели Леонтьева, с той лишь разницей, что х заменен нар, у — на v, А — на А Т .
Модель равновесных цен позволяет при известных величинах норм добавленной стоимости прогнозировать цены на продукцию отраслей, а также изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.
Замечание 2Л6. Если умножить уравнение Леонтьева (2.34) слева на вектор равновесных цен р т , то с учетом (2.35) получим
В левой части этого равенства находится суммарная стоимость, выпускаемой отраслями продукции. В правой части первое слагаемое представляет собой суммарную добавленную стоимость всех отраслей, а второе слагаемое — стоимость конечного спроса.
Пример 2.7. Рассмотрим экономическую систему, состоящую из трех условных отраслей — топливно-энергетической промышленности и сельского хозяйства. Пусть
— транспонированная матрица прямых затрат, v = (4, 10, 4) — вектор норм добавленной стоимости. Определим равновесные цены. Для этого, как и в модели Леонтьева, воспользуемся формулой
где S T = <(Е – А)1 ) — транспонированная матрица полных затрат.
Модель равновесных цен
Рассмотрим теперь балансовую модель – так называемую модель равновесных цен. Пусть, как и прежде, А – матрица прямых затрат,
х =( – вектор валового выпуска. Обозначим через вектор цен, i-я координата которого равна цене единицы продукции i-й отрасли; тогда, например, первая отрасль получит доход, равный . Часть своего дохода эта отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции, ей необходима продукция первой отрасли в объеме , второй отрасли в объеме , и т.д., n-й отрасли в объеме . На покупку этой продукции ею будет затрачена сумма, равная + + … + . Следовательно, для выпуска продукции в объеме первой отрасли необходимо потратить на закупку продукции других отраслей сумму, равную
(++…+ ). Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим через (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
Таким образом, имеет место следующее равенство:
Разделив это равенство на получаем:
где = / – норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции). Подобным же образом получаем для остальных отраслей
Найденные равенства могут быть записаны в матричной форме следующим образом:
где v = (,…,),Т – вектор норм добавленной стоимости. Как мы видим, полученные уравнения очень похожи на уравнения модели Леонтьева, с той лишь разницей, что х заменен на р, у – на v, А – на [7, С. 200].
5. Примеры решения задач
Рассмотрим сначала простую макроэкономическую модель, которая предполагает наличие всего двух секторов экономики: производители потребители. От производителей идет поток товаров и услуг, а от потребителей-поток денег.
Все потоки будем измерять в стоимостных (денежных) величинах.
Вся произведенная продукция (товары и услуги) делится на промежуточный продукт и конечный продукт.
Промежуточный продукт- это та часть совокупного продукта, которой производители обмениваются между собой или используют для собственных нужд.
Конечный продукт (конечный спрос) – вся продукция, которая используется вне сферы материального производства.
Пример 1.Пусть производители состоят всего из двух фирм . Предположим, что совокупный продукт, выпускаемый за один год, составляет в стоимостном выражении 400 ден.ед. Для этого производства используется продукция собственный подразделений в объеме 40 ден.ед. и закупленном у фирмы в объеме 320 ден.ед. Аналогичные цифры для совокупный продукт- 500, поставки собственных подразделений – 100, закупки у – 200. Таким образом, поставляет сама себе 40 единиц и – 200 единиц. Если из совокупного продукта ,равного 400, вычесть промежуточный продукт, то получится конечный продукт – 160.
Аналогично поставляет сама себе 100 единиц и – 320, что дает в сумме промежуточный продукт, а конечный продукт:
Далее удобно перейти к нормированным величинам, т.е. к затратам, отнесенным к единице (в стоимостном выражении) продукции (см. рис.3).
Модель равновесных цен
Дата добавления: 2015-07-09 ; просмотров: 4594 ; Нарушение авторских прав
Рассмотрим теперь балансовую модель, двойственную к модели Леонтьева – так называемую модель равновесных цен. Пусть, как и прежде, А – матрица прямых затрат, х=(х1, х2. хn) – вектор валового выпуска. Обозначим через р=( p1, p2. pn) – вектор цен, i-я координата которого равна цене единицы продукции i-й отрасли.
1. Часть своего дохода каждая i-я отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции ей необходима продукция первой отрасли в объеме а1i, второй отрасли в объеме а2i, п-й отрасли в объеме аni и т.д. На покупку этой продукции ею будет затрачена сумма, равная a1i р1 + a2i р2 +. + ani рn. Следовательно, для выпуска продукции в объеме хi отрасли необходимо потратить на закупку продукции других отраслей сумму, равную хi(a1i р1 + a2i р2 +. + ani рn). Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим через Vi (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
Таким образом, имеет место следующее равенство:
Разделив это равенство на хi, получаем
где vi = Vi/хi – норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
Найденные равенства могут быть записаны в матричной форме следующим образом:
p = A T p + v,
где v = (v1, v2 . vп) – вектор норм добавленной стоимости, A T – транспонированная матрица.
Как мы видим, полученные уравнения очень похожи на уравнения модели Леонтьева с той лишь разницей, что х заменен на р, у – на v, А – на А T .
Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукцию отраслей Она также позволяет прогнозировать изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.
Пример1.2.2. Рассмотрим экономическую систему, состоящую из трех отраслей. Назовем их условно: топливно-энергетическая отрасль, промышленность и сельское хозяйство. Пусть
– транспонированная матрица прямых затрат;
– столбец норм добавленной стоимости.
Определим равновесные цены. Для этого, как и в модели Леонтьева, воспользуемся формулой р=С T v, где С T = (Е–А Т ) -1 – транспонированная матрица полных затрат. После необходимых вычислений имеем
0,58 0,14 0,18
С T = (1/0,444) 0,28 0,68 0,24
10
Отсюда получаем, что р = С T v = 20 .
Допустим теперь, что в топливно-энергетической отрасли произойдет увеличение нормы добавленной стоимости на 1,11. Определим равновесные цены в этом случае. Принимая во внимание, что v = (5,11; 10; 4), находим, что
11,45
р = С T v = 20,7 .
Таким образом, продукция первой отрасли подорожала на 14,5%, второй – на 3,5%, третьей отрасли – на 4,17%. Нетрудно также, зная объемы выпуска, подсчитать вызванную этим повышением инфляцию.
| | | следующая лекция ==> | |
| Модель Леонтьева многоотраслевой экономики | | | Модель международной торговли. |
Не нашли то, что искали? Google вам в помощь!
[spoiler title=”источники:”]
http://vuzlit.ru/1729300/model_ravnovesnyh
http://life-prog.ru/2_32503_model-ravnovesnih-tsen.html
[/spoiler]
Рассмотрим
теперь балансовую модель, двойственную
к модели Леонтьева – так называемую
модель равновесных цен. Пусть, как и
прежде, А
– матрица прямых затрат, х=(х1,
х2,…,
хn)
– вектор валового выпуска. Обозначим
через р=(
p1,
p2,…,
pn)
– вектор цен, i-я
координата которого равна цене единицы
продукции i-й
отрасли.
-
Часть
своего дохода каждая
i-я отрасль
потратит на закупку продукции у других
отраслей. Так, для выпуска единицы
продукции ей необходима продукция
первой отрасли в объеме а1i,
второй отрасли в объеме а2i,
п-й
отрасли в объеме аni
и т.д. На покупку этой продукции ею
будет затрачена сумма, равная a1i
р1
+ a2i
р2
+…+ ani
рn.
Следовательно, для выпуска продукции
в объеме хi
отрасли необходимо потратить на
закупку продукции других отраслей
сумму, равную хi(a1i
р1
+ a2i
р2
+…+ ani
рn).
Оставшуюся часть дохода, называемую
добавленной стоимостью, мы обозначим
через Vi
(эта часть дохода идет на выплату
зарплаты и налогов, предпринимательскую
прибыль и инвестиции).
Таким образом,
имеет место следующее равенство:
хiрi
= хi(a1i
р1
+ a2i
р2
+…+ ani
рn)+
Vi.
Разделив
это равенство на хi,
получаем
рi
= хi(a1i
р1
+ a2i
р2
+…+ ani
рn)+
vi.
где
vi
= Vi/хi
– норма добавленной стоимости (величина
добавленной стоимости на единицу
выпускаемой продукции).
Найденные равенства
могут быть записаны в матричной форме
следующим образом:
p
= ATp
+ v,
где
v
= (v1,
v2
,…, vп)
– вектор норм добавленной стоимости,
AT
– транспонированная матрица.
Как
мы видим, полученные уравнения очень
похожи на уравнения модели Леонтьева
с той лишь разницей, что х
заменен
на р,
у
– на v,
А – на АT.
Модель равновесных
цен позволяет, зная величины норм
добавленной стоимости, прогнозировать
цены на продукцию отраслей Она также
позволяет прогнозировать изменение
цен и инфляцию, являющиеся следствием
изменения цены в одной из отраслей.
Пример
1.2.2. Рассмотрим
экономическую систему, состоящую из
трех отраслей. Назовем их условно:
топливно-энергетическая отрасль,
промышленность и сельское хозяйство.
Пусть
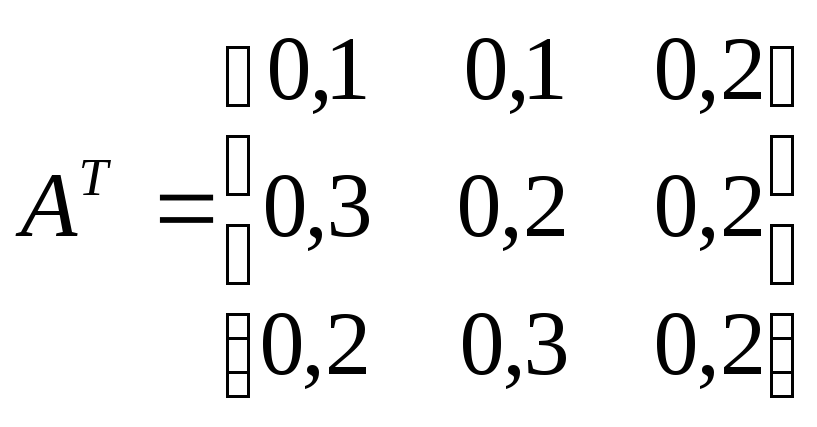 –транспонированная
–транспонированная
матрица прямых затрат;
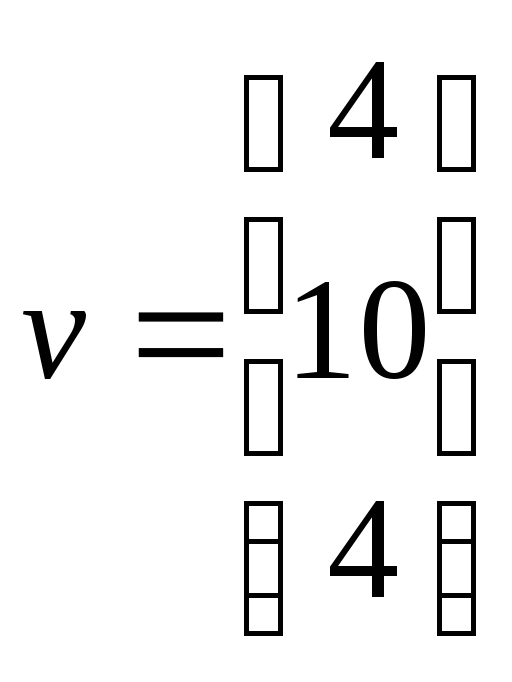 –столбец
–столбец
норм добавленной стоимости.
Определим
равновесные цены. Для этого, как и в
модели Леонтьева, воспользуемся формулой
р=СTv,
где СT
= (Е–АТ)-1
– транспонированная матрица полных
затрат. После необходимых вычислений
имеем
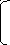
 0,58
0,58
0,14 0,18
СT
= (1/0,444) 0,28 0,68 0,24
0,25
0,29 0,69 .

 10
10
Отсюда
получаем, что р
= СTv
= 20 .
15
Допустим
теперь, что в топливно-энергетической
отрасли произойдет увеличение нормы
добавленной стоимости на 1,11. Определим
равновесные цены в этом случае. Принимая
во внимание, что v
= (5,11; 10; 4), находим, что

 11,45
11,45
р
= СTv
= 20,7 .
15,625
Таким образом,
продукция первой отрасли подорожала
на 14,5%, второй – на 3,5%, третьей отрасли
– на 4,17%. Нетрудно также, зная объемы
выпуска, подсчитать вызванную этим
повышением инфляцию.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Некоторые приложения в экономике собственных чисел и собственных векторов матрицы.
-
Линейные модели обмена.
Пусть
имеется система из n
отраслей производства, каждая из которых
выпускает продукцию одного вида.
Примем за единицу
объёма продукции каждой отрасли в
рассматриваемом периоде. Обмен продукции
происходит только внутри системы
(экономика замкнута) и известна матрица
А:

,
где
а
– доля продукции j-й
отрасли, которая поступает в i-ю
отрасль.
Ясно, что для
матрицы А
выполнимы два условия:
1.
![]()
,
для
j=![]()
; 2.
а
![]()
,
для i
=
,
j=
.
Первое
условие вызвано тем, что вся продукция
j-й отрасли предназначена
для обмена внутри системы.
Матрица, для которой
выполнимы условие 1 и 2, называется
матрицей
обмена.
Требуется
установить такие цены на продукцию
каждой отрасли, при которых вся система
находится в равновесии, то есть ни одна
отрасль не обогащается за счет другой.
Пусть хi
– цена одной единицы продукции i-й
отрасли, а
![]()
– вектор цен. Тогда расход i-й
отрасли, то есть стоимость всей закупаемой
ею продукции, таков:
![]()
.
Чтобы
отрасль могла развиваться, её расход
не должен превышать дохода, который
равен стоимости произведённой ею
продукции, то есть хi.
![]()
, i
=
(1)
Если
искомые равновесные цены существуют,
то система неравенств выполняется для
них как система равенств.
Доказательство.
Пусть
числа
![]()
удовлетворяют условию (1), подставим их
в эти неравенства и сложим почленно все
полученные неравенства
![]()
; ![]()
; ![]()
,
но это
неравенство является равенством
![]()
и все слагаемые в сумме неотрицательны,
то и исходные неравенства (1) выполняются
для чисел
.
Как равенства:
![]()
![]()
.
Итак,
надо найти вектор
![]()
такой, что

Таким
образом, задача свелась к следующему:
-
Является
ли число=1
собственным числом матрицы обмена А. -
Если
да, то найти соответствующий ему
положительный собственный вектор
матрицы А.
Для того, чтобы
![]()
было собственным числом матрицы обмена,
необходимо и достаточно, чтобы выполнялось
равенство
![]()
,
т.е.


.
Элементы
первой строки равны 0, т.к. в матрице
обмена
![]()
в силу этого
определитель, содержащий нулевой ряд,
равен 0.
Итак,
число 1 собственное число матрицы обмена,
для отыскания соответствующего ему
собственного вектора
![]()
,
следует найти полуположительное решение
однородной системы.
Такое
решение существует и найденный
полуположительный вектор
![]()
,
является искомым
вектором равновесных цен.
Задача.
Экономическая
система состоит из 3-х отраслей
производства, каждая из которых выпускает
один вид продукции. Обмен внутри системы
происходит в соответствии с данной
матрицей обмена
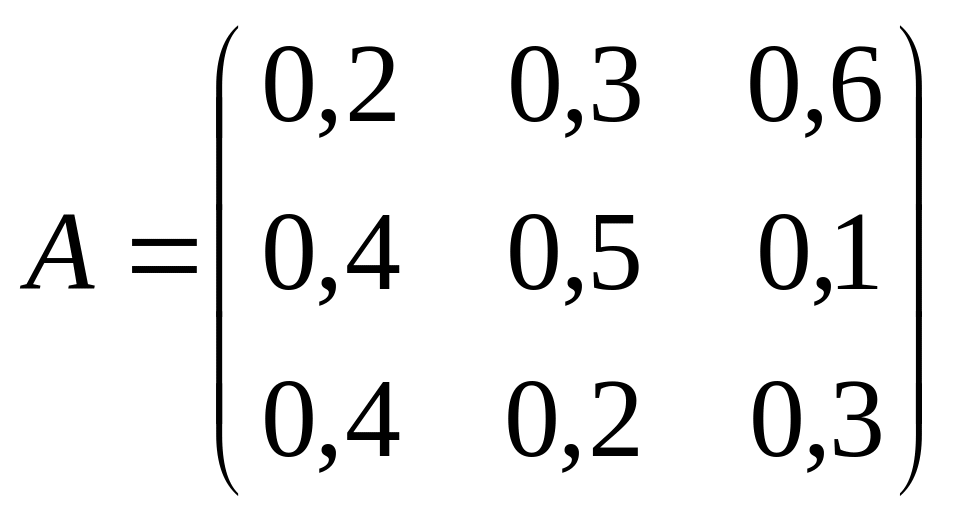
.
Найти вектор равновесных цен.
Решение.
Сначала найдём
матрицу
![]()
:

.
Составим однородную
систему линейных уравнений
![]()
,
где
![]()
.

; 
эта система
равносильна системе уравнений
![]()
находим её общее
решение:
![]()
.
Принимая
![]()
,
получим
![]()
.
Таким образом,
равновесные цены на продукцию каждой
отрасли:
![]()
,
где к
можно трактовать как множитель, связанный
с денежной единицей.
-
Модель международной торговли
Рассмотрим систему
из N
стран, торгующих только друг с другом
(т.е. система замкнута). Известна матрица
![]()
,
где
–
доля средств j
– ой страны, затрачиваемая на импорт
из i
– ой страны . Матрица А
является матрицей обмена, т.е.
![]()
и
(![]()
).
Требуется найти первоначальное
распределение средств между странами,
обеспечивающие равновесие всей системы,
т.е. такое положение, при котором в каждой
стране после каждого цикла обмена
остается столько же средств, сколько
было до обмена.
Пусть Хi
– количество средств i
– ой страны, т.е. вектор
![]()
описывает искомое распределение средств.
Ясно, что надо найти вектор
,
удовлетворяющий условиям:
![]()
.
Число 1 есть
собственное число матрицы обмена А
и существует полуположительный
собственный вектор
матрицы А,
соответствующий этому числу. Вектор
и является искомым первоначальным
распределением средств.
Система при этом
будет находиться в равновесии, т.е.
расход каждой страны в каждом цикле
обмена совпадает с её доходом от экспорта
и не изменяется от цикла к циклу.
Проанализируем
структуру равновесных векторов на
модели.
Международная
модель 6 стран описывается матрицей
обмена

I
II III IY Y YI
Найти равновесный
вектор этой системы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Файлы
Никитина Е.К.
1
1 Самарский государственный экономический университет
Аппарат линейной алгебры может быть использован для построения микроэкономических моделей, а именно отыскание собственных чисел и собственных векторов квадратной матрицы.
При исследовании различных экономических ситуаций возникает необходимость рассматривать матрицу обмена и находить ее собственные векторы.
Рассмотрим задачу о равновесии цен в простой модели обмена.
Пусть имеется система из n отраслей производства, каждая из которых выпускает продукцию одного вида. Примем за единицу объем продукции каждой отрасли в рассматриваемом периоде. Обмен продукцией происходит только внутри системы (экономика замкнута) и известна матрица А:
 (1)
(1)
где αij – доля продукции j-й отрасли, которая поступает в i-ю отрасль.
Ясно, что для матрицы А выполнены два условия:
αij ≥ 0, I = 1,2,…n;
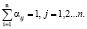
Второе условие вызвано тем, что вся продукция j-ой отрасли предназначена для обмена внутри системы. Матрица (1), для которой выполнены условия 1 и 2, называется матрицей обмена. Требуется установить такие цены на продукцию каждой отрасли, при которых вся система находится в равновесии, т.е. ни одна отрасль не обогащается за счёт другой.
Пусть хi – цена одной единицы продукции i-й отрасли, а 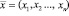 – вектор цен. Тогда расход i-й отрасли, т.е. стоимость всей закупаемой ею продукции, таков:
– вектор цен. Тогда расход i-й отрасли, т.е. стоимость всей закупаемой ею продукции, таков: 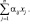
Чтобы отрасль могла развиваться, её расход не должен превышать дохода, который равен стоимости произведённой ею продукции, т.е. xi:
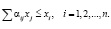 (2)
(2)
Если искомые равновесные цены существуют, то система неравенств (2) выполняется для них как система равенств: 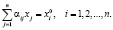
Таким образом, задача свелась к следующему:
1. выяснить, является ли число λ=1 собственным числом матрицы обмена А;
2. если да, то найти соответствующий этому собственному числу полуположительный собственный вектор матрицы А.
Для того чтобы число λ=1 было собственным числом матрицы обмена А, необходимо и достаточно, чтобы выполнялось равенство 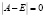 .
.
Итак, число 1 является собственным числом матрицы обмена и для отыскания соответствующего ему собственного вектора следует найти полуположительное решение однородной системы (A – E) 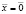 . Найденный полуположительный вектор
. Найденный полуположительный вектор 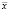 является искомым вектором равновесных цен.
является искомым вектором равновесных цен.
Рассмотрим пример: экономическая система состоит из трёх отраслей производства, каждая из которых выпускает один вид продукции. Обмен внутри системы происходит в соответствии с данной матрицей обмена
 .
.
Найдем вектор равновесных цен. Составим однородную систему линейных уровнений (А-Е) 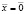 :
:
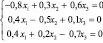
Решив её, получим:
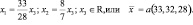
Полагая а > 0, находим равновесные цены на продукцию каждой отрасли: х1=33а; х2=32а; х3=28а, где а можно трактовать как множитель, связанный с денежной единицей.
Другая экономическая модель, где решается математическая задача того же вида, – это модель международной торговли. Рассмотрим систему из п стран, торгующих только друг с другом (т.е. система замкнута). Известна матрица 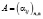 , где
, где 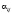 – доля средств j-й страны, затрачиваемая на импорт из i-й страны. Матрица А является матрицей обмена (1), т.е.
– доля средств j-й страны, затрачиваемая на импорт из i-й страны. Матрица А является матрицей обмена (1), т.е. 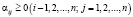 и
и 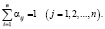
Требуется найти первоначальное распределение средств между странами, обеспечивающее равновесие всей системы, т.е. такое положение, при котором в каждой стране после каждого цикла обмена остаётся столько же средств, сколько было до обмена.
Пусть хi – количество средств i-й страны, т.е. вектор 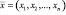 описывает искомое распределение средств. Ясно, что надо найти вектор
описывает искомое распределение средств. Ясно, что надо найти вектор  , удовлетворяющий условиям
, удовлетворяющий условиям
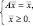
Ранее было показано, что число 1 есть собственное число матрицы обмена А и что существует полуположительный собственный вектор  матрицы А, соответствующий этому собственному числу. Вектор
матрицы А, соответствующий этому собственному числу. Вектор  и является искомым первоначальным распределением средств. Система при этом будет находиться в равновесии, т.е. расход каждой страны в каждом цикле обмена совпадает с её доходом от экспорта и не изменяется от цикла к циклу.
и является искомым первоначальным распределением средств. Система при этом будет находиться в равновесии, т.е. расход каждой страны в каждом цикле обмена совпадает с её доходом от экспорта и не изменяется от цикла к циклу.
Библиографическая ссылка
Никитина Е.К. ЛИНЕЙНЫЕ МОДЕЛИ ОБМЕНА // Современные наукоемкие технологии. – 2013. – № 10-2.
– С. 213-214;
URL: https://top-technologies.ru/ru/article/view?id=33432 (дата обращения: 19.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
