Пусть векторы
и
заданы своими проекциями на оси координат
,
и
или, что то же самое
,
.
Линейные операции над векторами
Так как линейные операции над векторами
сводятся к соответствующим линейным
операциям над проекциями этих векторов,
то можно записать:
1.
![]()
,
или кратко
![]()
![]()
.
То есть при сложении (вычитании) векторов
их одноименные координаты складываются
(вычитаются).
2.
![]()
или короче
![]()
.
То есть при умножении вектора на скаляр
координаты вектора умножаются на этот
скаляр.
Равенство векторов
Из определения вектора как направленного
отрезка, который можно передвигать в
пространстве параллельно самому себе,
следует, что два вектора
и
равны тогда и только тогда, когда
выполняются равенства:
![]()
,
![]()
,
![]()
,
т.е.

Коллинеарность векторов
Выясним условия коллинеарности векторов
и
,
заданных своими координатами.
Так как
,
то можно записать
![]()
,
где
– некоторое число. То есть
![]()
.
Отсюда
![]()
,
![]()
,
![]()
,
т.е.

,

,

или
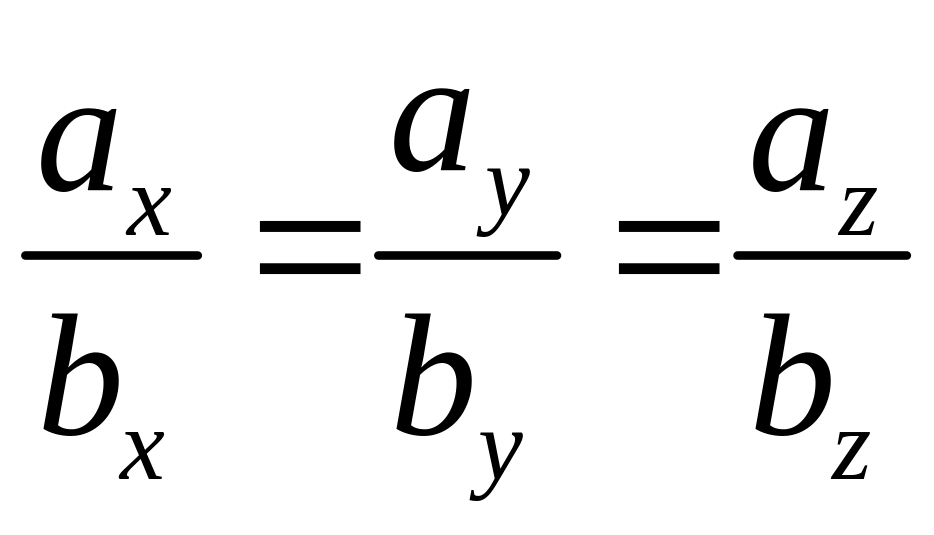
.
Таким образом, проекции коллинеарных
векторов пропорциональны. Верно и
обратное утверждение: векторы, имеющие
пропорциональные координаты, коллинеарны.
Координаты точки
Пусть в пространстве задана прямоугольная
декартова система координат
.
Для любой точки
координаты вектора
называются координатами точки
.
Вектор
называется радиус-вектором точки
,
обозначается
![]()
,
т.е.
![]()
.
Следовательно, координаты точки – это
координаты ее радиус-вектора
![]()
или
![]()
.
Координаты точки
записываются в виде
![]()
.
Координаты вектора
Найдем координаты вектора
![]()
,
если известны координаты точек
![]()
и
![]()
.
Имеем

![]()
![]()
![]()
.
Следовательно, координаты вектора равны
разностям соответствующих координат
его конца и начала:
![]()
.
2. Скалярное произведение векторов и его свойства
2.1. Определение скалярного произведения
Определение.
Скалярным произведением двух ненулевых
векторов
и
называется число, равное произведению
длин этих векторов на косинус угла между
ними.
Обозначается
![]()
,
![]()
(или
![]()
).
Итак, по определению,
![]()
, (6)
где
![]()
.
Формуле
(6) можно придать иной вид. Так как
![]()
,

а
![]()
,
то получаем:
![]()
, (7)
т.е. скалярное
произведение двух векторов равно модулю
одного из них, умноженному на проекцию
другого на ось, сонаправленную с первым
вектором.
2.2. Свойства скалярного произведения
1.
Скалярное произведение обладает
переместительным свойством:
![]()
.
2.
Скалярное произведение обладает
сочетательным свойством относительно
скалярного множителя:
![]()
.
3.
Скалярное произведение обладает
распределительным свойством:
![]()
.
4.
Скалярный квадрат вектора равен квадрату
его длины:
![]()
.
В
частности:
![]()
.
Если
вектор
возвести скалярно в квадрат и затем
извлечь корень, то получим не первоначальный
вектор, а его модуль
![]()
,
т.е.
![]()
(![]()
).
5. Если
векторы
и
(ненулевые) взаимно перпендикулярны,
то их скалярное произведение равно
нулю, т.е. если
![]()
,
то
![]()
.
Справедливо и обратное утверждение:
если
и
![]()
,
то
.
2.3. Выражение скалярного произведения через координаты
Пусть
заданы два вектора
и
.
Найдем
скалярное произведение векторов,
перемножая их как многочлены (что законно
в силу свойств линейности скалярного
произведения) и пользуясь таблицей
скалярного произведения векторов
,
,
:
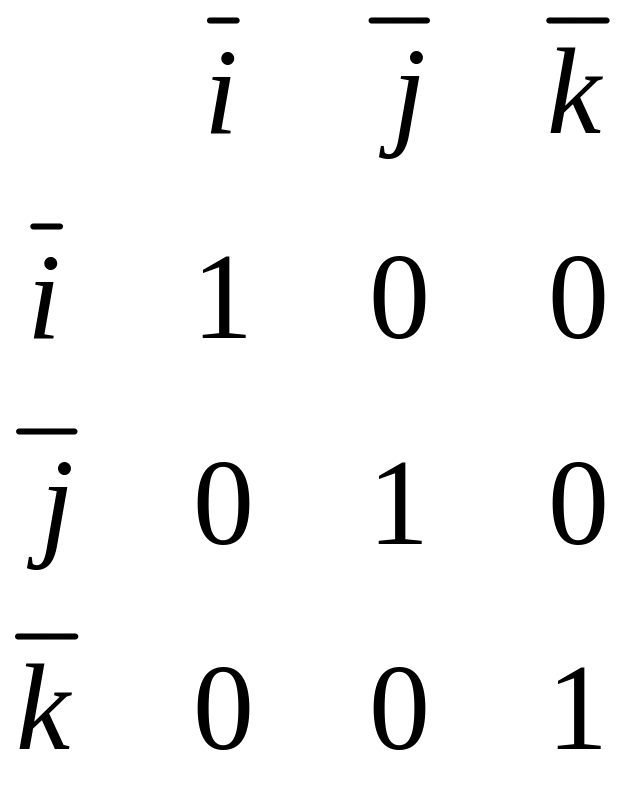
![]()
![]()
![]()
![]()
![]()
,
т.е.
![]()
.
Итак, скалярное
произведение векторов равно сумме
произведений их одноименных координат.


Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти проекцию вектора на вектор?
Для того, чтобы найти проекцию вектора на вектор ($overline{a}$ на $overline{b}$) нужно разделить скалярное произведение этих векторов на длину последнего вектора $overline{b}$ по формуле: $$text{Пр}_{overline{b}} overline{a} = frac{(overline{a},overline{b})}{|overline{b}|}$$
| Пример 1 |
| Найти проекцию вектора $overline{a} = (1,2)$ на вектор $overline{b} = (-1,2)$ |
| Решение |
|
Вычисляем скалярное произведение векторов. Умножаем соответствующие координаты и складываем $$(overline{a},overline{b}) = 1 cdot (-1) + 2 cdot 2 = -1 + 4 = 3$$ Находим модуль вектора, на который ищем проекцию $$|overline{b}| = sqrt{(-1)^2 + 2^2} = sqrt{5}$$ Подставляя в формулу проекции вектора $overline{a}$ на направляющий вектор $overline{b}$ получаем искомое значение $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ |
| Пример 2 |
| Вычислить проекцию вектора на вектор, если $overline{a} = (1,2,-3)$ и $overline{b} = (2,1,1)$ |
| Решение |
|
Берем скалярное произведение двух векторов. Перемножаем попарно соответствующие координаты и суммируем полученные значения $$(overline{a},overline{b}) = 1 cdot 2 + 2 cdot 1 + (-3) cdot 1 = 2 + 2 – 3 = 1$$ Так как ищем проекцию на вектор $overline{b}$, то вычисляем его модуль (длину) $$|overline{b}| = sqrt{2^2 + 1^2 + 1^2} = sqrt{6}$$ По главной формуле получаем ответ к задаче $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
ВИДЕО УРОК
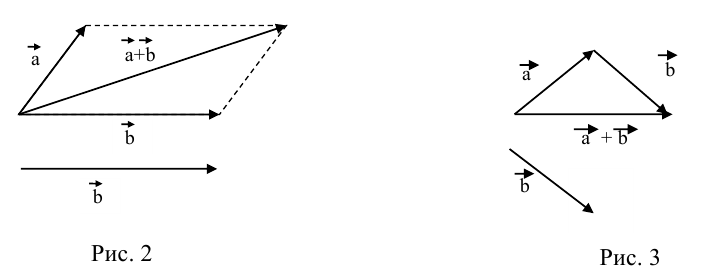
Сложение векторов.
ЗАДАЧА:
Пешеходу, стоящему на
перекрёстке двух улиц, надо перейти с угла, обозначенного М1, на угол М2.

Он мог бы направиться
непосредственно к этому углу по прямой М1М2.
Тогда мы сказали бы, что перемещение пешехода равно

Но на улицах с оживлённым
движением такой переход запрещён. Поэтому дисциплинированный пешеход перейдёт
сначала из точки М1 в точку А,
а затем из точки А в точку
М2.
Конечный результат будет таким же, как если бы он прошёл по прямой М1М2.
Перемещение

достигнуто в результате двух
перемещений:

Эти перемещения заменили одно.
Естественно считать, что перемещени

еесть сумма двух перемещений

Приведённый пример показывает, что векторы складываются геометрически.
Чтобы сложить два вектора, нужно их расположить так,
чтобы конец первого вектора примыкал к началу второго.
Вектор, соединяющий начало
первого вектора с концом второго, есть сумма обоих векторов.
Правило параллелограмма.
Если нужно сложить два вектора

их располагают так, чтобы они исходили из одной точки.

Затем, считая, что расположенные таким образом векторы образуют две стороны
параллелограмма, достраивают параллелограмм и проводят диагональ из точки, где
совмещены начала обоих векторов. Эта диагональ и есть сумма векторов или
результирующий вектор.
Другой способ сложения двух векторов состоит в том, что складываемые векторы

располагаются так, чтобы конец одного из них примыкал к началу другого.
Сумма обоих векторов – это вектор, направленный от начала первого вектора к
концу второго.

Этим же способом пользуются, если нужно сложить не два, а больше векторов.
Все складываемые векторы располагаются так, чтобы конец первого вектора
примыкал к началу второго, конец второго – к началу третьего и т. д. Сумма всех
векторов или результирующий вектор – это вектор, направленный от начала первого
вектора к концу последнего.

Чтобы сложить несколько векторов, надо расположить их
так, чтобы конец первого вектора примыкал к началу второго, конец второго – к
началу третьего и т. д.
Результирующим будет вектор, направленный от начала
первого вектора к концу последнего.
По этому же правилу складывают векторы, направленные вдоль одной прямой
(коллинеарные векторы). Сложение коллинеарных векторов, направленных в одну и
ту же сторону и в стороны, противоположные друг другу показано на рисунках:

Из этих рисунков видно, что параллельные (коллинеарные) векторы
складываются, как алгебраические величины, если приписать одному из направлений
знак <<+>> , а противоположному знак <<–>>.
Как найти проекцию вектора, являющегося суммой нескольких векторов ?
На
рисунке

проведены векторы

и показан результирующий вектор

равный сумме этих векторов:

Из этого рисунка видно, что проекции векторов

на ось Х положительны, а
проекция вектора

отрицательна. Видно также, что проекция результирующего вектора

получается, если сложить проекции всех трёх складываемых векторов
алгебраически, т. е. с учётом того, что знак проекции вектора

отрицательный.
Следовательно,
проекция суммы векторов на заданную ось
равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Поэтому, для того чтобы найти проекцию суммы векторов, нет необходимости
находить результирующий вектор и определить его проекцию. Надо просто сложить
проекции всех векторов, учитывая их знаки.
Задачей, обратной сложению вектора, является разложение вектора на
составляющие. Так, в частности, нахождение по данной скорости её составляющих
называется разложением скорости. Данная
скорость

раскладывается на составляющие самым различным образом, так как можно
построить сколько угодно параллелограммов с заданной диагональю, равной вектору


чтобы задача разложения данного вектора

на две составляющие была бы однозначной, нужно дополнительно знать
направления составляющих векторов

или величину и направление одного из них.

Вычитание векторов.
Чтобы найти вектор

равный разности двух векторов

нужно сложить векторы

Вектор

равен по модулю и направлен противоположно вектору

Чтобы найти разность двух векторов, нужно расположить их
так, чтобы они исходили из одной точки, и соединить концы обоих векторов
отрезком, направленным от второго вектора к первому (от вычитаемого к
уменьшаемому). Этот направленный
отрезок и есть вектор-разность.
По такому же правилу производят вычитание коллинеарных векторов

Если нам нужно найти проекцию разности двух векторов

то, так же как в случае сложения векторов, нет необходимости выполнять
геометрические построения. Нетрудно убедиться в том, что
проекция
разности векторов на ось равна алгебраической разности их проекций на эту ось.
Умножение вектора на скаляр.
ЗАДАЧА:
Два автомобиля, выехавшие из
гаража, к исходу дня оказались один в 100
км, а другой в 200
км к северу от места, где расположен
гараж. Что можно сказать о перемещении этих двух автомобилей ? Очевидно, что
одно из них вдвое больше другого. Если обозначить перемещение в 100
км через

то перемещение в 200
км будет равно

т. е. вектору

умноженному на 2. Вектор

имеет то же направление, что и
вектор

но его модуль вдвое больше.
Если бы второй автомобиль
отправился не на север, а на юг, то его перемещение было бы равно

т. е. вектору

умноженному на и –2. Вектор

вдвое больше (по абсолютной
величине) вектора

но направлен в противоположную
сторону.

Вектор

умноженный на скаляр k, представляет собой вектор, модуль которого равен
произведению модуля вектора на модуль скаляра:

Вектор

направлен так же, как вектор

если знак k положительный.
Если же знак k отрицательный, то
вектор

направлен в сторону, противоположную вектору

Проекция вектора

на ось равна умноженной на k проекции вектора

на эту ось:
bx = kax.
Итак, действия над векторами производят по правилам геометрии.
При умножении вектора на скалярную величину k изменяется его
модуль:
увеличивается при k ˃ 1 или уменьшается
при k < 1.
Если величина k положительна, то
направление вектора

совпадает с направлением вектора

Если же величина k отрицательна, то
вектор

направлен противоположно вектору

Действия же над проекциями векторов производят по обычным правилам алгебры.
Если известны проекции ax и ay вектора

на оси координат, то абсолютное значение самого вектора равно

(теорема Пифагора).
ЗАДАЧА:
Камень, который кинули из окна второго
этажа с высоты 4 м, упал на поверхность земли на расстоянии 3
м от стены здания. Найдите модуль перемещения
камня.
РЕШЕНИЕ:
Перемещение камня

Проверим единицы измерения:

Числовое значение:

ОТВЕТ: 5 м
Относительность движения.
Положение тела (точки) в пространстве всегда задаётся относительно какого-то
другого тела, выбранного телом отсчёта. Через какую-нибудь точку тела отсчёта
связана система координат.
Но за тело отсчёта мы можем принять любое тело и с каждым из них связать
свою систему координат. Тогда положение одного и того же тела мы можем
одновременно рассматривать в разных системах координат. Очевидно, что
относительно разных тел отсчёта в разных системах координат положение одного и
того же тела может быть совершенно различным.
ПРИМЕР:
Положение автомобиля на дороге
можно определить, указав, что он находится на расстоянии l1 км к северу от
населённого пункта А.

Пункт А служит в данном случае телом отсчёта, а
прямая, мысленно проведённая от него к северу, – координатной осью, связанной с
телом отсчёта. Но можно выбрать за тело отсчёта и какой-нибудь другой
населённый пункт, например В,
и сказать, что автомобиль расположен в l2 км к востоку от
него.
Это значит, что положение тела относительно:
оно
различно относительно разных тел отсчёта и связанных с ними разных систем
координат.
Но не только положение тела относительно.
Относительно
и его движение.
В чём состоит относительность движения ?
Часто бывает, что движение одного и того же тела приходится рассматривать
относительно разных тел отсчёта, которые сами
движутся друг относительно друга.
ПРИМЕР:
Артиллеристу важно знать, как
движется снаряд не только относительно Земли, на которой его орудие стоит
неподвижно, но и относительно танка, в который он стреляет и который сам
движется относительно Земли.
Пилот интересуется движением
самолёта и относительно Земли, и относительно воздуха, который в бурную погоду
сам движется.
Движение одного и того же тела относительно разных тел отсчёта, движущихся
одно относительно другого, могут сильно различаться. Различными могут быть и
траектории, и скорости движения этого тела.
Рассмотрим движения одного и того же тела относительно двух тел отсчёта,
движущихся друг относительно друга. Предположим, что одно тело отсчёта
неподвижно, а второе движется относительно первого. Примем для простоты, что оно
движется прямолинейно и равномерно. Выясним, как найти перемещение тела
относительно этих двух тел отсчёта (конечно, за одно и то же время).
ПРИМЕР:
Представим себе человека,
плывущего вниз по течению реки с некоторой скоростью, которую он поддерживает постоянной,
работая руками и ногами (если бы он не работал руками и ногами, он бы
просто лежал на воде и относительно воды находился в покое). Примем за неподвижное тело отсчёта берег,
а за подвижное – воду.
Как же движется пловец
относительно берега и относительно воды ? предположим, что за движением пловца
следит два наблюдателя: один – на берегу, а другой – на лодке, которая без
гребца плывёт по течению реки. Относительно воды лодка покоится, а относительно
берега она движется равномерно с такой же скоростью, как и сама вода.
Проведём мысленно через
точку О на берегу, в которой расположился
наблюдатель, оси координат X и Y,
причём ось Х направим вдоль течения реки.

С лодкой (с водой) мы тоже свяжем систему координат X‘O‘Y‘,
оси X‘ и Y‘ которой параллельны осям X и Y.
Лодка и вода движутся поступательно.
Найдём перемещение пловца
относительно этих двух систем координат (систем отсчёта).
Для наглядности посмотрим, как
движение пловца будет представляться наблюдателям в лодке и на берегу. Наблюдатель
в лодке через некоторое время отметит,
что пловец относительно него совершил перемещение

Разделив это перемещение на
время, он получит скорость пловца:


– это скорость пловца относительно
воды (лодки),
т. е. в подвижной системе
координат X‘O‘Y‘.
Наблюдатель на берегу отмети,
что за это же время t перемещение пловца равно

а сама лодка совершила
перемещение

относительно берега. Из рисунка
видно, что перемещение

пловца относительно берега, т.
е. в системе координат, XOY, равно сумме обоих перемещений:

Разделив

на t,
наблюдатель на берегу получит скорость

пловца относительно берега:

Первое слагаемое

– это скорость пловца
относительно подвижной системы координат (воды или лодки). Слагаемое же

– это, очевидно, скорость лодки
(воды) относительно
неподвижной системы координат (берега). Обозначим её через

Значит,

– это скорость подвижной
системы координат относительно покоящейся.
Следовательно

Эта формула называется формулой
сложения скоростей.
Точно такую же формулу сложения скоростей мы получили бы и в том случае,
если бы пловец плыл против течения.

Скорость движения тела относительно неподвижной системы
координат равна геометрической сумме двух скоростей: скорости тела
относительно подвижной системы координат и скорости самой подвижной системы относительно
неподвижной.
Скорости тела относительно различных систем отсчёта, движущихся друг
относительно друга, различны. В этом и проявляется относительность движения.
В рассмотренном примере движущееся тело (пловец) и подвижная система координат
(лодка или вода) движутся вдоль одной прямой – вдоль оси Х.
Поэтому вместо векторов

мы можем воспользоваться их проекциями на ось Х.
Тогда формула сложения скоростей будет иметь вид:
v = v1 + v2.
Величины v, v1 и v2 в этой формуле
могут быть как положительными, так и отрицательными в зависимости от
направлений векторов

по отношению оси Х.
Может случиться и так, что тело, которое движется в одной системе
координат, находится в покое относительно другой. Если бы тот же пловец
перестал работать руками и ногами и просто лежал бы на воде, то относительно
лодки он находился бы в покое, а относительно берега он двигался бы со
скоростью течения. Наоборот, если бы пловец плыл со скоростью течения, но в противоположном
направлении, то в покое он находился ба относительно берега, а относительно
воды он двигался бы со скоростью – v1. Следовательно, относительно не только движение, но и
покой. Если тело относительно какой-то системы координат покоится, то всегда
можно найти такие системы координат, относительно которых оно движется. Это
значит, что абсолютно покоящихся тел не существует. Движение свойственно всем
телам и вообще всему, что существует в природе, т. е. всему материальному миру.
Не всегда скорости движущегося тела и подвижной системы координат
направлены вдоль одной прямой, как в примере с пловцом в предыдущем примере.
ПРИМЕР:
Предположим, что пловцу понадобилось
переплыть реку с одного берега на другой, так что двигаться он должен всё время
перпендикулярно течению, т. е. перпендикулярно оси Х.

По-прежнему будем считать
движение пловца равномерным.
Каким будет это движение для
наблюдателя в лодке (относительно подвижной системы
координат X‘O‘Y‘) и каким оно будет
для наблюдателя на берегу (в
покоящейся системе координат XOY) ?
Наблюдатель в лодке видит, что
пловец всё время удаляется от него, двигаясь вдоль оси Y‘.
Он видит это, находясь и в точке А,
и в точке В,
и в любой другой точке. Через промежуток времени t, когда лодка будет находиться в точке С,
пловец окажется на противоположном берегу в точке C1,
совершив перемещение

Перемещение самого наблюдателя
вдоль оси Х равно

Разделив перемещение

На время t,
наблюдатель в лодке получит скорость

пловца относительно подвижной
системы координат X‘O‘Y‘:

Направлена она вдоль оси Y‘.
Совсем другим будет
представляться движение пловца, переплывающего реку, наблюдателю, находящемуся
на берегу. Для этого наблюдателя перемещаться будет и ось Y‘. B <<его>> системе координат перемещение пловца за то же
время t представится направленным отрезком

Пловца отнесло вниз по течению.
Из рисунка видно, что перемещение

равно геометрической сумме
перемещения

пловца относительно подвижной
системы координат X‘O‘Y‘ и перемещения

cамой системы координат X‘O‘Y‘ относительно неподвижной системы XOY.
Следовательно, и теперь так же, как и в примере, рассмотренном выше,

Скорость пловца

Относительно системы XOY найдём так:

т. е.

Видно, что правило сложения скоростей осталось таким же как и раньше, но
теперь алгебраически скорости складывать нельзя, так как векторы

не параллельны друг другу.
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами 
Длина отрезка, изображающего вектор называется его длиной и обозначается через
называется его длиной и обозначается через  Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение
Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение 
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
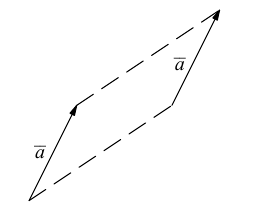
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора  называются коллинеарными (обозначение
называются коллинеарными (обозначение  ), если отрезки их изображающие параллельны.
), если отрезки их изображающие параллельны.
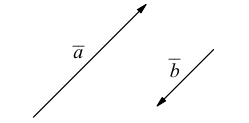
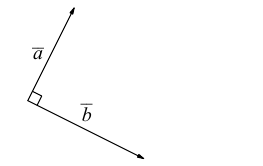
Аналогично, векторы а и b называются ортогональными (обозначение  ), если соответствующие отрезки перпендикулярны.
), если соответствующие отрезки перпендикулярны.
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
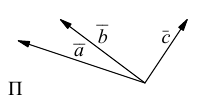
Углом между векторами  приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами
приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами 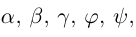 … или через
… или через 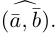
Два ненулевых вектора 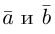 мы будем считать одинаково направленными, если
мы будем считать одинаково направленными, если 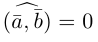 и противоположно направленными, если
и противоположно направленными, если 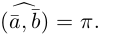
Введем теперь линейные операции над векторами.
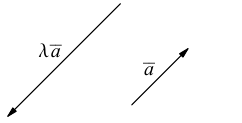
а) Умножение числа на вектор.
Произведением действительного числа 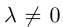 на вектор
на вектор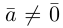 называется вектор
называется вектор 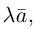 длина которого равна
длина которого равна 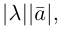 а направление его совпадает с направлением вектора
а направление его совпадает с направлением вектора 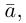 если
если 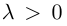 и имеет противоположное с ним направление, если
и имеет противоположное с ним направление, если 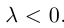 Если
Если 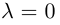 или
или 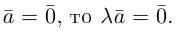
В частности, вектор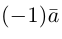 обозначается через
обозначается через 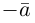 и называется вектором, противоположным вектору
и называется вектором, противоположным вектору 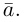
Если 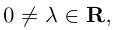 то произведение
то произведение 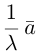 мы будем иногда записывать в виде
мы будем иногда записывать в виде 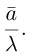
Из приведенного определения сразу же следует, что коллинеарные векторы 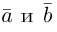 линейно связаны, т. е. существует константа
линейно связаны, т. е. существует константа 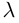 такая,что
такая,что 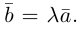 В качестве такой константы следует
В качестве такой константы следует
взять число 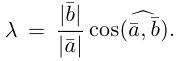 Если
Если 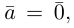 то
то 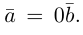 В частности, если
В частности, если 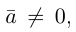 то вектором единичной длины с направлением данного вектора является вектор
то вектором единичной длины с направлением данного вектора является вектор 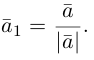
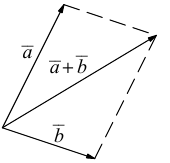
b) Сложение векторов.
Суммой двух векторов  называется вектор
называется вектор  который находится по правилу треугольника
который находится по правилу треугольника
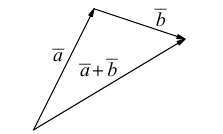
или по равносильному ему правилу параллелограмма
Вектор 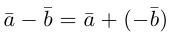 называется разностью векторов
называется разностью векторов 
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора  на вектор
на вектор  называется число
называется число
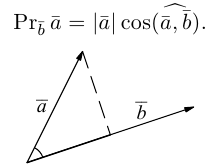
Геометрически очевидны следующие свойства проекции:
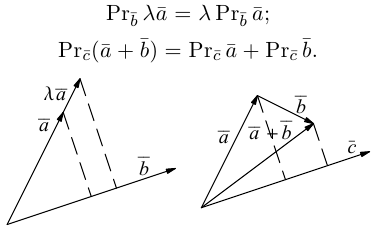
Пример №1
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
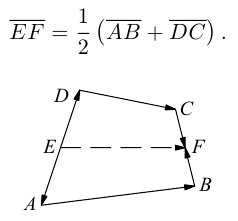
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
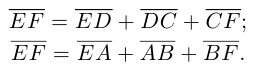
Сложив данные равенства и учитывая, что 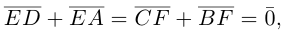 будем иметь:
будем иметь:
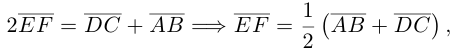
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 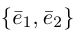 — базис на плоскости,
— базис на плоскости, 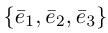 — базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора
— базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора 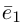 к вектору
к вектору 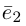 совершается против часовой стрелки, если наблюдение ведется со стороны вектора
совершается против часовой стрелки, если наблюдение ведется со стороны вектора Сформулируем теперь фундаментальное свойство базиса.
Сформулируем теперь фундаментальное свойство базиса.
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 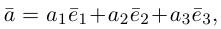 где действительные числа
где действительные числа 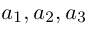 – координаты вектора
– координаты вектора 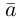 в базисе
в базисе
Приведем геометрическое доказательство этого утверждения.
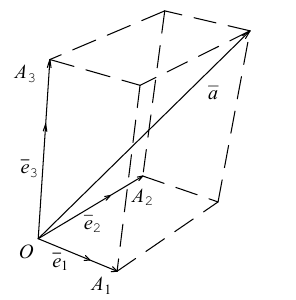
Вектор можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов
можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов 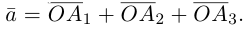 В виду коллинеарности векторов
В виду коллинеарности векторов 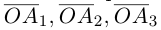 соответствующим базисным векторам, мы можем записать, что
соответствующим базисным векторам, мы можем записать, что 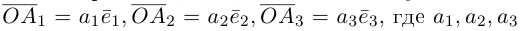 — некоторые действительные числа. Отсюда и следует искомое разложение.
— некоторые действительные числа. Отсюда и следует искомое разложение.
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 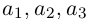 коротко записывается как
коротко записывается как 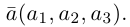
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 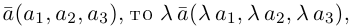 если
если 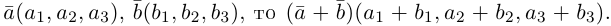 Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
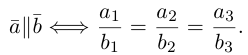
Рассмотрим теперь ортонормированный базис 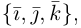 т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе
т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе 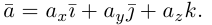
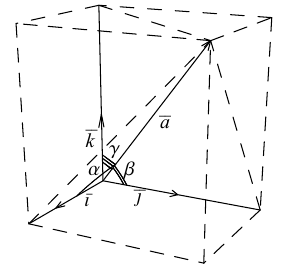
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
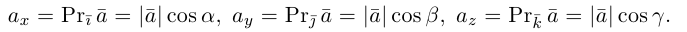
Величины 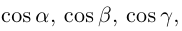 т. е. косинусы углов, которые образует данный вектор с ортами
т. е. косинусы углов, которые образует данный вектор с ортами 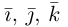 к соответственно, называются направляющими косинусами вектора
к соответственно, называются направляющими косинусами вектора 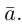 Единичный вектор
Единичный вектор 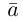 имеет координаты
имеет координаты 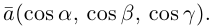
Очевидно также, что
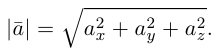
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 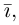 ось
ось 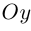 (ординат) — вдоль орта
(ординат) — вдоль орта 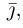 наконец, ось
наконец, ось  (аппликат) направим вдоль орта
(аппликат) направим вдоль орта

В выбранной системе координат координаты радиуса-вектора 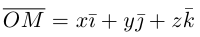 мы будем называть координатами точки М и записывать
мы будем называть координатами точки М и записывать 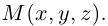
Если известны координаты начальной 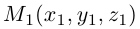 и конечной
и конечной 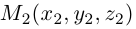 точек вектора, то из равенства
точек вектора, то из равенства 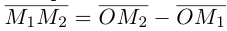 слезет, что его координаты равны
слезет, что его координаты равны
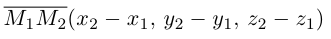 и, значит, расстояние между точками
и, значит, расстояние между точками 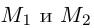 вычисляется по формуле
вычисляется по формуле
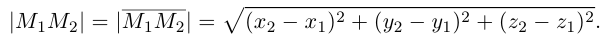
Найдем теперь координаты точки М, делящей отрезок с концами в точках 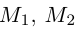 в данном
в данном
отношении 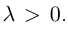 Так как
Так как 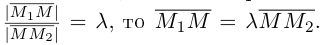 Отсюда, переходя к координатам получим:
Отсюда, переходя к координатам получим:
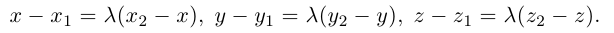
Следовательно, координаты искомой точки вычисляются по формулам:
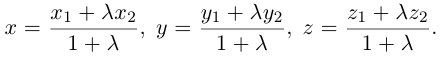
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
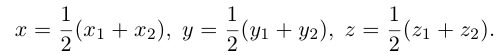
Пример №2
Треугольник задан координатами своих вершин 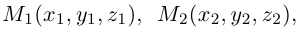
 Найти координаты точки пересечения его медиан. Решение.
Найти координаты точки пересечения его медиан. Решение.
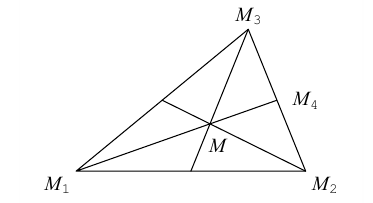
Пусть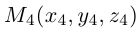 – середина отрезка
– середина отрезка 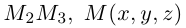 – точка пересечения медиан. Тогда
– точка пересечения медиан. Тогда
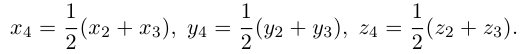
По известному свойству точки пересечения медиан 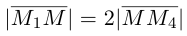 и потому
и потому
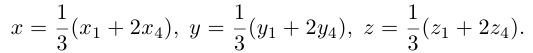
Подставив сюда найденные координаты точки 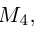 ползучим:
ползучим:
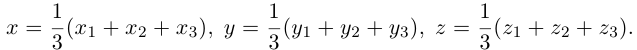
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 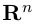 называется упорядоченная совокупность n векторов
называется упорядоченная совокупность n векторов

обладающая тем свойством, что любой вектор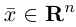 единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа
единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа 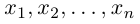 (координаты вектора
(координаты вектора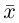 в базисе (1)) такие, что
в базисе (1)) такие, что

В качестве базиса в 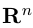 мы можем взять, например, векторы
мы можем взять, например, векторы
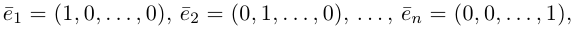
так как, очевидно, любой вектор 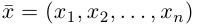 однозначно представляется в виде (2).
однозначно представляется в виде (2).
Скалярное произведение векторов
Определение: Скалярным произведением векторов 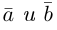 называется число
называется число
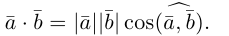
Из этого определения сразу же следует, что
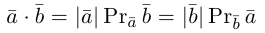
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
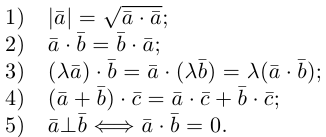
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 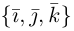 векторы
векторы 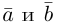 имеют координаты
имеют координаты 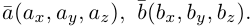 Заметив, что по свойствам 1) и 5) скалярного произведения
Заметив, что по свойствам 1) и 5) скалярного произведения
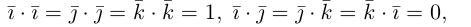
перемножим векторы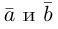 скалярно, используя свойства 2) – 4):
скалярно, используя свойства 2) – 4):
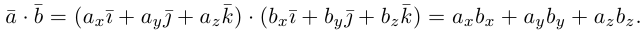
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 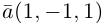 на две ортогональные составляющие, одна из которых коллинеарна вектору
на две ортогональные составляющие, одна из которых коллинеарна вектору 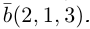
Решение.
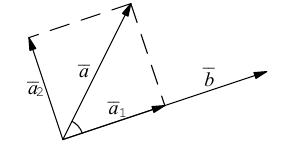
Из чертежа следует, что 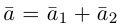 – искомое разложение. Найдем векторы
– искомое разложение. Найдем векторы 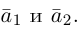 Составляющая
Составляющая 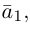 коллинеарная вектору
коллинеарная вектору 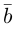 равна, очевидно, вектору проекции
равна, очевидно, вектору проекции  и, следовательно,
и, следовательно,
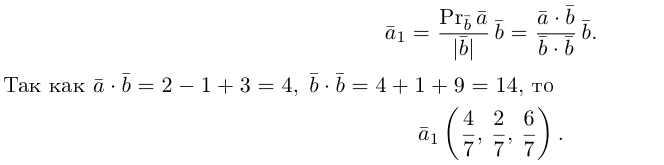
Тогда вторая ортогональная составляющая вектора 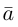 равна
равна
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы  материальная тотп<а переместилась по прямой из положения В в положение С.
материальная тотп<а переместилась по прямой из положения В в положение С.
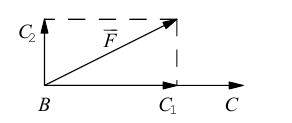
Найдем работу этой силы. Для этого разложим вектор силы 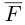 на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения
на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения 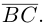 Тогда
Тогда
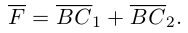
Составляющая 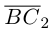 работы не совершает, следовательно, работа силы
работы не совершает, следовательно, работа силы 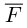 равна работе составляющей
равна работе составляющей 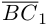 и, таким образом,
и, таким образом,
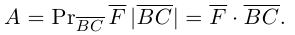
Окончательно, работа силы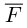 , под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
, под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
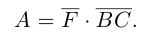
Замечание. Скалярным произведением векторов 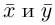 n-мерного пространства
n-мерного пространства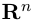 называется число
называется число 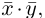 равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
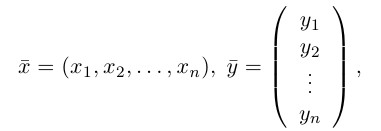
то
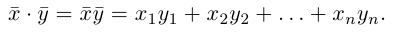
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в  обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
Длиной вектора 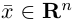 называется число
называется число
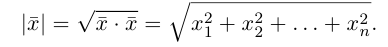
Векторы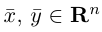 называются ортогональными, если
называются ортогональными, если 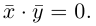 Векторы
Векторы
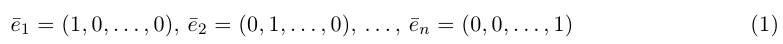
составляют ортонормированный базис пространства 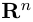 , так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
, так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
Любой вектор  мы можем рассматривать как точку
мы можем рассматривать как точку
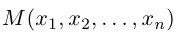
n-мерного пространства с координатами 
Взяв еще одну точку 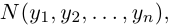 соответствующую вектору
соответствующую вектору 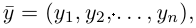 мы под расстоянием между точками М и N будем понимать длину вектора
мы под расстоянием между точками М и N будем понимать длину вектора 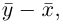 т. е. число
т. е. число
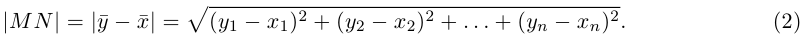
Таким образом переопределенное пространство 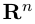 с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов 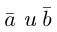 называется вектор
называется вектор  такой, что
такой, что
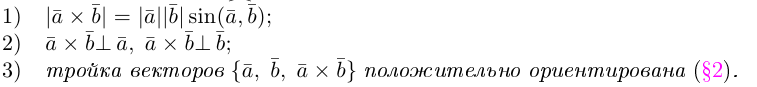
Из этого определения следует, что площадь параллелограмма, построенного на векторах 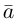 и
и 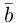 равна длине векторного произведения
равна длине векторного произведения  , т. е.
, т. е.
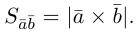
Сформулируем основные свойства векторного произведения.
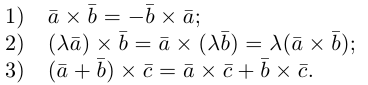
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы  и
и 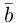 в ортонормированном базисе
в ортонормированном базисе 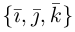 имеют координаты
имеют координаты 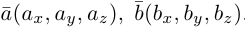 Учитывая, tito по определению векторного произведения
Учитывая, tito по определению векторного произведения
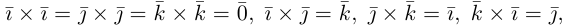
раскроем скобки в векторном произведении 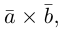 принимая во внимание свойства 1) – 3):
принимая во внимание свойства 1) – 3): 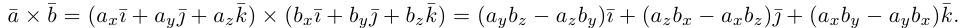
Полученный вектор мы можем записать в виде следующего символического определителя.
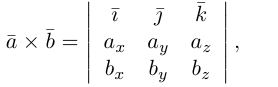
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 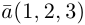 , ортогональную плоскости векторов
, ортогональную плоскости векторов  .
.
Решение.
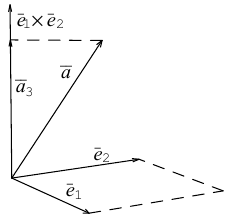
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора  на векторное произведение
на векторное произведение и, следовательно.
и, следовательно.
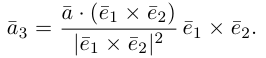
Переходим к вычислениям:
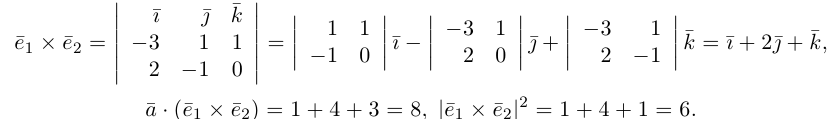
Тогда 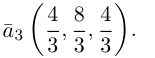
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
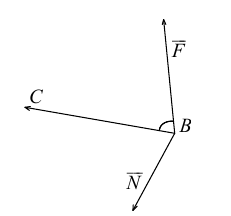
Итак, пусть сила  приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
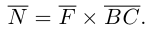
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 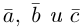 называется число
называется число
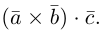
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
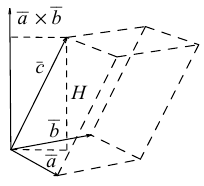
По определению смешанного произведения
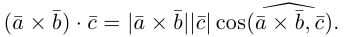
Поскольку 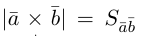 – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах 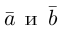 (§4)
(§4)
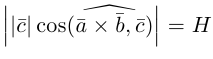 -высота параллелепипеда построенного на векторах
-высота параллелепипеда построенного на векторах 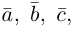 то
то
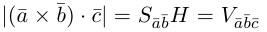
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 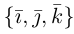 , т.е.
, т.е. 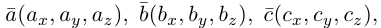 то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
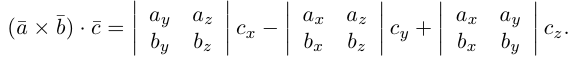
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
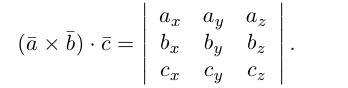
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
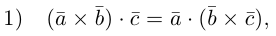
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение  . которым мы и будем пользоваться в дальнейшем.
. которым мы и будем пользоваться в дальнейшем.
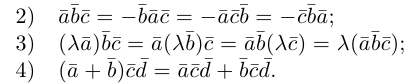
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 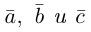 компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 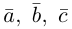 компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение
компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение 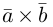 ортогонально вектору с и, следовательно,
ортогонально вектору с и, следовательно, 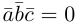 . Аналогично проверяется достаточность условия теоремы.
. Аналогично проверяется достаточность условия теоремы.
Следствие. Три вектора 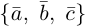 образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
Заметим, кроме того, что, если 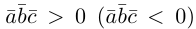 , то угол между векторами
, то угол между векторами 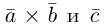 -острый (тупой) и, следовательно, базис
-острый (тупой) и, следовательно, базис 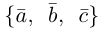 является положительно (отрицательно) ориентированным.
является положительно (отрицательно) ориентированным.
Пример №5
Доказать, что пять точек
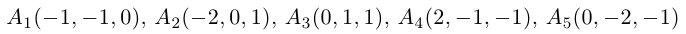
расположены в одной плоскости.
Решение. Рассмотрим векторы 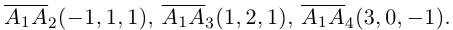 Так как
Так как
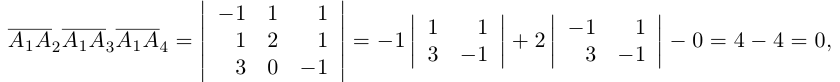
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 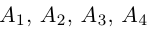 находятся в одной плоскости
находятся в одной плоскости  Аналогично покажем, что и точки
Аналогично покажем, что и точки 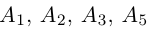 также принадлежат одной плоскости
также принадлежат одной плоскости  . Действительно,
. Действительно, 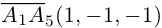
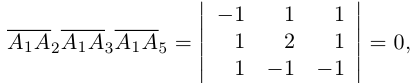
так как первая и третья строки в определителе пропорциональны. Плоскости  имеют три общие точки
имеют три общие точки  , следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
, следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
Векторы и линейные операции над ними
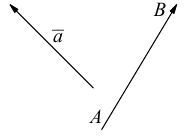
Определение: Вектором называется направленный отрезок (рис. 1).
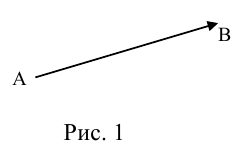 А – начало, В – конец вектора
А – начало, В – конец вектора 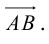
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 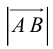 – расстояние между его началом и концом.
– расстояние между его началом и концом.
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
 – нулевой вектор: его направление не определено, а длина
– нулевой вектор: его направление не определено, а длина 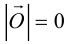 .
.
Определение: Векторы 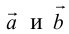 называются коллинеарными, если они лежат на параллельных прямых:
называются коллинеарными, если они лежат на параллельных прямых: 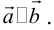
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 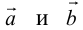 совмещаются в одной точке, и
совмещаются в одной точке, и 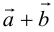 – диагональ параллелограмма, построенного на
– диагональ параллелограмма, построенного на 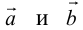 .
.
б) Правило треугольника (рис. 3): начало 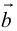 совмещается с концом
совмещается с концом 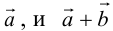 направлен от начала
направлен от начала  к концу
к концу  .
.
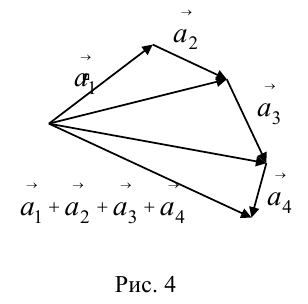
в) Правило сложения нескольких векторов (рис. 4).
Вектор 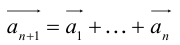 замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и
замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и  направлен от начала
направлен от начала  к концу
к концу .
.
Умножение на число
Определение: Произведением вектора 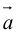 на число
на число 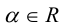 называется вектор
называется вектор 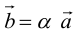 , aудовлетворяющий условиям:
, aудовлетворяющий условиям:
а) 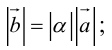
б) 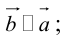
в)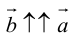 , если
, если 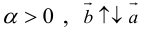 ,a если
,a если 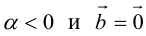 , если
, если 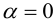 .
.
Произведение 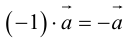 называется вектором, противоположным вектору
называется вектором, противоположным вектору . Очевидно,
. Очевидно, 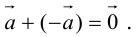 .
.
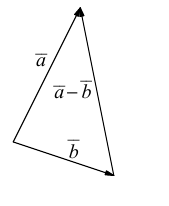
Определение: Разностью 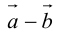 называется сумма вектора
называется сумма вектора 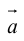 и вектора, противоположного
и вектора, противоположного 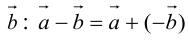 (рис. 5).
(рис. 5).

Начала 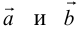 совмещаются в одной точке, и
совмещаются в одной точке, и 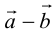 направлен от конца
направлен от конца 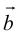 к концу
к концу 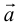 .
.
Свойства линейных операций
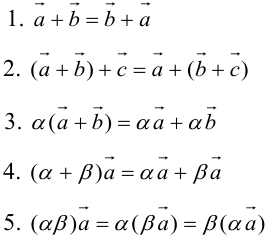
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: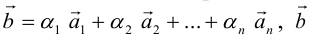 – линейная комбинация векторов
– линейная комбинация векторов 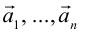 с коэффициентами
с коэффициентами 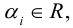
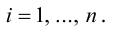
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить  как линейную комбинацию
как линейную комбинацию
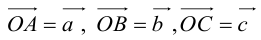 (рис. 6).
(рис. 6).
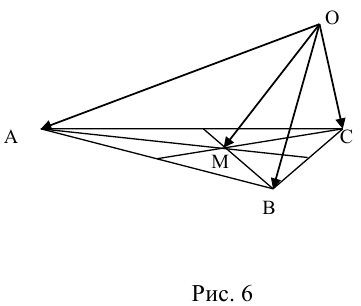
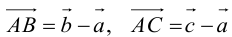 . Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что
. Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что 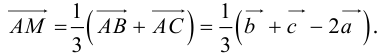
По правилу треугольника 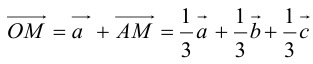 , то есть
, то есть 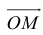 – линейная комбинация
– линейная комбинация 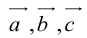 с коэффициентами
с коэффициентами 
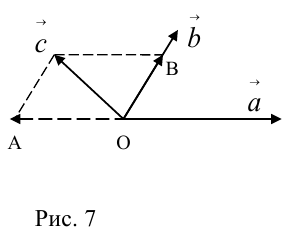
Теорема: Пусть 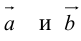 – неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
– неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
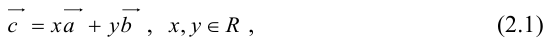
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 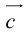 в виде (2.1) называется разложением его по двум неколлинеарным векторам.
в виде (2.1) называется разложением его по двум неколлинеарным векторам.
Доказательство:
- Пусть среди
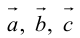 есть два коллинеарных, например:
есть два коллинеарных, например: 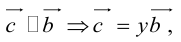
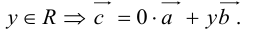
- Пусть среди
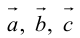 коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с 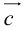 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 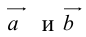 (рис. 7).
(рис. 7).
Тогда c 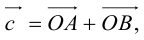 но
но 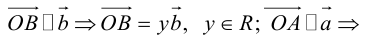
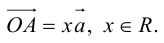 Поэтому
Поэтому 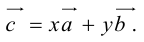
Докажем единственность разложения. Предположим, что 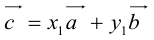 и
и 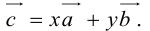 Тогда, вычитая одно равенство из другого, получим:
Тогда, вычитая одно равенство из другого, получим: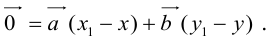
Если 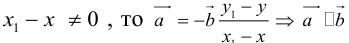 , что противоречит условию. Теорема доказана.
, что противоречит условию. Теорема доказана.
Теорема: Пусть  – некомпланарные векторы. Тогда любой вектор
– некомпланарные векторы. Тогда любой вектор 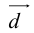 может быть представлен в виде
может быть представлен в виде
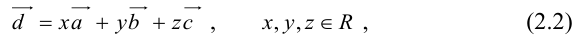
причем единственным образом.
Представление вектора 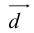 в виде (2.2) называется разложением его по трем некомпланарным.
в виде (2.2) называется разложением его по трем некомпланарным.
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси  называется единичный вектор
называется единичный вектор 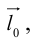
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось  называется основание
называется основание  перпендикуляра, опущенного из М на
перпендикуляра, опущенного из М на  .
.
Определение: Ортогональной проекцией вектора 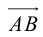 на ось
на ось 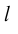 называется длина отрезка
называется длина отрезка  этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора
этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора 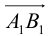 совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
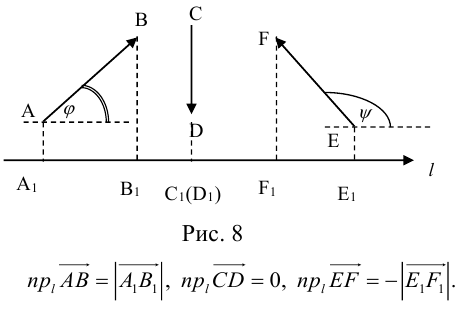
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
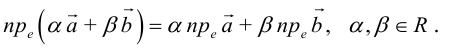
В частности, проекция суммы векторов равна сумме их проекций:
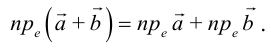
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим  – орт оси ОХ,
– орт оси ОХ,  – орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).
– орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).

Аналогично в пространственной системе OXYZ  – орты координатных осей) (рис. 10):
– орты координатных осей) (рис. 10):
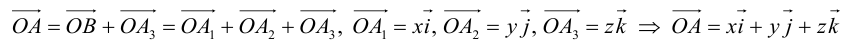
– разложение  по ортам координатных осей (единственно по теореме 2).
по ортам координатных осей (единственно по теореме 2).
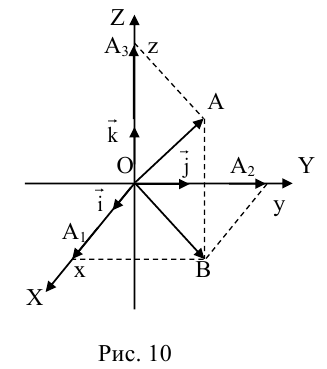
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 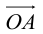 можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
Определение: Координатами вектора 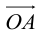 в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 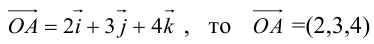 и наоборот, если
и наоборот, если
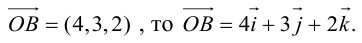
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
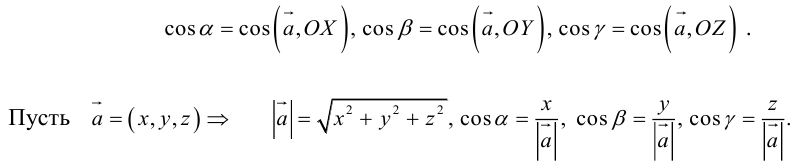
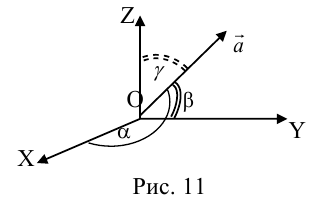
Из этих формул очевидно следует основное свойство направляющих косинусов:
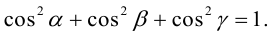
Если известны длина 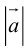 и направляющие косинусы вектора, то его координаты вычисляются по формулам:
и направляющие косинусы вектора, то его координаты вычисляются по формулам:
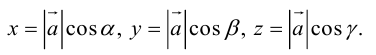
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
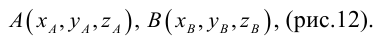
Тогда
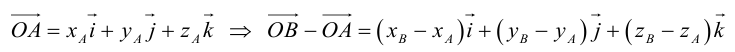 (см. свойства линейных операций над векторами). Таким образом,
(см. свойства линейных операций над векторами). Таким образом,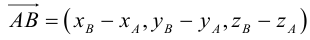 , то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
, то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если  – базис, то
– базис, то 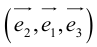 – другой базис, так как изменился порядок следования векторов.
– другой базис, так как изменился порядок следования векторов.
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать 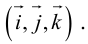
Из теоремы 2 следует, что всякий вектор 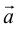 может быть разложен по базису
может быть разложен по базису 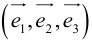 , то есть представлен в виде:
, то есть представлен в виде: 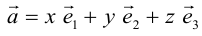 . Числа x,y,z называются координатами
. Числа x,y,z называются координатами 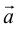 в базисе
в базисе 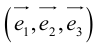 .
.
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если  – базис, то представление вектора в виде
– базис, то представление вектора в виде 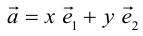 называется разложением
называется разложением 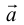 по базису
по базису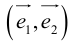 и x, y – координаты
и x, y – координаты 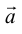 в этом базисе.
в этом базисе.
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 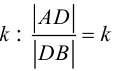 (рис. 14).
(рис. 14).
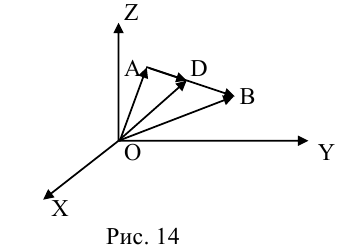
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
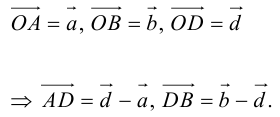
Так как 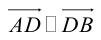 (лежат на одной прямой) и
(лежат на одной прямой) и 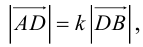 то
то
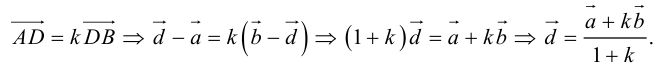
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
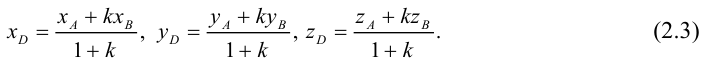
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
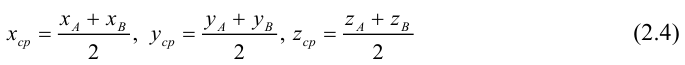
ЗАМЕЧАНИЕ 2. Если k < 0, 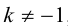 , то точка D лежит за пределами AB : так как
, то точка D лежит за пределами AB : так как 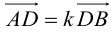 , то при
, то при 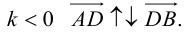
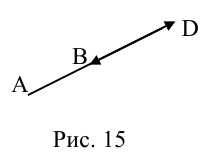
В этом случае 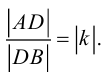
Скалярное произведение векторов
Определение: Скалярным произведением векторов 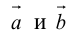 называется скаляр (число), равный
называется скаляр (число), равный 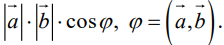
Скалярное произведение обозначается так: 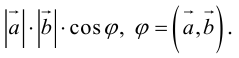 или
или 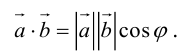
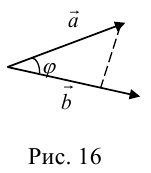
Так как 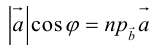 (рис. 16) или
(рис. 16) или 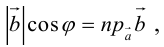 то
то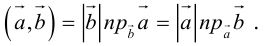
Свойства скалярного произведения
1.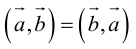 – очевидно из определения.
– очевидно из определения.
2.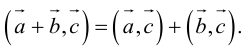
Доказательство:
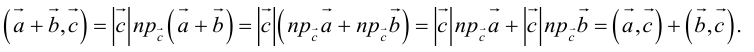
3.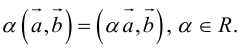
Доказательство:
а) 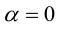 – очевидно.
– очевидно.
б) 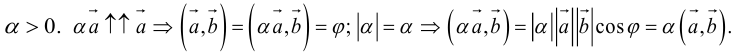
в) 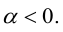 В этом случае
В этом случае
4.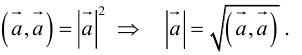
Отсюда следует, что 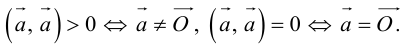
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.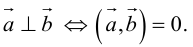
Доказательство:
а) пусть 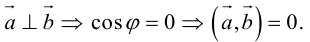
б) пусть 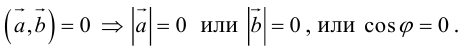
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 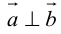 . В третьем случае
. В третьем случае 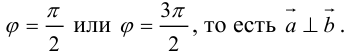
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов 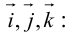
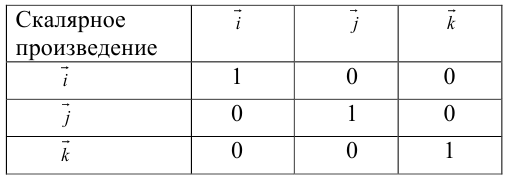
Пусть в некоторой пдск 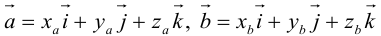 . Найдем скалярное произведение этих векторов:
. Найдем скалярное произведение этих векторов:
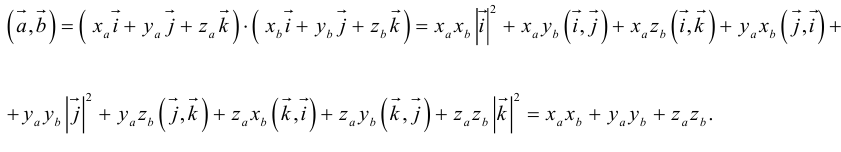
Таким образом, 
Пример №8
Найти, при каком значении x векторы 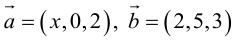 перпендикулярны.
перпендикулярны.
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5): 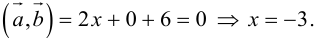
Пример №9
Найти угол между биссектрисой AD и медианой  если
если 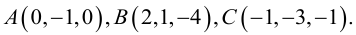
Так как 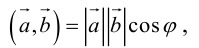
то 
Найдем координаты векторов 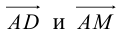 . Точка M – середина BC , поэтому по формулам (2.4)
. Точка M – середина BC , поэтому по формулам (2.4)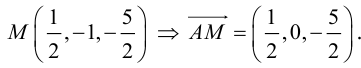
По теореме о биссектрисе внутреннего угла треугольника 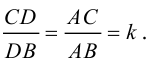
Чтобы найти k , вычислим длины AC и AB :
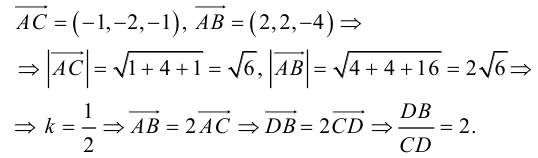
Разделим отрезок CB в данном отношении по формулам (2.3):
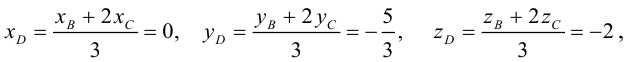
отсюда 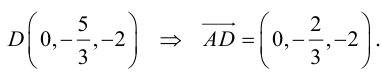
Заметим, что 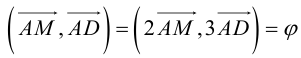 . Это замечание позволит нам не иметь дело с дробями, так как
. Это замечание позволит нам не иметь дело с дробями, так как
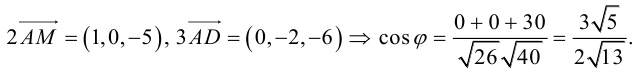
Пример №10
Найти 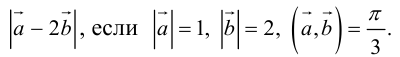
Воспользуемся свойствами 1–4 скалярного произведения:
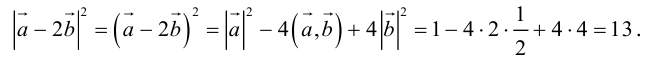
Отсюда 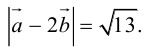
ЗАМЕЧАНИЕ. Так как работа силы 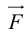 по перемещению материальной точки вдоль вектора
по перемещению материальной точки вдоль вектора 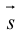 вычисляется по формуле
вычисляется по формуле 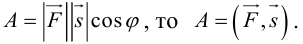
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 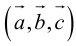 , имеющих общее начало, называется правой (левой), если
, имеющих общее начало, называется правой (левой), если 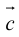 конца третьего вектора c вращение первого вектора
конца третьего вектора c вращение первого вектора 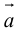 ко второму вектору
ко второму вектору 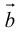 по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
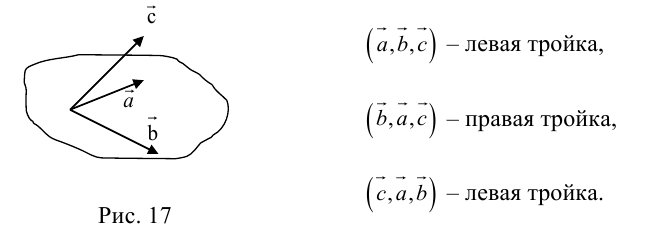
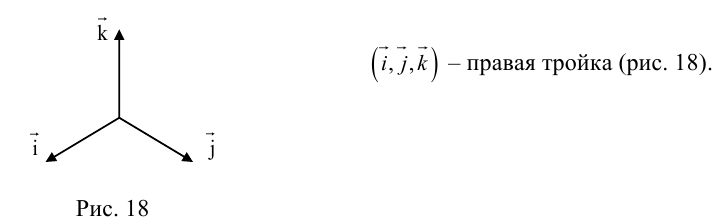
Определение: Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор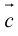 , удовлетворяющий условиям:
, удовлетворяющий условиям:
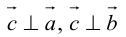 (
(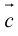 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 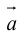 и
и 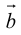 ).
). - Направление
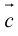 таково, что тройка
таково, что тройка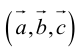 – правая.
– правая. 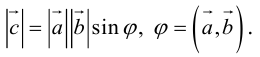
Векторное произведение обозначается так: 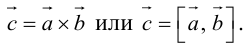
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
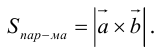
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
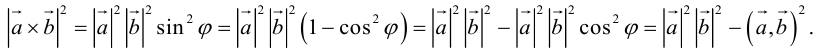
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
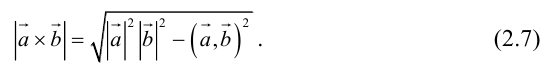
Пример №11
Найти площадь параллелограмма, построенного на векторах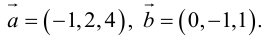
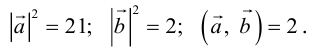
По формуле (2.7): 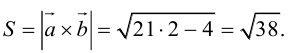
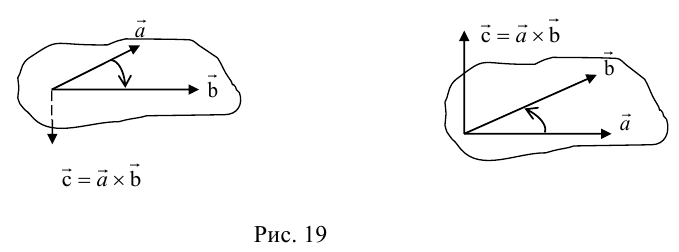
ЗАМЕЧАНИЕ 2. Направление вектора  можно также (кроме п.2) определить по правилу винта: направление вектора
можно также (кроме п.2) определить по правилу винта: направление вектора  совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора
совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора  ко второму вектору
ко второму вектору  по кратчайшему пути (рис. 19).
по кратчайшему пути (рис. 19).
Свойства векторного произведения
1.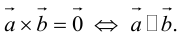
Доказательство:
а)пусть 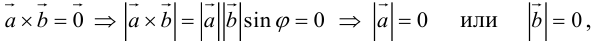 или
или 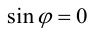 . В первом и втором случаях один из сомножителей – нулевой вектор.
. В первом и втором случаях один из сомножителей – нулевой вектор.
Его направление не определено, поэтому можно считать, что 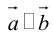 . Если
. Если 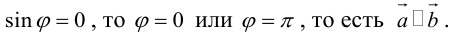
б)пусть 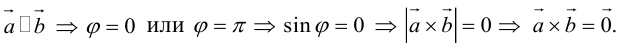
2. 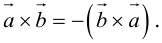
Доказательство: По определению направления векторов 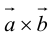 и
и 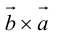 противоположны, а модули равны, значит, векторы отличаются лишь знаком.
противоположны, а модули равны, значит, векторы отличаются лишь знаком.
3.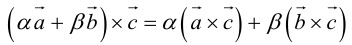 – свойство линейности векторного произведения по первому сомножителю (без доказательства).
– свойство линейности векторного произведения по первому сомножителю (без доказательства).
Векторное произведение также линейно и по второму сомножителю.
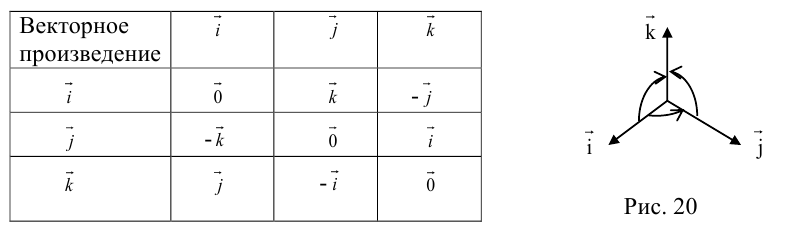
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов  : векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
: векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
Пусть в некоторой пдск 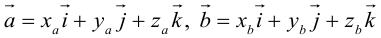 . Найдем векторное произведение этих векторов:
. Найдем векторное произведение этих векторов:
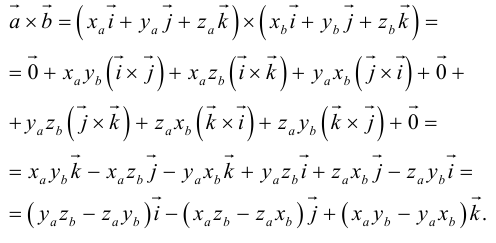
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
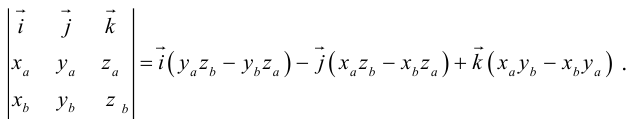
Таким образом,
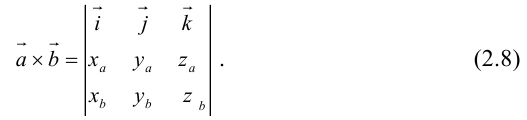
Пример №12
Вычислить векторное произведение векторов 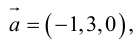
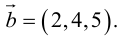
По формуле (2.8): 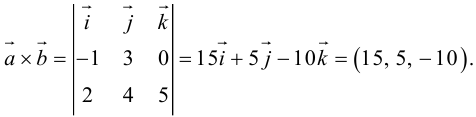
Заметим, что площадь треугольника, построенного на векторах 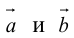 , можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что
, можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что 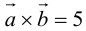
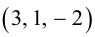
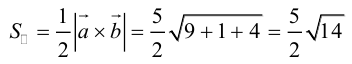
или
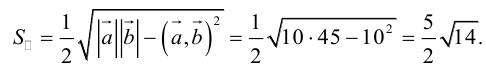
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 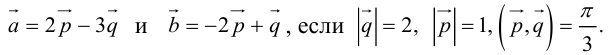
Так как 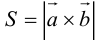 , то вычислим векторное произведение, используя его свойства:
, то вычислим векторное произведение, используя его свойства: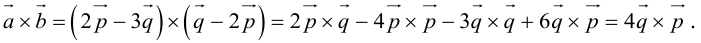
Отсюда 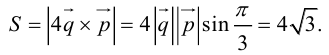
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 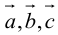 называется число
называется число 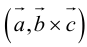 – скалярное произведение a на векторное произведение
– скалярное произведение a на векторное произведение 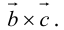
Смешанное произведение обозначается так: 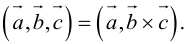
Пусть в некоторой пдск 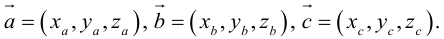
Обозначим
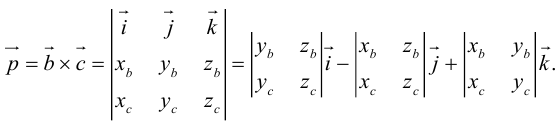
Тогда
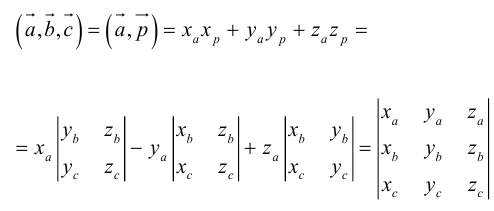
по 7 свойству определителей.
Таким образом,
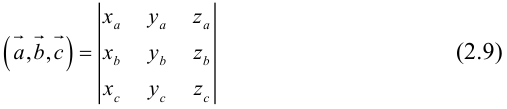
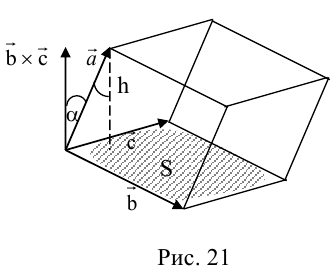
По определению скалярного произведения 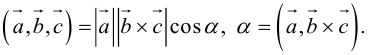
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
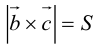 – площадь параллелограмма,
– площадь параллелограмма,
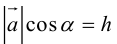 – высота параллелепипеда,
– высота параллелепипеда,
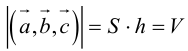 – объем параллелепипеда.
– объем параллелепипеда.
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом  – правая тройка, и
– правая тройка, и  – левая тройка.
– левая тройка.
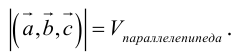
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 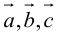 компланарны
компланарны
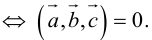
Доказательство: а) 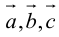 компланарны
компланарны 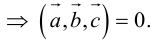
Если 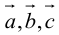 компланарны, то на них нельзя построить параллелепипед, а потому
компланарны, то на них нельзя построить параллелепипед, а потому 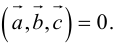
б)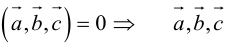 компланарны.
компланарны.
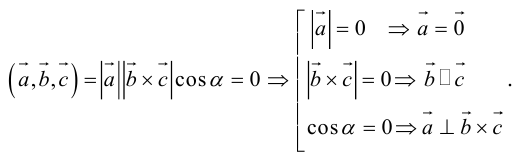
Во всех трех случаях 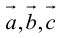 компланарны: в частности, если
компланарны: в частности, если 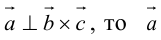 параллелен плоскости векторов
параллелен плоскости векторов 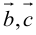 , что означает их компланарность.
, что означает их компланарность.
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
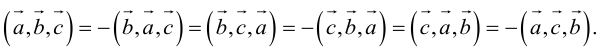
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами: 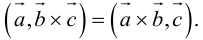
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим: 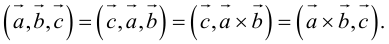
4. Смешанное произведение линейно по каждому из трех сомножителей.
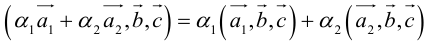 – линейность по первому сомножителю.
– линейность по первому сомножителю.
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
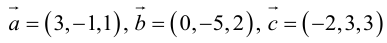 , и его высоту, перпендикулярную плоскости векторов
, и его высоту, перпендикулярную плоскости векторов 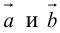 .
.
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому 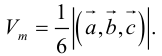
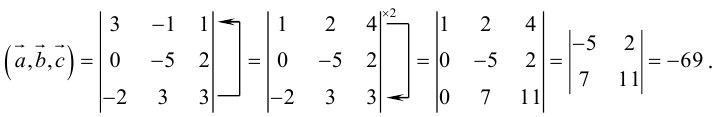
Отсюда 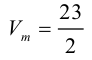 (заметим, что
(заметим, что 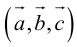 – левая тройка, так как смешанное произведение отрицательно).
– левая тройка, так как смешанное произведение отрицательно).
Чтобы найти высоту, воспользуемся формулой
По формуле (2.7) 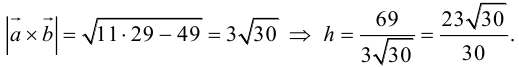
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
1.7.1. Как найти проекцию вектора на вектор?
Рассмотрим ненулевые векторы ![]() и
и ![]() :
:
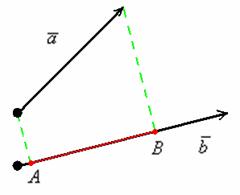
Спроецируем вектор ![]() на вектор
на вектор ![]() , для этого из начала и конца вектора
, для этого из начала и конца вектора ![]() опустим перпендикуляры на вектор
опустим перпендикуляры на вектор ![]() (зелёные пунктирные линии).
(зелёные пунктирные линии).
Представьте,
что на вектор ![]() перпендикулярно сверху падают
перпендикулярно сверху падают
лучи света. Тогда отрезок ![]() будет «тенью»
будет «тенью»
вектора ![]() . Проекцией вектора
. Проекцией вектора ![]() на вектор
на вектор ![]() является ДЛИНА отрезка
является ДЛИНА отрезка ![]() . То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Это ЧИСЛО обозначается следующим образом: ![]() , «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
, «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись ![]() читается так: «проекция
читается так: «проекция
вектора «а» на вектор «бэ»».
Если угол между векторами ![]() острый (как на рисунке выше), то
острый (как на рисунке выше), то ![]()
Если векторы ![]() ортогональны, то
ортогональны, то ![]() (проекцией является точка, размеры которой считаются нулевыми).
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами ![]() тупой (на рисунке мысленно переставьте стрелочку вектора
тупой (на рисунке мысленно переставьте стрелочку вектора ![]() ), то
), то ![]() (та же длина с добавленным знаком «минус»).
(та же длина с добавленным знаком «минус»).
Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую
вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую
вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на
прямую, содержащую вектор «бэ».
Из вышесказанного следует, что проекция вектора ![]() на любой ненулевой сонаправленный вектор
на любой ненулевой сонаправленный вектор
![]() будет точно такой же:
будет точно такой же:
![]() – фактически это проекция вектора
– фактически это проекция вектора
![]() на прямую
на прямую ![]() , которая содержит сонаправленные векторы
, которая содержит сонаправленные векторы ![]() (и поскольку векторы свободны, то таких прямых будет
(и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно ![]() , то
, то
добавится знак «минус»:
![]()
Отложим наши подопытные векторы от одной точки:
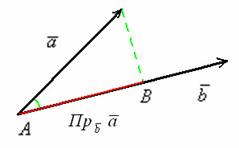
и рассмотрим прямоугольный треугольник. Косинус угла ![]() – есть отношение прилежащего катета к гипотенузе:
– есть отношение прилежащего катета к гипотенузе:
![]() , но с другой стороны, у нас уже получена
, но с другой стороны, у нас уже получена
формула косинуса угла между векторами:
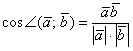
…все ли догадались, что будет дальше?
Приравниваем формулы:
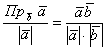
и сокращаем знаменатели обеих частей на ![]() ,
,
получая формулу для вычисления проекции:
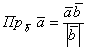
Распишем её в координатах:
Если векторы плоскости ![]() и
и ![]() заданы в ортонормированном базисе
заданы в ортонормированном базисе ![]() , то проекция вектора
, то проекция вектора ![]() на вектор
на вектор ![]() выражается формулой:
выражается формулой:
![]()
Если векторы пространства ![]() заданы в ортонормированном базисе
заданы в ортонормированном базисе ![]() , то проекция вектора
, то проекция вектора ![]() на вектор
на вектор ![]() выражается формулой:
выражается формулой:
![]()
Легко убедиться, что проекция вектора ![]() на
на
коллинеарный вектор ![]() может
может
отличаться лишь знАком, приведу выкладки для «плоского» случая ![]() :
:
![]()
![]() , если
, если ![]() , и
, и ![]() , если
, если ![]()
Задача 34
Найти проекцию вектора ![]() на вектор
на вектор ![]()
Решение в одну строчку:
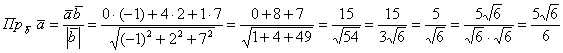 , на завершающем шаге я умножил числитель и
, на завершающем шаге я умножил числитель и
знаменатель на ![]() , избавившись тем самым от
, избавившись тем самым от
иррациональности в знаменателе.
Ответ: ![]()
Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это
будет своеобразно.
Задача 35
Треугольник задан своими вершинами ![]() .
.
Найти:
а) проекцию стороны ![]() на сторону
на сторону ![]() ;
;
б) проекцию стороны ![]() на сторону
на сторону ![]() .
.
Это задача для самостоятельного решения.
Итак, как найти проекцию вектора ![]() на отрезок с известными концами
на отрезок с известными концами ![]() ? (как вариант, на продолжение этого отрезка). Находим вектор
? (как вариант, на продолжение этого отрезка). Находим вектор ![]() и используем формулу
и используем формулу 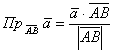 . Либо вектор
. Либо вектор ![]() и формулу
и формулу 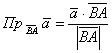 . В
. В
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант 🙂
О проекции же вектора на прямую поговорим в следующей главе, а пока
выясним геометрический смысл координат векторов в ортонормированном базисе:
 1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
 1.6.9. Как найти угол между векторами в координатах?
1.6.9. Как найти угол между векторами в координатах?
| Оглавление |
Автор: Aлeксaндр Eмeлин
