Операции над векторами и их свойства: сложение и умножение
Прежде чем приступить к тематике статьи, напомним основные понятия.
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.
Геометрически сложение векторов выглядит так:
– для неколлинеарных векторов:
– для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
Сложение нескольких векторов
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Геометрически оно выглядит следующим образом:
Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и – b → .
Умножение вектора на число
Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
– если k > 1 , то это число приведет к растяжению вектора в k раз;
– если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
– если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
– если k = 1 , то вектор остается прежним;
– если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = – 1 3 .
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .
- Свойство коммутативности: a ⇀ + b → = b → + a → .
- Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
- Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
- Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
- Любой ненулевой вектор a → имеет противоположный вектор – a → и верным является равенство: a → + ( – a → ) = 0 → . Указанное свойство – очевидное.
- Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
- Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
- Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
Геометрически это свойство определяется подобием треугольников:
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Задача: упростить выражение a → – 2 · ( b → + 3 · a → )
Решение
– используя второе распределительное свойство, получим: a → – 2 · ( b → + 3 · a → ) = a → – 2 · b → – 2 · ( 3 · a → )
– задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → – 2 · b → – 2 · ( 3 · a → ) = a → – 2 · b → – ( 2 · 3 ) · a → = a → – 2 · b → – 6 · a →
– используя свойство коммутативности, меняем местами слагаемые: a → – 2 · b → – 6 · a → = a → – 6 · a → – 2 · b →
– затем по первому распределительному свойству получаем: a → – 6 · a → – 2 · b → = ( 1 – 6 ) · a → – 2 · b → = – 5 · a → – 2 · b → Краткая запись решения будет выглядеть так: a → – 2 · ( b → + 3 · a → ) = a → – 2 · b → – 2 · 3 · a → = 5 · a → – 2 · b →
Ответ: a → – 2 · ( b → + 3 · a → ) = – 5 · a → – 2 · b →
Векторы на ЕГЭ по математике. Действия над векторами
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения 
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор 
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора 
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
Сложение векторов
Для сложения векторов есть два способа.
1 . Правило параллелограмма. Чтобы сложить векторы 



Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 



По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов 

Вычитание векторов
Вектор 



Теперь понятно, что такое вычитание векторов. Разность векторов 



Умножение вектора на число
При умножении вектора 



Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 

Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
Примеры решения задач с векторами
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме – координаты вектора.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vektory-na-ege-po-matematike-v-zadache-v6-dejstviya-nad-vektorami/
http://www.webmath.ru/poleznoe/formules_4_14.php
[/spoiler]
Эта статья — о понятии вектора в геометрии. Об общем понятии вектора в математике см. Вектор (математика).
Вектор
Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом[1].
Вектор с началом в точке 




Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector, несущий). Итак, каждый направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства: скажем, вектор 






Интерпретация вектора как переноса позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число.
Основные понятия[править | править код]
Вектором называется направленный отрезок построенный по двум точкам, одна из которых считается началом, а другая концом.
Координаты вектора определяются как разность координат точек его конца и начала. Например, на координатной плоскости, если даны координаты начала и конца: 


Длиной вектора 



Роль нуля среди векторов играет нулевой вектор, у которого начало и конец совпадают 
Проекция вектора на направленную прямую
Для координатного представления векторов большое значение имеет понятие проекции вектора на ось (направленную прямую, см. рисунок). Проекцией называется длина отрезка, образованного проекциями точек начала и конца вектора на заданную прямую, причём проекции приписывается знак плюс, если направление проекции соответствует направлению оси, иначе — знак минус. Проекция равна длине исходного вектора, умноженной на косинус угла между исходным вектором и осью; проекция вектора на перпендикулярную ему ось равна нулю.
Применения[править | править код]
Векторы находят широкое применение в геометрии и в прикладных науках, где используются для представления величин, имеющих направление (силы, скорости и т. п.). Применение векторов упрощает ряд операций — например, определение углов между прямыми или отрезками, вычисление площадей фигур. В компьютерной графике векторы-нормали используются, чтобы создать правильное освещение тела. Использование векторов может быть положено в основу метода координат.
Виды векторов[править | править код]
Иногда вместо того, чтобы рассматривать в качестве векторов множество всех направленных отрезков (рассматривая как различные все направленные отрезки, начала и концы которых не совпадают), берут только некоторую модификацию этого множества (фактормножество), то есть, некоторые направленные отрезки рассматривают как равные, если они имеют одинаковое направление и длину, хотя они могут иметь разное начало (и конец), то есть направленные отрезки одинаковой длины и направления считаются представляющими один и тот же вектор; таким образом, каждому вектору оказывается соответствующим целый класс направленных отрезков, одинаковых по длине и направлению, но различающихся началом (и концом).
Так, говорят о «свободных», «скользящих» и «фиксированных» векторах. Эти виды отличаются понятием равенства двух векторов.
- Говоря о свободных векторах, отождествляют любые векторы, имеющие одинаковое направление и длину;
- говоря о скользящих векторах — добавляют, что начала равных скользящих векторов должны совпадать или лежать на одной прямой, на которой лежат изображающие эти векторы направленные отрезки (так что один может быть совмещен с другим перемещением в направлении, им же самим задаваемом);
- говоря о фиксированных векторах — говорят, что равными считаются только векторы, у которых совпадают и направления, и начала (то есть в этом случае факторизации нет: нет двух фиксированных векторов с различными началами, которые считались бы равными).
Формально:
Говорят, что свободные векторы 





Говорят, что скользящие векторы 

Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила, действующая на твердое тело. Перенос начала вектора силы вдоль прямой, на которой он лежит, не меняет момента силы относительно любой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (даже почти всегда вызовет): поэтому при вычислении момента нельзя рассматривать силу как свободный вектор, то есть, нельзя её считать приложенной к произвольной точке твердого тела.
Говорят, что фиксированные векторы 





Вектором в одном случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Все операции над векторами (сложение, умножение на число, скалярное и векторное произведения, вычисление модуля или длины, угла между векторами и т. д.) в принципе определены одинаково для всех типов векторов, различие в типах сводится в этом отношении только к тому, что для скользящих и фиксированных наложено ограничение на возможность осуществления операций между двумя векторами, имеющими разное начало (так, для двух фиксированных векторов запрещено — или лишено смысла — сложение, если их начала отличаются; однако для всех случаев, когда эта операция разрешена — или имеет смысл — она такова же, как для свободных векторов). Поэтому часто тип вектора вообще явно не указывается, подразумевается, что он очевиден из контекста. Более того, один и тот же вектор в зависимости от контекста задачи может рассматриваться как фиксированный, скользящий или свободный, например, в механике векторы сил, приложенных к телу, могут суммироваться независимо от точки приложения при нахождении равнодействующей (и в статике, и в динамике при исследовании движения центра масс, изменения импульса и т. п.), но не могут складываться друг с другом без учета точек приложения при вычислении вращающего момента (также и в статике и в динамике).
Отношения между векторами[править | править код]
Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны. Есть и другое определение: два ненулевых вектора 



Три вектора называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости[3].
Координатное представление[править | править код]
Разложение вектора 
При работе с векторами часто вводят некоторую декартову систему координат и в ней определяют координаты вектора, раскладывая его по базисным векторам. Разложение по базису геометрически можно представить при помощи проекций вектора на координатные оси. Если известны координаты начала и конца вектора, координаты самого вектора получаются вычитанием из координат конца вектора координат его начала.
За базис часто выбирают координатные орты, обозначаемые 


Любое геометрическое свойство можно записать в координатах, после чего исследование из геометрического становится алгебраическим и при этом часто упрощается. Обратное, вообще говоря, не совсем верно: обычно принято говорить[4], что «геометрическое истолкование» имеют лишь те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).
Операции над векторами[править | править код]
Модуль вектора[править | править код]
Модулем вектора 


Сложение векторов[править | править код]
Два вектора 
В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:
Для геометрического построения вектора суммы 
Правило треугольника[править | править код]
Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов 


Для сложения двух векторов 

Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:
Правило трёх точек[править | править код]
Если отрезок 





Правило многоугольника[править | править код]
Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же 

Правило параллелограмма[править | править код]
Для сложения двух векторов 

Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.
Модуль суммы двух векторов можно вычислить, используя теорему косинусов:
, где
— косинус угла между векторами
и
.
Если векторы изображены в соответствии с правилом треугольника и берется угол по рисунку — между сторонами треугольника — что не совпадает с обычным определением угла между векторами, а значит и с углом в приведенной формуле, то последний член приобретает знак минус, что соответствует теореме косинусов в её прямой формулировке.
Для суммы произвольного количества векторов применима аналогичная формула, в которой членов с косинусом больше: по одному такому члену существует для каждой пары векторов из суммируемого набора. Например, для трех векторов формула выглядит так:
Вычитание векторов[править | править код]
Два вектора 
Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:
Для получения вектора разности 




Модуль разности векторов[править | править код]
Три вектора 
где 


Отличие от формулы модуля суммы в знаке перед косинусом, при этом надо хорошо следить, какой именно угол берется (вариант формулы модуля суммы с углом между сторонами треугольника при суммировании по правилу треугольника по виду не отличается от данной формулы для модуля разности, но надо иметь в виду, что тут берутся разные углы: в случае суммы берётся угол, когда вектор 

Умножение вектора на число[править | править код]
Вектор 
Умножение вектора 


Умножение вектора 


Умножение вектора на число в координатной форме производится умножением всех координат на это число:
Исходя из определения получается выражение для модуля вектора, умноженного на число:
Аналогично как и числами, операции сложение вектора с самим с собой можно записать через умножение на число:
А вычитание векторов можно переписать через сложение и умножение:
Исходя из того, что умножение на 
Скалярное произведение векторов[править | править код]
Для геометрических векторов скалярное произведение определяется через их геометрические характеристики и вводится следующим образом:
Здесь для вычисления косинуса берётся угол между векторами, который определяется как величина угла, образованного векторами, если приложить их к одной точке (совместить их начала).
Это выражение можно переписать через координаты (здесь формула для трехмерного пространства):
Скалярным квадратом вектора называется его скалярное произведение само на себя и может быть вычислено через модуль вектора:
Векторное произведение векторов[править | править код]
Векторным произведением двух векторов 




Смешанное произведение векторов[править | править код]
Смешанным произведением трёх векторов 
Модуль этой величины даёт объём параллелепипеда, построенного на векторах 
См. также[править | править код]
- Линейное пространство
- Векторная величина
- Кортеж (математика)
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.
- Башмаков М. Что такое вектор? // Квант. — 1976. — № 4. — С. 2—5.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Примечания[править | править код]
- ↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия 7-9 классы. — Москва: Просвещение, 2010. — 384 с. — ISBN 978-5-09-023915-8.
- ↑ Элементарная математика, 1976, с. 249..
- ↑ 1 2 Выгодский М. Я. Справочник по высшей математике. — Москва: Астрель, 2006. — 991 с. — ISBN 5-271-03651-0.
- ↑ Это утверждение, очевидно, до некоторой степени условно, поскольку конкретная фиксированная система координат при желании может быть явно включена в число объектов, для которых соотношения устанавливаются, и тогда алгебраические утверждения для этой фиксированной частной системы координат могут быть переформулированы так, что будут инвариантными при записи в любой другой, произвольной, системе координат.
Операции над векторами, скалярное,
векторное и смешанное произведения
векторов.
Вводная информация
I. Геометрический вектор.
Определение.
Вектором
(геометрическим
вектором)
называется направленный прямолинейный
отрезок, т.е. отрезок, имеющий определенную
длину и определенное направление. Если
– начало вектора, а
– его конец, то вектор обозначается
символомили
.
Вектор(
)
называетсяпротивоположным
вектору
.
Длиной вектора
или его модулем
называется длина отрезка и обозначается
.
Вектор, длина которого равна нулю,
называетсянулевым
вектором и
обозначается
.
Вектор, длина которого равна единице,
называетсяединичным
вектором.
Единичный вектор, направление которого
совпадает с направлением вектора
,
называетсяортом
этого
вектора и обозначается
.
Векторы
и
называютсяколлинеарными,
если они
лежат на одной прямой или на параллельных
прямых. Для
коллинеарных векторов принято обозначение
.
Два вектора называютсяравными
(),
если они одинаково направлены и имеют
одинаковые длины. Три вектора в
пространстве называютсякомпланарными,
если они лежат в одной плоскости или в
параллельных плоскостях.
II. Операции над векторами.
На множестве
векторов вводится бинарная операция,
которая называется сложением
векторов. Эту операцию можно определить
либо правилом
параллелограмма (если
векторы
и
,
являются сторонами параллелограмма,
то их суммой будет вектор,
где– четвертая вершина параллелограмма),
либо правиломтреугольника
(если
векторы
и
являются сторонами треугольника, то их
суммой называют вектор).
Легко убедиться
в следующих свойствах этой бинарной
операции на множестве векторов:
1)
;
2)
;
3);
4)
.
Следовательно,
относительно сложения множество векторов
образует абелеву группу.
Произведением
вектора
на число
называется вектор
,
который имеет длинуи направление вектора
,
если;
направление противоположного вектора
к,
если.
Отметим, что.
Произведение
вектора на число обладает свойствами:
1)
;
2)
;
3)
.
Множество
геометрических векторов
с
введенными на нем операциями называетсявекторным
пространством.
III.
Координаты вектора.
Рассмотрим
пространство
с введенной на нем декартовой системой
координат. Пустьи
–
три единичных вектора, исходящих из
начала координат в направлениях
соответственно декартовых осейи
.
Эти векторы называютсяортами
координатных осей.
Пусть вектор
имеет начало также в точке
(начале координат). Спроектируем конец
векторана координатные оси. Полученные проекции
можно записать в видеи
,
гдеи
– углы, которые образует вектор
соответственно с координатными осями
и
.
Числаи
называютсянаправляющими
косинусами вектора
.
Вектори его проекции на координатные оси
удовлетворяют равенству
.
Тройка векторов
называетсябазисом
векторного пространства
,
а написанное выше равенство – разложением
вектора
по базису
.
При этом числаносят названиекоординат
вектора
относительно базиса
.
Поскольку координаты вектораотносительно данного базиса являются
проекциями этого вектора на координатные
оси, длина вектора и его координаты
связаны формулой
.
Подставляя в эту
формулу координаты вектора, выраженные
через направляющие косинусы, легко
получить равенство
,
которому удовлетворяют
направляющие косинусы любого вектора.
Заметим, что направляющие косинусы
являются координатами орта вектора
.
Поскольку
координаты вектора
полностью его определяют, можно ввести
обозначениеи заменить введенные операции над
векторами операциями над их координатами.
Так сложение векторовможно заменить сложением их координат:
,
т.е.,
а умножение вектора
на число
– умножением координат на это число:
или
.
Равенство векторов
на координатном языке предполагает
равенство их координат,
а коллинеарность– пропорциональность их координат
.
Пусть имеются
две точки
и
.
Тогда векторможно записать в виде
или
.
В частности, длярадиус-вектора
точки
имеем формулы
или
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор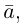
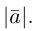
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 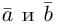
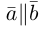
Аналогично, векторы а и b называются ортогональными (обозначение 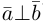
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
Углом между векторами 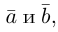
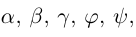
Два ненулевых вектора 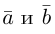
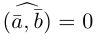
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 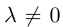
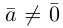
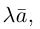
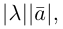
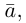
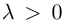
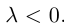
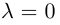
В частности, вектор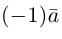
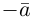
Если 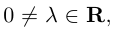
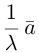
Из приведенного определения сразу же следует, что коллинеарные векторы 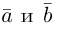
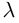
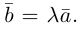
взять число 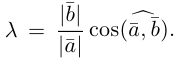
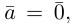
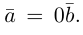
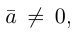
b) Сложение векторов.
Суммой двух векторов 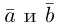
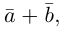
или по равносильному ему правилу параллелограмма
Вектор 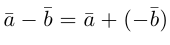
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 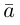
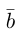
Геометрически очевидны следующие свойства проекции:
Пример №1
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 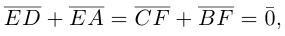
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 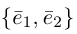
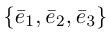
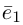
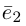
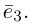
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 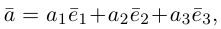
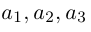
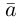
Приведем геометрическое доказательство этого утверждения.
Вектор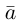
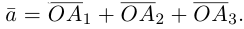
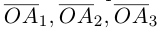
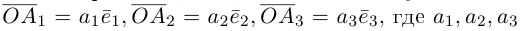
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 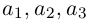
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 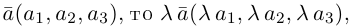
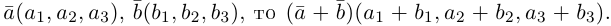
Рассмотрим теперь ортонормированный базис 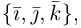
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 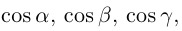
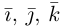
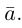
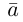
Очевидно также, что
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 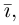
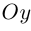
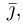
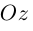
В выбранной системе координат координаты радиуса-вектора 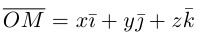
Если известны координаты начальной 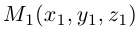
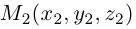
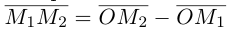
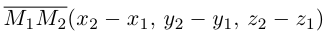
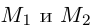
Найдем теперь координаты точки М, делящей отрезок с концами в точках 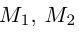
отношении 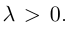
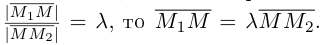
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
Пример №2
Треугольник задан координатами своих вершин 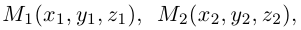
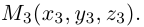
Пусть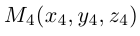
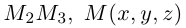
По известному свойству точки пересечения медиан 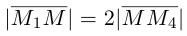
Подставив сюда найденные координаты точки 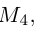
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 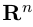
обладающая тем свойством, что любой вектор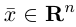
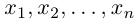
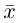
В качестве базиса в 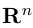
так как, очевидно, любой вектор 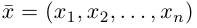
Скалярное произведение векторов
Определение: Скалярным произведением векторов 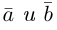
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 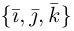
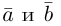
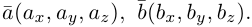
перемножим векторы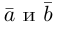
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 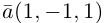
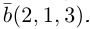
Решение.
Из чертежа следует, что 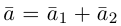
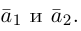
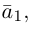
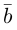
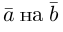
Тогда вторая ортогональная составляющая вектора 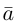
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 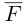
Найдем работу этой силы. Для этого разложим вектор силы 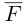
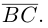
Составляющая 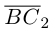
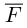
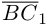
Окончательно, работа силы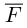
Замечание. Скалярным произведением векторов 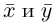
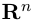
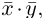
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 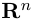
Длиной вектора 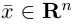
Векторы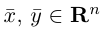
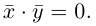
составляют ортонормированный базис пространства 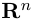
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 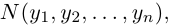
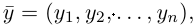
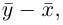
Таким образом переопределенное пространство 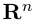
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов 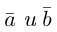

Из этого определения следует, что площадь параллелограмма, построенного на векторах 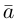
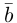

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 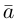
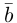
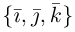
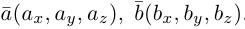
раскроем скобки в векторном произведении 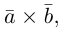
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 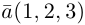
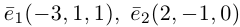
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 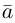

Переходим к вычислениям:
Тогда
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 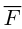
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 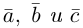
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 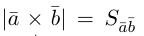
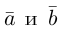
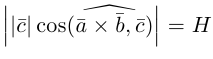
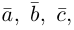
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 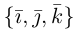
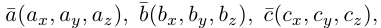
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 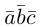
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 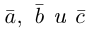
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 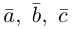
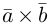
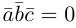
Следствие. Три вектора 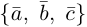
Заметим, кроме того, что, если 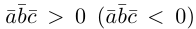
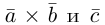
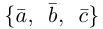
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 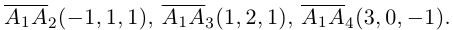
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 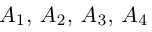
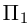
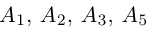
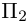
так как первая и третья строки в определителе пропорциональны. Плоскости 
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
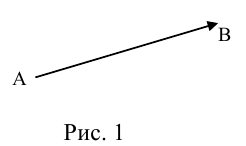
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 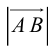
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
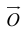
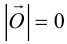
Определение: Векторы 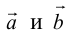
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 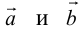
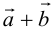
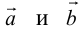
б) Правило треугольника (рис. 3): начало 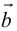
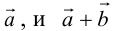
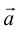
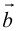
в) Правило сложения нескольких векторов (рис. 4).
Вектор 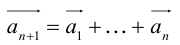
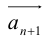
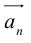
Умножение на число
Определение: Произведением вектора 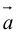
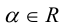
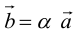
а) 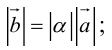
б) 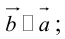
в)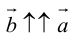
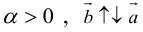
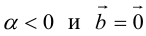
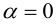
Произведение 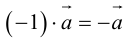
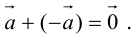
Определение: Разностью 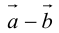
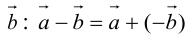
Начала 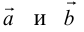
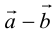
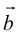
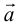
Свойства линейных операций
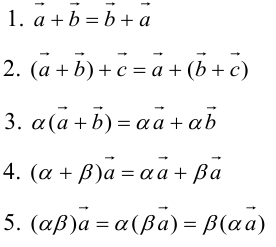
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: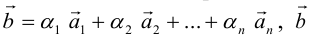
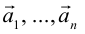
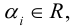
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 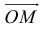
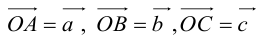
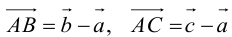
По правилу треугольника 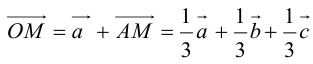
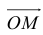
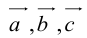
Теорема: Пусть 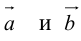
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 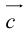
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 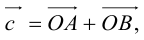
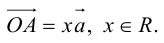
Докажем единственность разложения. Предположим, что 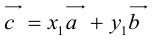
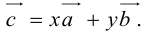
Если 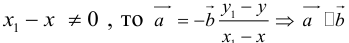
Теорема: Пусть 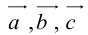
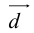
причем единственным образом.
Представление вектора 
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 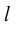
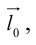
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 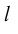
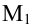
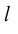
Определение: Ортогональной проекцией вектора 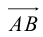
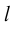
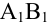
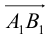
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
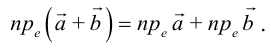
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 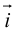
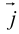

Аналогично в пространственной системе OXYZ 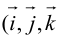
– разложение 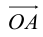
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 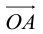
Определение: Координатами вектора 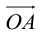
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 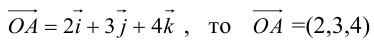
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если известны длина 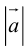
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
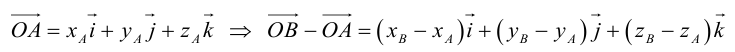
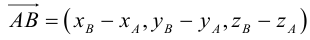
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 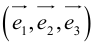
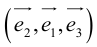
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 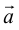
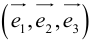
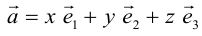
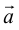
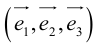
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 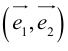
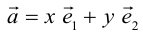
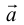
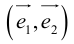
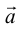
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 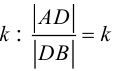
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
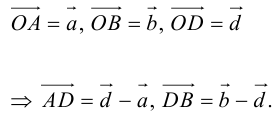
Так как 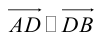
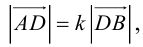
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
ЗАМЕЧАНИЕ 2. Если k < 0, 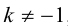
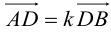
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 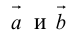
Скалярное произведение обозначается так: 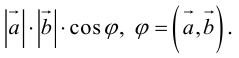
Так как 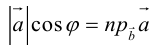
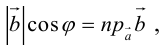
Свойства скалярного произведения
1.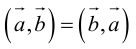
2.
Доказательство:
3.
Доказательство:
а) 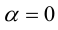
б)
в) 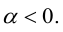
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 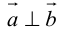
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 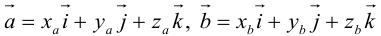
Таким образом,
Пример №8
Найти, при каком значении x векторы 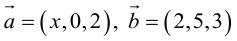
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 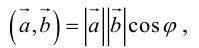
то
Найдем координаты векторов 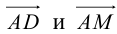
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 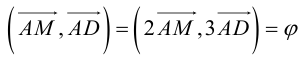
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 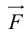
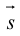
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 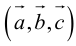
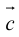
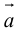
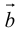
Определение: Векторным произведением вектора 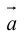
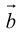
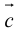
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 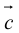
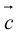
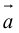
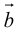
Свойства векторного произведения
1.
Доказательство:
а)пусть 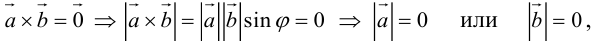
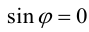
Его направление не определено, поэтому можно считать, что 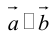
б)пусть
2. 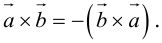
Доказательство: По определению направления векторов 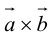
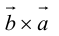
3.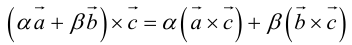
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 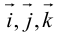
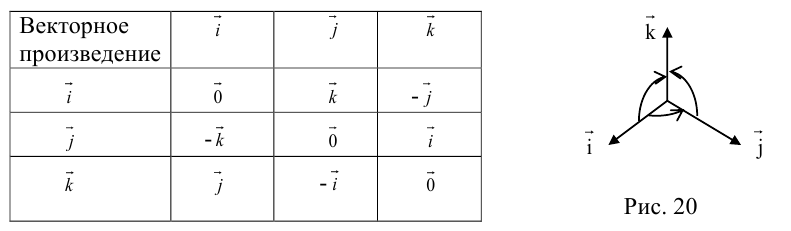
Пусть в некоторой пдск 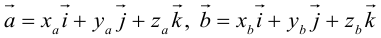
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
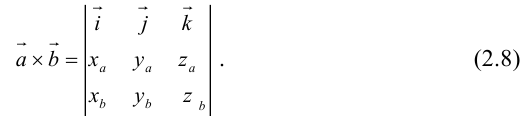
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 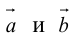
или
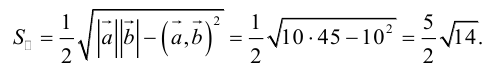
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 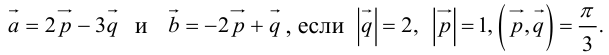
Так как 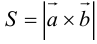
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 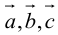
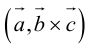
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
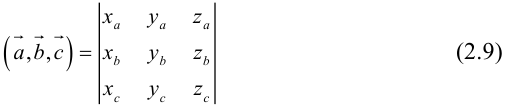
По определению скалярного произведения
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
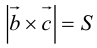
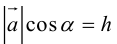
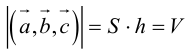
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 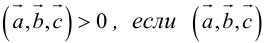
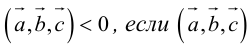
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 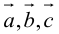
Доказательство: а) 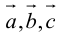
Если 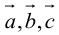
б)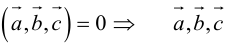
Во всех трех случаях 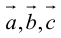
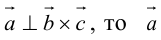
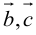
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
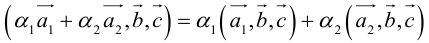
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
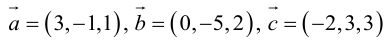
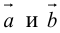
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 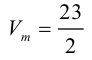

Чтобы найти высоту, воспользуемся формулой
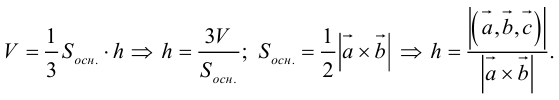
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
Содержание:
- Векторы
- Действия над векторами
- Умножение вектора на число
- Скалярное произведение векторов
- Векторное произведение
- Смешенное произведение векторов
- Разложение вектора по базису
- Действия над векторами, заданными своими координатами
- Проекция вектора на ось
- Проекции вектора на оси координат
- Направляющие косинусы вектора
- Разложение вектора по ортам
- Действия над векторами, заданными в координатной форме
- Вектор – основные определения
- Операции над векторами и их свойства
- Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
- Координаты вектора
- Скалярное произведение векторов и его свойства
- Векторы и их решение
- Собственные числа и собственные векторы
- Векторная алгебра
- Векторы: основные определения, линейные операции
- Линейные операции над векторами
- Умножения вектора на скаляр
- Основные свойства проекции вектора на ось
- Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
- Скалярное, векторное, смешанное произведения векторов
- Векторное произведение двух векторов
- Смешанное произведение векторов, заданных в координатной форме
- Простейшие задачи аналитической геометрии
- Задача об определении площади треугольника
- Задача о деление отрезка в заданном отношении
Векторы
В математике вектором называют величину, которая характеризуется только числом и направлением. Так определённые векторы ещё называют свободными векторами. Примером физических величин, которые имеют векторный характер являются скорость, сила, ускорение. Геометрически вектор — это направленный отрезок, хотя правильней говорить про целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковые длину и направление.
Векторы обозначают малыми латинскими буквами с чертой сверху 


Действия над векторами
Рассмотрим основные действия, определённые над векторами.
1. Сложение векторов. Суммой векторов 





Учитывая, что 

Вычитание векторов сводится к сложению противоположного вектора
Запишем основные свойства действий сложения векторов:
Заметим, что сумма нескольких векторов находится последовательным сложением двух из них, например:
Геометрически сумма нескольких векторов находится их последовательным отложением один за одним так, чтоб начало следующего совпадало с концом предыдущего. Суммой является вектор, который будет соединять начало первого с концом последнего (рис. 4). Если такая последовательность векторов даёт замкнутую ломаную то суммой векторов является 
Умножение вектора на число
Произведением вектора 


а) 
б) 




Запишем основные свойства действий умножения вектора на число:
Скалярное произведение векторов
Скалярным произведением 






Очевидно, что скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда когда эти вектора перпендикулярны (ортогональны). Действительно, если 

Наоборот, если 

Например, скалярное произведение 
Запишем основные свойства действий скалярного умножения векторов:
Векторное произведение
Векторным произведением 



1) модуль вектора 


2) вектор 


3) вектор 





Модуль векторного произведения равен площади параллелограмма, построенного на векторах 







Приведём основные свойства векторного произведения:
1) векторное произведение 


2) от перестановки местами векторов-сомножителей векторное произведение меняет знак на противоположный: 
3) 
4) 
Физическое содержание векторного произведения такое. Если 







Смешенное произведение векторов
Смешенным произведением векторов 



Как результат скалярного произведения векторов 


Действительно, 




Объём V параллелепипеда, построенного на векторах 
Однако, знак смешенного произведения совпадает со знаком 




Из геометрического содержания смешенного произведения выходит, что
1) смешанное произведение равно нулю тогда и только тогда, когда перемноженные вектора копланарные (условие компланарных векторов);
2)
Учитывая коммутативность скалярного произведения и антикоммутативность векторного, для произвольных векторов 
Пример 1.
Доказать, что когда М — точка АВС и О — произвольные точки пространства, то выполняется равенство:
Решение.
Пусть 



тогда
Пример 2.
У прямоугольного параллелепипеда рёбра 




Решение.
Пусть 

рис. 9.
Далее,
Этим закончен “перевод” условия задачи на “язык” векторов.
Теперь произведём вычисления с векторами:
Наконец “переводим” полученные вектора равенства снова на “геометрический язык”. Поскольку 

Далее поскольку 




Разложение вектора по базису
Базисом на площади называют упорядоченную пару неколлинеарных векторов и точку отсчёта.
Теорема. Любой вектор 



Доказательство.
Пусть векторы 





Тогда по правилу параллелограмма 
Но 

Числа, которые стоят при базисных векторах в разложении вектора за двумя неколлинеарными векторами называют координатами вектора в данном базисе и обозначают 
Соответственно в пространстве базисом называется упорядоченная тройка некомпланарных векторов и точки отсчёта. Для четырёх некомпланарных векторов справедлива следующая теорема.
Теорема. Любой вектор 




Доказательство.
От точки О отложим векторы 


в котором вектор 
Числа х,у,z которые стоят при базисных векторах в разложении вектора по трём некомпланарным векторам называют координатами вектора в пространстве и обозначают 






Отсюда легко установить длину вектора как расстояние между двумя точками:
Действия над векторами, заданными своими координатами
1. При сложении двух, или более векторов их соответствующие координаты складываются:
Действительно:
2. При вычитании векторов соответствующие координаты вычитаются:
Доказательство аналогично предыдущему.
3. При умножении вектора на число все координаты умножаются на это число.
Правда, для вектора 

4. Скалярное произведение двух векторов 
Правда:
Поскольку 

5. Векторное произведение векторов 
6. Смешенное произведение трёх векторов 
Пример 1.
Зная координаты векторов 

Решение:
Ответ: 
Пример 2.
Зная координаты векторов 

Решение.
Ответ: 
Пример 3.
Зная координаты векторов 
а) скалярное произведение векторов
б) векторное произведение векторов
в) смешенное произведение векторов 
Решение.
Ответ:
На основании приведённых выше формул действий над векторами можно установить следующие условия и соотношения для нулевых векторов
1. Угол между векторами.
2. Условие перпендикулярности двух векторов:
(векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю).
3. Условие коллинеарности двух векторов: 
4. Условие компланарности трёх векторов.
(три вектора компланарны тогда и только тогда, когда их смешенное произведение равно нулю).
5. Деление отрезка АВ в заданном отношении.
Если точка 

Если точка М делит отрезок АВ на пополам то 
Действия над векторами (теория)
а) Произведение вектора на число.
Определение 1. Произведением вектора 

который имеет длину 

Рис. 12.
Условие 
является условием коллинеарности двух векторов.
б) Сложение векторов.
Определение 2. Суммой двух векторов 






Рис. 13.
Понятно, что вектор 


Для векторной суммы справедливый переместительный закон
Легко убедиться, что для векторной суммы имеет место соединительный
закон 
Исходя из определения 2, легко находим сумму, например, четырех векторов 
Рис. 14.
Вектор 


в) Вычитание векторов.
Действие вычитание векторов можно рассматривать как обратное действие относительно сложения векторов.
Определение. Разностью 



Рис. 15.
Как видно из рис. 15, одна диагональ 




Дадим еще одно определение разности векторов.
Определение. Разностью двух векторов 


Проекция вектора на ось
Пусть имеем произвольную ось l на плоскости и некоторый вектор 
Рис. 16.
Опустим из начала A вектора и из конца B перпендикуляры на ось l. Основаниями перпендикуляров будут точки A1 и B1, которые называются проекциями точек A и B.
Величина A1B1 называется проекцией вектора 


Определение 1. Проекцией вектора 
Из точки A проведем прямую, параллельную оси l, которая пересечет отрезок BB1 в точке C. Вектор 


Определение 2. Проекция вектора на любую ось равна произведению длины этого вектора на косинус угла между осью и вектором.
Если угол φ острый, то проекция 

Свойства проекций.
1. Если векторы 


2. Проекция суммы векторов на любую ось равна сумме проекций слагаемых на ту же ось, то есть:
3. Проекция разности двух векторов на ось l равна разности величин проекций на ту же ось, то есть:
4. Если вектор 

Проекции вектора на оси координат
Рассматривается прямоугольная система координат Oxyz в пространстве и произвольный вектор 
Пусть 
Проекции x, y, z вектора 

Если заданы две точки A (x1; y1; z1) и B (x2; y2; z2), то координаты вектора 
x = x2 – x1, y = y2 – y1, z = z2 – z1 .
Рис. 17
Действительно, проведем через точки A и B плоскости, перпендикулярные оси Ox и обозначим точки их пересечения соответственно A1 и B1 (рис.17). Точки A1 и B1 имеют на оси Ox координаты x1 и x2 , но 
x = x2 – x1 . Аналогично доказывается, что y = y2 – y1, z = z2 – z1 .
Направляющие косинусы вектора
Пусть имеем вектор 
Рис. 18
Через точку M проведем плоскости, перпендикулярные к осям координат, и вместе с координатными плоскостями они образуют параллелепипед, диагональ которого — отрезок OM (рис.18). Через α, β, γ обозначим углы, которые образует вектор 


Квадрат диагонали прямоугольного параллелепипеда равна сумме квадратов длин трех его измерений.
Поэтому


Формула (2.8) выражает длину вектора через его координаты. Тогда на основе формул (2.7) и (2.8) получим
Отсюда для направляющих косинусов получаем

Для направляющих косинусов справедливо равенство 
Разложение вектора по ортам
Рассмотрим прямоугольную систему координат в пространстве и вектор, начало которого в точке O (рис.19) .
Рис. 19.
Обозначим орты осей координат Ox, Oy, Oz соответственно через 
Спроецируем вектор 
Из прямоугольника ODMC видно, что вектор 

Тогда

Вектор 
Векторы 




Подставляя эти значения в равенство (2.10), учитывая, что 

Слагаемые 

Тройка векторов 

Пример 1. Построить вектор 
Рис. 20.
Решение. Компоненты вектора 


соответствует прямоугольный параллелепипед, диагональ которого является искомый вектор (рис. 20).
Действия над векторами, заданными в координатной форме
Если векторы заданы в координатной форме, то действия сложения, вычитания, умножения вектора на число можно заменить простыми арифметическими операциями над координатами этих векторов по таким правилам.
Правило 1. При сложении векторов их одноименные координаты складываются
Пусть имеем векторы 





Сложив эти равенства, получим

Итак, координаты вектора 
Правило 2. Чтобы отнять от вектора 



Правило 3. Чтобы умножить вектор 


Пример 1. Найти вектор 
Решение. Выполним действия последовательно и найдем

Значит,
Вектор – основные определения
Определение вектора в пространстве ничем не отличается от определения вектора на плоскости.
Определение 1. Вектором называется направленный отрезок, т.е. отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Так же как и на плоскости, векторы обозначаются 
Определение 2. Длиной (или модулем) вектора 


Длина вектора 


Любая точка пространства также считается вектором, который называется нулевым. Начало такого вектора совпадает с его концом, а длина равна нулю. Обозначения нулевого вектора:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Определение 3. Векторы 

Если ненулевые векторы 







Ясно, что сонаправленные векторы, в силу их определения, коллинеарны. Если два коллинеарных вектора не сонаправлены, то они называются противоположно направленными. Обозначения остаются обычными: 





Определение 4. Векторы 



Теорема 1. От любой тонки пространства можно отложить вектор, равный данному, и притом только один.
Доказательство этой теоремы аналогично доказательству соответствующей планиметрической теоремы.
Возможно вам будут полезны данные страницы:
Операции над векторами и их свойства
Операции над векторами в пространстве аналогичны соответствующим операциям на плоскости.
Пусть даны два вектора 








Теорема 2. Сумма 




Правило треугольника можно сформулировать и так: для любых трёх точек 
Кроме того, сумму двух неколлинеарных векторов с общим началом можно построить и по правилу параллелограмма: 




Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве:
1)
2) 
3) 
Здесь 
Определение 5. Два ненулевых вектора называются противоположными, если их длины равны и эти векторы противоположно направлены.
Вектор, противоположный данному ненулевому вектору 
Определение 6. Разностью двух векторов 



Разность векторов 



Разность векторов 



Из законов сложения векторов следует, что сумма нескольких векторов не зависит от порядка слагаемых.
Умножение (произведение) вектора на число и его свойства, так же как и свойства операции сложения, не претерпевают изменений и в пространстве.
Определение 7. Произведением ненулевого вектора 








Таким образом, по определению, 






Свойства умножения вектора на число не отличаются от аналогичных свойств на плоскости:
-
— ассоциативность (сочетательный закон);
-
—дистрибутивность относительно сложения векторов (1-й распределительный закон);
-
— дистрибутивность относительно сложения чисел (2-й распределительный закон).
Здесь 


Справедлива также и лемма о коллинеарных векторах: если векторы 


что 

Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
Теорема 3. Пусть 



Доказательство
1. Из равенства 





2. Пусть 




З. Компланарные и некомпланарные векторы
Следующее понятие уже не имеет аналога в планиметрии.
Определение 8. Векторы называются компланарными, если лучи, задающие их направления, параллельны некоторой плоскости.
Замечание. Из определения 8 следует, что при откладывании от одной точки векторов, равных нескольким данным компланарным векторам, получим векторы, лежащие в одной плоскости. Таким образом, компланарные векторы лежат либо в одной плоскости, либо в параллельных плоскостях.
Очевидно, что любые два вектора компланарны и любые три вектора, два из которых коллинеарны, также являются компланарными (поясните). Рассмотрим теперь условия, при которых три вектора, из которых никакие два не коллинеарны, являются компланарными.
Теорема 4. Векторы 




Доказательство
1. Пусть векторы 
точки 
















Докажем, что векторы 






Отложим от произвольной точки 







Если векторы 






Следующая теорема, называемая теоремой о разложении вектора по трём некомпланарным векторам, является основной во всей элементарной (школьной) векторной алгебре.
Теорема 5. Любой вектор 




2. Пусть векторы 





















3. Докажем теперь, что разложение вектора 



Тогда
отсюда
– т. е. векторы
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
по данным векторам
единственно. Теорема доказана.
Итак, любой вектор 





Координаты вектора
Так же как и на плоскости, в пространстве помимо координат точки вводятся координаты вектора. Рассмотрим три попарно перпендикулярных вектора 












Свойства векторов пространства, заданных своими координатами, аналогичны соответствующим свойствам векторов на плоскости:
- Два вектора равны в том и только том случае, если равны их координаты.
- Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат этих векторов, т.е. для векторов
получаем
- При умножении вектора на число каждая его координата умножается на это число, т.е. для вектора
и действительного числа
получаем
Докажем, например, свойство 2. Так как 



Скалярное произведение векторов и его свойства
Определение скалярного произведения векторов 

Определение 11. Скалярным произведением векторов 

Теорема 8. Два ненулевых вектора 

Доказательство этой теоремы вытекает из формулы (9).
Определение 12. Скалярным квадратом вектора 


Так как 
Таким образом, длина вектора равна квадратному корню из его скалярного квадрата.
Замечание. Скалярное произведение есть число, поэтому грубой ошибкой явилась бы запись:
Если векторы 


Теорема 9. Скалярное произведение векторов равно сумме произведений их соответственных координат, т. е.
Доказательство. Отложим от произвольной точки 







итак как 


поэтому
Решение любой геометрической задачи на вычисление сводится, в сущности, к нахождению величин двух типов: расстояний и углов. Если в пространстве задан некоторый базис (в частности, прямоугольный), т. е. тройка некомпланарных векторов, то на основании теоремы 5 любой вектор пространства можно разложить по векторам этого базиса, причём единственным образом.
Если известны длины векторов, образующих базис, углы между ними и разложение некоторого вектора по векторам этого базиса, то, используя свойства скалярного произведения, можно определить длину такого вектора и угол, образуемый им с любым другим вектором, разложение которого по векторам этого базиса известно.
Таким образом, векторы позволяют находить решения довольно широкого класса геометрических задач, а умение определять разложение вектора по базисным векторам является важнейшим фактором их решения.
Для решения задач о разложении вектора по трём данным некомпланарным векторам, разумеется, необходимо, помимо теоремы 5, знание предшествующего ей материала.
Примеры с решением
Задача 1.
Основанием четырёхугольной пирамиды 






Решение (см. рис. 14).
1. 

2. Так как 


Ответ:
Заметим, что в разложении вектора 








Задача 2.
Пусть 


Решение (см. рис. 15). Пусть 






Ответ:
Векторы и их решение
Вектором называется направленный отрезок. Направление отрезка показывается стрелкой. Различают начало и конец отрезка.
Два вектора называются равными между собой, если каждый из них можно получить параллельными перенесениями другого.
Равные векторы являются параллельными (колинеарными), имеют одно и то же направление и одинаковую длину. Длина вектора 
Вектор называется нулевым (ноль- вектором), если он имеет нулевую длину, то есть его конец сходится с началом.
Чтобы найти сумму двух векторов 



Суммой 






Для складывания векторов имеют место такие законы:
1) переставной (коммутативный)
2) связующий
3) для каждого вектора 

4)
5) для некоторых двух векторов 

Если вектор 



Пусть вектор имеет начало в точке 





Если вектор 
Произведением вектора 






Любой вектор 
где 



Пример 1.73
Даны два вектора: 

Найти вектор
Решение
Признаком колинеарности двух векторов 

Скалярным произведением двух векторов 


Скалярное произведение можно записать в таком виде:
Если векторы 

Учитывая формулы (1.18) и (1.19), можно найти косинус угла между векторами 

Отсюда получается условие перпендикулярности двух векторов: если 

Среди свойств скалярного произведения отметим так:
Векторным произведением вектора 


1) длина вектора 
2) вектор 

3) из конца вектора 


Заметим, что 


В координатной форме векторное произведение векторов 

Смешанным или скалярно – векторным произведением трех векторов 



Если векторы 
Если известные координаты сомножителей 
Если три ненулевых 
Следует, в координатной форме условие компланарности трех ненулевых векторов имеет вид:
Решение примеров:
Пример 1.74
Заданы координатами точек 


1) вектор 
2) угол между векторами 
3) координаты вектора
4) объем пирамиды с вершинами в точках
Решение
1) По формуле (1.14) находим
тогда
2) Косинус угла между векторами 

Поскольку косинус угла отрицательный, то угол 
3) Координаты векторного произведения находим по формуле (1.22):
4) Чтобы найти объем пирамиды, найдем сначала смешанное произведение векторов, что выходят из одной вершины пирамиды:
Тогда объем пирамиды
Собственные числа и собственные векторы
Вектор – столбец 




Тут 



Координаты собственного вектора 

Собственный вектор обозначаются с точностью к постоянному множителю.
Решение примеров:
Пример 1.90.
Обозначить собственные определения и собственные векторы матрицы
Решение. Характеристические уравнения данной матрицы имеет вид (1.24):

отсюда получается, что матрица 





которое приводится к одному уравнению
Возьмем 
Следует, первый собственный вектор является
Второй вектор 

Эта система уравнений так же приводится к одному уравнению 


Таким образом, матрица 




Пример 1.91
Найти собственные векторы и собственные значения матрицы
Решение. Характеристическое уравнение
Раскрыв определитель получим:
Корень 


Система уравнений для определения собственных векторов имеет вид:
Последовательно подставим 

Фундаментальная система уравнений получается, если свободным переменным 
Получили два линейно независимые собственные векторы. Вся совокупность векторов, что соответствуют собственному значению 
Фундаментальная система решений получается, если взять
Векторная алгебра
Понятие «вектор» (от лат. vector – носитель), как отрезка, имеет определенную длину и определенное направление, впервые появилось в работах по построению числовых систем в ирландского математика Уильяма Гамильтона (1805-1865). Это понятие связано с объектами, которые характеризуются величиной и направлением, например, скорость, сила, ускорение. При этом скорость можно понимать в широком смысле: скорость изменения издержек производства, доходов, спроса, потребления и предложения и др. Вектор может указывать направление наибольшего возрастания или убывания функции, описывающей различные экономические процессы. Векторы, рассмотренные в данном разделе, является частным случаем 
Для графического изображения решения экономических задач на плоскости и в пространстве применяются средства аналитической геометрии. Аналитическая геометрия – математическая наука, объектом изучения которой являются геометрические фигуры, а предметом – установление их свойств средствами алгебры с помощью координатного метода. Теоретической базой этой науки является частично известна из школы векторная алгебра.
Основателем метода координат и, вместе с тем, аналитической геометрии является Рене Декарт (1596-1650) – французский философ, математик, физик и физиолог. Его именем и названа известная «декартова прямоугольная система координат», которая позволяет определить положение фигуры на плоскости и тела в пространстве.
После изучения данной темы вы сможете:
● использовать инструмент векторной алгебры для геометрического изображения и анализа объектов экономических процессов;
● применять уравнение прямой линии на плоскости для геометрической интерпретации зависимости между функциональному признаку и аргументом, что на нее влияет;
● применять уравнение кривых второго порядка при построении нелинейных математических моделей экономических задач;
● осуществлять геометрическую интерпретацию решений экономических задач с помощью поверхностей и плоскостей.
Векторы: основные определения, линейные операции
Выберем на произвольной прямой (в 






алфавита с чертой: 
Рис. 6.1
В применимых задачах естественных наук существенным является обстоятельство – где, в какой точке находится начало вектора. Например, результат действия силы зависит не только от ее величины и направления действия, но и от того, в какой точке она прикладывается.
Вектор, для которого фиксированная (не фиксирована) начальная точка называется связанным (свободным). Векторы, которые применяются в экономических задачах, как правило, не являются связанными, поэтому в дальнейшем будем рассматривать преимущественно свободные векторы
Длиной, или модулем, вектора называется длина соответствующего отрезка и обозначается одним из символов:
Нулевым вектором 0, или ноль-вектором, называется вектор, длина которого равна нулю, а направление его считается произвольным (неопределенным).
Единичным вектором 
Равными векторами называются векторы, которые принадлежат одной прямой или параллельным прямым, одинаково направлены и имеют равные длины.
Взаимно противоположными называются векторы, которые принадлежат одной прямой или параллельным прямым, имеют равные длины, но противоположно направлены. Вектор, противоположный вектору 

Коллинеарными называют векторы, которые принадлежат одной прямой или параллельным прямым.
Компланарными называются векторы, которые принадлежат одной плоскости или параллельным плоскостям.
Линейные операции над векторами
Будем считать, что векторы 



1. Суммой векторов 


Параллельный перенос можно осуществить и так, что объединятся начала векторов 

Рис. 6.2
Правило треугольника обобщается на произвольное конечное число векторов. Если параллельным переносом расположить векторы так, что конец предыдущего вектора (начиная с первого) является началом следующего, то результирующим будет вектор, соединяющий начало первого вектора слагаемого с концом последнего (рис. 6.3):
Рис. 6.3
Соответствующее правило называют правилом многоугольника.
Свойства суммы векторов:
1) переставная, или коммутативна:
2) соединительная, или ассоциативная:
3)
4)
Разницу 

Умножения вектора на скаляр
Пусть 










Рис. 6.4
При


Свойства умножения вектора на скаляр:
1) переставной или коммутативных закон:

2) соединительный, или ассоциативный закон:

3) распределительный или дистрибутивный закон:

4)
5)
Из определения умножения вектора на скаляр следует необходимое и достаточное условие коллинеарности двух векторов: вектора 

Известно, что три ненулевые векторы 


Рассмотрим понятие, имеет очень важное значение в теории векторов – проекции вектора на ось (прямую, имеет направление; заданное направление считать положительным, противоположное направление – отрицательным).
Компонентой вектора 





Рис. 6.5
Проекцией вектора 






Основные свойства проекции вектора на ось
1. Проекция вектора на ось 

2. Проекция суммы двух векторов на эту ось равна сумме их проекций на эту ось:
Это свойство обобщается на любое конечное число векторов.
3. Проекция на ось произведения вектора со скаляром равна произведению со скаляром проекции самого вектора на ось:
Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
Пусть в трехмерном векторном пространстве 


Рис. 6.6
Выберем в пространстве произвольную точку 





Под декартовыми прямоугольными координатами точки 

Точка 





Измерениями параллелепипеда есть модули координат точки 
Углы 


откуда:
Косинусы направляющих углов называются направляющими косинусами радиус-вектора 
1) направляющие косинусы являются координатами единичного радиус-вектора:
2) сумма квадратов направляющих косинусов вектора 
Понятие «координата», «направляющие углы», «направляющие косинусы» без изменений переносятся на любые свободные векторы, потому начало каждого из них параллельным переносом можно поместить в начало 
Координатами любого вектора 



Задача вектора тройкой его координат 
Для единичных векторов 

Длина произвольного вектора 
Найти длину и направляющие косинусы вектора
По формулам (6.5) имеем:
Установим связь между координатами вектора – числами – и его компонентами – векторами – с помощью единичных векторов 
Рис. 6.7
Компонентами вектора 


Следовательно, любой вектор 
Изображение вектора с 
Согласно свойствами операций над векторами, алгебраическая форма задания дает возможность установить результаты действий над векторами, заданными в координатной форме.
1. При добавлении (вычитании) двух векторов с 


Действительно, по свойствам ассоциативности и дистрибутивности имеем:
2. При умножении вектора 

Действительно, согласно распределительным свойствам умножения скаляра на сумму векторов имеем:
Скалярное, векторное, смешанное произведения векторов
Скалярным произведением двух векторов 



Вместо 


Для определения угла 







Основные свойства скалярного произведения векторов вытекают из его определения (6.7).
1. Скалярное произведение 
2. Скалярный квадрат вектора равен квадрату его модуля, то есть
3. Скалярное произведение подчиняется всем законам арифметики чисел относительно линейных операций:
4. Скалярное произведение двух векторов равно произведению модуля одного из них с проекцией второго на ось, направление которого определяется первым вектором:
Доказательство этого свойства основывается на определении (6.3).
Скалярное произведение векторов 

1. Вычислим скалярные произведения единичных векторов 

2. Находим произведение 
Раскрываем скобки и получаем:
Скалярное произведение двух векторов равно сумме произведений одноименных координат. Это полностью совпадает с определением скалярного произведения 
Как следствие из (6.12) при 
Определим угол между двумя ненулевыми векторами 

Следовательно, косинус угла между двумя векторами определяется формулой:
Отсюда
В результате с соотношением (6.13) получим критерий ортогональности двух векторов, заданных в координатной форме:
Критерием коллинеарности векторов 

Векторное произведение двух векторов
Пусть 








1) модуль его численно равен площади параллелограмма, построенного на векторах 

2) он перпендикулярный плоскости параллелограмма 



Рис. 6.9
Векторное произведение обозначается символами: 
Следовательно,
где 




Основные свойства векторного произведения вытекают из его определения.
1. Векторное произведение ненулевых векторов равно ноль-вектору тогда и только тогда, когда векторы 

Еще одним критерием коллинеарности векторов является равенство нулевому вектору их векторного произведения.
2. Векторные произведения с разным порядком сомножителей являются взаимно противоположными векторами:
Это означает, что векторное произведение не подчиняется переставному (коммутативному) закону.
3. Векторное произведение подчиняется ассоциативному закону относительно скалярного множителя и дистрибутивному закону относительно сложения:
где
Векторное произведение векторов 

1. Определяем векторные произведения ортов 
Векторное произведение одноименных векторов по свойству 1 дает ноль вектор:
Однако все векторные произведения разноименных единичных векторов будут давать единичные векторы:
Рис. 6.10
Рассмотрим, например, произведение 




2. Находим произведение 
Множители при 
Коэффициенты при единичных векторах в соотношении (6.20) являются координатами вектора 


Если символы 

Найдем векторное произведение векторов 
Модуль векторного произведения 

Смешанным произведением трех векторов 


Смешанное произведение можно обозначать тройкой векторов 





Геометрическая интерпретация смешанного произведения. Пусть 

Рис. 6.11
Вектор 





Согласно (6.11) скалярное произведение 



где 




Модуль смешанного произведения трех векторов численно равен объему параллелепипеда 
Основные свойства смешанного произведения вытекают из его определения и геометрической интерпретации.
1. Смешанное произведение ненулевых векторов равно нулю, если по крайней мере два из трех векторов коллинеарны или все три – компланарны, и наоборот.
Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения:

Свяжем с изображенными на плоскости векторами 
2. Циклическая перестановка трех сомножителей смешанного произведения не меняет его величины, а отрицательное перестановки меняет его знак на противоположный:
Смешанное произведение векторов, заданных в координатной форме
Пусть имеем три ненулевые векторы 
Полученная сумма произведений является расписанием определителя 3-го порядка, составленный из координат векторов, по элементам его третьей строки, то есть:
Векторы 

С помощью смешанного произведения векторов легко определить, относятся ли четыре точки 
Простейшие задачи аналитической геометрии
Задача об определении длины отрезка. Найти длину отрезка 

1. Введем в рассмотрение вектор 



2. Определим координаты вектора 


3. Находим модуль вектора 

Задача об определении площади треугольника
Найдем площадь треугольника, заданного координатами вершин:
По аксиомой стереометрии известно, что три точки в пространстве определяют плоскость и притом только одну. Для упрощения изложения, не нарушает общего подхода к решению задачи, договоримся рассматривать треугольник 



1. Введем в рассмотрение векторы:
и найдем их векторное произведение
По соотношению (6.20) имеем:
2. Вычислим модуль вектора 


Тогда для площади треугольника 
Знак 

Если треугольник принадлежит не плоскости 
Найдем площадь треугольника с вершинами 

Введем в рассмотрение векторы: 


Тогда

Задача о деление отрезка в заданном отношении
Пусть в пространстве заданы две точки 







Рис. 6.15
Число 
называется отношением, в котором точка 



Задача о деление отрезка в заданном отношении формулируется так: найти координаты точки 




Пусть точкам 




С этого векторного равенства найдем вектор
или в координатах:
Отсюда, если отрезок разделить на две равные части точкой 

Можно доказать, что координаты точки пересечения медиан треугольника, заданного координатами его вершин 
Лекции:
- Объем конуса
- Разложение на множители
- Деление многочлена на многочлен
- Правила дифференцирования
- Теорема Пифагора
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Прямая линия на плоскости
- Выпуклость и вогнутость графика функции
- Матанализ для чайников
- Производные некоторых элементарных функций
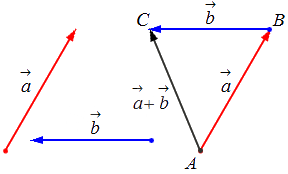
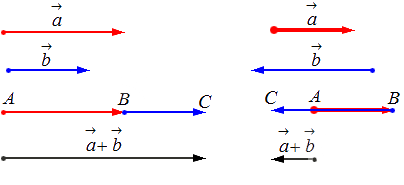
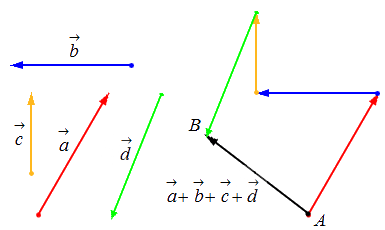
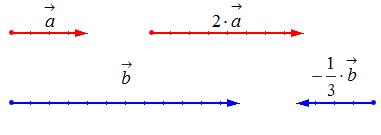
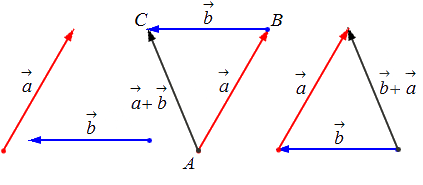
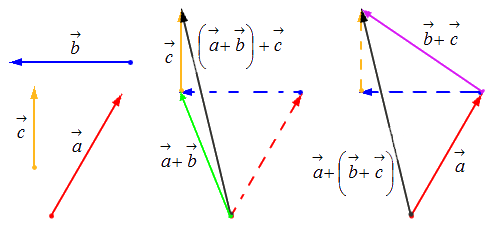
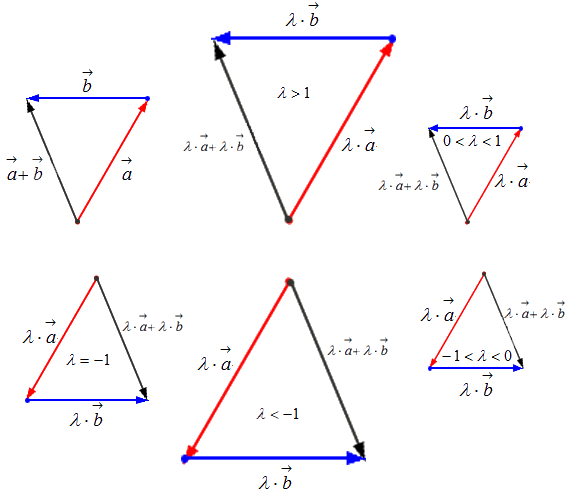

















 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»






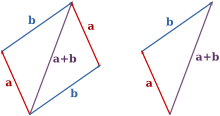
















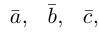
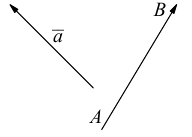
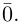
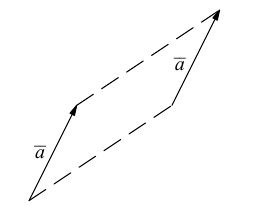
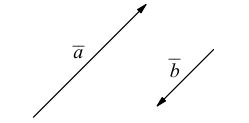
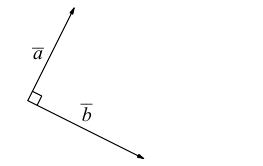
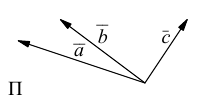
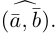
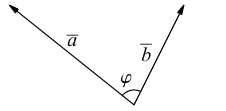
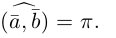
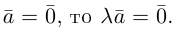
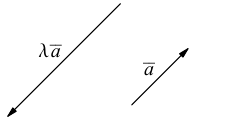
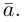
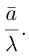
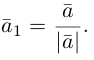
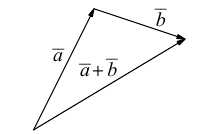
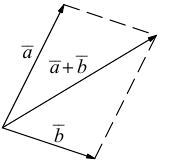
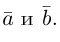
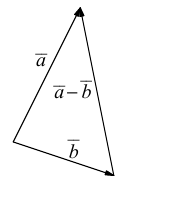
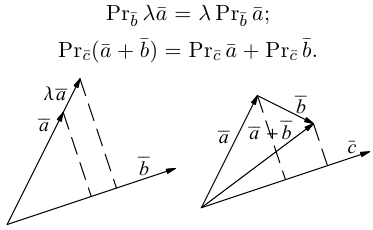
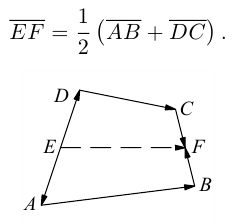
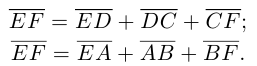
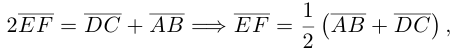
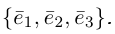
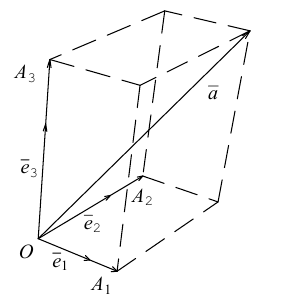
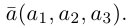
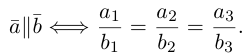
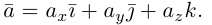
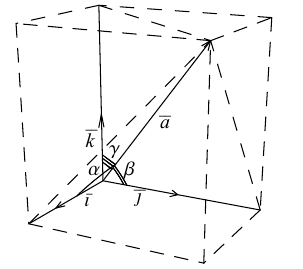
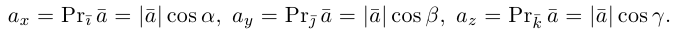
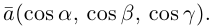
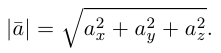
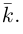

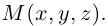
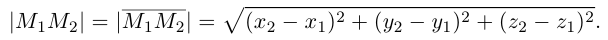
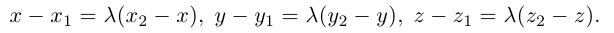
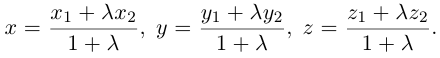
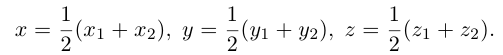
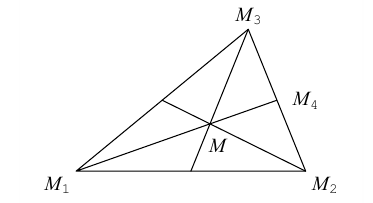
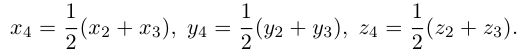
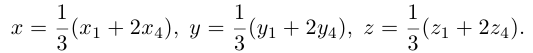
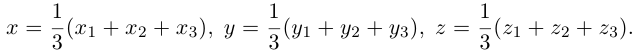


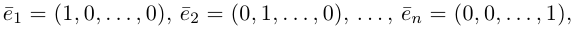
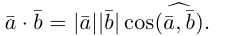
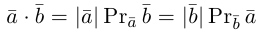
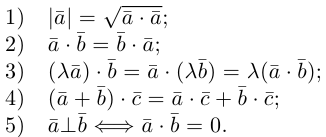
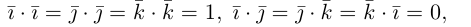
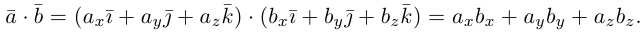
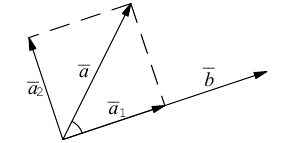
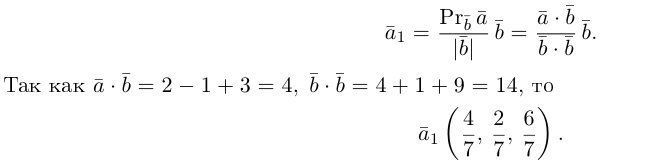
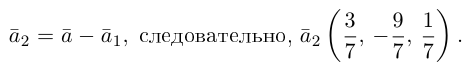
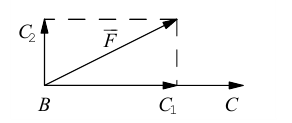
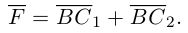
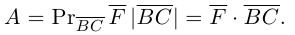
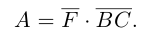
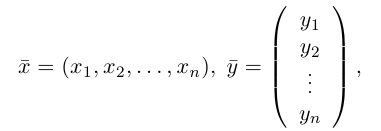
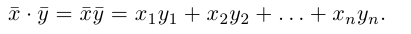
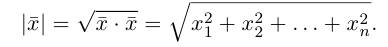
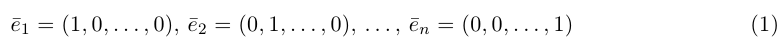
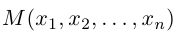

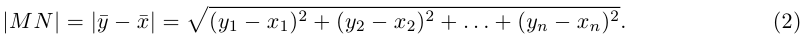
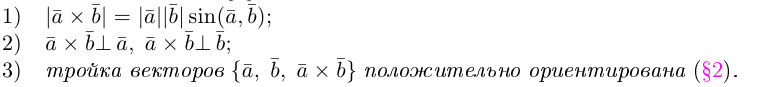
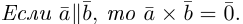
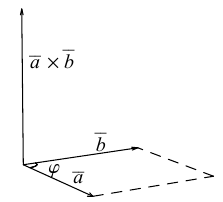
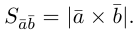
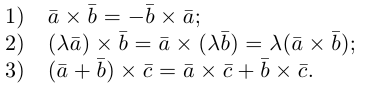
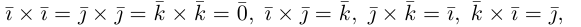
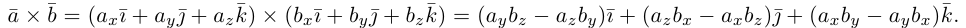
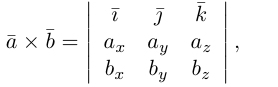
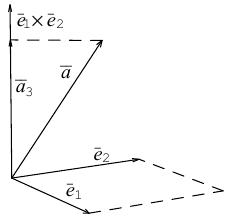
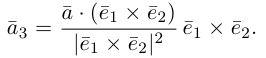
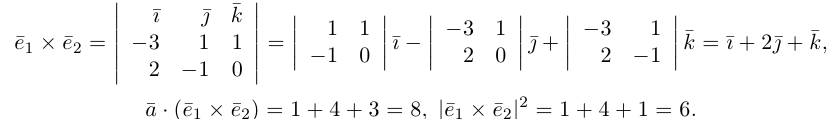
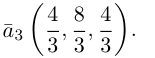
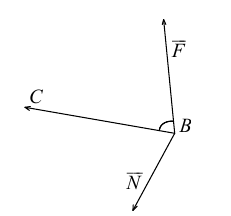
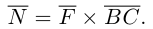
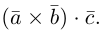
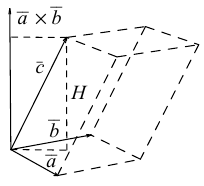
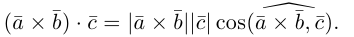
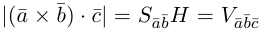
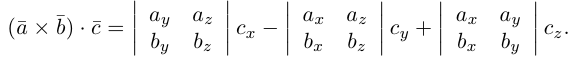
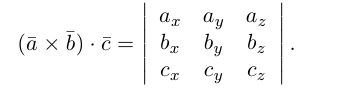
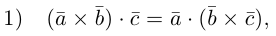
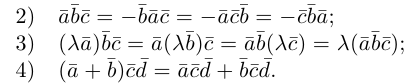
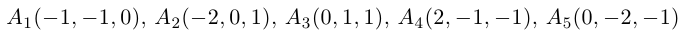
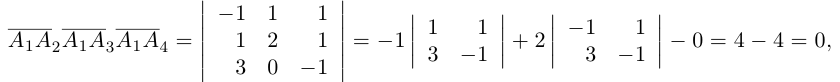
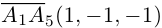
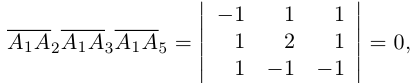
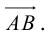
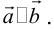
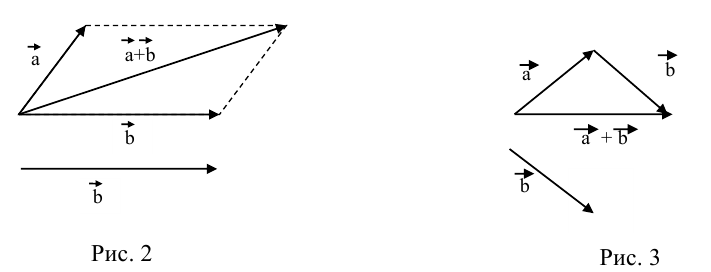
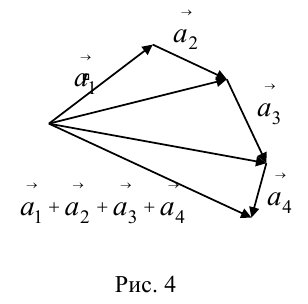

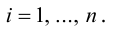
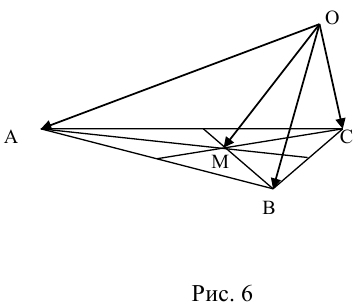
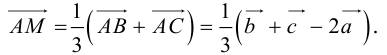
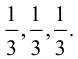
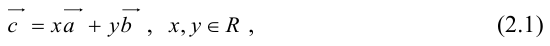
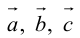 есть два коллинеарных, например:
есть два коллинеарных, например: 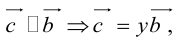
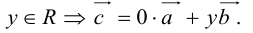
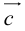 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 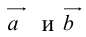 (рис. 7).
(рис. 7). 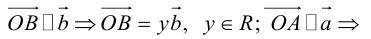
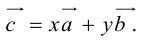
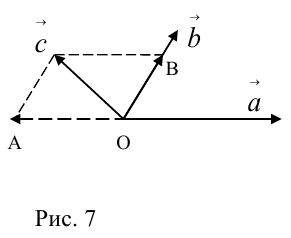
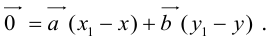
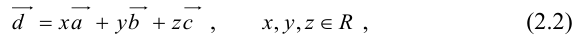
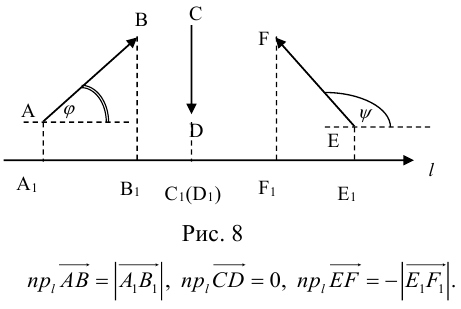
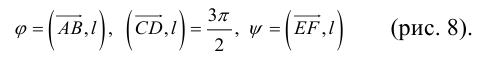
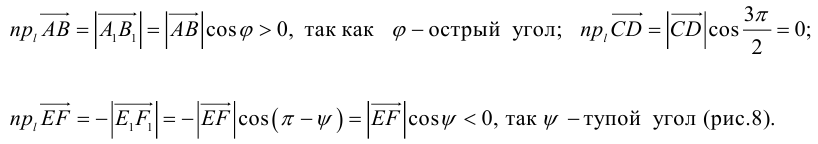
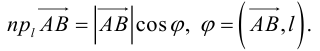
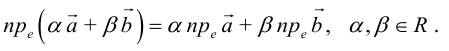
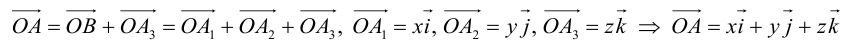
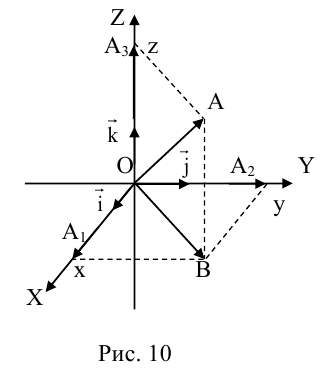
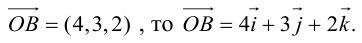
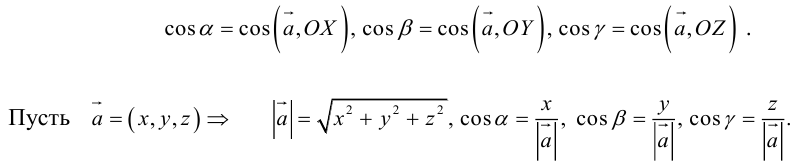
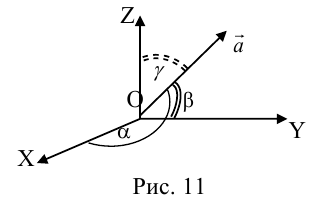
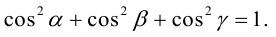
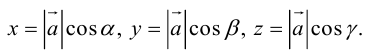
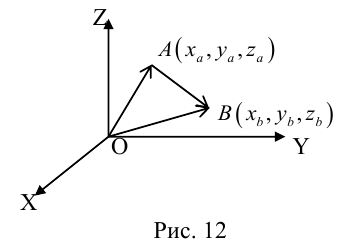
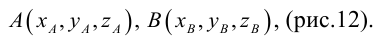
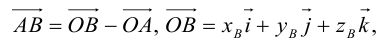
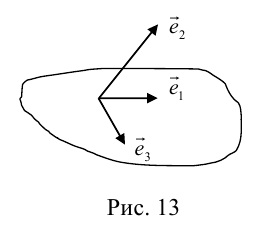
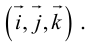
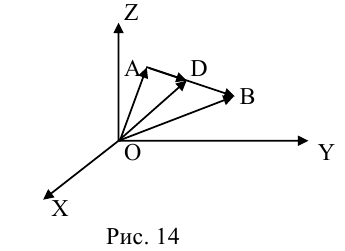
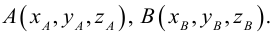

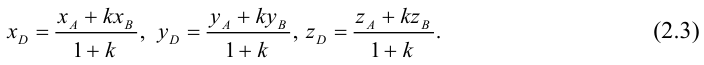
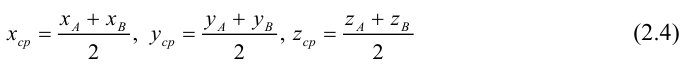
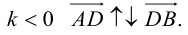
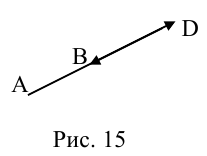
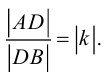
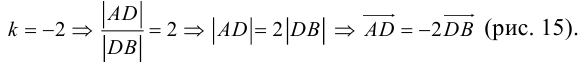
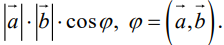
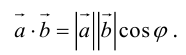
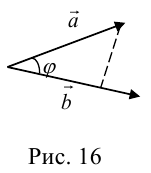
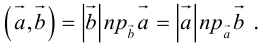
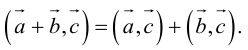
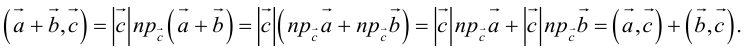
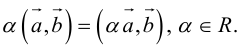
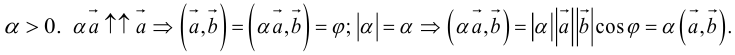
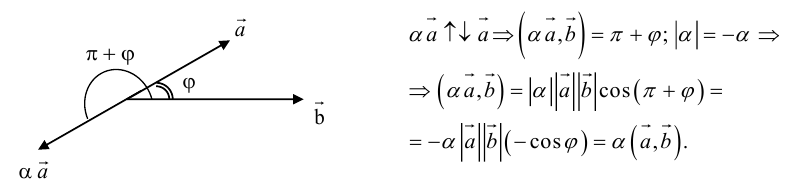
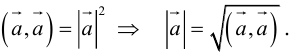
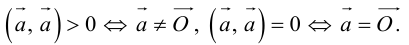
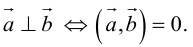
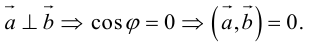
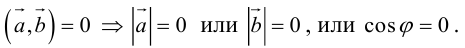
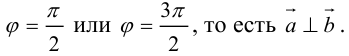
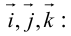
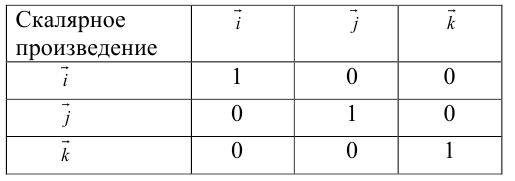
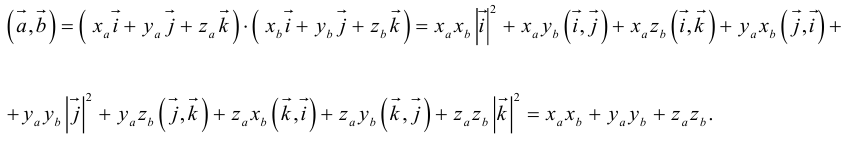

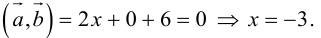
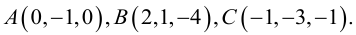

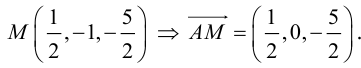
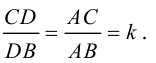
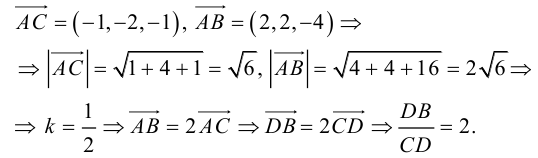
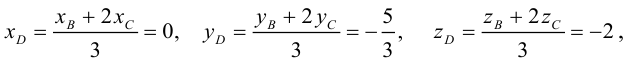
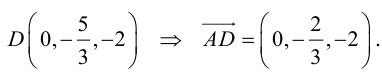
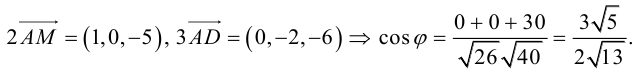
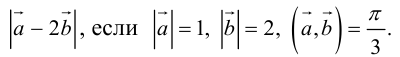
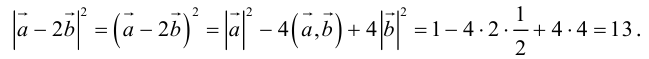
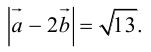
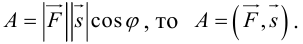
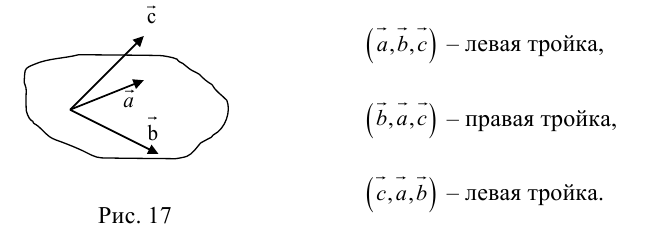
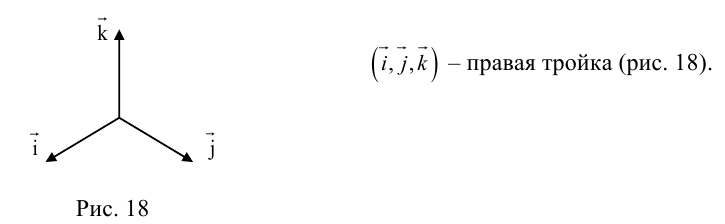
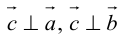 (
(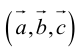 – правая.
– правая.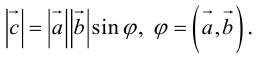
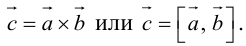
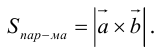
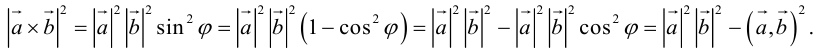
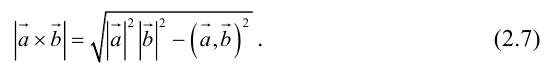
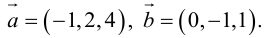
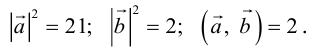
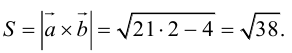
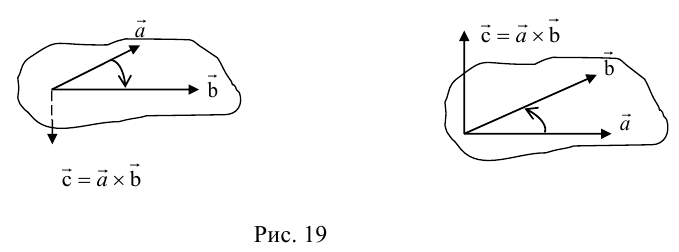
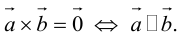
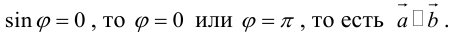
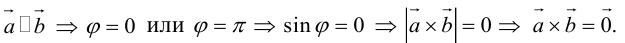
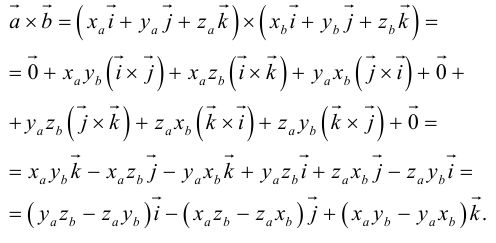
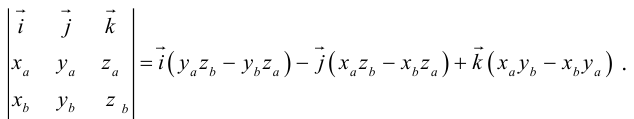
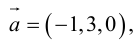
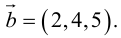
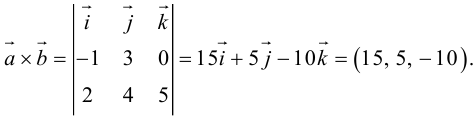
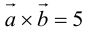
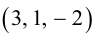
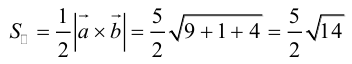
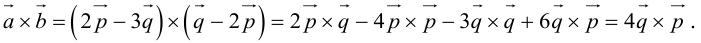
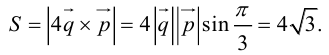
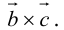
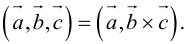
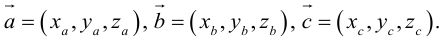
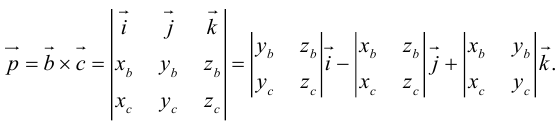
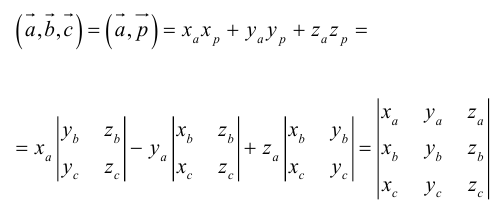
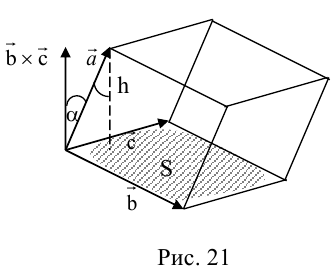
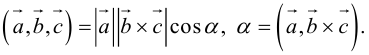
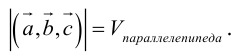
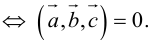
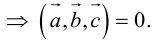
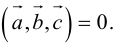
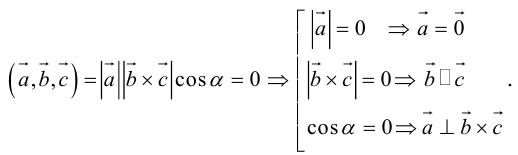
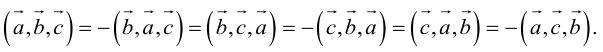
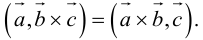
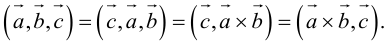
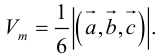
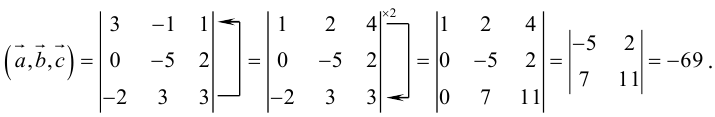
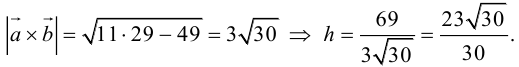























































































 — ассоциативность (сочетательный закон);
— ассоциативность (сочетательный закон); —дистрибутивность относительно сложения векторов (1-й распределительный закон);
—дистрибутивность относительно сложения векторов (1-й распределительный закон); — дистрибутивность относительно сложения чисел (2-й распределительный закон).
— дистрибутивность относительно сложения чисел (2-й распределительный закон).











 отсюда
отсюда 
 – т. е. векторы
– т. е. векторы  компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора  по данным векторам
по данным векторам  единственно. Теорема доказана.
единственно. Теорема доказана.

 получаем
получаем 
 и действительного числа
и действительного числа  получаем
получаем 












































































































































































































