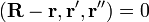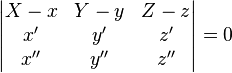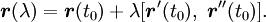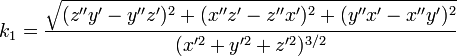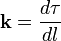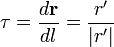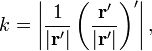-
Нормальная плоскость.
Начать изучение
-
Главная нормаль.
Начать изучение
Нормальная плоскость.
Плоскость (mathcal{P}), проходящую через точку (M_{0}) кривой (Gamma) и перпендикулярную касательной к этой кривой в точке (M_{0}), называют нормальной плоскостью кривой (Gamma) в точке (M_{0}).
Если кривая (Gamma) задана уравнением в векторной форме
$$
Gamma={textbf{r}=textbf{r}(t), alphaleq tleqbeta},label{ref3}
$$
где
$$
textbf{r}=(x,y,z),quad textbf{r}(t)=(x(t),y(t),z(t)),nonumber
$$
(t_{0}in[alpha,beta]), (overrightarrow{OM_0}=textbf{r}(t_0)) и (textbf{r}'(t_0)neq 0), то вектор (textbf{r}'(t_0)) параллелен касательной к кривой (Gamma) в точке (M_{0}). Пусть (M) — произвольная точка нормальной плоскости (mathcal{P}) (рис. 22.5), (overrightarrow{OM}=textbf{r}). Тогда вектор (overrightarrow{MM}_{0}=textbf{r}-textbf{r}(t_0)) перпендикулярен вектору (textbf{r}'(t_{0})), и поэтому уравнение нормальной плоскости (mathcal{P}) к кривой (Gamma) в точке (M_{0}) можно записать в виде
$$
(textbf{r}-textbf{r}(t_{0}),textbf{r}'(t_{0}))=0nonumber
$$
или
$$
(x-x(t_{0}))x'(t_0)+(y-y(t_{0}))y'(t_{0})+(z-z(t_0))z'(t_0)=0.nonumber
$$
Главная нормаль.
Любую прямую, лежащую в нормальной плоскости (mathcal{P}) к кривой (Gamma) в точке (M_{0}), называют нормалью кривой (Gamma) в точке (M_{0}). Среди всех нормалей выделяют одну — главную нормаль.
Понятие главной нормали требует введения дополнительных ограничений на вектор-функции, с помощью которых записываются уравнения кривых. Пусть (Gamma) — гладкая кривая, заданная уравнением eqref{ref3}, причем для всех (tin[alpha,beta]) существует (textbf{r}″(t)). В этом случае говорят, (Gamma) — дважды дифференцируемая кривая без особых точек.
Утверждение 1.
Если (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref{ref3}, (s) — переменная длина дуги кривой (Gamma), то существуют (displaystyle frac{dtextbf{r}}{ds}) и (displaystyle frac{d^{2}textbf{r}}{ds^{2}}) и справедливы равенства
$$
frac{dtextbf{r}}{ds}=frac{textbf{r}'(t)}{s'(t)},label{ref26}
$$
$$
frac{d^{2}rtextbf{}}{ds^{2}}=frac{s'(t)textbf{r}″(t)-s″(t)textbf{r}'(t)}{(s(t))^{3}}.label{ref27}
$$
Доказательство.
(circ) Применяя правило дифференцирования вектор-функции при замене переменного, получаем формулу eqref{ref26}:
$$
frac{dtextbf{r}}{ds}=frac{dtextbf{r}}{dt}frac{dt}{ds}=frac{dtextbf{r}}{dt}frac{1}{s'(t)}=frac{textbf{r}'(t)}{s'(t)}.nonumber
$$
Используя формулу eqref{ref26} и правило дифференцирования произведения векторной функции на скалярную, находим
$$
frac{d^{2}textbf{r}}{ds^{2}}=frac{d}{dt}left(frac{dtextbf{r}}{ds}right)frac{dt}{ds}=frac{d}{dt}left(frac{textbf{r}'(t)}{s'(t)}right)frac{1}{s'(t)}=left(frac{textbf{r}″(t)}{s'(t)}-frac{s″(t)textbf{r}'(t)}{(s(t))^{2}}right)frac{1}{s'(t)},nonumber
$$
откуда следует формула eqref{ref27}.
Заметим, что (s″(t)) существует, так как (s'(t)=|textbf{r}'(t)|),
$$
s″(t)=frac{d}{dt}(|textbf{r}'(t)|)=frac{d}{dt}(textbf{r}'(t),textbf{r}'(t))^{1/2},nonumber
$$
а (textbf{r}″(t)) существует и (|textbf{r}'(t)|neq 0). (bullet)
Перейдем к определению главной нормали. Будем считать, что (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref{ref3}. Тогда существуют (displaystyle frac{dtextbf{r}}{ds}) и (displaystylefrac{d^{2}textbf{r}}{ds^{2}}), причем (displaystyle frac{dtextbf{r}}{ds}) — единичный вектор в силу данного утверждения. Обозначим этот вектор буквой (tau). Тогда
$$
frac{dtextbf{r}}{ds}=tau,quad |tau|=1,label{ref28}
$$
и поэтому (см. данный пример) вектор (displaystyle frac{dtau}{ds}=frac{d^{2}textbf{r}}{ds^{2}}) ортогонален вектору (tau).
Предположим, что
$$
frac{dtau}{ds}neq 0,label{ref29}
$$
и обозначим
$$
k=|frac{dtau}{ds}|.label{ref30}
$$
Пусть (nu) — единичный вектор, параллельный вектору (displaystyle frac{dtau}{ds}). Тогда
$$
frac{dtau}{ds}=knu,quad|nu|=1,label{ref31}
$$
причем вектор (nu) ортогонален вектору (tau).
Так как вектор (tau=displaystyle frac{dtextbf{r}}{ds}) параллелен вектору касательной (r'(t)) к кривой (Gamma) в силу равенства eqref{ref26}, то из eqref{ref31} следует, что вектор (nu) параллелен нормальной плоскости кривой (Gamma) в точке (M) ((overrightarrow{OM}=r(t))). Поэтому вектор (nu) параллелен одной из нормалей кривой (Gamma) в точке (M). Эту нормаль называют главной.
Итак, если в точке (MinGamma) выполняется условие eqref{ref29}, то нормаль к кривой (Gamma) в точке (M), параллельная вектору (nu) (формула eqref{ref31}), называется главной нормалью.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end
Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.
Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).
Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:
Если расписать покоординатно, то получим следующее уравнение:
begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x”(t_0) & y”(t_0) & z”(t_0) \ end right|=0 end
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:
Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$
Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end
begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end
begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$
— правая). Изменим направление одного из векторов. Например, пусть
Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end
begin (X-t_0)cdot t_0^2 – (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.
Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
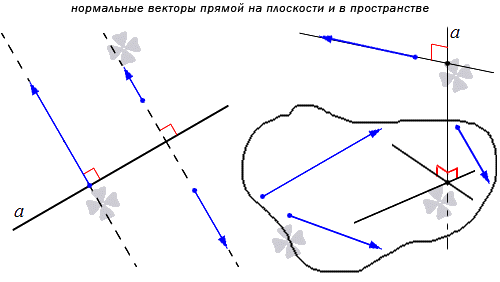
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .
Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2 x + 7 y – 4 = 0 _, найти координаты нормального вектора.
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y – 3 = 0 .
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y – 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .
Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x 1 3 – y = 1 .
Для начала необходимо перейти от уравнения в отрезках x 1 3 – y = 1 к уравнению общего вида. Тогда получим, что x 1 3 – y = 1 ⇔ 3 · x – 1 · y – 1 = 0 .
Отсюда видно, что координаты нормального вектора имеют значение 3 , – 1 .
Ответ: 3 , – 1 .
Если прямая определена каноническим уравнением прямой на плоскости x – x 1 a x = y – y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x – x 1 a x = y – y 1 a y ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 = 0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x – 2 7 = y + 3 – 2 .
Из прямой x – 2 7 = y + 3 – 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , – 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , – 2 ) .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , – 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x – 2 · n y = 0 .
Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 – 2 · n y = 0 ⇔ n y = 7 2 .
Значит, нормальный вектор имеет координаты 1 , 7 2 .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x – 2 7 = y + 3 – 2 ⇔ 7 · ( y + 3 ) = – 2 · ( x – 2 ) ⇔ 2 x + 7 y – 4 + 7 3 = 0
Полученный результат координат нормального вектора равен 2 , 7 .
Ответ: 2 , 7 или 1 , 7 2 .
Указать координаты нормального вектора прямой x = 1 y = 2 – 3 · λ .
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x = 1 y = 2 – 3 · λ ⇔ x = 1 + 0 · λ y = 2 – 3 · λ ⇔ λ = x – 1 0 λ = y – 2 – 3 ⇔ x – 1 0 = y – 2 – 3 ⇔ ⇔ – 3 · ( x – 1 ) = 0 · ( y – 2 ) ⇔ – 3 · x + 0 · y + 3 = 0
Отсюда видно, что координаты нормального вектора равны – 3 , 0 .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .
Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x – x 1 a x = y – y 1 a y = z – z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .
Нормальная плоскость и главная нормаль кривой
Нормальная плоскость.
Плоскость (mathcal
), проходящую через точку (M_<0>) кривой (Gamma) и перпендикулярную касательной к этой кривой в точке (M_<0>), называют нормальной плоскостью кривой (Gamma) в точке (M_<0>).
Рис. 22.5
Если кривая (Gamma) задана уравнением в векторной форме
$$
Gamma=<textbf=textbf(t), alphaleq tleqbeta>,label
$$
где
$$
textbf=(x,y,z),quad textbf(t)=(x(t),y(t),z(t)),nonumber
$$
(t_<0>in[alpha,beta]), (overrightarrow=textbf(t_0)) и (textbf'(t_0)neq 0), то вектор (textbf'(t_0)) параллелен касательной к кривой (Gamma) в точке (M_<0>). Пусть (M) — произвольная точка нормальной плоскости (mathcal
) (рис. 22.5), (overrightarrow=textbf). Тогда вектор (overrightarrow_<0>=textbf-textbf(t_0)) перпендикулярен вектору (textbf'(t_<0>)), и поэтому уравнение нормальной плоскости (mathcal
) к кривой (Gamma) в точке (M_<0>) можно записать в виде
$$
(textbf-textbf(t_<0>),textbf'(t_<0>))=0nonumber
$$
или
$$
(x-x(t_<0>))x'(t_0)+(y-y(t_<0>))y'(t_<0>)+(z-z(t_0))z'(t_0)=0.nonumber
$$
Главная нормаль.
Любую прямую, лежащую в нормальной плоскости (mathcal
) к кривой (Gamma) в точке (M_<0>), называют нормалью кривой (Gamma) в точке (M_<0>). Среди всех нормалей выделяют одну — главную нормаль.
Понятие главной нормали требует введения дополнительных ограничений на вектор-функции, с помощью которых записываются уравнения кривых. Пусть (Gamma) — гладкая кривая, заданная уравнением eqref, причем для всех (tin[alpha,beta]) существует (textbf″(t)). В этом случае говорят, (Gamma) — дважды дифференцируемая кривая без особых точек.
Если (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref, (s) — переменная длина дуги кривой (Gamma), то существуют (displaystyle frac>) и (displaystyle fractextbf>>) и справедливы равенства
$$
frac>=frac<textbf'(t)>,label
$$
$$
fracrtextbf<>>>=frac″(t)-s″(t)textbf'(t)><(s(t))^<3>>.label
$$
(circ) Применяя правило дифференцирования вектор-функции при замене переменного, получаем формулу eqref:
$$
frac>=frac>
$$
Используя формулу eqref и правило дифференцирования произведения векторной функции на скалярную, находим
$$
fractextbf>>=frac
$$
откуда следует формула eqref.
Перейдем к определению главной нормали. Будем считать, что (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref. Тогда существуют (displaystyle frac>) и (displaystylefractextbf>>), причем (displaystyle frac>) — единичный вектор в силу данного утверждения. Обозначим этот вектор буквой (tau). Тогда
$$
frac>=tau,quad |tau|=1,label
$$
и поэтому (см. данный пример) вектор (displaystyle frac=fractextbf>>) ортогонален вектору (tau).
Пусть (nu) — единичный вектор, параллельный вектору (displaystyle frac). Тогда
$$
frac=knu,quad|nu|=1,label
$$
причем вектор (nu) ортогонален вектору (tau).
Так как вектор (tau=displaystyle frac>) параллелен вектору касательной (r'(t)) к кривой (Gamma) в силу равенства eqref, то из eqref следует, что вектор (nu) параллелен нормальной плоскости кривой (Gamma) в точке (M) ((overrightarrow=r(t))). Поэтому вектор (nu) параллелен одной из нормалей кривой (Gamma) в точке (M). Эту нормаль называют главной.
Итак, если в точке (MinGamma) выполняется условие eqref, то нормаль к кривой (Gamma) в точке (M), параллельная вектору (nu) (формула eqref), называется главной нормалью.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-prjamoj-koordinaty-normalnogo-vek/
http://univerlib.com/mathematical_analysis/derivative/normal_plane/
[/spoiler]
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
-
Векторное уравнение $gamma:, vec{r}=vec{r}(t)$.
-
Параметрическое уравнение $gamma:,, x=x(t),, y=y(t),, z=z(t)$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin{equation*}
vec{r_0}=vec{r}(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0).
end{equation*}
Пусть в точке $M$ $ vec{r’}(t_0)neqvec{0}$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec{r’}(t_0)$.
Пусть $vec{R}$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
begin{equation*}
vec{R}=vec{r}(t_0)+lambdavec{r’}(t_0).
end{equation*}
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec{R}$).
Если $vec{R}={X,Y,Z}$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
begin{equation*}
frac{X-x(t_0)}{x'(t_0)}=frac{Y-y(t_0)}{y'(t_0)}=frac{Z-z(t_0)}{z'(t_0)}.
end{equation*}
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec{R}$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec{R}-vec{r}(t_0)$ и $vec{r’}(t_0)$:
begin{equation*}
(vec{R}-vec{r}(t_0))cdotvec{r’}(t_0)=0.
end{equation*}
Если расписать покоординатно, то получим следующее уравнение:
begin{equation*}
x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0.
end{equation*}
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec{r’}(t_0)$, $vec{r”}(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec{R}$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec{R}-vec{r}(t_0)$, $vec{r’}(t_0)$, $vec{r”}(t_0)$:
begin{equation*}
(vec{R}-vec{r}(t_0), vec{r’}(t_0), vec{r”}(t_0))=0.
end{equation*}
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin{equation*}
left|
begin{array}{ccc}
X-x(t_0) & Y-y(t_0) & Z-z(t_0) \
x'(t_0) & y'(t_0) & z'(t_0)\
x”(t_0) & y”(t_0) & z”(t_0) \
end{array}
right|=0
end{equation*}
Плоская кривая лежит в своей соприкасающейся плоскости.
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec{r’}(t_0)timesvec{r”}(t_0)$, тогда ее уравнение можно записать в виде:
begin{equation*}
vec{R}=vec{r}(t_0)+lambda,vec{r’}(t_0)timesvec{r”}(t_0).
end{equation*}
Как и раньше, $vec{R}$ — радиус-вектор произвольной точки бинормали.
Каноническое уравнение прямой:
begin{equation*}
frac{X-x(t_0)}{left|
begin{array}{cc}
y'(t_0) & z'(t_0) \
y”(t_0) & z”(t_0) \
end{array}
right|
}=frac{Y-y(t_0)}{left|
begin{array}{cc}
z'(t_0) & x'(t_0) \
z”(t_0) & x”(t_0) \
end{array}
right|
}=frac{Z-z(t_0)}{left|
begin{array}{cc}
x'(t_0) & y'(t_0) \
x”(t_0) & y”(t_0) \
end{array}
right|
}.
end{equation*}
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec{r’}(t_0) timesleft[vec{r’}(t_0),vec{r”}(t_0)right]$:
begin{equation*}
vec{R}=vec{r}(t_0)+lambda,vec{r’}(t_0) timesleft[vec{r’}(t_0),vec{r”}(t_0)right].
end{equation*}
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение:
Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec{R}-vec{r}(t_0)$, $vec{r’}(t_0)$, $vec{r’}(t_0)timesvec{r”}(t_0)$:
begin{equation*}
left(vec{R}-vec{r}(t_0),, vec{r’}(t_0),, vec{r’}(t_0)timesvec{r”}(t_0)right)=0.
end{equation*}
Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим:
$$ vec{tau}=frac{vec{r’}(t_0)}{|vec{r’}(t_0)|}. $$
Орт бинормали:
$$ vec{beta}=frac{vec{r’}(t_0)timesvec{r”}(t_0)}{|vec{r’}(t_0)timesvec{r”}(t_0)|}. $$
Орт главной нормали:
$$ vec{nu}=frac{vec{r’}(t_0) times[vec{r’}(t_0),,vec{r”}(t_0)]}{|vec{r’}(t_0) times [vec{r’}(t_0),,vec{r”}(t_0)]|}. $$
Правая тройка векторов $vec{tau}$, $vec{nu}$, $vec{beta}$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
$$
x=t,,, y=t^2,,, z=e^t.
$$
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$.
Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin{gather*}
gamma: vec{r}(t)=left{ t,, t^2,, e^tright} ,, Rightarrow \
vec{r’}(t)=left{ 1,, 2t,, e^tright},\
vec{r”}(t)=left{ 0,, 2,, e^tright}.
end{gather*}
В точке $M(t_0=0)$:
begin{gather*}
vec{r}(t_0)={ 0,, 0,, 1},\
vec{r’}(t_0)={ 1,, 0,, 1},\
vec{r”}(t_0)={ 0,, 2,, 1}.
end{gather*}
-
Зная координаты точки $M(0,0,1)$ и направляющего вектора $ vec{r’}(t_0)={ 1,0,1 }$, можем записать уравнение касательной:
begin{equation*}
frac{X}{1}=frac{Y}{0}=frac{Z-1}{1}.
end{equation*}
-
Нормальная плоскость проходит через точку $M(0,0,1)$ перпендикулярно вектору $vec{r’}(t_0)={ 1,0,1 }$, поэтому ее общее уравнение имеет вид:
begin{equation*}
1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1.
end{equation*}
-
Запишем теперь уравнение соприкасающейся плоскости, определяемой точкой $M(0,0,1)$ и векторами: $vec{r’}(t_0)={ 1,, 0,, 1}$, $vec{r”}(t_0)={ 0,, 2,, 1}$:
begin{equation*}
left|
begin{array}{ccc}
X-0 & Y-0 & Z-1 \
1 & 0 & 1\
0 & 2 & 1 \
end{array}
right|=0
end{equation*}
Раскрываем определитель, получаем уравнение:
begin{equation*}
-2X-Y+2Z-2=0
end{equation*}
-
Направление бинормали задается вектором $vec{r’}(t_0) times vec{r”}(t_0)$. Координаты этого вектора мы уже нашли, когда вычисляли миноры в определителе, задающем уравнение соприкасающейся плоскости.
$$
{ 1,, 0,, 1} times { 0,, 2,, 1}= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 1\
0 & 2 & 1 \
end{array}
right|= {-2,, -1,, 2}.
$$
Уравнение бинормали:
begin{equation*}
frac{X}{-2}=frac{Y}{-1}=frac{Z-1}{2}.
end{equation*}
-
Направление главной нормали задается вектором $vec{r’}(t_0) times (vec{r’}(t_0)timesvec{r”}(t_0))$.
$$
{ 1,, 0,, 1} times {-2,, -1,, 2}= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 1\
-2 & -1 & 2 \
end{array}
right|= {1,, -4,, -1} ,, Rightarrow ,,
frac{X}{1}=frac{Y}{-4}=frac{Z-1}{-1}.
$$
-
Спрямляющая плоскость перпендикулярна главной нормали, а значит, вектору ${1,, -4,, -1}$, поэтому можем сразу записать ее общее уравнение:
begin{equation*}
1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0.
end{equation*}
Орт касательной: $vec{tau} =frac{1}{sqrt{2}}{1,,0,,1}$,
Орт главной нормали: $vec{nu} =frac{1}{sqrt{18}}{1,,-4,,-1}$,
Орт бинормали: $vec{beta }=frac{1}{3}{-2,,-1,,2}$.
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec{tau}$, $vec{nu}$, $vec{beta}$ не будет правой (по определению векторного произведения вектор $vec{tau}timesvec{beta}$ направлен так, что тройка векторов $vec{tau}$, $vec{beta}$, $vec{nu}=vec{tau}timesvec{beta}$ — правая). Изменим направление одного из векторов. Например, пусть
$$ vec{nu} =frac{1}{sqrt{18}}{-1,,4,,1}.$$
Теперь тройка $vec{tau}$, $vec{nu}$, $vec{beta}$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой
$$
x=t,,, y=frac{t^2}{2},,, z=frac{t^3}{3},
$$
проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
begin{align*}
gamma: vec{r}(t)&=left{ t,, frac{t^2}{2},, frac{t^3}{3}right} ,, Rightarrow \
vec{r’}(t)&=left{ 1,, t,, 3t^2right},\
vec{r”}(t)&=left{ 0,, 1,, 6tright}.
end{align*}
В точке $M(t=t_0)$:
begin{align*}
vec{r}(t_0)&=left{t_0,, frac{t_0^2}{2},, frac{t_0^3}{3}right} \
vec{r’}(t_0)&=left{1,, t_0,, 3t_0^2right},\
vec{r”}(t_0)&=left{0,, 1,, 6t_0right}.
end{align*}
Соприкасающаяся плоскость определяется векторами $vec{r’}(t_0)$, $vec{r”}(t_0)$, поэтому записываем определитель
begin{equation*}
left|
begin{array}{ccc}
X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \
&&\
1 & t_0 & t^2_0 \
&&\
0 & 1 & 2t_0
end{array}
right|=0 quad Rightarrow
end{equation*}
begin{equation*}
(X-t_0)cdot t_0^2 – (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0.
end{equation*}
Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$:
begin{equation*}
9-t_0^3/3=0 quad Rightarrow quad t_0=3.
end{equation*}
Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости:
$$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой:
$$
x=t^2,,, y=1+t,,, z=2t.
$$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec{r’}(t_0)$ и $vec{r’}(t_0)timesvec{r”}(t_0)$.
В произвольной точке $M(t=t_0)$:
begin{align*}
vec{r}(t_0)&=left{t^2_0,, 1+t_0,, 2t_0right} \
vec{r’}(t_0)&=left{2t_0,, 1,, 2right},\
vec{r”}(t_0)&=left{2,, 0,, 0right}.
end{align*}
begin{equation*}
vec{r’}(t_0)timesvec{r”}(t_0)= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
2t_0 & 1 & 2\
2 & 0 & 0
end{array}
right|= {0,, 4,, -2}
end{equation*}
Записываем уравнение спрямляющей плоскости:
begin{equation*}
left|
begin{array}{ccc}
X-t_0^2 & Y-1-t_0 & Z-2t_0 \
2t_0 & 1 & 2\
0 & 4 & -2
end{array}
right|= 0
end{equation*}
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$:
begin{equation*}
5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_{01}=2,, t_{02}=-frac25.
end{equation*}
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид:
begin{align*}
& 5X-4Y-8Z+24=0,\
& 25X+4Y+8Z=0.
end{align*}
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end
Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.
Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).
Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:
Если расписать покоординатно, то получим следующее уравнение:
begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:
Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$
Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end
begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end
begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$
— правая). Изменим направление одного из векторов. Например, пусть
Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end
begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.
Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end
Нормальная плоскость и главная нормаль кривой
Нормальная плоскость.
Плоскость (mathcal
), проходящую через точку (M_<0>) кривой (Gamma) и перпендикулярную касательной к этой кривой в точке (M_<0>), называют нормальной плоскостью кривой (Gamma) в точке (M_<0>).
Рис. 22.5
Если кривая (Gamma) задана уравнением в векторной форме
$$
Gamma=<textbf=textbf(t), alphaleq tleqbeta>,label
$$
где
$$
textbf=(x,y,z),quad textbf(t)=(x(t),y(t),z(t)),nonumber
$$
(t_<0>in[alpha,beta]), (overrightarrow=textbf(t_0)) и (textbf‘(t_0)neq 0), то вектор (textbf‘(t_0)) параллелен касательной к кривой (Gamma) в точке (M_<0>). Пусть (M) — произвольная точка нормальной плоскости (mathcal
) (рис. 22.5), (overrightarrow=textbf). Тогда вектор (overrightarrow_<0>=textbf-textbf(t_0)) перпендикулярен вектору (textbf‘(t_<0>)), и поэтому уравнение нормальной плоскости (mathcal
) к кривой (Gamma) в точке (M_<0>) можно записать в виде
$$
(textbf-textbf(t_<0>),textbf‘(t_<0>))=0nonumber
$$
или
$$
(x-x(t_<0>))x'(t_0)+(y-y(t_<0>))y'(t_<0>)+(z-z(t_0))z'(t_0)=0.nonumber
$$
Главная нормаль.
Любую прямую, лежащую в нормальной плоскости (mathcal
) к кривой (Gamma) в точке (M_<0>), называют нормалью кривой (Gamma) в точке (M_<0>). Среди всех нормалей выделяют одну — главную нормаль.
Понятие главной нормали требует введения дополнительных ограничений на вектор-функции, с помощью которых записываются уравнения кривых. Пусть (Gamma) — гладкая кривая, заданная уравнением eqref, причем для всех (tin[alpha,beta]) существует (textbf″(t)). В этом случае говорят, (Gamma) — дважды дифференцируемая кривая без особых точек.
Если (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref, (s) — переменная длина дуги кривой (Gamma), то существуют (displaystyle frac>) и (displaystyle fractextbf>>) и справедливы равенства
$$
frac>=frac<textbf‘(t)>,label
$$
$$
fracrtextbf<>>>=frac″(t)-s″(t)textbf‘(t)><(s(t))^<3>>.label
$$
(circ) Применяя правило дифференцирования вектор-функции при замене переменного, получаем формулу eqref:
$$
frac>=frac>
$$
Используя формулу eqref и правило дифференцирования произведения векторной функции на скалярную, находим
$$
fractextbf>>=frac
$$
откуда следует формула eqref.
Перейдем к определению главной нормали. Будем считать, что (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref. Тогда существуют (displaystyle frac>) и (displaystylefractextbf>>), причем (displaystyle frac>) — единичный вектор в силу данного утверждения. Обозначим этот вектор буквой (tau). Тогда
$$
frac>=tau,quad |tau|=1,label
$$
и поэтому (см. данный пример) вектор (displaystyle frac=fractextbf>>) ортогонален вектору (tau).
Пусть (nu) — единичный вектор, параллельный вектору (displaystyle frac). Тогда
$$
frac=knu,quad|nu|=1,label
$$
причем вектор (nu) ортогонален вектору (tau).
Так как вектор (tau=displaystyle frac>) параллелен вектору касательной (r'(t)) к кривой (Gamma) в силу равенства eqref, то из eqref следует, что вектор (nu) параллелен нормальной плоскости кривой (Gamma) в точке (M) ((overrightarrow=r(t))). Поэтому вектор (nu) параллелен одной из нормалей кривой (Gamma) в точке (M). Эту нормаль называют главной.
Итак, если в точке (MinGamma) выполняется условие eqref, то нормаль к кривой (Gamma) в точке (M), параллельная вектору (nu) (формула eqref), называется главной нормалью.
Касательная и нормаль к графику функции
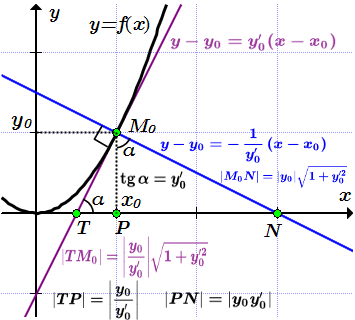
Основные формулы
Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной
Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓
Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓
Определения
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.
Определение касательной приводится здесь. Уравнение касательной:
.
Касательная TM0, нормаль M0N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .
Полезные формулы из аналитической геометрии
Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.
Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.
Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .
Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :
Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.
Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.
Уравнение прямой в отрезках, пересекающей оси координат в точках :
.
Примеры решения задач
Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓
Пример 1
Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.
Находим значение функции при :
.
Находим производную:
.
Находим производную в точке :
;
.
Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .
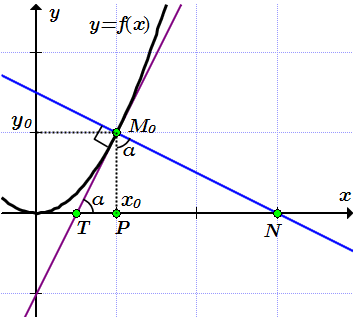Касательная и нормаль к графику функции y=x 2 в точке M0(1;1).
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.
Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .
Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.
Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка поднормали . Из прямоугольника имеем:
.
Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.
Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .
Пример 2
Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .
Находим значения переменных при .
;
.
Обозначим эту точку как .
Находим производные переменных x и y по параметру t .
;
;
;
;
.
Подставляя , находим производную y по x в точке .
.
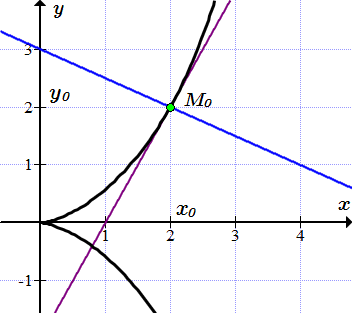Касательная и нормаль к циссоиде в точке (2;2).
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.
Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.
Уравнение касательной: .
Уравнение нормали: .
Пример 3
Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .
Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.
Находим производную в заданной точке, подставляя .
;
.
Находим уравнение касательной по формуле (2).
;
;
;
.
Находим уравнение нормали по формуле (3).
;
;
;
.
Касательная и нормаль к циссоиде изображены на рисунке ⇑.
Уравнение касательной: .
Уравнение нормали: .
Пример 4
Найти угол между кривыми и .
Найдем множество точек пересечения кривых, решая систему уравнений.
Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .
Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.
Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.
Вывод формулы для угла между кривыми
Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .
Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .
Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.
В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .
На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .
При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.
1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).
2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:
.
Этот случай изображен на рисунке ⇑.
3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).
Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.
Автор: Олег Одинцов . Опубликовано: 30-06-2021
источники:
http://univerlib.com/mathematical_analysis/derivative/normal_plane/
http://1cov-edu.ru/mat-analiz/proizvodnaya/kasatelnaya-i-normal-k-grafiku-funktsii/
Главная
»
Общенаучные дисциплины
»
Математика (2 семестр)
»
Главная нормаль. Бинормаль. Сопровождающий трехгранник. Кривизна и кручение.
Главная нормаль. Бинормаль. Сопровождающий трехгранник. Кривизна и кручение.
Соприкасающаяся плоскость и нормали
Если взять в качестве m плоскость, проходящую через точку O кривой M, то условие соприкосновения при 
определяет соприкасающуюся плоскость кривой (рис. 1). Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость. Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся.
Пусть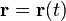 
— уравнение кривой. Тогда уравнение 
её соприкасающейся плоскости определяется из соотношения:
В координатах оно имеет вид:
Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Также нормалью и бинормалью для краткости могут называть единичные векторы вдоль этих прямых (при этом направление вектора главной нормали обычно выбирают совпадающим с направлением вектора кривизны кривой).
Векторное уравнение бинормали в точке, отвечающей значению t0 параметра t, имеет вид:
Направление главной нормали может быть получено как двойное векторное произведение: 
.
Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке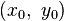 
имеет следующий вид.
- Параметрическое задание:
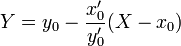
- Явное задание:
- Неявное задание:
- Кривизна
-
При движении вдоль кривой её касательная меняет направление. Скорость этого вращения (отношение угла поворота касательной за бесконечно малый промежуток времени к этому промежутку) при равномерном, с единичной скоростью, движении вдоль кривой называется кривизной кривой. Производная же по времени положительного единичного вектора касательной называется в этом случае вектором кривизны кривой. То и другое – функции точки кривой. Кривизна есть абсолютная величина вектора кривизны.
В случае произвольного параметрического задания кривой кривизна кривой в трехмерном пространстве определяется по формуле
- ,
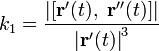где
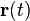— вектор-функция с координатами 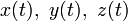.В координатах:
Для кривой в более многомерном пространстве можно заменить векторное произведение, обозначенное здесь квадратными скобками, на внешнее произведение.
Также для кривой в любой размерности пространства можно воспользоваться формулой вектора кривизны:
и фактом, что кривизна есть его модуль, а также выражением для единичного вектора касательной
и
и получить для кривизны формулу:
или, раскрыв скобки:
Прямые и только прямые имеют всюду равную нулю кривизну. Поэтому кривизна наглядно показывает, насколько (в данной точке) кривая отличается от прямой линии: чем ближе кривизна к нулю, тем это отличие меньше. Кривизна окружности радиуса R равна 1 / R.
Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость.
Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения. Кривизна плоской кривой, задаваемой уравнениями
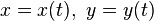, определяется по формуле- .
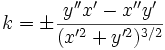Знак + или – берётся по соглашению, но сохраняется вдоль всей кривой.
Кручение
При движении вдоль кривой в окрестности заданной точки соприкасающаяся плоскость вращается, причём касательная к кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении называется кручением. Направление вращения определяет знак кручения.
Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определённое кручение. В случае параметрического задания кривой уравнениями (1) кручение кривой определяется по формуле
здесь ( * , * , * ) обозначает смешанное произведение. В координатах для натуральной параметризации:
Для прямой кручение не определено, поскольку неоднозначно определяется соприкасающаяся плоскость. Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением — плоская.
,
— вектор-функция с координатами
.
, определяется по формуле
.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
