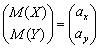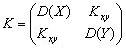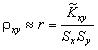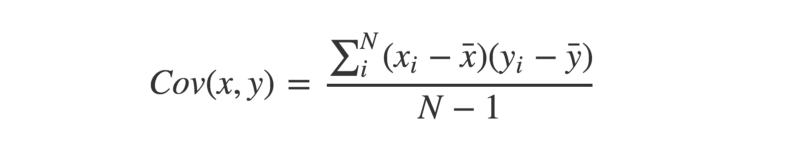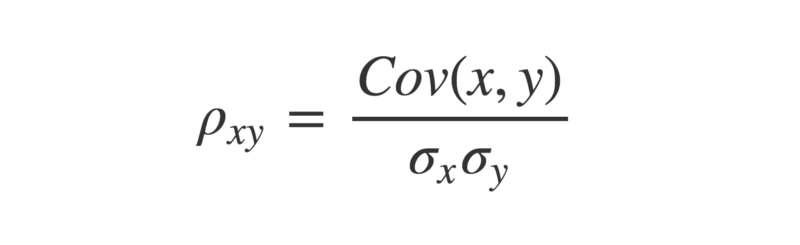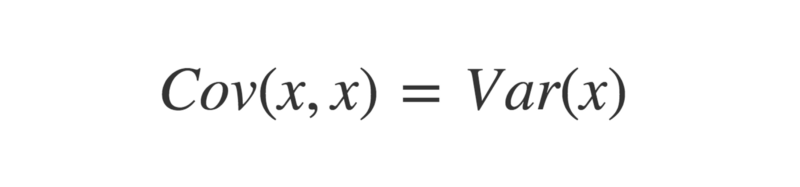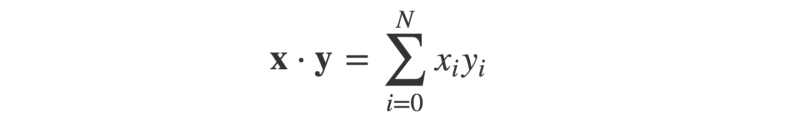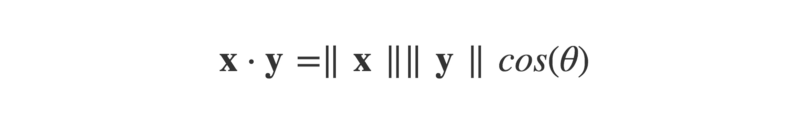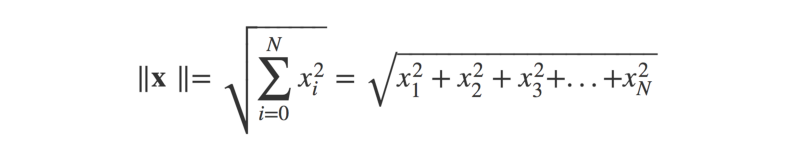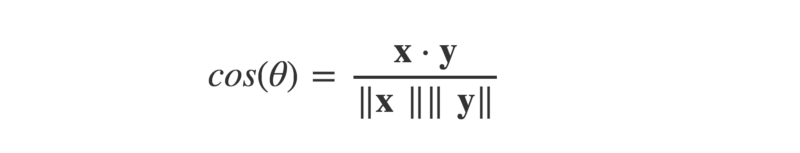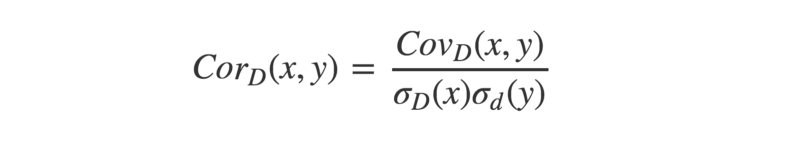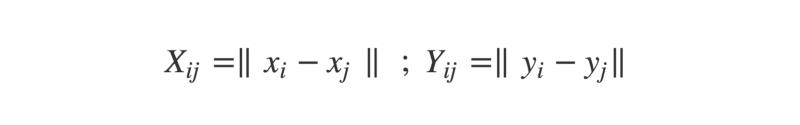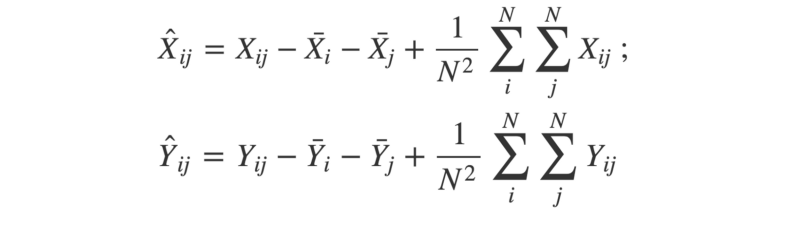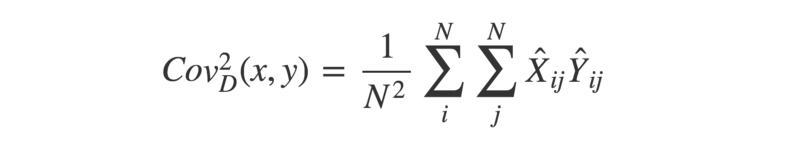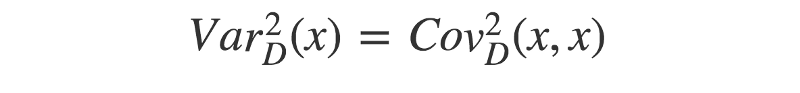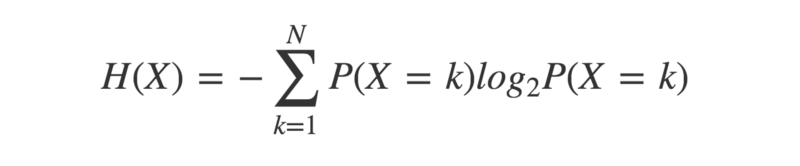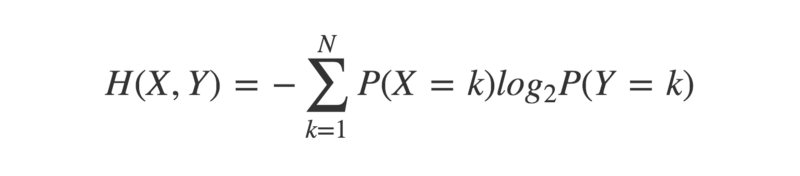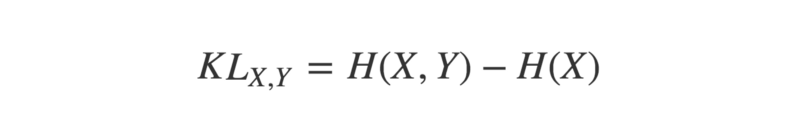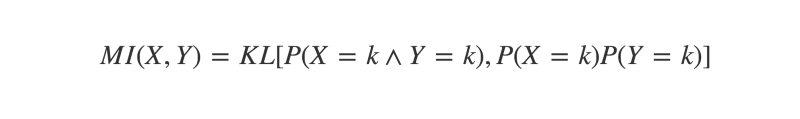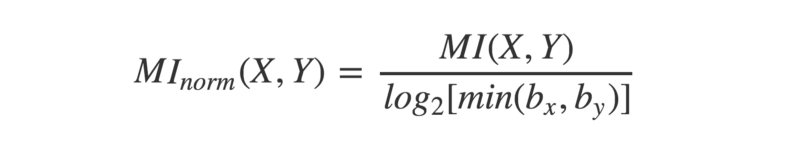Как найти вектор корреляции

Корреляция, ковариация и девиация (часть 3)

В первой части показано, как на основе матрицы расстояний между элементами получить матрицу Грина. Ее спектр образует собственную систему координат множества, центром которой является центроид набора. Во второй рассмотрены спектры простых геометрических наборов.

В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.

7. Векторизация и нормирование одномерных координат

Пусть значения некой характеристики элементов заданы рядом чисел . Для того, чтобы данный набор можно было сравнивать с другими характеристиками, необходимо его векторизовать и обезразмерить (нормировать).
Для векторизации находим центр (среднее) значений

и строим новый набор как разность между исходными числами и их центроидом (средним):

Получили вектор. Основной признак векторов состоит в том, что сумма их координат равна нулю. Далее нормируем вектор, — приведем сумму квадратов его координат к 1. Для выполнения данной операции нам нужно вычислить эту сумму (точнее среднее):

Теперь можно построить ССК исходного набора как совокупность собственного числа S и нормированных координат вектора:

Квадраты расстояний между точками исходного набора определяются как разности квадратов компонент собственного вектора, умноженные на собственное число. Обратим внимание на то, что собственное число S оказалось равно дисперсии исходного набора (7.3).

Итак, для любого набора чисел можно определить собственную систему координат, то есть выделить значение собственного числа (она же дисперсия) и рассчитать координаты собственного вектора путем векторизации и нормирования исходного набора чисел. Круто.

Упражнение для тех, кто любит «щупать руками». Построить ССК для набора <1, 2, 3, 4>.

8. Векторизация и ортонормирование многомерных координат

Что, если вместо набора чисел нам задан набор векторов — пар, троек и прочих размерностей чисел. То есть точка (узел) задается не одной координатой, а несколькими. Как в этом случае построить ССК? Стандартный путь следующий.

Введем обозначение характеристик (компонент) набора. Нам заданы точки (элементы) и каждой точке соответствует числовое значение характеристики . Обращаем внимание, что второй индекс — это номер характеристики (столбцы матрицы), а первый индекс — номер точки (элемента) набора (строки матрицы).

Далее векторизуем характеристики. То есть для каждой находим центроид (среднее значение) и вычитаем его из значения характеристики:

Получили матрицу координат векторов (МКВ) .
Следующим шагом как будто бы надо вычислить дисперсию для каждой характеристики и их нормировать. Но хотя таким образом мы действительно получим нормированные векторы, нам-то нужно, чтобы эти векторы были независимыми, то есть ортонормированными. Операция нормирования не поворачивает вектора (а лишь меняет их длину), а нам нужно развернуть векторы перпендикулярно друг другу. Как это сделать?

Правильный (но пока бесполезный) ответ — рассчитать собственные вектора и числа (спектр). Бесполезный потому, что мы не построили матрицу, для которой можно считать спектр. Наша матрица координат векторов (МКВ) не является квадратной — для нее собственные числа не рассчитаешь. Соответственно, надо на основе МКВ построить некую квадратную матрицу. Это можно сделать умножением МКВ на саму себя (возвести в квадрат).

Но тут — внимание! Неквадратную матрицу можно возвести в квадрат двумя способами — умножением исходной на транспонированную. И наоборот — умножением транспонированной на исходную. Размерность и смысл двух полученных матриц — разный.

Умножая МКВ на транспонированную, мы получаем матрицу корреляции:

Из данного определения (есть и другие) следует, что элементы матрицы корреляции являются скалярными произведениями векторов (грамиан на векторах). Значения главной диагонали отражают квадрат длины данных векторов. Значения матрицы не нормированы (обычно их нормируют, но для наших целей этого не нужно). Размерность матрицы корреляции совпадает с количеством исходных точек (векторов).

Теперь переставим перемножаемые в (8.1) матрицы местами и получим матрицу ковариации (опять же опускаем множитель 1/(1-n), которым обычно нормируют значения ковариации):

Здесь результат выражен в характеристиках. Соответственно, размерность матрицы ковариации равна количеству исходных характеристик (компонент). Для двух характеристик матрица ковариации имеет размерность 2×2, для трех — 3×3 и т.д.

Почему важна размерность матриц корреляции и ковариации? Фишка в том, что поскольку матрицы корреляции и ковариации происходят из произведения одного и того же набора векторов, то они имеют один и тот же набор собственных чисел, один и тот же ранг (количество независимых размерностей) матрицы. Как правило, количество векторов (точек) намного превышает количество компонент. Поэтому о ранге матриц судят по размерности матрицы ковариации.

Диагональные элементы ковариации отражают дисперсию компонент. Как мы видели выше, дисперсия и собственные числа тесно связаны. Поэтому можно сказать, что в первом приближении собственные числа матрицы ковариации (а значит, и корреляции) равны диагональным элементам (а если межкомпонентная дисперсия отсутствует, то равны в любом приближении).

Если стоит задача найти просто спектр матриц (собственные числа), то удобнее ее решать для матрицы ковариации, поскольку, как правило, их размерность небольшая. Но если нам необходимо найти еще и собственные вектора (определить собственную систему координат) для исходного набора, то необходимо работать с матрицей корреляции, поскольку именно она отражает скалярное произведение векторов.

Отметим, что метод главных компонент как раз и состоит в расчете спектра матрицы ковариации/корреляции для заданного набора векторных данных. Найденные компоненты спектра располагаются вдоль главных осей эллипсоида данных. Из нашего рассмотрения это вытекает потому, что главные оси — это и есть те оси, дисперсия (разброс) данных по которым максимален, а значит, и максимально значение спектра.

Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.

9. Матрица Грина — это матрица корреляции векторов

Рассмотрим теперь ситуацию, когда нам известен не набор чисел, характеризующих точки (элементы), а набор расстояний между точками (причем между всеми). Достаточно ли данной информации для определения ССК (собственной системы координат) набора?

Ответ дан в первой части — да, вполне. Здесь же мы покажем, что построенная по формуле (1.3′) матрица Грина и определенная выше матрица корреляции векторов (8.1) — это одна и та же матрица.

Как такое получилось? Сами в шоке. Чтобы в этом убедиться, надо подставить выражение для элемента матрицы квадратов расстояний

в формулу преобразования девиации:

Отметим, что среднее значение матрицы квадратов расстояний отражает дисперсию исходного набора (при условии, что расстояния в наборе — это сумма квадратов компонент):

Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):

Итак, матрица Грина и матрица корреляции векторов — суть одно и то же. Ранг матрицы корреляции совпадает с рангом матрицы ковариации (количеством характеристик — размерностью пространства). Это обстоятельство позволяет строить спектр и собственную систему координат для исходных точек на основе матрицы расстояний.

Для произвольной матрицы расстояний потенциальный ранг (количество измерений) на единицу меньше количества исходных векторов. Расчет спектра (собственной системы координат) позволяет определить основные (главные) компоненты, влияющие на расстояния между точками (векторами).

Таким образом можно строить собственные координаты элементов либо на основании их характеристик, либо на основании расстояний между ними. Например, можно определить собственные координаты городов по матрице расстояний между ними.

Расчет значений вектора и матрицы корреляции

В разд. 1.3 отмечалось, что для оценивания силы линейной зависимости объясняемой переменной у от потенциальных объясняющих переменных х_ь х₂, . х_т рассчитываются коэффициенты корреляции по формуле (1.19), которые формируют вектор корреляции R₀:

Также рассчитываются коэффициенты корреляции между потенциальными объясняющими переменными х_и х₂, . х_т по формуле (1.21)

а их значения записываются в виде матрицы корреляции R, симметричной относительно единичной диагонали.

Задание. Для представленного ниже множественного линейного уравнения и соответствующих ему данных следует оценить силы линейной зависимости объясняемой переменной у от потенциальных объясняющих переменных а также рассчитать коэффициенты корреляции между потенциальными объясняющими переменными х, и Xj, где i * j.

Расчеты следует выполнить по приведенным формулам, а затем с использованием функции КОРРЕЛ табличного процессора Excel и инструмента КОРРЕЛЯЦИЯ, входящего в пакет Анализ данных. Результаты расчетов необходимо представить в виде вектора R₀ и матрицы R корреляции.

А. Расчет коэффициентов корреляции по формулам (1.19) и (1.21).

Проведем расчет средних значений факторов:

Далее приведен пример расчета коэффициента корреляции между X] и у:

Рассчитаем далее r_yxl(rj):

Последующие расчеты коэффициентов корреляции между как у и Xj, так и Xj и Xj проведите самостоятельно.

В. Расчет коэффициентов корреляции с использованием функции КОРРЕЛ табличного процессора Excel.

Для расчета коэффициента корреляции г_уХ[ вызывается функция КОРРЕЛ и задаются в первом массиве значения из столбца у, а во втором массиве значения из столбцах!. Результат будет равен 0,631 (рис. 1.3).

Рис. 1.3. Задание аргументов функции КОРРЕЛ

Аналогичные действия необходимо повторить, меняя значения во втором массиве. Выполните эти действия самостоятельно и запишите полученные результаты в виде вектора корреляции R₀. После этого самостоятельно рассчитайте значения коэффициентов корреляции между х, и х₇ и запишите результаты в виде матрицы корреляции R.

С. Расчет коэффициентов корреляции с использованием инструмента КОРРЕЛЯЦИЯ пакета Анализ данных.

Для выполнения расчета вызывается инструмент КОРРЕЛЯЦИЯ, а в раздел Входные данные в окно Входной интервал вводятся все исходные данные с метками в первой строке. Ставится знак «V» в окне Метки в первой строке. Выполнив эти действия, следует указать параметры вывода (рис. 1.4):

Рис. 1.4. Задание моста вывода результата

6.5.1 лПЧБТЙБГЙС. лПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ

рХУФШ ЪБДБОП ЧЕТПСФОПУФОПЕ РТПУФТБОУФЧП ( W , F, P) Й ДЧЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η ОБ ОЕН.

пртедемеойе 6.5.1.1
лпчбтйбгйек ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η ОБЪЩЧБЕФУС ЮЙУМП, ПРТЕДЕМСЕНПЕ РП ЖПТНХМЕ: M((ξ – Mξ)(η – Mη)).

пвпъобюеойе: cov(ξ, η) = M((ξ – Mξ)(η – Mη))

(6.5.1.1)

пЮЕЧЙДОП, ЮФП cov(ξ, η) НПЦОП ОБКФЙ ФПМШЛП Ч ФПН УМХЮБЕ, ЛПЗДБ УХЭЕУФЧХАФ УППФЧЕФУФЧХАЭЙЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС.

ъбнеюбойе. жПТНХМБ (6.5.1.1) Ч ТБУЮЕФБИ ЙУРПМШЪХЕФУС ТЕДЛП. пРЙТБСУШ ОБ УЧПКУФЧБ НБФЕНБФЙЮЕУЛПЗП ПЦЙДБОЙС Й ДЙУРЕТУЙЙ, НПЦОП РПМХЮЙФШ ВПМЕЕ ХДПВОЩЕ ДМС ТБУЮЕФПЧ ЖПТНХМЩ.

M((ξ – Mξ)(η – Mη)) = M(ξη – ηMξ – ξMη + MξMη) =

= M(ξη) – MξMη – MξMη + MξMη = M(ξη) – MξMη. уМЕДПЧБФЕМШОП,

D(ξ + η) = Dξ + Dη + 2M(ξη) – 2MξMη = Dξ + Dη + 2cov(ξ, η) (уНПФТЙ 6.2.2).

D(ξ – η) = D(ξ + (-η)) = Dξ + D(-η) – 2M(ξ(-η)) – MξM(-η) =
= Dξ + D(-η) – 2(M(ξη) – MξMη) = Dξ + Dη – 2cov(ξ, η).

фептенб 6.5.1.1 (уЧПКУФЧБ ЛПЧБТЙБГЙЙ ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО)
1. еУМЙ ξ Й η – ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ, ФП cov(ξ, η) = 0.
2. cov(ξ, η) = cov(η, ξ).
3. cov(ξ, ξ) = Dξ.
4. cov(ξ, Cη) = Ccov(ξ, η),
cov(Cξ, η) = Ccov(ξ, η), ” C п R.
5. cov(ξ₁ + ξ₂, η) = cov(ξ₁, η) + cov(ξ₂, η);
cov(ξ, η₁ + η₂) = cov(ξ, η₁) + cov(ξ, η₂).

уРТБЧЕДМЙЧПУФШ ХФЧЕТЦДЕОЙК 2-3 УМЕДХЕФ ЙЪ ЖПТНХМЩ (6.5.1.2). дМС ДПЛБЪБФЕМШУФЧБ ПУФБМШОЩИ ЧПУРПМШЪХЕНУС УППФЧЕФУФЧХАЭЙНЙ УЧПКУФЧБНЙ НБФЕНБФЙЮЕУЛПЗП ПЦЙДБОЙС.

1) cov(ξ, η) = M(ξη) – MξMη = MξMη – MξMη = 0, ФБЛ ЛБЛ ДМС ОЕЪБЧЙУЙНЩИ η, ξ M(ξη) = MξMη.

4) cov(ξ, Cη) = M(ξCη) – MξM(Cη) = CM(ξη) – CMξMη = Ccov(ξ, η).

уРТБЧЕДМЙЧПУФШ ЧФПТПК ЖПТНХМЩ НПЦОП ДПЛБЪБФШ МЙВП БОБМПЗЙЮОП, МЙВП, ЙУРПМШЪХС УЧПКУФЧП 2.

уРТБЧЕДМЙЧПУФШ ЧФПТПК ЖПТНХМЩ НПЦОП ДПЛБЪБФШ МЙВП БОБМПЗЙЮОП, МЙВП ЙУРПМШЪХС УЧПКУФЧП 2.

умедуфчйе 6.5.1.1
1. cov(ξ, C) = cov(C, ξ) = 0, ” C п R.
2. cov(ξ, Aξ + B) = cov(Aξ+B, ξ) = ADξ, ” A, B п R.

1) рПУФПСООХА у НПЦОП ТБУУНБФТЙЧБФШ ЛБЛ УМХЮБКОХА ЧЕМЙЮЙОХ η, РТЙОЙНБАЭХА ПДОП ЪОБЮЕОЙЕ у У ЧЕТПСФОПУФША 1. пЮЕЧЙДОП, ЮФП Ч ЬФПН УМХЮБЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η – ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ Й, УМЕДПЧБФЕМШОП, cov(ξ, η) = 0.

2) cov(ξ, Aξ + B) = cov(ξ, Aξ) + cov(ξ, B) = Acov(ξ, ξ) + 0 = ADξ.

ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЙЪ cov(ξ, η) = 0 ОЕ УМЕДХЕФ ОЕЪБЧЙУЙНПУФЙ УМХЮБКОЩИ ЧЕМЙЮЙО ξ, η.

оБРТЙНЕТ, РХУФШ ξ – УМХЮБКОБС ЧЕМЙЮЙОБ ДЙУЛТЕФОПЗП ФЙРБ, ЙНЕАЭБС УМЕДХАЭЙК ЪБЛПО ТБУРТЕДЕМЕОЙС:

x_k	-2	-1	1	2
p_k	1/4	1/4	1/4	1/4

Mξ = (1/4)ћ(-2) + (1/4)ћ(-1) + (1/4)ћ2 + (1/4)ћ1 = 0.

тБУУНПФТЙН η = ξ 2 (η Й ξ Ч ФБЛПН УМХЮБЕ ЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ!) ъБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ η ЙНЕЕФ ЧЙД:

Mη = (1/2)ћ1 + (1/2)ћ4 = 5/2.

cov(ξ, η) = M(ξη) – MξMη = M(ξћξ 2 ) – 0ћ(5/2) = M(ξ 3 ).

уМХЮБКОБС ЧЕМЙЮЙОБ ξ 3 ЙНЕЕФ ЪБЛПО ТБУРТЕДЕМЕОЙС:

x_k	-8	-1	1	8
p_k	1/4	1/4	1/4	1/4

Mξ 3 = (1/4)ћ(-8) + (1/4)ћ(-1) + (1/4)ћ1 + (1/4)ћ8 = 0. уМЕДПЧБФЕМШОП, cov (ξ, η) = 0, Б УМХЮБКОЩЕ ЧЕМЙЮЙОЩ СЧМСАФУС ЪБЧЙУЙНЩНЙ.

пртедемеойе 6.5.1.2
лПЬЖЖЙГЙЕОФПН лпттемсгйй ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η ОБЪЩЧБЕФУС ЮЙУМП, ПРТЕДЕМСЕНПЕ РП ЖПТНХМЕ:

ъбнеюбойе. пЮЕЧЙДОП, ЮФП ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО НПЦОП ПРТЕДЕМЙФШ МЙЫШ Ч ФПН УМХЮБЕ, ЛПЗДБ УХЭЕУФЧХАФ УППФЧЕФУФЧХАЭЙЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС Й Dξ 0, Dη 0.

пРЙТБСУШ ОБ УЧПКУФЧБ ЛПЧБТЙБГЙЙ Й ДЙУРЕТУЙЙ (6.2.2), НПЦОП РПМХЮЙФШ ЕЭЕ ФТЙ ДПРПМОЙФЕМШОЩЕ ЖПТНХМЩ ДМС ЧЩЮЙУМЕОЙС ЛПЬЖЖЙГЙЕОФБ ЛПТТЕМСГЙЙ.

(уНПФТЙ ЖПТНХМХ 6.5.1.3). уМЕДПЧБФЕМШОП,

уПЧЕТЫЕООП БОБМПЗЙЮОП, ПРЙТБСУШ ОБ ЖПТНХМХ 6.5.1.4, НПЦОП ДПЛБЪБФШ, ЮФП:

фептенб 6.5.1.2 (уЧПКУФЧБ ЛПЬЖЖЙГЙЕОФБ ЛПТТЕМСГЙЙ)
1. еУМЙ ξ Й η – ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ, ФП ρ(ξ, η) = 0.
2. ρ(ξ, η) = ρ(η, ξ).
3. ρ(Cξ, η) = ρ(ξ, Cη) = signC ρ(Cξ, η), ” C п R (C 0).
4. |ρ(ξ, η)| ≤ 1.
5. |ρ(ξ, η)| = 1 щ $ A, B п R (A 0): η = Aξ + B.

уЧПКУФЧБ 1-2 УМЕДХАФ ЙЪ УЧПКУФЧ ЛПЧБТЙБГЙЙ.

4) фБЛ ЛБЛ ДЙУРЕТУЙС МАВПК УМХЮБКОПК ЧЕМЙЮЙОЩ (ЕУМЙ ПОБ УХЭЕУФЧЕФ) – ЧЕМЙЮЙОБ ОЕПФТЙГБФЕМШОБС, ФП ЙЪ ЖПТНХМ (6.5.1.7 Й 6.5.1.8) УМЕДХЕФ:

5) ( а ) (ОЕПВИПДЙНПУФШ)

Б) ρ(ξ, η) = 1 а ЙЪ ЖПТНХМЩ 6.5.1.8 УМЕДХЕФ, ЮФП .

ч ФБЛПН УМХЮБЕ, $ C п R:

фБЛЙН ПВТБЪПН, η = Aξ + B, ЗДЕ

ъБНЕФЙН, ЮФП .

В) ρ(ξ, η) = -1. тБУУХЦДБС БОБМПЗЙЮОП Й ЙУРПМШЪХС ЖПТНХМХ 6.5.1.7, НПЦОП ДПЛБЪБФШ, ЮФП

( ш ) η = Aξ + B; A, B п R Й A 0. (дПУФБФПЮОПУФШ.)

умедуфчйе 6.5.1.2
ρ(ξ, ξ) = 1.

ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЙЪ ρ(ξ, η) = 0 ОЕ УМЕДХЕФ ОЕЪБЧЙУЙНПУФШ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η. (фБЛ ЛБЛ ρ(ξ, η) = 0 щ cov(ξ,η)=0; Б ЙЪ cov(ξ,η)=0 ОЕ УМЕДХЕФ, ЮФП ξ Й η ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ).

пртедемеойе 6.5.1.3
еУМЙ ρ(ξ, η) = 0, ФП УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η ОБЪЩЧБАФУС оелпттемйтхенщнй.

ъбнеюбойе. еУМЙ ρ(ξ, η) 0, ФП УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η СЧМСАФУС ЪБЧЙУЙНЩНЙ (РТЙ ρ(ξ, η) = 0 ПОЙ НПЗХФ ВЩФШ ЛБЛ ЪБЧЙУЙНЩНЙ, ФБЛ Й ОЕЪБЧЙУЙНЩНЙ).

еУМЙ ρ(ξ, η) 1, ФП ОБЙМХЮЫЕЕ МЙОЕКОПЕ РТЙВМЙЦЕОЙЕ ДМС η ЙНЕЕФ ЧЙД:

ьФП РТЙВМЙЦЕОЙЕ СЧМСЕФУС ОБЙМХЮЫЕН Ч УНЩУМЕ:

рХУФШ ОБ ЧЕТПСФОПУФОПН РТПУФТБОУФЧЕ ( W , F, P) ЪБДБО УМХЮБКОЩК ЧЕЛФПТ (ξ₁, ξ₂, . , ξ_n).

фБЛ ЛБЛ k_ij = cov(ξ_i, ξ_j) = cov(ξ_j, ξ_i) = k_ji, ” i, j, ФП НБФТЙГБ K – УЙННЕФТЙЮОБС НБФТЙГБ (ПФОПУЙФЕМШОП ЗМБЧОПК ДЙБЗПОБМЙ); k_ii = Dξ_i, i= 1, . , n.

пртедемеойе 6.5.1.5
пРТЕДЕМЙФЕМШ ЛПЧБТЙБГЙПООПК НБФТЙГЩ ОБЪЩЧБЕФУС пвпвэеоопк дйуретуйек УМХЮБКОПЗП ЧЕЛФПТБ.

еУМЙ ξ₁, ξ₂, . , ξ_n РПРБТОП ОЕЪБЧЙУЙНЩ ЙМЙ cov(ξ_i, ξ_j) = 0, i j, ФП НБФТЙГБ K СЧМСЕФУС ДЙБЗПОБМШОПК::

фептенб 6.5.1.3
еУМЙ ЙЪЧЕУФОБ ЛПЧБТЙБГЙПООБС НБФТЙГБ л = (k_ij)_n УМХЮБКОПЗП ЧЕЛФПТБ (ξ₁, ξ₂, . , ξ_n) Й η_i = c_i1ξ₁ + c_i2ξ₂ + . + c_inξ_n, i = 1, . , n; ФП ЕУФШ

ФП ЛПЧБТЙБГЙПООБС НБФТЙГБ H = (h_ij), h_ij = cov(η_i, η_j) УМХЮБКОПЗП ЧЕЛФПТБ (η₁, η₂, . , η_n) НПЦЕФ ВЩФШ ОБКДЕОБ РП ЖПТНХМЕ:
H = CћKћC T .

уМЕДПЧБФЕМШОП, ЛПТТТЕМСГЙПООБС НБФТЙГБ R СЧМСЕФУС УЙННЕФТЙЮОПК.

еУМЙ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ₁, ξ₂, . , ξ_n РПРБТОП ОЕЪБЧЙУЙНЩ ЙМЙ ОЕЛПТТЕМЙТХЕНЩ, ФП ЛПТТЕМСГЙПООБС НБФТЙГБ R СЧМСЕФУС ЕДЙОЙЮОПК:

ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЮФП ЪОБС ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ₁, ξ₂, . , ξ_n), НПЦОП ОБКФЙ ЮЙУМПЧЩЕ ИБТБЛФЕТЙУФЙЛЙ ЛПНРБОЕФ (ЕУМЙ ПОЙ УХЭЕУФЧХАФ).

оБРТЙНЕТ, ЕУМЙ ЧЕЛФПТ – УМХЮБКОБС ЧЕМЙЮЙОБ БВУПМАФОП ОЕРТЕТЧЩОПЗП ФЙРБ У РМПФОПУФША ТБУРТЕДЕМЕОЙС , ФП

ъБРЙЫЙФЕ УБНПУФПСФЕМШОП УППФЧЕФУФЧХАЭЙЕ ЖПТНХМЩ ДМС УМХЮБКОПЗП ЧЕЛФПТБ ДЙУЛТЕФОПЗП ФЙРБ.

ъбдбюб 6.5.1.1 йЪЧЕУФОП, ЮФП Mξ = 1, Dξ = 2; η = 5ξ + 7. оБКФЙ cov(ξ, η).

cov(ξ, η) = cov(ξ, 5ξ + 7) = 5Dξ = 10.

ъбдбюб 6.5.1.2 йЪЧЕУФОП, ЮФП Mξ = 3, Dξ = 8. оБКФЙ ρ(ξ, η), ЕУМЙ η = – 15ξ + 2.

ъбдбюб 6.5.1.3 дБО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ₁, ξ₂) ДЙУЛТЕФОПЗП ФЙРБ:

	5	6	7
0	0,2	0	0
0,1	0,1	0,15	0
0,2	0,05	0,15	0,1
0,3	0,05	0,1	0,1

оБКФЙ: ЛПЧБТЙБГЙПООХА Й ЛПТТЕМСГЙПООХА НБФТЙГЩ УМХЮБКОПЗП ЧЕЛФПТБ (ξ₁, ξ₂).

1) рТЕЦДЕ ЧУЕЗП ОБКДЕН ЪБЛПО ТБУРТЕДЕМЕОЙС ЛБЦДПК ЛПНРПОЕОФЩ (БМЗПТЙФН УНПФТЙ 4.4.2)

ξ₁	5	6	7
0,4	0,4	0,2

Mξ₁ 2 = 25ћ0,4 + 36ћ0,4 + 49ћ0,2 = 34,2;

ξ₂	0	0,1	0,2	0,3
0,2	0,25	0,3	0,25

Mξ₂ = 0ћ0,2 + 0,1ћ0,25 + 0,2ћ0,3 + 0,3ћ0,25 = 0,16;

Mξ₂ 2 = 0ћ0,1 + 0,01ћ0,25 + 0,04ћ0,3 + 0,09ћ0,25 = 0,037;

ъБНЕФЙН, ЮФП УМХЮБКОБС ЧЕМЙЮЙОБ ξ₁ћξ₂ РТЙОЙНБЕФ УМЕДХАЭЙЕ ЪОБЮЕОЙС Ч ЪБЧЙУЙНПУФЙ ПФ ЪОБЮЕОЙК ЛПНРПОЕОФ:

	5	6	7
0	0	0	0
0,1	0,5	0,6	0,7
0,2	1	1,2	1,4
0,3	1,5	1,8	2,1

уМЕДПЧБФЕМШОП, ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ₁ћξ₂ ЙНЕЕФ УМЕДХАЭЙК ЧЙД:

x_k	0	0,5	0,6	0,7	1	1,2	1,4	1,5	1,8	2,1
p_k	0,2	0,1	0,15	0	0,05	0,15	0,1	0,05	0,1	0,1

M(ξ₁ξ₂) = 0ћ0,2 + 0,1ћ0,5 + 0,6ћ0,15 + 0,7ћ0 + 0,05ћ1 + 0,15ћ1,2 +
+ 1,4ћ0,1 + 1,5ћ0,05 + 0,1ћ1,8 + 0,1ћ2,1 = 0,975.

Dξ₁Dξ₂ = 0,56ћ0,0114 = 0,006384 а ρ₁₂ = ρ₂₁ = 0,588.

ъбдбюб 6.5.1.4 йЪЧЕУФЕО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ:

	0	1
-1	0,1	0,2
0	0,2	0,3
1	0	0,2

оБКФЙ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ Й ДЙУРЕТУЙА УМХЮБКОПК ЧЕМЙЮЙОЩ q = 2ξ₁ + ξ 2 ₂.

уМЕДПЧБФЕМШОП, РТЕЦДЕ ЧУЕЗП ПРТЕДЕМЙН ЪБЛПОЩ ТБУРТЕДЕМЕОЙС ξ₁ Й ξ₂.

ξ₁	x_k	0	1
p_k	0,3	0,7

ξ₂	x_k	-1	0	1
p_k	0,3	0,5	0,2

ξ₂ 2	x_k	0	1
p_k	0,5	0,5

ξ₁ξ₂ 2	x_k	0	1
p_k	0,6	0,4

cov(ξ₁, ξ₂ 2 ) = 0,4 – 0,7 ћ 0,5 = 0,05. фБЛЙН ПВТБЪПН,

M q = 2ћ0,7 + 0,5 = 1,9;

D q = 4ћ0,21 + 0,25 + 2ћ0,05 = 0,84 + 0,25 + 0,1 = 1,29.

ъбдбюб 6.5.1.5 йЪЧЕУФОБ РМПФОПУФШ ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ, η):

оБКФЙ ЛПЧБТЙБГЙА УМХЮБКОЩИ ЧЕМЙЮЙО ξ, η.

Cov(ξ, η) = π/2 – 1 – π 2 /16.

(чУЕ ЧЩЮЙУМЕОЙС РТПЧЕТШФЕ!)

ъБДБЮЙ ДМС УБНПУФПСФЕМШОПЗП ТЕЫЕОЙС.

ъбдбюб 6.5.1.1(у) дБО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ₁, ξ₂):

	0	2	5
1	0,1	0	0,2
2	0	0,3	0
4	0,1	0,3	0

уПУФБЧЙФШ ЛПЧБТЙБГЙПООХА Й ЛПТТЕМСГЙПООХА НБФТЙГЩ.

ъбдбюб 6.5.1.2(у) ъБДБО УМХЮБКОЩК ЧЕЛФПТ (ξ, η). йЪЧЕУФОП, ЮФП Mξ = 0, Mη = 2, Dξ = 2, Dη = 1, ρ(ξ, η) = – . оБКФЙ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ Й ДЙУРЕТУЙА УМХЮБКОПК ЧЕМЙЮЙОЩ q = 2ξ – 3η.

ъбдбюб 6.5.1.3(у) йЪЧЕУФОБ РМПФОПУФШ ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ, η):

D – ФТЕХЗПМШОЙЛ, ПЗТБОЙЮЕООЩК РТСНЩНЙ x + y = 1, x = 0, y = 0. оБКФЙ ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ.

[spoiler title=”источники:”]

http://studref.com/707005/ekonomika/raschet_znacheniy_vektora_matritsy_korrelyatsii

http://cde.osu.ru/courses2/course8/p_6_5_1.html

[/spoiler]

Источник

Время на прочтение
5 мин

Количество просмотров 42K

В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.

7. Векторизация и нормирование одномерных координат

и строим новый набор как разность между исходными числами и их центроидом (средним):

Упражнение для тех, кто любит «щупать руками». Построить ССК для набора {1, 2, 3, 4}.

Ответ.

Собственное число (дисперсия): 1.25.
Собственный вектор: {-1.342, -0.447, 0.447, 1.342}.

8. Векторизация и ортонормирование многомерных координат

Умножая МКВ на транспонированную, мы получаем матрицу корреляции:

Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.

9. Матрица Грина — это матрица корреляции векторов

в формулу преобразования девиации:

Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):

Источник

Двумерной называют случайную величину

, возможные значения
которой есть пары чисел

. Составляющие

, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку

на плоскости

либо как случайный вектор

Дискретной называют двумерную величину, составляющие которой дискретны.

Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих

Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.

Закон
распределения дискретной двумерной случайной величины может быть задан:

а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;

б) аналитически, например в виде функции распределения.

Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность

, надо просуммировать
вероятности столбца

. Аналогично сложив
вероятности строки

получим вероятность

Пусть
составляющие

дискретны и имеют соответственно следующие
возможные значения:

;

Условным распределением составляющей

при

(j сохраняет одно и то же
значение при всех возможных значениях

) называют совокупность
условных вероятностей:

Аналогично
определяется условное распределение

Условные
вероятности составляющих

вычисляют соответственно по формулам:

Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Ковариация (корреляционный момент)

Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки

Ковариацию
(корреляционный момент) можно найти по формуле:

Свойства ковариации

Свойство 1.

Ковариация двух независимых случайных величин равна нулю.

Свойство 2.

Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.

Свойство 3.

Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.

Коэффициент корреляции

Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.

Формула коэффициента корреляции:

Две
случайные величины

называют коррелированными, если их коэффициент
корреляции отличен от нуля.

называют некоррелированными величинами, если
их коэффициент корреляции равен нулю

Свойства коэффициента корреляции

Свойство 1.

Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.

Свойство 2.

Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.

Свойство 3.

Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Линейная регрессия

Рассмотрим
двумерную случайную величину

, где

– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины

в виде линейной функции величины

где

– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.

Линейная
средняя квадратическая регрессия

на

имеет вид:

Коэффициент

называют
коэффициентом регрессии

на

, а прямую

называют
прямой среднеквадратической регрессии

на

Аналогично
можно получить прямую среднеквадратической регрессии

на

Смежные темы решебника:

Двумерная непрерывная случайная величина
Линейный выборочный коэффициент корреляции
Парная линейная регрессия и метод наименьших квадратов

Задача 1

Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.

Требуется:

–
определить одномерные законы распределения случайных величин X и Y;

– найти
условные плотности распределения вероятностей величин;

–
вычислить математические ожидания m_x и m_y;

–
вычислить дисперсии σ_x и σ_y;

–
вычислить ковариацию μ_xy;

–
вычислить коэффициент корреляции r_xy.

xy	3	5	8	10	12
-1	0.04	0.04	0.03	0.03	0.01
1	0.04	0.07	0.06	0.05	0.03
3	0.05	0.08	0.09	0.08	0.05
6	0.03	0.04	0.04	0.06	0.08

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 2

Задана
дискретная двумерная случайная величина (X,Y).

а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.

Y	X
1	2	3	4	5
30	0.05	0.03	0.02	0.01	0.01
40	0.03	0.02	0.02	0.04	0.01
50	0.05	0.03	0.02	0.02	0.01
70	0.1	0.03	0.04	0.03	0.01
90	0.1	0.04	0.01	0.07	0.2

Задача 3

Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.

x y	1	2	3
1.5	0.03	0.02	0.02
2.9	0.06	0.13	0.03
4.1	0.4	0.07	0.02
5.6	0.15	0.06	0.01

Задача 4

Двумерная
случайная величина (X,Y) распределена по закону

XY	1	2
-3	0,1	0,2
0	0,2	0,3
-3	0	0,2

Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.

Задача 5

Случайные
величины ξ и η имеют следующий совместный закон распределения:

P(ξ=1,η=1)=0.14

P(ξ=1,η=2)=0.18

P(ξ=1,η=3)=0.16

P(ξ=2,η=1)=0.11

P(ξ=2,η=2)=0.2

P(ξ=2,η=3)=0.21

1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.

2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).

3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}

4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.

Задача 6

Дан закон
распределения двумерной случайной величины (ξ,η):

	ξ=-1	ξ=0	ξ=2
η=1	0,1	0,1	0,1
η=2	0,1	0,2	0,1
η=3	0,1	0,1	0,1

1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания M_ξ,
M_η и дисперсии D_ξ, D_η

2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).

3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?

4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти M_γ и D_γ.

Задача 7

Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.

XY	1	2	4
-2	0,25	0	0,25
1	0	0,25	0
3	0	0,25	0

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 8

Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.

YX	-1	1
-1	0,4	0,1
1	0,2	0,3

Задача 9

Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:

	X=-3	X=0	X=1
Y=-2	0,3	?	0,1
Y=1	0,1	0,1	0,2

Задача 10

Совместный
закон распределения пары

задан таблицей:

xh	-1	0	1
-1	1/12	1/4	1/6
1	1/4	1/12	1/6

Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.

Задача 11

Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции r_xy?

X	20	25	30	35
P	0.1	0.1	0.4	0.4

Задача 12

Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):

XY	0	1	2
-1	?	0,1	0,2
1	0,1	0,2	0,3

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 13

Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:

ξη	-1	1	2
0	1/7	2/7	1/7
1	1/7	1/7	1/7

Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?

Задача 14

Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.

XY	2,3	2,9	3,1	3,4
0,2	0,15	0,15	0	0
2,8	0	0,25	0,05	0,01
3,3	0	0,09	0,2	0,1

Задача 15

Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.

xy	1	4
-10	0,1	0,2
0	0,3	0,1
20	0,2	0,1

Задача 16

Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:

а) законы
распределения ее компонент и их числовые характеристики;

b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.

с)
ковариацию и коэффициент корреляции случайных величин X и Y;

d) составить матрицу ковариаций и матрицу корреляций;

e) вероятность попадания в область, ограниченную линиями y=16-x² и y=0.

f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.

XY	-1	0	1	2
-1	0	1/6	0	1/12
0	1/18	1/9	1/12	1/9
2	1/6	0	1/9	1/9

Задача 17

Совместный
закон распределения случайных величин X и Y задан таблицей:

XY	0	1	3
0	0,15	0,05	0,3
-1	0	0,15	0,1
-2	0,15	0	0,1

Найдите:

а) закон
распределения случайной величины X и закон распределения
случайной величины Y;

б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.

Задача 18

Известен
закон распределения двумерной случайной величины (X,Y).

а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);

б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;

в)
построить поле распределения и линию регрессии Y по X и X по Y;

г)
вычислить корреляционный момент (коэффициент ковариации) μ_xy и
коэффициент корреляции r_xy.

	5	20	35
100	—	—	0.05
115	—	0.2	0.15
130	0.15	0.35	—
145	0.1	—	—-

Источник

5.1 Теоретическое введение

5.1.1 Двумерный случайный вектор. Линейная корреляция

Рассмотрим
систему двух случайных величин
или двумерный
случайный вектор (X,
Y)^T c
центром распределения
и
ковариационной матрицей

(5.1)

где a_x и a_y –
математические ожидания; D(X )
= σ_x² и D(Y )
= σ_y² –
дисперсии случайных
величин X и Yсоответственно; K_xy –
ковариация между величинами X и Y,
определяется следующим образом:

K_xy =
cov(X,Y)
= M[(X
– a_x )(Y
– a_y )].

(5.2)

В
качестве нормированной ковариации
вводится коэффициент
корреляции:

(5.3)

который
характеризует степень линейной
зависимости между
случайными величинами X и Y.

Свойства коэффициента
корреляции следующие.

1. Коэффициент
корреляции является безразмерным
коэффициентом, не зависящим от начала
отсчета величинX и Y.

2. Коэффициент
корреляции по абсолютной величине не
превышает единицу : –1 ≤ ρ_xy ≤
1.

3. Если
|ρ_xy |
= 1, случайные величины X и Y
связаны линейной функциональной
зависимостью.

4. Если
ρ_xy =
0, случайные величины X и Y
некоррелированы,
т.е. между ними отсутствует
линейная зависимость.

5. Чем
ближе значение |ρ_xy |
к единице, тем сильнее линейная зависимость
между X и Y.
Чем ближе значение |ρ_xy |
к нулю, тем слабее линейная зависимость
между X и Y.

6. Если
ρ_xy >
0, то с увеличением одной случайной
величины математическое ожидание
(среднее значение) другой увеличивается;
если ρ_xy <
0, то с увеличением одной случайной
величины математическое ожидание
(среднее значение) другой уменьшается.

Для
случайного вектора (X,
Y)^T вводятся условные
математические ожидания M(X
/ Y = y)
и M(Y
/ X = x). M(X
/ Y = y)
– это математическое ожидание случайной
величины X при
условии, что Y приняло
одно из своих возможных значений y.
Аналогично, M(Y
/ X = x)
– это математическое ожидание случайной
величины Y при
условии, что X приняло
одно из своих возможных значений x.

Функцией
регрессии Y на X называется
зависимость величины M(Y
/ X = x)
от аргумента х.
Она характеризует зависимость
математического ожидания величины Y от
значения, принимаемого величиной X.
Аналогичнофункцией
регрессии X на Y называется
зависимость величины M(X
/ Y = y)
от аргумента y.
Она характеризует зависимость
математического ожидания величины X от
значения, принимаемого величиной Y.
Если обе функции регрессии Y на X и X на Y являются
линейными, корреляционная
зависимость между
случайными величинами X и Y называется линейной.
В случае линейной корреляционной
зависимости уравнения регрессии
– Y на X и X на Y –
называются уравнениями
линейной регрессии.

Уравнение
линейной регрессии Y на X имеет
вид

(5.4)

а
уравнение линейной регрессии X на Y –

(5.5)

5.1.2
Выборочные характеристики двумерного
случайного вектора

Пусть
(X_i, Y_i ), i =
1,2,…, n –
выборка объема n из
наблюдений случайного двумерного
вектора (X,
Y)^T.
Определим оценки числовых характеристик
этого вектора. За оценку математических
ожиданий a_x и a_yпринимаются
средние арифметические
и
(см.
формулу (3.2)), за оценку дисперсий σ_x² и
σ_y² –
соответствующие эмпирические
дисперсии S_x² и S_y²,
вычисленные по формуле (3.3). Здесь и далее
ссылки на формулы с первой цифрой 3
даются на текст типового расчета
10.3.

Несмещенной
оценкой ковариации K_xy является
величина

(5.6)

Для практических расчетов формулу (5.6)
удобно преобразовать к виду:

(5.7)

Расчет упрощается, если, как и при
нахождении оценок параметров одномерной
случайной величины, ввести линейную
замену (3.6):

X_i = C₁ + h₁U_i ;
Y_i = C₂ + h₂V_i .

(5.8)

При такой замене формула (5.7) принимает
вид

(5.9)

Оценку
коэффициента корреляции ρ_xy находят
по формуле

(5.10)

Уравнения
оценочных (выборочных) прямых регрессии
получают по следующим формулам.

Уравнение
линейной регрессии Y на X :

(5.11)

Уравнение
линейной регрессии X на Y :

(5.12)

Выборочные уравнения
прямых регрессии используют для
предсказания среднего значения одной
переменной по значению другой.

5.1.3
Построение доверительного интервала
для коэффициента корреляции. Проверка
гипотезы о существовании линейной
зависимости

Будем
предполагать, что заданная двумерная
выборка имеет двумерное нормальное
распределение. Тогда доверительный
интервал для коэффициента корреляции
можно найти по номограммам. В Приложении
(см. [1]) приведены такие номограммы (рис.
П1) для доверительной вероятности P =
0,95. По горизонтальной оси номограммы
отложены значения выборочного коэффициента
корреляции r,
по вертикальной оси – значения истинного
коэффициента корреляции ρ_xy ,
числа над кривыми указывают объемы
выборок n.
Отложив по горизонтальной оси вычисленное
значение выборочного коэффициента
корреляции, следует подняться над этой
точкой вертикально вверх и найти две
точки пересечения с кривыми, соответствующими
объему заданной выборки. Ординаты этих
двух точек являются границами
доверительного интервала истинного
коэффициента корреляции.

Эти
же графики можно использовать для
проверки гипотезы H₀ об
отсутствии линейной зависимости между
величинами X и Y,
т.е. о том, что истинный коэффициент
корреляции ρ_xy =
0 при альтернативной гипотезе H₁:
ρ_xy ≠
0. Гипотеза H₀ принимается,
т.е. линейная зависимость между величинами
не существует (с уровнем значимости α
= 1 – P),
если значение ρ_xy =
0 принадлежит найденному доверительному
интервалу. Здесь P –
доверительная вероятность при определении
доверительного интервала.
Гипотеза H₀ отвергается,
т.е. принимается альтернативная
гипотеза H₁ (линейная
зависимость между величинами существует),
если значение ρ_xy =
0 не принадлежит найденному доверительному
интервалу.

Для
проверки гипотезы H₀ :
ρ_xy =
0 при альтернативной гипотезе H₁ :
ρ_xy ≠
0 можно использовать другой критерий.
Гипотеза H₀ принимается
с уровнем значимости α, т.е. линейная
зависимость между величинами не
существует, если

(5.13)

в
противоположном случае принимается
гипотеза H₁,
т.е. предполагается, что линейная
зависимость между величинами
существует; t_1–

α/2(n –
2) – квантиль распределения Стьюдента
с числом степеней свободы k = n –
2.

Если
принята гипотеза о существовании
линейной зависимости между случайными
величинами, то, зная доверительный
интервал для коэффициента корреляции,
можно сделать вывод о силе взаимосвязи
между X и Y.
Если доверительный интервал примыкает
к единице или минус единице, то говорят,
что связь сильная. Если доверительный
интервал примыкает к нулю, то говорят,
что связь слабая. Если доверительный
интервал расположен примерно посередине
интервала (–1; 0) или (0; 1), то говорят, что
связь средней величины.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
16.09.2019717.31 Кб1lk.doc
#
16.09.2019423.42 Кб0lk.doc
#
#
#
#

Источник

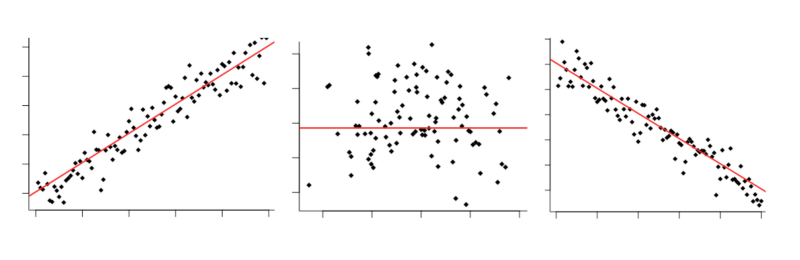
From a signalling perspective, the world is a noisy place. In order to make sense of anything, we have to be selective with our attention.

We humans have, over the course of millions of years of natural selection, become fairly good at filtering out background signals. We learn to associate particular signals with certain events.

For instance, imagine you’re playing table tennis in a busy office.

To return your opponent’s shot, you need to make a huge array of complex calculations and judgements, taking into account multiple competing sensory signals.

To predict the motion of the ball, your brain has to repeatedly sample the ball’s current position and estimate its future trajectory. More advanced players will also take into account any spin their opponent applied to the shot.

Finally, in order to play your own shot, you need to account for the position of your opponent, your own position, the speed of the ball, and any spin you intend to apply.

All of this involves an amazing amount of subconscious differential calculus. We take it for granted that, generally speaking, our nervous system can do this automatically (at least after a bit of practice).

Just as impressive is how the human brain differentially assigns importance to each of the myriad competing signals it receives. The position of the ball, for example, is judged to be more relevant than, say, the conversation taking place behind you, or the door opening in front of you.

This may sound so obvious as to seem unworthy of stating, but that is testament to the just how good we are at learning to make accurate predictions out of noisy data.

Certainly, a blank-state machine given a continuous stream of audiovisual data would face a difficult task knowing which signals best predict the optimal course of action.

Luckily, there are statistical and computational methods that can be used to identify patterns in noisy, complex data.

Correlation 101

Generally speaking, when we talk of ‘correlation’ between two variables, we are referring to their ‘relatedness’ in some sense.

Correlated variables are those which contain information about each other. The stronger the correlation, the more one variable tells us about the other.

You may have seen it all before: Positive correlation, zero correlation, negative correlation

You may well already have some understanding of correlation, how it works and what its limitations are. Indeed, it’s something of a data science cliche:

“Correlation does not imply causation”

This is of course true — there are good reasons why even a strong correlation between two variables is not a guarantor of causality. The observed correlation could be due to the effects of a hidden third variable, or just entirely down to chance.

That said, correlation does allow for predictions about one variable to made based upon another. There are several methods that can be used to estimate correlated-ness for both linear and non-linear data. Let’s take a look at how they work.

We’ll go through the math and the code implementation, using Python and R. The code for the examples this article can be found here.

Pearson’s Correlation Coefficient

What is it?

Pearson’s Correlation Coefficient (PCC, or Pearson’s r) is a widely used linear correlation measure. It’s often the first one taught in many elementary stats courses. Mathematically speaking, it is defined as “the covariance between two vectors, normalized by the product of their standard deviations”.

Tell me more…

The covariance between two paired vectors is a measure of their tendency to vary above or below their means together. That is, a measure of whether each pair tend to be on similar or opposite sides of their respective means.

Let’s see this implemented in Python:

def mean(x):
    return sum(x)/len(x)

def covariance(x,y):
    calc = []
    for i in range(len(x)):
        xi = x[i] - mean(x)
        yi = y[i] - mean(y)
        calc.append(xi * yi)
    return sum(calc)/(len(x) - 1)
    
a = [1,2,3,4,5] ; b = [5,4,3,2,1]
print(covariance(a,b))

The covariance is calculated by taking each pair of variables, and subtracting their respective means from them. Then, multiply these two values together.

If they are both above their mean (or both below), then this will produce a positive number, because a positive×positive=positive, and likewise a negative×negative=positive.
If they are on different sides of their means, then this produces a negative number (because positive×negative=negative).

Once we have all these values calculated for each pair, sum them up, and divide by n-1, where n is the sample size. This is the sample covariance.

If the pairs have a tendency to both be on the same side of their respective means, the covariance will be a positive number. If they have a tendency to be on opposite sides of their means, the covariance will be a negative number. The stronger this tendency, the larger the absolute value of the covariance.

If there is no overall pattern, then the covariance will be close to zero. This is because the positive and negative values will cancel each other out.

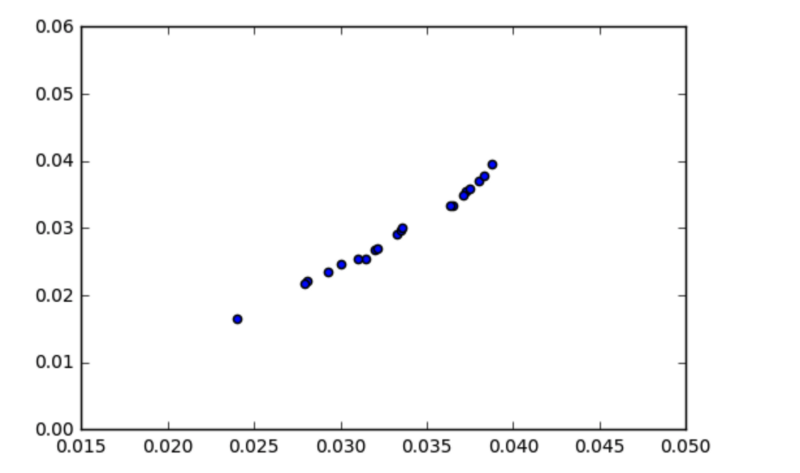
At first, it might appear that the covariance is a sufficient measure of ‘relatedness’ between two variables. However, take a look at the graph below:

Covariance = 0.00003. From a question posted recently on stackexchange

Looks like there’s a strong relationship between the variables, right? So why is the covariance so low, at approximately 0.00003?

The key here is to realise that the covariance is scale-dependent. Look at the x and y axes — pretty much all the data points fall between the range of 0.015 and 0.04. The covariance is likewise going to be close to zero, since it is calculated by subtracting the means from each individual observation.

To obtain a more meaningful figure, it is important to normalize the covariance. This is done by dividing it by the product of the standard deviations of each of the vectors.

The Greek letter rho is often used to denote Pearson’s r

In Python:

import math

def stDev(x):
    variance = 0
    for i in x:
        variance += (i - mean(x) ** 2) / len(x)
    return math.sqrt(variance)
    
def Pearsons(x,y):
    cov = covariance(x,y)
    return cov / (stDev(x) * stDev(y))

The reason this is done is because the standard deviation of a vector is the square root of its variance. This means if two vectors are identical, then multiplying their standard deviations will equal their variance.

Funnily enough, the covariance of two identical vectors is also equal to their variance.

Therefore, the maximum value the covariance between two vectors can take is equal to the product of their standard deviations, which occurs when the vectors are perfectly correlated. It is this which bounds the correlation coefficient between -1 and +1.

Which way do the arrows point?

As an aside, a much cooler way of defining the PCC of two vectors comes from linear algebra.

First, we center the vectors, by subtracting their means from their individual values.

a = [1,2,3,4,5] ; b = [5,4,3,2,1]

a_centered = [i - mean(a) for i in a]
b_centered = [j - mean(b) for j in b]

Now, we can make use of the fact that vectors can be considered as ‘arrows’ pointing in a given direction.

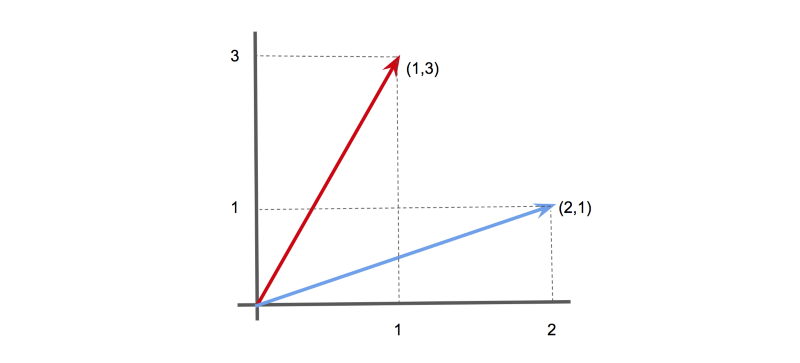
For instance, in 2-D, the vector [1,3] could be represented as an arrow pointing 1 unit along the x-axis, and 3 units along the y-axis. Likewise, the vector [2,1] could be represented as an arrow pointing 2 units along the x-axis, and 1 unit along the y-axis.

Two vectors (1,3) and (2,1) shown as arrows.

Similarly, we can represent our data vectors as arrows in an n-dimensional space (although don’t try visualising when n > 3…)

The angle ϴ between these arrows can be worked out using the dot product of the two vectors. This is defined as:

Or, in Python:

def dotProduct(x,y):
    calc = 0
    for i in range(len(x)):
        calc += x[i] * y[i]
    return calc

The dot product can also be defined as:

Where ||x|| is the magnitude (or ‘length’) of the vector x (think Pythagoras’ theorem), and ϴ is the angle between the arrow vectors.

As a Python function:

def magnitude(x):
    x_sq = [i ** 2 for i in x]
    return math.sqrt(sum(x_sq))

This lets us find cos(ϴ), by dividing the dot product by the product of the magnitudes of the two vectors.

def cosTheta(x,y):
    mag_x = magnitude(x)
    mag_y = magnitude(y)
    return dotProduct(x,y) / (mag_x * mag_y)

Now, if you know a little trigonometry, you may recall that the cosine function produces a graph that oscillates between +1 and -1.

Source

The value of cos(ϴ) will vary depending on the angle between the two arrow vectors.

When the angle is zero (i.e., the vectors point in the exact same direction), cos(ϴ) will equal 1.
When the angle is -180°, (the vectors point in exact opposite directions), then cos(ϴ) will equal -1.
When the angle is 90° (the vectors point in completely unrelated directions), then cos(ϴ) will equal zero.

This might look familiar — a measure between +1 and -1 that seems to describe the relatedness of two vectors? Isn’t that Pearson’s r?

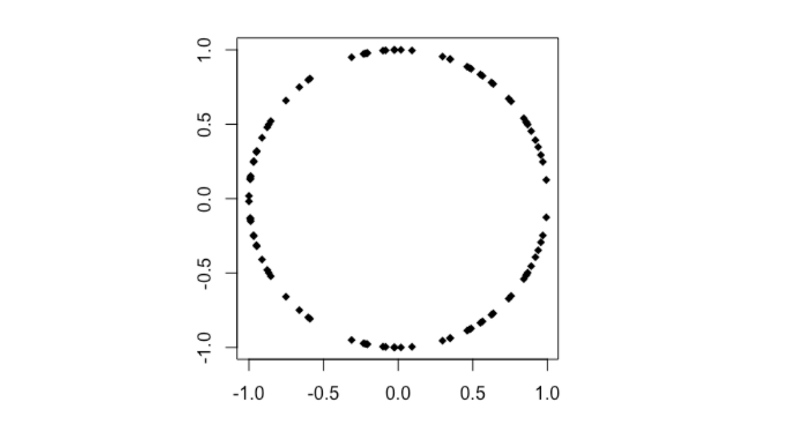
Well — that is exactly what it is! By considering the data as arrow vectors in a high-dimensional space, we can use the angle ϴ between them as a measure of similarity.

A) Positively correlated vectors; B) Negatively correlated vectors; C) Uncorrelated vectors

The cosine of this angle ϴ is mathematically identical to Pearson’s Correlation Coefficient.

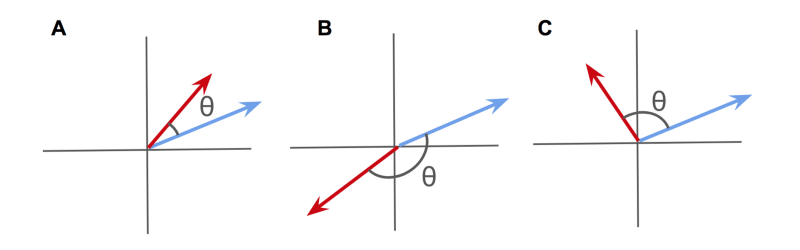
When viewed as high-dimensional arrows, positively correlated vectors will point in a similar direction.

Negatively correlated vectors will point towards opposite directions.

And uncorrelated vectors will point at right-angles to one another.

Personally, I think this is a really intuitive way to make sense of correlation.

Statistical significance?

As is always the case with frequentist statistics, it is important to ask how significant a test statistic calculated from a given sample actually is. Pearson’s r is no exception.

Unfortunately, whacking confidence intervals on an estimate of PCC is not entirely straightforward.

This is because Pearson’s r is bound between -1 and +1, and therefore isn’t normally distributed. An estimated PCC of, say, +0.95 has only so much room for error above it, but plenty of room below.

Luckily, there is a solution — using a trick called Fisher’s Z-transform:

Calculate an estimate of Pearson’s r as usual.
Transform r→z using Fisher’s Z-transform. This can be done by using the formula z = arctanh(r), where arctanh is the inverse hyperbolic tangent function.
Now calculate the standard deviation of z. Luckily, this is straightforward to calculate, and is given by SDz = 1/sqrt(n-3), where n is the sample size.
Choose your significance threshold, alpha, and check how many standard deviations from the mean this corresponds to. If we take alpha = 0.95, use 1.96.
Find the upper estimate by calculating z +(1.96 × SDz), and the lower bound by calculating z – (1.96 × SDz).
Convert these back to r, using r = tanh(z), where tanh is the hyperbolic tangent function.
If the upper and lower bounds are both the same side of zero, you have statistical significance!

Here’s a Python implementation:

r = Pearsons(x,y)
z = math.atanh(r)
SD_z = 1 / math.sqrt(len(x) - 3)
z_upper = z + 1.96 * SD_z
z_lower = z - 1.96 * SD_z
r_upper = math.tanh(z_upper)
r_lower = math.tanh(z_lower)

Of course, when given a large data set of many potentially correlated variables, it may be tempting to check every pairwise correlation. This is often referred to as ‘data dredging’ — scouring the data set for any apparent relationships between the variables.

If you do take this multiple comparison approach, you should use stricter significance thresholds to reduce your risk of discovering false positives (that is, finding unrelated variables which appear correlated purely by chance).

One method for doing this is to use the Bonferroni correction.

The small print

So far, so good. We’ve seen how Pearson’s r can be used to calculate the correlation coefficient between two variables, and how to assess the statistical significance of the result. Given an unseen set of data, it is possible to start mining for significant relationships between the variables.

However, there is a major catch — Pearson’s r only works for linear data.

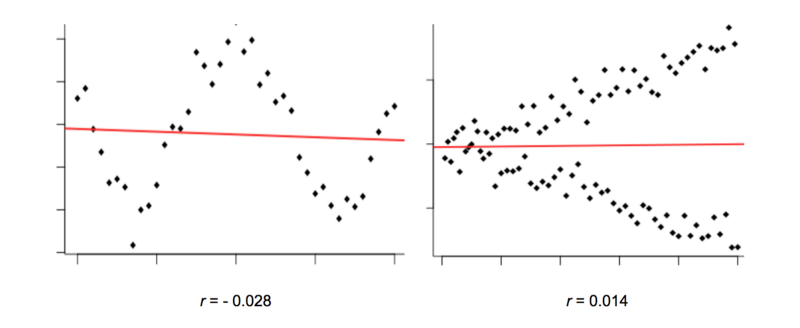
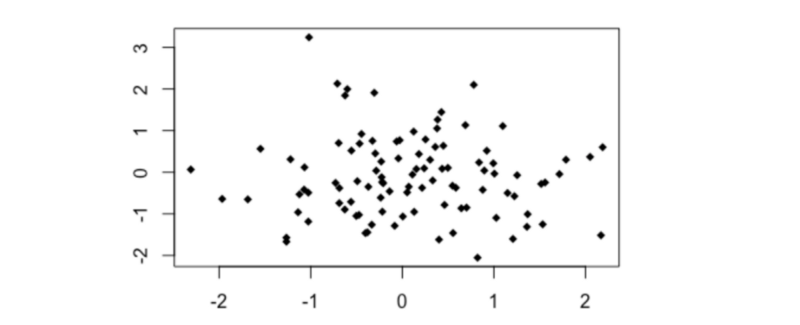
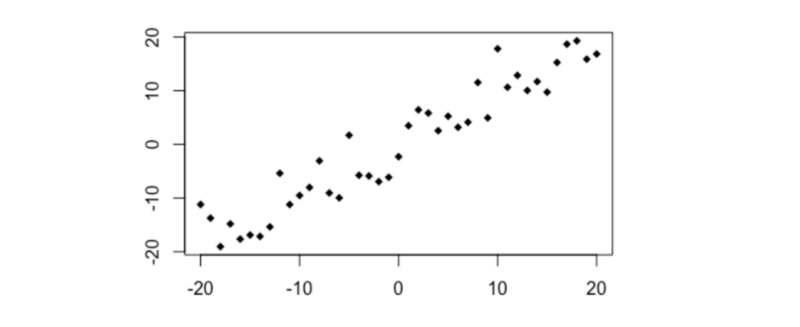
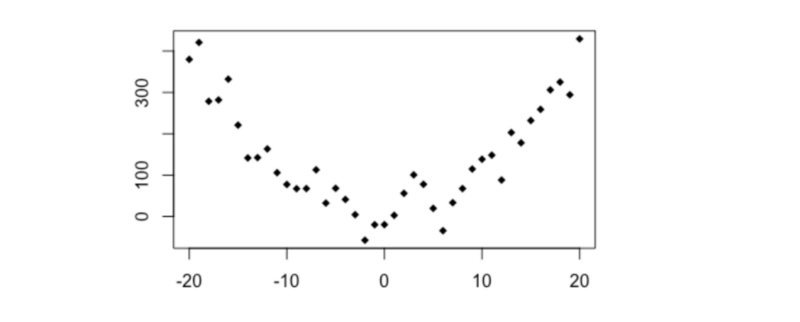
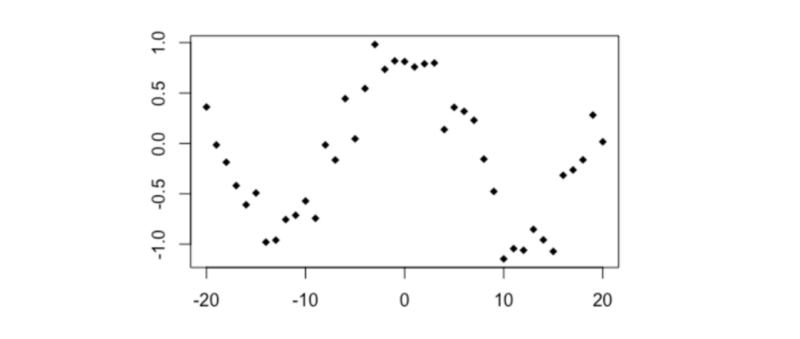
Look at the graphs below. They clearly show what looks like a non-random relationship, but Pearson’s r is very close to zero.

The reason why is because the variables in these graphs have a non-linear relationship.

We can generally picture a relationship between two variables as a ‘cloud’ of points scattered either side of a line. The wider the scatter, the ‘noisier’ the data, and the weaker the relationship.

However, Pearson’s r compares each individual data point with only one other (the overall means). This means it can only consider straight lines. It’s not great at detecting any non-linear relationships.

In the graphs above, Pearson’s r doesn’t reveal there being much correlation to talk of.

Yet the relationship between these variables is still clearly non-random, and that makes them potentially useful predictors of each other. How can machines identify this? Luckily, there are different correlation measures available to us.

Let’s take a look at a couple of them.

Distance Correlation

What is it?

Distance correlation bears some resemblance to Pearson’s r, but is actually calculated using a rather different notion of covariance. The method works by replacing our everyday concepts of covariance and standard deviation (as defined above) with “distance” analogues.

Much like Pearson’s r, “distance correlation” is defined as the “distance covariance” normalized by the “distance standard deviation”.

Instead of assessing how two variables tend to co-vary in their distance from their respective means, distance correlation assesses how they tend to co-vary in terms of their distances from all other points.

This opens up the potential to better capture non-linear dependencies between variables.

The finer details…

Robert Brown was a Scottish botanist born in 1773. While studying plant pollen under his microscope, Brown noticed tiny organic particles jittering about at random on the surface of the water he was using.

Little could he have suspected a chance observation of his would lead to his name being immortalized as the (re-)discoverer of Brownian motion.

Even less could he have known that it would take nearly a century before Albert Einstein would provide an explanation for the phenomenon — and hence proving the existence of atoms — in the same year he published papers on E=MC², special relativity and helped kick-start the field of quantum theory.

Brownian motion is a physical process whereby particles move about at random due to collisions with surrounding molecules.

The math behind this process can be generalized into a concept known as the Weiner process. Among other things, the Weiner process plays an important part in mathematical finance’s most famous model, Black-Scholes.

Interestingly, Brownian motion and the Weiner process turn out to be relevant to a non-linear correlation measure developed in the mid-2000’s through the work of Gabor Szekely.

Let’s run through how this can be calculated for two vectors x and y, each of length N.

First, we form N×N distance matrices for each of the vectors. A distance matrix is exactly like a road distance chart in an atlas — the intersection of each row and column shows the distance between the corresponding cities. Here, the intersection between row i and column j gives the distance between the i-th and j-th elements of the vector.

2. Next, the matrices are “double-centered”. This means for each element, we subtract the mean of its row and the mean of its column. Then, we add the grand mean of the entire matrix.

The ‘hat’ symbols mean ‘double-centred’; the ‘bar’ symbols mean ‘mean’

3. With the two double-centered matrices, we can calculate the square of the distance covariance by taking the average of each element in X multiplied by its corresponding element in Y.

4. Now, we can use a similar approach to find the “distance variance”. Remember — the covariance of two identical vectors is equivalent to their variance. Therefore, the squared distance variance can be described as below:

5. Finally, we have all the pieces to calculate the distance correlation. Remember that the (distance) standard deviation is equal to the square-root of the (distance) variance.

If you prefer to work through code instead of math notation (after all, there is a reason people tend to write software in one and not the other…), then check out the R implementation below:

set.seed(1234)

doubleCenter <- function(x){
  centered <- x
  for(i in 1:dim(x)[1]){
    for(j in 1:dim(x)[2]){
      centered[i,j] <- x[i,j] - mean(x[i,]) - mean(x[,j]) + mean(x)
      }
    }
  return(centered)
}

distanceCovariance <- function(x,y){
  N <- length(x)
  distX <- as.matrix(dist(x))
  distY <- as.matrix(dist(y))
  centeredX <- doubleCenter(distX)
  centeredY <- doubleCenter(distY)
  calc <- sum(centeredX * centeredY)
  return(sqrt(calc/(N^2)))
 }

distanceVariance <- function(x){
  return(distanceCovariance(x,x))
}
distanceCorrelation <- function(x,y){
  cov <- distanceCovariance(x,y)
  sd <- sqrt(distanceVariance(x)*distanceVariance(y))
  return(cov/sd)
}

# Compare with Pearson's r
x <- -10:10
y <- x^2 + rnorm(21,0,10)
cor(x,y) # --> 0.057
distanceCorrelation(x,y) # --> 0.509

The distance correlation between any two variables is bound between zero and one. Zero implies the variables are independent, whereas a score closer to one indicates a dependent relationship.

If you’d rather not write your own distance correlation methods from scratch, you can install R’s energy package, written by very researchers who devised the method. The methods available in this package call functions written in C, giving a great speed advantage.

Physical interpretation

One of the more surprising results relating to the formulation of distance correlation is that it bears an exact equivalence to Brownian correlation.

Brownian correlation refers to the independence (or dependence) of two Brownian processes. Brownian processes that are dependent will show a tendency to ‘follow’ each other.

A simple metaphor to help grasp the concept of distance correlation is to picture a fleet of paper boats floating on the surface of a lake.

If there is no prevailing wind direction, then each boat will drift about at random — in a way that’s (kind of) analogous to Brownian motion.

Boats drifting under no prevailing wind

If there is a prevailing wind, then the direction the boats drift in will be dependent upon the strength of the wind. The stronger the wind, the stronger the dependence.

Under a prevailing wind, the boats will tend to drift in the same direction

In a comparable way, uncorrelated variables can be thought of as boats drifting without a prevailing wind. Correlated variables can be thought of as boats drifting under the influence of a prevailing wind. In this metaphor, the wind represents the strength of the relationship between the two variables.

If we allow the prevailing wind direction to vary at different points on the lake, then we can bring a notion of non-linearity into the analogy. Distance correlation uses the distances between the ‘boats’ to infer the strength of the prevailing wind.

Confidence Intervals?

Confidence intervals can be established for a distance correlation estimate using a ‘resampling’ technique. A simple example is bootstrap resampling.

This is a neat statistical trick that requires us to ‘reconstruct’ the data by randomly sampling (with replacement) from the original data set. This is repeated many times (e.g., 1000), and each time the statistic of interest is calculated.

This will produce a range of different estimates for the statistic we’re interested in. We can use these to estimate the upper and lower bounds for a given level of confidence.

Check out the R code below for a simple bootstrap function:

set.seed(1234)

bootstrap <- function(x,y,reps,alpha){
  estimates <- c()
  original <- data.frame(x,y)
  N <- dim(original)[1]
  for(i in 1:reps){
    S <- original[sample(1:N, N, replace = TRUE),]
    estimates <- append(estimates, distanceCorrelation(S$x, S$y))
  }
  u <- alpha/2 ; l <- 1-u
  interval <- quantile(estimates, c(l, u))
  return(2*(dcor(x,y)) - as.numeric(interval[1:2]))
}

# Use with 1000 reps and threshold alpha = 0.05
x <- -10:10
y <- x^2 + rnorm(21,0,10)
bootstrap(x,y,1000,0.05) # --> 0.237 to 0.546

If you want to establish statistical significance, there is another resampling trick available, called a ‘permutation test’.

This is slightly different to the bootstrap method defined above. Here, we keep one vector constant and ‘shuffle’ the other by resampling. This approximates the null hypothesis — that there is no dependency between the variables.

The ‘shuffled’ variable is then used to calculate the distance correlation between it and the constant variable. This is done many times, and the distribution of outcomes is compared against the actual distance correlation (obtained from the unshuffled data).

The proportion of ‘shuffled’ outcomes greater than or equal to the ‘real’ outcome is then taken as a p-value, which can be compared to a given significance threshold (e.g., 0.05).

Check out the code to see how this works:

permutationTest <- function(x,y,reps){
  estimates <- c()
  observed <- distanceCorrelation(x,y)
  N <- length(x)
  for(i in 1:reps){
    y_i <- sample(y, length(y), replace = T)
    estimates <- append(estimates, distanceCorrelation(x, y_i))
  }
  p_value <- mean(estimates >= observed)
  return(p_value)
}

# Use with 1000 reps
x <- -10:10
y <- x^2 + rnorm(21,0,10)
permutationTest(x,y,1000) # --> 0.036

Maximal Information Coefficient

What is it?

The Maximal Information Coefficient (MIC) is a recent method for detecting non-linear dependencies between variables, devised in 2011. The algorithm used to calculate MIC applies concepts from information theory and probability to continuous data.

Diving in…

Information theory is a fascinating field within mathematics that was pioneered by Claude Shannon in the mid-twentieth century.

A key concept is entropy — a measure of the uncertainty in a given probability distribution. A probability distribution describes the probabilities of a given set of outcomes associated with a particular event.

Entropy of a probability distribution is minus “the sum of the probability of each outcome, multiplied by the logarithm of itself”

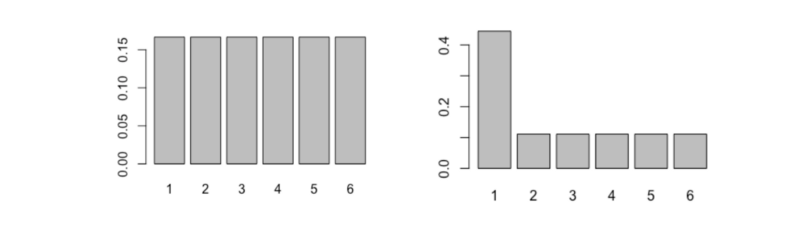
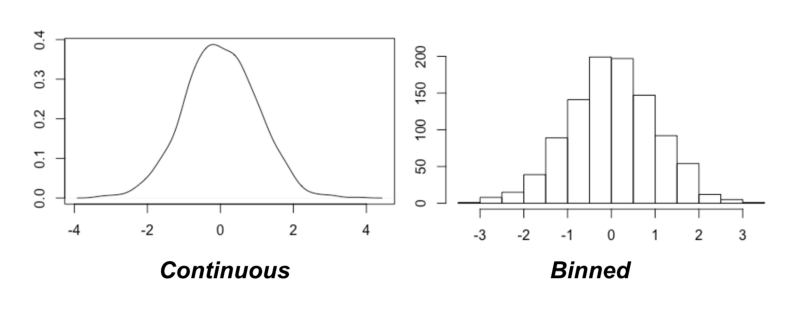
To understand how this works, compare the two probability distributions below:

Possible outcomes are on the X-axis; their respective probabilities are on the Y-axis

On the left is that of a fair six-sided dice, and on the right is the distribution of a not-so-fair six-sided dice.

Intuitively, which would you expect to have the higher entropy? For which dice is the outcome the least certain? Let’s calculate the entropy and see what the answer turns out to be.

entropy <- function(x){
  pr <- prop.table(table(x))
  H <- sum(pr * log(pr,2))
  return(-H)
}

dice1 <- 1:6
dice2 <- c(1,1,1,1,2:6)
entropy(dice1) # --> 2.585
entropy(dice2) # --> 2.281

As you may have expected, the fairer dice has the higher entropy.

That is because each outcome is as likely as any other, so we cannot know in advance which to favour.

The unfair dice gives us more information — some outcomes are much more likely than others — so there is less uncertainty about the outcome.

By that reasoning, we can see that entropy will be highest when each outcome is equally likely. This type of probability distribution is called a ‘uniform’ distribution.

Cross-entropy is an extension to the concept of entropy, that takes into account a second probability distribution.

crossEntropy <- function(x,y){
  prX <- prop.table(table(x))
  prY <- prop.table(table(y))
  H <- sum(prX * log(prY,2))
  return(-H)
}

This has the property that the cross-entropy between two identical probability distributions is equal to their individual entropy. When considering two non-identical probability distributions, there will be a difference between their cross-entropy and their individual entropies.

This difference, or ‘divergence’, can be quantified by calculating their Kullback-Leibler divergence, or KL-divergence.

The KL-divergence of two probability distributions X and Y is:

KL-divergence of probability distributions X and Y equals their cross-entropy, minus the entropy of X

The minimum value of the KL-divergence between two distributions is zero. This only happens when the distributions are identical.

KL_divergence <- function(x,y){
  kl <- crossEntropy(x,y) - entropy(x)
  return(kl)
}

One use for KL-divergence in the context of discovering correlations is to calculate the Mutual Information (MI) of two variables.

Mutual Information can be defined as “the KL-divergence between the joint and marginal distributions of two random variables”. If these are identical, MI will equal zero. If they are at all different, then MI will be a positive number. The more different the joint and marginal distributions are, the higher the MI.

To understand this better, let’s take a moment to revisit some probability concepts.

The joint distribution of variables X and Y is simply the probability of them co-occurring. For instance, if you flipped two coins X and Y, their joint distribution would reflect the probability of each observed outcome. Say you flip the coins 100 times, and get the result “heads, heads” 40 times. The joint distribution would reflect this.

P(X=H, Y=H) = 40/100 = 0.4

jointDist <- function(x,y){
  N <- length(x)
  u <- unique(append(x,y))
  joint <- c()
  for(i in u){
    for(j in u){
      f <- x[paste0(x,y) == paste0(i,j)]
      joint <- append(joint, length(f)/N)
    }
  }
  return(joint)
}

The marginal distribution is the probability distribution of one variable in the absence of any information about the other. The product of two marginal distributions gives the probability of two events’ co-occurrence under the assumption of independence.

For the coin flipping example, say both coins produce 50 heads and 50 tails. Their marginal distributions would reflect this.

P(X=H) = 50/100 = 0.5 ; P(Y=H) = 50/100 = 0.5

P(X=H) × P(Y=H) = 0.5 × 0.5 = 0.25

marginalProduct <- function(x,y){
  N <- length(x)
  u <- unique(append(x,y))
  marginal <- c()
  for(i in u){
    for(j in u){
      fX <- length(x[x == i]) / N
      fY <- length(y[y == j]) / N 
      marginal <- append(marginal, fX * fY)
    }
  }
  return(marginal)
}

Returning to the coin flipping example, the product of the marginal distributions will give the probability of observing each outcome if the two coins are independent, while the joint distribution will give the probability of each outcome, as actually observed.

If the coins genuinely are independent, then the joint distribution should be (approximately) identical to the product of the marginal distributions. If they are in some way dependent, then there will be a divergence.

In the example, P(X=H,Y=H) > P(X=H) × P(Y=H). This suggests the coins both land on heads more often than would be expected by chance.

The bigger the divergence between the joint and marginal product distributions, the more likely it is the events are dependent in some way. The measure of this divergence is defined by the Mutual Information of the two variables.

The Mutual Information of X and Y equals “the KL divergence of their joint distribution, and the product of their marginal distributions”

mutualInfo <- function(x,y){
  joint <- jointDist(x,y)
  marginal <- marginalProduct(x,y)
  Hjm <- - sum(joint[marginal > 0] * log(marginal[marginal > 0],2))
  Hj <- - sum(joint[joint > 0] * log(joint[joint > 0],2))
  return(Hjm - Hj)
}

A major assumption here is that we are working with discrete probability distributions. How can we apply these concepts to continuous data?

Binning

One approach is to quantize the data (make the variables discrete). This is achieved by binning (assigning data points to discrete categories).

The key issue now is deciding how many bins to use. Luckily, the original paper on the Maximal Information Coefficient provides a suggestion: try most of them!

That is to say, try differing numbers of bins and see which produces the greatest result of Mutual Information between the variables. This raises two challenges, though:

How many bins to try? Technically, you could quantize a variable into any number of bins, simply by making the bin size forever smaller.
Mutual Information is sensitive to the number of bins used. How do you fairly compare MI between different numbers of bins?

The first challenge means it is technically impossible to try every possible number of bins. However, the authors of the paper offer a heuristic solution (that is, a solution which is not ‘guaranteed perfect’, but is a pretty good approximation). They also suggest an upper limit on the number of bins to try.

The maximum number of bins to try is determined by the sample size, N

As for fairly comparing MI values between different binning schemes, there’s a simple fix… normalize it! This can be done by dividing each MI score by the maximum it could theoretically take for that particular combination of bins.

The binning combination that produces the highest normalized MI overall is the one to use.

Mutual Information can be normalized by dividing by the logarithm of the smallest number of bins

The highest normalized MI is then reported as the Maximal Information Coefficient (or ‘MIC’) for those two variables. Let’s check out some code that will estimate the MIC of two continuous variables.

MIC <- function(x,y){
  N <- length(x)
  maxBins <- ceiling(N ** 0.6)
  MI <- c()
  for(i in 2:maxBins) {
    for (j in 2:maxBins){
      if(i * j > maxBins){
        next
      }
      Xbins <- i; Ybins <- j
      binnedX <-cut(x, breaks=Xbins, labels = 1:Xbins)
      binnedY <-cut(y, breaks=Ybins, labels = 1:Ybins)
      MI_estimate <- mutualInfo(binnedX,binnedY)
      MI_normalized <- MI_estimate / log(min(Xbins,Ybins),2)
      MI <- append(MI, MI_normalized)
    }
  }
  return(max(MI))
}

x <- runif(100,-10,10)
y <- x**2 + rnorm(100,0,10)
MIC(x,y) # --> 0.751

The above code is a simplification of the method outlined in the original paper. A more faithful implementation of the algorithm is available in the R package minerva. In Python, you can use the minepy module.

MIC is capable of picking out all kinds of linear and non-linear relationships, and has found use in a range of different applications. It is bound between 0 and 1, with higher values indicating greater dependence.

Confidence Intervals?

To establish confidence bounds on an estimate of MIC, you can simply use a bootstrapping technique like the one we looked at earlier.

To generalize the bootstrap function, we can take advantage of R’s functional programming capabilities, by passing the technique we want to use as an argument.

bootstrap <- function(x,y,func,reps,alpha){
  estimates <- c()
  original <- data.frame(x,y)
  N <- dim(original)[1]
  for(i in 1:reps){
    S <- original[sample(1:N, N, replace = TRUE),]
    estimates <- append(estimates, func(S$x, S$y))
  }
  l <- alpha/2 ; u <- 1 - l
  interval <- quantile(estimates, c(u, l))
  return(2*(func(x,y)) - as.numeric(interval[1:2]))
}

bootstrap(x,y,MIC,100,0.05) # --> 0.594 to 0.88

Summary

To conclude this tour of correlation, let’s test each different method against a range of artificially generated data. The code for these examples can be found here.

Noise

set.seed(123)

# Noise
x0 <- rnorm(100,0,1)
y0 <- rnorm(100,0,1)
plot(y0~x0, pch = 18)

cor(x0,y0)
distanceCorrelation(x0,y0)
MIC(x0,y0)

Pearson’s r = – 0.05
Distance Correlation = 0.157
MIC = 0.097

Simple linear

# Simple linear relationship
x1 <- -20:20
y1 <- x1 + rnorm(41,0,4)
plot(y1~x1, pch =18)

cor(x1,y1)
distanceCorrelation(x1,y1)
MIC(x1,y1)

Pearson’s r =+0.95
Distance Correlation = 0.95
MIC = 0.89

Simple quadratic

# y ~ x**2
x2 <- -20:20
y2 <- x2**2 + rnorm(41,0,40)
plot(y2~x2, pch = 18)

cor(x2,y2)
distanceCorrelation(x2,y2)
MIC(x2,y2)

Pearson’s r =+0.003
Distance Correlation = 0.474
MIC = 0.594

Trigonometric

# Cosine
x3 <- -20:20
y3 <- cos(x3/4) + rnorm(41,0,0.2)
plot(y3~x3, type='p', pch=18)

cor(x3,y3)
distanceCorrelation(x3,y3)
MIC(x3,y3)

Pearson’s r = – 0.035
Distance Correlation = 0.382
MIC = 0.484

Circle

# Circle

n <- 50
theta <- runif (n, 0, 2*pi)
x4 <- append(cos(theta), cos(theta))
y4 <- append(sin(theta), -sin(theta))
plot(x4,y4, pch=18)

cor(x4,y4)
distanceCorrelation(x4,y4)
MIC(x4,y4)

Pearson’s r < 0.001
Distance Correlation = 0.234
MIC = 0.218

Thanks for reading!

Learn to code for free. freeCodeCamp’s open source curriculum has helped more than 40,000 people get jobs as developers. Get started

Источник

Корреляция, ковариация и девиация (часть 3)

7. Векторизация и нормирование одномерных координат

8. Векторизация и ортонормирование многомерных координат

9. Матрица Грина — это матрица корреляции векторов

Расчет значений вектора и матрицы корреляции