Как найти вектор кривизны

Как найти вектор кривизны

Рассмотрим плоскую кривую, заданную уравнением (y = fleft( x right).) Пусть в точке (Mleft( right)) проведена касательная к данной кривой, которая образует угол (alpha) с осью абсцисс (рисунок (1)). При смещении (Delta s) вдоль дуги кривой точка (M) переходит в точку (.) При этом положение касательной также изменяется: угол наклона касательной к оси (Ox) в точке () будет составлять (alpha + Deltaalpha.) Таким образом, при смещении точки кривой на расстояние (Delta s) касательная поворачивается на угол (Deltaalpha.) (Будем считать, что угол (alpha) возрастает при вращении против часовой стрелки.)

Абсолютное значение отношения (largefrac<<Delta alpha >><<Delta s>>normalsize) называется средней кривизной дуги (M.) В пределе, при (Delta s to 0,) мы получаем кривизну кривой в точке (M:) [K = limlimits_ <Delta s to 0>left| <frac<<Delta alpha >><<Delta s>>> right|.] Из приведенного определения следует, что кривизна в какой-либо точке кривой характеризует скорость вращения касательной в этой точке.

Для плоской кривой (y = fleft( x right)) кривизна в точке (Mleft( right)) выражается через первую и вторую производные функции (fleft( x right)) по формуле [K = frac <<left| right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] Если кривая задана в параметрической форме уравнениями (x = xleft( t right),) (y = yleft( t right),) то ее кривизна в произвольной точке (Mleft( right)) равна [K = frac <<left| right|>> <<<<left[ <<<left( right)>^2> + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] В случае, если кривая задана полярным уравнением (r = rleft( theta right),) кривизна находится по формуле [K = frac <<left| <+ 2 <<left( right)>^2> – rr”> right|>> <<<<left[ <+ <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] Радиусом кривизны кривой в точке (Mleft( right)) называется величина, обратная кривизне (K) данной кривой в рассматриваемой точке: [R = frac<1>.] Следовательно, для плоских кривых, заданных явным уравнением (y = fleft( x right),) радиус кривизны в точке (Mleft( right)) будет определяться выражением [R = frac <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>> <<left| right|>>.]

Очевидно, достаточно найти кривизну эллипса в точках (Aleft( right)) и (Bleft( <0,b>right)) (рисунок (2)), поскольку в силу симметрии кривой кривизна в двух противоположных вершинах эллипса будет такой же.

Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме : [x = acos t,;;;y = bsin t.] где (t) − параметр. В точке (Aleft( right)) параметр имеет значение (t = 0,) а в точке (Bleft( <0,b>right)) его значение равно (t = largefrac<pi ><2>normalsize.)

Данная функция достигает максимума в точках (x = largefrac<<2pi n>>normalsize,;n in Z.) В силу периодичности кривизна во всех точках максимума одинакова, поэтому достаточно рассмотреть лишь точку (x = 0).

В данном случае точка (x = 0) является точкой перегиба функции (y = arctan x.) Поскольку в точке перегиба вторая производная равна нулю, то кривизна здесь также должна быть равна нулю, что и показывает полученное решение.

Экспоненциальная функция (y = ) − это единственная уникальная функция, у которой производные любого порядка равны самой функции. Поэтому для кривизны данной кривой можно сразу написать следующую формулу: [ right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>> > = <frac<<>><<<<left( <1 + >> right)>^<largefrac<3><2>normalsize>>>>.> ] Знак модуля в числителе опущен, поскольку экспоненциальная функция всегда положительна.

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Кривизна и кручение. Натуральные уравнения кривой

Краткие теоретические сведения

Кривизна кривой

Кривизной $k$ кривой в данной точке называют модуль скорости вращения касательной по отношению к длине дуги.

Регулярная дважды дифференцируемая без особых точек кривая $gamma$, заданная векторной функцией $vec=vec(t)$, имеет в каждой точке определенную кривизну, причем $$ |k(t)|=frac<|vec(t)times vec(t)|><|vec|^3>. $$

Для кривой, заданной параметрически $$ x=x(t), ,, y=y(t), ,, z=z(t), $$ кривизна в точке $P(t=t_0)$ находится по формуле: $$ k^2(t_0)=frac<left| begin y’ & z’ \ y”& z” \ end right|^2+left| begin z’ & x’ \ z”& x” \ end right|^2+left| begin x’ & y’ \ x” & y” \ end right|^2><Bigl((x’)^2+(y’)^2+(z’)^2Bigr)^3>, $$ где все производные вычисляются при $t=t_0$.

Если кривая задана естественной параметризацией $vec=vec(s)$, то векторы $vec(s)$ и $vec(s)$ перпендикулярны, причем $|vec(s)|=1$. Тогда выражение для кривизны принимает вид: $$ k(s)= |vec(s)|. $$

Что вы скажете о кривой, которая в каждой свой точке имеет нулевую кривизну?

Кручение

Абсолютным кручением $varkappa$ кривой называют скорость вращения соприкасающейся плоскости вокруг касательной. $$ |varkappa (t)|=frac<|(vec(t), vec(t), vec(t))|><|vec(t)times vec(t)|^2>. $$

В случае естественной параметризации $$ |varkappa(s)|=frac<|(vec(s), vec(s), vec(s))|> $$

Натуральные уравнения кривой

Если кривая задана естественной параметризацией $vec=vec(s)$, то кривизна и кручение будут являться функциями длины дуги $$ k=k(s), quad varkappa=varkappa(s). $$ Система этих двух соотношений называется натуральными уравнениями кривой.

Натуральные уравнения полностью определяют форму кривой, ибо связывают инварианты, которые не меняются при преобразовании координат (при изменении положения указанной кривой в пространстве относительно системы координат).

Решение задач

Задача 1 (Феденко №351)

Найдите кривизну кривой: $$ x=a,mbox^3t,,,y=a,mbox^3t. $$

Задача 2 (Феденко №380)

Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=mboxx$ в точке $A(pi/2,1)$ общие касательную и кривизну.

Задача 3 (Феденко №405)

Составьте натуральные уравнения кривой: $$ x=a(mbox,t+t,mbox,t), ,, y=a(mbox,t-t,mbox,t). $$

Краткое решение задачи 3

Натуральные уравнения: $$ k=frac<1>,,,s=frac <2>$$ или $$ k^2=frac<1><2as>. $$

Феденко записывает ответы через радиус кривизны: $R=frac<1>$.

Задача 4 (Феденко №486, №514)

Найдите кривизну и кручение, составьте натуральные уравнения кривой: $$ x=a,mboxt, , y=a,mboxt, , z=a, t. $$

Решение задачи 4

Задачу можно решать двумя способами:

1 способ. Найти $k(t), varkappa(t), s(t)$.

2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $vec=vec(s)$. А далее найти $k(s)$ и $varkappa(s)$.

В задаче №473 была та же кривая и мы получили, что $$s=asqrt<2>,mbox,t.$$ Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения: begin s=asqrt<2>,mboxt=asqrt<2>,sqrt<mbox^2t-1> ,, Rightarrow ,, mbox^2t=frac<2a^2>+1 ,, Rightarrow end begin k(s)=varkappa(s)=frac<1><2a,mbox^2t> = frac. end

Вычисления сделаны для $a>0$.

Задача 5 (Феденко №496)

Найдите функцию $f(t)$, для которой данная кривая — плоская: $$ vec(t)=t, , a,mboxt, , f(t)> $$

Решение задачи 5

Для плоской кривой кручение равно нулю: begin varkappa(t) = left| begin -a,mboxt & a,mboxt & f'(t) \ -a,mboxt & -a,mboxt & f”(t) \ a,mboxt & -a,mboxt & f”'(t) \ end right| = left( f'(t) + f”'(t) right)cdot2a^2=0. end begin f'(t)=-f”'(t) quad Rightarrow quad f(t)=c_1+c_2,mboxt+c_3,mboxt. end

Как найти уравнение плоскости, в которой лежит кривая?

Известно, что плоская кривая лежит в своей соприкасающейся плоскости! Второй способ — составить уравнение плоскости по трем точкам.

Кривизна плоской кривой

Под кривизной линии понимают степень ее отклонения от прямой. Не давая пока точных определений, заметим, что чем больше радиус окружности, тем менее она искривлена, тем больше ее участок заданной длины напоминает отрезок прямой той же длины. При этом окружность одинаково искривлена во всех точках. В то же время парабола наиболее искривлена в ее вершине, а по мере удаления от вершины кривизна становится меньше.

Чтобы дать точное определение кривизны, рассмотрим гладкую дугу . Если бы эта дуга не была искривлена, т. е. если бы она была отрезком прямой линии, то касательные в начале и конце дуги имели бы одинаковое направление (совпадающее с направлением отрезка). Таким образом, за меру искривленности данной дуги в целом следует принять угол поворота касательной к этой дуге при движении от начала дуги к ее концу. Например, для полуокружности этот угол равен (рис. 55), для всей окружности он равен , а для дуги синусоиды, изображенной на рисунке 56, этот угол равен нулю, так как при обходе дуги касательная возвращается в исходное положение, не сделав при этом полного оборота.

Угол поворота касательной считают положительным, если вращение происходит против часовой стрелки, и отрицательным в противном случае.

Однако угол поворота касательной показывает лишь полную искривленность линии. Поэтому полуокружности малого и большого радиусов дают один и тот же угол поворота , в то время как искривленность большой окружности в каждой точке меньше, чем малой. Это показывает, что нам надо учитывать не только угол поворота , но и длину дуги, на протяжении которой получился этот поворот касательной. Иными словами, следует рассчитывать угол поворота на единицу длины дуги, или, иначе, отношение величины этого угла к длине дуги. Назовем это отношение средней кривизной данной дуги:

Например, длина полуокружности радиуса равна , а соответствующий ей угол поворота равен . Значит, средняя кривизна полуокружности равна

т. е. обратно пропорциональна радиусу. Очевидно, что тот же результат получился бы, если бы мы взяли любую другую дугу окружности радиуса .

Мы уже говорили, что, вообще говоря, кривизна данной линии различна в разных точках. Поэтому надо перейти от средней кривизны дуги к ее кривизне в данной точке. Введем следующее определение:

Определение. Кривизной дуги кривой в данной точке называется предел средней кривизны дуги , когда длина этой дуги стремится к нулю:

(разумеется, если этот предел не существует, то кривизна линии в данной точке не определена).

Перейдем к выводу расчетной формулы для кривизны. Выберем декартову систему координат (рис. 57). Из рисунка видно, что угол между касательными в точках и равен разности углов и , т. е. углов наклона касательных в этих точках к оси абсцисс. Это можно записать следующим образом: , где — угол наклона касательной к оси абсцисс. Поэтому формулу для кривизны можно переписать так:

Мы доказали, что кривизна дуги кривой является производной угла наклона касательной к положительному направлению оси абсцисс по длине дуги.

Пусть кривая задана уравнением на отрезке , где функция дважды дифференцируема. Тогда эта кривая спрямляема и имеет касательную в любой точке. При этом , а так как , то , и потому

Пример 1. Найти кривизну гиперболы в точке .

Решение. Воспользуемся формулой (2) кривизны кривой. Имеем:

Вычислить значения производных в данной точке . Таким образом,

Пример 2. Найти наибольшую кривизну линии кубической параболы .

Решение. Мы имеем: .

Чтобы найти наибольшее значение кривизны, вычислим

Приравнивая производную нулю, получаем: . В этой точке . Отметим, что при имеем , а при будет . Поэтому вдоль кривой кривизна плавно возрастает от нуля до , а потом плавно убывает.

Это используется при строительстве железных дорог для построения переходных кривых, вдоль которых кривизна плавно возрастает от нуля до требуемого значения.

[spoiler title=”источники:”]

http://vmath.ru/vf5/diffgeom/seminar3

http://mathhelpplanet.com/static.php?p=krivizna-ploskoi-krivoi

[/spoiler]

Определение кривизны по формуле (1.5) имеет место и в пространственном случае. В качестве основного “естественного параметра” принимаем длину дуги кривой , так что текущий радиус-вектор кривой запишем как

.

Рассмотрим модуль вектора , а именно

,

Т. е. в любой точке кривой.

Пусть вектор направлен по касательной к кривой в некоторой точке А (рис.1.4). Задавая приращение параметра , переходим к точке В, а вектор , направленный по касательной к кривой в точке В, обозначим через . Так как , о является равнобедренным, поэтому, обозначив угол поворота касательной через , запишем

.

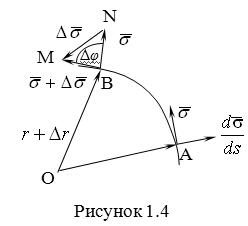Отсюда получаем

И, следовательно, в пределе при находим, что

,

Как следует из определения кривизны. С другой стороны,

.

Итак, мы получаем следующую формулу для вычисления кривизны

(1.8)

Далее, поскольку – единичный вектор, то из формулы (1.4) следует, что вектор ортогонален вектору и, следовательно, этот последний вектор лежит в нормальной плоскости к кривой в данной её точке. Соответствующее направление называют направлением главной нормали. Обозначив единичный вектор главной нормали через , запишем так называемую Первую формулу Френе

, (1.9)

Где коэффициент пропорциональности и является кривизной, поскольку , т. е. . (Направление главной нормали выбирается таким образом, чтобы величина была положительной).

Перейдем теперь к вычислению кривизны в более общем случае, когда радиус-вектор кривой есть функция произвольного параметра . Справедливо равенство

, (1.10)

Поскольку ранее было установлено, что .

Дифференцируя равенство (1.10) по параметру T, имеем

. (1.11)

Вновь возводя в квадрат, получим

(1.12)

Теперь вычисляем

И

.

Отсюда

.

В последнюю формулу, исключая естественный параметр , подставим вместо , и соответствующие выражения из вспомогательных формул (1.10), (1.11), (1.12). Получаем

, (1.13)

Где знак ‘‘´’’ означает векторное произведение. В том, что и совпадают, можно легко убедиться непосредственным вычислением (здесь для краткости введён символ (¢) как знак дифференцирования по параметру T). В случае если , из (1.13) получаем

. (1.14)

Если рассматриваемая кривая представляет собой траекторию движения некоторой материальной точки, а – время, то, вводя векторы скорости и ускорения , можно переписать формулу (1.13) в виде

Пример. Винтовая линия, которая задана уравнениями , , , где – некоторые постоянные. Выпишем векторы

и .

Тогда

;

И, следовательно,

.

Итак, по формуле (1.13)

,

Т. е. кривизна винтовой линии одна и та же во всех точках данной кривой.

< Предыдущая		Следующая >

Кинема́тика
(греч.
κινειν —
двигаться) в физике — раздел механики,
изучающий математическое описание
(средствами геометрии,
алгебры,
математического
анализа…) движения идеализированных
тел (материальная
точка, абсолютно
твердое тело, идеальная
жидкость), без рассмотрения
причин движения (массы,
сил
и т. д.). Исходные понятия кинематики —
пространство
и время.
Например, если тело движется по окружности,
то кинематика предсказывает необходимость
существования центростремительного
ускорения без уточнения того,
какую природу имеет сила, его порождающая.
Причинами возникновения механического
движения занимается другой
раздел механики — динамика.

Различают
классическую кинематику, в которой
пространственные (длины отрезков) и
временные (промежутки времени)
характеристики движения считаются
абсолютными, то есть не зависящими от
выбора системы отсчёта, и релятивистскую.
В последней длины отрезков и промежутки
времени между двумя событиями
могут изменяться при переходе от одной
системы отсчёта к другой. Относительной
становится также одновременность. В
релятивистской механике вместо отдельных
понятий пространство
и время
вводится понятие пространства-времени,
в котором инвариантным
относительно преобразований
Лоренца является величина,
называемая интервалом.

Ра́диус-ве́ктор
(обычно обозначается

или
просто

)
— вектор,
задающий положения точки
в пространстве
относительно некоторой заранее
фиксированной точки, называемой началом
координат.

Для
произвольной точки в пространстве,
радиус-вектор — это вектор, идущий из
начала координат в эту точку.

Длина
радиус-вектора, или его модуль,
определяет расстояние, на котором точка
находится от начала координат, а стрелка
указывает направление на эту точку
пространства.

На
плоскости углом радиус-вектора называется
угол, на который радиус-вектор повёрнут
относительно оси
абсцисс в направлении против
часовой стрелки.

Траекто́рия
материа́льной то́чки  — линия
в трёхмерном пространстве,
представляющая собой множество
точек, в которых находилась, находится
или будет находиться материальная
точка при своём перемещении в
пространстве.^[1].
Существенно, что понятие о траектории
имеет физический смысл даже при отсутствии
какого-либо по ней движения. Кроме того,
и при наличии движущегося по ней объекта,
траектория сама по себе не может ничего
дать в отношении причин движения, то
есть о действующих силах.^[2]

Принято
описывать траекторию материальной
точки при помощи радиус-вектора,
направление, длина и начальная точка
которого зависят от времени.
При этом кривая, описываемая концом
радиус-вектора в пространстве может
быть представлена в виде сопряжённых
дуг
различной кривизны,
находящихся в общем случае в пересекающихся
плоскостях.
При этом кривизна каждой дуги определяется
её радиусом
кривизны, направленном к дуге
из мгновенного центра
поворота, находящегося в той
же плоскости, что и сама дуга. При том
прямая
линия рассматривается как предельный
случай кривой,
радиус кривизны которой может считаться
равным бесконечности.И
потому траектория в общем случае может
быть представлена как совокупность
сопряжённых
дуг.

Существенно,
что форма траектории зависит от системы
отсчёта, избранной для описания
движения материальной точки. Так
прямолинейное движение в инерциальной
системе в общем случае будет параболическим
в равномерно ускоряющейся системе
отсчёта.

Скорость
материальной точки всегда направлена
по касательной к дуге, используемой для
описания траектории точки. При этом
существует связь между величиной
скорости v,
нормальным
ускорением
a_n
и радиусом кривизны траектории ρ в
данной точке:

Представление
траектории как следа, оставляемого
движением материальной точки,
связывает чисто кинематическое
понятие о траектории, как геометрической
проблеме, с динамикой
движения материальной точки, то есть
проблемой определения причин её движения.
Фактически, решение уравнений
Ньютона (при наличии полного
набора исходных данных) даёт траекторию
материальной точки. И наоборот, зная
траекторию материальной точки в
инерциальной системе отсчёта и её
скорость
в каждый момент времени, можно определить
силы, действовавшие на неё.

В
соответствии с Первым законом Ньютона,
иногда называемым законом
инерции должна существовать
такая система, в которой свободное тело
сохраняет (как вектор) свою скорость.
Такая система отсчёта называется
инерциальной.
Траекторией такого движения является
прямая
линия, а само движение называется
равномерным и прямолинейным.

В
соответствии с принципом
относительности Галилея,
существует бесконечное множество
равноправных инерциальных систем,
движение которых одна относительно
другой не может быть установлено никаким
образом путём наблюдения любых процессов
и явлений, происходящих только в этих
системах. Прямая траектория движения
объекта в одной системе будет выглядеть
также прямой в любой другой инерциальной
системе.

Если
же в некоторой системе отсчёта свободное
тело двигается по криволинейной
траектории и/или с переменной скоростью,
то такая система является неинерциальной.

Если
в заведомо инерциальной системе скорость

движения
объекта с массой m
меняется по направлению, даже оставаясь
прежней по величине, то есть тело
производит поворот
и движется по дуге с радиусом кривизны
R,
то объект испытывает нормальное ускорение
a_n.
Причиной, вызывающей это ускорение,
является сила, прямо пропорциональная
этому ускорению. В этом состоит суть
Второго закона Ньютона:

(1)

Где

есть
векторная сумма сил, действующих на
тело,

его
ускорение, а m —
инерционная масса.^[3]

Ско́рость
(часто обозначается

,
от англ. velocity
или фр. vitesse) —
векторная
физическая
величина, характеризующая быстроту
перемещения
и направление движения материальной
точки в пространстве относительно
выбранной системы
отсчёта (например, угловая
скорость). Этим же словом может
называться скалярная
величина, точнее модуль
производной
радиус-вектора.

В
науке используется также скорость в
широком смысле, как быстрота изменения
какой-либо величины (не обязательно
радиус-вектора) в зависимости от другой
(чаще изменения во времени,
но также в пространстве или любой
другой). Так, например, говорят о скорости
изменения температуры, скорости
химической реакции, групповой
скорости, скорости соединения,
угловой
скорости и т. д. Математически
характеризуется производной
функции.

Вектор
скорости материальной
точки в каждый момент времени
определяется производной по времени
радиус-вектора

этой
точки:

Здесь

 —
модуль
скорости,

 —
направленный вдоль скорости единичный
вектор касательной к траектории
в точке

.

Скорость
направлена вдоль касательной
к траектории
и равна по модулю производной дуговой
координаты по времени.

Говорят,
что тело совершает мгновенно-поступательное
движение, если в данный момент
времени скорости всех составляющих его
точек равны. Так, например, равны скорости
всех точек кабинки колеса обозрения
(если, конечно, пренебречь колебаниями
кабинки).

В
общем случае, скорости точек, образующих
твёрдое тело, не равны между собой. Так,
например, для катящегося без проскальзывания
колеса величина скорости точек на ободе
относительно дороги принимает значения
от нуля (в точке касания с дорогой) до
удвоенного значения скорости автомобиля
(в точке, диаметрально противоположной
точке касания). Распределение скоростей
в твёрдом теле определяется с помощью
кинематической
формулы Эйлера.

Если
скорость тела (как векторная величина)
не меняется во времени, то движение
тела — равномерное (ускорение
равно нулю) и тогда:

Скорость —
характеристика движения точки, при
равномерном движении численно
равная отношению пройденного
пути s к промежутку времени t, за который
этот путь пройден

Полезно
отличать понятие средней скорости
перемещения от понятия средней скорости
пути, равной отношению пройденного
точкой пути ко времени, за которое этот
путь был пройден. В отличие от скорости
перемещения, средняя скорость пути —
скаляр.

Когда
говорят о средней
скорости , для различения,
скорость согласно выше приведённому
определению называют мгновенной
скоростью. Так, хотя мгновенная
скорость бегуна, кружащего по стадиону,
в каждый момент времени отлична от нуля,
его средняя скорость (перемещения) от
старта до финиша оказывается равной
нулю, если точки старта и финиша совпадают.
Заметим, что при этом, средняя путевая
скорость остаётся отличной от нуля.

Основная
статья:
Теорема
о сложении скоростей

В
классической механике Ньютона скорости
преобразуются при переходе из одной
инерциальной
системы отсчёта
в другую согласно преобразованиям
Галилея.
Если скорость тела в системе отсчёта S
была равна

,
а скорость системы отсчёта S’ относительно
системы отсчёта S равна

,
то скорость тела при переходе в систему
отсчёта S’ будет равна

.

Для
скоростей, близких к скорости света
преобразования Галилея становятся
несправедливы. При переходе из системы
S в систему S’ необходимо использовать
преобразования
Лоренца
для скоростей:

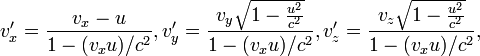
в
предположении, что скорость

направлена
вдоль оси х системы S. Легко убедиться,
что в пределе нерелятивистских скоростей
преобразования Лоренца сводятся к
преобразованиям Галилея.

скоре́ние
(обычно обозначается

,
в теоретической
механике

)
— производная скорости
по времени, векторная
величина, показывающая, насколько
изменяется вектор скорости
точки (тела) при её движении за единицу
времени (т.е. ускорение учитывает не
только изменение величины скорости, но
и её направления).

Например,
вблизи Земли
падающее на Землю
тело, в случае, когда можно пренебречь
сопротивлением
воздуха, увеличивает свою
скорость примерно на 9,8 м/с каждую
секунду, то есть, его
ускорение равно 9,8 м/с².

Единицей
ускорения служит метр
в секунду
за секунду (m/s², м/с²),
существует также внесистемная единица
Гал
(Gal), применяемая в гравиметрии
и равная 1 см/с².

Производная
ускорения по времени, т.е. величина,
характеризующая скорость изменения
ускорения, называется рывок.

Вектор
ускорения материальной
точки
в любой момент времени находится путём
дифференцирования вектора скорости
материальной точки по времени:

.

сли
вектор

не
меняется со временем, движение называют
равноускоренным.
При равноускоренном движении справедливы
формулы:

.

Частным
случаем равноускоренного движения
является случай, когда ускорение равно
нулю в течение всего времени движения.
В этом случае скорость постоянна, а
движение происходит по прямолинейной
траектории (если скорость тоже равна
нулю, то тело покоится), поэтому такое
движение называют прямолинейным и
равномерным.

Равноускоренное
движение точки всегда является плоским,
а твёрдого
тела
— плоскопараллельным (поступательным).
(Обратное, вообще говоря, не верно).

Вектор
ускорения

при
движении точки по окружности можно
разложить на два слагаемых (компоненты):

Тангенциальное
ускорение
—

направлено
по касательной к траектории (обозначается
иногда

итд,
в зависимости от того, какой буквой в
данной книге принято обозначать
ускорение). Является составляющей
вектора ускорения a.
Характеризует изменение скорости по
модулю.

Центростремительное
или Нормальное
ускорение

—
возникает (не равно нулю) всегда при
движении точки по окружности (конечного
радиуса) (также обозначается иногда

итд).
Является составляющей вектора ускорения
a,
перпендикулярной вектору мгновенной
скорости. Вектор нормального ускорения
всегда направлен к центру окружности,
а модуль равен:

Угловое
ускорение
— показывает, на сколько изменилась
угловая скорость за единицу времени,
и, по аналогии с линейным ускорением,
равно:

Направление
вектора здесь показывает, увеличивается
или уменьшается модуль скорости. Если
векторы углового ускорения и скорости
сонаправлены, значение скорости растёт,
и наоборот.

Вектор
ускорения

можно
разложить по сопутствующему
базису

:

,

где

•  —
  величина
  скорости,

•  —
  единичный
  касательный к траектории вектор,
  направленный вдоль скорости (касательный
  орт),

• 
   —
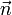
  орт
  главной
  нормали
  к траектории, который можно определить
  как единичный вектор в направлении
  
  ,

• 
   —
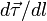
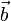
  орт
  бинормали
  к траектории,

• R —
  радиус
  кривизны
  траектории.

,
называемое бинормальным ускорением,
всегда равно нулю. Это можно считать
прямым следствием определения векторов

:
можно сказать, что они выбираются именно
так, чтобы первый всегда совпадал с
нормальным ускорением, второй же
ортогонально первому.

Векторы

и

называются
касательным (тангенциальным)
и нормальным
ускорениями
соответственно.

Итак,
учитывая сказанное выше, вектор ускорения
всегда можно записать как:

,

Преобразова́ния
Ло́ренца — линейные (или аффинные)
преобразования векторного (соответственно,
аффинного) псевдоевклидова
пространства, сохраняющее длины
или, что эквивалентно, скалярное
произведение векторов.

Преобразования
Лоренца псевдоевклидова пространства
сигнатуры
(n-1,1) находят широкое применение в физике,
в частности, в специальной
теории относительности (СТО),
где в качестве аффинного псевдоевклидова
пространства выступает
четырёхмерный пространственно-временной
континуум (пространство
Минковского).

Преобразование Лоренца
представляет собой естественное
обобщение понятия ортогонального
преобразования (т.е. преобразования,
сохраняющего скалярное произведение
векторов) с евклидовых
на псевдоевклидовы
пространства. Различие между ними
состоит в том, что скалярное произведение
предполагается не положительно
определённым, а лишь невырожденным (так
называемое индефинитное скалярное
произведение).

Преобразование
Лоренца
(лоренцево
преобразование)
псевдоевклидова векторного
пространства

—
это линейное
преобразование

,
сохраняющее индефинитное скалярное
произведение
векторов. Это означает, что для любых
двух векторов

выполняется
равенство

где
треугольными скобками обозначено
индефинитное скалярное произведение

в
псевдоевклидовом пространстве

.

Аналогично,
преобразование
Лоренца
(лоренцево
преобразование)
псевдоевклидова аффинного
пространства
— это аффинное
преобразование,
сохраняющее расстояние между точками
этого пространства.

• Так
  как любое аффинное преобразование
  является композицией параллельного
  переноса
  (очевидным образом, сохраняющего
  расстояние между точками) и преобразования,
  имеющего неподвижную точку, то группа
  преобразований Лоренца аффинного
  пространства (группа
  Пуанкаре)
  получается из группы преобразований
  Лоренца векторного пространства (группа
  Лоренца)
  такой же размерности путём добавления
  к ней всевозможных параллельных
  переносов.

где
звёздочка означает транспонирование
матрицы. И обратно, любая матрица

,
удовлетворяющая соотношению ( * ), является
матрицей преобразования Лоренца. В
частности, всегда можно выбрать базис

таким
образом, что индефинитное скалярное
произведение имеет вид

и
в равенстве ( * ) матрица

―
диагональная с элементами

(первые
k)
и

(последние
n
− k).

• Из
  соотношения ( * ) следует, что, как и в
  случае ортогонального преобразования,
  определитель
  
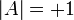
  или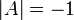

  
  .

Вид
преобразований при коллинеарных
(параллельных) пространственных осях

Если
ИСО K‘
движется относительно ИСО K
с постоянной скоростью V
вдоль оси x,
а начала
пространственных координат
совпадают в начальный момент времени
в обеих системах, то преобразования
Лоренца (прямые) имеют вид:

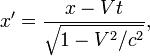
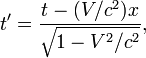
где
c
— скорость
света,
величины со штрихами измерены в системе
K‘,
без штрихов — в K.

Эта
форма преобразования (то есть при выборе
коллинеарных осей), называемая иногда
бустом
(англ. boost)
или лоренцевским
бустом
(особенно в англоязычной литературе),
несмотря на свою простоту, включает, по
сути, всё специфическое физическое
содержание преобразований Лоренца, так
как пространственные оси всегда можно
выбрать таким образом, а при желании
добавить пространственные повороты не
представляет трудности (см. это в явном
развёрнутом виде ниже), хотя и делает
формулы более громоздкими.

• Формулы,
  выражающие обратное преобразование,
  то есть выражающие x‘,y‘,z‘,t‘
  через x,y,z,t
  можно получить просто заменой V
  на − V
  (абсолютная величина относительной
  скорости движения систем отсчёта | V
  | одинакова при измерении её в обеих
  системах отсчёта, поэтому можно при
  желании снабдить V
  штрихом, только при этом надо внимательно
  следить за тем, чтобы знак и определение
  соответствовали друг другу) и взаимной
  заменой штрихованных x
  и t
  с нештрихованными. Или решая систему
  уравнений (1) относительно x‘,y‘,z‘,t‘.

• Надо
  иметь в виду, что в литературе
  преобразования Лоренца часто записывается
  для упрощения в системе единиц, где c
  = 1, что действительно делает их вид
  более изящным.

• Видно,
  что при преобразованиях Лоренца события,
  одновременные
  в одной системе отсчёта, не являются
  одновременными в другой (относительность
  одновременности), кроме того, у движущегося
  тела сокращается продольный размер по
  сравнению с тем, какой оно имеет в
  сопутствующей ему системе отсчёта
  (лоренцево
  сокращение),
  а ход движущихся часов замедляется,
  если наблюдать их из «неподвижной»
  системы отсчёта (релятивистское
  замедление времени).

В
дифференциальной
геометрии, кривизна́ —
собирательное название ряда количественных
характеристик (скалярных,
векторных,
тензорных),
описывающих отклонение того или иного
геометрического «объекта» (кривой,
поверхности,
риманова
пространства и т. д.) от
соответствующих «плоских» объектов
(прямая,
плоскость,
евклидово
пространство и т. д.).

Обычно
кривизна определяется для каждой точки
на «объекте» и выражается как значение
некоторого дифференциального
выражения 2-го порядка. Иногда
кривизна определяется в интегральном
смысле, например, как мера,
такие определения используют для
«объектов» пониженной гладкости. Как
правило, тождественное обращение в нуль
кривизны во всех точках влечёт локальное
совпадение изучаемого «объекта» с
«плоским» объектом.

Кривизна кривой

Пусть
γ(t) — регулярная кривая в d-мерном
евклидовом
пространстве, параметризованная
длиной.
Тогда

называется
кривизной кривой γ в точке p =
γ(t), здесь

обозначает
вторую производную по t. Вектор

называется
вектором кривизны γ в точке p =
γ(t).

Очевидно,
это определение можно переписать через
вектор касательной

:

где
одна точка над буквой означает первую
производную по t.

Для
кривой, заданной параметрически в общем
случае (параметр не обязательно является
длиной), кривизна отображается формулой

,

где

и

соответственно
обозначают первую и вторую производную
радиус-вектора γ в требуемой точке (при
этом под крестом

для
кривой в трехмерном пространстве можно
понимать векторное
произведение, для кривой в
двумерном пространстве — псевдоскалярное
произведение, а для кривой в
пространстве произвольной размерности
— внешнее
произведение).

Для
того чтобы кривая γ совпадала с некоторым
отрезком прямой или со всей прямой,
необходимо и достаточно, чтобы кривизна
(или вектор кривизны) тождественно
равнялась нулю.

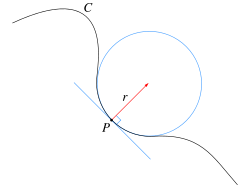
Величина,
обратная кривизне кривой (r = 1 / κ),
называется радиусом кривизны; он
совпадает с радиусом соприкасающейся
окружности в данной точке
кривой. Центр этой окружности называется
центром кривизны.

Дина́мика
(греч.
δύναμις —
сила) — раздел механики,
в котором изучаются причины возникновения
механического
движения. Динамика оперирует
такими понятиями, как масса,
сила,
импульс,
энергия.

Также
динамикой нередко называют, применительно
к другим областям физики (например, к
теории поля), ту часть рассматриваемой
теории, которая более или менее прямо
аналогична динамике в механике,
противопоставляясь обычно кинематике
(к кинематике в таких теориях обычно
относят, например, соотношения,
получающиеся из преобразований величин
при смене системы отсчета).

Иногда
слово динамика применяется в физике и
не в описанном смысле, а в более
общелитературном: для обозначения
просто процессов, развивающихся во
времени, зависимости от времени каких-то
величин, не обязательно имея в виду
конкретный механизм или причину этой
зависимости.

Динамика,
базирующаяся на законах Ньютона,
называется классической динамикой.
Классическая динамика описывает движения
объектов со скоростями от долей
миллиметров в секунду до километров в
секунду.

Однако
эти методы перестают быть справедливыми
для движения объектов очень малых
размеров (элементарные частицы) и при
движениях со скоростями, близкими к
скорости света. Такие движения подчиняются
другим законам.

С
помощью законов динамики изучается
также движение сплошной среды, т. е.
упруго и пластически деформируемых
тел, жидкостей и газов.

В
результате применения методов динамики
к изучению движения конкретных объектов
возник ряд специальных дисциплин:
небесная
механика, баллистика,
динамика
корабля, самолёта
и т. п.

Исторически
деление на прямую и обратную задачу
динамики сложилось следующим образом.

• Прямая
  задача динамики: по заданному характеру
  движения определить равнодействующую
  сил, действующих на тело.

• Обратная
  задача динамики: по заданным силам
  определить характер движения тела.

Макеты страниц

Пусть (Gamma={textbf{r}=textbf{r}(t), alphaleq tleqbeta}) — дважды дифференцируемая кривая, не имеющая особых точек. Тогда существует (displaystyle frac{dr}{ds}=tau) и (displaystyle frac{dtau}{ds}=frac{d^2textbf{r}}{ds^2}), где (s=s(t)) — переменная длина дуги кривой (Gamma). Число (k), определяемое формулой
$$
k=left|frac{dtau}{ds}right|,label{ref30}
$$
называют кривизной кривой в точке (MinGamma (overrightarrow{OM}=textbf{r}(t))).

Если (textbf{r}(t)=(x(t),y(t),z(t))), то (textbf{r}'(t)=(x'(t),y'(t),z'(t))), (r″(t)=(x″(t),y″(t),z″(t))),
$$
s'(t)=|r'(t)|=sqrt{(x'(t))^{2}+(y'(t))^{2}+(z'(t))^{2}},nonumber
$$
и из формулы eqref{ref32}, опуская аргументы, получаем
$$
k=frac{sqrt{begin{vmatrix}y’&z’\y″&z″end{vmatrix}^2+begin{vmatrix}z’&x’\z″&x″end{vmatrix}^2+begin{vmatrix}x’&y’\x″&y″end{vmatrix}^2}}{((x’)^2+(y’)^2+(z’)^2)^{3/2}}label{ref34}
$$
Если (z(t)=0) ((Gamma) — плоская кривая), то формула eqref{ref34} примет вид
$$
k=frac{|x’y″-y’x″|}{((x)^{2}+(y)^{2})^{3/2}}.label{ref35}
$$
В частности, если плоская кривая (Gamma) задана уравнением (y=f(x)), то из формулы eqref{ref35} находим
$$
k=frac{|f″(x)|}{(1+(f'(x))^{2})^{3/2}}.label{ref36}
$$

Выясним физический смысл кривизны кривой. Пусть кривая (Gamma) задана натуральным уравнением, и пусть в точке (MinGamma), где (overrightarrow{OM}=textbf{r}(s)), существует кривизна (k(s)). Тогда (k(s)=left|displaystyle frac{dtau}{ds}right|), где (|tau (s)|=1). Обозначим
$$
Delta tau=tau(s+Delta s)-tau(s),nonumber
$$
где (tau(s+Delta s)) и (tau(s)) — единичные векторы, параллельные касательным к кривой (Gamma) в точках кривой, определяемых значениями параметра (s+Delta s) и (s).

Пусть (Deltavarphi) — угол поворота касательной к кривой (Gamma) при изменении ее параметра от (s) до (s+Delta s), то есть угол между векторами (tau(s+Delta s)) и (tau(s)), тогда (рис. 22.6)
$$
frac{1}{2}|Deltatau|=sinfrac{|Deltavarphi|}{2}.label{ref37}
$$
Назовем скоростью вращения вектора (tau) величину
$$
lim_{Delta srightarrow 0}left|frac{Deltavarphi}{Delta s}right|.label{ref38}
$$
Так как
$$
k(s)=left|frac{dtau}{ds}right|=lim_{Delta srightarrow 0}left|frac{Deltatau}{Delta s}right|.label{ref39}
$$
то, используя равенство eqref{ref37} и учитывая, что (2 displaystyle sinfrac{|Deltavarphi|}{2}sim|Deltavarphi|) при (Deltavarphirightarrow 0), запишем формулу eqref{ref39} в следующем виде:
$$
k(s)=lim_{Delta srightarrow 0}left|frac{Deltavarphi}{Delta s}right|.label{ref40}
$$

Из равенств eqref{ref40} и eqref{ref38} следует, что кривизна кривой (Gamma), заданной натуральным уравнением, в точке (MinGamma) равна скорости вращения вектора касательной к этой кривой в точке (M).

Число (R=displaystyle frac{1}{k(s)}) называют радиусом кривизны кривой (Gamma) в точке (MinGamma (overrightarrow{OM}=textbf{r}(s))). Заметим, что если (Gamma) — окружность радиуса (R) (рис. 22.7), то угол (Deltavarphi) равен углу между векторами (textbf{r}(s)) и (textbf{r}(s+Delta s)). В этом случае (Delta s|=R|Deltavarphi|), и поэтому (displaystyle lim_{Delta srightarrow 0}left|frac{Deltavarphi}{Delta s}right|=k=frac{1}{R}), то есть кривизна окружности равна обратной величине ее радиуса.