Формулы для вычисления магнитного момента
В
случае плоского контура с электрическим
током магнитный момент вычисляется как
![]() ,
,
где I — сила
тока в
контуре, S —
площадь контура, ![]() —
—
единичный вектор нормали к плоскости
контура. Направление магнитного момента
обычно находится по правилу
буравчика:
если вращать ручку буравчика в направлении
тока, то направление магнитного момента
будет совпадать с направлением
поступательного движения буравчика.
Для
произвольного замкнутого контура
магнитный момент находится из:
![]() ,
,
где ![]() — радиус-вектор,
— радиус-вектор,
проведенный из начала координат до
элемента длины контура ![]()
В
общем случае произвольного распределения
токов в среде:
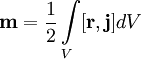 ,
,
где ![]() — плотность
— плотность
тока в
элементе объёма dV.
8. Принцип суперпозиции
За
положительное направление
вектора![]() принимается
принимается
направление от южного полюсаS к
северному полюсу N магнитной
стрелки, свободно ориентирующийся в
магнитном поле. Таким образом, исследуя
магнитное поле, создаваемое током или
постоянным магнитом, с помощью маленькой
магнитной стрелки, можно в каждой точке
пространства определить направление
вектора ![]() .
.
Направление
этого вектора для поля прямого проводника
с током и соленоида можно определить
по правилу буравчика:
если направление поступательного
движения буравчика (винта) с правой
нарезкой совпадает с направлением тока
в проводнике, то направление вращения
ручки буравчика совпадает с направлением
вектора магнитной индукции.
Модуль
индукции B магнитного
поля прямолинейного проводника с
током I на
расстоянии R от
него выражается соотношением:
|
|
где
μ0 –
постоянная величина, которую
называют магнитной
постоянной.
Ее численное значение равно μ0 =
4π∙10–7 H/A2 ≈
1,26∙10–6 H/A2.
Принцип
суперпозиции магнитных полей:
если магнитное поле создано несколькими
проводниками с токами, то вектор магнитной
индукции в какой-либо точке этого поля
равен векторной сумме магнитных индукций,
созданных в этой точке каждым током в
отдельности:
|
|
9. Поток магнитного поля
Магни́тный
пото́к — поток ![]() как
как
интеграл вектора магнитной
индукции ![]() через
через
конечную поверхность ![]() .
.
Определяется через интеграл по поверхности
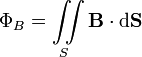
при
этом векторный элемент площади поверхности
определяется как
![]()
где ![]() — единичный
— единичный
вектор, нормальный к
поверхности.
Также
магнитный поток можно рассчитать как
скалярное произведение вектора магнитной
индукции на вектор площади:
![]()
где α —
угол между вектором магнитной индукции
и нормалью к
плоскости площади.
Магнитный
поток через контур также можно выразить
через циркуляцию векторного
потенциала магнитного
поля по этому контуру:
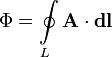
В
системе СИ единицей магнитного
потока является Вебер (Вб, размерность — В·с = кг·м²·с−2·А−1),
в системе СГС — максвелл (Мкс);
1 Вб = 108 Мкс.
10. *Момент сил, действующих на контур с током в магнитном поле
Опыт показывает, что моментсил,действующихнаконтур,
зависит от его ориентации в пространстве,
следовательно, физическая величина,
описывающее магнитноеполе,
должна быть векторной. В общем случае
этот вектор может изменяться от точки
к точке, поэтому магнитноеполедолжно
описываться математически как уже
знакомое намвекторной поле.
Так как мы хотим определить «точечную»
характеристику магнитного поля, то
такой контур(или магнитную
стрелку)следует считать бесконечно
малым.
В очередной раз мы должны сделать
традиционную оговорку – бесконечно
малый контурфизически
нереализуем – даже провода имеют
конечную толщину, поэтому переход к
бесконечно малому контуру следует
понимать в физическом смысле – мал,
настолько, что с математической точки
можно считать бесконечно малым, но
реально реализуемым.
Чтобы избавиться от неоднозначности
измеряемого момента сил, связанной
с ориентацией контура, выберем такое
положение контура, при котором модель
моментасилмаксималенMmax.
Наконец, учтем еще один экспериментальный
факт –момент сил, действующих на контур,
пропорционален силе тока в контуре I и
площади контура S.
Следовательно, отношение момента сил к
произведению силы тока в контуре на его
площадь является величиной, не зависящей
от свойств контура, поэтому является
характеристикой поля, которая называется
индукцией магнитного поля
![]() .
.
(8)
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 декабря 2020 года; проверки требуют 7 правок.
| Магнитный момент | |
|---|---|
 |
|
| Размерность | L2I |
| Единицы измерения | |
| СИ | А⋅м2 |
| Примечания | |
| векторная величина |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная физическая величина, характеризующая магнитные свойства вещества, то есть способность создавать и воспринимать магнитное поле. Вычисляется как
где 


Магнитный момент измеряется в А⋅м2, или в Вб·м, или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10−3 Дж/Тл. Специфическими единицами элементарного магнитного момента являются магнетон Бора и ядерный магнетон.
Объекты, обладающие магнитным моментом[править | править код]
Магнитными свойствами обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Как показала квантовая механика, магнитный момент электронов, протонов, нейтронов и других частиц обусловлен наличием у них собственного момента импульса — спина. Он обычно представляется как вращение частицы вокруг своей оси, однако это сугубо модельная картина, служащая лишь для демонстрации аналогии с явлениями макромира.
Среда, состоящая из частиц (например, молекул), индивидуальные магнитные моменты которых ориентированы не хаотично, будет обладать магнитным моментом и характеризоваться намагниченностью.
Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток.
Формулы для вычисления магнитного момента[править | править код]
В случае плоского контура с электрическим током магнитный момент вычисляется как
где 


Для произвольного замкнутого контура магнитный момент равен
где 

В общем случае произвольного распределения токов в среде:
где 

Магнитный момент во внешнем поле[править | править код]
Потенциальная энергия магнитного диполя в магнитном поле:
Минимизации энергии отвечает сонаправленность момента и поля. Поэтому, скажем, рамка с током «стремится» расположиться в плоскости, ортогональной к 


Момент силы, действующий со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
Эти выражения аналогичны соответствующим выражениям для электрического дипольного момента во внешнем электрическом поле.
Создание магнитного поля самим моментом[править | править код]
Магнитный момент 

.
Предполагается, что начало координат произвольно выбрано в области токов, формирующих магнитный момент, а расстояние 

Приведённое выражение также имеет аналог для электрического поля, создаваемого электрическим дипольным моментом на большом расстоянии от него.
См. также[править | править код]
- Электрический дипольный момент
- Аномальный магнитный момент
Литература[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
Магнитный момент тока. Рамка с током.
Магнитный момент тока это произведение площади контура, в котором он протекает на силу тока в нем. Магнитный момент направлен перпендикулярно плоскости контура. Это направление можно определить с помощью правила буравчика. Если буравчик вращать по направлению движения тока в контуре, то его поступательное движение укажет направление магнитного момента.
Для наглядности рассмотрим действие магнитного момента тока на примере. Возьмем прямоугольную рамку с током. Поместим ее в постоянное магнитное поле, так чтобы плоскость рамки была параллельна вектору магнитной индукции.
Как известно на проводник, с током помещённый в магнитное поле действует сила Лоренца. Направление, которой можно определить с помощью правила левой руки. Рассматривая действие силы Лоренца на стороны рамки в отдельности можно прийти к выводу, что на них будут действовать силы равные по величине, но противоположные по знаку.
Поскольку эти силы зависят от длинны проводника силы тока в нем и угла между направлением тока и вектором магнитной индукции. А ток в этом контуре протекает один и тот же. Длинна сторон рамки одинакова. И стороны рамки находятся параллельно магнитному полю. Но ток движется в противоположные стороны. Значит и силы будут направлены противоположно.
Две другие стороны рамки не будут взаимодействовать с полем поскольку ток в них течет параллельно силовым линиям поля. Следовательно, исходя из закона Лоренца сила, действующая на них, будет равна нулю.
Далее если мысленно провести вдоль рамки вертикальную осевую линию. То силы, действующие на ее края, будут стремиться ее развернуть. До тех пор пока рамка не примет такое положение, при котором все силы не уравновесятся. При этом рамка повернется своей плоскостью перпендикулярно силовым линия поля.
Таким образом, вращающий момент можно представить в таком виде
где B вектор магнитной индукции
I сила тока в контуре
S площадь рамки с током
sinb угол между вектором магнитной индукции и плоскостью рамки
МАГНИ́ТНЫЙ МОМЕ́НТ
В книжной версии
Том 18. Москва, 2011, стр. 382-383
Скопировать библиографическую ссылку:
МАГНИ́ТНЫЙ МОМЕ́НТ, физич. величина, характеризующая магнитные свойства замкнутого контура, обтекаемого электрич. током, или другого, эквивалентного ему физич. объекта (напр., атома или др. системы движущихся зарядов). Для замкнутого тока силой $I$ М. м. определяется выражением: $$boldsymbol p_М=Iint_σ boldsymbol ndσ,$$ где $σ$ – геометрич. поверхность произвольной формы, ограниченная контуром с током; $dσ$ – малый элемент этой поверхности, который можно принять за часть плоскости; $boldsymbol n$ – единичный вектор, направленный перпендикулярно к $dσ$ в сторону, согласующуюся с направлением протекания тока по правилу винта. Величина и направление М. м. не зависят от выбора поверхности $σ$ , и для контура с током, целиком лежащего в плоскости, $boldsymbol p_м=IS boldsymbol n$ , где $S$ – площадь части плоскости, ограниченной контуром с током, $boldsymbol n$ – единичный вектор, направленный перпендикулярно $S$ в сторону, согласующуюся с направлением протекания тока по правилу винта. Размерность М. м. – А · м 2 .
МАГНИТНЫЙ МОМЕНТ. ВЕКТОРЫ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
Практическое значение имеет вращение прямоугольной рамки с током в однородном магнитном поле. Вращение рамки происходит под действием момента пары сил, возникающих, как отмечалось в предыдущем параграфе, за счет непосредственного взаимодействия магнита и проводника с током. Момент вращения для случая контура с током в поле постоянного магнита меняется от нуля до некоторого максимального значения. Конкретное значение его определяется положением рамки относительно полюсов постоянного магнита и его силовых линий. Рассмотрим два крайних варианта компоновки системы рамка—магнит с заданным направлением силы тока в рамке. Вначале плоскость рамки расположена вдоль поля (рис. 11.2). Направление действующей силы на проводник ЛВ с током в магнитном поле можно определить по правилу левой руки. Руку располагают так, чтобы силовые линии постоянного магнита, исходящие из северного полюса к южному, входили в ладонь, а четыре пальца были расположены вдоль тока. Отставленный на 90° большой палец указывает направление действующей на проводник силы.
Применяя правило левой руки, найдем, что на проводник ЛВ рамки действует сила F<, направленная от наблюдателя, к проводнику CD приложена сила F2, направленная к наблюдателю. На участки АС и BD рамки, расположенные вдоль силовых линий поля, силы не действуют. Силы F< и F2 равны, параллельны и противоположны друг другу, так как ЛВ и CD равны и параллельны. К рамке с током, таким образом, приложена пара сил, под действием которых она повернется по часовой стрелке. Момент пары сил будет максимальным, Мтах.
Рассмотрим положение рамки, когда ее плоскость перпендикулярна полю постоянного магнита (рис. 11.3). В таком положении рамки момент вращения, действующий на нее, равен нулю, М = 0. Силы, действующие на рамку в этом случае, только деформируют ее, но не поворачивают. Состояние рамки является равновесным. Однако при рассмотрении ряда последовательных положений рамки с током в магнитном поле легко догадаться, что положение рамки, представленное на рис. 11.3, всего лишь промежуточное состояние, вращающий момент сил в котором равен нулю.
Движение проводника с током, и в том числе вращательное движение контура с током в магнитном поле, имеет широкое применение в электродвигателях, измерительных приборах с вращающейся катушкой и ряде других электротехнических устройств.
Важной характеристикой рамки с током является ее магнитный момент рт = Is, А-м 2 (рис. 11.4). Это векторная величина. И совпадает
она с направлением положительной нормали к плоскости рамки. То есть направление вектора магнитного момента рамки с током определяется по правилу буравчика (,правого винта).
Вращающий момент сил зависит от свойств рамки с током и свойств магнитного поля в данной точке, т.е. прямо пропорционален вектору магнитного момента рамки с током: М = Гд„.я1,
М = Bis, Н • м. Свойства магнитного поля сконцентрированы в коэффициенте пропорциональности В, называемом магнитной индукцией. Чтобы разобраться в его физическом содержании, проделаем следующие рассуждения. Если в фиксированную точку магнитного поля последовательно размещать параллельно полю рамки с различными значениями магнитного момента рт, то естественно, что на них действуют различные вращающие моменты М, в данном случае максимальные. Однако, как показывает опыт, отношение Mmax / рт = const для всех контуров
и поэтому может служить характеристикой магнитного поля в данной точке, называемой магнитной индукцией:
Прирт = 1 А • м 2 В = Л/тах, т.е. магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Следовательно, магнитная индукция характеризует способность магнитного поля оказывать силовое действие на прямолинейный или замкнутый проводник с током или движущийся электрический заряд.
Магнитное поле является силовым, и по аналогии с электрическим его изображают с помощью линий магнитной индукции — линий, касательные к которым совпадают с направлением вектора В. Направление силовых линий магнитного поля задается правилом правого винта. Если ввинчивать винт так, чтобы он перемещался по направлению тока, то направление вращения его головки указывает направление силовых линий. Для кольцевых проводников винт вкручивается так, чтобы он продвигался по направлению поля, т.е. вдоль силовой линии, и тогда направление вращения его «шляпки» укажет направление тока в витке. Линии магнитной индукции всегда замкнуты и охватывают проводники с током в отличие от силовых линий электрического поля (рис. 11.5). Поэтому магнитное поле называют вихревым.
Итак, на проводник с током в магнитном поле действует сила. Из изложенного только что известно, от чего зависит направление этой силы. А вот величина ее, как показали опыты А. Ампера, прямо пропорциональна силе тока в проводнике, его длине, напряженности магнитного поля, ориентации относительно силовых линий магнитного поля
(sina) и зависит от свойств среды (р.0р.), в которой находится проводник:
где ц0 = 4 л: • 10 -7 Гн/м, Гн = Дж/А 2 — магнитная постоянная; ц — магнитная проницаемость среды.
Эта безразмерная характеристика магнитных свойств вещества показывает, во сколько раз магнитное поле макротоков усиливается за счет микротоков в веществе. Подробно физическое содержание р
будет рассмотрено несколько позже; a = | Ш j — угол между прямолинейным проводником и вектором магнитной индукции. Величину Н называют напряженностью магнитного поля: Н = F/ (p0p//sina), А/м. Это важная характеристика магнитного поля. Она является векторной величиной. Вектор напряженности магнитного поля в фиксированной точке направлен, как и вектор магнитной индукции, по касательной к силовой линии, проходящей через эту точку. Величина напряженности магнитного поля служит его силовой характеристикой, подобно тому, как вектор электрической напряженности служит силовой характеристикой электрического поля. И еще один момент: вектор напряженности Н характеризует магнитное поле, создаваемое макротоками.
Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое микро- и макротоками или постоянным магнитом и микротоками. Для однородной изотропной среды связь между векторами магнитной индукции и напряженности следующая:
Из последних двух уравнений очевидно, что при всех равных условиях векторы В и Н в различных средах будут иметь разное значение.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
Расчет векторов В и Н для конкретных полей будет рассмотрен несколько позже, после изучения законов Био—Савара—Лапласа и полного тока.
[spoiler title=”источники:”]
http://bigenc.ru/physics/text/2153456
http://studref.com/596837/tehnika/magnitnyy_moment_vektory_induktsii_napryazhennosti_magnitnogo_polya
[/spoiler]
In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include loops of electric current (such as electromagnets), permanent magnets, elementary particles (such as electrons), various molecules, and many astronomical objects (such as many planets, some moons, stars, etc).
More precisely, the term magnetic moment normally refers to a system’s magnetic dipole moment, the component of the magnetic moment that can be represented by an equivalent magnetic dipole: a magnetic north and south pole separated by a very small distance. The magnetic dipole component is sufficient for small enough magnets or for large enough distances. Higher-order terms (such as the magnetic quadrupole moment) may be needed in addition to the dipole moment for extended objects.
The magnetic dipole moment of an object is readily defined in terms of the torque that the object experiences in a given magnetic field. The same applied magnetic field creates larger torques on objects with larger magnetic moments. The strength (and direction) of this torque depends not only on the magnitude of the magnetic moment but also on its orientation relative to the direction of the magnetic field. The magnetic moment may be considered, therefore, to be a vector. The direction of the magnetic moment points from the south to north pole of the magnet (inside the magnet).
The magnetic field of a magnetic dipole is proportional to its magnetic dipole moment. The dipole component of an object’s magnetic field is symmetric about the direction of its magnetic dipole moment, and decreases as the inverse cube of the distance from the object.
Definition, units, and measurement[edit]
Definition[edit]
The magnetic moment can be defined as a vector relating the aligning torque on the object from an externally applied magnetic field to the field vector itself. The relationship is given by:[1]
where τ is the torque acting on the dipole, B is the external magnetic field, and m is the magnetic moment.
This definition is based on how one could, in principle, measure the magnetic moment of an unknown sample. For a current loop, this definition leads to the magnitude of the magnetic dipole moment equaling the product of the current times the area of the loop. Further, this definition allows the calculation of the expected magnetic moment for any known macroscopic current distribution.
An alternative definition is useful for thermodynamics calculations of the magnetic moment. In this definition, the magnetic dipole moment of a system is the negative gradient of its intrinsic energy, Uint, with respect to external magnetic field:
Generically, the intrinsic energy includes the self-field energy of the system plus the energy of the internal workings of the system. For example, for a hydrogen atom in a 2p state in an external field, the self-field energy is negligible, so the internal energy is essentially the eigenenergy of the 2p state, which includes Coulomb potential energy and the kinetic energy of the electron. The interaction-field energy between the internal dipoles and external fields is not part of this internal energy.[2]
Units[edit]
The unit for magnetic moment in International System of Units (SI) base units is A⋅m2, where A is ampere (SI base unit of current) and m is meter (SI base unit of distance). This unit has equivalents in other SI derived units including:[3][4]
where N is newton (SI derived unit of force), T is tesla (SI derived unit of magnetic flux density), and J is joule (SI derived unit of energy).[5] Although torque (N·m) and energy (J) are dimensionally equivalent, torques are never expressed in units of energy.[6]
In the CGS system, there are several different sets of electromagnetism units, of which the main ones are ESU, Gaussian, and EMU. Among these, there are two alternative (non-equivalent) units of magnetic dipole moment:
(ESU)
(Gaussian and EMU),
where statA is statamperes, cm is centimeters, erg is ergs, and G is gauss. The ratio of these two non-equivalent CGS units (EMU/ESU) is equal to the speed of light in free space, expressed in cm⋅s−1.
All formulae in this article are correct in SI units; they may need to be changed for use in other unit systems. For example, in SI units, a loop of current with current I and area A has magnetic moment IA (see below), but in Gaussian units the magnetic moment is IA/c.
Other units for measuring the magnetic dipole moment include the Bohr magneton and the nuclear magneton.
Measurement[edit]
The magnetic moments of objects are typically measured with devices called magnetometers, though not all magnetometers measure magnetic moment: Some are configured to measure magnetic field instead. If the magnetic field surrounding an object is known well enough, though, then the magnetic moment can be calculated from that magnetic field.
Relation to magnetization[edit]
The magnetic moment is a quantity that describes the magnetic strength of an entire object. Sometimes, though, it is useful or necessary to know how much of the net magnetic moment of the object is produced by a particular portion of that magnet. Therefore, it is useful to define the magnetization field M as:
where mΔV and VΔV are the magnetic dipole moment and volume of a sufficiently small portion of the magnet ΔV. This equation is often represented using derivative notation such that
where dm is the elementary magnetic moment and dV is the volume element. The net magnetic moment of the magnet m therefore is
where the triple integral denotes integration over the volume of the magnet. For uniform magnetization (where both the magnitude and the direction of M is the same for the entire magnet (such as a straight bar magnet) the last equation simplifies to:
where V is the volume of the bar magnet.
The magnetization is often not listed as a material parameter for commercially available ferromagnetic materials, though. Instead the parameter that is listed is residual flux density (or remanence), denoted Br. The formula needed in this case to calculate m in (units of A⋅m2) is:
,
where:
- Br is the residual flux density, expressed in teslas.
- V is the volume of the magnet (in m3).
- μ0 is the permeability of vacuum (4π×10−7 H/m).[7]
Models[edit]
The preferred classical explanation of a magnetic moment has changed over time. Before the 1930s, textbooks explained the moment using hypothetical magnetic point charges. Since then, most have defined it in terms of Ampèrian currents.[8] In magnetic materials, the cause of the magnetic moment are the spin and orbital angular momentum states of the electrons, and varies depending on whether atoms in one region are aligned with atoms in another.
Magnetic pole model[edit]
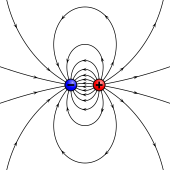
An electrostatic analog for a magnetic moment: two opposing charges separated by a finite distance.
The sources of magnetic moments in materials can be represented by poles in analogy to electrostatics. This is sometimes known as the Gilbert model.[9] In this model, a small magnet is modeled by a pair of fictitious magnetic monopoles of equal magnitude but opposite polarity. Each pole is the source of magnetic force which weakens with distance. Since magnetic poles always come in pairs, their forces partially cancel each other because while one pole pulls, the other repels. This cancellation is greatest when the poles are close to each other i.e. when the bar magnet is short. The magnetic force produced by a bar magnet, at a given point in space, therefore depends on two factors: the strength p of its poles (magnetic pole strength), and the vector 
It points in the direction from South to North pole. The analogy with electric dipoles should not be taken too far because magnetic dipoles are associated with angular momentum (see Relation to angular momentum). Nevertheless, magnetic poles are very useful for magnetostatic calculations, particularly in applications to ferromagnets.[8] Practitioners using the magnetic pole approach generally represent the magnetic field by the irrotational field H, in analogy to the electric field E.
Amperian loop model[edit]

The Amperian loop model: A current loop (ring) that goes into the page at the x and comes out at the dot produces a B-field (lines). The north pole is to the right and the south to the left.
After Hans Christian Ørsted discovered that electric currents produce a magnetic field and André-Marie Ampère discovered that electric currents attract and repel each other similar to magnets, it was natural to hypothesize that all magnetic fields are due to electric current loops. In this model developed by Ampère, the elementary magnetic dipole that makes up all magnets is a sufficiently small amperian loop of current I. The dipole moment of this loop is
where S is the area of the loop. The direction of the magnetic moment is in a direction normal to the area enclosed by the current consistent with the direction of the current using the right hand rule.
Localized current distributions[edit]

Moment 
The magnetic dipole moment can be calculated for a localized (does not extend to infinity) current distribution assuming that we know all of the currents involved. Conventionally, the derivation starts from a multipole expansion of the vector potential. This leads to the definition of the magnetic dipole moment as:
where × is the vector cross product, r is the position vector, and j is the electric current density and the integral is a volume integral.[10] When the current density in the integral is replaced by a loop of current I in a plane enclosing an area S then the volume integral becomes a line integral and the resulting dipole moment becomes
which is how the magnetic dipole moment for an Amperian loop is derived.
Practitioners using the current loop model generally represent the magnetic field by the solenoidal field B, analogous to the electrostatic field D.
Magnetic moment of a solenoid[edit]

A generalization of the above current loop is a coil, or solenoid. Its moment is the vector sum of the moments of individual turns. If the solenoid has N identical turns (single-layer winding) and vector area S,
Quantum mechanical model[edit]
When calculating the magnetic moments of materials or molecules on the microscopic level it is often convenient to use a third model for the magnetic moment that exploits the linear relationship between the angular momentum and the magnetic moment of a particle. While this relation is straightforward to develop for macroscopic currents using the amperian loop model (see below), neither the magnetic pole model nor the amperian loop model truly represents what is occurring at the atomic and molecular levels. At that level quantum mechanics must be used. Fortunately, the linear relationship between the magnetic dipole moment of a particle and its angular momentum still holds, although it is different for each particle. Further, care must be used to distinguish between the intrinsic angular momentum (or spin) of the particle and the particle’s orbital angular momentum. See below for more details.
Effects of an external magnetic field[edit]
Torque on a moment[edit]
The torque τ on an object having a magnetic dipole moment m in a uniform magnetic field B is:
.
This is valid for the moment due to any localized current distribution provided that the magnetic field is uniform. For non-uniform B the equation is also valid for the torque about the center of the magnetic dipole provided that the magnetic dipole is small enough.[11]
An electron, nucleus, or atom placed in a uniform magnetic field will precess with a frequency known as the Larmor frequency. See Resonance.
Force on a moment[edit]
A magnetic moment in an externally produced magnetic field has a potential energy U:
In a case when the external magnetic field is non-uniform, there will be a
force, proportional to the magnetic field gradient, acting on the magnetic moment itself. There are two expressions for the force acting on a magnetic dipole, depending on whether the model used for the dipole is a current loop or two monopoles (analogous to the electric dipole).[12] The force obtained in the case of a current loop model is
.
Assuming existence of magnetic monopole, the force is modified as follows:
In the case of a pair of monopoles being used (i.e. electric dipole model), the force is
.
And one can be put in terms of the other via the relation
.
In all these expressions m is the dipole and B is the magnetic field at its position. Note that if there are no currents or time-varying electrical fields or magnetic charge, ∇×B = 0, ∇·B = 0 and the two expressions agree.
Relation to Free Energy[edit]
One can relate the magnetic moment of a system to the free energy of that system.[13] In a uniform magnetic field B, the free energy F can be related to the magnetic moment M of the system as

where S is the entropy of the system and T is the temperature. Therefore, the magnetic moment can also be defined in terms of the free energy of a system as

Magnetism[edit]
In addition, an applied magnetic field can change the magnetic moment of the object itself; for example by magnetizing it. This phenomenon is known as magnetism. An applied magnetic field can flip the magnetic dipoles that make up the material causing both paramagnetism and ferromagnetism. Additionally, the magnetic field can affect the currents that create the magnetic fields (such as the atomic orbits) which causes diamagnetism.
Effects on environment[edit]
Magnetic field of a magnetic moment[edit]
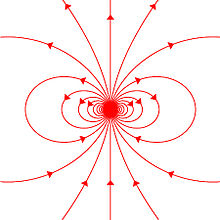
Magnetic field lines around a “magnetostatic dipole”. The magnetic dipole itself is located in the center of the figure, seen from the side, and pointing upward.
Any system possessing a net magnetic dipole moment m will produce a dipolar magnetic field (described below) in the space surrounding the system. While the net magnetic field produced by the system can also have higher-order multipole components, those will drop off with distance more rapidly, so that only the dipole component will dominate the magnetic field of the system at distances far away from it.
The magnetic field of a magnetic dipole depends on the strength and direction of a magnet’s magnetic moment 
where 



The equivalent equations for the magnetic 
Forces between two magnetic dipoles[edit]
As discussed earlier, the force exerted by a dipole loop with moment m1 on another with moment m2 is
where B1 is the magnetic field due to moment m1. The result of calculating the gradient is[14][15]
where r̂ is the unit vector pointing from magnet 1 to magnet 2 and r is the distance. An equivalent expression is[15]
The force acting on m1 is in the opposite direction.
Torque of one magnetic dipole on another[edit]
The torque of magnet 1 on magnet 2 is
Theory underlying magnetic dipoles[edit]
The magnetic field of any magnet can be modeled by a series of terms for which each term is more complicated (having finer angular detail) than the one before it. The first three terms of that series are called the monopole (represented by an isolated magnetic north or south pole) the dipole (represented by two equal and opposite magnetic poles), and the quadrupole (represented by four poles that together form two equal and opposite dipoles). The magnitude of the magnetic field for each term decreases progressively faster with distance than the previous term, so that at large enough distances the first non-zero term will dominate.
For many magnets the first non-zero term is the magnetic dipole moment. (To date, no isolated magnetic monopoles have been experimentally detected.) A magnetic dipole is the limit of either a current loop or a pair of poles as the dimensions of the source are reduced to zero while keeping the moment constant. As long as these limits only apply to fields far from the sources, they are equivalent. However, the two models give different predictions for the internal field (see below).
Magnetic potentials[edit]
Traditionally, the equations for the magnetic dipole moment (and higher order terms) are derived from theoretical quantities called magnetic potentials[16] which are simpler to deal with mathematically than the magnetic fields.
In the magnetic pole model, the relevant magnetic field is the demagnetizing field 


.
In the amperian loop model, the relevant magnetic field is the magnetic induction 
Both of these potentials can be calculated for any arbitrary current distribution (for the amperian loop model) or magnetic charge distribution (for the magnetic charge model) provided that these are limited to a small enough region to give:
where 


where 
where × is the vector cross product, r is the position vector, and j is the electric current density and the integral is a volume integral.
In the magnetic pole perspective, the first non-zero term of the scalar potential is
Here 
The same symbol 
External magnetic field produced by a magnetic dipole moment[edit]
The magnetic flux density for a magnetic dipole in the amperian loop model, therefore, is
Further, the magnetic field strength 
Internal magnetic field of a dipole[edit]
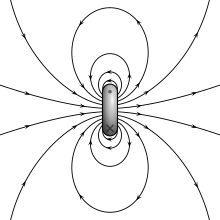
The magnetic field of a current loop
The two models for a dipole (magnetic poles or current loop) give the same predictions for the magnetic field far from the source. However, inside the source region, they give different predictions. The magnetic field between poles (see the figure for Magnetic pole model) is in the opposite direction to the magnetic moment (which points from the negative charge to the positive charge), while inside a current loop it is in the same direction (see the figure to the right). The limits of these fields must also be different as the sources shrink to zero size. This distinction only matters if the dipole limit is used to calculate fields inside a magnetic material.[8]
If a magnetic dipole is formed by taking a “north pole” and a “south pole”, bringing them closer and closer together but keeping the product of magnetic pole charge and distance constant, the limiting field is[8]
If a magnetic dipole is formed by making a current loop smaller and smaller, but keeping the product of current and area constant, the limiting field is
Unlike the expressions in the previous section, this limit is correct for the internal field of the dipole.[8][17]
These fields are related by B = μ0(H + M), where M(r) = mδ(r) is the magnetization.
Relation to angular momentum[edit]
The magnetic moment has a close connection with angular momentum called the gyromagnetic effect. This effect is expressed on a macroscopic scale in the Einstein–de Haas effect, or “rotation by magnetization”, and its inverse, the Barnett effect, or “magnetization by rotation”.[1] Further, a torque applied to a relatively isolated magnetic dipole such as an atomic nucleus can cause it to precess (rotate about the axis of the applied field). This phenomenon is used in nuclear magnetic resonance.
Viewing a magnetic dipole as current loop brings out the close connection between magnetic moment and angular momentum. Since the particles creating the current (by rotating around the loop) have charge and mass, both the magnetic moment and the angular momentum increase with the rate of rotation. The ratio of the two is called the gyromagnetic ratio or 
where 
In the amperian loop model, which applies for macroscopic currents, the gyromagnetic ratio is one half of the charge-to-mass ratio. This can be shown as follows. The angular momentum of a moving charged particle is defined as:
where μ is the mass of the particle and v is the particle’s velocity. The angular momentum of the very large number of charged particles that make up a current therefore is:
where ρ is the mass density of the moving particles. By convention the direction of the cross product is given by the right-hand rule.[20]
This is similar to the magnetic moment created by the very large number of charged particles that make up that current:
where 

Comparing the two equations results in:
where 

Even though atomic particles cannot be accurately described as orbiting (and spinning) charge distributions of uniform charge-to-mass ratio, this general trend can be observed in the atomic world so that:
where the g-factor depends on the particle and configuration. For example the g-factor for the magnetic moment due to an electron orbiting a nucleus is one while the g-factor for the magnetic moment of electron due to its intrinsic angular momentum (spin) is a little larger than 2. The g-factor of atoms and molecules must account for the orbital and intrinsic moments of its electrons and possibly the intrinsic moment of its nuclei as well.
In the atomic world the angular momentum (spin) of a particle is an integer (or half-integer in the case of spin) multiple of the reduced Planck constant ħ. This is the basis for defining the magnetic moment units of Bohr magneton (assuming charge-to-mass ratio of the electron) and nuclear magneton (assuming charge-to-mass ratio of the proton). See electron magnetic moment and Bohr magneton for more details.
Atoms, molecules, and elementary particles[edit]
Fundamentally, contributions to any system’s magnetic moment may come from sources of two kinds: motion of electric charges, such as electric currents; and the intrinsic magnetism of elementary particles, such as the electron.
Contributions due to the sources of the first kind can be calculated from knowing the distribution of all the electric currents (or, alternatively, of all the electric charges and their velocities) inside the system, by using the formulas below. On the other hand, the magnitude of each elementary particle’s intrinsic magnetic moment is a fixed number, often measured experimentally to a great precision. For example, any electron’s magnetic moment is measured to be −9.284764×10−24 J/T.[21] The direction of the magnetic moment of any elementary particle is entirely determined by the direction of its spin, with the negative value indicating that any electron’s magnetic moment is antiparallel to its spin.
The net magnetic moment of any system is a vector sum of contributions from one or both types of sources.
For example, the magnetic moment of an atom of hydrogen-1 (the lightest hydrogen isotope, consisting of a proton and an electron) is a vector sum of the following contributions:
- the intrinsic moment of the electron,
- the orbital motion of the electron around the proton,
- the intrinsic moment of the proton.
Similarly, the magnetic moment of a bar magnet is the sum of the contributing magnetic moments, which include the intrinsic and orbital magnetic moments of the unpaired electrons of the magnet’s material and the nuclear magnetic moments.
Magnetic moment of an atom[edit]
For an atom, individual electron spins are added to get a total spin, and individual orbital angular momenta are added to get a total orbital angular momentum. These two then are added using angular momentum coupling to get a total angular momentum. For an atom with no nuclear magnetic moment, the magnitude of the atomic dipole moment, 
where j is the total angular momentum quantum number, gJ is the Landé g-factor, and μB is the Bohr magneton. The component of this magnetic moment along the direction of the magnetic field is then[23]
The negative sign occurs because electrons have negative charge.
The integer m (not to be confused with the moment, 
Due to the angular momentum, the dynamics of a magnetic dipole in a magnetic field differs from that of an electric dipole in an electric field. The field does exert a torque on the magnetic dipole tending to align it with the field. However, torque is proportional to rate of change of angular momentum, so precession occurs: the direction of spin changes. This behavior is described by the Landau–Lifshitz–Gilbert equation:[25][26]
where γ is the gyromagnetic ratio, m is the magnetic moment, λ is the damping coefficient and Heff is the effective magnetic field (the external field plus any self-induced field). The first term describes precession of the moment about the effective field, while the second is a damping term related to dissipation of energy caused by interaction with the surroundings.
Magnetic moment of an electron[edit]
Electrons and many elementary particles also have intrinsic magnetic moments, an explanation of which requires a quantum mechanical treatment and relates to the intrinsic angular momentum of the particles as discussed in the article Electron magnetic moment. It is these intrinsic magnetic moments that give rise to the macroscopic effects of magnetism, and other phenomena, such as electron paramagnetic resonance.
The magnetic moment of the electron is
where μB is the Bohr magneton, S is electron spin, and the g-factor gS is 2 according to Dirac’s theory, but due to quantum electrodynamic effects it is slightly larger in reality: 2.00231930436. The deviation from 2 is known as the anomalous magnetic dipole moment.
Again it is important to notice that m is a negative constant multiplied by the spin, so the magnetic moment of the electron is antiparallel to the spin. This can be understood with the following classical picture: if we imagine that the spin angular momentum is created by the electron mass spinning around some axis, the electric current that this rotation creates circulates in the opposite direction, because of the negative charge of the electron; such current loops produce a magnetic moment which is antiparallel to the spin. Hence, for a positron (the anti-particle of the electron) the magnetic moment is parallel to its spin.
Magnetic moment of a nucleus[edit]
The nuclear system is a complex physical system consisting of nucleons, i.e., protons and neutrons. The quantum mechanical properties of the nucleons include the spin among others. Since the electromagnetic moments of the nucleus depend on the spin of the individual nucleons, one can look at these properties with measurements of nuclear moments, and more specifically the nuclear magnetic dipole moment.
Most common nuclei exist in their ground state, although nuclei of some isotopes have long-lived excited states. Each energy state of a nucleus of a given isotope is characterized by a well-defined magnetic dipole moment, the magnitude of which is a fixed number, often measured experimentally to a great precision. This number is very sensitive to the individual contributions from nucleons, and a measurement or prediction of its value can reveal important information about the content of the nuclear wave function. There are several theoretical models that predict the value of the magnetic dipole moment and a number of experimental techniques aiming to carry out measurements in nuclei along the nuclear chart.
Magnetic moment of a molecule[edit]
Any molecule has a well-defined magnitude of magnetic moment, which may depend on the molecule’s energy state. Typically, the overall magnetic moment of a molecule is a combination of the following contributions, in the order of their typical strength:
- magnetic moments due to its unpaired electron spins (paramagnetic contribution), if any
- orbital motion of its electrons, which in the ground state is often proportional to the external magnetic field (diamagnetic contribution)
- the combined magnetic moment of its nuclear spins, which depends on the nuclear spin configuration.
Examples of molecular magnetism[edit]
- The dioxygen molecule, O2, exhibits strong paramagnetism, due to unpaired spins of its outermost two electrons.
- The carbon dioxide molecule, CO2, mostly exhibits diamagnetism, a much weaker magnetic moment of the electron orbitals that is proportional to the external magnetic field. The nuclear magnetism of a magnetic isotope such as 13C or 17O will contribute to the molecule’s magnetic moment.
- The dihydrogen molecule, H2, in a weak (or zero) magnetic field exhibits nuclear magnetism, and can be in a para- or an ortho- nuclear spin configuration.
- Many transition metal complexes are magnetic. The spin-only formula is a good first approximation for high-spin complexes of first-row transition metals.[27]
-
Number of
unpaired
electronsSpin-only
moment
(μB)1 1.73 2 2.83 3 3.87 4 4.90 5 5.92
Elementary particles[edit]
In atomic and nuclear physics, the Greek symbol μ represents the magnitude of the magnetic moment, often measured in Bohr magnetons or nuclear magnetons, associated with the intrinsic spin of the particle and/or with the orbital motion of the particle in a system. Values of the intrinsic magnetic moments of some particles are given in the table below:
-
Intrinsic magnetic moments and spins
of some elementary particles[28]Particle
name (symbol)Magnetic
dipole moment
(10−27 J⋅T−1)Spin
quantum number
(dimensionless)electron (e−) −9284.764 1/2 proton (H+) –0 014.106067 1/2 neutron (n) 0 00−9.66236 1/2 muon (μ−) 0 0−44.904478 1/2 deuteron (2H+) –0 004.3307346 1 triton (3H+) –0 015.046094 1/2 helion (3He++) 0 0−10.746174 1/2 alpha particle (4He++) –0 000 0
For the relation between the notions of magnetic moment and magnetization see magnetization.
See also[edit]
- Moment (physics)
- Electric dipole moment
- Toroidal dipole moment
- Magnetic susceptibility
- Orbital magnetization
- Magnetic dipole–dipole interaction
- Electron magnetic moment
- Nucleon magnetic moment
References and notes[edit]
- ^ a b
Cullity, B. D.; Graham, C. D. (2008). Introduction to Magnetic Materials (2nd ed.). Wiley-IEEE Press. p. 103. ISBN 978-0-471-47741-9. - ^ See, for example, Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics (2nd ed.). John Wiley & Sons. p. 200. ISBN 978-0-471-86256-7. where the relevant U is U[Be].
- ^ “Magnetic units”. IEEE Magnetics. Retrieved 19 February 2016.
- ^ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (21 Jul 2015). “CODATA Recommended Values of the Fundamental Physical Constants: 2014”. Reviews of Modern Physics. 88 (3): 035009. arXiv:1507.07956. Bibcode:2016RvMP…88c5009M. doi:10.1103/RevModPhys.88.035009. S2CID 1115862.
- ^ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, ISBN 978-92-822-2272-0, pp. 20-21
- ^ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, ISBN 978-92-822-2272-0, p. 23
- ^ “K&J Magnetics – Glossary”. www.kjmagnetics.com.
- ^ a b c d e f Brown, William Fuller Jr. (1962). Magnetostatic Principles in Ferromagnetism. North-Holland.
- ^ Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. p. 258. ISBN 978-0-13-805326-0. OCLC 40251748.
- ^ Jackson, John David (1975). “5.6 Magnetic fields of a Localized Current Distribution, Magnetic Moment”. Classical Electrodynamics. Vol. 2. ISBN 978-0-471-43132-9.
- ^ Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. p. 257. ISBN 978-0138053260.
- ^ Boyer, Timothy H. (1988). “The Force on a Magnetic Dipole”. Am. J. Phys. 56 (8): 688–692. Bibcode:1988AmJPh..56..688B. doi:10.1119/1.15501.
- ^ Landau, L. D.; Lifshitz, E. M.; Pitaevskii, L. P. (January 15, 1984). Electrodynamics of Continuous Media: Volume 8 (Course of Theoretical Physics) (2 ed.). Butterworth-Heinemann. p. 130. ISBN 978-0750626347.
- ^ Furlani, Edward P. (2001). Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications. Academic Press. p. 140. ISBN 978-0-12-269951-1.
- ^ a b Yung, K. W.; Landecker, P. B.; Villani, D. D. (1998). “An Analytic Solution for the Force between Two Magnetic Dipoles” (PDF). Magnetic and Electrical Separation. 9: 39–52. doi:10.1155/1998/79537. Retrieved November 24, 2012.
- ^ Jackson, John David (1975). “5.6”. Classical electrodynamics (2nd ed.). New York: Wiley. ISBN 9780471431329.
- ^ Jackson, John David (1975). Classical electrodynamics (2nd ed.). New York: Wiley. p. 184. ISBN 978-0-471-43132-9.
- ^ Krey, Uwe; Owen, Anthony (2007). Basic Theoretical Physics. Springer. pp. 151–152. ISBN 978-3-540-36804-5.
- ^ Buxton, Richard B. (2002). Introduction to functional magnetic resonance imaging. Cambridge University Press. p. 136. ISBN 978-0-521-58113-4.
- ^ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2006). The Feynman Lectures on Physics. Vol. 2. pp. 13–12. ISBN 978-0-8053-9045-2.
- ^ “CODATA Value: electron magnetic moment”. physics.nist.gov.
- ^ Tilley, R. J. D. (2004). Understanding Solids. John Wiley and Sons. p. 368. ISBN 978-0-470-85275-0.
- ^ Tipler, Paul Allen; Llewellyn, Ralph A. (2002). Modern Physics (4th ed.). Macmillan. p. 310. ISBN 978-0-7167-4345-3.
- ^ Crowther, J.A. (1949). Ions, Electrons, and Ionizing Radiations (8th ed.). London: Edward Arnold. p. 270.
- ^ Rice, Stuart Alan (2004). Advances in chemical physics. Wiley. pp. 208ff. ISBN 978-0-471-44528-9.
- ^ Steiner, Marcus (2004). Micromagnetism and Electrical Resistance of Ferromagnetic Electrodes for Spin Injection Devices. Cuvillier Verlag. p. 6. ISBN 978-3-86537-176-8.
- ^ Figgis, B.N.; Lewis, J. (1960). “The magnetochemistry of complex compounds”. In Lewis, J.; Wilkins, R.G. (eds.). Modern Coordination Chemistry: Principles and methods. New York: Interscience. pp. 405–407.
- ^ “Search results matching ‘magnetic moment’“. CODATA internationally recommended values of the Fundamental Physical Constants. National Institute of Standards and Technology. Retrieved 11 May 2012.
External links[edit]
- Bowtell, Richard (2009). “μ – Magnetic Moment”. Sixty Symbols. Brady Haran for the University of Nottingham.
Содержание:
- Магнитное поле
- Магнитный момент
- Сила Ампера
- Сила, действующая на движущийся заряд
- Магнитное поле, создаваемое постоянными магнитами
- Напряженность магнитного поля
- Взаимодействия токов и магнитов
- Эквивалентность токов и магнитов
- Вихревой характер магнитного поля
- Закон электромагнитной индукции и сила Лоренца
- Измерения магнитного поля методом индукционного толчка
- Ограниченные тела в магнитном поле
- Связь между магнитной проницаемостью и восприимчивостью
- Искажение магнитного поля при внесении в него магнетика
- Магнитный гистерезис
Магнитное поле – особая форма материи, существующая вокруг движущихся электрических зарядов – токов. Источниками магнитного поля являются постоянные магниты, проводники с током.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Магнитное поле
Магнитное поле можно назвать особым видом материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом. В специальной теории относительности магнитные поля являются необходимым следствием существования электрических полей.
Магнитный момент
Магнитные поля действуют на токи, движущиеся заряженные тела или частицы, на намагниченные тела. Можно осуществить множество различных приборов и с их помощью судить о свойствах магнитного поля. Наиболее целесообразно характеризовать свойства магнитного поля, изучая его механические действия на контур тока. Вполне возможно осуществление проволочного контура весьма малой площади. Такой прибор позволит промерить магнитное поле достаточно детально. Таким образом, «пробный» контур тока играет в теории магнитного поля ту же роль, что «пробный» заряд в теории электрического поля.
Производя опыты с подобным прибором, мы придем к следующим основным фактам. В каждой точке поля свободно вращающийся контур займет определенное положение равновесия. При этом положение устойчивого равновесия определяется не только расположением в пространстве оси контура, но также и тем, как располагается в пространстве определенная сторона контура, скажем, та, смотря на которую мы видим ток идущим против часовой стрелки. Назовем эту сторону положительной, или северной; условимся проводить нормаль к контуру так, чтобы она образовывала правовинтовую систему с направлением тока. Смотря против нормали, мы будем видеть положительную (северную) сторону контура.
Сравнивая поведение контура тока с поведением магнитных стрелок, можно обнаружить, что нормаль контура, находящегося в устойчивом равновесии, смотрит туда же, куда и магнитная стрелка. Таким образом, называя направлением магнитного поля то направление, куда смотрит нормаль свободного пробного контура, мы не разойдемся с элементарным определением.
Отклоняя пробный контур от положения равновесия, мы обнаружим действие на него момента сил (рис. 105). При этом отклонение контура от равновесия однозначно описывается отклонением нормали контура от направления поля — синус угла  и вращающий момент сил N оказываются пропорциональными:
и вращающий момент сил N оказываются пропорциональными:
 При том же угле а вращательный момент пропорционален произведению площади контура S на силу протекающего тока
При том же угле а вращательный момент пропорционален произведению площади контура S на силу протекающего тока  Уменьшение площади в какое-то число раз приводит к такому же изменению вращающего момента, что и уменьшение силы тока в такое же количество раз.
Уменьшение площади в какое-то число раз приводит к такому же изменению вращающего момента, что и уменьшение силы тока в такое же количество раз.

Из сказанного следует, что магнитное поведение контура зависит от расположения нормали контура и от величины произведения Эти данные можно объединить в одну векторную величину, называемую магнитным моментом кольцевого тока. В электротехнике, где используется система СИ, принято называть магнитным моментом вектор
Эти данные можно объединить в одну векторную величину, называемую магнитным моментом кольцевого тока. В электротехнике, где используется система СИ, принято называть магнитным моментом вектор  — единичная нормаль). В системе СГС, чаще используемой физиками, в эту формулу вводят коэффициент пропорциональности 1 /с:
— единичная нормаль). В системе СГС, чаще используемой физиками, в эту формулу вводят коэффициент пропорциональности 1 /с:  — скорость распространения электромагнитных волн в вакууме). Введение числового коэффициента, да еще вдобавок размерного, может показаться ненужным усложнением. Однако другие формулы при этом упрощаются; оценить это упрощение читатель сумеет значительно позднее.
— скорость распространения электромагнитных волн в вакууме). Введение числового коэффициента, да еще вдобавок размерного, может показаться ненужным усложнением. Однако другие формулы при этом упрощаются; оценить это упрощение читатель сумеет значительно позднее.
Результаты опытов с пробным контуром могут быть записаны в виде:  где В — коэффициент пропорциональности. Для разных полей или для разных точек пространства одного поля величина В будет иметь разные значения. По смыслу написанной формулы В равно максимальному вращательному моменту, действующему на единичный пробный контур
где В — коэффициент пропорциональности. Для разных полей или для разных точек пространства одного поля величина В будет иметь разные значения. По смыслу написанной формулы В равно максимальному вращательному моменту, действующему на единичный пробный контур  Этот коэффициент В, характеризующий магнитное поле, носит название магнитной индукции. Векторная величина, имеющая направление магнитного поля и численно равная В, носит название вектора магнитной индукции.
Этот коэффициент В, характеризующий магнитное поле, носит название магнитной индукции. Векторная величина, имеющая направление магнитного поля и численно равная В, носит название вектора магнитной индукции.
Если вращательный момент описывать вектором, направленным вдоль оси вращения (в соответствии с правилами правовинтовой системы), то формула для него может быть записана в виде так называемого векторного произведения векторов, а именно: 
Если  параллельно
параллельно  это значит, что любой контур тока стремится установиться в магнитном поле таким образом, чтобы его магнитный момент совпал с направлением поля. На тело действует максимальный магнитный момент в том случае, если магнитный момент образует угол 90° с направлением поля. Для контура это соответствует положению плоскости витка проволоки вдоль силовых линий.
это значит, что любой контур тока стремится установиться в магнитном поле таким образом, чтобы его магнитный момент совпал с направлением поля. На тело действует максимальный магнитный момент в том случае, если магнитный момент образует угол 90° с направлением поля. Для контура это соответствует положению плоскости витка проволоки вдоль силовых линий.
Определив магнитное поле с помощью контура тока, у которого магнитный момент подсчитывается из измерений силы тока и площади, мы можем, наоборот, воспользоваться формулой  для определения магнитных моментов таких систем, для которых нельзя измерить ток. Более того, мы переносим понятие магнитного момента и на такие системы, где понятие кольцевого электрического тока теряет смысл. Именно таким образом поступает физик, когда он говорит о магнитном моменте электрона, ядерной частицы. Магнитный момент магнитной стрелки также является нерасчленяемым понятием. Впрочем, к магнитному моменту постоянного магнита мы еще вернемся на стр. 442, обсудив некоторые специфические влияния среды. Как бы то ни было, магнитный момент системы, находящейся в вакууме, всегда может быть определен по приведенной формуле вращательного момента.
для определения магнитных моментов таких систем, для которых нельзя измерить ток. Более того, мы переносим понятие магнитного момента и на такие системы, где понятие кольцевого электрического тока теряет смысл. Именно таким образом поступает физик, когда он говорит о магнитном моменте электрона, ядерной частицы. Магнитный момент магнитной стрелки также является нерасчленяемым понятием. Впрочем, к магнитному моменту постоянного магнита мы еще вернемся на стр. 442, обсудив некоторые специфические влияния среды. Как бы то ни было, магнитный момент системы, находящейся в вакууме, всегда может быть определен по приведенной формуле вращательного момента.
Поворот от положения равновесия тела, обладающего магнитным моментом, требует затраты работы. При повороте на малый угол  работа вращения может быть представлена в виде
работа вращения может быть представлена в виде

Отклонение тела от положения равновесия связано с накоплением потенциальной энергии  Написанное произведение есть скалярное произведение двух векторов; следовательно,
Написанное произведение есть скалярное произведение двух векторов; следовательно, 

В положении равновесия потенциальная энергия минимальна и равна  , при повороте магнитного момента на 90° потенциальная энергия возрастает до нуля, и, наконец, когда магнитный момент устанавливается антипараллельно полю (положение неустойчивого равновесия), потенциальная энергия максимальна и равна
, при повороте магнитного момента на 90° потенциальная энергия возрастает до нуля, и, наконец, когда магнитный момент устанавливается антипараллельно полю (положение неустойчивого равновесия), потенциальная энергия максимальна и равна 
Примеры. 1. Магнитный момент ядра атома водорода (ядерный магнетон)  СГС. Магнитный момент электрона (магнетон Бора)
СГС. Магнитный момент электрона (магнетон Бора) 

2. Электрический ток в 1 А, текущий по витку с площадью  создает магнитный момент
создает магнитный момент 
3. В абсолютной системе единиц магнитная индукция измеряется в гауссах (Гс), в системе СИ В измеряется в теслах (Т) и имеет размерность 
 Для магнитного поля Земли
Для магнитного поля Земли 
4. В воздушном зазоре мощной электрической машины магнитная индукция достигает нескольких тысяч гауссов. Академик П. Л. Капица получал импульсные магнитные поля с 
Сила Ампера
Наличие вращательного момента, действующего на контур тока, является несомненно результатом действия сил на каждый участок проводника, по которому текут заряды. Закон силы, действующей на элемент тока, можно установить опытным путем. Для этого необходимо выделить участок провода, например, с помощью ртутных контактов. Тогда этот участок может перемещяться под действием

силы. Если это смещение уравновесить натяжением пружины, то магнитная сила может быть измерена (рис. 106).
Закон силы, действующей на элемент тока малой длины, был впервые установлен Ампером и имеет вид

Векторная запись напоминает нам известное правило левой руки. Сила, действующая на элемент длины провода, всегда образует прямой угол с плоскостью, проходящей через ток и вектор магнитной индукции в этом месте. Чтобы выяснить направление силы, надо посмотреть, с какой стороны вращение вектора  к вектору
к вектору  представится идущим против часовой стрелки по кратчайшему пути. Эта сторона будет положительной в правовинтовой системе и вектор силы будет «смотреть» на наблюдателя. Сила имеет максимальное значение тогда, когда элемент тока образует прямой угол с вектором поля. Сила обращается в нуль для элемента провода, лежащего вдоль силовой линии.
представится идущим против часовой стрелки по кратчайшему пути. Эта сторона будет положительной в правовинтовой системе и вектор силы будет «смотреть» на наблюдателя. Сила имеет максимальное значение тогда, когда элемент тока образует прямой угол с вектором поля. Сила обращается в нуль для элемента провода, лежащего вдоль силовой линии.
Выше записаны формулы в системе СГС. В системе СИ коэффициент 1 /с отсутствует и формула силы Ампера имеет вид 

Чтобы определить величину силы, действующей на кусок провода конечной длины, написанное выражение силы надо проинтегрировать:

Только в простейшем случае прямолинейного куска провода длиной  находящегося в однородном магнитном поле В, закон Ампера можно применить непосредственно в форме
находящегося в однородном магнитном поле В, закон Ампера можно применить непосредственно в форме

Представляется совершенно естественной связь между законом Ампера и выражением для вращательного момента, выведенным в

предыдущем параграфе. Мы проведем рассмотрение лишь для простейшего случая прямоугольной рамки, расположенной в однородном магнитном поле параллельно силовым линиям (рис. 107). Две стороны рамки перпендикулярны к силовым линиям, две другие лежат вдоль силовых линий. Следовательно, все силы, действующие на элементы провода, можно свести к двум, показанным на рис. 107. Эти силы равны друг другу и по закону Ампера могут быть записаны в виде  Тот же рисунок показывает, что силы Ампера приводят к моменту сил
Тот же рисунок показывает, что силы Ампера приводят к моменту сил  есть площадь рамки, следовательно,
есть площадь рамки, следовательно,  что совпадает с формулой для момента сил, выведенной в предыдущем параграфе. Предоставляем читателю сделать это доказательство более общим.
что совпадает с формулой для момента сил, выведенной в предыдущем параграфе. Предоставляем читателю сделать это доказательство более общим.
Пример. На проводник длиной 3 м с током 50 А в поле 3000 Гс=0,3 Т действует сила  При диаметре ротора ~1 м на виток действует вращающий момент
При диаметре ротора ~1 м на виток действует вращающий момент  Эти величины по порядку соответствуют параметрам крупной электрической машины. В электроизмерительном при боре на проводник длиной 2 см в поле 100 Гс при токе 0,01 А действует сила
Эти величины по порядку соответствуют параметрам крупной электрической машины. В электроизмерительном при боре на проводник длиной 2 см в поле 100 Гс при токе 0,01 А действует сила При диаметре рамки ~1 см на виток действует вращающий момент
При диаметре рамки ~1 см на виток действует вращающий момент 
Сила, действующая на движущийся заряд
Мы можем пойти еще дальше и сделать попытку рассмотрения магнитных сил, действующих на токи, как сил, приложенных к элементарным частицам электричества.
Электрический ток есть не что иное, как поток электрических частиц. Если заряд каждой частицы есть е, направленная скорость частицы  й концентрация частиц (т. е. их число в единице объема) есть
й концентрация частиц (т. е. их число в единице объема) есть  то выражение для силы тока можно представить в виде
то выражение для силы тока можно представить в виде Действительно, через сечение провода
Действительно, через сечение провода пройдут все частицы, которые занимали объем
пройдут все частицы, которые занимали объем  т. е. протечет количество
т. е. протечет количество

электричества  (рис. 108). Подставляя это выражение в закон Ампера, получим
(рис. 108). Подставляя это выражение в закон Ампера, получим

Но  есть число частиц в рассматриваемом объеме проводника; значит, на одну частицу действует сила
есть число частиц в рассматриваемом объеме проводника; значит, на одну частицу действует сила

Эту силу называют иногда лоренцевой силой, в честь выдающегося физика Лоренца, много сделавшего для развития теории электронов.
Написанное выражение силы (мы его будем писать только в системе СГС, с коэффициентом 1/с) позволяет сразу же ответить на крайне интересный вопрос о характере движения электрической частицы (электрона, протона и т. д.) в магнитном поле. Сила, действующая на движущийся заряд, направлена перпендикулярно к силовым линиям и к вектору скорости частицы. Если частица движется вдоль силовых линий, то сила на нее не действует. Напротив, сила максимальна, если движение происходит в плоскости, перпендикулярной к силовым линиям. В этом последнем случае 
Если поле однородно, то электрическая частица, движущаяся перпендикулярно к полю, будет описывать окружность, поскольку движение под действием постоянной силы, направленной под прямым углом к движению, не может быть иным, согласно основному закону механики. Мы вернемся к движению частицы в магнитном поле на стр. 407.
Пример. Электрона в катодной лампе, ускоряемые разностью потенциалов 70 В, приобретают скорость  При вхождении под прямым углом в магнитное поле 500 Гс каждый электрон испытывает отклоняющую силу Лоренца
При вхождении под прямым углом в магнитное поле 500 Гс каждый электрон испытывает отклоняющую силу Лоренца  Под действием этой силы электрон начнет двигаться по круговой орбите такого радиуса
Под действием этой силы электрон начнет двигаться по круговой орбите такого радиуса 
Магнитное поле, создаваемое постоянными магнитами
Каждый постоянный магнит имеет два полюса *): из северного линии выходят, в южный входят. Мысленно построим поверхность, охватывающую северный полюс магнита. Мы можем найти полное число линий, пронизывающих эту поверхность. Это число по аналогии с соответствующей электрической величиной мы будем называть магнитным потоком и обозначать буквой Ф. Поток через элементарную площадку, перпендикулярную к силовым линиям, равен  через произвольную площадку
через произвольную площадку  — угол, образованный нормалью к площадке с силовыми линиями;
— угол, образованный нормалью к площадке с силовыми линиями;
через поверхность  ,и наконец, через замкнутую поверхность
,и наконец, через замкнутую поверхность 
Поток  выходящий из северного полюса магнита и входящий в южный, является основной характеристикой магнита. Чем сильнее магнит, тем больше
выходящий из северного полюса магнита и входящий в южный, является основной характеристикой магнита. Чем сильнее магнит, тем больше  Это несколько оправдывает название «количество магнетизма» (имеющее только историческое значение) для величины, пропорциональной потоку, а именно, равной
Это несколько оправдывает название «количество магнетизма» (имеющее только историческое значение) для величины, пропорциональной потоку, а именно, равной Иногда называют
Иногда называют  (еще более неудачно) магнитной массой. В электротехнике пользуются магнитной массой
(еще более неудачно) магнитной массой. В электротехнике пользуются магнитной массой 
Если полюсы магнита имеют небольшой размер (магнитная спица), то силовые линии вблизи таких полюсов расходятся радиально.
При помощи закона Гаусса — Остроградского

мы обосновали формулу для электрической индукции уединенного заряда, Очевидно, что «уединенный» магнитный полюс должен дать магнитную индукцию, удовлетворяющую аналогичному равенству:
Очевидно, что «уединенный» магнитный полюс должен дать магнитную индукцию, удовлетворяющую аналогичному равенству:



Разумеется, никаких «уединенных» магнитных полюсов не существует. Написанная формула имеет смысл лишь в случае длинного магнита с точечным полюсом и при этом не слишком далеко от полюса. Подобный подход к магнитному полю постоянного магнита имеет все же полное право на существование. Это хорошо видно при составлении выражения для поля стержневого магнита, рассматриваемого как магнитный диполь с двумя полюсами  находящимися на расстоянии
находящимися на расстоянии  друг от друга. На рис. 109 показано поле стержневого магнита и идеальное поле, рассчитанное по формуле
друг от друга. На рис. 109 показано поле стержневого магнита и идеальное поле, рассчитанное по формуле
где —расстояния от полюсов до рассматриваемой точки. Совпадение картин вполне удовлетворительное.
—расстояния от полюсов до рассматриваемой точки. Совпадение картин вполне удовлетворительное.
Хорошие результаты получаются при расчетах полей на больших расстояниях от магнита. Действительно, если расстояния  велики по сравнению с длиной магнита
велики по сравнению с длиной магнита  (плечом магнитного диполя), то рассмотрение полюсов как точек вполне оправдано. Расчеты ничуть не отличаются от соответствующих подсчетов электрических взаимодействий. Сравним, например, значения магнитной индукции, создаваемой стержневым магнитом на большом расстоянии от него вдоль оси магнита и перпендикулярно к его оси. В первом случае имеем
(плечом магнитного диполя), то рассмотрение полюсов как точек вполне оправдано. Расчеты ничуть не отличаются от соответствующих подсчетов электрических взаимодействий. Сравним, например, значения магнитной индукции, создаваемой стержневым магнитом на большом расстоянии от него вдоль оси магнита и перпендикулярно к его оси. В первом случае имеем

где  носит название магнитного момента постоянного магнита. Во втором случае (рис. 110)
носит название магнитного момента постоянного магнита. Во втором случае (рис. 110)


Итак, поле вдоль оси в два раза сильнее. В системе СИ две последние формулы будут иметь вид соответственно

Пример. Вычислим магнитную индукцию, создаваемую стержневым магнитом длиной на расстоянии
на расстоянии от магнита вдоль оси. Площадь поперечного сечения магнита
от магнита вдоль оси. Площадь поперечного сечения магнита  индукция в магните 500 Гс.
индукция в магните 500 Гс.
Магнитный поток в магните (он же выходящий из полюса)  максвелл (Мкс). Тогда на полюсе магнита сосредоточена «магнитная масса»
максвелл (Мкс). Тогда на полюсе магнита сосредоточена «магнитная масса»  СГС. Магнитный момент магнита
СГС. Магнитный момент магнита 
Искомая магнитная индукция 
Напряженность магнитного поля
Рассмотрим взаимодействие уединенного магнитного полюса и элемента тока (рис. 111). Магнитный полюс создает поле В в месте нахождения электрического тока. Следовательно, по закону Ампера на элемент тока будет действовать сила

Мы можем вместо величины магнитной индукции поставить ее выражение для точечного полюса. Учитывая, что поле направлено по радиусу, мы получим для силы взаимодействия следующие выражения:


Вполне естественно принять, что сила, с которой элемент тока действует на магнитный полюс, представится той же формулой с обращением направления силы. Это допущение Рис. 111. нельзя проверить непосредственно на опыте,
так как мы нё можем осуществить ни уединенного полюса, ни отдельно взятого элемента постоянного тока. Однако мы можем проверить правильность высказанного положения, интегрируя силы взаимодействия для опытных случаев. Теория действительно совпадает с опытом.
Итак, сила действия элемента тока на магнитный полюс может быть представлена в виде или в системе СИ, без коэффициента
или в системе СИ, без коэффициента  и с заменой
и с заменой  на
на 

Мы не ставим знака минус в этой формуле, так как полагаем обращенным радиус-вектор. За направление всегда принимают направление от источника поля до точки наблюдения. Поэтому, когда речь шла о силе, действующей на ток,
всегда принимают направление от источника поля до точки наблюдения. Поэтому, когда речь шла о силе, действующей на ток,  предполагалось направленным от полюса к элементу тока. Теперь же, когда речь идет, о силе, действующей со стороны тока на полюс, радиус-вектор
предполагалось направленным от полюса к элементу тока. Теперь же, когда речь идет, о силе, действующей со стороны тока на полюс, радиус-вектор  предполагается направленным от элемента тока к полюсу.
предполагается направленным от элемента тока к полюсу.
Сила, действующая на единичный магнитный полюс, носит название напряженности магнитного поля:

Нашим рассуждением доказано, что напряженность магнитного поля, создаваемого элементом тока, выражается формулой

В системе СИ формула, определяющая напряженность магнитного поля, создаваемого током, будет иметь вид

Итак, существуют две характеристики магнитного поля: вектор индукции, измеряемый действием магнитного поля на токи, и вектор напряженности, который может быть получен в эксперименте измерением воздействия поля на магниты.
Практически измерения напряженности удобнее сводить к измерению вращательного момента, действующего на магнитную стрелку (рис. 112). Такая стрелка, помещенная в однородное поле, будет подвергаться действию пары сил; величина силы равна  а плечо равно
а плечо равно Отсюда для вращательного момента получим выражение
Отсюда для вращательного момента получим выражение

или в векторной форме — магнитный момент стрелки, что весьма напоминает формулу момента сил, действующих на контур тока.
— магнитный момент стрелки, что весьма напоминает формулу момента сил, действующих на контур тока.

Вопрос о связи между напряженностью магнитного поля и магнитной индукцией должен быть решен опытом. Оказывается, что во всех случаях,.за исключением анизотропных тел, векторы напряженности и индукции параллельны друг другу. Это значит, что магнитная стрелка и ось пробного контура всегда установятся параллельно. Далее, во всех случаях, за исключением ферромагнитных веществ, между  имеется простая линейная зависимость:
имеется простая линейная зависимость:  — универсальная постоянная, так называемая магнитная проницаемость вакуума, а
— универсальная постоянная, так называемая магнитная проницаемость вакуума, а  — коэффициент, характеризующий среду,— относительная магнитная проницаемость среды.
— коэффициент, характеризующий среду,— относительная магнитная проницаемость среды.
В системе СГС полагают  Это приводит к одинаковой размерности магнитной индукции и напряженности. Эта одинаковость достигнута, однако, не даром, а ценой введения размерного коэффициента 1/с в законе Ампера. В системе СИ магнитная проницаемость вакуума равна
Это приводит к одинаковой размерности магнитной индукции и напряженности. Эта одинаковость достигнута, однако, не даром, а ценой введения размерного коэффициента 1/с в законе Ампера. В системе СИ магнитная проницаемость вакуума равна 
Взаимодействия токов и магнитов
Законы, рассмотренные в предыдущих параграфах, позволяют в принципе рассчитать взаимодействие любых магнитных систем. Мы располагаем формулами сил и моментов сил, действующих на приборы со стороны магнитного поля любого происхождения:

Формулы, связывающие поля с их источниками:

Подставляя любую нижнюю формулу в любую из верхнего ряда и используя связь  мы получим формулы магнитных, электромагнитных, магнитоэлектрических и электродинамических взаимодействий. Каждый тип взаимодействия проиллюстрируем одним примером.
мы получим формулы магнитных, электромагнитных, магнитоэлектрических и электродинамических взаимодействий. Каждый тип взаимодействия проиллюстрируем одним примером.
Магнитное взаимодействие, т. е. действие магнита на магнит. Два полюса на расстоянии г взаимодействуют по закону Кулона, т. е.

Сила взаимодействия обратно пропорциональна магнитной проницаемости.
Электромагнитное действие, т. е. действие тока на магнит. Магнитная стрелка испытывает вращательный момент со стороны элемента тока. Для простоты принято т. е. магнитная стрелка расположена поперек силовых линий.
т. е. магнитная стрелка расположена поперек силовых линий.


Взаимодействие не зависит от магнитной проницаемости, т. е. от свойств среды.
Магнитоэлектрическое действие, т. е. действие магнита наток. Контур тока расположен на продолжении оси стержневого магнита на расстоянии  от него (рис. 113). Контур испытывает вращательный момент
от него (рис. 113). Контур испытывает вращательный момент

Взаимодействие не зависит от магнитной проницаемости.
Пример. Контур площадью  обтекаемый током
обтекаемый током  взаимодействует на расстоянии 100 см со стержневым магнитом, магнитный момент которого
взаимодействует на расстоянии 100 см со стержневым магнитом, магнитный момент которого  На контур будет действовать вращающий момент
На контур будет действовать вращающий момент

Электродинамическое действие, т. е. действие тока на ток. Два параллельных тока притягиваются с силой

Взаимодействие прямо пропорционально магнитной проницаемости.
Таким же точно образом можно составить формулы для любых взаимодействий магнитных систем.
Пример: Электродинамическое взаимодействие надо серьезным образом учитывать при прокладке токопроводящих шин. В случае короткого замыкания шины и поддерживающие их изоляторы должны оказаться достаточно прочными, чтобы выдержать большие электродинамические нагрузки. Пусть по параллельным шинам, отстоящим на расстоянии  текут токи
текут токи На единицу длины одной из шин действует сила
На единицу длины одной из шин действует сила  — напряженность магнитного поля, создаваемого прямолинейным током, текущим по другой шине (см. стр. 250). Имеем
— напряженность магнитного поля, создаваемого прямолинейным током, текущим по другой шине (см. стр. 250). Имеем т. е. на каждый метр шины действует сила —
т. е. на каждый метр шины действует сила — Этот же результат можно было получить интегрированием последней формулы для
Этот же результат можно было получить интегрированием последней формулы для
Эквивалентность токов и магнитов
Мы обращали внимание на сходство между выражениями для вращательных моментов, действующих на магнитную стрелку и контур тока. Действительно, поведение этих двух систем во внешнем поле чрезвычайно похоже. Если характеризовать каждую из систем стрелкой ее магнитного момента, то сходство будет еще более полным. Каждая система стремится расположиться в магнитном поле так, чтобы ее магнитный момент совпал с силовыми линиями поля. Если магнитный момент отклонен от положения устойчивого равновесия, то на систему действует вращательный момент  — для магнитной стрелки и
— для магнитной стрелки и  — для контура тока. Соответственно потенциальные энергии этих двух систем представятся формулами
— для контура тока. Соответственно потенциальные энергии этих двух систем представятся формулами 
Так как  то становится очевидным различие между
то становится очевидным различие между
формулами: они переходят одна в другую введением в формулы магнитной проницаемости. Отсюда следует, что в отношении механического воздействия магнитная стрелка с моментом М эквивалентна контуру тока с моментом 
Однако сходство этих двух систем еще не кончается на сказанном. Мы покажем сейчас, что магнитная стрелка и контур тока обладают собственными полями, совпадающими с точностью до постоянного множителя. Такое сходство имеет место на расстояниях, существенно больших размера системы. Докажем это для точки пространства, лежащей на линии магнитного момента на расстоянии  от центра системы. Поле магнита для такой точки было уже вычислено, оно равно
от центра системы. Поле магнита для такой точки было уже вычислено, оно равно  Остается найти поле кругового тока на его оси.
Остается найти поле кругового тока на его оси.
На рис. 114 произведено построение векторов напряженности, создаваемых двумя элементами длины окружности, пересекающими чертеж. Векторы напряженности направлены перпендикулярно к соответствующему элементу тока и к радиусу-вектору, т. е. лежат в плоскости чертежа. В какую именно сторону смотрит вектор напряженности, следует определить либо при помощи правила векторного произведения, либо при помощи правила буравчика (что в общем одно и то же).
Элементарное поле равно в рассматриваемом случае 
 так как элемент тока и радиус-вектор образуют прямой угол. Сложим изображенные на рисунке два вектора. Для поля, созданного двумя «противоположными» элементами, получим
так как элемент тока и радиус-вектор образуют прямой угол. Сложим изображенные на рисунке два вектора. Для поля, созданного двумя «противоположными» элементами, получим

смысл обозначений ясен из чертежа. Такую же величину поля даст любая пара «противоположных» элементов. Поэтому полное поле мы получим, заменив в последнем выражении длину элемента  на длину половины окружности
на длину половины окружности  . Напряженность поля кругового тока на его оси на расстоянии
. Напряженность поля кругового тока на его оси на расстоянии  от тока *) представится формулой
от тока *) представится формулой

Но есть момент кругового тока. Следовательно,
есть момент кругового тока. Следовательно, а магнитная индукция
а магнитная индукция 
Этим доказано, что магнитный диполь и контур тока эквивалентны не только в отношении действующих на них сил, но и в отношении создаваемых ими полей. Эквивалентность имеет и здесь тот же характер. Чтобы заменить магнитную стрелку с моментом М, нужно взять контур тока с моментом 
В вакууме и для системы  и принцип эквивалентности еще проще: магнитная стрелка с моментом М эквивалентна контуру тока с таким же магнитным моментом.
и принцип эквивалентности еще проще: магнитная стрелка с моментом М эквивалентна контуру тока с таким же магнитным моментом.
Примеры. 1. Вернемся к примеру на стр. 242. Рассчитаем магнитную индукцию того же магнита в системе СИ:

в полном соответствии с результатом на стр. 242.
2. Контур с током  имеющий площадь
имеющий площадь  создает на расстоянии
создает на расстоянии  см вдоль оси, перпендикулярной к его плоскости, магнитное поле с напряженностью
см вдоль оси, перпендикулярной к его плоскости, магнитное поле с напряженностью

Вихревой характер магнитного поля
Исследование хода магнитных линий показывает принципиальное различие между электрическим и магнитным полем. Электрические линии имеют начало и конец, не существует замкнутых линий у постоянного электрического поля. Напротив, опыт показывает, что силовые линии магнитного поля (т. е. векторные линии магнитной индукции) всегда замкнуты, не существуют линии, имеющие начало и конец.
По причинам, обсуждавшимся выше, силы и поля сил, в которых работа по замкнутому пути равна нулю, получили название потенциальных. Векторные поля, характеризующиеся замкнутыми силовыми линиями, носят название вихревых. Магнитное поле является вихревым.
Если провести в магнитном поле замкнутую поверхность, то магнитный поток  через такую поверхность будет всегда равен нулю. Иначе говоря, число линий, входящих в эту поверхность, будет равно числу линий, выходящих из нее. Уравнение
через такую поверхность будет всегда равен нулю. Иначе говоря, число линий, входящих в эту поверхность, будет равно числу линий, выходящих из нее. Уравнение  и является математическим выражением того факта, что у магнитных силовых линий нет начала и конца.
и является математическим выражением того факта, что у магнитных силовых линий нет начала и конца.
Связь магнитных линий с создающими поле токами состоит в том, что магнитные линии всегда охватывают токи. Поэтому интегралы, взятые вдоль силовой линии от индукции или напряженности, должны быть отличны от нуля. Целесообразнее
должны быть отличны от нуля. Целесообразнее
рассматривать второй интеграл, так как его величина должна быть пропорциональна силе электрического тока, охватываемого силовой линией; ведь согласно основной формуле напряженности между  и силой тока имеет место прямая пропорциональность.
и силой тока имеет место прямая пропорциональность.
По аналогии с электростатикой  называют магнитным напряжением. Если интеграл берется вдоль силовой линии, то
называют магнитным напряжением. Если интеграл берется вдоль силовой линии, то
Магнитное напряжение вдоль замкнутой линии должно быть пропорционально току, около которого эта линия обворачивается:

где  — коэффициент пропорциональности.
— коэффициент пропорциональности.
Силовая линия может охватывать не один ток, а несколько. Для создаваемого поля существенна алгебраическая сумма токов, и уравнение имеет вид
Более глубокий теоретический анализ, на котором мы здесь не можем останавливаться, показывает, что написанное уравнение подвергается еще двум обобщениям. Во-первых, магнитное напряжение можно взять не только вдоль силовой линии, но и вдоль произвольного контура; во-вторых, коэффициент пропорциональности в уравнении является константой, зависящей лишь от свойств среды и одинаковой для любых геометрических условий. Таким образом, магнитное напряжение, взятое для любой замкнутой кривой линии, одинаково, если только эта кривая охватывает токи определенной силы. Безразлична форма кривой, размеры кривой; кривая может охватывать один ток или десяток токов; эти токи могут быть прямыми, круговыми,— все это безразлично, магнитное напряжение будет одним и тем же, если только алгебраическая сумма токов, пронизывающих кривую, будет иметь одинаковое значение.
Так как коэффициент пропорциональности в формуле магнитного напряжения есть величина универсальная, то мы можем найти  если сумеем вычислить магнитное напряжение для любой системы, поле которой нам известно.
если сумеем вычислить магнитное напряжение для любой системы, поле которой нам известно.
Мы познакомились с общим выражением для напряженности магнитного поля элементарного тока. Вычисление магнитного напряжения с помощью формулы напряженности

представляет математические трудности. Кроме того, нам известна формула напряженности магнитного поля на оси кругового тока,  Вычисление магнитного напряжения вдоль оси кругового тока не представит особых затруднений. Нас не должно смущать, что интегрирование происходит вдоль прямой линии, в то время как нас интересует магнитное напряжение вдоль замкнутой кривой. Дело в том, что прямая, идущая от отрицательной бесконечности в положительную, является замкнутой кривой — она замыкается в бесконечности. Выражение для магнитного напряжения
Вычисление магнитного напряжения вдоль оси кругового тока не представит особых затруднений. Нас не должно смущать, что интегрирование происходит вдоль прямой линии, в то время как нас интересует магнитное напряжение вдоль замкнутой кривой. Дело в том, что прямая, идущая от отрицательной бесконечности в положительную, является замкнутой кривой — она замыкается в бесконечности. Выражение для магнитного напряжения  взятого вдоль такой замкнутой кривой, т. е. вдоль оси кругового тока от отрицательной бесконечности до положительной бесконечности, можно записать в виде
взятого вдоль такой замкнутой кривой, т. е. вдоль оси кругового тока от отрицательной бесконечности до положительной бесконечности, можно записать в виде
 где
где  — радиус,
— радиус,  — расстояние, откладываемое по оси контура. Интеграл легко берется, если перейти к новой переменной
— расстояние, откладываемое по оси контура. Интеграл легко берется, если перейти к новой переменной  по формуле
по формуле и оказывается равным
и оказывается равным  Подставляя
Подставляя
 и приравнивая значение магнитного напряжения величине
и приравнивая значение магнитного напряжения величине  получим
получим

Закон магнитного напряжения имеет вид

Закон магнитного напряжения может оказать существенные услуги в подсчете магнитных полей ряда систем. В его применении нам должны помочь соображения симметрии, и в этом отношении рассуждения, к которым мы сейчас переходим, очень похожи на соответствующие задачи, которые решались в электростатике с помощью закона Гаусса — Остроградского.
Рассмотрим, прежде всего, бесконечный прямолинейный ток. Из соображений симметрии очевидно, что силовая линия может иметь лишь форму окружности, центр которой совладает с осью провода. Также несомненно, что во всех точках окружности числовое значение напряженности одно и то же. Применяя к такой силовой
линии закон магнитного напряжения, получим:  При
При
этом  есть не что иное как длина силовой линии. Если рассматриваются точки, расположенные на расстоянии
есть не что иное как длина силовой линии. Если рассматриваются точки, расположенные на расстоянии  от оси провода, то
от оси провода, то  и, таким образом, для магнитного поля бесконечного прямолинейного тока в пространстве вне провода мы получим:
и, таким образом, для магнитного поля бесконечного прямолинейного тока в пространстве вне провода мы получим:

Найдем теперь напряженность магнитного поля внутри провода. Обозначим радиус провода через а и допустим, что ток распределен вдоль сечения провода вполне равномерно. Силовые линии внутри провода также должны иметь вид окружностей. Рассмотрим такую линию радиуса  Через нее протекает доля тока
Через нее протекает доля тока  и, следовательно, закон магнитного напряжения даст
и, следовательно, закон магнитного напряжения даст
 или в системе СИ
или в системе СИ
Мы видим, что напряженность магнитного поля на оси провода равна нулю, далее она возрастает, становится максимальной на поверхности провода, а затем убывает обратно пропорционально расстоянию (рис. 115).
Если поле определяется в такой точке, для которой расстояние  много меньше ее расстояния до конца провода, то формула
много меньше ее расстояния до конца провода, то формула  может быть применена для провода конечных размеров.
может быть применена для провода конечных размеров.

Пример. Подсчитаем, какова напряженность магнитного поля на расстоянии 5 см от оси прямолинейного тока силой 20 А.
В системе 

Другой важный пример использования закона магнитного напряжения — это вычисление поля соленоида.
Положим, что на окружность длиной  равномерно навиты витки соленоида. Поле внутри кругового соленоида должно быть однородным, и все силовые линии должны быть окружностями, концентрическими с
равномерно навиты витки соленоида. Поле внутри кругового соленоида должно быть однородным, и все силовые линии должны быть окружностями, концентрическими с  Такая система для вопросов теории магнитного поля играет ту же роль, что бесконечный плоский конденсатор в теории электрического поля. Каждая силовая линия охватывает все
Такая система для вопросов теории магнитного поля играет ту же роль, что бесконечный плоский конденсатор в теории электрического поля. Каждая силовая линия охватывает все  витков, и поэтому магнитное напряжение, взятое вдоль силовой линии длиной
витков, и поэтому магнитное напряжение, взятое вдоль силовой линии длиной будет равно
будет равно

Так как

Напряженность магнитного поля катушки определяется ее «ампер-витками», т. е. произведением силы тока на число витков на единицу длины соленоида. Последняя формула — одно из оправданий электротехнической системы записи уравнений поля. Соленоид является одним из основных элементов электротехнических устройств, поэтому упрощение формулы для вычисления напряженности его магнитного поля очень полезно для практики.
Формулу  можно применять и для открытого соленоида, однако лишь для тех внутренних точек, которые находятся достаточно далеко от краев.
можно применять и для открытого соленоида, однако лишь для тех внутренних точек, которые находятся достаточно далеко от краев.
Пример. Напряженность магнитного поля в центре узкого и длинного соленоида 

В системе СГС тот же расчет примет вид

Закон электромагнитной индукции и сила Лоренца
Как известно, явление электромагнитной индукции, открытое великим английским физиком Фарадеем, состоит в том, что в замкнутом проводнике возникает электрический ток, если только изменяется значение магнитного потока, проходящего через замкнутый провод. При этом э. д. с. индукции оказывается пропорциональной скорости изменения магнитного потока, т. е. производной по времени


Покажем, что закон электромагнитной индукции тесно связан с существованием лоренцовой силы. Если электромагнитная индукция возникает при перемещении провода в магнитном поле, то закон индукции является прямым следствием выражения для силы Лоренца.
Чтобы не загромождать изложения чисто математическими трудностями, проведем упрощенное доказательство, а именно, допустим, что э. д. с. индукции возникает в прямоугольном контуре, расположенном перпендикулярно к силовым линиям однородного магнитного поля. Изменение потока вызывается поступательным перемещением одной из сторон прямоугольника длиной так, как показано на рис. 116. В перемещающемся проводнике находятся свободные заряды, поэтому при движении проводника со скоростью V эти заряды подвергнутся действию силы Лоренца
так, как показано на рис. 116. В перемещающемся проводнике находятся свободные заряды, поэтому при движении проводника со скоростью V эти заряды подвергнутся действию силы Лоренца  (Ввиду того, что углы между направлением скорости, магнитным полем и направлением проводника равны 90°, мы опустили векторные символы в формуле силы, а синус угла при этом равен единице.) Сила Лоренца направлена перпендикулярно к плоскости, проходящей через направление
(Ввиду того, что углы между направлением скорости, магнитным полем и направлением проводника равны 90°, мы опустили векторные символы в формуле силы, а синус угла при этом равен единице.) Сила Лоренца направлена перпендикулярно к плоскости, проходящей через направление  скорости перемещения зарядов (вместе с проводом) и магнитные линии, т. е. вдоль провода. Таким образом, заряды придут в движение вдоль провода, создастся индукционный ток.
скорости перемещения зарядов (вместе с проводом) и магнитные линии, т. е. вдоль провода. Таким образом, заряды придут в движение вдоль провода, создастся индукционный ток.
Электродвижущей силой называется работа перемещения единицы заряда вдоль замкнутого контура. Сила, действующая на единицу заряда, равна  работа этой силы вдоль движущегося провода равна
работа этой силы вдоль движущегося провода равна  но на остальных участках контура работа не производится. Поэтому последнее выражение и есть искомое выражение для э. д. с. индукции.
но на остальных участках контура работа не производится. Поэтому последнее выражение и есть искомое выражение для э. д. с. индукции.
Оно имеет вид
Пусть за время  провод передвинулся на расстояние
провод передвинулся на расстояние  Площадь контура возросла при этом на величину
Площадь контура возросла при этом на величину  а магнитный поток — на величину
а магнитный поток — на величину  Так как
Так как  э.д.с индукции может быть представлена и в такой форме:
э.д.с индукции может быть представлена и в такой форме:  Но это выражение
Но это выражение
—  в системе СГС и
в системе СГС и  в системе СИ — и есть закон электромагнитной индукции Фарадея.
в системе СИ — и есть закон электромагнитной индукции Фарадея.
Этим показано, что электромагнитная индукция и отклонение движущихся электрических зарядов во внешнем поле представляют собой проявления одних и тех же законов природы. Мы еще раз вернемся к этому интересному вопросу в следующей главе. Сейчас нам нужно было лишь напомнить смысл и содержание закона электромагнитной индукции.
Измерения магнитного поля методом индукционного толчка
Используя явление электромагнитной индукции, можно разработать весьма совершенные методы измерения магнитного поля. Допустим, что имеется необходимость определить значение магнитного поля в каком-либо месте пространства. Изготовляется плоская катушка малого размера (или берется один проволочный виток) и помещается в магнитное поле в положение, перпендикулярное к силовым линиям. К катушке (витку) идут провода от клемм баллистического гальванометра. Если теперь быстрым движением повернуть плоскость катушки на 90° так, чтобы ее плоскость совпала с силовыми линиями, то за время поворота по катушке пробежит електрический индукционный ток. Этот кратковременный ток, быстро достигающий максимума, а затем спадающий к нулю, носит название индукционного толчка (рис. 117). За время толчка по проводу пройдет определенное количество электричества, которое с большой точностью может быть измерено баллистическим гальванометром—прибором, позволяющим из-за инертности своей поворотной рамки интегрировать электрический ток за время толчка.
Если сопротивление катушки  число витков
число витков  то сила протекающего по катушке индукционного тока запишется в виде
то сила протекающего по катушке индукционного тока запишется в виде 

Количество электричества, протекшее через провод за время индукционного толчка, будет равно

где — значение потока, проходящего через катушку в первом положении, а
— значение потока, проходящего через катушку в первом положении, а  — во втором.
— во втором.
Если Ф1 или Ф2 равно нулю (магнитные линии не проходят через катушку в начальном или конечном положении), то проведенное измерение дает значение магнитной индукции. Остается лишь разделить величину магнитного потока на площадь сечения S катушки: B=QRI(nS).
Разумеется, возможны и другие варианты измерения. Скажем, вместо того чтобы поворачивать катушку, можно включать или выключать поле. Можно также, если надо увеличить эффект, поворачивать катушку не на 90, а на 180°, это удвоит эффект. Для этой же цели прибегают не к включению или выключению поля, а изменяют знак поля на обратный.
Так как измерительная катушка может быть сделана очень маленькой, вплоть до квадратного миллиметра, то измерения этим способом могут помочь в точном зондировании магнитного поля в небольших объемах.
Этот же самый метод применяется для измерения магнитного напряжения. Для этой цели изготовляется измерительный пояс (его называют поясом Роговского) — длинная катушка, надетая на гибкий ремень. Поясу может быть придана любая форма, и два конца его могут быть подведены к любым двум точкам пространства. Концы пояса могут быть также при желании приведены в соприкосновение. Покажем, что такой измерительный пояс, соединенный с баллистическим гальванометром, будет давать при выключении поля величину, пропорциональную магнитному напряжению вдоль того пути, по которому он уложен.
Баллистический гальванометр измерит величину магнитного потока, проходящего через все витки катушки. Пусть — плотность намотки, т. е. число витков, приходящееся на единицу длины измерительного пояса. Тогда на малом отрезке пояса
— плотность намотки, т. е. число витков, приходящееся на единицу длины измерительного пояса. Тогда на малом отрезке пояса  уложится
уложится  витков, и магнитный поток, проходящий через эти
витков, и магнитный поток, проходящий через эти  витков, будет равен
витков, будет равен
Если среда однородна и все витки имеют одинаковую площадь, то
 и суммарный магнитный поток, пронизывающий весь измерительный пояс, будет
и суммарный магнитный поток, пронизывающий весь измерительный пояс, будет
Переходя к пределу при  получим
получим

Так как измерения проводятся в среде, для которой  мало отличается от
мало отличается от  есть константа прибора. Отбросы баллистического гальванометра при измерениях с помощью пояса будут в точности пропорциональны магнитному напряжению между точками, где находятся концы пояса.
есть константа прибора. Отбросы баллистического гальванометра при измерениях с помощью пояса будут в точности пропорциональны магнитному напряжению между точками, где находятся концы пояса.
Этим прибором легко продемонстрировать закономерности, обсуждавшиеся в § 104. Обводя катушку вокруг одного и того же тока, мы увидим, что при любой конфигурации напряжение будет одним и тем же; мы также легко проверим, что магнитное напряжение вдоль контура, не охватывающего тока, равно нулю. Обводя катушку около одного тока несколько раз, мы убедимся в возрастании магнитного напряжения в соответствующее число раз, и т. д.
Необходимо подчеркнуть особенное значение измерений магнитного поля методом индукционного толчка для тех случаев, когда нас интересует магнитное поле внутри твердого тела. Кроме обсуждаемого метода, можно прибегнуть лишь к вырезыванию в твердом теле щелей. Обычно это невозможный путь.
Остановимся на самой распространенной задаче — измерении магнитной проницаемости железных тел. Наиболее точные результаты могут быть получены, если исследуемое вещество изготовляется в виде тороида. На это кольцо наматываются две обмотки, одна из которых присоединена к источнику тока, а другая — к баллистическому гальванометру. Если ток включен, то через кольцо проходит магнитный поток  Переключая направление первичного тока на обратное, мы вызовем во второй катушке индукционный ток. Протекшее по гальванометру количество электричества
Переключая направление первичного тока на обратное, мы вызовем во второй катушке индукционный ток. Протекшее по гальванометру количество электричества  будет связано с магнитной индукцией внутри кольца уже обсуждавшимся выше соотношением
будет связано с магнитной индукцией внутри кольца уже обсуждавшимся выше соотношением

где  — сечение тороида (предполагается, что витки плотно прилегают к кольцу),
— сечение тороида (предполагается, что витки плотно прилегают к кольцу),  — число витков и сопротивление вторичной обмотки. Что же касается напряженности магнитного поля, то ее мы можем определить по формуле, справедливой для кругового
— число витков и сопротивление вторичной обмотки. Что же касается напряженности магнитного поля, то ее мы можем определить по формуле, справедливой для кругового
соленоида: Частное от деления
Частное от деления  даст значение магнитной проницаемости материала кольца.
даст значение магнитной проницаемости материала кольца.
Ограниченные тела в магнитном поле
В той или иной степени все тела обладают магнитными свойствами. Магнитные свойства скажутся, во-первых, в том, что тела будут испытывать силы и моменты сил со стороны магнитного поля; во-вторых, магнитное поле исказится, если поместить в него тело. Как указывалось выше, магнитные свойства вещества характеризуются коэффициентом  — магнитной проницаемостью вещества. По значениям
— магнитной проницаемостью вещества. По значениям  тела могут быть отчетливо разбиты натри класса веществ: ферромагнетики, к которым относятся железо, никель и кобальт, обладающие положительными значениями относительной магнитной проницаемости, много большими единицы; парамагнетики — тела с проницаемостью, несколько большей единицы, и диамаг-нетики, у которых магнитная проницаемость чуть меньше единицы. Типичные цифры приведены в таблице.
тела могут быть отчетливо разбиты натри класса веществ: ферромагнетики, к которым относятся железо, никель и кобальт, обладающие положительными значениями относительной магнитной проницаемости, много большими единицы; парамагнетики — тела с проницаемостью, несколько большей единицы, и диамаг-нетики, у которых магнитная проницаемость чуть меньше единицы. Типичные цифры приведены в таблице.

Искажение магнитного поля, происходящее при внесении в него диамагнитных и парамагнитных тел, совершенно незначительно. Напротив, магнитное поле искажается весьма существенно, если в пространство будут внесены ферромагнитные тела.
Что же касается силовых действий магнитного поля, то они без особого труда обнаруживаются и для пара- и диамагнитных тел. Не приходится и говорить о значительных силах, которые испытываются со стороны магнитного поля железными телами; эти силы превосходно знакомы каждому.
Остановимся сначала на изучении магнитных сил. Каждое тело, не обладавшее магнитными свойствами, становится магнитным, будучи внесенным в поле. Этот процесс есть намагничивание тела, проявляющееся в приобретении телом магнитного момента. Как нам известно, система, обладающая магнитным моментом, может обнаружить себя двояко. В однородном поле такое тело поворачивается так, чтобы направление момента совпало с внешним полем. В неоднородном поле тело будет, кроме того, испытывать силу, действующую так, что тело придет в движение вдоль силовых линий.
Вращательный момент может быть без труда обнаружен у ферромагнитных тел. По формуле  можно найти магнитный момент тела. Однако большей частью нас интересует не тело случайной формы, а вещество. Поэтому по возможности пересчитывают измеренную величину на магнитный момент единицы объема. Век-гор, направленный вдоль магнитного момента и численно равный величине магнитного момента, приходящегося па единицу объема, называют вектором намагничения
можно найти магнитный момент тела. Однако большей частью нас интересует не тело случайной формы, а вещество. Поэтому по возможности пересчитывают измеренную величину на магнитный момент единицы объема. Век-гор, направленный вдоль магнитного момента и численно равный величине магнитного момента, приходящегося па единицу объема, называют вектором намагничения  Разумеется, перерасчет от магнитного момента тела к вектору намагничения не вызывает труд-костей лишь в том случае, если мы уверены в том, что намагничение образца однородно. Это имеет место тогда, когда образец обладает формой эллипсоида или вырожденного эллипсоида, т. е. цилиндра, пластинки, шара (ср. стр. 233). С такими телами и проводят подобные эксперименты.
Разумеется, перерасчет от магнитного момента тела к вектору намагничения не вызывает труд-костей лишь в том случае, если мы уверены в том, что намагничение образца однородно. Это имеет место тогда, когда образец обладает формой эллипсоида или вырожденного эллипсоида, т. е. цилиндра, пластинки, шара (ср. стр. 233). С такими телами и проводят подобные эксперименты.
Определение вектора намагничения измерением вращательного момента легко проводится для ферромагнитных тел. Для парамагнитных и диамагнитных тел вращательные моменты очень малы и измерять их трудно. В этих случаях предпочитают измерение силы, действующей на тело, находящееся в неоднородном поле.
Рассмотрим элемент объема магнетика, находящегося в неоднородном поле. Для простоты положим, что поле меняется вдоль одной оси и градиент поля равен  Каждый элемент объема магнетика будет вести себя, как магнитный диполь; поэтому потенциальная энергия единицы объема может быть записана в виде
Каждый элемент объема магнетика будет вести себя, как магнитный диполь; поэтому потенциальная энергия единицы объема может быть записана в виде  Если его момент установился вдоль поля, то сила, действующая на единицу объема магнетика, будет равна производной потенциальной энергии по координате, т. е.
Если его момент установился вдоль поля, то сила, действующая на единицу объема магнетика, будет равна производной потенциальной энергии по координате, т. е.

Таким образом, зная градиент поля и измеряя силу, можно найти величину магнитного момента единицы объема исследуемого тела. Практически это осуществляется в различных установках. Простейшими из них являются так называемые магнитные весы. В одной из чашек аналитических микровесов делается отверстие, через которое пропускается пить. На конец нити подвешивается образец н помещается между полюсами магнита. Образец уравновешивается сначала при невключенном магните, а затем при наложении поля. Разность показаний весов дает значение силы 
Весы должны быть достаточно точными, что видно из следующего примера. Кусок висмута (наиболее сильное диамагнитное вещество),помещенный в магнитное поле, напряженность которого  имеет намагничение
имеет намагничение  При неоднородности магнитного поля
При неоднородности магнитного поля  на каждый кубический сантиметр висмута будет действовать сила лишь в 1 дин, т. е.
на каждый кубический сантиметр висмута будет действовать сила лишь в 1 дин, т. е.


Опыт показывает, что для дна- и парамагнитных тел между вектором намагничения и напряженностью магнитного поля имеется простая зависимость
 где
где  носит название магнитной восприимчивости. Для диамагнитных тел
носит название магнитной восприимчивости. Для диамагнитных тел  отрицательно, для парамагнитных — положительно. Значения
отрицательно, для парамагнитных — положительно. Значения  были приведены в таблице на стр. 256. При положительных значениях х вектор намагничения параллелен вектору напряженности поля, при отрицательных значениях
были приведены в таблице на стр. 256. При положительных значениях х вектор намагничения параллелен вектору напряженности поля, при отрицательных значениях  т. е. для диамагнитных тел, направления векторов намагничения и напряженности магнитного поля противоположны.
т. е. для диамагнитных тел, направления векторов намагничения и напряженности магнитного поля противоположны.
Эта разница в знаке делает весьма непохожим поведение тел обоих классов в тождественных условиях. Это иллюстрируется рис. 118. Различия действительно разительны. Парамагнитное тело втягивается в область сильного поля, диамагнитное тело выталкивается. В однородном поле парамагнитная стрелка стремится расположить свою ось вдоль силовых линий, диамагнитная — поперек (ср. аналогичный пример с диэлектриком, стр. 231).
Определение магнитной восприимчивости измерением силы в неоднородном поле можно производить для твердых тел как в виде монокристаллов, так и в виде порошков. Без всякого труда метод приложим и к жидкостям. В этом случае можно поставить опыт так, чтобы измеряемой величиной явилось повышение или понижение уровня жидкости, втягиваемой или выталкиваемой из пространства между полюсами магнита.
Связь между магнитной проницаемостью и восприимчивостью
Обе эти величины могут быть измерены непосредственно: магнитная проницаемость определяется измерением индукции и напряженности с дальнейшим вычислением по формуле  а восприимчивость — по силовым действиям на магнетик, как описано только что. Разумеется, можно установить на опыте связь между этими двумя характеристиками магнитных свойств вещества. В этом, однако, нет нужды, так как между
а восприимчивость — по силовым действиям на магнетик, как описано только что. Разумеется, можно установить на опыте связь между этими двумя характеристиками магнитных свойств вещества. В этом, однако, нет нужды, так как между  существует строгая и простая связь, следующая из таких соображений.
существует строгая и простая связь, следующая из таких соображений.
Вернемся к опыту по определению магнитной проницаемости тела, выполненного в виде тороида. Первичная катушка, которой обернут тороид, создает поле с напряженностью не зависящей от вещества тороида; без тороида напряженность поля представится той же формулой. Иное дело — магнитный поток. Мы убеждаемся опытным путем, что значение В зависит от магнитной проницаемости. Если сердечник катушки сделан из железа, то В возрастает в сотни и тысячи раз. Это увеличение магнитного потока мы связываем с явлением намагничивания.
не зависящей от вещества тороида; без тороида напряженность поля представится той же формулой. Иное дело — магнитный поток. Мы убеждаемся опытным путем, что значение В зависит от магнитной проницаемости. Если сердечник катушки сделан из железа, то В возрастает в сотни и тысячи раз. Это увеличение магнитного потока мы связываем с явлением намагничивания.
Обратим прежде всего внимание на то обстоятельство, что в отсутствие железа магнитная индукция кругового соленоида имеет смысл магнитного момента в единице объема.
имеет смысл магнитного момента в единице объема.
Магнитный момент витка катушки равняется  (будем вести рассуждения применительно к системе СИ). Полный магнитный момент системы будет равен
(будем вести рассуждения применительно к системе СИ). Полный магнитный момент системы будет равен  а магнитный момент токов в единице объема
а магнитный момент токов в единице объема  есть не что иное как напряженность поля. Магнитный момент эквивалентных диполей будет в
есть не что иное как напряженность поля. Магнитный момент эквивалентных диполей будет в  раз больше (ср. § 103). Следовательно, магнитная индукция однородного магнитного поля, создаваемого витками кругового соленоида при отсутствии сердечника,
раз больше (ср. § 103). Следовательно, магнитная индукция однородного магнитного поля, создаваемого витками кругового соленоида при отсутствии сердечника, может быть представлена как магнитный момент эквивалентных диполей, приходящихся на единицу объема.
может быть представлена как магнитный момент эквивалентных диполей, приходящихся на единицу объема.
С полным основанием мы можем полагать, что магнитная индукция сохранит свой смысл, если, не нарушая однородности поля, равномерно заполнить пространство катушки дополнительным числом магнитных диполей. Если на единицу объема от дополнительных диполей приходится магнитный момент  то магнитная индукция возрастет на эту величину и станет равной
то магнитная индукция возрастет на эту величину и станет равной
Такое возрастание В и происходит, когда соленоид заполняется веществом. Так как и, следовательно, магнитная восприимчивость и проницаемость связаны равенством
и, следовательно, магнитная восприимчивость и проницаемость связаны равенством
Аналогичное рассуждение применительно к системе СГС приведет к формулам с другими коэффициентами. Магнитный момент токов (и диполей) в единице объема равен

Поэтому при наличии среды

Полагая получим
получим следовательно,
следовательно,
Пример. Проведем расчет примера на стр. 258 в системе СИ. Для висмута
 кусок висмута находится в магнитном поле
кусок висмута находится в магнитном поле
 обладающем неоднородностью
обладающем неоднородностью

Намагничение висмута будет  Тогда на единицу объема
Тогда на единицу объема  будет действовать сила
будет действовать сила

Ясно, что  что совпадает с результатом предыдущего примера.
что совпадает с результатом предыдущего примера.
что совпадает с результатом предыдущего примера.
Искажение магнитного поля при внесении в него магнетика
Вопрос об искажении магнитного поля имеет практическое значение только при внесении в поле железных тел. В значительной части нам придется повторить рассуждения, аналогичные приведенным на стр. 232 для диэлектриков.
На границе двух сред, обладающих разными магнитными про-ницаемостями, векторы магнитного поля (как индукция, так и напряженность) преломляются. Чтобы найти законы этого преломления, рассмотрим, прежде всего, магнитное напряжение, взятое вдоль малого контура A BCD, тесно прилегающего к поверхности раздела так, как это показано на рис. 119. Так как через этот контур токи не протекают, то магнитное напряжение равно нулю. Разложим вектор напряженности магнитного поля с обеих сторон границы на

нормальную и тангенциальную составляющие. Из рисунка ясно, что обращение в нуль магнитного напряжения может иметь место лишь в том случае, если тангенциальные составляющие будут равны друг другу:
Другое условие на границе двух сред мы найдем рассмотрением магнитного потока, проходящего через прилегающий к поверхности раздела небольшой цилиндр (на рисунке не показан). Так как у магнитных линий источников нет, то число силовых линий, входящих в верхнее основание цилиндра, должно равняться числу линий, выходящих через нижнее основание. Боковая поверхность бесконечно мала и поток через нее равен нулю. Разложим вектор магнитной индукции с обеих сторон границы на две составляющие: нормальную и тангенциальную. Очевидно, равенство потоков через основания может иметь место в том случае, если нормальные составляющие вектора индукции не изменятся при переходе через границу:
Из этих двух правил мы находим закон преломления силовых линий. Из рисунка ясно, что

При переходе из воздуха в железо магнитные линии отклоняются от перпендикуляра чрезвычайно значительно и поэтому сильно сгущаются. Именно поэтому железное тело, обладающее магнитной проницаемостью в сотни и тысячи раз больше «вбирает» в себя силовые линии. На этом явлении основана магнитная защита. В пространство, огражденное железом, магнитный поток не пройдет: подавляющая часть магнитных линий будет идти внутрь железа (рис. 120).
«вбирает» в себя силовые линии. На этом явлении основана магнитная защита. В пространство, огражденное железом, магнитный поток не пройдет: подавляющая часть магнитных линий будет идти внутрь железа (рис. 120).
В совершенной аналогии с диэлектриками решается задача о характере искажений, вносимых в магнитное поле телом определенной формы. Если тело имеет форму эллипсоида, цилиндра или пластинки, то поле внутри такого тела, как показывают теоретические

расчеты, будет однородным, если поле было однородным и до внесения в него железного тела. Между внешним однородным полем  (тем, которое было) И полем внутри железного тела
(тем, которое было) И полем внутри железного тела  (которое стало) существует соотношение, полностью аналогичное обсужденному в § 96. Напряженность поля, образовавшегося в железном теле, становится меньше той, которая была ранее, на величину, пропорциональную намагничению:
(которое стало) существует соотношение, полностью аналогичное обсужденному в § 96. Напряженность поля, образовавшегося в железном теле, становится меньше той, которая была ранее, на величину, пропорциональную намагничению:

Чтобы фактор размагничения был безразмерным, намагничение поделено на магнитную проницаемость вакуума. Продолжая и далее пользоваться соотношениями системы СИ и подставляя
 получим следующую связь между внешним и внутренним полем
получим следующую связь между внешним и внутренним полем
В системе СГС

и связь между внешним и внутренним полем будет иметь вид

Коэффициент размагничения имеет те же значения, что и в случае диэлектриков:  для пластины и т. д.
для пластины и т. д.
Магнитный гистерезис
Говоря о магнитной проницаемости железных уел, мы могли создать ложное впечатление, что магнитные свойства ферромагнетиков отличаются от магнитных свойств парамагнитных тел только величиной магнитной проницаемости. Это совсем не так. Принципиальное отличие ферромагнетиков от других тел заключается в отсутствии линейной и, более того, однозначной зависимости магнитного состояния тела от напряженности магнитного поля. Поэтому понятие магнитной проницаемости для ферромагнетиков носит весьма условный характер. Правильное представление о магнитных свойствах железа можно получить, рассматривая кривую зависимости намагничения от напряженности или магнитной индукции от напряженности поля. Обе эти кривые довольно близки друг К другу.


Будем измерять намагничение железного тела в функции напряженности. Сначала намагничение будет расти медленно, затем быстро и, наконец, наступит магнитное насыщение. Такого типа кривые намагничения, впервые построенные А. Г. Столетовым, типичны для всех ферромагнитных тел (рис. 121). Повторяем, что кривые намагничения и магнитной индукции весьма похожи. Ход кривой намагничения дает магнитную восприимчивость, ход кривой индукции дает магнитную проницаемость. Из приведенной кривой видно, что магнитная проницаемость (восприимчивость) изменяется по кривой с максимумом. При малых полях магнитная проницаемость мала, затем она возрастает до максимума, потом падает и по достижении насыщения остается неизменной. Большей частью, когда приводят значения магнитной проницаемости, не оговаривая внешних условий, имеют в виду максимальную магнитную проницаемость.
Однако описанным не исчерпывается своеобразие поведения ферромагнетиков. Положим, что железо доведено до состояния магнитного насыщения, и начнем уменьшать напряженность магнитного поля. Оказывается, что индукция будет убывать теперь по другой кривой, лежащей выше кривой начального намагничения. Напряженность поля может быть доведена до нуля, но намагничение не будет снято. Соответствующие значения намагничения и индукции называют остаточными. Чтобы снять остаточное намагничение, необходимо переменить направление поля. Если иметь в виду опыт, о котором говорилось на стр. 255, то это значит, что нужно изменить

направление тока в первичной катушке, обмотанной около железного тела, на обратное. Размагничивание произойдет тогда, когда напряженность поля достигнет некоторой величины  называемой коэрцитивной (задерживающей) силой. При дальнейшем увеличении тока тело начнет намагничиваться в обратном направлении, т. е. там, где был южный полюс, возникнет северный. Магнитный поток будет расти до той же степени насыщения, что и в начальном процессе. Достигнув отрицательного максимума индукции, можно повести процесс в обратную сторону и получить изображенную на рис. 122 петлю гистерезиса.
называемой коэрцитивной (задерживающей) силой. При дальнейшем увеличении тока тело начнет намагничиваться в обратном направлении, т. е. там, где был южный полюс, возникнет северный. Магнитный поток будет расти до той же степени насыщения, что и в начальном процессе. Достигнув отрицательного максимума индукции, можно повести процесс в обратную сторону и получить изображенную на рис. 122 петлю гистерезиса.
Из этого рисунка следует, что напряженность поля, в которое помещено железо, не определяет еще ни магнитной индукции, ни, следовательно, магнитной проницаемости. Для абсциссы  например, возможны три значения индукции: первое имеет место при начальном намагничивании, второе — в процессе размагничивания и третье — по прохождении почти всей петли при повторном намагничивании. Значение магнитной индукции и магнитной проницаемости зависит от предыдущей «исторйи» образца. Отсюда и название «петля гистерезиса».
например, возможны три значения индукции: первое имеет место при начальном намагничивании, второе — в процессе размагничивания и третье — по прохождении почти всей петли при повторном намагничивании. Значение магнитной индукции и магнитной проницаемости зависит от предыдущей «исторйи» образца. Отсюда и название «петля гистерезиса».
Обычно рисуют петлю, построенную при условии, что ферромагнитное тело доводится до магнитного насыщения. В то же время ясно, что можно осуществить с куском железа любые петли гистерезиса меньшего размера, как бы вписанные в основную петлю. Для этого надо начать размагничивание, не доходя до насыщения. Тогда каждому значению  соответствует сколь угодно большое число значений В.
соответствует сколь угодно большое число значений В.
Отсюда следует способ приведения ферромагнитного тела в состояние, при котором одновременно равны нулю и индукция, и напряженность. Такое приведение магнитного тела в «нулевую точку» осуществляют серией последовательных перемагничиваний, начиная каждый следующий цикл при меньшем значении напряженности, чем предыдущий.
Магнитное состояние железа нельзя характеризовать только значением проницаемости или только величиной напряженности или индукции. Нужно знать две величины, скажем, индукцию и напряженность, которые определят магнитное состояние железа точкой внутри основной гистерезисной петли.
Характер петли гистерезиса сильно зависит от материала. Магнитно-мягкими называют гела, у которых коэрцитивная сила мала (а значит, мала и площадь петли). К мягким материалам относятся чистое железо, кремнистая сталь, сплав железа с никелем (среди них выделяется пермаллой — 78% никеля). Углеродистые и иные стали принадлежат к магнитно-твердым материалам; их используют для изготовления постоянных магнитов.
Опыт показывает, что при перемагничивании ферромагнетик нагревается. Это очень существенно для электротехники, так как при помещении железа в переменное магнитное поле точка графика  изображающая магнитное состояние железа, непрерывно обегает петлю гистерезиса. Пробег по петле сопровождается выделением тепла, которое связывается теорией магнитного поля с площадью петли. Разумеется, чем меньше максимальная индукция, тем меньше площадь петли. Поэтому можно попытаться подыскать эмпирические формулы,” связывающие выделяющееся тепло с максимальной индукцией. В электротехнике имеет распространение, например, формула такого вида:
изображающая магнитное состояние железа, непрерывно обегает петлю гистерезиса. Пробег по петле сопровождается выделением тепла, которое связывается теорией магнитного поля с площадью петли. Разумеется, чем меньше максимальная индукция, тем меньше площадь петли. Поэтому можно попытаться подыскать эмпирические формулы,” связывающие выделяющееся тепло с максимальной индукцией. В электротехнике имеет распространение, например, формула такого вида:

где  — коэффициент, значения которого приводятся в таблицах.
— коэффициент, значения которого приводятся в таблицах.
Пример. Для хорошего трансформаторного железа 
 потери будут
потери будут

Это значит, что при перемагничппании железа переменным током частоты  мощность потерь в железе составит
мощность потерь в железе составит  на каждый кубический сантиметр объема железа.
на каждый кубический сантиметр объема железа.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
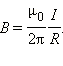
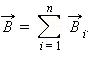
![{displaystyle mathbf {m} ={1 over 2}int limits _{V}[mathbf {r} ,mathbf {j} ]dV,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc99ebe55c27a99af52051c04a4bae1958f1213c)

![{displaystyle mathbf {m} ={I over 2}oint [mathbf {r} ,dmathbf {l} ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d2fef9d96691e532108dd6c77e508adaf1acd48)





























![{displaystyle mathbf {H} (mathbf {r} )={frac {1}{4pi }}left[{frac {3mathbf {hat {r}} (mathbf {hat {r}} cdot mathbf {m} )-mathbf {m} }{|mathbf {r} |^{3}}}-{frac {4pi }{3}}mathbf {m} delta (mathbf {r} )right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1b635de5e52b7fd68571a72866d50392b0b7213)
![{displaystyle mathbf {B} (mathbf {r} )={frac {mu _{0}}{4pi }}left[{frac {3mathbf {hat {r}} (mathbf {hat {r}} cdot mathbf {m} )-mathbf {m} }{|mathbf {r} |^{3}}}+{frac {8pi }{3}}mathbf {m} delta (mathbf {r} )right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47f91d20595386326b2945ac17533fd823321db)











