Как найти вектор магнитной индукции в точке

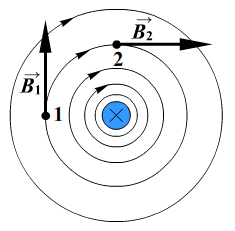
По двум тонким прямым проводникам, параллельным друг другу, текут одинаковые токи I (см. рисунок). Как направлен вектор индукции создаваемого ими магнитного поля в точке С?

Вектор магнитной индукции в точке C есть сумма векторов магнитной индукции от двух проводников. Согласно правилу правой руки: «Если отведенный в сторону большой палец правой руки расположить по направлению тока, то направление обхвата провода четырьмя пальцами покажет направление линий магнитной индукции». Следовательно, вектор магнитной индукции от нижнего проводника направлен в точке C от нас, а вектор магнитной индукции от верхнего проводника — к нам. Однако модуль вектора магнитной индукции ослабевает по мере удаления от проводника. Таким образом, суммарный вектор магнитной индукции в точке C направлен к нам.

Направление поля можно искать, используя также правило буравчика: «Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током».

Магнитное поле и его характеристики

теория по физике 🧲 магнетизм

Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.

Основные свойства магнитного поля

Магнитное поле порождается электрическим током (движущимися зарядами).
Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
Магнитное поле существует независимо от нас, от наших знаний о нем.

Вектор магнитной индукции

Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как → B . Единица измерения — Тесла (Тл).

За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.

Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:

B = F A m a x I l . .

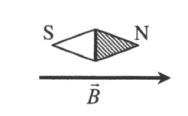
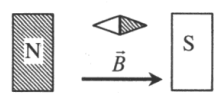
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.

Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.

Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.

Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.

Напряженность магнитного поля

Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как → H . Единица измерения — А/м.

μ — магнитная проницаемость среды (у воздуха она равна 1), μ 0 — магнитная постоянная, равная 4 π · 10 − 7 Гн/м.

Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: → H ↑↑ → B .

Направление вектора магнитной индукции и способы его определения

Чтобы определить направление вектора магнитной индукции, нужно:

Расположить в магнитном поле компас.
Дождаться, когда магнитная стрелка займет устойчивое положение.
Принять за направление вектора магнитной индукции направление стрелки компаса «север».

В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:

При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:

При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора → B магнитной индукции.

Отсюда следует, что:

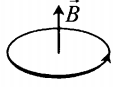
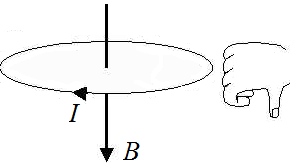
Если по витку ток идет против часовой стрелки, то вектор магнитной индукции → B направлен вверх.

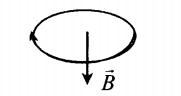
Если по витку ток идет по часовой стрелке, то вектор магнитной индукции → B направлен вниз.

Способы обозначения направлений векторов:

Вверх
Вниз
Влево
Вправо
На нас перпендикулярно плоскости чертежа
От нас перпендикулярно плоскости чертежа

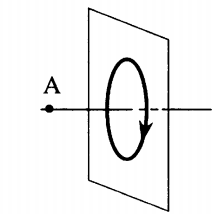
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?

Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.

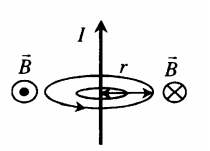
Магнитное поле прямолинейного тока

Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.

Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:

Правило буравчика (правой руки)

Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.

Модуль вектора магнитной индукции на расстоянии r от оси проводника:

B = μ μ 0 I 2 π r . .

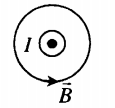
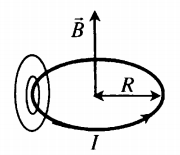
Магнитное поле кругового тока

Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.

Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:

Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.

Модуль вектора магнитной индукции в центре витка, радиус которого равен R:

Модуль напряженности в центре витка:

Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?

Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.

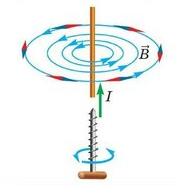
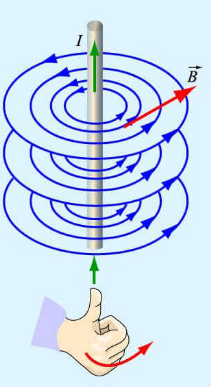
Магнитное поле электромагнита (соленоида)

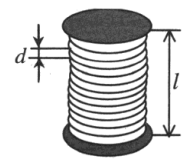
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.

Число витков в соленоиде N определяется формулой:

l — длина соленоида, d — диаметр проволоки.

Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.

Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции → B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.

Модуль вектора магнитной индукции в центральной области соленоида:

B = μ μ 0 I N l . . = μ μ 0 I d . .

Модуль напряженности магнитного поля в центральной части соленоида:

H = I N l . . = I d . .

Алгоритм определения полярности электромагнита

Определить полярность источника.
Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
Определить направление вектора магнитной индукции.
Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).

Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.

Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.

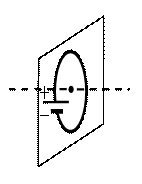
На рисунке изображён круглый проволочный виток, по которому течёт электрический ток. Виток расположен в вертикальной плоскости. В центре витка вектор индукции магнитного поля тока направлен

а) вертикально вверх в плоскости витка

б) вертикально вниз в плоскости витка

в) вправо перпендикулярно плоскости витка

г) влево перпендикулярно плоскости витка

Алгоритм решения

Решение

По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора → B магнитной индукции мы будем использовать правило правой руки.

Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.

Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.

pазбирался: Алиса Никитина | обсудить разбор | оценить

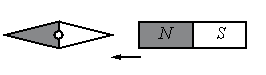
Магнитная стрелка компаса зафиксирована на оси (северный полюс затемнён, см. рисунок). К компасу поднесли сильный постоянный полосовой магнит и освободили стрелку. В каком положении установится стрелка?

а) повернётся на 180°

б) повернётся на 90° по часовой стрелке

в) повернётся на 90° против часовой стрелки

г) останется в прежнем положении

Алгоритм решения

Вспомнить, как взаимодействуют магниты.
Определить исходное положение полюсов.
Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.

Решение

Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.

pазбирался: Алиса Никитина | обсудить разбор | оценить

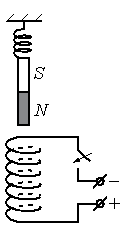
Непосредственно над неподвижно закреплённой проволочной катушкой вдоль её оси на пружине подвешен полосовой магнит (см. рисунок). Куда начнёт двигаться магнит сразу после замыкания ключа? Ответ поясните, указав, какие физические явления и законы Вы использовали для объяснения.

Алгоритм решения

Определить направление тока в соленоиде.
Определить полюса соленоида.
Установить, как будет взаимодействовать соленоид с магнитом.
Установить, как будет себя вести магнит после замыкания электрической цепи.

Решение

Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.

Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.

Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).

pазбирался: Алиса Никитина | обсудить разбор | оценить

Физика. 11 класс

Конспект урока

Физика, 11 класс

Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу

Перечень вопросов, рассматриваемых на уроке:

1) магнитное поле;

2) вектор магнитной индукции, линии магнитной индукции;

3) сила Ампера, сила Лоренца;

4) правило буравчика, правило левой руки.

Глоссарий по теме

Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.

Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.

Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.

Правило «буравчика» – правило для определения направления магнитного поля проводника с током.

Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.

Соленоид – проволочная катушка.

Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.

Основная и дополнительная литература по теме урока

Мякишев Г.Я., Буховцев Б.Б. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20

2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. – М: Дрофа, 2009. – С.109 – 112

Основное содержание урока

Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.

Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.

Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции. Поля с замкнутыми линиями называются вихревыми.

Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.

Она обозначается символом За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.

Направление магнитного поля устанавливают с помощью вектора магнитной индукции.

Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).

Правило буравчика звучит следующим образом:

если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.

Направление магнитного поля внутри соленоида определяют по правилу правой руки.

Определим модуль вектора магнитной индукции.

Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.

Тогда, зависимость силы от этих двух величин выглядит следующим образом

Отношение зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.

Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:

Единицей измерения магнитной индукции является 1 тесла (Тл).

Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:

где α – угол между вектором B и направлением тока.

Направление силы Ампера определяется правилом левой руки:

Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 0 большой палец покажет направление силы Ампера.

Сила Ампера – сила, действующая на проводник с током со стороны магнитного поля.

Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:

– заряд частицы;

– скорость частицы;

B – модуль магнитной индукции;

– угол между векторами скорости частицы и магнитной индукции.

Направление силы Лоренца также определяют по правилу левой руки:

Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 90 0 большой палец покажет направление силы Лоренца. Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.

Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.

Согласно 2-му закону Ньютона

Время, за которое частица делает полный оборот (период обращения), равно:

Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия. Им кажется, что теперь всё известно и никаких открытий на их долю не осталось.

Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…

Одна из возможных гипотез.

Как известно, ядро Земли имеет высокую температуру

и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.

Разбор тренировочных заданий

1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?

– точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.

Используя правило левой руки, определяем направление силы Ампера:

Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 90 0 большой палец покажет направление силы Ампера, т. е. она направлена влево.

2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?

(Ответ выразите в мТл).

3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл. (Ответ выразите в мН).

4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)

5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10 – ¹² Н? Ответ выразите в км/с.

6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)

Запишем формулу модуля магнитной индукции:

B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.

Запишем формулу силы Ампера:

F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН

Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,

масса протона: m = l,67·l0⁻²⁷ кг.

Согласно 2-му закону Ньютона:

v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.

Ответ: v ≈ l00 км/с.

Найти:

Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.

Используем формулу силы Лоренца:

Выразим из формулы силы скорость, учитывая, что sin90°=l,

v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.

Ответ: v = l2500 км/с.

B = 3,l4 мТл = 3,l4·l0⁻³ Tл,

Масса электрона равна: m = 9,l·l0⁻³¹ кг.

Время, за которое частица делает полный оборот (период обращения), равно:

T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.

[spoiler title=”источники:”]

Магнитное поле и его характеристики

http://resh.edu.ru/subject/lesson/3806/conspect/

[/spoiler]

Источник

Свойством поля магнитного в любой его точке с позиции силы выступает вектор магнитной индукции [overrightarrow{mathrm{B}}].

Вектор индукции магнитного поля: главные понятия

Рассмотрим определение вектора индукции магнитного поля. Индукцию определяют как предел отношения F силы, воздействующий на магнитное поле, на ток [text { Idl }] к произведению элементарного тока [text { I }] со значением элемента проводника [text { dl }]. Другими словами, магнитная индукция действует по направлению перпендикулярно [perp] по направлению тока (или по-другому к элементу проводника [text { dl }Rightarrow] из (1), а также вектор магнитной индукции поля перпендикулярен [perp] к направлению силы, которая действует с магнитного поля.

Вектор магнитной индукции однородного поля и неоднородного

Если [overrightarrow{mathrm{B}}=mathrm{const}], то поле является однородным. Если оно не изменяется с течением времени, то про него говорят, что поле постоянное.

Вектор индукции магнитного поля: важные формулы

Важно!

Формула с векторами преобразуется в модульную форму, потому что векторы задают направление, а модульная форма — значения, которые необходимы для решения задачи.

Формула

Модуль вектора индукции однородного поля находят следующим образом:

[mathrm{B}=frac{mathrm{M}_{max }}{mathrm{P}_{mathrm{m}}}].

где [mathrm{M}_{max }] — вращающий момент в максимуме действует на контур с элементарным током, помещенный в магнитное поле, где в данном случае [mathrm{P}_{mathrm{m}}=mathrm{I} cdot mathrm{S}] — магнитный момент контура (S — площадь определенного контура).

Модуль вектора индукции магнитного поля: производные формулы

Есть еще формулы для определения модуля магнитной индукции. Она определяется как отношение силы в максимуме [mathrm{F}_{max }], которое реагирует на проводник длины (при этом L= 1 м) к силе элементарного тока [text { I }] в проводнике:

[B=frac{F_{max }}{I cdot L}]

В вакууме модуль индукции будет равен:

[mathrm{B}=mu 0 cdot mathrm{H}]

Чтобы найти вектор индукции через силу Лоренца, следует преобразовать формулу: [overrightarrow{mathrm{F}}=mathrm{q} cdot[overrightarrow{mathrm{V}} times overrightarrow{mathrm{B}}]] (Крестом обозначается произведение векторов)

[vec{F}=B cdot q cdot v cdot sin alpha]

[B=frac{F}{sin alpha cdot q v}]

В данном случае угол α — это угол между вектором индукции и скорости. Стоит отметить, что направление силы Лоренца [overrightarrow{mathrm{F}}] перпендикулярно [perp] каждому вектору, направлено по правилу Буравчика. Под символом q подразумевается заряд в магнитном поле.

Интересно

В СИ единицей модуля магнитной индукции принимается 1 Тесла (кратко — Тл), где [1 Tл=frac{H}{Aм}]

Как определяется направление вектора индукции магнитного поля?

За направление вектора индукции магнитного поля [overrightarrow{mathrm{B}}] используют направление, в котором устанавливается под воздействием поля утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.

Вектор индукции [overrightarrow{mathrm{B}}] обладает направлением, которое начинается со стрелки южного полюса [text { S }] (она свободна передвигается в поле) к полюсу северному [text { N }].

Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.

Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:

Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на [90^{circ}] указывает на направление магнитной индукции [overrightarrow{mathrm{B}}] в середине катушки.

Для прямого проводника с элементарным током: большой палец руки, который оставляется на [90^{circ}], направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.

Задания по теме

Разберем примеры, в которых будет задействована данная формула и свойства.

Пример 1

Условие задачи:

Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.

Решение задачи следующее:

Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.

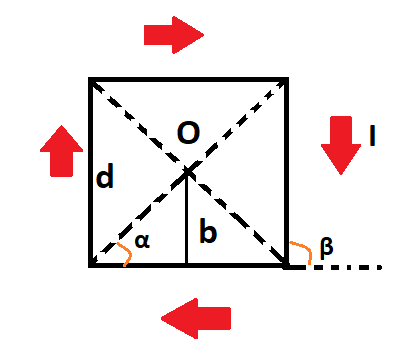
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B₁+B₂+B₃+B₄

Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B₁

В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.

Чтобы формула подошла к данной задачи, ее применяют в следующем виде:

[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{4 mathrm{pi b}}(cos alpha-cos beta)]

углы α и β, которые отмечены на рисунке:

[beta=pi-alpha rightarrow cos beta=cos (pi-alpha)=-cos alpha]

Используем формулу [B_{1}=frac{I cdot mu_{0}}{4 pi b}(cos alpha-cos beta)] и преобразуем с применением тригонометрического свойства:

[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{2 mathrm{pi b}} cdot cos alpha]

Поскольку у нас квадратная форма, то следует заметить следующее:

[mathrm{b}=mathrm{d} 2, alpha=frac{pi}{4} rightarrow cos alpha=frac{sqrt{2}}{2}]

Возьмем выведенные формулы и получим конечное выражение, то есть:

[mathrm{B}=4 cdot frac{mathrm{I} cdot mu_{0}}{pi mathrm{d}} cdot frac{sqrt{2}}{2}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]

Ответ: [mathrm{B}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]

Нет времени решать самому?

Наши эксперты помогут!

Пример 2

Условие задачи:

Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.

Решение задачи:

В точке А получается из двух частей проводника, то есть:

[overrightarrow{mathrm{B}}=mathrm{B}_{mathrm{II}}+mathrm{B}_{perp}]

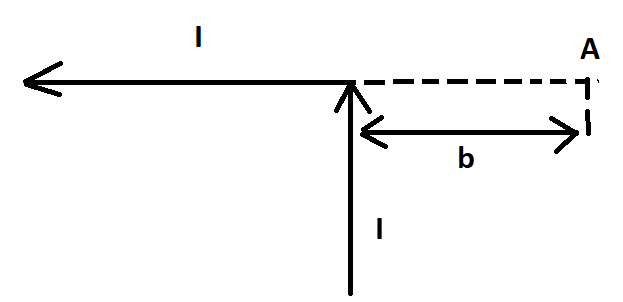
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля [mathrm{B}_{mathrm{II}}] равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.

Следовательно, произведение векторов [[mathrm{d} vec{ l } vec{r}]] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:

[overrightarrow{mathrm{B}}=frac{mu_{0}}{4 pi} oint frac{mathrm{I}[mathrm{d} vec{l} vec{r}]}{mathrm{r}^{3}}]

В этом случае [vec{r}] — радиус-вектор, который идет от элемента [mathrm{Idvec{l}}] к точке А, в которой находится индукция магнитного поля [overrightarrow{mathrm{B}}].

Индукция бесконечного проводника в точке А была бы равна:

[mathrm{B}^{prime}=frac{mu_{0}}{2 pi} frac{mathrm{I}}{mathrm{b}}]

Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:

[mathrm{B}=mathrm{B}_{perp}=frac{1}{2} mathrm{~B}^{prime}=frac{mu_{0}}{Pi} frac{mathrm{I}}{mathrm{b}}]

Ответ: [mathrm{B}=frac{mu_{0}}{pi} frac{mathrm{I}}{mathrm{b}}]

Источник

Определение

Основные свойства магнитного поля

Магнитное поле порождается электрическим током (движущимися зарядами).
Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
Магнитное поле существует независимо от нас, от наших знаний о нем.

Вектор магнитной индукции

Определение

Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как→B. Единица измерения — Тесла (Тл).

B=FAmaxIl

Напряженность магнитного поля

Определение

→H=→Bμμ0

μ — магнитная проницаемость среды (у воздуха она равна 1), μ0 — магнитная постоянная, равная 4π·10−7 Гн/м.

Направление вектора магнитной индукции и способы его определения

Чтобы определить направление вектора магнитной индукции, нужно:

Расположить в магнитном поле компас.
Дождаться, когда магнитная стрелка займет устойчивое положение.
Принять за направление вектора магнитной индукции направление стрелки компаса «север».

В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:

При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.

Отсюда следует, что:

Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.

Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.

Способы обозначения направлений векторов:

Вверх
Вниз
Влево
Вправо
На нас перпендикулярно плоскости чертежа
От нас перпендикулярно плоскости чертежа

Магнитное поле прямолинейного тока

Вид сверху:

Правило буравчика (правой руки)

Модуль вектора магнитной индукции на расстоянии r от оси проводника:

B=μμ0I2πr

Модуль напряженности:

H=I2πr

Магнитное поле кругового тока

Модуль вектора магнитной индукции в центре витка, радиус которого равен R:

B=μμ0I2R

Модуль напряженности в центре витка:

H=I2R

Магнитное поле электромагнита (соленоида)

Определение

Число витков в соленоиде N определяется формулой:

N=ld

l — длина соленоида, d — диаметр проволоки.

Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции →B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.

Модуль вектора магнитной индукции в центральной области соленоида:

B=μμ0INl=μμ0Id

Модуль напряженности магнитного поля в центральной части соленоида:

H=INl=Id

Алгоритм определения полярности электромагнита

Определить полярность источника.
Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
Определить направление вектора магнитной индукции.
Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).

Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.

Задание EF17530

Ответ:

а) вертикально вверх в плоскости витка

б) вертикально вниз в плоскости витка

в) вправо перпендикулярно плоскости витка

г) влево перпендикулярно плоскости витка

Алгоритм решения

1.Определить правило, по которому можно определить направление вектора магнитной индукции в данном случае.

2.Применить выбранное правило и определить направление вектора магнитной индукции относительно рисунка.

Решение

По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора →B магнитной индукции мы будем использовать правило правой руки.

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18109

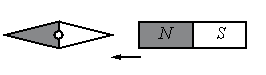
Ответ:

а) повернётся на 180°

б) повернётся на 90° по часовой стрелке

в) повернётся на 90° против часовой стрелки

г) останется в прежнем положении

Алгоритм решения

Вспомнить, как взаимодействуют магниты.
Определить исходное положение полюсов.
Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.

Решение

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18266

Алгоритм решения

Определить направление тока в соленоиде.
Определить полюса соленоида.
Установить, как будет взаимодействовать соленоид с магнитом.
Установить, как будет себя вести магнит после замыкания электрической цепи.

Решение

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 22.3k

Источник

Природа магнетизма

Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.

Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.

Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.

Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.

Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).

Магнитные линии и магнитный поток

Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.

Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.

Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.

Если приблизить два разноименных полюса, то произойдет притягивание магнитов

Если же приблизить одноименными полюсами, то произойдет их отталкивание

Итак, ниже важные свойства магнитных силовых линий.

Магнитные линии не поддаются гравитации.
Никогда не пересекаются между собой.
Всегда образуют замкнутые петли.
Имеют определенное направление с севера на юг.
Чем больше концентрация силовых линий, тем сильнее магнитное поле.
Слабая концентрация силовых линий указывает на слабое магнитное поле.

Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.

Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?

Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».

В физике формула магнитного потока записывается как

где

Ф — магнитный поток, Вебер

В — плотность магнитного потока, Тесла

а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах

S — площадь, через которую проходит магнитный поток, м2

Магнитная индукция

Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.

Изображение магнитного поля при помощи силовых линий

Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.

Магнитная индукция – это силовая векторная характеристика магнитного поля.

Она обозначается буквой B и измеряется вТесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.

Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.

Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.

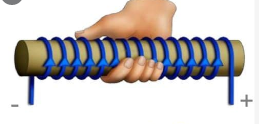
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!

Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.

Формула индукции магнитного поля

ОПРЕДЕЛЕНИЕ

Векторной характеристикой магнитного поля является вектор магнитной индукции. Его обозначают как:

Направлением вектора магнитной индукции считают направление на север магнитной стрелки, которая может свободно вращаться в магнитном поле. Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.

Модуль вектора магнитной индукции можно установить, используя силу, которая действует на проводники с током, помещенные в магнитное поле (силу Ампера). Тогда модуль вектора
равен частному от деления максимальной силы ( $F_{max}$ ), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():

$[B=frac{F_{max}}{IDelta l} qquad(1)]$

Рассматривая силу Лоренца, которая действует на заряженную частицу, движущуюся в магнитном поле, получают формулу для магнитной индукции в виде:

$[B=frac{F_L}{qvsin alpha } } qquad(2)]$

где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления ${overline{F}}_L$ , векторов и связаны между собой правилом левой руки.

Формулой, которая определяет величину вектора магнитной индукции в данной точке магнитного поля, считают так же следующее выражение:

$[B=frac{M_{max}}{p_m} qquad(3)]$

где $M_{max}$ – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля. Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:

где S – площадь, которую обтекает ток I. Следует помнить, что максимальный вращающий момент получается тогда, когда плоскость контура параллельна линиям магнитной индукции поля ().

Физический смысл магнитной индукции

Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка металлическая). В кристаллической решетке металла есть электрические заряды – электроны. Если на металл не действует магнитное воздействие, заряды (электроны) покоятся и никуда не движутся.

Если металл попадает под действие переменного магнитного поля (из-за движения постоянного магнита внутри катушки – точное смещение), то заряды начинают двигаться под действием влияние этого магнитного поля.

В результате в металле образуется электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости движения одного относительно другого.

Когда металлическую катушку помещают в магнитное поле, заряженные частицы металлической решетки (в каштане) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.

Чем больше напряженность магнитного поля, тем большее количество частиц вращается и тем более равномерным будет их расположение.

Магнитные поля, ориентированные в одном направлении, не нейтрализуют друг друга, а складываются в единое поле.

Другие формулы, где встречается B

Эти формулы также можно использовать для его расчета.

Сила Ампера

Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:

Это и есть сила Ампера. Угол альфа– угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.

Сила Лоренца

Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.

Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа– это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:

Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.

Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:

Магнитный поток

Магнитный поток: Ф = BS cosα

Где:

Ф — магнитный поток (в Вб — вебер)
B — индукция (в Тл)
S — площадь рамки (в м²)
α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))

Взаимодействие магнита с контуром

Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?

Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.

1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.

Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.

Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .

Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1

Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.

Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.

Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .

Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.

Частные случаи формул для вычисления величины вектора магнитной индукции

Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):

$[B=frac{{mu }_0mu }{2}frac{I}{R} qquad(6)]$

где R – радиус витка.

Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:

$[B=frac{{mu }_0mu }{2pi }frac{I}{r} qquad(7)]$

где r – расстояние от оси проводника до точки, в которой рассматривается поле.

В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:

$[B={mu }_0mu nI qquad(8)]$

где n – количество витков соленоида на единицу длины; I – сила тока в витке.

Основные формулы раздела «Магнитное поле»

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Закон Фарадея

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Закон Фарадея для контура из N витков

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

N — количество витков [-]

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:

Закон Ома для проводящего контура

Ɛi — ЭДС индукции [В]

I — сила индукционного тока [А]

R — сопротивление контура [Ом]

Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:

ЭДС индукции для движущегося проводника

Ɛi — ЭДС индукции [В]

B — магнитная индукция [Тл]

v — скорость проводника [м/с]

l — длина проводника [м]

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Примеры решения задач по теме «Магнитная индукция»

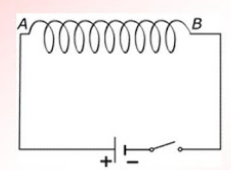
ПРИМЕР 1

Задание

Какова магнитная индукция поля в вакууме, которую создают два тока в точке находящейся на равном расстоянии от каждого проводника (рис.1)? Проводники являются бесконечно длинными, прямыми. Расстояние между ними равно r. Провода параллельные, текущие в них токи равны I, они имеют одинаковые направления.

Решение

В соответствии с принципом суперпозиции результирующая индукция магнитного поля должна быть найдена как векторная сумма:

$[overline{B}={overline{B}}_1+{overline{B}}_2 qquad(1.1)]$

где ${overline{B}}_1$
– индукция, которую создает первый ток; ${overline{B}}_2$
– индукция, которую создает второй ток. Из рис. 1 видно, что векторы ${overline{B}}_1$
и ${overline{B}}_2$
направлены вдоль одной прямой , но в разные стороны, следовательно:

Величину вектора магнитной индукции в точке А поля, которое создает первый проводник можно найти используя формулу:

$[B_1=frac{{mi}_0mu }{2pi }frac{I}{r_1} qquad(1.3)]$

где $r_1=frac{r}{2}$ <br>;
. Второй проводник в точке А создает точно такую же по величине магнитную индукцию:

$[B_2=frac{{mu }_0mu }{2pi }frac{I}{r_2} qquad(1.4)]$

$r_2=frac{r}{2}$
. Получаем, что в точке А:

Ответ

ПРИМЕР 2

Задание

Какова магнитная индукция в центре тонкого кольца, находящегося в вакууме, если по нему течет ток, равный

А? Радиус кольца равен

м.

Решение

В качестве основы для решения задачи используем закон Био-Савара-Лапласа для вакуума. Выделим на круговом токе элементарный участок, который можно считать прямолинейным. В центре окружности этот участок создает поле равное:

$[dB=frac{{mu }_0}{4pi }frac{Idl}{R^2} qquad(2.1)]$

Все векторы магнитной индукции от всех элементов тока при движении по окружности будут направлены вдоль одной прямой, поэтому векторное суммирование заменим простым интегрированием:

$[B=int_L{frac{{mu }_0}{4pi }frac{Idl}{R^2}}=frac{{mu }_0}{4pi }frac{I2pi R}{R^2}=frac{{mu }_0}{2R}I ]$

Проведем вычисление:

$[B=frac{4pi cdot {10}^{-7}}{2cdot 0,05}cdot 10=12,56cdot {10}^{-5}(Tl)]$

Ответ

$B=1,256cdot {10}^{-4}$

Тл

Причины возникновения индукционного тока в движущихся и неподвижных проводниках

Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:

Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
Изменение магнитного поля при неподвижном контуре.

Перейдем к рассмотрению этих случаев подробнее.

Перемещение контура или его частей в неизменном магнитном поле

При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.

Пример 2

На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.

Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон

На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:

FЛ=eυ→B.

Работа силы FЛ на пути l равна:

A=FЛ·l=eυBl.

По определению ЭДС:

δинд=Ae=υBl.

Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.

Следовательно,

δинд=∆Φ∆t.

Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.

При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:

∆Q=RIинд2∆t=υ2B2l2R∆t

Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.

Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:

Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t

Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.

Изменение магнитного поля при неподвижном контуре

Определение

Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.

В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.

В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.

Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.

Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Рисунок. Модель электромагнитной индукции

Рисунок. Модель опытов Фарадея

Рисунок . Модель генератора переменного тока

Источники

https://www.RusElectronic.com/magnetic-field/
https://Zaochnik.ru/blog/magnetizm-dlya-chajnikov-osnovnye-formuly-kotorye-prigodyatsya-pri-reshenii-zadach/
http://ru.solverbook.com/spravochnik/formuly-po-fizike/formula-indukcii-magnitnogo-polya/
https://www.radiochipi.ru/magnitnaya-indukcziya-magnitnyj-potok-opredelenie-formuly-smysl/
https://www.uznaychtotakoe.ru/magnitnaya-indukciya/
https://ege-study.ru/ru/ege/materialy/fizika/elektromagnitnaya-indukciya/
http://ru.solverbook.com/spravochnik/formuly-po-fizike/formula-magnitnoj-indukcii/
https://fizi4ka.ru/egje-2018-po-fizike/magnitnoe-pole.html
https://skysmart.ru/articles/physics/zakon-elektromagnitnoj-indukcii
https://Zaochnik.com/spravochnik/fizika/magnitnoe-pole/elektromagnitnaja-induktsija-pravilo-lentsa/

Как вам статья?

Павел

Бакалавр “210400 Радиотехника” – ТУСУР. Томский государственный университет систем управления и радиоэлектроники

Написать

Пишите свои рекомендации и задавайте вопросы

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 мая 2021 года; проверки требуют 16 правок.

Магнитная индукция

Размерность	MT⁻²I⁻¹
Единицы измерения
СИ	Тл
СГС	Гс
Примечания
Векторная величина

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Магни́тная инду́кция — векторная физическая величина, являющаяся силовой характеристикой магнитного поля, а именно характеристикой его действия на движущиеся заряженные частицы и на обладающие магнитным моментом тела.

Стандартное обозначение: ; единица измерения в СИ — тесла (Тл), в СГС — гаусс (Гс) (связь: 1 Тл = 10⁴ Гс).

Величина магнитной индукции фигурирует в ряде важнейших формул электродинамики, включая уравнения Максвелла.

Для измерения магнитной индукции используются магнитометры-тесламетры. Также она может быть найдена расчётным путём — в статической ситуации для этого достаточно знать пространственное распределение токов.

Вектор в общем случае зависит от координат рассматриваемой точки и времени . Он не инвариантен относительно преобразований Лоренца и изменяется при смене системы отсчёта.

Физический смысл[править | править код]

Магнитная индукция — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд ${displaystyle q^{*}}$ , движущийся со скоростью , равна

${displaystyle {vec {F}}=q^{*}left[{vec {v}}times {vec {B}}right]}$

(по величине ${displaystyle F=q^{*}vBsin alpha }$

Косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (вектор перпендикулярен им обоим и направлен по правилу левой руки).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в предполагаемое однородным (на расстояниях порядка размера рамки) магнитное поле, к произведению силы тока I^* в рамке на её площадь. Момент сил зависит от ориентации рамки и достигает максимального значения при каких-то определённых углах. Звёздочка у символа указывает на то, что заряд или ток являются «пробными», то есть используемыми именно для регистрации поля, в отличие от тех же величин без звёздочки.

Магнитная индукция выступает основной, фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля .

Способы расчёта[править | править код]

Общий случай[править | править код]

В общем случае расчёт магнитной индукции проводится совместно с расчётом электрической составляющей электромагнитного поля посредством решения системы уравнений Максвелла:

${displaystyle mathrm {div} ,(varepsilon {vec {E}})={frac {rho }{varepsilon _{0}}}, mathrm {rot} ,{vec {E}}=-{frac {partial {vec {B}}}{partial t}},}$

${displaystyle mathrm {div} ,{vec {B}}=0, ,mathrm {rot} ,{frac {vec {B}}{mu }}=mu _{0}{vec {j}}+{frac {varepsilon }{c^{2}}}{frac {partial {vec {E}}}{partial t}}}$

где $mu _{0}$ — магнитная постоянная, — магнитная проницаемость, — диэлектрическая проницаемость, а — скорость света в вакууме. Через rho обозначена плотность заряда (Кл/м³) и через vec{j} плотность тока (А/м²).

Магнитостатика[править | править код]

В магнитостатическом пределе^[3] расчёт магнитного поля может быть выполнен с использованием формулы Био—Савара—Лапласа. Вид этой формулы несколько различен для ситуаций, когда поле создаётся текущим по проводу $L_{1}$ током и когда оно создаётся объёмным распределением тока:

${displaystyle {vec {B}}left({vec {r}}right)={mu _{0} over 4pi }int limits _{L_{1}}{frac {Ileft({vec {r}}_{1}right)d{vec {l}}_{1}times left({vec {r}}-{vec {r}}_{1}right)}{left|{vec {r}}-{vec {r}}_{1}right|^{3}}},qquad {vec {B}}left({vec {r}}right)={mu _{0} over 4pi }int {frac {{vec {j}}left({vec {r}}_{1}right)dV_{1}times left({vec {r}}-{vec {r}}_{1}right)}{left|{vec {r}}-{vec {r}}_{1}right|^{3}}}}$

В магнитостатике эта формула играет ту же роль, что закон Кулона в электростатике. Формула позволяет вычислить магнитную индукцию в вакууме. Для случая магнитной среды необходимо использовать уравнения Максвелла (без слагаемых с производными по времени).

Если заранее очевидна геометрия поля, помогает теорема Ампера о циркуляции магнитного поля^[4] (эта запись является интегральной формой уравнения Максвелла для в вакууме):

${displaystyle oint limits _{L}{vec {B}}cdot d{vec {l}}=mu _{0}int limits _{S}{vec {j}}cdot d{vec {S}}}$

Здесь — произвольная поверхность, натянутая на выбранный замкнутый контур .

Простые примеры

Вектор магнитной индукции прямого провода с током на расстоянии от него составляет

${displaystyle {vec {B}}={frac {mu _{0}mu I}{2pi a}}cdot {vec {e}}_{varphi }}$

где ${displaystyle {vec {e}}_{varphi }}$ — единичный вектор вдоль окружности, по оси симметрии которой проложен провод. Предполагается, что среда однородна.

Вектор магнитной индукции прямого внутри соленоида с током и числом витков на единицу длины равен

${displaystyle {vec {B}}=mu _{0}mu nIcdot {vec {e}}_{z}}$

где ${displaystyle {vec {e}}_{z}}$ — единичный вектор вдоль оси соленоида. Здесь также предполагается однородность магнетика, которым заполнен соленоид.

Связь с напряжённостью[править | править код]

Магнитная индукция и напряжённость магнитного поля связаны через соотношение

${displaystyle {vec {B}}=mu _{0}mu {vec {H}}}$

где — магнитная проницаемость среды (вообще говоря, это тензорная величина, но в большинстве реальных случаев её можно считать скаляром, то есть просто константой конкретного материала).

Основные уравнения[править | править код]

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в большое число уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, — это электростатика.

Некоторые из уравнений:

из которого следуют выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле,

Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

${displaystyle {vec {F}}=K{frac {q_{m}^{*}{vec {r}}}{r^{3}}}.}$

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

Выражение для плотности энергии магнитного поля

${displaystyle w={frac {B^{2}}{2mu _{0}mu }}}$ .

Оно входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля, и в лагранжиан электромагнитного поля, и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Типичные значения[править | править код]

характерные значения магнитной индукции

объект	, Тл	объект	, Тл
магнитоэкранируемая комната	10^-14	солнечное пятно	0,15
межзвёздное пространство	10^-10	небольшой магнит (Nd-Fe-B)	0,2
магнитное поле Земли	5*10^-5	большой электромагнит	1,5
1 см от провода с током 100 А	2*10^-3	сильный лабораторный магнит	10
небольшой магнит (феррит)	0,01	поверхность нейтронной звезды	10⁸

Примечания[править | править код]

См. также[править | править код]

Векторный потенциал
Уравнения Максвелла
Электромагнитное поле
Тензор электромагнитного поля
Напряжённость магнитного поля

Источник