Как найти вектор намагниченности

Количественной
характеристикой намагничивания
магнетиков служит вектор
намагниченности,
определяемый, как магнитный
момент единицы объема
магнетика:

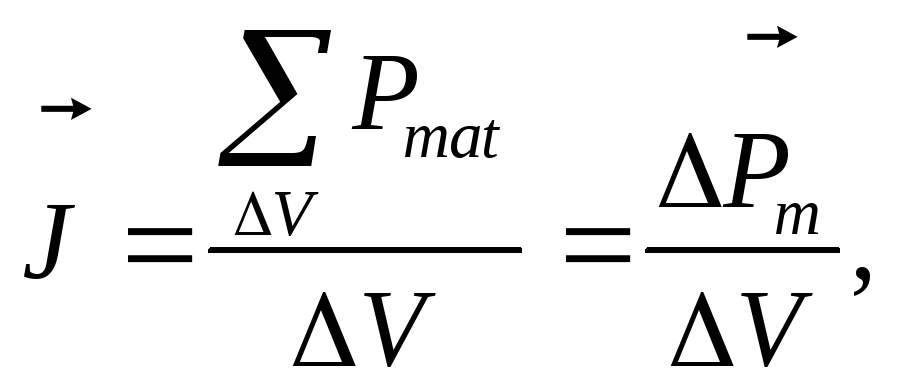(13.3)

где

векторная сумма магнитных моментов
отдельных атомов (молекул) в малом объеме
V
магнетика.

В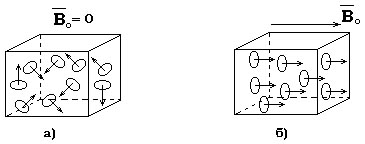отсутствие внешнего магнитного поля
()
магнетик обычно не намагничен, то есть
для него=
0. В диамагнитных веществах это обусловлено
равенством нулю результирующего
магнитного момента у каждого атома. В
парамагнитных телах вследствие
хаотичности теплового движения, магнитные
моменты отдельных атомов (молекул)
ориентированы беспорядочно, поэтому,
в отсутствие поляи вектор намагниченности оказывается
равным нулю в среднем для не слишком
малых объемовV
(рис. 13.1, а).

Рис.
13.1

Поместим
магнетик в однородное внешнее магнитное
поле с индукцией
.
Под действием этого поля элементарные
токи магнетика сориентируются. Магнетик
намагнитится и приобретет в расчете на
единицу объема магнитный момент(рис. 13.1, б). Ориентированные моменты
атомов создают собственное магнитное
поле магнетика с индукцией
.

Найдем
связь между
и
.
Для этого рассмотрим в намагниченном
веществе малый элемент объема V=(Sl)
в форме тонкого цилиндра, ось которого
параллельна направлению вектора
намагниченности
.

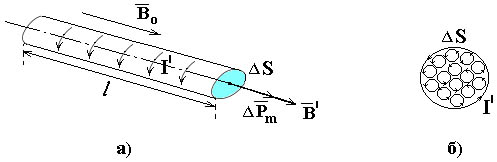
Рис. 13.2

Магнитные
моменты микротоков будут ориентированы
вдоль оси стержня, а их плоскости –
перпендикулярны оси (см. рис. 13.2, а). В
любом перпендикулярном оси сечении S
cтержня
соседние токи на внутренних участках
компенсируют друг друга. Нескомпенсированными
будут лишь отрезки токов, примыкающие
к поверхности магнетика (рис. 13.2, б).
Поэтому действие всех микротоков
эквивалентно действию сплошного
поверхностного микротока I
, обтекающего
намагниченный стержень.

Магнитный момент
этого тока численно равен

Р_m
= I


S.

Магнитный
момент цилиндра (как совокупность
магнитных моментов атомов) выразим из
формулы (13.3)

Р_m
=J 
V
=J 
Sl.

Приравнивая эти
выражения, получим условие эквивалентности
магнитных действий микротока и атомов
цилиндра:

I
= Jl.
(13.4)

Теперь
собственное поле магнетика с индукцией

можно рассматривать как поле, созданное
током I.
Цилиндр, обтекаемый этим током, можно
представить как тонкий соленоид с одним
витком и применить к нему формулу (12.32)
при N=1:

Подставляя
I
из (13.4) с
учетом векторного характера величин,
получим:

.
(13.5)

Таким
образом, индукция
собственного поля
внутри магнетика пропорциональна
вектору намагниченности.

1. Поле в магнетиках. Напряженность магнитного поля

Согласно
принципу суперпозиции результирующее
поле
,
действующее в намагниченном магнетике,
равно

=


+,
(13.6)

где
– индукция (намагничивающего) поля,

–
индукция собственного поля.

С учетом формулы
(13.5) получим:

(13.7)

Чтобы
рассчитать поле
,
надо знать

(или
),
которое, в свою очередь, зависит от.
Можно избежать этого противоречия и
облегчить расчет магнитных полей в
веществе, если ввестивспомогательную
векторную характеристику – напряженность
магнитного поля
:

(13.8)

В вакууме микротоки
отсутствуют, и вектор намагниченности
тождественно равен нулю:

поэтому, согласно
(13.8), напряженность магнитного поля для
вакуума равна

(13.9)

Подставив (13.7) в
(13.8), получим:

Таким образом

(13.10)

Это
означает, что напряженность магнитного
поля
в веществе совпадает с напряженностью
внешнего магнитного поля (поля в вакууме)₀.
Т.е., вектор
зависит только от внешних (макроскопических)
токов. В теории магнетизмаиграет такую же роль, как вектор смещенияв теории электричества. (Соответственно,
вектор индукциипо своей роли для магнитных полей подобен
вектору электрической напряженностив теории электрического поля).

Формула
(13.8) показывает, что в системе СИ
напряженность
магнитного поля, как и вектор намагниченности,
имеет размерность.
(В системе СГС единицей измеренияявляетсяэрстед
(э): 1э = 79,6).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Намагниченность
Размерность	L−1I
Единицы измерения
СИ	А/м
СГС	эрг·Гс−1·см−3
Примечания
векторная величина

Намагни́ченность (также: ве́ктор намагни́чивания) — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно буквой , реже . Определяется как магнитный момент единицы объёма вещества:

,

где  — вектор магнитного момента всей совокупности атомов в объёме , а  — магнитный дипольный момент -го отдельного атома. В системе СИ измеряется в А/м (амперах на метр).

В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность является функцией координат и выражается как:

где  — суммарный магнитный момент молекул в объёме .

Намагниченность выступает количественной характеристикой намагничивания — эффекта частичного упорядочения направлений магнитных моментов отдельных атомов и/или магнитных доменов вещества при наложении магнитного поля. Смысловое соотношение между понятиями «намагничивание» и «намагниченность» аналогично соотношению между «эффектом поляризации» и «вектором поляризации» в физике диэлектриков. В англоязычной литературе и для эффекта, и для его численной характеристики используется одно слово англ. magnetization. Эффект намагничивания наиболее заметен в ферромагнитных средах.

Магнитные моменты, на микроскопическом уровне, создаются так называемыми молекулярными токами, обусловленными локальным движением зарядов (например, электронов) в пределах молекулы. Они появляются в магнетиках там, где текут токи проводимости, и в местах неоднородности среды.

Намагниченность математически связана с объёмной плотностью молекулярных токов через соотношение^[1]:

Связь между и напряженностью магнитного поля в диамагнитных и парамагнитных материалах обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля):

величину называют магнитной восприимчивостью, а (система СИ) или
(СГС) — магнитной проницаемостью.

В ферромагнитных материалах нет однозначной связи между и из-за магнитного гистерезиса, эта связь зависит от предыстории намагничивания тела.

Магнитная индукция определяется через намагниченность как:

(в системе СИ);

(в системе СГС).

Применительно к анизотропным средам различают продольную и поперечную намагниченность по отношению к направлению вектора . В таких случаях вводится тензор магнитной восприимчивости.

Примечания[править | править код]

См. также[править | править код]

• Остаточная намагниченность

Литература[править | править код]

• Намагниченность // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
• Вонсовский С. В. Магнетизм. — М., 1971.
• Киренский Л. В. Магнетизм. — 3-е изд. — М., 1967.
• Савельев И. В. Электричество и магнетизм. — 2001.

В ненамагниченных магнетиках молекулярные токи распределены хаотично, их магнитные поля в среднем взаимно компенсируют друг друга. Намагниченный магнетик можно характеризовать упорядоченным характером молекулярных токов, благодаря чему результирующее магнитное поле вещества не равно нулю.

В тех магнетиках, которые являются проводниками (например, металлы) различают токи проводимости (плотность тока проводимости $overrightarrow{j_{pr}}$), которые относят к упорядоченному движению заряда в макроскопическом понимании (например, движению свободных электронов в металле) и молекулярные токи ($overrightarrow{j_m}$), тогда микроскопическую плотность тока ($overrightarrow{j_{mik}}$) в среде вычисляют как:

[overrightarrow{j_{mik}}=overrightarrow{j_m}+overrightarrow{j_{pr}} left(1right).]

Часто предполагают, что отличие токов проводимости от молекулярных токов в том, что молекулярные токи замыкаются внутри микроскопически малых объектов пространства. Подобное разделение токов на два типа упрощает вывод макро уравнений поля из посылок электронной теории.

Молекулярные токи и индукция магнитного поля

Для того, чтобы вычислить индукцию макроскопического поля молекулярные токи заменяют макроскопическими токами, которые непрерывно изменяются в пространстве. Такие токи имеют название токов намагничивания. Дальше эти плотность этих токов будем обозначать $overrightarrow{j_m}$. Плотность токов проводимости будем обозначать $overrightarrow{j}$. Так получаем, что магнитное поле порождается токами проводимости и токами намагничивания. Если известны эти токи, то можно вычислять индукцию поля $overrightarrow{B},$ используя формулы для вакуума. В таком случае теорема о циркуляции вектора индукции магнитного поля будет иметь вид:

[ointlimits_L{overrightarrow{B}overrightarrow{dl}}={mu }_0left(I+I_mright)left(2right)]

или в дифференциальной форме:

[rotoverrightarrow{B}={mu }_0left(overrightarrow{j}+{overrightarrow{j}}_mright)left(3right),]

где I — ток проводимости, $I_m$ — ток намагничивания, полные токи, которые пронизывают контур L.

Итак, возникновение магнитных моментов связано с наличием круговых токов. Токи в элементарных объемах, которые приводят к возникновению магнитных моментов, назвали молекулярными токами. Однако не следует воспринимать этот термин буквально. Молекулярные токи, строго говоря, могут течь только внутри молекулы. При определении намагниченности и других параметров имеют в виду усредненные величины. Магнитные моменты представляют размазанными по объему вещества, а молекулярные токи текущими по всему объему.

Намагниченность

Для характеристики состояния намагниченного состояния магнетика используют вектор намагниченности $(overrightarrow{J})$.

Намагниченностью ($overrightarrow{J}$) называют физическую величину, которая равна:

[overrightarrow{J}=frac{1}{triangle V}sumlimits_{triangle V}{{overrightarrow{p}}_{mi}(4)},]

где $triangle V$ — элементарный объем, $overrightarrow{p_{mi}}$ — магнитные моменты молекул, суммирование осуществляется по всем молекулам в объеме $triangle V$. Из формулы (4) имеем, что:

[p_m=overrightarrow{J}dVleft(5right).]

Связь намагниченности с молекулярными токами

Рассмотрим бесконечно маленький замкнутый контур L, который ограничивает элемент площади $triangle S$ (рис.1). Вычислим циркуляцию намагниченности ($overrightarrow{J}$) по контуру:

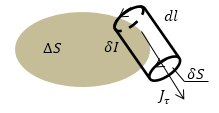
Рис. 1

[intlimits_L{overrightarrow{J}overrightarrow{dl}=intlimits_L{J_{tau }dl}left(6right),}]

где $J_{tau }$- тангенциальная составляющая вектора намагниченности вдоль контура L. Эта составляющая возникает за счет токов, которые текут по замкнутым контурам вокруг линии, вдоль которой проводится интегрирование. Умножим и разделим правую часть выражения (6) на величину $delta S$ (площадь которую обтекает ток в плоскости, которая перпендикулярная линии интегрирования), проведем преобразования в том числе используя выражение (5):

[intlimits_L{J_{tau }dl}=intlimits_L{J_фfrac{dldelta S}{delta S}}=intlimits_L{J_{tau }frac{dV}{delta S}}=intlimits_L{frac{dp_m}{delta S}}left(7right).]

В соответствии с определением магнитного момента ($p_m=ISto {dp}_m=delta Idelta S, $)$ где delta I сила тока, который обтекает площадку delta S,$ причем$ delta I$ пересекает $triangle S$ по нармали. Получаем из (7):

[intlimits_L{frac{dp_m}{delta S}}=intlimits_L{frac{delta I delta S}{дS}}=intlimits_L{delta I}=triangle I_nleft(8right),]

где $triangle I_n$- нормальная составляющая силы тока, которая пересекает площадку $triangle S.$ В результате мы получили:

[intlimits_L{overrightarrow{J}overrightarrow{dl}=triangle I_nleft(9right).}]

Из выражения (9) легко получить:

[overrightarrow{j_m}=rotoverrightarrow{J}left(10right).]

Формула (10) — выражение для объемной плотности молекулярных токов, которые являются причиной намагниченности $overrightarrow{J}$.

Молекулярные токи могут течь и по поверхности раздела меду магнетиками или между магнетиком и вакуумом. Тогда поверхностная плотность молекулярного тока ($i_{m.p}=frac{triangle I_{m.pov}}{l}$) равна:

[overrightarrow{i_{m.p}}=overrightarrow{n}times left(overrightarrow{J_2}-overrightarrow{J_1}right)left(11right),]

где $overrightarrow{n}$ — единичные вектор нормали к поверхности раздела, направленные во вторую среду.