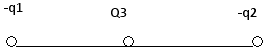Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.
Задачи урока:
- формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля; - научить учащихся применять формулу E=kq/r2 в решении
несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности
электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями; - между зарядами нигде не прерываются.
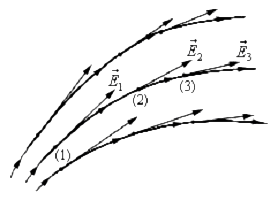
Рис.1
Силовые линии положительного заряда:
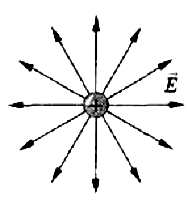
Рис.2
Силовые линии отрицательного заряда:
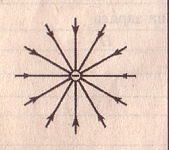
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
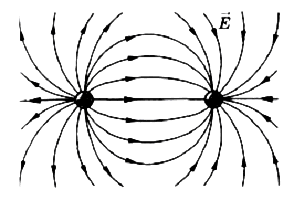
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
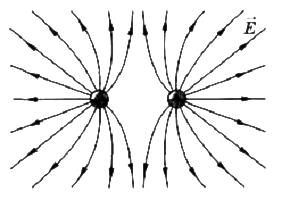
Рис.5
Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
![]() или
или
![]() .
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда
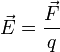
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда
![]()
где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.
В системе СИ
![]() Н·м2/Кл2,
Н·м2/Кл2,
где ε0 – электрическая
постоянная, равная 8,85·10-12 Кл2/Н·м2;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:
![]()
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
Е = kq1/x2 + kq2/(r – x)2
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
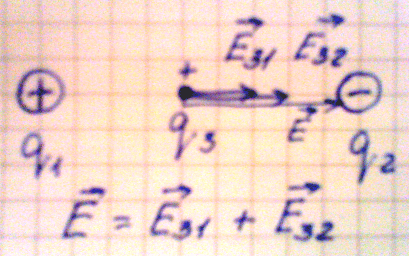
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a)2 – kq2/a2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
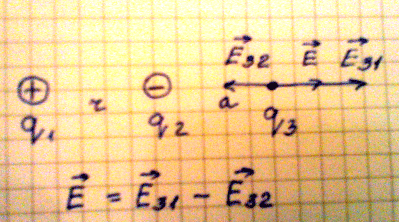
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
Е = (Е312 +Е322)1/2
Следовательно:
Е = ((kq1/r2 )2 + (kq2/b2)2)1/2
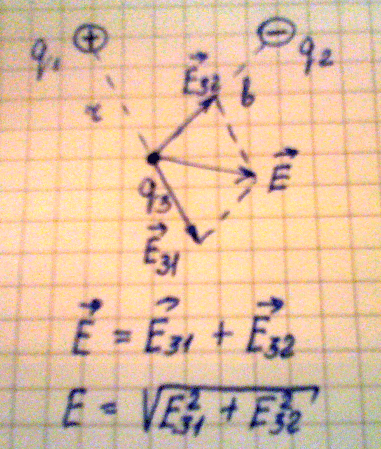
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
Проверочная работа.
Вариант № 1.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
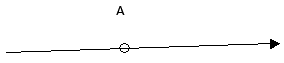
3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Вариант № 2.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Задачи на дом:
1. Два заряда q1 = +3·10-7 Кл и q2 = −2·10-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10-9 Кл действует сила 3·10-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.
Для школьников.
Приведём решение трёх задач на применение принципа суперпозиции (наложения) электростатических полей.
Задача 1. Два точечных одинаковых положительных заряда по 20 нКл каждый расположены в двух вершинах равностороннего треугольника со стороной 2 м в вакууме. Найти напряжённость поля в третьей вершине треугольника.
В точке А вектора напряженности электрических полей каждого заряда направлены вдоль их силовых линий (от зарядов).
Применим принцип суперпозиции для проекций указанных векторов на оси х и у:
Таким образом, вектор напряжённости результирующего электрического поля в точке А направлен вертикально вверх, а модуль напряжённости равен 77 В/м.
Задача 2. Электрическое поле образовано двумя одинаковыми разноимёнными точечными зарядами по 5 нКл. Расстояние между зарядами 10 см. Определить напряжённость поля: 1) в точке, лежащей посередине между зарядами; 2) в точке, лежащей на продолжении линии, соединяющей центры зарядов, на расстоянии 10 см от отрицательного заряда; 3) в точке, лежащей на расстоянии 10 см от положительного и отрицательного зарядов.
В точке А оба вектора напряжённости, создаваемых положительным и отрицательным зарядами, направлены вправо (на рисунке не показаны). Тогда результирующее поле находится через сумму полей, создаваемых первым и вторым зарядами:
В точке В результирующее поле направлено влево и равно:
В точке С вектор напряжённости результирующего электрического поля направлен вправо. Его модуль найдём из треугольника:
Ответ: 36000 В/м; 3400 В/м; 4500 В/м.
Задача 3. Электрическое поле создано двумя точечными зарядами 30 нКл и -10 нКл. Расстояние между зарядами 20 см. Определить напряжённость электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии второго (отрицательного) зарядов.
Покажем направления векторов напряжённости, создаваемых в искомой точке первым и вторым зарядами. Их модули найдём из формул:
Складывая вектора находим вектор результирующего поля. Модуль напряжённости результирующего поля находим по теореме косинусов:
Косинус угла найдём отдельно из треугольника образованного расстояниями:
Косинус угла оказался равным 0,25. Подставив все численные значения в формулу, получим результирующую напряжённость равную 16, 7 кВ/м.
Итак, приведено решение трёх задач на применение принципа суперпозиции (наложения) полей. Сначала в интересующей точке поля рисуем вектора напряжённости электрического поля, создаваемого каждым зарядом в отдельности. Затем, складывая их, находим напряжённость суммарного поля. В первой задаче проще просуммировать проекции векторов напряжённости на оси. Там, где угол между векторами напряжённости, создаваемыми отдельными зарядами, отличен от нуля, пользуются теоремой косинусов (задачи 2 и 3).
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Нахождение напряжённости электростатического поля.
Следующая запись:Как рассчитать напряжённость поля заряженной пластины. Поле конденсатора.
Ссылки на другие занятия (до электростатики) даны в Занятии 1.
Ссылки на занятия (начиная с электростатики) даны в Занятии 45.
По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.
Характеристика электрического поля
Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:
E→=F→q, где F→ – сила, действующая со стороны поля на неподвижный (пробный) заряд q. Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.
У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.
Силовые линии
Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.
Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
E→=∑i=1nE→i.
Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:
E→=∫dE→.
Интегрирование E→=∫dE→ проводится по области распределения зарядов. Если их распределение идет по линии (τ=dqdl – линейная плотность распределения заряда), то интегрирование E→=∫dE→ тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ=dqdS, тогда интегрируют по поверхности.
Интегрирование по объему выполняется, если имеется объемное распределение заряда:
ρ=dqdV, где ρ – объемная плотность распределения заряда.
Что называется напряженностью электрического поля
Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E0→ и связанные Ep→ заряды:
E→=E0→+Ep→.
Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:
E→=E0→ε, где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.
Отсюда следует, что по выражению E→=E0→ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равняется:
E→=14πε0∑i=1nqiεri3ri→.
В системе СГС напряженность поля точечного заряда в вакууме:
E→=qr→r3.
Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ. Необходимо найти напряженность поля в точке А, являющейся центром окружности.
Решение
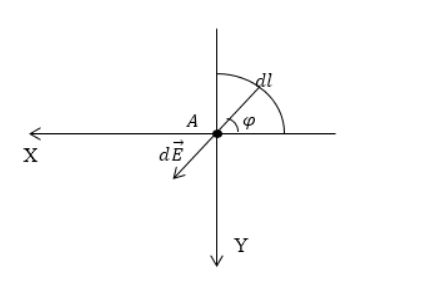
Рисунок 1
Произведем выделение на заряженной части окружности элементарного участка dl, который будет создавать элемент поля в точке А. Следует записать выражение для напряженности, то есть для dE→. Тогда формула примет вид:
dE→=dqR3R→R.
Проекция вектора dE→ на ось Ох составит:
dEx=dEcosφ=dqcosφR2.
Произведем выражение dq через линейную плотность заряда τ:
dq=τdl=τ·2πRdR.
Необходимо использовать dq=τdl=τ·2πRdR для преобразования dEx=dEcosφ=dqcosφR2:
dEx=2πRτdRcos φR2=2πτdRcos φR=τcos φdφR,
где 2πdR=dφ.
Далее перейдем к нахождению полной проекции Ex при помощи интегрирования dEx=2πRτdRcos φR2=2πτdRcos φR=τcos φdφR,
по dφ с изменением угла 0≤φ≤2π.
Ex=∫02πτcos φdφR=τR∫02πcosφ dφ=τRsin φ02π=τR.
Перейдем к проекции вектора напряженности на Оу:
dEy=dEsin φ=τRsin φdφ.
Следует проинтегрировать с изменяющимся углом π2≤φ≤0:
Ey∫π20τRsin φdφ=τR∫π20sin φdφ=-τRcos φπ20=-τR.
Произведем нахождение модуля вектора напряженности в точке А, применив теорему Пифагора:
E=Ex2+Ey2=τR2+-τR2=τR2.
Ответ: E=τR2.
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R. Поверхностная плотность заряда равняется σ.
Решение
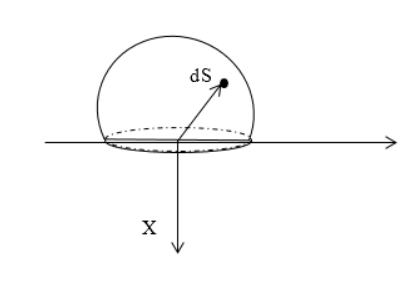
Рисунок 2
Следует выделить на поверхности заряженной сферы элементарный заряд dq, располагаемый на элементе площади dS. Запись, используя сферические координаты dS, равняется:
dS=R2sinθdθdφ,
при 0≤φ≤2π, 0≤θ≤π2.
Элементарная напряженность поля точечного заряда в системе СИ:
dE→=dq4πε0R3R→R.
Необходимо спроецировать вектор напряженности на Ох:
dEx=dqcosθ4πε0R2.
Произведем выражение заряда через поверхностную плотность заряда:
dq=σdS.
Подставим dq=σdS в dEx=dqcosθ4πε0R2, используя dS=R2sinθdθdφ, проинтегрируем и запишем:
Ex=σR24πε0R2∫02πdφ∫0π2cosθsinθdθ=σ4πε02π·12=σ4ε0.
Тогда EY=0.
Отсюда следует, что E=Ex.
Ответ: напряженность полусферы в центре равняется E=σ4ε0.
Электростатика – раздел электродинамики,
изучающий взаимодействие неподвижных
электрических зарядов.
Электрический заряд – физическая
величина, определяющая силу электромагнитного
взаимодействия. Заряд обозначается
буквой q, измеряется
в кулонах (Кл).
В природе существует два вида
электрических зарядов, которые условно
назвали «положительный» и «отрицательный».
Заряды одного знака отталкиваются,
разных знаков – притягиваются.
Электрический заряд всегда связан с
частицей. Существуют частицы без заряда,
но не существует заряда без частицы.
Величина электрического заряда не
зависит от скорости движения частицы.
Минимальный заряд, встречающийся в
природе, называется элементарным.
Величина элементарного заряда е =
1,610-19
Кл. Заряды электрона, протона, позитрона
(античастица для электрона) равны по
модулю элементарному. Заряд любого
макроскопического тела кратен
элементарному, т. е. электрический заряд
– дискретная величина.
Все вещества состоят из атомов или
молекул. Атом состоит из положительно
заряженного ядра и отрицательно
заряженных электронов, движущихся
вокруг ядра. Поэтому любое макроскопическое
тело содержит электрически заряженные
частицы. Если суммарный заряд тела равен
нулю, то говорят что тело электрически
нейтральное или незаряженное. Электрический
заряд любой системы равен алгебраической
сумме зарядов тел, входящих в систему.
Заряды могут перераспределятся между
телами системы. Если система тел
электрически изолирована (через границу
системы не проникают другие заряды), то
в ней выполняется закон сохранения
заряда:
алгебраическая сумма зарядов электрически
изолированной системы постоянна:
q1
+ q2
+ … + qn
= const.
Электризация – это процесс получения
электрически заряженных тел из
нейтральных.
При электризации трением одни вещества
отдают электроны, а другие их присоединяют.
Причина этого явления – в различии
энергии связи электронов с атомами в
этих веществах. Атом, потерявший электрон
называется положительным ионом,
присоединивший к себе электрон –
отрицательным ионом.
Точечный заряд – это заряженное
тело, размер которого много меньше
расстояния его возможного действия на
другие тела.
Закон Кулона (1875 г.): Сила взаимодействия
между двумя неподвижными точечными
зарядами, находящимися в вакууме, прямо
пропорциональна произведению модулей
зарядов, обратно пропорциональна
квадрату расстояния между ними и
направлена по прямой, соединяющей
заряды:
![]() .
.
Коэффициент k, входящий
в закон Кулона, зависит от выбора системы
единиц. В системе СИ
![]() .
.
Здесь
![]()
– электрическая постоянная.
Закон Кулона был получен экспериментально.
Он справедлив только для точечных
зарядов или равномерно заряженных
шаров. Электростатические взаимодействия
осуществляются посредством
электростатического поля.
Электростатическое поле это вид
материи который образуется неподвижными
электрическими зарядами и его можно
обнаружить по его действию на неподвижные
электрические заряды.
Силовой характеристикой электростатического
поля является напряженность –
векторная физическая величина, численно
равная силе с которой поле действует
на единичный пробный положительный
заряд, помещенный в заданной точке поля.
![]() .
.
Направление вектора напряженности
совпадает с направлением вектора силы,
действующей на положительный заряд,
помещенный в данной точке поля. Из закона
Кулона на основании определения
напряженности поля получаем формулу
для напряженности поля точечного заряда
на расстоянии r от него:
![]() .
.
Для наглядности электростатическое
поле представляют непрерывными линиями
напряженности – касательные к которым
в каждой точке совпадают по направлению
с направлением вектора напряженности
электростатического поля в данной
точке.
Линии напряженности не пересекаются
(в противном поле напряженность поля в
точке пересечения не имела бы определенного
значения); начинаются на положительных
зарядах (источники поля) и стекаются к
отрицательным зарядам (стоки). Модуль
вектора напряженности пропорционален
числу линий напряженности на густоте
линий напряженности можно судить о
модуле вектора напряженности на единицу
поверхности (густоте линий напряженности).
Электростатическое поле, векторы
напряженности которого одинаковы во
всех точках пространства, называется
однородным.
Принцип суперпозиции электрических
полей: напряженность поля системы
зарядов в данной точке равна векторной
сумме напряженностей полей, созданным
в этой точке каждым зарядом в отдельности:
![]() .
.
Теорема Гаусса.
Потоком вектора напряженности через
замкнутый контур площадью S
называется произведение проекции
вектора напряженности на нормаль к
контуру на площадь контура:
![]() .
.
Поток вектора напряженности через
произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
расположенных внутри этой поверхности,
деленной на электрическую постоянную:
![]() .
.
Напряженность поля точечного заряда.
Д ля
ля
определения напряженности проведем
сферическую поверхность S
радиусом r с центром
совпадающим с зарядом и воспользуемся
теоремой Гаусса. Так как внутри указанной
области находится только один заряд q,
то согласно указанной теореме получим
равенство:
![]()
(1), где En
– нормальная составляющая напряженности
электрического поля. Из соображений
симметрии нормальная составляющая
должна быть равна самой напряженности
и постоянна для всех точек сферической
поверхности, поэтому E=En=const.
Поэтому ее можно вынести за знак суммы.
Тогда равенство (1) примет вид
![]() ,
,
что и было получено из закона Кулона и
определения напряженности электрического
поля.
Электрическое поле заряженной сферы
Е сли
сли
сфера проводящая, то весь заряд находится
на поверхности. Рассмотрим две области
I – внутри сферы радиуса
R с зарядом q
и вне сферы область II.
Для определения напряженности в области
I проведем сферическую
поверхность S1
радиусом r1 (0<r1<R)
и воспользуемся теоремой Гаусса. Так
как внутри указанной области зарядов
нет, то согласно указанной теореме
получим равенство:
![]()
(1), где En
– нормальная составляющая напряженности
электрического поля. Из соображений
симметрии нормальная составляющая
должна быть равна самой напряженности
и постоянна для всех точек сферической
поверхности, поэтому E1=En=const.
Поэтому ее можно вынести за знак суммы.
Тогда равенство (1) примет вид
![]() .
.
Т. к. площадь сферы не равна нулю, то Е1=0
(во всех точках области I)
– внутри проводника зарядов нет и
напряженность поля равна нулю.
В области II Rr2
проведем сферическую поверхность S2
радиусом r2 и
воспользуемся теоремой Гаусса:
![]()
(2),
![]()
– напряженность поля вне сферы
рассчитывается по той же формуле, что
и напряженность поля точечного заряда.
Электрическое поле заряженного шара
Заряд равномерно распределен по всему
объему шара, поэтому введем понятие
объемной плотности заряда:
![]() .
.
Рассмотрим две области I
– внутри сферы радиуса R
с зарядом q и вне сферы
область II.
Для определения напряженности в области
I проведем сферическую
поверхность S1
радиусом r1 (0<r1<R)
и воспользуемся теоремой Гаусса:

– напряженность поля внутри шара
увеличивается прямо пропорционально
расстоянию до центра шара.
В области II R
r2
проведем сферическую поверхность S2
радиусом r2 и
воспользуемся теоремой Гаусса:
![]()
(2),
![]()
– напряженность поля вне шара рассчитывается
по той же формуле, что и напряженность
поля точечного заряда.
Электрическое поле заряженной нити
Д ля
ля
равномерно заряженной нити введем
понятие линейной плотности заряда![]() .
.
Для определения напряженности окружим
участок проволоки длиной ℓ
цилиндрической поверхностью S
радиусом r с осью совпадающей
с проволокой и воспользуемся теоремой
Гаусса. При этом весь поток вектора
напряженности будет проходить только
через боковую поверхность цилиндра,
площадь которой
![]() ,
,
т.к. поток через оба основания цилиндра
равен нулю. Тогда
![]()
– напряженность поля нити убывает обратно
пропорционально расстоянию.
Напряженность поля заряженной плоскости
Е сли
сли
плоскость бесконечна и заряжена
равномерно, т. е. поверхностная плотность
заряда = q/S
одинакова в любом ее месте, то линии
напряженности электрического поля в
любой точке перпендикулярны этой
плоскости. Такое же направление они
сохраняют и на любом расстоянии от
плоскости, т.е. поле заряженной плоскости
однородное.
Для нахождения напряженности электрического
поля заряженной плоскости мысленно
выделим в пространстве цилиндр, ось
которого перпендикулярна заряженной
плоскости, а основания параллельны ей
и одно из оснований проходит через
интересующую нас точку поля. Цилиндр
вырезает из заряженной плоскости участок
площадью S, и такую же
площадь имеют основания цилиндра,
расположенные по разные стороны от
плоскости (рис.). Согласно теореме Гаусса
поток Ф вектора напряженности
электрического поля через поверхность
цилиндра связан с электрическим зарядом
внутри цилиндра выражением
![]() .
.
С другой стороны, так как линии
напряженности пересекают лишь основания
цилиндра, поток вектора напряженности
можно выразить через напряженность
электрического поля у обоих оснований
цилиндра:
![]() .
.
В самом деле, поток через боковую
поверхность цилиндра (см. рис.), равен
нулю, поскольку линии напряженности
параллельны боковой поверхности
цилиндра.
Из двух выражений для потока вектора
напряженности получим:
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
Содержание:
- Определение и формула напряженности электрического поля
- Принцип суперпозиции напряженностей электрических полей
- Напряженность поля в диэлектрике
- Напряженность поля точечного заряда
- Связь напряженности и потенциала
- Единицы измерения напряженности электрического поля
- Примеры решения задач
Определение и формула напряженности электрического поля
Определение
Вектор напряженности $bar{E}$ – это силовая характеристика электрического поля. В некоторой точке поля, напряженность равна
силе, с которой поле действует на единичный положительный заряд, размещенный в указанной точке, при этом направление силы и напряженности
совпадают. Математическое определение напряженности записывается так:
$$bar{E}=frac{bar{F}}{q}$$
где $bar{F}$ – сила, с которой электрическое поле действует на
неподвижный, «пробный», точечный заряд q, который размещают в рассматриваемой точке поля. При этом считают, что «пробный» заряд
мал на столько, что не искажает исследуемого поля.
Если поле является электростатическим, то его напряженность от времени не зависит.
Если электрическое поле является однородным, то его напряженность во всех точках поля одинакова.
Графически электрические поля можно изображать при помощи силовых линий. Силовыми линиями (линиями напряженности) называют
линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности в этой точке поля.
Принцип суперпозиции напряженностей электрических полей
Если поле создано несколькими электрическими полями, то напряженность результирующего поля равна векторной сумме напряженностей отдельных полей:
$$bar{E}=sum_{i=1}^{n} bar{E}_{i}(2)$$
Допустим, что поле создается системой точечных зарядов и их распределение непрерывно, тогда результирующая напряженность находится как:
$$bar{E}=int d bar{E}(3)$$
интегрирование в выражении (3) проводят по всей области распределения заряда.
Напряженность поля в диэлектрике
Напряженность поля $bar{E}$ в диэлектрике равна векторной сумме
напряженностей полей, создаваемых свободными зарядами $bar{E}_0$ и
связанными (поляризационными зарядами) $bar{E}_p$:
$$bar{E}=bar{E}_{0}+bar{E}_{p}(4)$$
В том случае, если вещество, которое окружает свободные заряды однородный и изотропный диэлектрик, то напряженность
$bar{E}$ равна:
$$bar{E}=frac{bar{E}_{0}}{varepsilon}(5)$$
где $varepsilon$ – относительная диэлектрическая проницаемость вещества в исследуемой точке
поля. Выражение (5) обозначает то, что при заданном распределении зарядов напряженность электростатического поля в однородном изотропном
диэлектрике меньше, чем в вакууме в $varepsilon$ раз.
Напряженность поля точечного заряда
Напряженность поля точечного заряда q равна:
$$bar{E}=frac{1}{4 pi varepsilon varepsilon_{0}} frac{q}{r^{3}} bar{r}(6)$$
где $varepsilon_{0}=8,85 cdot 10^{-12}$ Ф/м (система СИ) – электрическая постоянная.
Связь напряженности и потенциала
В общем случае напряженность электрического поля связана с потенциалом как:
$$bar{E}=-operatorname{grad} varphi-frac{partial bar{A}}{partial t}(7)$$
где $varphi$ – скалярный потенциал,
$bar{a}$ – векторный потенциал.
Для стационарных полей выражение (7) трансформируется в формулу:
$$bar{E}=-operatorname{grad} varphi(8)$$
Единицы измерения напряженности электрического поля
Основной единицей измерения напряженности электрического поля в системе СИ является: [E]=В/м(Н/Кл)
Примеры решения задач
Пример
Задание. Каков модуль вектора напряженности электрического поля
$bar{E}$ в точке, которая определена радиус- вектором
$bar{r}_{2}=7 bar{i}+3 bar{j}$ (в метрах), если электрическое поле создает положительный точечный
заряд (q=1Кл), который лежит в плоскости XOY и его положение задает радиус вектор
$bar{r}_{1}=bar{i}-5 bar{j}$, (в метрах)?
Решение. Модуль напряжения электростатического поля, которое создает точечный заряд, определяется формулой:
$$E=frac{1}{4 pi varepsilon varepsilon_{0}} frac{q}{r^{2}}(1.1)$$
r- расстояние от заряда, создающего поле до точки в которой ищем поле.
$$bar{r}=bar{r}_{2}-bar{r}_{1}=6 bar{i}-8 bar{j}(1.2)$$
Из формулы (1.2) следует, что модуль $bar{r}$ равен:
$$r=|bar{r}|=sqrt{36+64}=10(mathrm{~m})$$
Подставим в (1.1) исходные данные и полученное расстояние r, имеем:
$$E=9 cdot 10^{9} frac{1}{100}=9 cdot 10^{7}left(frac{B}{m}right)$$
Ответ. $E=9 cdot 10^{7}left(frac{B}{m}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Запишите выражение для напряженности поля в точке, которая определена радиус – вектором
$bar{r}$, если поле создается зарядом, который распределен по объему V с плотностью
$rho=rho(r)$ .
Решение. Сделаем рисунок.
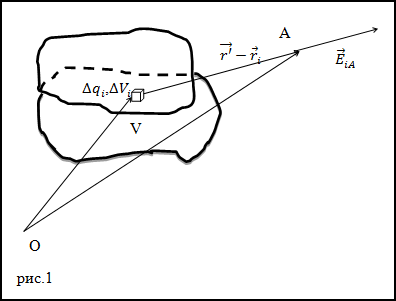
Проведем разбиение объема V на малые области с объемами
$Delta V_{i}$ заряды этих объемов
$Delta q_{i}$, тогда напряженность поля точечного заряда в точке А (рис.1) будет равна:
$$bar{E}_{i A}=frac{1}{4 pi varepsilon_{0}} frac{Delta q_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.1)$$
Для того чтобы найти поле, которое создает все тело в точке А, используем принцип суперпозиции:
$$bar{E}_{A}=sum_{i=1}^{N} bar{E}_{i A}=frac{1}{4 pi varepsilon_{0}} sum_{i=1}^{N} frac{Delta q_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.2)$$
где N – число элементарных объемов, на которые разбивается объем V.
Плотность распределения заряда можно выразить как:
$rholeft(bar{r}_{i}right)=frac{Delta q_{i}}{Delta V_{i}}(2.3)$
Из выражения (2.3) получим:
$Delta q_{i}=rholeft(bar{r}_{i}right) Delta V_{i}(2.4)$
Подставим выражение для элементарного заряда в формулу (2.2), имеем:
$$bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} sum_{i=1}^{N} frac{rholeft(bar{r}_{i}right) Delta V_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.5)$$
Так ка распределение зарядов задано непрерывное, то если устремить
$Delta V_i$ к нулю, то можно перейти от суммирования к интегрированию, тогда:
$$bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} int_{V} frac{rho(bar{r})}{left|bar{r}^{prime}-bar{r}right|^{3}}left(bar{r}^{prime}-bar{r}right) d V$$
Ответ. $bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} int_{V} frac{rho(bar{r})}{left|bar{r}^{prime}-bar{r}right|^{3}}left(bar{r}^{prime}-bar{r}right) d V$
Читать дальше: Формула пути.