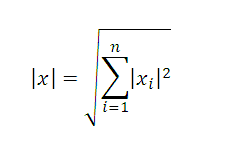Норма (модуль, длина) вектора
В пространстве V каждому вектору x∈V ставим в соответствие некоторое неотрицательное число 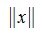
тогда и только тогда, когда x=0.
.
(неравенство треугольника).
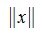
Примеры норм в линейных пространствах
1. max-норма, или m – норма:
2. l-норма:
3. Евклидова норма:
Пример вычисления нормы (длины, модуля) вектора
Вычислим нормы вектора
1. m-норма:
2. l-норма:
3. Евклидова норма:
|
|
Загрузить PDF
Загрузить PDF
Вектор является геометрическим объектом, он характеризуется направлением и величиной. Его можно представить в виде отрезка с начальной точкой на одном конце и стрелкой на втором, при этом длина отрезка соответствует величине вектора, а стрелка указывает на его направление. Нормирование вектора является стандартной операцией в математике, на практике она используется в компьютерной графике.
-
1
Определим единичный вектор. Единичным вектором вектора A называется такой вектор, направление которого совпадает с направлением вектора A, а длина равна 1. Можно строго доказать, что каждый вектор имеет один и только один соответствующий ему единичный вектор.
-
2
Узнайте, что такое нормирование вектора. Это процедура нахождения единичного вектора для заданного вектора A.
-
3
Определим связанный вектор. В декартовой системе координат связанный вектор выходит из начала координат, то есть для 2-мерного случая из точки (0,0). Это позволяет задавать вектор лишь координатами его конечной точки.
-
4
Освойте запись векторов. Если ограничиться связанными векторами, то в записи A = (x, y) пара координат (x,y) указывает на конечную точку вектора A.
Реклама
-
1
Установите, что известно. Из определения единичного вектора мы знаем, что начальная точка и направление этого вектора совпадают с аналогичными характеристиками вектора A. Кроме того, длина единичного вектора равна 1.
-
2
Определите, что необходимо найти. Требуется найти координаты конечной точки единичного вектора.
Реклама
- Найдите конечную точку единичного вектора для вектора A = (x, y). Единичный вектор и вектор А образуют подобные прямоугольные треугольники, поэтому конечная точка единичного вектора будет иметь координаты (x/c, y/c), где необходимо найти c. Кроме того, длина единичного вектора равна 1. Таким образом, согласно теореме Пифагора имеем: [x^2/c^2 + y^2/c^2]^(1/2) = 1 -> [(x^2 + y^2)/c^2]^(1/2) -> (x^2 + y^2)^(1/2)/c = 1 -> c = (x^2 + y^2)^(1/2). То есть единичный вектор вектора A = (x, y) задается выражением u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2)).
- Предположим, что вектор A начинается в начале координат, а его конечная точка расположена в (2,3), то есть A = (2,3). Найдем единичный вектор: u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2)) = (2/(2^2 + 3^2)^(1/2), 3/(2^2 + 3^2)^(1/2)) = (2/(13^(1/2)), 3/(13^(1/2))). Таким образом, нормирование вектора A = (2,3) приводит к вектору u = (2/(13^(1/2)), 3/(13^(1/2))).
- Обобщим формулу для нормирования вектора на случай пространства с произвольным числом измерений. Чтобы нормировать вектор A (a, b, c, …), необходимо найти вектор u = (a/z, b/z, c/z, …), где z = (a^2 + b^2 + c^2 …)^(1/2).
Об этой статье
Эту страницу просматривали 29 237 раз.
Была ли эта статья полезной?
Скалярное
произведение вектора самого на себя
называется скалярным квадратом. Эта
величина
определяет
квадрат длины вектора x.
Для обозначения длины (называемой
также нормой вектора)
используется обозначение
Например,
Рис.
16 Норма вектора
Вектор
единичной длины (||x||
= 1) называется нормированным. Ненулевой
вектор (x ≠ 0)
можно нормировать, разделив его на
длину, т.е. x =
||x||
(x/||x||)
= ||x|| e.
Здесь e =x/||x||
— нормированный вектор.
Векторы называются
ортонормированными, если все они
нормированы и попарно ортогональны.
Содержание
1.10. Угол между векторами
Скалярное
произведение определяет и угол φ
между двумя векторами x и y
Если вектора
ортогональны, то cosφ = 0 и φ = π/2, а если
они колинеарны, то cosφ = 1 и φ = 0.
Содержание
1.11. Векторное представление матрицы
Каждую
матрицу A размера I×J можно
представить как набор векторов
Здесь
каждый вектор aj является j-ым
столбцом, а вектор-строка bi является i-ой
строкой матрицы A
Содержание
1.12. Линейно зависимые векторы
Векторы
одинаковой размерности (N)
можно складывать и умножать на число,
также как матрицы. В результате получится
вектор той же размерности. Пусть имеется
несколько векторов одной
размерности x1, x2,…,xK и
столько же чисел α α1,
α2,…,αK.
Вектор
y =
α1x1+
α2x2+…+
αKxK
называется линейной
комбинацией векторов xk.
Если
существуют такие ненулевые числа αk ≠
0, k =
1,…, K,
что y = 0,
то такой набор векторов xk называется линейно
зависимым.
В противном случае векторы называются
линейно независимыми. Например,
векторы x1 =
(2, 2)t и x2 =
(−1, −1)t линейно
зависимы, т.к. x1 +2x2 = 0
Содержание
1.13. Ранг матрицы
Рассмотрим
набор из K векторов x1, x2,…,xK размерности N.
Рангом этой системы векторов называется
максимальное число линейно-независимых
векторов. Например в наборе
имеются
только два линейно независимых вектора,
например x1 и x2,
поэтому ее ранг равен 2.
Очевидно,
что если векторов в наборе больше, чем
их размерность (K>N),
то они обязательно линейно зависимы.
Рангом
матрицы (обозначается
rank(A))
называется ранг системы векторов, из
которых она состоит. Хотя любую матрицу
можно представить двумя способами
(векторы столбцы или строки), это не
влияет на величину ранга, т.к.
rank(A)
= rank(At).
Содержание
1.14. Обратная матрица
Квадратная
матрица A называется
невырожденной, если она имеет
единственную обратную матрицу A-1,
определяемую условиями
AA−1 = A−1A = I.
Обратная матрица
существует не для всех матриц. Необходимым
и достаточным условием невырожденности
является
det(A)
≠ 0 или rank(A)
= N.
Обращение матрицы
— это сложная процедура, для выполнения
которой существуют специальные программы.
Например,
Рис.
17 Обращение матрицы
Приведем формулы
для простейшего случая — матрицы 2×2
Если
матрицы A и B невырождены,
то
(AB)−1 = B−1A−1.
Содержание
1.15. Псевдообратная матрица
Если
матрица A вырождена
и обратная матрица не существует, то в
некоторых случаях можно
использовать псевдообратную матрицу,
которая определяется как такая матрица A+,
что
AA+A = A.
Псевдобратная
матрица — не единственная и ее вид
зависит от способа построения. Например
для прямоугольной матрицы можно
использовать метод
Мура-Пенроуза.
Если число столбцов
меньше числа строк, то
A+=(AtA)−1At
Например,

Рис.
17a Псевдообращение
матрицы
Если же число
столбцов больше числа строк, то
A+=At(AAt)−1
Содержание
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 июня 2021 года; проверки требуют 2 правки.
У этого термина существуют и другие значения, см. норма.
Норма — функционал, заданный на векторном пространстве и обобщающий понятие длины вектора или абсолютного значения числа.
Определение[править | править код]
Норма вектора[править | править код]
Норма в векторном пространстве 

-
(неравенство треугольника);
Эти условия являются аксиомами нормы.
Векторное пространство с нормой называется нормированным пространством, а условия (1—3) — также аксиомами нормированного пространства.
Из аксиом нормы очевидным образом вытекает свойство неотрицательности нормы:

Действительно, из третьего свойства следует: 

Чаще всего норму обозначают в виде: 



Вектор с единичной нормой 
Любой ненулевой вектор 

Норма матрицы[править | править код]
Нормой матрицы 

, причём
только при
;
, где
;
;
.
Если выполняется также и четвёртое свойство, норма называется субмультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы субмультипликативны.
Матричная норма 





для всех 
Норма оператора[править | править код]
Норма оператора 
,
- где
— оператор, действующий из нормированного пространства
в нормированное пространство
.
- где
Это определение эквивалентно следующему:
- Свойства операторных норм:
, причём
только при
;
, где
;
;
.
В конечномерном случае, оператору в некотором базисе соответствует матрица — матрица оператора. Если норма на пространстве(пространствах), где действует оператор, допускает одно из стандартных выражений в базисе, то свойства нормы оператора повторяют аналогичные свойства нормы матрицы.
Свойства нормы[править | править код]
[косинус угла]
Эквивалентность норм[править | править код]
Примеры[править | править код]
Линейные нормированные пространства[править | править код]
- Любое предгильбертово пространство можно считать нормированным, так как скалярное произведение порождает естественную норму
где 
В частности:
- Нормы функций в
— пространстве вещественных (или комплексных) непрерывных функций на отрезке [0,1]:
«L0 норма»[править | править код]
Особым случаем является 

Некоторые виды матричных норм[править | править код]
- Порожденные нормы
:
- Здесь
— сопряжённая к
матрица,
— след матрицы.
Связанные понятия[править | править код]
Топология пространства и норма[править | править код]
Норма задаёт на пространстве метрику (в смысле — функцию расстояния метрического пространства), порождая таким образом метрическое пространство, а значит топологию, базой которой являются всевозможные открытые шары, то есть множества вида 
См. также[править | править код]
- Полунорма
- Метрика
- Скалярное произведение
Примечания[править | править код]
- ↑ М. Вербицкий. Начальный курс топологии. Задачи и теоремы. — Litres, 2018-12-20. — С. 163-164. — 346 с.
Норма вектораФормулы, примеры, калькулятор нормы вектора Определение 1. Норма вектора ( эвклидова норма, модуль вектора, длина вектора) x=(x1,x2, …xn) Пример 1. Найти норму вектора a = (5,-2,7) Решение. Подставляем координаты вектора, получаем норму вектора Как нормировать векторНормированный вектор – это единичный вектор по направлению. То есть, сохраняется информация только о направлении вектора: Для того чтобы получить нормированный вектор, необходимо каждую координату исходного вектора разделить на норму вектора. Пример 2. Нормировать вектор a = (5,-2,7) Решение. Подставляем координаты вектора, получаем нормированный вектор Проверить правильность вычисления нормы вектора, а также найти нормированный вектор можно с помощью калькулятора. |
Категория: Аналитическая геометрия | Просмотров: 12351 | | Теги: вектор | Рейтинг: 0.0/0 |
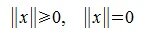 тогда и только тогда, когда x=0.
тогда и только тогда, когда x=0.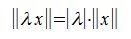 .
.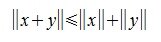 (неравенство треугольника).
(неравенство треугольника).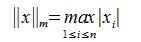

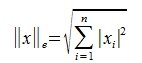
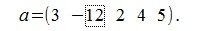

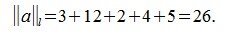














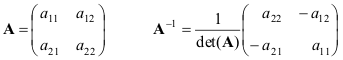


















![{frac {|x|^{2}+|y|^{2}-|x-y|^{2}}{2|x||y|}}in [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6683fcada4bd27b0d0cc5b5cc268d7f2c7ba534)




![C[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e160d783783c799aae07cf78d250747461af0ff9)