5.2.3. Вектор нормали плоскости (нормальный вектор)
Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.
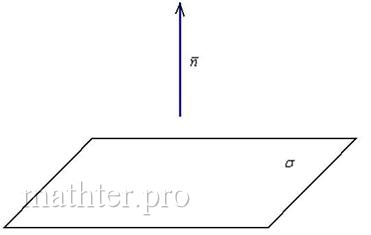
Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением в прямоугольной (!) системе координат, то вектор
является нормальным вектором данной плоскости.
Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:
Задача 134
Найти единичный нормальный вектор плоскости .
Решение: принципиально ситуация выглядит так:
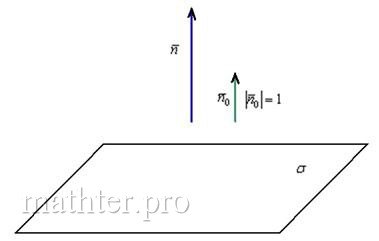
Сначала из уравнения плоскости «снимем» вектор нормали: .
И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора
разделить на длину вектора
.
Вычислим длину вектора нормали:
Таким образом:
Контроль: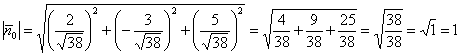
Ответ:
Вспоминаем, что координаты этого вектора – есть в точности направляющие косинусы вектора :
.
И, как говорится, обещанного три страницы ждут 🙂 – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке и двум векторам
, и в результате решения мы получили уравнение
.
Проверяем:
Во-первых, подставим координаты точки в полученное уравнение:
– получено верное равенство, значит, точка
лежит в данной плоскости.
На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы
параллельны плоскости, а вектор
ей перпендикулярен, то должны иметь место следующие факты:
. Ортогональность векторов элементарно проверяется с помощью скалярного произведения:
Вывод: уравнение плоскости найдено правильно.
В ходе проверки я фактически процитировал следующее утверждение теории: вектор параллелен плоскости
в том и только том случае, когда
.
Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Нормальный вектор плоскости – наиболее компактный и наглядный способ определить плоскость в трехмерной системе координат.
Определение 1
Вектор нормали к плоскости – любой ненулевой вектор, принадлежащий прямой, перпендикулярной к рассматриваемой плоскости. По отношению к такой прямой нормальный вектор является направляющим.
Для каждой плоскости существует бесконечное множество коллинеарных друг по отношению к другу нормальных векторов.
В качестве примера плоскостей, задаваемых нормальными векторами, можно рассматривать координатные плоскости системы координат $Oxyz$: $Oxy$, $Oxz$, $Oyz$. Для них нормальными векторами будут, векторы, направляющие оси, т.е., соответственно, $Oz$, $Oy$ и $Ox$ ($vec{k}, vec{j}, vec{i}$).
Рисунок 1. Векторы в трехмерной системе координат. Автор24 — интернет-биржа студенческих работ
Рассмотрим основные математические закономерности, показываюшие как найти вектор нормали к плоскости.
Формула нормального вектора выводится из общего уравнения плоскости, которое имеет вид $Ax + By + Cz + D = 0$.
Плоскости, в уравнениях которых один из коэффициентов равен $0$, соответствуют базовым плоскостям системы координат ($Oxy, Oxz, Oyz$).
Уравнения вида
$Ax + D = 0 \ By + D = 0 \ Cz + D = 0$
описывают плоскости, параллельные $Oxy, Oxz, Oyz$ и отстоящие от них на расстояние, равное отношению свободного члена $D$ к соответствующему коэффициенту, например:
$x = frac{D}{A}$
Нормальный вектор плоскости $Ax + By + Cz + D = 0$ можно выразить как $bar{n}(A; B; C)$. Существует бесконечное множество плоскостей, перпендикулярных данному вектору. Для определения плоскости нужна еще точка на ней. Через любую точку также можно провести бесконечное количество плоскостей (их совокупность называется связкой). Нормальный вектор и точка взаимодополняют друг друга, определяя единственную плоскость.
«Нормальный вектор плоскости» 👇
Точку на плоскости можно обозначить как $M_1(x; y; z)$. Вектор, соединяющий ее с любой другой точкой $M$ данной плоскости, при скалярном умножении на вектор нормали к плоскости $N$ дает ноль:
$overline{M_1M} cdot N = 0$
Переписав уравнение через проекции, получим
$overline{M_1M} cdot N = A(x – x_1) + B(y – y_1) + C(z – z_1) = 0$
Это дает нам возможность выводить уравнение плоскости через координаты точки и параметры нормального вектора плоскости.
Замечание 1
Определить плоскость в пространстве можно и другими способами, например, с помощью указания координат трех ее точек, не лежащих на одной прямой, двух неколлинеарных векторов и точки и т.д. Однако форма записи с помощью нормального вектора плоскости и точки наиболее компактна. К ней другие методы задания плоскости можно привести путем алгебраических преобразований.
С помощью нормального вектора плоскости как ее определителя могут быть решены задачи на доказательство параллельности или перпендикулярности плоскостей, на составление уравнения плоскости, на нахождение угла между прямой и плоскостью, на нахождение угла между плоскостями.
Пример 1
Сформулируем уравнение плоскости, проходящей через точку с координатами $M(1; -2; 3)$ и перпендикулярной вектору $N = 2i + 4k$.
Для начала найдем коэффициенты, соответствующие координатам:
$A = 2 \ B = 0 \ C = 4$
Заметим, что $B = 0$ следует из того, что направляющий вектор $vec{j}$ оси $Oy$ в исходном уравнении не упоминается.
Подставим значения в формулу:
$2(x – 1) + 0(y + 2) + 4(z – 3) = 0$
После стандартных преобразований получим ответ:
$x + 2z – 7 = 0$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Как найти нормаль плоскости
Нормаль плоскости n (вектор нормали к плоскости) – это любой направленный перпендикуляр к ней (ортогональный вектор). Дальнейшие выкладки по определении нормали зависят от способа задания плоскости.
Инструкция
Если задано общее уравнение плоскости – AX+BY+CZ+D=0 или его форма A(x-x0)+B(y-y0)+C(z-z0)=0, то можно сразу записать ответ – n(А, В, С). Дело в том, что это уравнение было получено, как задача определения уравнения плоскости по нормали и точке.
Для получения общего ответа, вам понадобится векторное произведение векторов из-за того, что последнее всегда перпендикулярно исходным векторам. Итак, векторным произведением векторов, является некоторый вектор, модуль которого равен произведению модуля первого (а) на модуль второго (b) и на синус угла между ними. При этом этот вектор (обозначьте его через n) ортогонален a и b – это главное. Тройка этих векторов правая, то есть из конца n кратчайший поворот от a к b совершается против часовой стрелки.
[a,b] – одно из общепринятых обозначений векторного произведения. Для вычисления векторного произведения в координатной форме, используется вектор-определитель (см. рис.1)
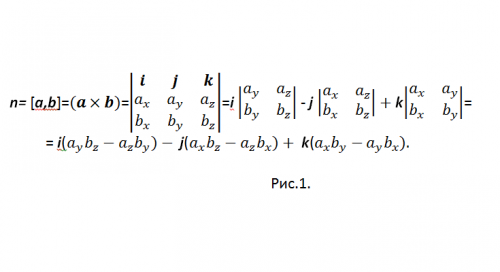
Для того чтобы не путаться со знаком «-», перепишите результат в виде: n={nx, ny, nz}=i(aybz-azby)+j(azbx-axbz)+k(axby-aybx), и в координатах: {nx, ny, nz}={(aybz-azby), (azbx-axbz), (axby-aybx)}.
Более того, дабы не путаться с численными примерами выпишете все полученные значения по отдельности: nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx.
Вернитесь к решению поставленной задачи. Плоскость можно задать различными способами. Пусть нормаль к плоскости определяется двумя неколлинеарными векторами, причем сразу численно.
Пусть даны векторы a(2, 4, 5) и b(3, 2, 6). Нормаль к плоскости совпадает с их векторным произведением и, как только что было выяснено будет равна n(nx, ny, nz),
nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx. В данном случае ax=2, ay=4, az=5, bx=3, by=2, bz=6. Таким образом,
nx=24-10=14, ny=12-15=-3, nz=4-8=-4. Нормаль найдена – n(14, -3, -4). При этом она является нормалью к целому семейству плоскостей.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

