Два вектора
a→
и
b→
всегда образуют угол.
Угол между векторами может принимать значения от
0°
до
180°
включительно.
Если векторы не параллельны, то их можно расположить на пересекающихся прямых.
Векторы могут образовать:
1. острый угол;

2. тупой угол;

3. прямой угол (векторы перпендикулярны).

Если векторы расположены на параллельных прямых, то они могут образовать:
4. угол величиной
0°
(векторы сонаправлены);

5. угол величиной
180°
(векторы противоположно направлены).

Если один из векторов или оба вектора нулевые, то угол между ними будет равен
0°
.
Угол между векторами записывают так:
Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
a→⋅b→=a→⋅b→⋅cosa→b→ˆ
.
Результат скалярного произведения векторов является числом (в отличие от результата рассмотренных ранее действий с векторами — сложения, вычитания и умножения на число. В таких случаях результатом был вектор). При умножении вектора на вектор получается число, так как длины векторов — это числа, косинус угла — число — соответственно, их произведение также будет являться числом.
1. Если угол между векторами острый, то скалярное произведение будет положительным числом (так как косинус острого угла — положительное число).
Если векторы сонаправлены, то угол между ними будет равен
0°
, а косинус равен (1), скалярное произведение также будет положительным.
2. Если угол между векторами тупой, то скалярное произведение будет отрицательным (так как косинус тупого угла — отрицательное число).
Если векторы направлены противоположно, то угол между ними будет равен
180°
. Скалярное произведение также отрицательно, так как косинус этого угла равен (-1).
Справедливы и обратные утверждения:
1. Если скалярное произведение векторов — положительное число, то угол между данными векторами острый.
2. Если скалярное произведение векторов — отрицательное число, то угол между данными векторами тупой.
Особенный третий случай!
Обрати внимание!
3. Если угол между векторами прямой, то скалярное произведение векторов равно нулю, так как косинус прямого угла равен (0).
Обратное суждение: если скалярное произведение векторов равно нулю, то эти векторы перпендикулярны.
Вектор, умноженный на самого себя, будет числом, которое называется скалярным квадратом вектора. Скалярный квадрат вектора равен квадрату длины данного вектора и обозначается как
a→2
.
Свойства скалярного произведения
Для любых векторов и любого числа справедливы следующие свойства:
1.
a→2≥0
, к тому же
a→2>0
, если
a→≠0→
.
2. Переместительный, или коммутативный, закон скалярного произведения:
a→⋅b→=b→⋅a→
.
3. Распределительный, или дистрибутивный, закон скалярного произведения:
a→+b→⋅c→=a→⋅c→+b→⋅c→
.
4. Сочетательный, или ассоциативный, закон скалярного произведения:
k⋅a→⋅b→=k⋅a→⋅b→
.
Использование скалярного произведения
Удобно использовать скалярное произведение векторов для определения углов между прямыми и между прямой и плоскостью.
Угол между прямыми
Ознакомимся с ещё одним определением.
Вектор называют направляющим вектором прямой, если он находится на прямой или параллелен этой прямой.

Чтобы определить косинус угла между прямыми, надо определить косинус угла между направляющими векторами этих прямых, то есть найти векторы, параллельные прямым, и определить косинус угла между векторами.
Для этого необходимо рассмотреть определение скалярного произведения, если векторы даны в координатной системе.
Если
a→x1;y1;z1
,
b→x2;y2;z2
, то
a→⋅b→=x1⋅x2+y1⋅y2+z1⋅z2
.
Прежде была рассмотрена формула определения длины вектора в координатной форме.
Теперь, объединив эти формулы, получим формулу для определения косинуса угла между векторами в координатной форме. Так как из формулы скалярного произведения следует, что
cosα=a→⋅b→a→⋅b→
, то
.
Угол между прямой и плоскостью
Введём понятие о нормальном векторе плоскости.
Нормальный вектор плоскости — это любой ненулевой вектор, лежащий на прямой, перпендикулярной к данной плоскости.

Используя следующий рисунок, легко доказать, что косинус угла
β
между нормальным вектором
n→
данной плоскости и неким вектором
b→
равен синусу угла
α
между прямой и плоскостью, так как
α
и
β
вместе образуют угол в
90°
.

При нахождении косинуса угла между
n→
и
b→
можно использовать это число как синус угла между прямой, на которой лежит вектор
b→
, и плоскостью.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно – 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = – 9 3 · 6 = – 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( – 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = – 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , – 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 2 2 + 0 2 + ( – 1 ) 2 · 1 2 + 2 2 + 3 2 = – 1 70 ⇒ a → , b → ^ = a r c cos ( – 1 70 ) = – a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( – 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 = – 1 cos a → , b → ^ = a → , b → ^ a → · b → = – 1 5 · 14 = – 1 70 ⇒ a → , b → ^ = – a r c cos 1 70
Ответ: a → , b → ^ = – a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , – 1 ) , B ( 3 , 2 ) , C ( 7 , – 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 – 2 , – 2 – ( – 1 ) ) = ( 5 , – 1 ) B C → = ( 7 – 3 , – 2 – 2 ) = ( 4 , – 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( – 1 ) · ( – 4 ) 5 2 + ( – 1 ) 2 · 4 2 + ( – 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 – 2 · O A · O B · cos ( ∠ A O B ) ,
b → – a → 2 = a → + b → – 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Угол между векторами
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На этом занятии мы поговорим об угле между векторами. Для начала дадим определение упомянутому понятию и используем его при обозначении скалярного произведения векторов. После рассмотрим примеры построения ненулевых векторов и вычисления угла между ними. Научимся находить скалярное произведение векторов.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
Скалярное произведение векторов

О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Угол между векторами
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Также векторы могут образовывать тупой угол. Это выглядит так:
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
→a * →b = →|a| * →|b| * cosα
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα
Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
Сначала докажем равенства
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.
Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB – →OA = →b – →a = (bx – ax, by – ay)
Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем
Записывайтесь на наши курсы по математике для учеников с 1 по 11 классы!
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:
a * b = ax * bx + ay * by
Формула скалярного произведения векторов для пространственных задач
В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:
a * b = ax * bx + ay * by + az * bz
Формула скалярного произведения n-мерных векторов
В n-мерном пространстве скалярное произведение векторов a = и b = можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + . + an * bn
Свойства скалярного произведения
Свойства скалярного произведения векторов:
Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.
→0 * →0 = 0
Скалярное произведение вектора самого на себя равно квадрату его модуля:
→a * →a = →∣∣a∣∣2
Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
→a * →b = →b * →a
Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
(→a + →b) * →c = →a * →c + →b * →c
Сочетательный закон для скалярного произведения:
(k * →a) * →b = k * (→a * →b)
Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
a ≠ 0, b ≠ 0, a * b = 0 a ┴ b
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)
По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.
Аналогично доказываются остальные свойства скалярного произведения.
Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.
Ответ: (→a,→b) = 21/2 = 10,5.
Пример 2.
Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.
Используем формулу →a * →b = →|a| * →|b| * cosα.
В данном случае:
→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3
Пример 3.
Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.
По свойству дистрибутивности скалярного произведения имеем
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
Итак, после применения свойств скалярного произведения имеем
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Пример 4.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.
Введем систему координат.
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
Пример 5.
а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
По условию чертеж выполнять не требуется, но для удобства можно сделать:
Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).
Вычислим скалярное произведение:
Вычислим длины векторов:
Найдем косинус угла:
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/geometry/9-klass/skalyarnoe-proizvedenie-vektorov/ugol-mezhdu-vektorami
http://skysmart.ru/articles/mathematic/skalyarnoe-proizvedenie-vektorov
[/spoiler]
образуют угол
зная, что
перпендикулярны; вектор
углы, равные
справедливость тождества
выяснить его геометрический смысл.
место знак равенства?
из векторов
от нуля, установить, при каком их взаимном
расположении справедливо равенство
вектторы
условию
условию
каждый из которых равен 600. Зная, что
модуль вектора
при каком значении
перпендикулярны.
должны удовлетворять векторы
вектор
вектор
вектор
перпендикулярен к вектору
совпадающие со сторонами
треугольника АВС. Найти разложение вектора,
приложенного к вершине В этого треугольника и
совпадающего с его высотой BD по базису
угол
угол, образованный медианами, проведенными из
вершин острых углов равноберденного
прямоугольного треугольника.
геометрическое место концов переменного вектора
точке А и вектор
вектор и
геометрическое место концов переменного вектора
точке А и вектор
неколлинеарные векторы и
работу произведет сила f={3; -5; 2}, когда ее точка
приложения перемещается из начала в конец
вектора
B(2; -1; 5), C(0; 1; -5). Вычислить:
векторов
работу производит сила f={3; -2; -5}, когда ее точка
приложения, двигаясь прямолинейно, перемещается
из положения A(2; -3; 5} в положение B(3; -2; -1).
Вычислить, какую работу производит
равнодействующая этих сил, когда ее точка
приложения, двигаясь прямолинейно, перемещается
из положения M1(5; 3; -7) в
положение M2(4; -1; -4).
четырехугольника A(1; -2; 2), B(1; 4; 0), C(-4; 1; 1), D(-5; -5; 3).
Доказать, что его диагонали AC и BD взаимно
перпендикулярны.
каком значении
перпендикулярны.
угла, образованного векторами
2; -6}.
треугольника A(-1; -2; 4), B(-4; -2; 0), C(3; -2; 1). Определить
его внутренний угол при вершине В.
треугольника A(3; 2; -3), B(5; 1; -1), C(1; -2; 1). Определить
его внешний угол при вершине А.
внутренние углы треугольника с вершинами A(1; 2; 1),
B(3; -1; 7), C(7; 4; -2), убедиться, что этот треугольник
равнобедренный.
вектору
-7,5}, образует острый угол с осью Oz.
Зная, что
к векторам
образует с осью Oy тупой угол.
Найти его координаты, зная, что
перпендикулярен к оси Oz и удовлетворяет условиям
вектор
вектора
с координатными осями равные острые углы.
вектора
осями Ox, Oz углы
с осью Oy – острый угол
B(2; 5; -2). Найти проекцию вектора
ось, составляющую с координатными осями Ox, Oy углы
угол
вектора
1; 4}. Вычислить
вектором
направлениям, одно из которых задано вектором
составляющую силы
N(7; -9; 9). Вычислить проекцию вектора
B(3; 2; 5), C(1; -1; 2), D(3; 2; -4). Вычислить
Федеральное агентство по образованию
Государственное
образовательное учреждение
высшего
профессионального образования
ПЕРМСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Теория поля
Индивидуальные
задания
-
Пособие
разработано ассистентом Оглезневой
А. Н..Одобрено методической комиссией
кафедры «Высшая математика»©
2007, каф. «Высшая математика» ПГТУ
Пермь 2007
Образец решения варианта.
Пример 1: Найти производную скалярного
поля![]() в точке
в точке![]() по направлению
по направлению
-
вектора

-
нормали к поверхности
 :
: ,
,
образующей острый угол с положительным
направлением оси
-
перпендикулярному к поверхности уровня
функции
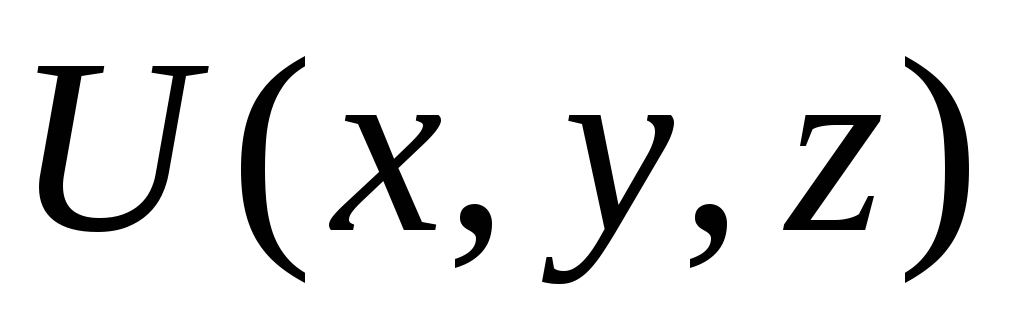 ,
,
проходящей через точку .
.
Решение:
Производную по направлению ищем по
формуле:
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
-
Найдем вектор
 ,
,
т.е. ,
,
Т.к.
![]() ,
,
тогда получаем![]() .
.
Таким образом
![]() .
.
-
Найдем вектор
 ,
,
т.е. ,
,
где ‑ вектор нормали к поверхности
‑ вектор нормали к поверхности .
.
![]()
Тогда
![]() ,
,

Получаем
![]() ,
,![]() ,
,![]() .
.
Заметим, что
![]() ,
,
то найденный вектор образует острый
угол с осью![]() ,
,
следовательно, требование задачи
выполнено.
Таким образом
![]() .
.
-
Найдем поверхность уровня функции
 ,
,
проходящей через точку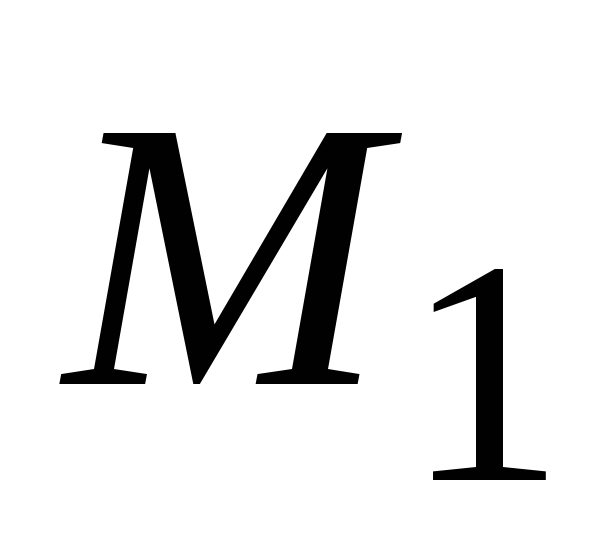 :
:
![]() .
.
Получаем поверхность
![]() :
:![]() .
.
Аналогично предыдущему пункту находим
вектор
![]() ,
,
где![]() ‑ вектор перпендикулярный поверхности
‑ вектор перпендикулярный поверхности
уровня![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
Таким образом
![]() .
.
Пример 2:Найти градиент скалярного
поля![]()
-

-
 .
.
Построить поверхности уровня для
заданных значений .
.
Решение
-
По определению градиента скалярного
поля
 .
.
Находим частные производные функции
![]() :
:
![]() ,
,![]() ,
,![]()
Таким образом
![]() .
.
-
Аналогично пункту а), получим:
![]() ,
,![]() ,
,![]()
Таким образом
![]() .
.
Построим поверхности уровня:
![]()
Тогда
![]() ,
,![]() ‑ конус с вершиной в начале координат.
‑ конус с вершиной в начале координат.

Если
![]() ,
,
то![]() :
:
![]()
![]()
![]()
![]()

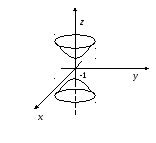
Однополостный Двуполостный
гиперболоид вращения гиперболоид
вращения
вокруг оси
![]() вокруг оси
вокруг оси![]()
Пример 3:Найти векторные линии
векторного поля![]() :
:
Решение:
-
Согласно определению, векторных линий:
![]() ,
,
или![]() .
.
Решая систему, получаем
![]() .
.
Таким образом, векторные линии данного
поля представляют собой окружности с
центрами на оси![]() ,
,
лежащие в плоскостях, перпендикулярных
этой оси.
-
Аналогично предыдущему пункту, составляем
систему
![]() .
.
Решим ее методом составления интегрируемых
комбинаций:
Равенство
![]() образует первую интегрируемую комбинацию.
образует первую интегрируемую комбинацию.
Получаем![]() .
.
Для получения еще одной интегрируемой
комбинации используем свойство пропорции:![]() .
.
Тогда, в нашем случае
![]() .
.
Интегрируя данное равенство, получаем![]() .
.
Таким образом, векторные линии задаются
системой:

Т.е. векторные линии данного поля являются
линиями пересечения гиперболических
цилиндров
![]() с плоскостями
с плоскостями![]() .
.
Пример 4.Вычислить поток векторного
поля![]() через внешнюю сторону боковой поверхности
через внешнюю сторону боковой поверхности
цилиндра![]() ,
,
ограниченного плоскостями![]()
![]() .
.
Решение:
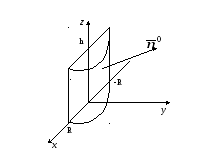
Вычислим поток векторного поля по
формуле:
![]() ,
,
где![]() ‑ нормальный единичный вектор к
‑ нормальный единичный вектор к
поверхности![]() .
.
Найдем вектор![]() .
.
Запишем уравнение поверхности![]() в неявном виде:
в неявном виде:![]() .
.
Тогда
![]() .
.
Т.к.![]() (по условию задачи), то
(по условию задачи), то![]() образует острый угол с осью
образует острый угол с осью![]() :
:
![]()
Следовательно,
![]() .
.
Поток векторного поля
![]() .
.
Спроектируем поверхность![]() :
:![]() на плоскость
на плоскость![]() ,
,
получим область![]() ,
,
ограниченную линиями:![]() .
.
![]() =
=![]()
Таким образом,
 (применяя
(применяя
подстановку![]() ,
,
получаем) =![]() .
.
Пример 5.Вычислить поток векторного
поля
![]()
через внешнюю сторону части поверхности
![]() ,
,
расположенной над плоскостью![]() .
.
Решение:

Замкнем данную поверхность куском
плоскости
![]() ,
,
который ограничен окружностью![]() .
.
Тогда можем применить формулу
Гаусса-Остроградского.
Пусть
![]() ‑
‑
объем полученного тела, ограниченного
замкнутой кусочно-гладкой поверхностью![]() ,
,
состоящей из части![]() параболоида вращения
параболоида вращения![]() и части
и части![]() плоскости
плоскости![]() .
.
Поток данного векторного поля через
поверхность
![]() по теореме Гаусса-Остроградского равен:
по теореме Гаусса-Остроградского равен:
![]()
![]() ,
,
где![]() .
.
![]() .
.
Следовательно, поток
![]() .
.
В силу аддитивности потока будем иметь
![]()
Отсюда искомый поток
![]()
Найдем
![]() .
.
Так как на плоскости![]() ,
,
имеем
![]() ,
,![]() и тогда
и тогда![]()
Таким образом, поток
![]() через круг
через круг![]() будет равен площади круга
будет равен площади круга![]() :
:![]() .
.
Искомый поток ![]() .
.
Пример 6.Вычислить работу векторного
поля![]() вдоль линии
вдоль линии![]() ,
,
являющейся пересечением параболического
цилиндра![]() с плоскостью
с плоскостью![]() от точки
от точки![]() до точки
до точки![]() .
.
Решение:
Зададим линию
![]() параметрически: положив
параметрически: положив![]() ,
,
получим![]() ,
,
а![]() .
.
Тогда![]() ,
,![]() ,
,![]() .
.
Точке![]() соответствует значение параметра
соответствует значение параметра![]() ,
,
а точке![]() ‑
‑
значение![]() .
.
Таким образом:
![]()
![]()
![]() .
.
Пример 7. Вычислить циркуляцию
векторного поля
![]()
вдоль периметра треугольника с вершинами
![]() .
.
Решение:
По определению циркуляции
![]() ,
,
получаем
![]() .
.
На отрезке
![]() ,
,
следовательно
![]() .
.
На отрезке
![]() ,
,
следовательно
![]() .
.
На отрезке
![]() ,
,
следовательно
![]() .
.
Следовательно,
![]()
Пример 8. Найти циркуляцию вектора![]() по контуру
по контуру непосредственно и по формуле Стокса.
непосредственно и по формуле Стокса.
Решение:

Iспособ.
Контур
![]() – окружность радиуса
– окружность радиуса![]() ,
,
лежащая в плоскости![]() .
.
Выберем ориентацию как показано на
рисунке, т.е. против часовой стрелки.
Параметрические уравнения окружности
имеют вид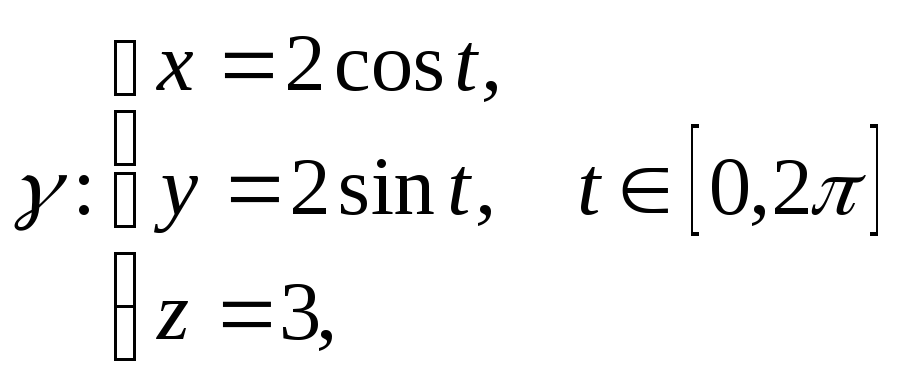 ,
,
так что![]()
![]()

IIспособ.
Для вычисления циркуляции по теореме
Стокса выберем какую-нибудь поверхность
![]() ,
,
натянутую на контур![]() .
.
Естественно в качестве![]() взять круг, имеющий контур
взять круг, имеющий контур![]() своей границей. Уравнение поверхности
своей границей. Уравнение поверхности![]() имеет вид:
имеет вид: .
.
Согласно выбранной ориентации контура
нормаль к поверхности необходимо взять
равной![]() .
.
Далее
 .
.
В силу теоремы Стокса
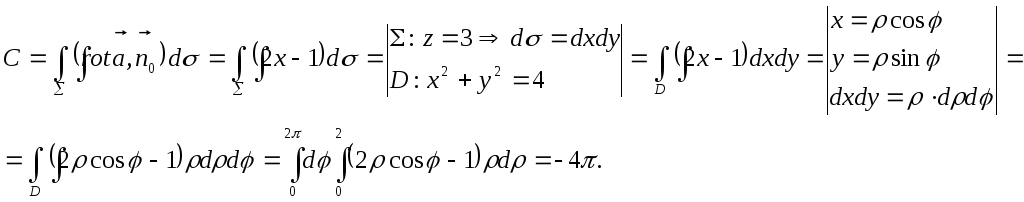
Пример 9. Доказать, что векторное
поле![]() является потенциальным. Найти его
является потенциальным. Найти его
потенциал.
Решение:
Необходимым и достаточным условием
потенциальности поля является равенство
нулю вихря поля. В нашем случае
 .
.
Таким образом, поле является потенциальным.
Обозначим
![]() – искомый потенциал. По определению
– искомый потенциал. По определению
потенциального поля, поле градиента
искомой функции![]() должно совпадать с векторным полем
должно совпадать с векторным полем![]() .
.
Поэтому
![]() .
.
Отсюда![]() ,
,
где![]() – некоторая функция аргументов
– некоторая функция аргументов![]() и
и![]() .
.
Из условия![]() ,
,
можно сделать вывод, что![]() .
.
Таким образом,![]() .
.
Неопределенную функцию![]() найдем из условия
найдем из условия![]() .
.
Решением последнего уравнения является
функция![]() .
.
В итоге потенциал имеет вид
![]() .
.
Пример 10. Пусть![]() – произвольные векторные поля. Показать,
– произвольные векторные поля. Показать,
что (символом
(символом![]() обозначено скалярное произведение
обозначено скалярное произведение
векторов).
Решение:
Пусть
![]() и
и![]() – произвольные векторные поля. Найдем
– произвольные векторные поля. Найдем
векторное произведение![]() .
.
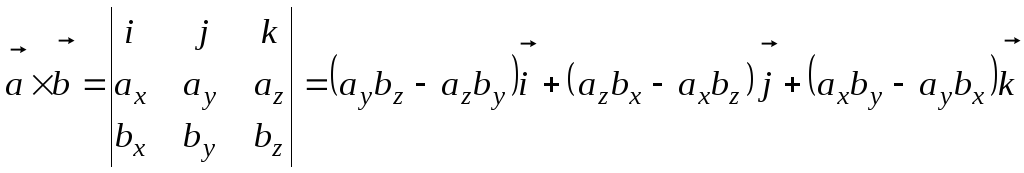 .
.

Соседние файлы в папке Индивидуальные_задания
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Опр. 1.5.6. Направляющими
косинусами вектора а назовём косинусы тех углов ![]() , которые этот вектор образует с
, которые этот вектор образует с
базисными векторами, соответственно, i, j, k.
Направляющие косинусы вектора а =
(х, у, z) находятся по формулам:
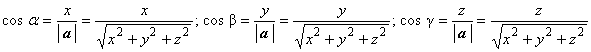 . Сумма
. Сумма
квадратов направляющих косинусов равна единице:
![]() .
.
 Направляющие косинусы вектора a являются координатами его орта:
Направляющие косинусы вектора a являются координатами его орта: ![]() .
.
1.5.4. Декартова прямоугольная система
координат.
Пусть базисные орты i, j, k отложены из общей точки О. Будем считать,
что орты задают положительные направления осей Ох, Оу, Oz. Совокупность точки О (начала координат)
и ортонормированного базиса i, j, k называется
декартовой прямоугольной системой координат в пространстве. Пусть А
– произвольная точка пространства. Вектор а = ОА = xi + yj + zk называется радиусом-вектором
точки А, координаты этого вектора (x,
y, z) называются
также координатами точки А ( обозначение: А(x,
y, z)). Оси
координат Ох, Оу, Oz называют
также, соответственно, осью абсцисс, осью ординат, осью аппликат.
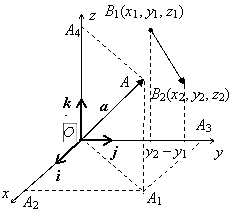
Если вектор ![]() задан координатами своей начальной
задан координатами своей начальной
точки В1(x1, y1, z1)
и конечной точки В2(x2,
y2, z2),
то координаты вектора ![]() равны разности координат
равны разности координат
конца и начала: ![]() (так как
(так как ![]() ).
).
Декартовы прямоугольные
системы координат на плоскости и на прямой определяются совершенно
аналогично с соответствующими количественными (в соответствии с размерностью)
изменениями.
Решение типовых
задач.
Пример 1. Найти длину и
направляющие косинусы вектора а = 6i
– 2j -3k.
Решение. Длину вектора: ![]() . Направляющие косинусы:
. Направляющие косинусы: ![]() .
.
Пример 2. Найти координаты
вектора а, образующего с координатными осями равные острые углы,
если длина этого вектора равна ![]() .
.
Решение. Так как ![]() , то подставляя
, то подставляя ![]() в формулу (1.6), получим
в формулу (1.6), получим ![]() . Вектор а образует с
. Вектор а образует с
координатными осями острые углы, поэтому орт ![]() .
.
Следовательно, находим координаты вектора ![]() .
.
Пример 3. Заданы три
некомпланарных вектора e1 = 2i – k,
e2 = 3i + 3j, e3 = 2i + 3k. Разложить
вектор d = i + 5j – 2k по базису e1,
e2, e3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
