Как найти вектор отклонений

Отклонение точки от прямой

В данной статье мы рассмотрим понятие отклонения точки от прямой на плоскости. Приведем примеры нахождения отклонения точки от прямой.

Отклонение точки от прямой на плоскости − это расстояние от точки до прямой, взятой со знаком “+”, если эта точка и начало координат лежат по разные стороны прямой, и со знаком “−”, если точка и начало координат лежат по одну сторону от прямой.

Если прямая проходит через начало координат, то отклонение точки от прямой предполагается равным расстоянию от точки до прямой, взятой со знаком “+”, если точка лежит по ту сторону от прямой, куда направлен пормальный вектор прямой, и равным расстоянию от точки до прямой, взятой со знаком “−”, в противном случае.

Обозначим отклонение точки от прямой символом δ, а расстояние от точки до прямой символом d. На рисунке Рис.1 отклонение точки M₁ от прямой L равно δ=+d₁, так как точка M₁ и начало координат O лежат по разные стороны прямой L, а отклонение точки M₂ от прямой L равно δ=−d₂, так как точка M₂ и начало координат O лежат по одну сторону от прямой L.

На рисунке Рис.2 прямая L проходит через начало координат. Поэтому, отклонение точки M₁ от прямой L равно δ=+d₁, так как точка M₁ лежит по ту сторону прямой L, куда направлен нормальный вектор n прямой L, а отклонение точки M₂ от прямой L равно δ=−d₂, так как точка M₂ лежит по противоположную сторону прямой, куда направлен нормальный вектор n прямой L

где r− расстояние начала координат до прямой L, а φ− угол между нормальным вектором прямой L и осью Ox.

Покажем, что левая часть нормального уравнения прямой дает отклонение точки M(x,y) от прямой, заданной уравнением (1). Для этого докажем следующую теорему:

Теорема 1. Пусть прямая L определяется нормальным уравнением прямой (1). Тогда отклонением точки M с координатами x, y от прямой L равно δ=xcosφ+ysinφ−r.

Доказательство. Проведем через нормальный вектор прямой L линию OQ (Рис.3). Проекция точки М на прямую OQ будет точка S. Отклонение δ точки M от прямой L будет равно SR.

,

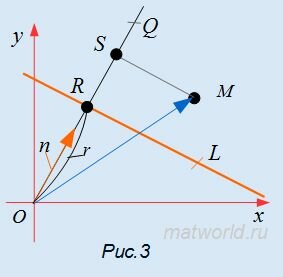
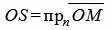(3)

где n− единичный нормальный вектор прямой L, α−угол между векторами n и .

Из (3) и (4) следует:

.

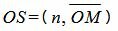(5)

С другой стороны

,

(6)

так как нормальный вектор прямой имеет координаты n=<cosφ, sinφ>, а точка M − M(x, y).

Сопоставляя (2), (5) и (6), получим:

Таким образом, как следует из теоремы 1, для вычисления отклонения некоторой точки M₀(x₀, y₀) от прямой, нужно в левую часть нормированного уравнения прямой (1) подставить координаты точки M₀:

Заметим, расстояние от точки M₀ до прямой L будет равно модулю отклонения данной точки от прямой.

Пример 1. Задано нормальное уравнение прямой:

.

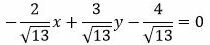(7)

Найти отклонение точки M(5,-3) от прямой (7).

Решение. Подставим координаты точки M(5,−3) в левую часть уравнения (7):

Ответ. Отклонение точки M(5,−3) от прямой (7) равно:

.

Пример 2. Задано общее уравнение прямой:

Найти отклонение точки M(1,1) от прямой (8).

Решение. Один из простых методов решения − это приведение общего уравнения прямой к нормальному виду (подробнее об этом читайте в статье “нормальное уравнение прямой”). Для приведения уравнения (8) к нормальному виду, нужно умножить данное уравнение на нормирующий множитель:

.

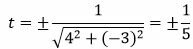Так как в уравнении (8) третий коэффициент равен +1, то знак нормирующего множителя должен быть противоположным:

.

Умножив уравнение (8) на нормирующий множитель, получим:

.

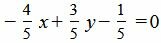Теперь найдем отклонение точки M(1,1) от прямой (8). Для этого вставим координаты точки M в левую часть уравнения(8):

.

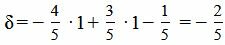Ответ. Отклонение точки M(1,1) от прямой (8) равно:

Стандартное отклонение

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

• среднеквадратическое отклонение,
• среднее квадратическое отклонение,
• среднеквадратичное отклонение,
• квадратичное отклонение,
• стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

• в финансах в качестве меры волатильности,
• в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

• А -> (19 + 21 + 19+ 21) / 4 = 20
• Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

• в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
• в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

• стандартное отклонение компании A = 1,
• стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ (“n” и “n–1”)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с “n–1”),
• полностью все данные – используется формула σ (с “n”).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 – μ = 15 – 20 = -5

x2 – μ = 26 – 20 = 6

x3 – μ = 15 – 20 = -5

x4 – μ = 24 – 20 = 4

3. Каждую полученную разницу возвести в квадрат:

4. Сделать сумму полученных значений:

Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi – μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:

1. Вычесть среднее значение из каждого числа
2. Возвести каждый результат в квадрат (так получатся квадраты разностей)
3. Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

• одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
• двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
• трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле “=СТАНДОТКЛОНА(“

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

• при 20 % — выборка сильно вариабельна.

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

[spoiler title=”источники:”]

http://www.uznaychtotakoe.ru/standartnoe-otklonenie/

[/spoiler]

Deviation typically means $X-E(X)$, where $E(X)$ is the expected value/mean.

Notice that in the first column you have values $-1$, $-1$ and $2$. Their average is $0$, so after subtracting the average you get $vec x=(-1,-1,2)$.

In the second column you have the values $1$, $2$ and $3$. The average of these values is $2$ after subtracting the average you get the values $1-2=-1$, $2-2=0$ and $3-2=1$. Your teacher written them into a single vector $vec y=(-1,0,1)$.

The formula $$r=frac{vec xcdotvec y}{|vec x||vec y|}$$
is then the formula for correlation coefficient. It is just written a bit differently. You can find this formula also in the Wikipedia article I linked above – in the section geometric interpretation. The example given there is very similar to this one. (Basically the only difference is that the Wikipedia article discusses uncentered and centered correlation coefficient.)

• 

sd(x)

#create dataset
data <- c(1, 3, 4, 6, 11, 14, 17, 20, 22, 23)

#find standard deviation
sd(data)

[1] 8.279157

#create dataset with missing values
data <- c(1, 3, 4, 6, NA, 14, NA, 20, 22, 23)

#attempt to find standard deviation
sd(data)

[1] NA

#find standard deviation and specify to ignore missing values
sd(data, na. rm = TRUE )

[1] 9.179753

#create data frame
data <- data.frame(a=c(1, 3, 4, 6, 8, 9),
 b=c(7, 8, 8, 7, 13, 16),
 c=c(11, 13, 13, 18, 19, 22),
 d=c(12, 16, 18, 22, 29, 38))

#find standard deviation of column a
sd(data$a)

[1] 3.060501

#create data frame
data <- data.frame(a=c(1, 3, 4, 6, 8, 9),
 b=c(7, 8, 8, 7, 13, 16),
 c=c(11, 13, 13, 18, 19, 22),
 d=c(12, 16, 18, 22, 29, 38))

#find standard deviation of specific columns in data frame
apply(data[ , c('a', 'c', 'd')], 2, sd)

 a c d 
3.060501 4.289522 9.544632 

Пункты	X1	X2	X3	X4	X5	X6	X7	X8	X9
d (Xi)	Б	Б	Б	Б	Б	Б	Б	Б	Б

Радиус, диаметр, центр, периферийные вершины.

В графе центра не существует, т.к.
компоненты вектора отклоненностей
являются бесконечными числами. Не
существует также и радиусом, т.к. радиусом
называется отклоненность его центра,
а последнего, для данного графа нет.

Периферийными вершинами для данного
графа являются все они, так как каждая
обладает максимальной отклоненностью.
Если считать данный граф неориентированным,
то его диаметр равен очевидно бесконечности.

Число внутренней и внешней устойчивости

Множество внутренней и внешней
устойчивости получается, если взять по
одному элементу из каждого класса
эквивалентности. В нашем случае число
классов эквивалентности равно 3, поэтому
и число внутренней устойчивости равно
3.

Для нашего случая множество внутренней
устойчивости совпадает с множеством
внешней устойчивости и таким образом
число внешней устойчивости также равно
3.

3) Для двух произвольно выбранных графов найти декартово произведение и декартову сумму.

Пусть
первым графом G₁
будут три точки находящиеся на расстоянии
3 единицы от начала координат, а графом
G₂ будут две точки
находящиеся на расстоянии 2 единицы от
начала координат.

Тогда G₁(X₀₁)={X₁₁,
X₂₁}, G₁(X₁₁)={X₀₁,
X₂₁}, G₁(X₂₁)={X₀₁,
X₁₁} и G₂(X₀₂)=X₁₂,
G₂(X₁₂)=X₀₂.

G(X₀₁,
X₀₂)={(X₁₁,
X₁₂),
(X₂₁,
X₁₂)}=G₁(X₀₁)
x G₂(X₀₂)

G(X₀₁,
X₁₂)={(X₁₁,
X₀₂),
(X₂₁,
X₀₂)}=G₁(X₀₁)
x G₂(X₁₂)

G(X₁₁,
X₀₂)={(X₀₁,
X₁₂),
(X₂₁,
X₁₂)}=G₁(X₁₁)
x G₂(X₀₂)

G(X₁₁,
X₁₂)={(X₀₁,
X₀₂),
(X₂₁,
X₀₂)}=G₁(X₁₁)
x G₂(X₁₂)

G(X₂₁,
X₀₂)={(X₀₁,
X₁₂),
(X₁₁,
X₁₂)}=G₁(X₂₁)
x G₂(X₀₂)

G(X₂₁,
X₁₂)={(X₀₁,
X₀₂),
(X₁₁,
X₀₂)}=G₁(X₂₁)
x G₂(X₁₂)

Декартово произведение графов G₁
x G₂.

Число вершин декартовой суммы графов
G₁ + G₂
также, как и для декартового произведения
равно 6. В соответствии с определением
декартовой суммы графов имеем:

G(X₀₁,
X₀₂)=[G₁(X₀₁)
x {X₀₂}]
U [{X₀₁}
x G₂(X₀₂)]=[{X₁₁,
X₂₁} x
{X₀₂}] U
[{X₀₁} x
{X₀₂}]={(X₁₁,
X₀₂), (X₂₁,
X₀₂)}U{(X₀₁,
X₁₂)}

G(X₀₁,
X₀₂)=[G₁(X₀₁)
x {X₀₂}]
U [{X₀₁}
x G₂(X₀₂)]={(X₁₁,
X₀₂), (X₂₁,
X₀₂)}U{(X₀₁,
X₁₂)}

G(X₁₁,
X₀₂)=[G₁(X₁₁)
x {X₀₂}]
U [{X₁₁}
x G₂(X₀₂)]={(X₀₁,
X₀₂), (X₂₁,
X₀₂)}U{(X₁₁,
X₁₂)}

G(X₁₁,
X₁₂)=[G₁(X₁₁)
x {X₁₂}]
U [{X₁₁}
x G₂(X₁₂)]={(X₀₁,
X₁₂), (X₂₁,
X₁₂)}U{(X₁₁,
X₀₂)}

G(X₂₁,
X₀₂)=[G₁(X₂₁)
x {X₀₂}]
U [{X₂₁}
x G₂(X₀₂)]={(X₀₁,
X₀₂), (X₁₁,
X₀₂)}U{(X₂₁,
X₁₂)}

G(X₂₁,
X₀₂)=[G₁(X₂₁)
x {X₁₂}]
U [{X₂₁}
x G₂(X₁₂)]={(X₀₁,
X₁₂), (X₁₁,
X₁₂)}U{(X₂₁,
X₀₂)}

Декартова сумма графов G₁
+ G₂.

Соседние файлы в папке Контрольная работа 2

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

К настоящему моменту мы определились с тем, какие точки исключать из торговой статистики и исследовать на нерациональность. Дальнейшее исследование проходит по следующей схеме.

– исследуемая торговая статистика, которая рационализируема с показателем нерациональности _.

Пусть – множество точек торговой статистики, которые не являются выбросами, т.е. не находятся в множестве _, – торговая статистика, суженная до множества , рационализируемая с показателем нерациональности – точка, которая является временным выбросом, а – вектор цен в данной точке.

Строится множество прогнозов на векторы спроса для торговой статистики . Множество состоит из векторов , таких, что – _{рационализируема с показателем нерациональности для .}

После построения множества ищется проекция вектора на множество . Удобнее всего решать данную задачу следующим образом.

_{Рассматривается оптимизационная задача:}

Решение данной задачи легко находится методами квадратичного программирования. После нахождения вектора вычисляется вектор разности _.

_{При дальнейшем анализе возникают определенные сложности, которые связаны в} первую очередь с нормировкой вектора .

4.7 Нормировка вектора отклонений и выявление выбросов

Номенклатура товаров имеет неоднородную структуру. Какие-то товары имеют небольшие объемы продаж и высокие цены, какие-то имеют большие денежные потоки, какие-то меньшие. Отклонение на 1000 акций по одному товару может составлять 1% от торгов, по другому 10%. Возникает задача выбора оптимальной нормировки вектора разности для дальнейшего анализа.

Автором сравнивались следующие варианты нормировки:

1. Отсутствие нормировки

2. Нормировка компонент вектора на средние объёмы, , где

3. Нормировка компонент вектора на текущие объёмы, .

4. Нормировка компонент вектора на компоненты вектора проекции, .

_{5. Вычисление вектора отклонений по денежным объёмам, .}

_{6. Вычисление вектора отклонений по денежным объёмам и его нормировка на средние денежные объёмы, , где .}

_{Таблица 1:} Различные варианты нормировок вектора и .

В таблице 1 приведены графики компонент векторов и в зависимости от _{нормировки.}

_{Автором был выбран вектор отклонения по бюджетам в качестве основного и отклонения на данном векторе и рассматривались как акции, где велись нерациональные торги. Данный выбор обусловлен тем соображением, что при активности спекулянтов мерой воздействия на рынок должна служить именно денежная сумма, которая участвовала в нерациональной торговле. Нормировка на объёмы не даёт полноты картины, т.к. даже большое отклонение в объёмах может быть незаметно для рынка, если цена на данные акции невелика.}