Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Сложное движение точки. Пример решения задачи
Теория, применяемая для решения приведенной ниже задачи, излагается на странице “Сложное движение точки, теорема Кориолиса”.
Условие задачи
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6 t 2 – 3 t 3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO 1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40( t – 2 t 3 ) – 40 ( s – в сантиметрах, t – в секундах). Расстояние b = 20 см . На рисунке точка M показана в положении, при котором s = AM > 0 (при s 0 точка M находится по другую сторону от точки A ).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t 1 = 1 с .
Указания. Эта задача – на сложное движение точки. Для ее решения необходимо воспользоваться теоремами о сложении скоростей и о сложении ускорений (теорема Кориолиса). Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка M на пластине в момент времени t 1 = 1 с , и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунке к задаче).
Решение задачи
Дано: b = 20 см , φ = 6 t 2 – 3 t 3 , s = |AM| = 40( t – 2 t 3 ) – 40 , t 1 = 1 c .
Определение положения точки
Определяем положение точки в момент времени t = t 1 = 1 c .
s = 40( t 1 – 2 t 1 3 ) – 40 = 40(1 – 2·1 3 ) – 40 = –80 см.
Поскольку s 0 , то точка M ближе к точке B, чем к D.
|AM| = |–80| = 80 см.
Делаем рисунок.
Определение абсолютной скорости точки
Согласно теореме о сложении скоростей, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Определение относительной скорости точки
Определяем относительную скорость . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD . Дифференцируя s по времени t , находим проекцию скорости на направление BD :
.
В момент времени t = t 1 = 1 с ,
см/с.
Поскольку , то вектор направлен в направлении, противоположном BD . То есть от точки M к точке B . Модуль относительной скорости
vот = 200 см/с .
Изображаем вектор на рисунке.
Определение переносной скорости точки
Определяем переносную скорость . Для этого считаем, что точка M жестко связана с пластиной, а пластина совершает заданное движение. То есть пластина вращается вокруг оси OO1. Дифференцируя φ по времени t , находим угловую скорость вращения пластины:
.
В момент времени t = t 1 = 1 с ,
.
Поскольку 0″ style=”width:48px;height:18px;vertical-align:-10px;background-position:-583px -267px”> , то вектор угловой скорости направлен в сторону положительного угла поворота φ , то есть от точки O к точке O1. Модуль угловой скорости:
ω = 3 с -1 .
Изображаем вектор угловой скорости пластины на рисунке.
Из точки M опустим перпендикуляр HM на ось OO1.
При переносном движении точка M движется по окружности радиуса |HM| с центром в точке H .
|HM| = |HK| + |KM| = 3 b + |AM| sin 30° = 60 + 80·0,5 = 100 см ;
Переносная скорость:
vпер = ω|HM| = 3·100 = 300 см/с .
Вектор направлен по касательной к окружности в сторону вращения.
Определение абсолютной скорости точки
Определяем абсолютную скорость . Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Проводим оси неподвижной системы координат Oxyz . Ось z направим вдоль оси вращения пластины. Пусть в рассматриваемый момент времени ось x перпендикулярна пластине, ось y лежит в плоскости пластины. Тогда вектор относительной скорости лежит в плоскости yz . Вектор переносной скорости направлен противоположно оси x . Поскольку вектор перпендикулярен вектору , то по теореме Пифагора, модуль абсолютной скорости:
.
Определение абсолютного ускорения точки
Согласно теореме о сложении ускорений (теорема Кориолиса), абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова ускорений:
,
где
– кориолисово ускорение.
Определение относительного ускорения
Определяем относительное ускорение . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD . Дважды дифференцируя s по времени t , находим проекцию ускорения на направление BD :
.
В момент времени t = t 1 = 1 с ,
см/с 2 .
Поскольку , то вектор направлен в направлении, противоположном BD . То есть от точки M к точке B . Модуль относительного ускорения
aот = 480 см/с 2 .
Изображаем вектор на рисунке.
Определение переносного ускорения
Определяем переносное ускорение . При переносном движении точка M жестко связана с пластиной, то есть движется по окружности радиуса |HM| с центром в точке H . Разложим переносное ускорение на касательное к окружности и нормальное ускорения:
.
Дважды дифференцируя φ по времени t , находим проекцию углового ускорения пластины на ось OO 1 :
.
В момент времени t = t 1 = 1 с ,
с –2 .
Поскольку , то вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ , то есть от точки O1 к точке O. Модуль углового ускорения:
ε = 6 с -2 .
Изображаем вектор углового ускорения пластины на рисунке.
Переносное касательное ускорение:
a τ пер = ε |HM| = 6·100 = 600 см/с 2 .
Вектор направлен по касательной к окружности. Поскольку вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ , то направлен в сторону, противоположную положительному направлению поворота φ . То есть направлен в сторону оси x .
Переносное нормальное ускорение:
a n пер = ω 2 |HM| = 3 2 ·100 = 900 см/с 2 .
Вектор направлен к центру окружности. То есть в сторону, противоположную оси y .
Определение кориолисова ускорения
Кориолисово (поворотное) ускорение:
.
Вектор угловой скорости направлен вдоль оси z . Вектор относительной скорости направлен вдоль прямой |DB| . Угол между этими векторами равен 150° . По свойству векторного произведения,
.
Направление вектора определяется по правилу буравчика. Если ручку буравчика повернуть из положения в положение , то винт буравчика переместится в направлении, противоположном оси x .
Определение абсолютного ускорения
Абсолютное ускорение:
.
Спроектируем это векторное уравнение на оси xyz системы координат.
;
;
.
Модуль абсолютного ускорения:
.
Абсолютная скорость ;
абсолютное ускорение .
Автор: Олег Одинцов . Опубликовано: 10-01-2016
Основные понятия кинематики. Скорость. Средняя скорость. Относительная скорость. Сложение перемещений и скоростей
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Этот урок посвящён разделу физики, который называется кинематика. Мы узнаем, что изучает кинематика, основные понятия этого раздела. Также на этом уроке будут подробно показаны решения трёх типовых задач различной сложности, которые взяты из сборника задач для подготовки к единому государственному экзамену. Задачи на нахождение средней и относительной скорости.
[spoiler title=”источники:”]
http://1cov-edu.ru/mehanika/kinematika/slozhnoe-dvizhenie-tochki-reshenie-zadachi/
http://interneturok.ru/lesson/physics/11-klass/podgotovka-k-ege/osnovnye-ponyatiya-kinematiki-skorost-srednyaya-skorost-otnositelnaya-skorost-slozhenie-peremescheniy-i-skorostey
[/spoiler]
Чтобы получить точное представление о движении двух объектов относительно друг друга относительная скорость является важным. Поэтому в этой статье мы подробно поговорим об относительной скорости между двумя объектами.
Относительная скорость — это, по сути, скорость одного объекта по отношению к другому. Рассмотрим следующие два объекта, А и В, которые движутся с разными скоростями. Скорость объекта А по отношению к объекту В или наоборот называется относительной скоростью. Он также известен как скорость изменения относительного положения одного объекта по отношению к другому с течением времени.
Как найти относительную скорость двух тел?
🠊 Техника определения скорости объекта требует определения скорости изменения положения объекта по отношению к неподвижному окружающему объекту.
Когда объекты A и B находятся в относительном движении, их соответствующие скорости также будут в относительном движении. Чтобы получить относительную скорость объекта A по отношению к B, нужно математически придать равную и противоположную скорость B как объекту A, так и объекту B, чтобы привести объект B в состояние покоя.
В результате равнодействующая обеих скоростей (скорости объекта А и Б) дает нам относительную скорость объекта А относительно объекта Б.
Уравнения относительной скорости следующие:
Скорость объекта А относительно объекта В можно рассчитать следующим образом:
Vab V =a – Vb
Скорость объекта B относительно объекта A можно рассчитать следующим образом:
Vba V =b – Va
Из двух выражений мы можем вывести следующее:
Vab = – Vba
Однако обе величины равны математически и могут быть представлены как:
|Vab |= |Вba|
Какова относительная скорость между двумя телами, когда они движутся с одинаковой скоростью в одном направлении?
🠊 Когда два тела А и В движутся в одном направлении с одинаковой скоростью, угол между ними равен 0°.
Предположим, что два транспортных средства A и B движутся в одном направлении, т. е. параллельно друг другу, с одинаковой скоростью или скоростью (поскольку они движутся в одном направлении), т. е. Va V =b.
В результате скорость автомобиля А относительно автомобиля В равна:
Vab V =a – Vb = 0
Аналогичным образом, скорость транспортного средства B относительная к транспортному средству А:
Vba V =b – Va = 0
Это означает, что если два объекта двигаться в одном направлении с одинаковой скоростью или скорость, их относительная скорость становится равной нулю. Это демонстрирует, что другой может казаться покоящимся для одного объекта.
Построение графика положение-время для двух объектов, движущихся в одном направлении с одинаковой скоростью, приводит к прямым параллельным линиям, как показано на графике ниже.
Какова относительная скорость между двумя телами, когда они движутся с разными скоростями в одном направлении?
🠊 Если два транспортных средства, A и B, движутся в одном направлении с разными скоростями, в первую очередь следует рассмотреть два сценария:
(1) Начальные точки одинаковы (Va > Vb):
Если два транспортных средства движутся с разными скоростями в одном направлении с одной и той же начальной точкой и Va > Vb, человек в транспортном средстве B воспринимает транспортное средство A как удаляющееся от него со скоростью:
Vab V =a – Vb
Транспортное средство B движется назад к пассажиру в транспортном средстве A со скоростью:
Vba V =b – Va = -( Вa – Vb) = -Vab
В результате обе скорости имеют одинаковую величину, но противоположные знаки.
(2) Различные отправные точки:
Мы можем думать о двух сценариях здесь:
(i) Предположим, что транспортное средство A имеет более высокую скорость, чем транспортное средство B, т. е. Va > Vb, и следует за автомобилем B.
В этой ситуации транспортное средство A в конечном итоге догонит транспортное средство B, как показано на их графике положение-время.
Vab V =a – Vb ≠ 0
(ii) Рассмотрим ситуацию, когда Va > Vb и автомобиль А движется впереди автомобиля В.
В этом случае транспортное средство B никогда не сможет обогнать транспортное средство A.. Графики положения и времени обоих транспортных средств не будут пересекаться по мере их удаления друг от друга.
Vab V =a – Vb ≠ 0
Какова будет относительная скорость двух тел, когда они движутся в противоположных направлениях?
🠊 Угол, образованный двумя телами, движущимися в противоположных направлениях по прямой, называется 180°.
Рассмотрим два автомобиля А и В, движущихся в противоположных направлениях по прямой.
В результате скорость автомобиля А относительно автомобиля В равна:
Vab V =a -(- Вb) = Вa +Vb
Скорость транспортного средства B по отношению к A аналогична:
Vba V =b-(- Вa) = Вa +Vb
В результате можем написать:
Vab V =ba
Это указывает на то, что если два объекта движутся в противоположных направлениях по прямой линии, кажется, что каждый объект движется очень быстро по сравнению с другим.
Какова относительная скорость, когда два тела движутся под углом?
🠊 Рассмотрим пример относительной скорости, который возникает, когда два объекта, A и B, движутся под углом со скоростями Va и Vb.
&
Диагональ даст нам относительную скорость, если мы построим параллелограмм, как показано на рисунке. В результате величина диагонального вектора параллелограмма или относительная скорость с использованием закона косинусов составляет:
Но Cos(180°-𝛳) = -Cos𝛳
Когда два объекта движутся под углом, приведенное выше уравнение дает нам их относительную скорость. Мы также можем вывести случай того же направления и случай противоположного направления из этого уравнения, изменив значение угла на 0° и 180° соответственно.
Однако, как показано на изображении, если вектор относительной скорости Vab образует угол ꞵ со скоростью объекта A, то
Но Sin(180°-𝛳) = Sin𝛳
Или,
Важность относительной скорости:
Важность относительной скорости резюмируется ниже:
- Рассчитать скорость звезд и астероидов относительно Земли.
- Для измерения расстояния между любыми двумя объектами в пространстве.
- Чтобы запустить ракету.
- Для определения скорости любого объекта.
- Это помогает нам, когда объект движется через жидкость.
Проблемы, связанные с относительной скоростью:
1. Автомобиль, едущий по шоссе со скоростью 110 км/ч, проезжает мимо автобуса, идущего со скоростью 85 км/ч. Какова скорость автомобиля с точки зрения пассажира автобуса?
Данный:
Скорость автомобиля Vc = 110 км/ч
Скорость автобуса Vb = 85 км/ч
Найти:
Относительная скорость автомобиля относительно автобуса Vcb знак равно
Решение:
Поскольку автомобиль и автобус едут в одном направлении, относительная скорость автомобиля с точки зрения пассажира автобуса равна:
Vcb V =c – Vb = (110 -85)км/ч = 25 км/ч
Таким образом, скорость автомобиля с точки зрения пассажира автобуса составляет 25 км/ч.
2. Две машины, находящиеся на некотором расстоянии друг от друга, начинают двигаться навстречу друг другу со скоростями 150 м/с и 200 м/с по прямой дороге. С какой скоростью они приближаются друг к другу?
Данный:
Скорость автомобиля 1 В1 = 150 м / с
Скорость автомобиля 2 В2 = 200 м / с
Найти:
Относительная скорость вагона 1 относительно вагона 2 V12 знак равно
Относительная скорость вагона 2 относительно вагона 1 V21 знак равно
Решение:
Так как оба автомобиля едут в противоположном направлении, относительная скорость:
V12 V =1 + V2 = (150 + 200) м/с = 350 м/с
Кроме того,
V21 V =1 + V2 = (150 + 200) м/с = 350 м/с
В результате два автомобиля движутся навстречу друг другу с относительной скоростью 350 м/с.
Резюме:
- Скорость одного объекта по отношению к другому объекту просто называется относительной скоростью этих двух объектов.
- Рассмотрим два объекта, которые движутся в одном направлении. В этой ситуации величина относительной скорости одного объекта по отношению к другому будет равна разнице в величине их скоростей.
- Если два объекта движутся в одном направлении и с одинаковыми скоростями, их относительная скорость будет ноль.
- Предположим, что любые два объекта движутся в противоположном направлении. В этом случае величина относительной скорости одного объекта по отношению к другому окажется суммой величины их скоростей.
Содержание:
- Сложное движение точки
- Абсолютный, относительный и переносной движения точки
- Теорема о сложении скоростей в сложном движении точки
- Теорема о сложении ускоренного в сложном движении точки (Теорема Кориолиса *)
- Кориолисово ускорения
- Правило Жуковского
- Примеры решения задач на сложное движение точки
- Сложное движение точки и решение задач
- Порядок решения задач на сложное движение точки
- Примеры решения задач
- Задание темы К4 (сложное движение точки)
- Пример решения задания темы К4
- Сложное движение точки образцы и примеры
- Относительное, переносное и абсолютное движение точки
- Относительные, переносные и абсолютные скорости и ускорение
- Сложение скоростей и ускорений при сложном движении точки
- Примеры решения задач
- Абсолютное, относительное и переносное движение точки
- Центральная операция кинематики и динамики. Абсолютная и относительная производные по времени от вектора функции
- Теорема о сложении скоростей
- Теорема о сложении ускорений
- Вращательное и осевое ускорение в случае вращения тела вокруг неподвижной оси
- Ускорение Кориолиса
- Случаи превращения в ноль ускорения Кориолиса
- Физические причины возникновения ускорения Кориолиса
- Сложное движение материальной точки. Относительное, переносное и абсолютное движение материальной точки
- Теорема о сложении скоростей в сложном движении материальной точки
- Теорема Кориолиса
- Модуль, направление и физические причины возникновения ускорения Кориолиса
- Методика решения задач на сложное движение материальной точки
Сложное движение точки – это такое движение, при котором точка (тело) одновременно участвует в двух или нескольких движениях. Примером сложного движения могут служить: движение пассажира. перемещающегося в вагоне движущегося поезда; движение человека, перемещающегося по лестнице движущегося эскалатора.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Сложное движение точки
Сложное движение точки – это такое движение, при котором точка участвует одновременно в двух или нескольких движениях. Примеры сложного движения точки (тела): лодка, переплывающая реку; человек, идущий по движущемуся эскалатору; камень подвижной кулисы, поршень качающегося цилиндра; шары центробежного регулятора Уатта. Для описания сложного движения точки или для представления движения в виде сложного используются неподвижная система отсчета, связанная с каким-либо условно неподвижным телом, например, с Землей, и подвижная система отсчета, связанная с каким-либо движущимся телом.
Абсолютный, относительный и переносной движения точки
В разделе 2 изучалось движение точки по отношению к системе координат (системы отсчета), которую считали условно неподвижной. В то же время, рассматривая многие задачи механики, целесообразнее, а в некоторых случаях просто необходимо, проводить исследования движения точки одновременно по отношению в двух (или более) систем отсчета, из которых одна считается неподвижной, а другая (другие) движется определенным образом по отношению к ней.
Движение точки по отношению к нескольким системам отсчета называется сложным.
Например, в сложном движении находятся поршень двигателя движущегося автомобиля; груз, который поднимается краном, одновременно перемещается вдоль направляющих и поворачивается вокруг своей вертикальной оси; движение человека по вагону подвижного состава.
В этом разделе будем рассматривать движение точки относительно двух систем отсчета.
Рассмотрим движущееся тело А, которое в отдельных случаях будем называть переносной средой, в отношении которого движется точка М, которая не принадлежит телу (рис. 7.1). С телом А неизменно свяжем систему координат 

Система координат 

Поскольку точка М движется относительно двух систем отсчета, то ее движение, по определению, будет сложным. Введем основные понятия и обозначения в случае сложного движения точки.
Движение точки М по отношению к неподвижной системе отсчета называется абсолютным движением. Уравнения абсолютного движения точки можно записать в виде:
Траектория, скорость и ускорение точки в абсолютном движении называются абсолютной траекторией, скоростью и ускорением точки. Абсолютные скорость и ускорение будем обозначать 
Движение точки М относительно подвижной системы отсчета 
относительным движением точки, а траектория, скорость и ускорение – относительной траекторией, скоростью и ускорением. Относительные скорость и ускорение обозначают 

Движение подвижной системы отсчета (а значит и тела А) относительно неподвижной
является для точки М переносным движением. Скорость и ускорение той точки тела А, с которой в данный момент времени совпадает движущаяся точка М, называется соответственно переносной скоростью и переносным ускорением точки в этот момент. Переносная скорость и ускорение обозначаются 

В приведенном выше примере о человеке, что перемещается в вагоне подвижного состава, с вагоном можно связать подвижную систему координат, а с поверхностью Земли – неподвижную. Тогда движение вагона будет переносным, движение человека относительно вагона – относительным, а движение человека относительно поверхности
Земли – абсолютным. Переносной скоростью и переносным ускорением человека будет скорость и ускорение той точки вагона, в которой в заданный момент находится человек.
Основная задача кинематики сложного движения точки заключается в том, чтобы, зная кинематические характеристики относительного и переносного движений, найти соответствующие им характеристики абсолютного движения.
Теорема о сложении скоростей в сложном движении точки
Теорема. В сложном движении точки ее абсолютная скорость равна векторной сумме относительной и переносной скоростей.
Доказательство. Для доказательства рассмотрим движение точки М (рис. 7.1) относительно подвижной системы отсчета 




точку 
Положение точки М в подвижной системе координат 






Если координаты точки М в подвижной системе отсчета обозначить через 

и тогда
Абсолютная скорость точки М равна производной по времени от радиусавектора

Изменение направлений ортов 


После подстановки (7,7) в (7.6) и преобразований с учетом зависимости (7.7), получим
где

Зависимость (7.8) определяет вектор абсолютной скорости точки М. Проведем ее анализ.
Поскольку в последних трех слагаемых зависимости (7.8) являются производные по времени от соответствующих уравнений относительного движения точки М (7.2), то согласно с (2.18) они являются проекциями вектора относительной скорости точки на оси
подвижной системы координат

Покажем, что первые две слагаемых зависимости (7.8) определяют вектор переносной скорости точки М. Действительно, переносная скорость точки, по определению, это скорость точки, неизменно связанной с подвижной системой отсчета, с которой в данный момент времени совпадает движущаяся точка М. Такой точкой в нашем случае является точка М тела А, находящегося в свободном движении. А по формуле (6.3) скорость этой точки равна сумме скорости полюса 
оси 
Учитывая (7.9) и (7.10), зависимость (7.8) перепишем в виде
то есть абсолютная скорость точки равна векторной сумме переносной и относительной скоростей. Теорема доказана.
Следует заметить, что в случае, когда переносным движением является движение свободного твердого тела, то переносная скорость сама определяется диагональю
параллелограмма, построенного на векторах скорости полюса

В случае вращательного переносного движения 

Исходя из того, что в общем случае абсолютная скорость точки М определяется диагональю параллелограмма, построенного на векторах 

Замечания. Если точка М находится в n движениях, то абсолютная скорость точки М равна векторной сумме векторов скоростей составляющих движений
Теорема о сложении ускоренного в сложном движении точки (Теорема Кориолиса *)
Теорема. В сложном движении точки ее абсолютное ускорение равно векторной сумме переносного, относительного и кориолисового ускоренний.
Доказательство. Вектор абсолютного ускорения точки М равна
и для его определения продифференцируем зависимость (7.6) по времени.
После возведения соответствующих членов, получим
Учитывая формулы (7.7),
Превратим зависимость (7.14), используя зависимости (7.5), (7.7), (7.9) и (7.15). Получим формулу, выражающую вектор абсолютного ускорения точки М
где 
Проведем анализ зависимости (7.16).
Учитывая, что переносным движением в нашем случае является движение свободного твердого тела, то соответственно формуле (6.10) первые три слагаемых формулы (7.16) является вектором переносного ускорения точки
Поскольку в выражении
Итак, мы установили механический смысл первых шести слагаемых зависимостях (7.16). Но, как видим, в формулу для вектора абсолютного ускорения точки М входит еще одно слагаемое.
Выражение
называется вектором кориолисового или поворотного ускорения точки М.
Подставляя формулы (7.17), (7.18) и (7.19) в (7.16), получим
Теорема доказана.
В случае поступательного переносного движения
И одинаковое для всех точек переносного среды. Кроме этого, кориолисово ускорения в этом
случае также равна нулю
Замечания. Относительные скорость и ускорение определяются в относительной системе отсчета по правилам кинематики точки: по координатного способа – через проекции на оси декартовой системы координат, как вторые производные от уравнений относительного движения точки (7.2) при натуральном способа – через проекции на оси натурального трехгранника относительной траектории.
Переносная скорость и ускорение определяются методами кинематики твердого тела. Если система 
разделах 5 и 6. Методы определения кориолисового ускорения рассмотрены ниже.
Кориолисово ускорения
Кориолисовым ускорением называется составляющая абсолютного ускорения точки в ее сложном движении, равна удвоенному векторном произведения вектора переносной угловой скорости на вектор относительной скорости этой точки.
В начале выясним физические причины появления кориолисового ускорения. Как известно, вектор ускорения характеризует изменение вектора скорости как по величине, так и по направлению. Так, переносное ускорение характеризует изменение переносной скорости, а относительное -относительной скорости в соответствующих движениях точки М. Какие же изменения и которых кинематических характеристик движения точки, при ее сложном движении, характеризует кориолисово ускорения? Для ответа на этот вопрос рассмотрим движение точки М, равномерно перемещается вдоль радиуса платформы, которая равномерно вращается вокруг оси, перпендикулярной к плоскости платформы (рис. 7.2).
В этом случае переносным движением будет вращения платформы с
относительным движением – прямолинейное движение точки вдоль радиуса
с
Пусть в момент времени 
переносной и относительной скоростей 




момент времени
Поскольку относительное движение равномерное прямолинейный, то относительное ускорение 



скорости 

скорости состоялась за счет переносного движения.
Учитывая, что переносное движение – равномерное вращение





Итак, появление кориолисового ускорения обусловлена взаимным влиянием переносного и относительных движений.
Ускорение Кориолиса характеризует изменение направления относительной скорости, обусловленной переносным движением, и величины переносной скорости за счет относительного движения.
Модуль кориолисового ускорения, исходя из (7.19), равна
Рассмотрим случаи отсутствия кориолисового ускорения точки.
Из формулы (7.22) следует, что 
1) 
2) 

3)


Направление вектора кориолисового ускорения определяется согласно правилу векторного произведения двух векторов 
Правило Жуковского
Чтобы найти направление кориолисового ускорения, необходимо спроектировать вектор относительной скорости 


Наличием кориолисового ускорения объясняются различные явления, которые происходят на поверхности Земли вследствие ее вращения. так замечено, что для рек, текущих в
северном полушарии, даже на прямолинейных участках, подмываются больше правы, чем левые берега; при аналогичных условиях на железнодорожных дорогах происходит интенсивнее износ правых рельсов колеи по сравнению с левыми. Все эти явления объясняются появлением кориолисова силы инерции, направленной в сторону, противоположную кориолисового ускорению, о чем пойдет речь в части «Динамика».
Примеры решения задач на сложное движение точки
Задача 1. Тележка А мостового крана, перемещает груз С в горизонтальной плоскости, движется по закону 






Решение. Рассмотрим движение груза С, как материальной точки, находится в сложном движении. выберем неподвижную 




точки С по кругу).
Для определения абсолютной скорости груза используем зависимость (7.11)
Чтобы определить переносную скорость, условно остановим относительное движение груза.
Тогда движение системы тележка-груз на подвесе рассматриваем как поступательное движение одного тела, происходит по закону
Переносная скорость определится
Если 

Чтобы найти относительную скорость груза, условно остановим переносное движение и тогда относительную скорость подсчитаем как скорость точки С при вращении вокруг точки 
где 
При
Знак минус показывает, что вращение в данный момент времени происходит против положительного направления отсчета угла φ, то есть по часовой стрелки.
Итак,
Вектор 

Модуль абсолютной скорости груза С определим по зависимости (7.12)
где α – угол между векторами
При
Тогда
Для определения абсолютного ускорения груза С используем зависимость (7.20)
Определим составляющие абсолютного ускорения груза. Методика определение переносного и относительного ускоренного аналогична определения переносной и относительной скоростей. переносное ускорение
Знаки 


Относительное ускорение точки, при ее движении по кругу, равна
Касательное ускорение
где 
При
Поскольку знаки 

совпадает по направлению с
Тогда
Вектор 
Нормальное ускорение точки в относительном движении определится зависимостью
и при
Вектор 

В этой задаче переносное движение является поступательным, так кориолисово ускорения равна нулю 
Проекции абсолютного ускорения груза будут такими
Тогда модуль абсолютного ускорения груза С будет равняться
Задача 2. Прямоугольный треугольник АВС вращается вокруг своего катета АС ривносповильнено с угловым ускорением 



Решение. Поскольку точка М одновременно находится в двух движениях, то
ее движение рассматриваем как сложный.
Выберем неподвижную 

Подвижная система связана с треугольником, вращающийся (на рис. 7.7 показана только ось 
Абсолютная скорость точки М определится согласно (7.11)
Переносную скорость точки М определим как скорость той точки гипотенузы АВ треугольника, вращающийся с которой в данный момент времени совпадает подвижная точка М. Определим положение точки М на гипотенузе АВ при
Переносная скорость равна
где DM – короткая расстояние от точки М до оси вращения АС; 
Тогда
Поскольку траектории переносного движения точки М в данный момент времени
является окружность радиуса DM, то вектор 
круга в сторону вращения. Если плоскость треугольника АВС при


и при
Вектор
Поскольку угол между векторами 


скорости будет равняться
В случае непоступального переносного движения абсолютное ускорение точки М в сложном движении по формуле (7.20) будет равняться
Переносное движение является вращательным, так переносное ускорение точки М в соответствии с (3.15) определится по формуле
Вектор 




При прямолинейном относительном движении относительно ускорения точки М имеет только касательную составляющую, равную
векторы


Модуль кориолисового ускорения определится по зависимости (7.23)
Согласно принятому направлением вращения вектор 





Вектор 
Для нахождения модуля абсолютного ускорения точки М воспользуемся методом проекций. Для этого введем вспомогательную систему координат 
тогда:
Модуль абсолютного ускорения точки М
Сложное движение точки и решение задач
Краткие сведения по теории:
Характер движения существенно зависит от того, в какой системе отсчета (подвижной или неподвижной) рассматривается это движение.
Движение точки относительно неподвижной системы отсчета называется абсолютным.
Движение точки по отношению к подвижной системе отсчета называется относительным.
Движение, которое имеет подвижная система отсчета со всеми неизменно связанными с ней точками пространства по отношению к условно неподвижной системы отсчета,
называется переносным.
Каждое из этих движений характеризуется своими скоростями и ускорениями.
В соответствии с законами сложения скоростей:
и ускорений:
где 



Величина Корриолисового ускорения определяется по формуле:
где 


Вектор Корриолисового ускорения 




Поскольку в случае плоского движения тела угол между векторами 


При плоском движении направление 


В случае, если переносное движение является поступательным
Если переносные и относительные движения являются криволинейными, переносными и относительными ускорениями можно изобразить в виде геометрических сумм соответствующих нормальных и касательных ускорений:
Порядок решения задач на сложное движение точки
При решении задач на сложное движение точки рекомендуется придерживаться такой последовательности:
1. Разложить движение точки на составляющие, определить абсолютное, относительное и переносное движения.
2. Выбрать две системы координат: абсолютную (неподвижную) и относительную (подвижную).
3. Мысленно остановить переносное движение, определить скорость и ускорение точки в относительном движении.
4. Мысленно остановить относительное движение, определить угловую скорость переносного движения, скорость и ускорение точки в переносном движении.
5. По известным угловым скоростям переносного движения и скоростью точки в относительном движении найти величину и направление кориолисового ускорения точки.
6. Используя метод проекций, определить проекции абсолютного ускорения и абсолютной скорости на оси неподвижной системы координат.
7. По определенным проекциям, найти модули и направления абсолютной скорости и абсолютного ускорения.
Примеры решения задач
Задача 1
Диск вращается вокруг оси, перпендикулярной к его плоскости, против хода часовой стрелки с угловой скоростью 
Определить модуль и направление корриолисового ускорения точки M в изображенном на рис. 1 положении, если относительная скорость
Решение. Точка M движется в плоскости диска которая перпендикулярна к оси вращения, то есть угол между векторами 

Учитывая 
Поскольку вектор относительной скорости находится в плоскости перпендикулярной к оси вращения, то для определения направления ускорения Кориолиса согласно правилу
Жуковского надо повернуть вектор 


Задача 2
Определить модуль и направление корриолисового ускорения точки M, которая движется по производной ВN кругового конуса от вершины В к точке N. Конус вращается вокруг своей оси с угловой скоростью 

Решение. Отложим вектор угловой скорости 

векторами 

Модуль ускорения Кориолиса точки M равен:
Чтобы найти направление ускорения Кориолиса (рис.1), спроектируем вектор относительной скорости 
Проекция относительной скорости 
Повернув проекцию 


Задача 3
По хорде АВ диска, что вращается от точки А до точки В (рис.1) движется точка М, согласно уравнению 
Определить абсолютные скорости и ускорение точки М в момент времени, когда она находится на расстоянии 
Решение. В данной задачи переносным движением будет вращение диска по закону

Запишем уравнение для определения абсолютной скорости точки М:
Для определения относительной скорости остановим переносное вращение диска и будем рассматривать движение точки по отношению к неподвижному диску.
Поскольку закон относительного движения 
Вектор 
Переносной скоростью 
Из условия задачи следует, что точка М в данный момент времени находится посередине хорды АВ на расстоянии 
Переносная скорость вращающегося движения определяется по формуле:
где 
Угловую скорость переносного вращательного движения найдем как первую производную от угла поворота 

Таким образом, переносная скорость вращательного движения равна:
Вектор переносной скорости направлен перпендикулярно радиусу OM в сторону вращения диска.
Поскольку векторы 

Тогда:
В зависимости от абсолютных значений скоростей 



Определить абсолютное ускорение точки M. Поскольку переносное движение является вращательным, то абсолютное ускорение точки равно:
Модуль относительного ускорения определим как производную от относительной скорости по времени:
Направленный вектор 
Переносное ускорение 

Вычислим модули нормального 

где 
Переносное нормальное ускорение направлено вдоль радиуса к центру вращения O (рис.2).
Поскольку движение точки M происходит в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется из формулы:
Для определения направления ускорения Кориолиса (рис.2) необходимо вектор относительной скорости 

переносного вращательного движения, то есть против хода часовой стрелки.
Для определения величины и направления абсолютного ускорения 


Найдена векторная сумма 

Таким образом, абсолютное ускорение точки M равняется сумме векторов:
Поскольку вектор 




Модуль абсолютного ускорения равняется:
Ответ:
Задание темы К4 (сложное движение точки)
Вдоль стороны AB (см. задачу К3 и рис. К4.1) движется ползун 2, шарнирно
соединённый со стержнем EK, который движется в неподвижных направляющих параллельно оси 
Определить путем построения планов скоростей и ускорений по известным из задачи К3 кинематическим характеристикам движения фигуры АВС абсолютные скорости и
ускорение точек Е и К.
Пример решения задания темы К4
Изобразим на стороне AB тела 1 (рис.К4.2, а) ползун 2, который соединен шарниром Е со стержнем 3. Ползун 2 может двигаться поступательно по стороне AB, а стержень
3 – поступательно в вертикальных направляющих. Положение шарнира Е на стороне AB определяем по заданному коэффициенту пропорциональности
1. Анализ движения стержня ЕК
Рассмотрим точку 
Очевидно, скорость и ускорение точки 

Тогда движение точки 



Одновременно ползун 2 движется вместе с фигурой ABC . Это движение для точки
является переносным. Переносные скорость и ускорение 


2. Определение переносной, абсолютной и относительной скорости точки Е2
Приняв точку A тела 1, осуществляющую плоское движение, за полюс (рис. К4.2, б), определим скорость точки 
ABС тела 1 и abc плана скоростей, в соответствии с какой:
Из этой пропорции определим отрезок
Отрезок откладываем на стороне ab фигуры abc плана скоростей (рис.К4.2, б) в направлении от точки “a” до точки “b”. Величине переносной скорости ползуна 2 на
плане будет соответствовать отрезок
Запишем уравнение для абсолютной скорости точки 
В этом уравнении нам известны:
- величина и направление переносной скорости
(из плана скоростей);
- направление относительной скорости
(вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно;
- направление абсолютной скорости
(вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
Для решения уравнения (2) воспользуемся планом скоростей (рис.К4.2, б). Поскольку согласно уравнению до вектора 

проведем прямую 



в масштабе 

3. Определение переносного и абсолютного ускорения точки Е2
Определить переносное ускорение точки 
Из условия сходства фигур ABС тела 1 и abc плана ускорений (рис.К4.2,в) следует, что точка 


ускорений 
Тогда отрезок 
в масштабе плана ускорений
Запишем векторное уравнение для абсолютного ускорения для точки 
Определим сначала величину и направление Кориолисового ускорения.
Поскольку движение происходит в плоскости 




Угловая переносная скорость 
Величину относительной скорости 

изображает 
Тогда:
Направление Кориолисового ускорения определим по правилу Жуковского Н.Е., для этого вектор относительной скорости 



Таким образом, в уравнении (3) нам известны:
- величина и направление переносного ускорения
- величина и направление Корриолисового ускорения
- направление относительного ускорения
(вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно;
- направление абсолютного ускорения
(вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
Все это позволяет нам построить многоугольник ускорений в соответствии с уравнением (3) на плане ускорений, или отдельным чертежом. Учитывая, что величины отрезков, которые будут изображать некоторые ускорения, слишком большие и выходят за пределы чертежа, для нахождения абсолютного ускорения точки 
Сначала из произвольной точки 



До этого вектора в направлении Кориолисового ускорения (рис. К4.2, г) добавим вектор 

Через конец вектора 





будет изображать абсолютное ускорение точек К и
Замерив отрезок 
Примечание. Поскольку все построения расчетные графических работ по кинематике К1, К3 и К4 рекомендуется выполнять на бумаге форматом А3, то после выполнения данной курсовой работы ее графическая часть будет иметь вид подобный изображенному на с. 188.
Сложное движение точки образцы и примеры
Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
Относительное, переносное и абсолютное движение точки
При исследовании движения точки выбирают некоторую систему отсчета (темы 1 и 2), относительно которой рассматривают движение точки.
В некоторых случаях приходится рассматривать движение точки относительно двух различных систем отсчета. Например, движение пассажира в поезде можно рассматривать как по отношению к поезду, так и по отношению к Земле.
При этом движение одной и той же точки относительно двух различных систем отсчета будет разным. Например, точка обода колеса движущегося железнодорожного вагона относительно Земли пишет циклоиду, а относительно вагона – окружение.
При рассмотрении движения точки по отношению к двум системам отсчета и система, которая в данной задаче условно принята за неподвижную, называется основной системой отсчета (неподвижной), а система, которая движется относительно основной, называется подвижной системой отсчета.
Движение точки относительно основной системы отсчета называется абсолютным движением, а ее движение относительно подвижной системы отсчета – относительным движением.
Пусть есть две системы координат 


Выберем систему координат 






Надо заметить, что переносным движением является движение не самой точки 


Основная задача этого раздела состоит в том, чтобы по известным относительным и переносным движениям определить абсолютное движение точки (движение точки 

Выбор основной и подвижной систем отсчета, а соответственно, и разделение движения точки на абсолютное и относительное зависит от постановки конкретной задачи. В большинстве случаев за основную систему отсчета принимают систему, которую связано с Землей.
Относительные, переносные и абсолютные скорости и ускорение
Относительной скоростью 
Абсолютной скоростью 
Переносной скоростью 
Аналогично введем понятие относительного, абсолютного и переносного ускорения точки.
Относительным ускорением 
Абсолютным ускорением 
Переносным ускорением 
Обратим внимание на то, что переносное движение – это движение всей подвижной системы отсчета, то есть некоторого тела, с которым связана подвижная система координат, а переносная скорость и переносное ускорение – это скорость и ускорение конкретной точки этого тела.
Сложение скоростей и ускорений при сложном движении точки
Зависимость между абсолютной, переносной и относительной скоростями точки определяется теоремой сложения скоростей, согласно которой абсолютная скорость точки равна векторной сумме переносной и относительной скоростей:

где 


Для определения относительной скорости точки достаточно мысленно остановить переносное движение и найти по правилам кинематики скорость точки относительно системы отсчета, которая была подвижной.
Для определения переносной скорости – достаточно мысленно остановить относительное движение и найти переносную скорость как скорость той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
Зависимость между абсолютным, относительным и переносным ускорением точки при поступательном движении подвижной системы отсчета выражается векторным уравнением:

где 


Если переносным движением является вращательный, или сложный, то теорема о сложении ускорений приобретает вид:

где 
3.4. Ускорение Кориолиса

Модуль ускорения Кориолиса равен:
где 


Ускорение Кориолиса характеризует:
- изменение модуля и направления переносной скорости точки вследствие ее относительного движения;
- изменение направления относительной скорости точки вследствие вращательного переносного движения.
Ускорение Кориолиса равно нулю в трех случаях:
Направление ускорения Кориолиса определяется как направление вектора векторного произведения 

Пусть точка 













Для определения направления ускорения Кориолиса удобно пользоваться правилом Жуковского: чтобы найти направление ускорения Кориолиса надо спроектировать относительную скорость точки 

Действительно, полученное направление 




Если вектор 








Такой случай возможен, если относительное движение точки происходит в плоскости перпендикулярной оси переносного вращения. В этом случае векторы 


Рассмотрим два примера определения модуля и направления ускорения Кориолиса .
Пример 1. Диск вращается вокруг оси, которая перпендикулярна его плоскости, против хода часовой стрелки с угловой скоростью 



Определить модуль и направление ускорения Кориолиса точки 

Точка 





Поскольку вектор относительной скорости лежит в плоскости перпендикулярной оси вращения, то для определения направления ускорение Кориолиса согласно правилу Жуковского надо повернуть вектор 


Пример 2. Определить модуль и направление ускорение Кориолиса точки 






Отложим вектор угловой скорости 







Модуль ускорения Кориолиса точки 








Чтобы найти направление ускорения Кориолиса (рис.3.6), спроектируем вектор относительной скорости 

Проекция относительной скорости 


Если повернуть проекцию 



Примеры решения задач
Задача №1
Клин 



Найти абсолютную скорость стержня 
Решение. Учитывая, что стержень 
Рассмотрим движение точки 
Поскольку точка 



По отношению к клину точка 



Клин 




Абсолютную скорость точки 



Для решения векторного уравнения (1) построим параллелограмм на векторах 


Поскольку угол между векторами 

Ответ:
Задача № 2
Круг радиусом 




Найти абсолютное ускорение точки 
Решение. Движение точки 



Абсолютное ускорение точки 


Поскольку переносное движение вращательное, то переносное ускорение точки круга с которой совпадает точка 


Учитывая, что при равномерном вращении угловое ускорение 
Величина переносного нормального ускорения 
где 
Направлено это ускорение вдоль радиуса от точки 

Учитывая то, что точка 



где 

Направлено это ускорение от точки 

Поскольку точка 


Учитывая, что 

Для определения направления ускорения Кориолиса повернем вектор относительной скорости 



Поскольку все ускорения направлены вдоль одной прямой, то их можно сложить алгебраически:



или с учетом выражений для 


Подставив зависимости для угловых скоростей 

Ответ:
Задача №3
По хорде 





Определить абсолютные скорости и ускорения точки 

Решение. В данной задаче переносным движением будет вращение диска по закону 


Запишем уравнение для определения абсолютной скорости точки 


Для определения относительной скорости остановим переносное вращение диска и будем рассматривать движение точки по отношению к неподвижному диску. Поскольку закон относительного движения 

Вектор относительной скорости направлен по хорде 


Переносной скоростью 


Из условия задачи вытекает, что точка 


Переносная скорость вращательного движения определяется по формулой:
где 
Угловую скорость переносного вращательного движения найдем как первую производную от угла поворота 
Таким образом, переносная скорость вращательного движения равна:
Вектор переносной скорости направлен перпендикулярно радиусу 
Поскольку векторы 

Тогда:


В зависимости от абсолютных значений скоростей 




Определим абсолютное ускорение точки 


Модуль относительного ускорения определим как производную от относительной скорости по времени:

Направлен вектор 



Переносное ускорение 




Вычислим модули нормального 

где 
Переносное нормальное ускорение направлено вдоль радиуса к центру вращения 
Поскольку движение точки 


Для определения направления ускорения Кориолиса (рис.3.10) необходимо вектор относительной скорости 


Для определения величины и направления абсолютного ускорения 




Таким образом, абсолютное ускорение точки 


Поскольку вектор от 




Модуль абсолютного ускорения будет равен:
Ответ:
Задача №4
В состав механизма Витворта (рис.3.11) входит: кривошип 1, ползун 2 и кулиса 3. Кривошип 
Определить скорость и ускорение точки 
когда:
Решение. Особенность этого механизма заключается в том, что в точке 
Пересечение

Кривошип 1 и ползун 2 между собой соединены цилиндрическим шарниром, что позволяет ползуну относительно кривошипа возвращаться, а на кулисе 3 параллельно ее оси сделаны направляющие, по которым ползун 2 может двигаться поступательно.
При повороте кривошипа 1 ползун 2 скользит по кулисе 3 и заставляет ее поворачиваться вокруг точки 


Такой механизм позволяет преобразовать вращательное движение кривошипа в колебательное движение кулисы, если 

Таким образом, в точке 



Перед решением задачи в произвольном масштабе построим схему механизма (рис.3.13,а) для заданного положения кривошипа.
Первой определим скорость точки 


Направлена скорость 

Скорость точки 

Для определения скорости точки 



Запишем уравнение для скоростей при сложном движении точки 

где 










Векторное уравнение (1) решим путем построения плана скоростей.
Поскольку направления скорости в правой и в левой части уравнения (1) известны, то из полюса плана скоростей сначала построим правую часть уравнения, а затем левую.
Согласно правой части уравнения (1) с полюса 










Теперь построим левую часть уравнения (1). Поскольку абсолютная скорость 





Вектор 



Поскольку на плане скоростей вектор 






Угол при вершине 




Таким образом треугольник 


Из плана скоростей определяем:


Учитывая, что кулиса 3 вращается вокруг точки 

где 

Поскольку ползун 2 относительно кулисы 3 движется поступательно, то 
Для определения направления угловой скорости 



Определим ускорение точек механизма.
Поскольку кривошип 1 вращается вокруг центра 


Направлено ускорение точки 

Ускорение точки 

Для ускорения точки 
где 










Поскольку относительное движение происходит в плоскости, перпендикулярной оси вращения ползуна 2, то ускорения Кориолиса определим из формулы:
где 



Для определения направления ускорения Кориолиса необходимо вектор относительной скорости 



С другой стороны, точка 


где 









Решим систему векторных уравнений (2, 3) графически, путем построения плана ускорений.
Первым построим векторное уравнение (2). Из произвольного полюса 





Длину отрезка 

От точки 



Длина вектора 
Через конец вектора 



Следующим построим векторное уравнение (3). С полюса 





Через конец вектора 



Решением системы (2, 3) будет точка пересечения линий 



Из плана ускорений определяем:
Угловое ускорение кулисы 3 и ползуна 2 определим через известное тангенциальное ускорение 
Для определения направления углового ускорения 



Ответ: 
Абсолютное, относительное и переносное движение точки
В кинематике точки, рассматривается движение точки относительно неподвижной системы координат (прямоугольной декартовой или относительно осей натурального трехгранника). Однако часто приходится исследовать движение точки в отношении двух и более систем координат (тел отсчета), из которых одна система координат осуществляет движение относительно другой, условно берется за неподвижную. Например, при изучении роботов-манипуляторов следует вводить несколько систем координат. Итак, предположим, что система координат 

Движение точки М относительно неподвижной системы координат называется абсолютным, а относительно подвижной системы координат – относительным. Скорости и ускорения точки, рассматриваемые в отношении данных систем, соответственно называются абсолютными и относительными.
Движение подвижной системы координат 

Основной задачей сложного движения точки является установление зависимости между кинематическими характеристиками абсолютного, переносного и относительного движений. Уравнениями абсолютного движения точки есть, например, зависимости координат точки М, заданных в неподвижной системе координат, как функции времени:

Аналогично для уравнения относительного движения:

Уравнения (9.1) и (9.2) определяют в параметрической форме в соответствии абсолютную и
относительную траектории. Если уравнение (9.1) и (9.2) известны, то проекции абсолютной и относительной скоростей определяются соответственно как первые производные по времени приведенных функций; тогда вторые производные по времени от этих функций
определяют проекции абсолютного и относительного ускорений. В дальнейшем введем такие обозначения: 

Пример 1. Пусть стержень ОА вращается вокруг неподвижной оси 
стержня движется гладкое кольцо, рассматриваемое как материальная точка М. Выясните характер относительного и переносного движений.
Решение. Выберем в точке О начало неподвижной системы координат 





Итак, сложное движение точки М (кольца) можно рассматривать как совокупность прямолинейного относительного (вдоль стержня ОА) и вращательного переносного вокруг неподвижной оси Oz вместе со стержнем. Установив характер абсолютного, относительного и переносного движений, можно решать, например, такие задачи:
а) по заданным относительным и переносным движениями определять сложное (абсолютное) движение точки;
б) по заданным сложным движениям точки определить составляющие простых движений.
Центральная операция кинематики и динамики. Абсолютная и относительная
производные по времени от вектора функции
Пусть 
за неподвижную, a 

Рассмотрим произвольную точку М, которая движется относительно как подвижной, так и неподвижной систем координат. Пусть положение этой точки в подвижной системе координат определяется радиусом-вектором 

Установим связь между производными от функции, вычисленными в подвижной и неподвижной системах координат. Для этого сначала найдем производную по времени от вектора 


Первые три члена этого выражения представляют собой производную от вектора 

Рассмотрим теперь последние три слагаемых в (9.4), которые обозначим через:

Умножив обе части (9.6) скалярно на 

Правые части этих выражений являются проекциями вектора 


Продифференцировав их по времени, получим:

Введем обозначения:

Тогда выражения (9.7) с учетом соотношений (9.8)-(9.10) можно записать в форме:

Если ввести на рассмотрение вектор:

то выражение (9.6) можно подать в виде:

Подставив (9.13) и (9.5) в выражение (9.4) получим формулу, которая устанавливает связь между производной не только вектора 


Отметим, что во второй формуле (9.14) указана система координат, в которой вычисляется соответствующая производная.
Здесь вектор to можно рассматривать как угловую скорость вращения подвижной системы координат Oxyz относительно неподвижной 
Бура. Она имеет следующее содержание: абсолютная производная произвольного вектора 




Поскольку формула (9.14) может быть распространена на любой вектор, то в дальнейшем будем широко пользоваться ею не только в кинематике, но и в динамике.
Рассмотрим теперь частные случаи.
1. Если система Oxyz неподвижная, то 


2. Если вектор 


3. Если вектор 


Отметим, что в формуле (9.14) не раскрыто пока физического смысла вектора
Полностью он будет установлен в кинематике в разделе “Движение свободного твердого тела”. Сейчас ограничимся рассмотрением некоторых случаев, которые частично отвечают на этот вопрос.
4. Рассмотрим движение подвижной системы координат, считая, что последняя неизменно связана с телом, которое вращается вокруг неподвижной оси, например 

являются скоростями точек, которые совпадают с концами векторов 



точек, которые совпадают с концами единичных векторов 


Сравнив эти выражения полученной ранее формуле Эйлера, делаем вывод, что вектор 
А именно – это вектор угловой скорости тела, которое вращается вокруг неподвижной оси.
Этот вывод легко обобщается на случай произвольной точки М, положение которой
в подвижной системе координат определяется радиусом-вектором 


что соответствует формуле (8.23)
5. Если скалярно умножить обе части выражения (9.18) соответственно на 

получим:

Левые части этих выражений являются соответственно проекциями вектора 









(рис. 9.3, б).
6. Рассмотрим подвижную систему координат и предположим, что она совершает вращательное движение как твердое тело вокруг неподвижной оси 

(Рис. 9.4). тогда:

где 
Отсюда получим соотношение, с которыми уже встречались в полярной системе
координат:

Умножив теперь скалярно обе части полученных выражений соответственно на j и
и, будем иметь:

Как видим, производная от угла поворота является ничем иным, как угловой скоростью вращения подвижной системы координат. Таким образом, для одной из компонентов в (9.10) также установлено физический смысл.
7. Пусть подвижная система отсчета осуществляет поступательное движение. Тогда:
Следовательно, 

Теорема о сложении скоростей
Теорема. Абсолютная скорость


Доказательство. Рассмотрим движение точки М относительно некоторого тела G (рис. 9.1), с которым неизменно связана подвижная система координат Oxyz, которая, в свою очередь, движется относительно условно неподвижной системы координат. Пусть положение точки М в подвижной системе координат определяется радиусом-вектором 




Продифференцировав это выражение в соответствии формуле (9.14):

Здесь индекс 


С учетом этих обозначений, выражение (9.25) будет иметь следующий вид:

который отражает теорему о распределении скоростей точек при сложном движении. Очевидно, что формула (9.27) отражает правило параллелограмма для сложения скоростей.
Модуль абсолютной скорости 

Пример 2. Вдоль хорды АВ (рис. 95) вращающегося диска движется точка М от точки
А к точке В в соответствии с уравнением 

Решение. Движение точки М вдоль хорды подвижного диска относительно. Поэтому относительная скорость и направлена по хорде АВ
Диск вращается вокруг оси, перпендикулярной к его плоскости. Итак, переносное движение диска будет вращательным, поэтому переносная скорость точки М направлена перпендикулярно к ОМ в сторону вращения диска. По теореме о сложении скоростей абсолютная скорость 
В некоторых задачах кинематики сложного движения точки нужно определить относительную скорость 
Итак, чтобы построить вектор относительной скорости, следует добавить вектор абсолютная скорости к вектору, направленному противоположно переносной скорости.
Теорема о сложении ускорений
Теорема Кориолиса. Абсолютное ускорение точки при сложном движении равно
векторной сумме относительного, переносного ускорений и ускорения Кориолиса.
Доказательство. По определению ускорения точки, с учетом (9.27), имеем:

где

С помощью формулы (9.14) для абсолютной производной, определим каждое слагаемое ускорения отдельно, учитывая, что векторы 

координат Oxyz и поэтому именно на них распространяются формулы (9.14):


Введем обозначения:

Тогда (9.32) перепишем в виде:

где
Введем обозначения в соответствии с определениями абсолютного, относительного и переносного ускорений:

Подставив (9.31) и (9.34) в выражение (9.29), с учетом (9.35), получим:

Последнее слагаемое в этой формуле, который не входит ни в относительное, ни в переносное ускорения, называется поворотным или кориолисовым ускорением 

Окончательно получим:

Теорема доказана.
Заметим, что в ряде случаев может стать полезной формула для определения ускорения, которая непосредственно следует из (9.14):

Отметим, что когда переносное движение подвижной системы координат Oxyz является поступательным 
принимает вид:

то есть при поступательном движении абсолютное ускорение точки равно геометрической
сумме относительного и переносного ускорений.
Следовательно, эта формула отражает правило параллелограмма для сложения ускорений в данном случае. В следующих разделах проанализируем выражения для каждой составляющей ускорения более детально.
Вращательное и осевое ускорение в случае вращения тела вокруг неподвижной оси
Проанализируем две составляющие переносного ускорение точки в выражении (9.35) 

Поскольку кинематическое содержание векторов 




Введем следующие обозначения:

и будем называть ускорение 

Рассмотрим ускорения произвольной точки М, неизменно связанной с телом, вращения вокруг неподвижной оси (рис. 9.6).
В этом случае 
(9.38), запишем в виде, опустив индекс 



Кроме того, ускорение этой же точки, согласно п. 8.3, можно представить в виде векторной суммы нормального и тангенциально ускорений:

Установим связь между составляющими ускорения точки М которые есть в выражениях (9.42) и (9.43). Прежде всего покажем, что составляющая ускорения точки 

подчеркнуть это обстоятельство, его называют осевым ускорением. Действительно, если 


будет направлен перпендикулярно к плоскости KLM, которая содержит прямую МК, параллельную оси вращения 


получим:

Сравнив последнее выражение с соответствующим выражением (8.27) для нормального ускорения точки, которое всегда направлено по главной нормали к абсолютной траектории с центром кривизны в точке N, которая лежит на оси вращения, получим:

Рассмотрим теперь вторую составляющую ускорения 

Далее будет показано, что в общем случае движение твердого тела 



Ускорение Кориолиса
По формуле (9.37) ускорение Кориолиса появляется тогда, когда переносное движение является вращательным:

Как видно из приведенной формулы, ускорение Кориолиса равно удвоенному векторному произведению вектора 

нормали к плоскости, в которой расположены векторы 

которой, если смотреть с конца вектора 


Модуль ускорения Кориолиса находим по формуле:

Спроектировав обе части равенства (9.50) на подвижные оси координат, получим такие выражения для проекций ускорения Кориолиса :

где 

Тогда модуль ускорения Кориолиса :

Направление 



Случаи превращения в ноль ускорения Кориолиса
Как следует из (9.51), ускорение Кориолиса равно нулю в те моменты (или на тех промежутках времени), когда:
1) вектор 
2) относительная скорость 
3) 


Следует отметить, что в те моменты времени, когда ускорения Кориолиса превращается в ноль, абсолютное ускорение точки определяется по правилу параллелограмма.
тогда:

а модуль этого ускорения определяется по теореме косинусов:

Физические причины возникновения ускорения Кориолиса
Покажем, что ускорение Кориолиса возникает вследствие таких двух причин:
1. Представим себе два прямолинейных отрезка 

точки 







займет положение 
скорости точки 

Переносным движением точки 




Итак, переносная скорость точки 





2. Вторая физическая причина возникновения ускорения Кориолиса такова:
относительная скорость точки 



Следовательно, скорость изменение во времени относительной скорости точки (т.е. ускорение точки, которое зависит от приведенной выше причины) также будет пропорционально относительной скорости 

А. И. Сомов обратил внимание на то, что ускорения Кориолиса как будто вращает вектор относительной скорости в направлении переносного вращательного движения, из-за чего назвал ускорение Кориолиса поворотным.
Подводя итог изложенного и обращаясь к формуле (9.34), видим, что изменение во времени переносной скорости при условии, что переносное движение является непоступательным, вызывается не только переносным, но и относительным движением точки. Дополнительное ускорение равно векторному произведению 
Ускорение Кориолиса 
векторов 


Пример 3. Определить абсолютное ускорение точки в примере 2, приведенном в п. 9.3.
Решение. Поскольку переносное движение является вращательным, то абсолютное ускорение точки М (Рис. 9.5) определим по теореме Кориолиса:
Поскольку 



Относительное движение точки М происходит вдоль прямой АВ, поэтому относительное ускорение 






Пример 4. На подвижных объектах (самолетах, кораблях и т.д.) используются гироскопические приборы маятникового типа для определения отклонения объектов от горизонтали. При движении относительно Земли в этих приборах возникают так называемые скоростные и баллистические девиации (погрешности), обусловленные тем, что эти объекты, двигаясь горизонтально по поверхности Земли (или по сфере радиусом 
угловую скорость вращения подвижного объекта и его ускорение в географической системе координат, если составляющая относительной скорости объекта к северу 


Решение. Движение объекта (точку О) задано в сферической системе координат: 




Ось 


Очевидно, что движение объекта с составляющей скорости 







С учетом этого, очевидно, что:

Если теперь учесть и угловую скорость вращения Земли 

В данном случае вращательное движение Земли является переносным, а движение объекта по поверхности относительным. С учетом этого и формул (2) приведем формулы для абсолютной скорости объекта в проекциях на оси географической системы координат:

Используя уравнение (3) выражение (2) можно переписать в форме:

Найдем теперь абсолютное ускорение подвижного объекта, воспользовавшись формулой
(9.39):

тут 

Проектируя (5) на оси 

Подставив в (6) выражения (3) и (4), получим:

При горизонтальном движении объекта 


В выражениях (8) не видно явно ускорения Кориолиса, хотя понятно, что оно должно было иметь место, потому что переносное движение Земли является вращательным.
Для того, чтобы выделить явно ускорение Кориолиса, осевое ускорение, вращательное и относительное, нужно формулы (8) записать в развернутом виде:

Перепишем в конечном итоге формулы (9) так, чтобы на первом месте было переносное, дальше относительное и в конце ускорения Кориолиса (таблица).
Таким образом, задача решена.
Пример 5. Точка М неравномерно движется по ободу колеса радиусом R с относительной
скоростью вращается с переменной угловой скоростью 
1) задавая движение точки в натуральной системе координат;
2) используя понятие сложного движения точки.
Решение. 1. При заданном движения точки в натуральной системе координат нужно учесть, что ускорение в данном случае имеет две составляющие – тангенциальное


Следовательно, для определения ускорений по формулам (1) нужно найти 
Очевидно, что 

Подставив (2) в (1), получим:

Если спроектировать эти ускорения на оси ортогональной системы координат 

При 


2. Использование понятия сложного движения точки. В этом случае (рис. 9.10,б)

Переносное ускорение имеет две составляющие 




Осевое ускорения будет направлено к оси вращения, проходящей через точку О (рис. 9.10, б) и равно:

Ускорение Кориолиса в этом случае направлено по оси Оу и равно:

Относительное ускорение в этом случае определяется по формуле (9.31), в которой нужно учесть только ту составляющую угловой скорости 

Очевидно, что

Спроектировав выражение (10) на оси 


Найдем теперь проекции абсолютных ускорений на осях 

Сравнивая выражения (3), (4) и (13), видим, что проекции ускорения на оси 


Для сравнения найдем ускорение по формуле (9.39)

Отметим, что в данном случае в формуле (15) нужно задать полную угловую скорость
вращения подвижной системы координат:

В нашем случае 


или

Нетрудно заметить, что выражения (3), (13) и (18) одинаковые, то есть приведенный способ решения задачи оказался достаточно эффективным. Задача решена.
Сложное движение материальной точки. Относительное, переносное и абсолютное движение материальной точки
Сложное движение материальной точки — это такое движение, при котором точка может одновременно участвовать в двух и более движениях.
Для представления о сложном движение приведем такой пример. Если человека принять за материальную точку, то ее движение по палубе корабля будет сложным, когда это движение рассматривать относительно палубы и относительно берега (поверхности Земли). Движение человека относительно палубы является относительным, вместе с кораблем — переносным, а относительно поверхности Земли — абсолютным.
При сложном движении можно рассматривать точку, тело переноса или подвижное переносное пространство, с которым связана подвижная система координат, и неподвижную систему координат, которая скреплена с поверхностью Земли.
Движение точки относительно тела переноса или подвижной системы отсчета называется относительным, а скорость и ускорение точки в этом движении — относительными скоростью и ускорением, они обозначаются 

Движение точки вместе с подвижным пространством, а точнее вместе с той точкой подвижного пространства, с которой в данный момент совпадает заданная точка, называется переносным движением, а скорость и ускорение точки в этом движении — переносными скоростью и ускорением, они обозначаются 

Движение материальной точки относительно неподвижной системы координат называется абсолютным, а скорость и ускорение — абсолютными, они обозначаются 

Теорема о сложении скоростей в сложном движении материальной точки
Сформулируем эту теорему.
Абсолютная скорость материальной точки при сложном ее движении равна геометрической сумме ее переносной и относительной скоростей:

Докажем это. Выберем материальную точку М (рис. 2.45), что движется независимо по своему закону относительно подвижной системы отсчета Oxyz, которая жестко связана с телом S, и вместе с ним перемещается относительно неподвижной системы координат 



Определим положение материальной точки М относительно выбранных осей координат. Так, относительно подвижной системы координат Oxyz ее положение определяется радиус-вектором 


Положение начала (центр O) подвижной системы координат Oxyz относительно неподвижной системы координат 

Как видно из образованного на рис. 2.46 векторного треугольника 

или, если представить радиус-вектор 




Используя выражение определим абсолютную скорость 
При произвольном переносном движении тела орты 



Перегруппируем правую часть выражения и перепишем его:

Рассмотрим подробно выражение. Так, в последней скобке в этом выражении можно сделать следующие обозначения:



Тогда она представляет собой

Рассмотрим далее первую скобку в выражении, где

По формулам Пуассона другие составляющие первой скобки выражения можно представить так:



где 



Подставим в первую скобку выражения:

Тогда выражение окончательно будет иметь следующий вид:

Сумма 

Поскольку переносное движение в общем случае является сложным, то он разделяется на поступательное вместе с полюсом (точкой О) и вращательное вокруг полюса
Окончательно имеем:

Что и необходимо было доказать.
Выражение называют параллелограммом скоростей.
Когда угол 

Если 


Теорема Кориолиса
Сформулируем эту теорему.
Абсолютное ускорение материальной точки при произвольном переносном движении равно геометрической сумме трех ускорений: переносного, относительного и дополнительного ускорения, которое называется поворотным ускорением или ускорением Кориолиса.
Итак:

где 



Предположим, что материальная точка М имеет сложное движение. Считаем, что она движется относительно подвижной системы координат Oxyz, которая сама произвольным образом перемещается относительно другой — неподвижной системы 



Как и в предыдущем случае, определим положение материальной точки М. Так, положение точки М в подвижной системе координат Oxyz определяется радиус-вектором 




Абсолютное ускорение материальной точки М равна производной по времени от абсолютной скорости:

Проведем преобразование и анализ выражения. В первой скобке составляющая

Превратим дальше выражение первой скобки, пользуясь формулами Пуассона:

Во второй скобке

В уравнении есть еще такие два выражения, которые также надо превратить:

Учитывая сделанные преобразования, окончательно запишем:

Что и требовалось доказать.

где 

Модуль, направление и физические причины возникновения ускорения Кориолиса
Рассмотрим подробно ускорения Кориолиса и его свойства. Оно, согласно формуле, имеет следующий вид:

Ускорение Кориолиса равна двойному векторном произведения векторов переносной угловой скорости и относительной скорости точки.
Как известно, модуль векторного произведения равен:
Из выражения видно, что модуль ускорения Кориолиса равен нулю 
1. 
2. 
3. 

Модуль ускорения Кориолиса будет максимальным, если угол между векторами 


Направление ускорения Кориолиса можно найти по двум методами: математическим — по определению векторного произведения двух векторов и физическим — по способу Жуковского.
Рассмотрим первый способ.
Предположим, что тело S вращается вокруг оси z против направления хода часовой стрелки.
Это тело переноса и вектор 






Таким образом, вектор ускорения Кориолиса перпендикулярен плоскости, которую образуют векторы переносной угловой скорости и относительной скорости, и направлен в ту сторону, откуда видим, что кратчайший переход от вектора угловой скорости к вектору относительной скорости происходит против часовой стрелки.
Переходим к рассмотрению определения направления вектора ускорения Кориолиса по методу Жуковского.
Для определения направления вектора ускорения Кориолиса этим методом необходимо вектор относительной скорости 


Нетрудно понять, что в плоских механизмах, которые являются объектом курсового проекта по теории механизмов и машин, вектор 

Рассмотрим далее физические причины возникновения поворотного ускорения или ускорение Кориолиса.
Пусть по пластине, расположенной в плоскости рисунка и равномерно вращается вокруг вертикальной оси с постоянной угловой скоростью 



Из выше приведенного можно сформулировать две физические причины возникновения ускорения Кориолиса:
— изменение направления вектора относительной скорости материальной точки в результате переносного вращения;
— изменение модуля и направления вектора переносной скорости точки в результате ее относительного движения; это видно из следующих выражений переносной скорости движения для различных ее положений M и M1 (расстояние 


Следовательно, ускорение Кориолиса — это новый кинематический эффект, который возникает в результате взаимодействия, взаимовлияния векторов относительной и переносной скоростей при вращательном переносном движении.
Влияние ускорения Кориолиса наблюдается в природе и технике.
Так, за счет сил инерции масс воды, которые формируются этим ускорением, размываются правые берега рек, текущих вдоль меридиана. Поэтому правые берега в северном полушарии всегда являются крутыми. В южном полушарии – наоборот, левые берега являются крутыми.
В технике ускорения Кориолиса возникает в так называемых кулисных механизмах (кулиса — это подвижная направляющая). Относительно кулисы движется кулисный камень, а переносным движением является поворот кулисы относительно недвижимого центра.
Методика решения задач на сложное движение материальной точки
1. Выяснить, движение точки является относительным, какое является переносным, проанализировать законы движения и условие задачи.
2. Для определения характеристик относительного движения необходимо условно остановить переносное движение. Найти положение точки в заданный момент времени на траектории относительного движения.
3. Для определения характеристик переносного движения необходимо условно остановить относительное движение и рассмотреть движение точки, принадлежащей телу переноса, которая совпадает в данный момент с этой точкой.
4. Для определения параметров абсолютного движения точки необходимо выбрать систему координат с началом в самой точке, затем методом проекций определить проекции абсолютных скорости и ускорения и, наконец, полные скорости и ускорения
Пример.
Кольцевая трубка (рис. 2.50) радиуса 16 см вращается вокруг горизонтальной диаметра ОА по закону 


Решение
Определяем положение точки М в момент времени t1. Положение точки M удобно определить углом α. Определим его с помощью такого выражения:


Точка М в заданный момент времени изображена на рис. 2.50. Выберем подвижную систему координат, жестко связанную с кольцевой трубкой.
Выделяем переносное движение точки M. Для этого скрепляем точку М с подвижной системой координат. В этом случае точка M будет описывать круг в плоскости, перпендикулярной к диаметру ОА, радиус которого будет равен:

Вычислим переносную скорость точки М как скорость вращения данной точки вокруг оси ОА. Она равна:
Определим угловую скорость вращения трубки.


Вектор угловой скорости направлен вдоль оси вращения.
Переносная скорость 

Для момента времени 

Вектор переносной скорости направлен перпендикулярно к плоскости чертежа в направлении вращения.
Относительное движение точки М — это движение жидкости относительно трубки. В этом случае точка М будет двигаться по кругу диаметром ОА.
Вычисляем относительную скорость точки М. Она равна:

Для момента времени 

Направляем вектор относительной скорости 
Векторы переносной 

Учитывая, что векторы 


Абсолютное ускорение точки M будет равно:

Находим переносное нормальное ускорение точки M:

При 

Направленный вектор переносного нормального ускорения 
Переносное касательное ускорение 

Определим угловое ускорение трубки. Оно будет равно:

Угловое ускорение 
Вычисляем переносное касательное ускорение 

Для 

Направленное переносное касательное ускорение 

Находим относительное касательное ускорение 

Вектор относительного касательного ускорения 


Вычислим относительное нормальное ускорение 

Для момента времени 

Направленный вектор нормального относительного ускорения 
Находим ускорение Кориолиса 

Направлено ускорение Кориолиса перпендикулярно плоскости, в которой лежат векторы






Находим относительное касательное ускорение 

Вектор относительного касательного ускорения 


Вычислим относительное нормальное ускорение 

Для момента времени 

Направленный вектор нормального относительного ускорения 
Находим ускорение Кориолиса 

Направлено ускорение Кориолиса перпендикулярно плоскости, в которой лежат векторы 





Векторы относительного, переносного и ускорение Кориолиса изображены на рис. 2.51.
Для нахождения абсолютного ускорения 



Модуль абсолютного ускорения 

Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.
Относительность перемещения
Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:
s′ = s1 + s2
s′ — перемещение МТ относительно НСО, s1— перемещение МТ относительно ПСО, s2 — перемещение ПСО относительно НСО.
Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.
Полезные факты
- Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = s1 + s2
- Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = s1 – s2
- Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = √(s12 + s22)
- Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s1=0, перемещение s′ = s2
- Если тело движется относительно двух НСО, то его перемещение относительно НСО1 равно перемещению движения относительно НСО2. В этом случае одну из систем можно принять за ПСО с нулевой скоростью. Тогда ее перемещение относительно НСО будет равно 0. При s2=0, перемещение s′ = s1
Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.
Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:
s′=|s1 – s2|=|10 – 2|=8 (м).
Относительность скорости в ПСО и НСО
Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:
v′ = v + u
v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.
Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.
Полезные факты
- Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = v + u
- Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = v – u
- Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = √(v2 + u2)
- Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0, скорость v′ = u
- Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2. В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.
Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:
Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):
Косинусу 0,5 соответствует угол, равный 60 градусам.
Относительная скорость двух тел
Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.
Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:
vотн = v1– v2
vотн — относительная скорость, или скорость первого тела относительно второго, v1 и v2 — скорость первого и второго тела относительно СО.
Варианты обозначения относительной скорости и их проекций:
- v12 — скорость первого тела относительно второго. Ее проекция равна:
v12x = v1x – v2x
- v21 — скорость второго тела относительно первого. Ее проекция равна v21x = v2x – v1x
Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.
Полезные факты
- Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:
vотн = |v1 – v2|
- Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:
vотн = |v1 + v2|
- Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:
vотн = √(v12 + v22)
Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.
Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:
Скорость второго автомобиля относительно дороги равна 80 км/час.
Правила сложения векторов
Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b. Результатом их сложения является вектор c .
| Сложение двух сонаправленных векторов | |
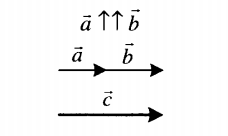 |
Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону.
Его длина равна сумме длин слагаемых векторов: c = a + b. |
| Сложение двух противоположно направленных векторов | |
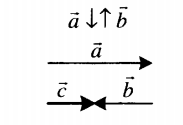 |
Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|. |
| Сложение двух векторов, расположенных друг к другу под углом | |
| Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
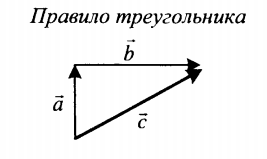 |
Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора:
|
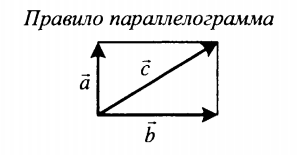 |
|
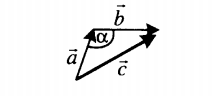 |
Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов:
|
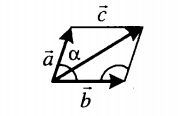 |
Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов:
|
Правила вычитания векторов
Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор
.
| Вычитание двух сонаправленных векторов | |
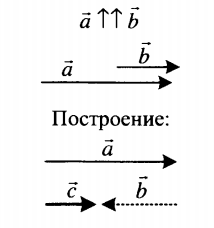 |
Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора.
Его длина равна модулю разности длин вычитаемых векторов: c = |a – b|. |
| Вычитание двух противоположно направленных векторов | |
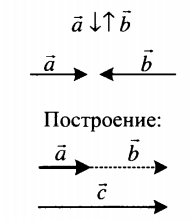 |
Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b. |
| Вычитание двух векторов, расположенных друг к другу под углом | |
| Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
 |
Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора:
|
 |
Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов:
|
Задание EF17727
Два автомобиля движутся по прямому шоссе, первый — со скоростью v, второй — со скоростью –4v. Найти скорость второго автомобиля относительно первого.
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно оси ОХ: v1 = v.
- Скорость второго автомобиля относительно оси ОХ: v2 = –4v.
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость второго автомобиля относительно оси ОХ (v2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ (v1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
v2 = v + v1
Отсюда:
v = v2 — v1 = –4v – v = –5v
Ответ: -5v
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17518
Два автомобиля движутся в одном направлении. Относительно Земли скорость первого автомобиля 110 км/ч, второго 60 км/ч. Чему равен модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Выбрать систему отсчета.
- Записать классический закон сложения скоростей в скалярном виде.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно неподвижной системы отсчета: v1 = 110 км/ч;
- Скорость второго автомобиля относительно Земли: v2 = 60 км/ч.
Изображаем графическую модель ситуации:
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость автомобиля относительно земли (v1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли (v2).
По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
v’ = v + u
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
v = v’ – u = v1 – v2 = 110 – 60 = 50 (км/ч).
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.4k
From Wikipedia, the free encyclopedia
The relative velocity 


Classical mechanics[edit]
In one dimension (non-relativistic)[edit]
Relative motion man on train
We begin with relative motion in the classical, (or non-relativistic, or the Newtonian approximation) that all speeds are much less than the speed of light. This limit is associated with the Galilean transformation. The figure shows a man on top of a train, at the back edge. At 1:00 pm he begins to walk forward at a walking speed of 10 km/h (kilometers per hour). The train is moving at 40 km/h. The figure depicts the man and train at two different times: first, when the journey began, and also one hour later at 2:00 pm. The figure suggests that the man is 50 km from the starting point after having traveled (by walking and by train) for one hour. This, by definition, is 50 km/h, which suggests that the prescription for calculating relative velocity in this fashion is to add the two velocities.
The diagram displays clocks and rulers to remind the reader that while the logic behind this calculation seem flawless, it makes false assumptions about how clocks and rulers behave. (See The train-and-platform thought experiment.) To recognize that this classical model of relative motion violates special relativity, we generalize the example into an equation:
where:
is the velocity of the Man relative to Earth,
is the velocity of the Man relative to the Train,
is the velocity of the Train relative to Earth.
Fully legitimate expressions for “the velocity of A relative to B” include “the velocity of A with respect to B” and “the velocity of A in the coordinate system where B is always at rest”. The violation of special relativity occurs because this equation for relative velocity falsely predicts that different observers will measure different speeds when observing the motion of light. [note 1]
In two dimensions (non-relativistic)[edit]
Relative velocities between two particles in classical mechanics
The figure shows two objects A and B moving at constant velocity. The equations of motion are:
where the subscript i refers to the initial displacement (at time t equal to zero). The difference between the two displacement vectors, 
Hence:
After making the substitutions 

Galilean transformation (non-relativistic)[edit]
To construct a theory of relative motion consistent with the theory of special relativity, we must adopt a different convention. Continuing to work in the (non-relativistic) Newtonian limit we begin with a Galilean transformation in one dimension:[note 2]
where x’ is the position as seen by a reference frame that is moving at speed, v, in the “unprimed” (x) reference frame.[note 3] Taking the differential of the first of the two equations above, we have, 

To recover the previous expressions for relative velocity, we assume that particle A is following the path defined by dx/dt in the unprimed reference (and hence dx′/dt′ in the primed frame). Thus 




where the latter form has the desired (easily learned) symmetry.
Special relativity[edit]
As in classical mechanics, in Special Relativity the relative velocity 
This peculiar lack of symmetry is related to Thomas precession and the fact that two successive Lorentz transformations rotate the coordinate system. This rotation has no effect on the magnitude of a vector, and hence relative speed is symmetrical.
Parallel velocities[edit]
In the case where two objects are traveling in parallel directions, the relativistic formula for relative velocity is similar in form to the formula for addition of relativistic velocities.
The relative speed is given by the formula:
Perpendicular velocities[edit]
In the case where two objects are traveling in perpendicular directions, the relativistic relative velocity 
where
The relative speed is given by the formula
General case[edit]
The general formula for the relative velocity 
where
The relative speed is given by the formula
See also[edit]
- Doppler effect
- Non-Euclidean geometry § Kinematic geometries
- Peculiar velocity
- Proper motion
- Range rate
- Radial velocity
- Rapidity
- Relativistic speed
- Space velocity (astronomy)
Notes[edit]
- ^ For example, replace the “Man” by a photon traveling at the speed of light.
- ^ This result is valid if all motion is restricted to the x-axis, but can be easily generalized by replacing the first equation by
- ^ It is easy to be confused about the minus sign before v, or whether v is defined in the prime or unprimed reference frame. It might help to visualize the fact that if x = vt, then x′ = 0, meaning that a particle that is following the path x = vt is at rest in the primed reference frame.
- ^ Keep in mind that, due to time dilation, dt = dt′ is valid only in the approximation that the speed is much less than that of light.
References[edit]
- ^ Fock 1964 The theory of Space Time and Gravitation, retrieved from https://archive.org/details/TheTheoryOfSpaceTimeGravitation
Further reading[edit]
- Alonso & Finn, Fundamental University Physics ISBN 0-201-56518-8
- Greenwood, Donald T, Principles of Dynamics.
- Goodman and Warner, Dynamics.
- Beer and Johnston, Statics and Dynamics.
- McGraw Hill Dictionary of Physics and Mathematics.
- Rindler, W., Essential Relativity.
- KHURMI R.S., Mechanics, Engineering Mechanics, Statics, Dynamics
External links[edit]
- Relative Motion at HyperPhysics
- A Java applet illustrating Relative Velocity, by Andrew Duffy
- Relatív mozgás (1)…(3) Relative motion of two train (1)…(3). Videos on the portal FizKapu. (in Hungarian)
- Sebességek összegzése Relative tranquility of trout in creek. Video on the portal FizKapu. (in Hungarian)












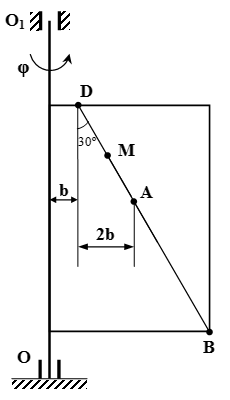
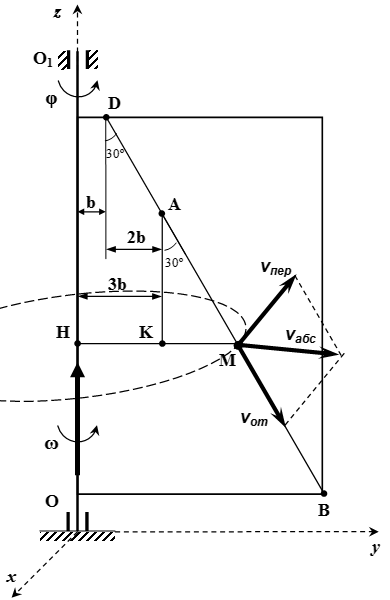
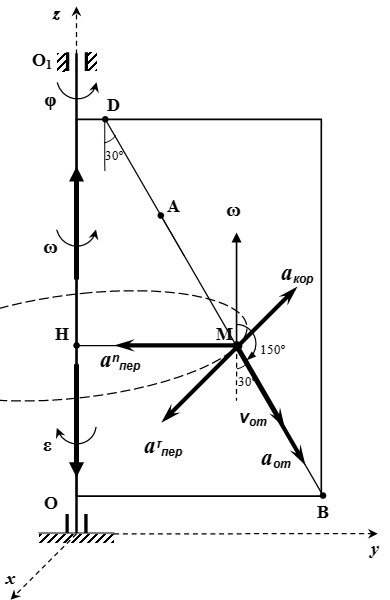












































































































































 (из плана скоростей);
(из плана скоростей); (вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно;
(вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно; (вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
(вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.














 (вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно;
(вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно; (вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
(вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
































































































































































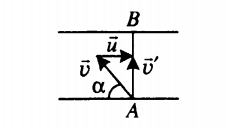

























![{displaystyle {vec {v}}_{mathrm {B|A} }={frac {1}{gamma _{mathrm {A} }left(1-{frac {{vec {v}}_{mathrm {A} }{vec {v}}_{mathrm {B} }}{c^{2}}}right)}}left[{vec {v}}_{mathrm {B} }-{vec {v}}_{mathrm {A} }+{vec {v}}_{mathrm {A} }(gamma _{mathrm {A} }-1)left({frac {{vec {v}}_{mathrm {A} }cdot {vec {v}}_{mathrm {B} }}{v_{mathrm {A} }^{2}}}-1right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df4dfe757c619047b27a74f71b219a91abc01113)


