Как найти вектор параллельного переноса

Как найти вектор параллельного переноса

Сегодня на уроке мы вспомним, какое отображение
плоскости на себя мы называли параллельным переносом, введём понятие
параллельного переноса в пространстве. Проверим, будет ли параллельный перенос
движением пространства.

Вернёмся в планиметрию и вспомним, что параллельным
переносом мы называли преобразование, при котором каждая точка фигуры
перемещается в одном и том же направлении и на одно и то же расстояние. Мы
говорили, что для того, чтобы задать перенос достаточно задать вектор.

Другими словами, параллельным переносом на
вектор  называется
отображение плоскости на себя, при котором каждая точка  отображается
в такую точку ,
что вектор  равен
вектору .

То, что параллельный перенос является примером
движения плоскости, мы уже доказывали. Давайте вспомним это доказательство.

Пусть при параллельном переносе на вектор  точки
 и
 отображаются
в точки  и
.
Так как векторы  и
,
то значит, эти векторы равны между собой .
То есть они параллельны  и
их длины равны, поэтому четырёхугольник  –
параллелограмм. Следовательно, ,
то есть расстояние между точками  и
 равно
расстоянию между точками  и
.

Случай, когда точки  и
 лежат
на прямой параллельной вектору ,
вы можете рассмотреть самостоятельно. Но и в этом случае расстояние между
точками  и
 будет
равно расстоянию между точками  и
.

Таким образом, параллельный перенос сохраняет
расстояние между точками и поэтому представляет собой движение. Это
движение можно представить себе как сдвиг всей плоскости в направлении данного
вектора  на
его длину.

В планиметрии мы говорили, что параллельный перенос
обладает некоторыми свойствами.

Свойства параллельного переноса:

·              
При
параллельном переносе отрезок переходит в равный ему отрезок.

·              
Угол
переходит в равный ему угол.

·              
Окружность
переходит в равную ей окружность.

·              
Любой
многоугольник переходит в равный ему многоугольник.

·              
Параллельные
прямые переходят в параллельные прямые.

·              
Перпендикулярные
прямые переходят в перпендикулярные прямые.

Теперь давайте определим, что мы будем понимать под
параллельным переносом в пространстве.

Определение:

Параллельным переносом на вектор  называется
такое отображение пространства на себя, при котором любая точка  переходит
в такую точку  что
.

Проверим, будет ли параллельный перенос в
пространстве примером движения пространства.

При параллельном переносе точки пространства  и
 переходят
в такие точки  и
,
что вектора  и
.

Сложим по правилу треугольника векторы

Поскольку левые части равенств равны, значит, равны
и правые части равенств.

Значит, можно записать, что .

Заменим вектора  и
 на
вектор .
Получим, что .
Отсюда получаем, что вектор .
Поскольку векторы равны, значит, равны и их длины, то есть .
То есть расстояние между точками при параллельном переносе в пространстве
сохраняется, значит, параллельный перенос в пространстве также является
движением, но уже не плоскости, а пространства.

Сформулируем свойства параллельного переноса.

Свойства параллельного переноса:

·                  
Параллельный
перенос является примером движения пространства.

·                  
При
параллельном переносе точки смещаются по параллельным или совпадающим прямым на
одно и то же расстояние.

·                  
При
параллельном переносе прямая переходит в параллельную прямую (или сама в себя).

·                  
Каковы
бы не были две точки  и
,
существует, и притом единственный, параллельный перенос, при котором точка  переходит
в точку .

·                  
При
параллельном переносе в пространстве каждая плоскость переходит либо в себя,
либо в параллельную ей плоскость.

Движение в пространстве обладает теми же свойствами,
что и движение плоскости.

Свойства движения пространства:

·                  
Движение
сохраняет расстояние между точками.

·                  
При
любом движении пространства отрезок отображается на отрезок, прямая – в прямую,
плоскость – в плоскость.

Решим несколько задач.

Задача:
начертить отрезок  и
вектор .
Построить отрезок ,
который получится из отрезка параллельным
переносом на вектор .

Решение:
для того, чтобы построить отрезок ,
отобразим точку  в
точку ,
точку  в
точку  с
помощью параллельного переноса. Тогда соединив точки ,
 мы
получим отрезок .

Задача:
начертить треугольник  и
вектор .
Построить треугольник ,
который получится из треугольникa
параллельным
переносом на вектор .

Решение:
отобразим с помощью параллельного переноса точки ,
,
 в
точки ,
,.
Соединив полученные точки, мы получим искомый треугольник .

Задача:
начертить пятиугольник  и
вектор .
Построить пятиугольник ,
который получится из пятиугольника параллельным
переносом на вектор .

Решение:
решать эту задачу будем аналогично тому, как мы решали предыдущую задачу.
Отобразим каждую вершину пятиугольника с помощью параллельного переноса на
вектор .
Соединим получившиеся точки и получим искомый пятиугольник .

Итоги:

Сегодня на уроке мы вспомнили, что мы понимали под
параллельным переносом в планиметрии. Ввели понятие параллельного переноса в пространстве.
Сформулировали основные свойства параллельного переноса, движения пространства.

Источник

Паралле́льный перено́с иногда трансляция[1] (от лат. translatio — перенос,перемещение) ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние.

Определение[править | править код]

Параллельный перенос ― перемещение всех точек пространства в одном и том же направлении на одно и то же расстояние.
Если M ― первоначальное положение, а M' ― смещённое в результате переноса положение точки, то вектор {displaystyle {overrightarrow {MM'}}} ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании.

Параллельный перенос на вектор vec a обозначается как {displaystyle T_{vec {a}}} (от лат. translatio – перенос,перемещение)

Параллельный перенос перемещает каждую точку фигуры или пространства на одно и то же расстояние в одном и том же направлении.

Координатное представление[править | править код]

На плоскости параллельный перенос выражается аналитически в прямоугольной системе координат (x,;y) при помощи

{textstyle (x,;y)mapsto (x+a,;y+b),}

где вектор {displaystyle {overrightarrow {MM'}}=(a,;b)}.

Свойства[править | править код]

  • Две различные точки и их образы, полученные параллельным переносом, являются вершинами параллелограмма, в котором отрезок, соединяющий две начальные точки, образует одну сторону, а отрезок, соединяющий два их образа — противоположную ей сторону.
  • У параллельного переноса нет неподвижных точек (если только это не тождественное преобразование, либо если прямая или плоскость не параллельны вектору параллельного переноса (т.к. именно он определяет направление переноса[2])).
  • Совокупность всех параллельных переносов образует группу, которая в евклидовом пространстве является нормальной подгруппой группы движений, а в аффинном ― нормальной подгруппой группы аффинных преобразований.
  • Параллельный перенос сохраняет направления ( т.е. для любого вектора {vec {a}} верно, что {displaystyle f({vec {a}})={vec {a}}})
  • Преобразование, обратное к параллельному переносу {displaystyle T_{vec {a}}} есть {displaystyle T_{-{vec {a}}}}
  • Композиция параллельных переносов {displaystyle T_{vec {a}}} и {displaystyle T_{vec {b}}} есть {displaystyle T_{{vec {a}}+{vec {b}}}}
  • Параллельный перенос переводит прямую в себя или в параллельную ей прямую, а плоскость – в себя или в параллельную ей плоскость.
  • Параллельный перенос {displaystyle T_{vec {0}}} – это тождественное преобразование.

Вариации и обобщения[править | править код]

  • Параллельное перенесение — обобщение понятия «параллельный перенос» на случай искривлённых пространств.
  • Поступательное движение — движение в механике, разница положений при котором в любые 2 момента времени представляет собой параллельный перенос.
  • Трансляция (кристаллография)
  • Трансляционная симметрия

Примечания[править | править код]

  1. ↑ Паралле́льный перено́с и трансляция ― полные синонимы в математике и физике, вторая форма термина особенно часто употребляется для образования прилагательного, например трансляционная симметрия), также, традиционно, ей отдается почти исключительное предпочтение в некоторых областях, таких, как кристаллография.
  2. ↑ Калинин А.Ю., Терешин Д.А. Геометрия. 10-11 классы (профильный уровень). — МЦНМО, 2011. — С. 231-250. — ISBN 978-5-94057-581-8.
Источник

Геометрия, 11 класс

Урок №4. Движения в пространстве

Перечень вопросов, рассматриваемых в теме:

  • понятие «движение» в пространстве;
  • свойства движений в пространстве;
  • виды движений в пространстве;
  • отличия движений в пространстве от движений на плоскости.

Глоссарий по теме

  1. Пусть каждой точке А пространства поставлена в соответствие точка А1 пространства. При этом каждая точка А1 поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А1.
  2. Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.
  3. Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.
  4. Центральная симметрия пространства относительно точки O – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O. Точка O – центр симметрии.
  5. Осевая симметрия пространства относительно прямой m – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой . Прямая m – ось симметрии.
  6. Зеркальная симметрия пространства относительно плоскости α – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α. Плоскость α – плоскость симметрии.
  7. Параллельный перенос на вектор – преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M’, что выполняется равенство .
  8. Поворот пространства на угол φ вокруг прямой n – преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 121-126.

Дополнительная литература:

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-63.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Определение движения в пространстве

Допустим, что каждой точке А пространства поставлена в соответствие точка А1 пространства. При этом каждая точка А1 поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А1. А1 – образ точки А.

Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.

Два преобразования называются равными, если образы любой точки при этих преобразованиях совпадают.

Точка А называется неподвижной точкой при некотором преобразовании f, если при этом преобразовании она отображается на себя.

Фигура F называется неподвижной фигурой при некотором преобразовании f, если при этом преобразовании она отображается на себя.

Преобразование пространства, которое каждую точку отображает на себя, называется тождественным преобразованием. Оно обычно обозначается Е. При тождественном преобразовании все точки и все фигуры пространства являются неподвижными.

Для любых двух преобразований можно рассмотреть третье, которое получается последовательным применением этих преобразований. Например, если преобразование f отображает точку М на точку М’, а преобразование g отображает точку М’ на точку M”, то преобразование f°g отображает точку М на точку M”: f°g(М)=g(f(M))=M”.

f°g – композиция преобразований f и g.

Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.

Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, можно доказать, что при движении в пространстве

 – прямые переходят в прямые,

– полупрямые — в полупрямые,

– отрезки — в отрезки,

– сохраняются углы между прямыми.

Новое свойство движения в пространстве: движение переводит плоскости в плоскости.

В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.

Можно доказать, что композиция двух движений пространства есть движение.

2. Виды движений.

Центральная симметрия.

Центральная симметрия в пространстве задается и определяется так же, как и на плоскости

Определение:

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O, называется центральной симметрией пространства относительно точки O. При этом точка O отображается на себя и называется центром симметрии.

Рисунок 1 – Центральная симметрия

На рисунке точка О – центр симметрии, АО=А1О, ВО=В1О, СО=С1О, DО=D1О (по определению точки, симметричной данной).

Центральная симметрия имеет только одну неподвижную точку – центр симметрии.

Сформулируем некоторые свойства центральной симметрии:

1) Прямая, проходящая через центр симметрии, отображается на себя.

2) Прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.

3) Плоскость, проходящая через центр симметрии, отображается на себя (то есть является неподвижной плоскостью этой центральной симметрии).

4) Плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость.

3. Осевая симметрия (симметрия относительно прямой):

Определение:

Точка M’ пространства, не лежащая на прямой m, называется симметричной точке М относительно прямой m, если отрезок ММ’ перпендикулярен этой прямой и делится ею пополам.

Определение:

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой m, называется осевой симметрией пространства относительно прямой m. Прямая m отображается на себя и называется осью симметрии.

Рисунок 2 – Осевая симметрия

Неподвижные точки осевой симметрии – любая точка прямой m.

Неподвижные прямые осевой симметрии:

1) сама прямая m

2) любая прямая, перпендикулярная прямой m

Неподвижные плоскости осевой симметрии:

1) любая плоскость, проходящая через прямую m

2) любая плоскость, перпендикулярная прямой m.

Зеркальная симметрия (симметрия относительно плоскости):

Определение:

Точка M’ пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ’ перпендикулярен этой плоскости и делится ею пополам.

Определение:

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется зеркальной симметрией пространства относительно плоскости α. Плоскость α отображается на себя и называется плоскостью симметрии.

Рисунок 3 – Зеркальная симметрия

Неподвижные точки зеркальной симметрии – любая точка плоскости α.

Неподвижные прямые зеркальной симметрии:

1) любая прямая плоскости α

2) любая прямая, перпендикулярная плоскости α

Неподвижные плоскости зеркальной симметрии:

1) сама плоскость α

2) любая плоскость, перпендикулярная плоскости α.

Параллельный перенос (точки переносятся на данный вектор):

 Рисунок 4 – параллельный перенос

Определение

Пусть дан вектор .

Преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M’, что выполняется равенство , называется параллельным переносом на вектор .

Перенос на нулевой вектор является тождественным преобразованием.

Параллельный перенос отображает прямую на параллельную ей прямую либо на себя; плоскость на параллельную ей плоскость либо на себя.

Неподвижных точек параллельный перенос на ненулевой вектор не имеет.

Неподвижными прямыми при параллельном переносе на вектор являются прямые, параллельные этому вектору.

Неподвижными плоскостями при параллельном переносе на вектор являются плоскости, параллельные этому вектору.

Поворот на данный угол вокруг данной оси:

Определение:

Поворотом пространства на угол φ вокруг прямой n называется такое преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.

Рисунок 5 – Поворот вокруг прямой

Неподвижными точками являются любая точка оси вращения.

Неподвижной прямой является ось поворота.

Неподвижной плоскостью является любая плоскость, перпендикулярная оси поворота.

Поворот вокруг оси на угол 1800 является осевой симметрией.

Примеры и разбор решения заданий тренировочного модуля

Дан треугольника АВС: А(3,- 2, 4), В (4, 6, 0), С (2, 2, 2)

В какую точку перейдет центр О пересечения медиан данного треугольника при:

Преобразование

Координата образа

Параллельный перенос на вектор (2; -2; 3)

(5; 0; 5)

Симметрия относительно начала координат

(-3; -2; -2)

Симметрия относительно координатной плоскости ZOY

(-3; 2; 2)

Поворот на угол 1800 относительно координатной оси OZ

(-3; -2; 2)

Симметрия относительно плоскости х=2

(1; 2; 2)

Решение:

Найдем точку пересечения медиант данного треугольника.

Найдем координаты точки М – середины отрезка ВС:

М (); М(3; 4; 1)

Так как медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины, то можем найти координаты точки О, зная координаты А и М:

О (3; 2; 2).

Теперь найдем координаты образа точки О при каждом из преобразований:.

  1. Параллельный перенос на вектор (2; -2; 3) означает, что координаты образа получаются так:

. То есть координаты образа: (5; 0; 5)

  1. Симметрия относительно начала координат задается уравнениями:

. То есть координаты образа: (-3; -2; -2)

  1. Симметрия относительно координатной плоскости ZOY задается уравнениями:

(ордината и аппликата точки остаются такими же, а абсцисса меняет знак). То есть координаты образа: (-3; 2; 2).

  1. Поворот на угол 1800 относительно координатной оси OZ означает симметрию относительно координатной оси OZ и задается уравнениями:

(аппликата точки остается такой же, а ордината и абсцисса меняют знак). То есть координаты образа: (-3; -2; 2).

  1. Симметрия относительно плоскости α: х=2.

Эта плоскость параллельная плоскости ZOY, поэтому ордината и аппликата точки остаются такими же. Так как абсцисса токи О хо =3, то расстояние от точки до плоскости α равно 1. Точка, симметричная точке О относительно плоскости α, будет иметь абсциссу, равную хо’ =1.

Поэтому координаты образа (1; 2; 2).

Источник

Параллельным переносом фигуры называется перенос всех точек пространства на одно расстояние в одном направлении.

Параллельный перенос определяет вектор, по которому совершается перенос.

Чтобы совершить параллельный перенос, нужно знать направление и расстояние, что означает задать вектор.

Pp.png

Рис. (1). Параллельный перенос треугольника (ABC) на вектор (a). 

Чтобы при параллельном переносе построить изображение многоугольника, достаточно построить изображения вершин этого многоугольника.

Первоначальная фигура и фигура, полученная после параллельного переноса, равны.

Параллельный перенос используется для конструирования графиков функций.

На рисунке изображена парабола и два результата параллельного переноса.

Grafiki_pp.png

Рис. (2). Параллельный перенос параболы.

Параллельный перенос можно встретить в реальной жизни.

nadia_if Shutterstock.jpg

Если одна фигура получена из другой фигуры поворотом всех её точек относительно центра (O) на один и тот же угол в одном и том же направлении, то такое преобразование фигуры называется поворотом.

Чтобы поворот имел место, должен быть задан центр (O) и угол поворота

α

.

Против часовой стрелки — положительный угол поворота, наоборот — отрицательный угол поворота (так же как углы поворота в единичной окружности).

Треугольник (ABC) повёрнут в положительном направлении (приблизительно на α (= 45) градусов).

Pagr.png

Рис. (4). Поворот треугольника (ABC) на угол

α

. 

Если угол поворота равен (180) или (-180) градусам, то фигура отображается как центрально симметричная данной, и этот поворот называется случаем центральной симметрии.

Pagr_180.png

Рис. (5). Поворот треугольника (ABC) на угол

180°

. 

Источники:

Рис. 3. Окна. nadia_if / Shutterstock.com

Источник
Автор статьи

оксана николаевна кузнецова

Эксперт по предмету «Математика»

Задать вопрос автору статьи

В данной статье мы будем рассматривать понятие параллельного переноса в трехмерном пространстве. Но вначале нам надо рассмотреть такие понятия как отображение и движение в пространстве.

Понятие движения

Перед тем, как ввести понятие движения в пространстве, надо ввести определение отображения пространства на себя.

Определение 1

Отображением пространства на себя будем называть такое соответствие любой точке данного пространства какой-либо точке этого же пространства, в котором участвуют все точки из этого пространства.

Введем теперь, непосредственно, определение движения.

Определение 2

Движением пространства будем называть отображением пространства на себя, которое сохраняется расстояния между соответствующими точками.

Пример – рисунок 1.

Введем теперь несколько теорем, связанных с понятием движения без доказательства.

При движении отрезок будет отображаться на ему же равный отрезок.

Теорема 2

При движении треугольник будет отображаться на равный ему же треугольник.

Теорема 3

При движении пирамида будет отображаться на равную ей пирамиду.

Основными примерами движений в геометрии являются осевая симметрия, центральная симметрия, зеркальная симметрия, поворот и параллельный перенос. Доказательство того, что параллельный перенос действительно является движением, нами будет рассмотрено ниже.

«Параллельный перенос» 👇

Параллельный перенос

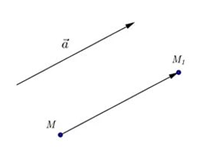
Введем теперь, непосредственно, понятие параллельного переноса на какой-либо вектор. Пусть нам дан вектор $overline{α}$.

Определение 3

Параллельным переносом на вектор $overline{α}$ будем называть такое отображение плоскости само на себя, при котором произвольная точка $M$ отображается на такую точку $M_1$, что выполняется равенство $overline{MM_1}=overline{α}$
(Рис. 2).

Введем следующую теорему, связанную с понятием параллельного переноса.

Теорема 4

Параллельный перенос – движение.

Доказательство.

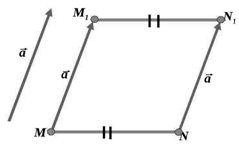
Рассмотрим в пространстве две произвольные точки $M$ и $N$. Будем рассматривать параллельный перенос на данный нам вектор $overline{α}$. Пусть при нашем параллельном переносе данные нам точки отображаются, соответственно, в точки $M_1$ и $N_1$ (рис. 3).

Из определения 3 параллельного переноса получим, что $overline{MM_1}=overline{a}$, а $overline{NN_1 }=overline{a}$, следовательно, получим, что $overline{MM_1}=overline{NN_1}$.

Тогда, из определения равных векторов будем получать, что

$|MM_1|=|NN_1|$, $MM_1||NN_1$

Получаем, что четырехугольник $MM_1N_1N$ будет являться параллелограммом и, как следствие, верно равенство: $|MN|=|M_1N_1|$. Отсюда получаем, что параллельный перенос будет сохранять расстояния, что и доказывает нашу теорему.

Пример задачи

Пример 1

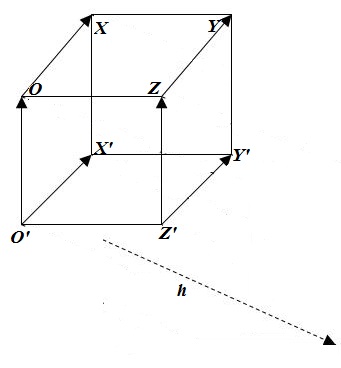
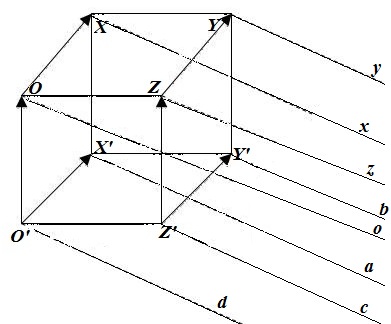
Постройте параллельный перенос куба на вектор $overline{h}$, изображенных на рисунке 4.

Решение.

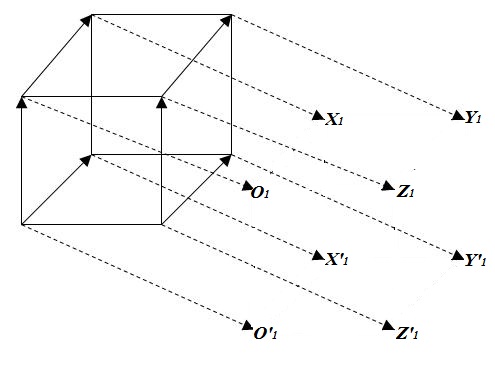
Для построения параллельного переноса сначала проведем через все точки тетраэдра прямые, параллельные заданному нам вектору $overline{h}$ (рис. 5).

Далее, для построения будем использовать определение 3. Точка $X$ перейдет в такую точку $X_1$, которая будет принадлежать прямой $x$. Точка $Y$ перейдет в такую точку $Y_1$, которая будет принадлежать прямой $y$. Точка $Z$ перейдет в такую точку $Z_1$, которая будет принадлежать прямой $z$. Точка $O$ перейдет в такую точку $O_1$, которая будет принадлежать прямой $o$. Точка $X’$ перейдет в такую точку $X’_1$, которая будет принадлежать прямой $a$. Точка $Y’$ перейдет в такую точку $Y’_1$, которая будет принадлежать прямой $b$. Точка $Z’$ перейдет в такую точку $Z’_1$, которая будет принадлежать прямой $c$. Точка $O’$ перейдет в такую точку $O’_1$, которая будет принадлежать прямой $o’$. Причем будут выполняться равенства:

$overline{XX_1}=overline{h}$, $overline{YY_1}=overline{h}$, $overline{ZZ_1}=overline{h}$, $overline{OO_1}=overline{h}$, $overline{X’X’_1}=overline{h}$, $overline{Y’Y’_1}=overline{h}$, $overline{Z’Z’_1}=overline{h}$, $overline{O’O’_1}=overline{h}$

Отметим эти точки (рис. 6).

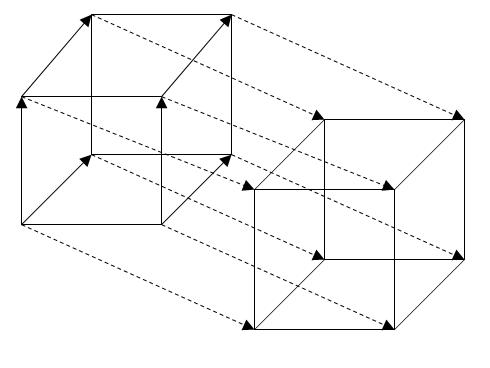
Соединив эти точки между собой, мы и получим искомый нами параллельный перенос на вектор $overline{h}$ (рис. 7).

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Добавить комментарий