- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Законы сложения векторов. Правило параллелограмма
Теорема
Доказательство
Дано:  ,
,  и
и  .
.
Доказать: 10.  +
+  =
=  +
+  ; 20. (
; 20. ( +
+  ) +
) +  =
=  + (
+ ( +
+  ).
).
Доказательство:
10. Пусть векторы  и
и  коллинеарны.
коллинеарны.
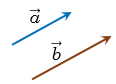
От произвольной точки А отложим векторы  =
=  и
и  =
=  , т.е. векторы
, т.е. векторы  и
и  будут лежать на одной прямой и на той же прямой от точки А отложим векторы
будут лежать на одной прямой и на той же прямой от точки А отложим векторы 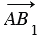 =
=  и
и 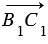 =
=  .
.
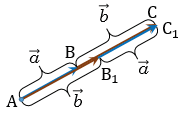
 +
+  =
= 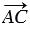 ,
,  +
+  =
= 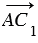 , тогда
, тогда 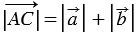 ,
, 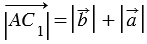 , при этом
, при этом 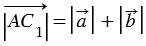 , так как модуль вектора – это длина отрезка, следовательно,
, так как модуль вектора – это длина отрезка, следовательно, 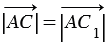 . Поэтому точки С и С1 совпадают, значит,
. Поэтому точки С и С1 совпадают, значит, 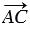 =
= 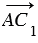 (по определению равных векторов), значит,
(по определению равных векторов), значит,  +
+  =
=  +
+  .
.
Пусть теперь векторы  и
и  не коллинеарны.
не коллинеарны.
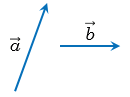
От произвольной точки А отложим векторы  =
=  и
и 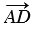 =
=  и на этих векторах построим параллелограмм АВСD. Противоположные стороны ВС и АD параллелограмма равны, при этом векторы
и на этих векторах построим параллелограмм АВСD. Противоположные стороны ВС и АD параллелограмма равны, при этом векторы  и
и 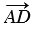 сонаправлены, следовательно,
сонаправлены, следовательно,  =
= 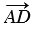 =
=  (по определению равных векторов), также DC = АВ (противоположные стороны параллелограмма) и векторы
(по определению равных векторов), также DC = АВ (противоположные стороны параллелограмма) и векторы 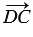 и
и  сонаправлены, следовательно,
сонаправлены, следовательно, 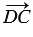 =
=  =
=  .
.
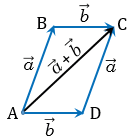
По правилу треугольника 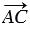 =
=  +
+  =
=  +
+  . Аналогично
. Аналогично 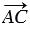 =
= 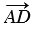 +
+ 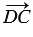 =
=  +
+  , поэтому
, поэтому  +
+  =
=  +
+  .
.
20. От произвольной точки А отложим вектор  =
=  , от точки В – вектор
, от точки В – вектор  =
=  , а от точки С – вектор
, а от точки С – вектор 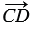 =
=  .
.
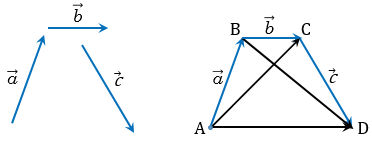
Применяя правило треугольника, получим:
( +
+  ) +
) +  = (
= ( +
+  ) +
) + 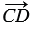 =
= 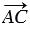 +
+ 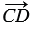 =
= 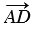 ,
,
 + (
+ ( +
+  ) =
) =  + (
+ ( +
+ 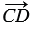 ) =
) =  +
+ 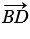 =
= 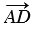 .
.
Следовательно, ( +
+  ) +
) +  =
=  + (
+ ( +
+  ).
).
Теорема доказана.
Правило параллелограмма

Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Сумма нескольких векторов
Вычитание векторов
Произведение вектора на число
Применение векторов к решению задач
Средняя линия трапеции
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 762,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 763,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 764,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 770,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 784,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 785,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 802,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 907,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Сложение векторов по правилу параллелограмма
Даны векторы
a→
и
b→
. Если векторы
a→
и
b→
исходят из одной точки, то вектор суммы
c→
исходит из общей начальной точки векторов и является диагональю параллелограмма, сторонами которого являются векторы
a→
и
b→
.
Запись:
или
AB→+AD→=AC→
.
Такой приём сложения векторов называется правилом параллелограмма.
Так как
DC→=AB→=b→
, то
a→+b→=AD→+DC→=AC→=c→
; выполняя сложение по правилу треугольника, убедимся, что суммой остаётся тот же вектор
c→
. Поэтому оба способа сложения равноценны.
1. Для любых двух векторов
a→
и
b→
в силе равенство
a→+b→=b→+a→
(коммутативный, или переместительный, закон сложения).
2. Для любых трёх векторов
a→
,
b→
,
c→
в силе равенство
a→+b→+c→=a→+b→+c→
(ассоциативный, или сочетательный, закон сложения).
Сложение векторов по правилу параллелограмма
Правило параллелограмма — что это такое
Чтобы сложить два вектора можно воспользоваться правилом параллелограмма.
Правило параллелограмма: если два неколлинеарных вектора a и b привести к общему началу, то вектор c=a+b совпадает с диагональю параллелограмма, построенного на векторах a и b. Начало вектора c совпадает с началом этих векторов.
Кроме того, по правилу параллелограмма можно осуществлять вычитание.
Сложение векторов по правилу параллелограмма
Для того чтобы сложить два вектора по правилу параллелограмма, необходимо:
- Взять произвольную точку А.
- Отложить от точки векторы a и b.
- Построить на векторах a и b параллелограмм.
- Диагональ параллелограмма и будет суммой векторов a+b
Также существуют еще два правила нахождения векторной суммы:
1. Правило треугольника.
Чтобы сложить два вектора, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор и построить вектор, который соединит начало первого с концом второго. Полученный вектор — искомая сумма.
2. Правило многоугольника.
Чтобы сложить несколько векторов, нужно от произвольной точки отложить первый вектор, из его конца — второй вектор, из конца второго — третий, и так далее. Затем соединить начальную точку с концом последнего вектора, полученный вектор — искомая сумма.
Переместительный и сочетательный законы, доказательство
Для более ясного понимания правила параллелограмма, важно знать законы сложения векторов.
Переместительный закон: от перемены мест слагаемых сумма не меняется a+b=b+a.
От произвольной точки A отложим векторы AB=a и AD=b.
Построим параллелограмм ABCD.
По правилу треугольника заметим: AC=AB+BC, то есть равен сумме векторов a+b.
AC=AB+BC, AC=a+b⇒ a+b=b+a.
С другой стороны, AC=AD+DC, AC=b+a.
Что и требовалось доказать.
Именно переместительный закон применяется в правиле параллелограмма.
Сочетательный закон: (a+b)+c=a+(b+c).
От произвольной точки A отложим вектор AB=a, от точки B вектор BC=b, от точки C вектор CD=c.
Запишем сумму (a+b)+c через векторы:
Сумма AB+BC=AC (по правилу треугольника).
Запишем сумму a+(b+c) через векторы:
Что и требовалось доказать.
Примеры решения задач
Дан параллелограмм, построенный на векторах AB=6 см, BC=8 см. ∠B=90º. Найти сумму векторов AB+BC.
По правилу параллелограмма сумма векторов AB+BC=BD.
BD-диагональ параллелограмма. Диагональ можно найти по формуле:
B D = √ ( A B ² + B C ² – 2 * A B * B C * cos B ) .
ABCD — прямоугольник, так как ∠B=90º ⇒cosB=0.
Векторы на ЕГЭ по математике. Действия над векторами

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения  направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.
направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор  .
.

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается:  или
или 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами: 
Здесь в скобках записаны координаты вектора  – по x и по y .
– по x и по y .
Находятся они просто: координата конца вектора минус координата его начала.

Если координаты вектора заданы, его длина находится по формуле

Сложение векторов
Для сложения векторов есть два способа.
1 . Правило параллелограмма. Чтобы сложить векторы  и
и  , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов
, помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов  и
и  .
.

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы  и
и  . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов
. К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов  и
и  .
.

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов  и
и  получаем:
получаем:


Вычитание векторов
Вектор  направлен противоположно вектору
направлен противоположно вектору  . Длины векторов
. Длины векторов  и
и  равны.
равны.

Теперь понятно, что такое вычитание векторов. Разность векторов  и
и  – это сумма вектора
– это сумма вектора  и вектора
и вектора  .
.

Умножение вектора на число
При умножении вектора  на число k получается вектор, длина которого в k раз отличается от длины
на число k получается вектор, длина которого в k раз отличается от длины  . Он сонаправлен с вектором
. Он сонаправлен с вектором  , если k больше нуля, и направлен противоположно
, если k больше нуля, и направлен противоположно  , если k меньше нуля.
, если k меньше нуля.

Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов  и
и  :
:

Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
Сложение и вычитание векторов
Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec – vec = vec <0>)
Длина нулевого вектора равна нулю:
( left| vec <0>right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec – vec = left( <- , – , – > right) )
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vektory-na-ege-po-matematike-v-zadache-v6-dejstviya-nad-vektorami/
http://calcsbox.com/post/slozenie-i-vycitanie-vektorov.html
[/spoiler]
2.1. Скалярные и векторные величины
Скалярная
величина
– это физическая величина, которая
имеет только одну характеристику –
численное значение.
Скалярная
величина может быть положительной или
отрицательной.
Примеры
скалярных величин: температура, масса,
объем, время, плотность. Математические
действия со скалярными величинами –
это алгебраические действия.
![]() Векторная
Векторная
величина
– это физическая величина, которая
имеет две характеристики:
1)
численное значение, которое всегда
положительно (модуль вектора);
2)
направление.
Примеры векторных
физических величин: скорость, ускорение,
сила.
Векторная величина
обозначается латинской буквой и стрелкой
над этой буквой. Например:
-
вектор
скорости обозначается символом
 ,
, -
вектор
ускорения обозначается символом
 ,
, -
вектор
силы обозначается символом
 .
.
Модуль
вектора обозначается так:
![]() или – модуль
или – модуль
вектора
![]() ,
,
![]() или – модуль
или – модуль
вектора
![]() ,
,
![]() или – модуль
или – модуль
вектора
![]() ,
,
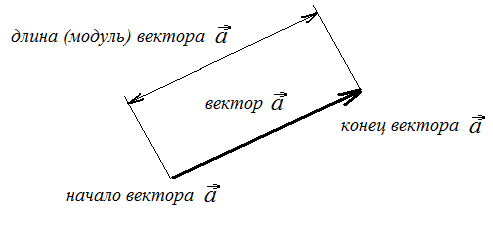
На
рисунке (графически) вектор изображается
направленным отрезком прямой линии.
Модуль вектора равен длине направленного
отрезка в заданном масштабе.
2.2. Действия с векторами
Математические
действия с векторными величинами – это
геометрические действия.
2.2.1 Сравнение векторов
Равные
векторы.
Два вектора
равны, если они имеют:
-
равные
модули, -
одинаковые
направления.
Противоположные
векторы.
Два вектора противоположны, если они
имеют:
-
равные
модули, -
противоположные
направления.
2.2.2 Сложение векторов
Мы
можем сложить два вектора геометрически
по правилу параллелограмма и по правилу
треугольника.
Пусть заданы два
вектора
![]() и
и![]() (см.
(см.
рис.). Найдем сумму этих векторов![]() +
+![]() =
=![]() .
.
Величины![]() и
и![]() – это составляющие векторы, вектор
– это составляющие векторы, вектор![]() – это результирующий вектор.
– это результирующий вектор.
Правило параллелограмма для сложения двух векторов:
1 .
.
Нарисуем вектор![]() .
.
2.
Нарисуем вектор
![]() так,
так,
что его начало совпадает с началом
вектора![]() ;
;
угол между векторами равен![]() (см. рисунок).
(см. рисунок).
3.
Через конец вектора
![]() проведем прямую линию, параллельную
проведем прямую линию, параллельную
вектору![]() .
.
4.
Через конец вектора
![]() проведем прямую линию, параллельную
проведем прямую линию, параллельную
вектору![]() .
.
Мы
построили параллелограмм. Стороны этого
параллелограмма – составляющие векторы
![]() и
и![]() .
.
5.
Проведем диагональ параллелограмма из
общей точки начала вектора
![]() и начала вектора
и начала вектора![]() .
.
6.
Модуль результирующего вектора
![]() равен длине диагонали параллелограмма
равен длине диагонали параллелограмма
и определяется по формуле:
![]() ;
;
начало
вектора
![]() совпадает
совпадает
с началом вектора![]() и началом вектора
и началом вектора![]() (направление
(направление
вектора![]() показано на рисунке).
показано на рисунке).
Правило треугольника для сложения двух векторов:

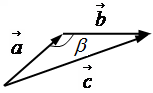
1.
Нарисуем составляющие векторы
![]() и
и![]() так, что начало вектора
так, что начало вектора![]() совпадает с концом вектора
совпадает с концом вектора![]() .
.
При этом угол между векторами равен![]() .
.
2.
Результирующий вектор
![]() направлен
направлен
так, что его начало совпадает с началом
вектора![]() ,
,
а конец совпадает с концом вектора![]() .
.
3.
Модуль результирующего вектора находим
по формуле:
![]()
2.2.3
Вычитание векторов
Вычитание векторов
– это действие, обратное сложению:
![]()
Найти разность
вектора
![]() и вектора
и вектора![]() – это тоже самое, что найти сумму вектора
– это тоже самое, что найти сумму вектора![]() и вектора
и вектора![]() ,
,
противоположного вектору![]() .
.
Мы можем найти вектор разности
геометрически по правилу параллелограмма
или по правилу треугольника (см. рис.).
Правило
параллелограмма.
Стороны параллелограмма
– вектор
![]() и вектор –
и вектор –![]() ;
;
диагональ параллелограмма – вектор
разности![]() .
.

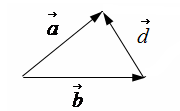
Правило
треугольника.
Вектор разности
![]() соединяет конец вектора
соединяет конец вектора![]() и конец вектора
и конец вектора![]() (начало
(начало
вектора![]() совпадает с концом вектора
совпадает с концом вектора![]() ).
).
![]()
2.2.4
Умножение вектора на скаляр
Пусть заданы вектор
![]() и скалярn.
и скалярn.
Найдем произведение вектора
![]() и скалярного вектораn.
и скалярного вектораn.
В
результате умножения вектора на скаляр
мы получаем новый вектор
![]() :
:![]()
Направление
вектора
![]() такое же, как направление вектора
такое же, как направление вектора![]() при
при![]() .
.
Направление
вектора
![]() противоположно направлению вектора
противоположно направлению вектора![]() при
при![]() .
.
Модуль
вектора
![]() вn
вn
раз больше модуля вектора![]() ,
,
если![]() .
.
2.3. Скалярное и
векторное произведения
2.3.1
Скалярное произведение
Из
двух векторов
![]() и
и![]() можно
можно
образовать скаляр по правилу:
![]()
Это
выражение называется скалярным
произведением векторов
![]() и
и![]() и обозначается одним из символов
и обозначается одним из символов![]() ,
,
или![]() .
.
Следовательно,
![]() .
.![]() =
=![]() .
.
По определению
скалярное произведение обладает
следующими свойствами:
1)
![]() ,
,
2)
![]() ,
,
3)
![]()
2.3.2
Векторное произведение
Из двух векторов
![]()
и
![]() можно
можно
образовать новый вектор:
![]() ,
,
где

Модуль
нового результирующего вектора находим
по формуле:
![]() .
.
Эта операция
называется векторным произведением
векторов
![]() и
и![]() и обозначается одним из символов
и обозначается одним из символов![]() или
или![]() .
.
Также общеизвестна
формула
![]() ,
,
где
![]() – угол между векторами
– угол между векторами![]() и
и![]() .
.
Направление
вектора
![]() можно найти, используя следующий прием.
можно найти, используя следующий прием.
Мысленно совмещаем продольную ось
буравчика (правого винта, штопора) с
перпендикуляром к плоскости, в которой
лежат перемножаемые векторы (в данном
примере – векторы
![]()
и
![]()
). Затем начинаем вращать головку винта
(ручку штопора) по направлению кратчайшего
поворота от первого сомножителя ко
второму, то есть от вектора
![]()
к вектору
![]() .
.
Направление движения тела винта и будет
являться направлением вектора
![]() .
.
Этот прием называетсяправилом
правого винта или правилом буравчика
(см.
рис.).

В терминах векторного
произведения выражаются момент силы,
момент импульса и др. Говоря о векторе,
всегда имеем ввиду его компоненты.
Вектор, в отличие от скаляра, определяется
тремя числами. Поэтому такие операции
как сложение, вычитание, скалярное и
векторное произведения сводятся к
привычным действиям с компонентами.
Соседние файлы в папке Введение в физику
- #
- #
- #
- #
- #
- #
С
прошлых уроков вам уже известно, что векторы можно складывать и делать это вы
уже умеете с помощью правила треугольника.
Для
того, чтобы изобразить вектор суммы двух векторов и
,
от некоторой точки А откладывают вектор .
Далее от точки B откладывают
вектор .
Тогда вектор .
Для
дальнейшей работы с векторами нам понадобится знание следующих законов сложения
векторов.
Сумма
векторов .
Этот закон называют переместительным законом: от перемены мест
слагаемых сумма не меняется.
И
ещё один закон. .
Этот закон называют сочетательным законом.
По
очереди докажем каждый из них.
Рассмотрим
переместительный закон для неколлинеарных векторов и
.
Доказательство.
Итак,
от произвольной точки А отложим вектор ,
и вектор .
На
этих векторах построим параллелограмм ABCD.
А
теперь, пользуясь правилом треугольника сложения двух векторов, заметим, что ,
то есть равен сумме векторов .
,
С
дугой стороны, ,
Отсюда
можем сделать вывод, что сумма векторов равна
сумме векторов .
Что
и требовалось доказать.
Теперь
перейдём к доказательству сочетательного закона для трёх неколлинеарных
векторов ,
,
.
От
произвольной точки А отложим Вектор ,
равный вектору .
От точки B отложим вектор ,
равный вектору .
А от точки C отложим вектор ,
равный вектору .
Рассмотрим
левую часть равенства, выражающего сочетательный закон. Запишем вектора ,
,
как
.
В
скобках записана сумма векторов .
Пользуясь правилом треугольника, можем записать, что эта сумма равна вектору .
А
сумма вектора и
,
в свою очередь, по правилу треугольника равна вектору .
Теперь
аналогично поступим с правой частью равенства, задающего сочетательный закон.
По
правилу треугольника .
Отсюда
делаем вывод, .
Что
и требовалось доказать.
Вернёмся
к рисунку из доказательства переместительного закона.
Обратите
внимание, если векторы ,
отложить
от одной точки и построить на них параллелограмм, то диагональ этого
параллелограмма задаёт вектор суммы векторов и
.
Такое
правило сложения векторов называют правилом параллелограмма.
Изобразим
вектор суммы для каждой пары векторов, пользуясь правилом параллелограмма.
Первым
изобразим вектор суммы векторов и
.
Отложим
от произвольной точки А вектор ,
равный вектору .
Далее
от точки А отложим вектор ,
равный вектору .
Теперь
на этих векторах построим параллелограмм ABCD.
Вектор является
вектором суммы векторов и
.
Далее
изобразим вектор суммы векторов и
.
Обратите
внимание, что каждый раз вектор суммы берёт своё начала из точки начала обоих
векторов-слагаемых.
Последним изобразим
вектор суммы векторов и
.
Задача.
В треугольнике сторона
равна
,
—
,
а .
Найти
длину векторов и
.
Решение.
Ответ:
,
.
Давайте
подведём итоги нашего урока.
Сегодня
вы познакомились с законами сложения векторов. А именно с переместительным и
сочетательным законами сложения векторов. А так же освоили правило
параллелограмма для сложения двух векторов.
Оно заключается в следующем: чтобы сложить
неколлинеарные векторы и
,
нужно отложить от произвольной точки А векторы и
равные
векторам и
соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор
равен
сумме векторов и
.
