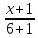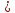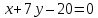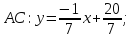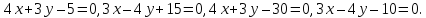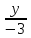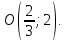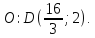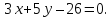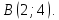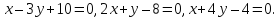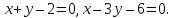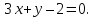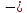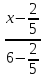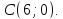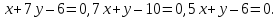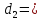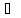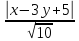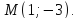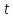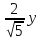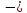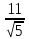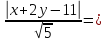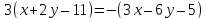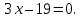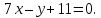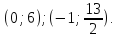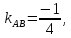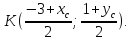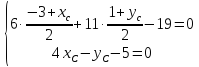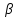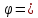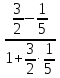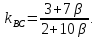2.2.5. Нормальный вектор прямой
Или вектор нормали.
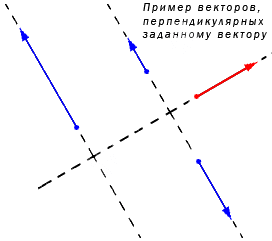
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением в декартовой системе координат, то вектор
является вектором нормали данной прямой.
Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора приходилось аккуратно «вытаскивать» из уравнения, то координаты вектора нормали
достаточно просто «снять».
Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».


| Оглавление |
Автор: Aлeксaндр Eмeлин
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а1 параллельные, а n→ считается нормальным вектором прямой a, также считается нормальным вектором для прямой a1. Когда прямая а имеет прямой вектор, тогда вектор t·n→ является ненулевым при любом значении параметра t, причем также является нормальным для прямой a.
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость Оху, то множеством векторов для Ох является координатный вектор j→. Он считается ненулевым и принадлежащим координатной оси Оу, перпендикулярной Ох. Все множество нормальных векторов относительно Ох можно записать, как t·j→, t∈R, t≠0.
Прямоугольная система Oxyz имеет нормальный вектор i→, относящийся к прямой Оz. Вектор j→ также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный Оz, считается нормальным для Oz.
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат Оху выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения Ax+By+C=0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2x+7y-4=0_, найти координаты нормального вектора.
Решение
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2, 7.
Ответ: 2, 7.
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y-3=0.
Решение
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0·x+1·y-3=0. Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0, 1.
Ответ: 0, 1.
Если дано уравнение в отрезках вида xa+yb=1 или уравнение с угловым коэффициентом y=k·x+b, тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x13-y=1.
Решение
Для начала необходимо перейти от уравнения в отрезках x13-y=1 к уравнению общего вида. Тогда получим, что x13-y=1 ⇔3·x-1·y-1=0.
Отсюда видно, что координаты нормального вектора имеют значение 3, -1.
Ответ: 3, -1.
Если прямая определена каноническим уравнением прямой на плоскости x-x1ax=y-y1ay или параметрическим x=x1+ax·λy=y1+ay·λ, тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a→=(ax, ay). Возможность нахождения координат нормального вектора n→ возможно, благодаря условию перпендикулярности векторов n→ и a→.
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax·(y-y1)⇔ay·x-ax·y+ax·y1-ay·x1x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔ay·x-ax·y+ax·y1-ay·x1=0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x-27=y+3-2.
Решение
Из прямой x-27=y+3-2 понятно, что направляющий вектор будет иметь координаты a→=(7, -2). Нормальный вектор n→=(nx, ny) заданной прямой является перпендикулярным a→=(7, -2).
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a→=(7, -2) и n→=(nx, ny) запишем a→, n→=7·nx-2·ny=0.
Значение nx – произвольное , следует найти ny. Если nx=1, отсюда получаем, что 7·1-2·ny=0⇔ny=72.
Значит, нормальный вектор имеет координаты 1, 72.
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x-27=y+3-2⇔7·(y+3)=-2·(x-2)⇔2x+7y-4+73=0
Полученный результат координат нормального вектора равен 2, 7.
Ответ: 2, 7 или 1, 72.
Указать координаты нормального вектора прямой x=1y=2-3·λ.
Решение
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x=1y=2-3·λ⇔x=1+0·λy=2-3·λ⇔λ=x-10λ=y-2-3⇔x-10=y-2-3⇔⇔-3·(x-1)=0·(y-2)⇔-3·x+0·y+3=0
Отсюда видно, что координаты нормального вектора равны -3, 0.
Ответ: -3, 0.
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат Охуz.
Когда прямая задается при помощи уравнений пересекающихся плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, тогда нормальный вектор плоскости относится к A2x+B2y+C2z+D2=0 и A2x+B2y+C2z+D2=0, тогда получаем запись векторов в виде n1→=(A1, B1, C1) и n2→=(A2, B2, C2).
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x-x1ax=y-y1ay=z-z1az или параметрического, имеющего вид x=x1+ax·λy=y1+ay·λz=z1+az·λ, отсюда ax, ay и az считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a→=(ax, ay, az). Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a→=(ax, ay, az).
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.
Замечание 1
Нормаль – синоним для слова перпендикуляр.
Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.
Можно выразить уравнение прямой и другим способом:
$y = kx + b$.
Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ – в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ
Нормальное уравнение прямой можно выразить и в тригонометрическом виде:
$x cdot cos{alpha} + y cdot sin{alpha} – p = 0$
где $alpha$ – угол между прямой и осью абсцисс, а $p$ – расстояние от начала координат до рассматриваемой прямой.
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:
- когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
- когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
- когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
- для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.
«Нормальный вектор прямой» 👇
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.
Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:
$y – y_0 = k cdot (x – x_0)$
Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой – самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.
Определение 1
Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.
Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.
Обозначив нормальный вектор прямой как $vec{n}(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как
$n_1 cdot (x – x_n) + n_2 cdot (y – y_0) = 0$
Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат
$Ax + By + C = 0$,
то нормальный вектор описывается формулой:
$bar{n}(A; B)$.
При этом говорят, что координаты нормального вектора “снимаются” с уравнения прямой.
Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar{p}(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar{p}(p_1; p_2)$ и точке $M_0(x_0; y_0)$:
$frac{x – x_0}{p_1} = frac{y – y_0}{p_2}$
В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:
$bar{p} cdot bar{n} = -B cdot A + A cdot B = 0 implies bar{p} perp bar{n}$
Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar{n}(A; B)$, можно выразить уравнение прямой в следующем виде:
$A(x – x_0) + B(y – y_0) = 0$
Пример 1
Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.
Для решения задействуем формулу $A cdot (x – x_0) + B cdot (y – y_0) = 0$
Подставив значения, получаем:
$3 cdot (x – (-1)) – (-1) cdot (y – (-3)) = 0$
$3 cdot (x + 1) – (y + 3) = 0$
$3x + 3 – y – 3 = 0$
$3x – y = 0$
Проверить правильность общего уравнения прямой можно “сняв” из него координаты для нормального вектора:
$3x – y = 0 implies A = 3; B = -1 implies bar{n}(A; B) = bar{n}(3; -1),$
Что соответствует числам исходных данных.
Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x – y = 0$:
$3 cdot (-1) – (-3) = 0$
Равенство верно. Осталось лишь найти формулу направляющего вектора:
$bar{p}(-B; A) implies bar{p}(1; 3)$
Ответ: $3x – y = 0; bar{p}(1; 3).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением 

Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора 

Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».
Нахождение вектора, перпендикулярного данному вектору, примеры и решения
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Скалярное произведение двух ненулевых векторов a → и b → равном нулю для выполнения равенства a → , b → = 0 достаточно для их перпендикулярности.
Пусть заданные векторы a → и b → перпендикулярны, тогда выполним доказательство равенства a ⇀ , b → = 0 .
Из определения про скалярное произведение векторов мы знаем, что оно равняется произведению длин заданных векторов на косинус угла между ними. По условию a → и b → перпендикулярны, а, значит, исходя из определения, угол между ними 90 ° . Тогда имеем a → , b → = a → · b → · cos ( a → , b → ^ ) = a → · b → · cos 90 ° = 0 .
Вторая часть доказательства
При условии, когда a ⇀ , b → = 0 доказать перпендикулярность a → и b → .
По сути доказательство является обратным предыдущему. Известно, что a → и b → ненулевые, значит, из равенства a ⇀ , b → = a → · b → · cos ( a → , b → ) ^ найдем косинус. Тогда получим cos ( a → , b → ) ^ = ( a → , b → ) a → · b → = 0 a → · b → = 0 . Так как косинус равен нулю, можем сделать вывод, что угол a → , b → ^ векторов a → и b → равен 90 ° . По определению это и есть необходимое и достаточное свойство.
Условие перпендикулярности на координатной плоскости
Раздел скалярного произведения в координатах демонстрирует неравенство ( a → , b → ) = a x · b x + a y · b y , справедливое для векторов с координатами a → = ( a x , a y ) и b → = ( b x , b y ) , на плоскости и ( a → , b → ) = a x · b x + a y · b y для векторов a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид a x · b x + a y · b y = 0 , для трехмерного пространства a x · b x + a y · b y + a z · b z = 0 .
Применим на практике и рассмотрим на примерах.
Проверить свойство перпендикулярности двух векторов a → = ( 2 , – 3 ) , b → = ( – 6 , – 4 ) .
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
( a → , b → ) = a x · b x + a y · b y = 2 · ( – 6 ) + ( – 3 ) · ( – 4 ) = 0 . Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.
Ответ: да, заданные векторы a → и b → перпендикулярны.
Даны координатные векторы i → , j → , k → . Проверить, могут ли векторы i → – j → и i → + 2 · j → + 2 · k → быть перпендикулярными.
Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i → – j → и i → + 2 · j → + 2 · k → имеются соответствующие координаты ( 1 , – 1 , 0 ) и ( 1 , 2 , 2 ) . Подставляем числовые значения и получаем: i → + 2 · j → + 2 · k → , i → – j → = 1 · 1 + ( – 1 ) · 2 + 0 · 2 = – 1 .
Выражение не равно нулю, ( i → + 2 · j → + 2 · k → , i → – j → ) ≠ 0 , а это означает, что векторы i → – j → и i → + 2 · j → + 2 · k → не перпендикулярны, так как условие не выполнилось.
Ответ: нет, векторы i → – j → и i → + 2 · j → + 2 · k → не перпендикулярны.
Даны векторы a → = ( 1 , 0 , – 2 ) и b → = ( λ , 5 , 1 ) . Найти значение λ , при котором данные векторы перпендикулярны.
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · λ + 0 · 5 + ( – 2 ) · 1 = 0 ⇔ λ = 2
Ответ: векторы перпендикулярны при значении λ = 2 .
Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.
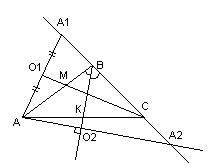
Дан треугольник А В С со сторонами А В = 8 , А С = 6 , В С = 10 см. проверить на перпендикулярность векторы A B → и A C → .
При перпендикулярности векторов A B → и A C → треугольник A B C считается прямоугольным. Тогда применим теорему Пифагора, где В С – гипотенуза треугольника. Равенство B C 2 = A B 2 + A C 2 должно выполниться. Отсюда следует, что 10 2 = 8 2 + 6 2 ⇔ 100 = 100 . Значит, А В и А С являются катетами треугольника А В С , следовательно, A B → и A C → перпендикулярны.
Нахождение вектора, перпендикулярного данному
Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Нахождение вектора, перпендикулярного данному в плоскости.
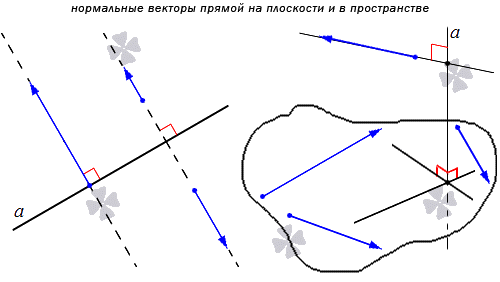
Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.
Задан ненулевой вектор a → , лежащий на прямой а. Тогда заданный b → , расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным и a → . Если вектору i → перпендикулярен вектор j → или любой из векторов λ · j → при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b → , перпендикулярному a → = ( a x , a y ) , сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a → = ( a x , a y ) . Для этого необходимо записать условие перпендикулярности векторов в такой форме a x · b x + a y · b y = 0 . Имеем b x и b y , являющиеся искомыми координатами перпендикулярного вектора. Когда a x ≠ 0 , значение b y является ненулевым, а b x вычислим из неравенства a x · b x + a y · b y = 0 ⇔ b x = – a y · b y a x . При a x = 0 и a y ≠ 0 присваиваем b x любое значение кроме нуля, а b y находим из выражения b y = – a x · b x a y .
Дан вектор с координатами a → = ( – 2 , 2 ) . Найти перпендикулярный данному вектор.
Обозначим искомый вектор как b → ( b x , b y ) . Найти его координаты можно из условия перпендикулярности векторов a → и b → . Тогда получим: ( a → , b → ) = a x · b x + a y · b y = – 2 · b x + 2 · b y = 0 . Присвоим b y = 1 и подставим: – 2 · b x + 2 · b y = 0 ⇔ – 2 · b x + 2 = 0 . Отсюда из формулы получим b x = – 2 – 2 = 1 2 . Значит, вектор b → = ( 1 2 , 1 ) является вектором, перпендикулярным a → .
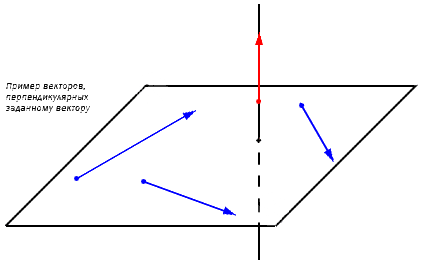
Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a → = ( a x , a y , a z ) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a → , лежащая на прямой a . Перпендикулярную прямой a плоскость обозначаем α . В этом случае любой ненулевой вектор b → из плоскости α перпендикулярен a → .
Необходимо найти координаты b → , перпендикулярного ненулевому вектору a → = ( a x , a y , a z ) .
Пусть задан b → с координатами b x , b y и b z . Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство a x · b x + a y · b y + a z · b z = 0 должно выполняться. Из условия a → – ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что a x ≠ 0 , ( a y ≠ 0 или a z ≠ 0 ). Следовательно, имеем право разделить на эту координату все неравенство a x · b x + a y · b y + a z · b z = 0 , получим выражение b x + a y · b y + a z · b z a x = 0 ⇔ b x = – a y · b y + a z · b z a x . Присваиваем координатам b y и b x любое значение, вычисляем значение b x , исходя из формулы, b x = – a y · b y + a z · b z a x . Искомый перпендикулярный вектор будет иметь значение a → = ( a x , a y , a z ) .
Рассмотрим доказательство на примере.
Дан вектор с координатами a → = ( 1 , 2 , 3 ) . Найти вектор, перпендикулярный данному.
Обозначим искомый вектор за b → = ( b x , b y , b z ) . Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.
a ⇀ , b ⇀ = 0 ⇔ a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · b x + 2 · b y + 3 · b z = 0 ⇔ b x = – ( 2 · b y + 3 · b z )
Если значение b y = 1 , b z = 1 , тогда b x = – 2 · b y – 3 · b z = – ( 2 · 1 + 3 · 1 ) = – 5 . Отсюда следует, что координаты вектора b → ( – 5 , 1 , 1 ) . Вектор b → является одним из перпендикулярных векторов заданному.
Ответ: b → = ( – 5 , 1 , 1 ) .
Нахождение координат вектора, перпендикулярного двум заданным векторам
Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторам a → ( a x , a y , a z ) и b → = ( b x , b y , b z ) . При условии коллинеарности векторов a → и b → в задаче достаточно будет найти вектор, перпендикулярный a → или b → .
При решении применяется понятие векторного произведения векторов.
Векторным произведением векторов a → и b → называют вектор, одновременно перпендикулярный и a → и b → . Для решения данной задачи применяется векторное произведение a → × b → . Для трехмерного пространства имеет вид a → × b → = a → j → k → a x a y a z b x b y b z
Разберем подробнее векторное произведение на примере задачи.
Заданы векторы b → = ( 0 , 2 , 3 ) и a → = ( 2 , 1 , 0 ) . Найти координаты любого перпендикулярного вектора данным одновременно.
Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :
a → × b → = i → j → k → 2 1 0 0 2 3 = i → · 1 · 3 + j → · 0 · 0 + k → · 2 · 2 – k → · 1 · 0 – j → · 2 · 3 – i → · 0 · 2 = 3 · i → + ( – 6 ) · j → + 4 · k →
Ответ: ( 3 , – 6 , 4 ) – координаты вектора, одновременно перпендикулярного заданным a → и b → .
Уравнение перпендикулярной прямой
Альтернативная формула
Прямая, проходящая через точку M1(x1; y1) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением
назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).
Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /9x – 1 /3 (a = 4 /9). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .
Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .
Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-vektora-perpendikuljarnogo-dannomu-vek/
http://math.semestr.ru/line/perpendicular.php
[/spoiler]
Определение.
Любой ненулевой вектор, перпендикулярный
прямой называется её нормальным
вектором,
и обозначается
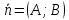
Теорема.
Алгебраическое уравнение 1-й степени
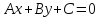
где
коэффициенты
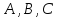
одновременно не равные нулю, являетсяуравнением
прямой на плоскости
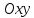
а вектор
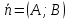
Верно
обратное:
на координатной плоскости
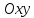
любой прямой с нормальным вектором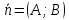
может быть записано в виде алгебраического
уравнения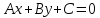
Определение.
Уравнение прямой вида
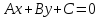
где
коэффициенты
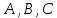
одновременно не равные нулю, называетсяобщим
уравнением прямой.
Известно,
что прямая определяется двумя точками.
Пусть
и
–
точки, лежащие на прямой
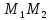
–
произвольная точка этой прямой. Тогда
векторы
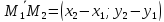
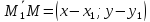
пропорциональны. Получаемуравнение
прямой, проходящей через две точки:
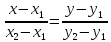
Определение.
Вектор,
параллельный прямой, называется
направляющим
вектором прямой.
Определение.
Пусть
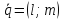
предыдущего уравнения получаемканоническое
уравнение прямой:
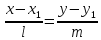
Определение.
В
тех же обозначениях, параметрическое
уравнение прямой
имеет вид:
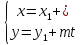
Определение.
Уравнение прямой вида
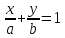
где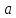
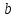
действительные числа, называетсяуравнением
прямой в отрезках.
Теорема.
Пусть
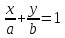
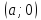
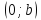
прямой с осями координат.
Определение.
Уравнение прямой вида

где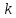
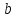
называетсяуравнением
прямой с угловым коэффициентом,
коэффициент
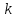
коэффициентом данной
прямой.
Теорема.
Пусть
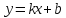
Тогда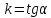
где угол
α
равен углу наклона данной прямой к оси
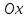
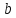
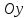
Если
известны угловые коэффициенты
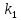
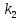
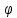
формуле:
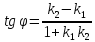
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:
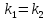
Признаком
перпендикулярности двух прямых является
соотношение:
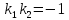
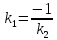
Теорема.
(Связь нормального вектора прямой с её
направляющим вектором и её угловым
коэффициентом.)
1)
Если
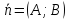
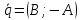
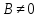
то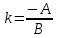
2)
Если
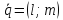
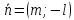
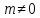
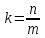
3)
Если
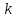
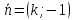
–
направляющий вектор.
Взаимное
расположение двух прямых на плоскости.
Две
прямые на плоскости могут пересекаться,
совпадать или быть параллельными.
Теорема.
Пусть прямые заданы общими уравнениями:
L1: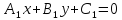
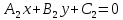
Тогда:
1)
если
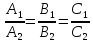
то прямые совпадают, и система уравнений
имеет
бесконечное множество решений;
2)
если
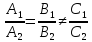
уравнений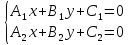
3)
если
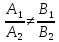
точки их пересечения являются единственным
решением системы уравнений
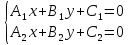
Определение.
Уравнение вида
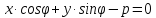
где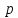
координат, называетсянормальным
уравнением прямой,
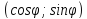
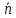
Чтобы
привести прямую к указанному виду,
разделим общее уравнение прямой на
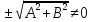
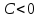
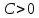
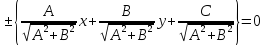
Теорема.
Орт нормального вектора
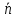
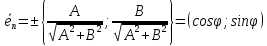
где
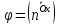
Теорема.
Расстояние от прямой до произвольной
точки
находится
по формуле:
Чтобы
найти расстояние
между двумя параллельными прямыми,
нужно взять произвольную точку на одной
из прямых и найти расстояние от нее до
другой прямой.
Чтобы
найти множество
точек, равноудаленных от двух прямых
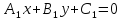
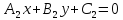
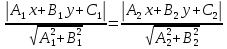
Раскрывая
модули в случае параллельных прямых,
получаем параллельную им прямую, лежащую
между данными прямыми, а в случае
пересекающихся прямых – биссектрисы
углов,
образованных пересечением прямых.
Определение.
Совокупность прямых, проходящих через
некоторую точку S,
называется пучком
прямых с центром S.
Теорема.
Если
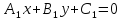
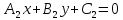
в точкеS,
то уравнение:
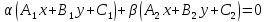
где
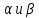
одновременно нулю, определяют прямую,
также проходящую через точкуS.
Более
того, в указанном уравнении числа всегда
возможно подобрать так, чтобы оно
определяло любую (заранее назначенную)
прямую, проходящую через точку S,
иначе говоря, любую прямую пучка с
центром S.
Поэтому уравнение вида называется
уравнением пучка с центром S.
Решение
типовых задач
Задача
№1:
Даны
уравнения двух сторон параллелограмма
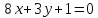
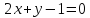
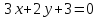
Определить координаты вершин этого
параллелограмма.
Решение:
Найдём
координаты т.
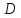
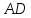
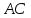
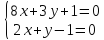
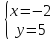
т.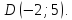
Подставим
координаты т.
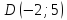
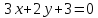
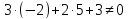
т.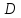
следовательно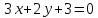
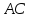
Найдём
координаты т.
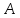
как точки пересечения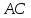
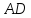
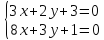
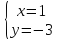
т.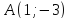
Найдём
координаты т.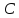
как точки пересечения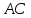
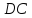
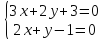

т.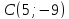
Найдём
координаты т.B:
в параллелограмме диагонали делят друг
друга пополам:
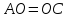
Найдём координаты т.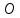
т.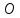
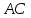
следовательно, т.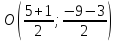
т.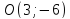
но т.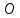
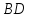
следовательно,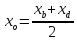
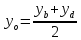
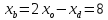
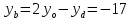
т.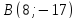
Ответ:
Задача
№2:
Дана
прямая
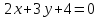
Составить уравнение прямой, проходящей
через точку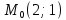
-
параллельно
данной прямой. -
перпендикулярно
к данной прямой.
Решение:
-
Искомая
прямая параллельна прямой
,
поэтому её уравнение имеет вид:.
Найдём
т.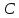
точка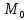
координаты удовлетворяют записанному
уравнению: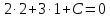
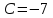
Итак, прямая принимает вид: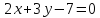
-
Т.к.
заданная и искомые прямые перпендикулярны,
то их угловые коэффициенты удовлетворяют
условию:
.
Найдём
угловой коэффициент прямой
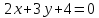
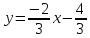
итак,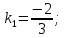
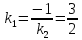
Запишем уравнение искомой прямой: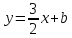
Точка
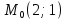
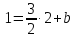
Уравнение
прямой принимает вид:
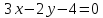
Ответ:
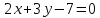
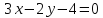
Задача
№3:
Определить,
при каких значениях a
и b
две прямые
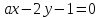
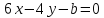
-
имеют
одну общую точку; -
параллельны;
-
совпадают.
Решение:
-
Прямые
имеют одну общую точку, когда они не
параллельны (их коэффициенты при x
и y
не пропорциональны):
;
-
Прямые
параллельны, когда коэффициенты при x
и y
пропорциональны:
;
.
-
Прямые
совпадают, когда все их коэффициенты
пропорциональны:
;
.
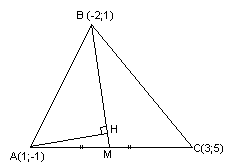
Задача
№4:
Найти
проекцию точки
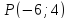
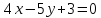
Решение:
Проведём
через т.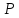
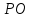
перпендикулярную прямой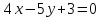
Точка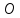
проекцией.
Прямая
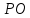
её направляющим вектором служит
нормальный вектор прямой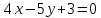
т.е.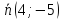
Запишем
уравнение прямой
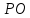
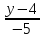
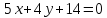
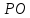
Найдём
координаты т.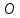
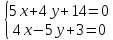
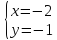
т.
Ответ:
Задача
№5:
Найти
точку
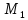
симметричную точке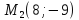
точки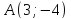
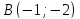
Решение:
Составим
уравнение
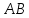
как прямой проходящей через 2 точки:
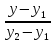
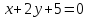
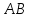
Найдём
уравнение прямой
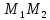
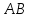
Нормальный
вектор
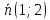
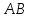
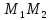
поэтому используем каноническое
уравнение прямой: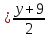
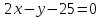
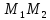
Найдём
координат т.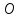
как точки пересечения прямых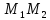
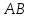
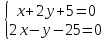
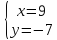
т.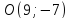
Так
как точка

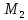
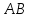
следовательно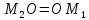
то есть т.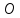
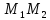
Найдём координаты точки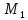
зная начало и середину отрезка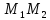
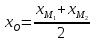
, тогда
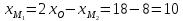
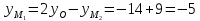
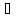
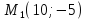
Ответ:
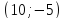
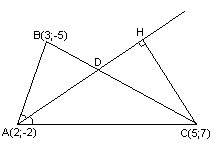
Задача
№6:
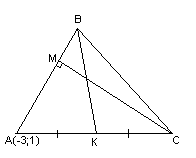
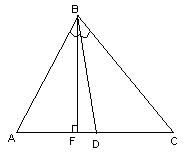
Даны
вершины треугольника
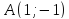
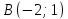
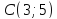
Составить уравнение перпендикуляра,
опущенного из вершины
Решение:
Найдём
координаты т.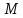
как середины отрезка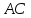
т.
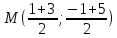
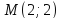
Запишем
уравнение медианы
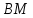
как прямой, проходящей через две известные
точки:
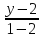
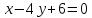
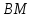
Нормальный
вектор для
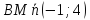
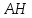
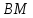
тогда уравнение примет вид:
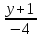
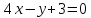
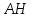
Ответ:
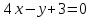
Задача
№7:
Даны
вершины треугольника

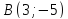
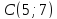
Составить уравнение перпендикуляра,
опущенного из вершины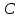
вершине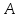
Решение:
Пусть
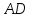
Найдём
координаты т.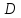
Тогда:
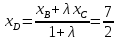
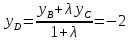
т.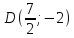
Уравнение
биссектрисы
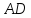
=
⇒
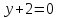
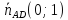
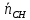
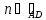
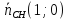
Точка
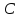
поэтому уравнение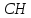
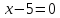
Ответ:
Задача
№8:
Две
стороны квадрата лежат на прямых
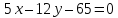
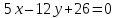
Вычислить его площадь.
Решение:
-
Выберем
на прямой
некоторую точку
:
пусть
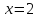
тогда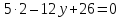
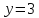
т.е.
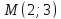
-
Найдём
расстояние от точки
до прямой
:
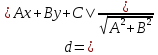
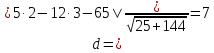
где
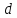
-
т.е.
.
Ответ:
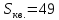
Задача
№9:
Даны
две противоположные вершины квадрата
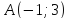
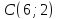
Составить уравнения его сторон.
Решение:
Зная
вершины
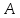

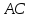
как прямой проходящей через две точки: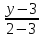
– уравнение прямой
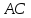
Т.к.
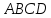
биссектрисами, поэтому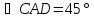
найдём угловой коэффициент
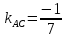
Зная
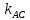

найдём угловой коэффициент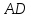
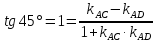
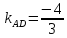
Уравнение
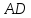
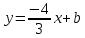
Найдём
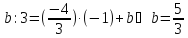
Тогда уравнение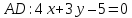
Т.к.
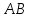
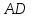
угловой коэффициент
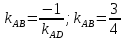
Уравнение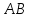
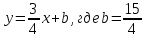
тогда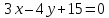
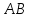
Т.к.
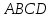
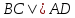
то уравнение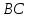
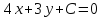
Зная,
что точка
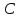
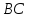
найдём свободный член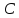
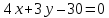
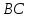
Аналогично
найдём уравнение стороны
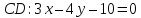
Ответ:
Задача
№10:
Вычислить
площадь треугольника, отсекаемого
прямой
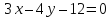
Решение:
Запишем
уравнение прямой
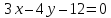
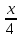
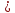
Из
этого уравнения следует, что длины
отрезков
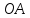
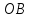
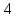
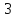
поэтому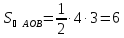
Ответ:
Задача
№11:
Составить
уравнения сторон треугольника, зная
одну из его вершин

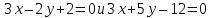
Решение:
Выясним,
что точка
Найдём
координаты точки
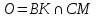
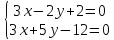
т.
Продолжим
медиану
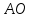
и на её продолжении отложим отрезок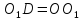
Соединим точку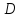
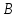
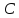
Полученный четырёхугольник
пересекаясь в точке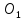
делятся пополам).
Найдём
координаты точки
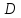
как конца отрезка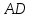

Найдём
уравнение прямой
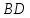
зная, что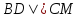

Найдём
координаты вершины
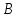
как точки пересечения прямых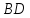
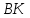
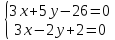
т.
Точка
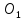
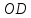
поэтому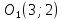
Найдём
координаты точки
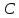
как конца отрезка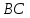
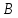
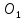
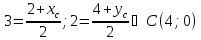
Зная
координаты всех вершин треугольника
найдём уравнения его сторон, как прямых
проходящих через две точки.
Ответ:
Задача
№12:
Составить
уравнения сторон треугольника, зная
одну из его вершин
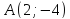
Решение:
Очевидно,
что точка

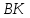
Найдём точку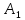
симметричную точке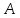
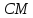
Можно доказать, что точка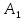
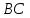
Опустим из т.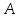
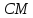
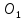
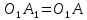
Т.к.
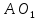
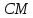
то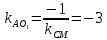
точка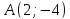
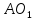
поэтому её уравнение примет вид:
Координаты
точки
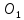
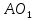
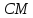
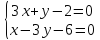
т.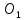
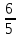
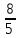
Найдём
координаты точки
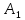
как конца отрезка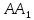
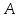
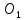
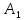
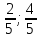
Аналогично
найдём точку
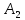
симметричную т.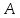
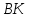
Точка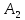
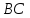
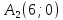
Тогда
уравнение стороны
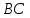
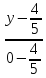
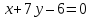
Найдём
координаты точек
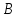
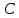
как точек пересечения прямой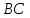
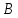
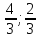
Зная
координаты вершин треугольника
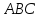
найдём уравнения его сторон.
Ответ:
Задача
№13:
Составить
уравнения биссектрис углов, образованных
двумя пересекающимися прямыми:
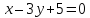
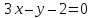
Решение:
Известно
свойство: биссектриса есть геометрическое
место точек, равноудалённых от сторон
угла.
Пусть
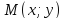
тогда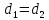
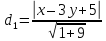
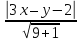
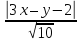
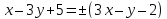
Тогда
уравнения биссектрис примут вид:
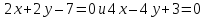
Ответ:
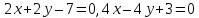
Задача
№14:
Составить
уравнение биссектрисы угла между прямыми
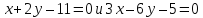
в котором лежит точка
Решение:
Найдём
отклонение точки
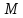
прямых, для этого приведём их уравнения
к нормальному виду: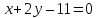
нормирующий множитель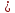
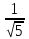
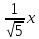
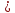
Найдём
отклонение
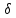
т.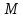
нормального уравнения подставим
координаты т.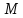
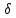
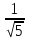
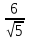
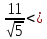
Аналогично
найдём отклонение
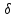
т.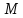
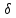
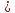
Отклонения имеют разные знаки, поэтому
при раскрытии модулей (см. решение
предыдущей задачи) справа ставим знак
«минус».
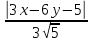
Уравнение
биссектрисы принимает вид:
Ответ:
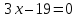
Задача
№15:
На
прямой
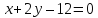
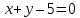
Решение:
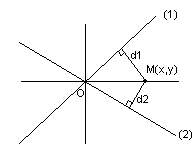
Точки
равноудалённые от прямых
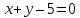
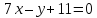
лежат на биссектрисах углов, образованных
этими прямыми. Аналогично решению
предыдущих задач найдём их:
Тогда
искомые точки являются точками пересечения
этих биссектрис и прямой
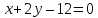
поэтому найдём их, решая системы: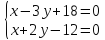
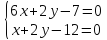
Ответ:
Задача
№16:
Составить
уравнения сторон треугольника, зная
одну из его вершин
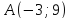
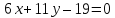
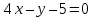
проведённых из различных вершин.
Решение:
Убедимся,
что точка
высоте.
Найдём
уравнение стороны
зная, что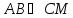
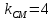
тогда уравнение примет вид:
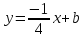
зная координаты т.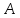
принадлежащей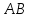
найдём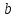
тогда уравнение примет вид: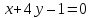
Найдём
координаты т.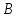
как точки пересечения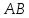
медианы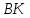
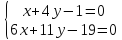
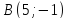
Пусть
точка
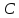
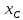
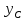
найдём их. Точка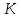
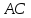
поэтому
Точка
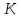
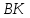
точка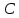
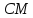
поэтому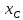
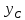
Откуда
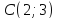
найдём уравнения всех его сторон.
Ответ:
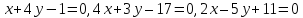
Задача
№17:
Через
точку
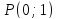
заключённый между прямыми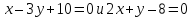
делился бы в точке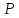
Решение:
Обозначим
через
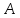
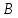
искомой прямой и пусть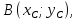
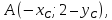
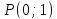
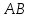
Координаты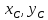
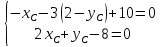
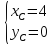
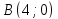
Составим
уравнение искомой прямой, которая
проходит через две точки, например,
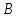
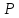
Ответ:
Задача
№18:
Составить
уравнения сторон треугольника
зная одну из его вершин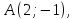
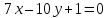
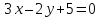
проведённых из одной вершины. Решить
задачу, не вычисляя координат вершин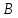
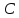
Решение:
Можно
проверить, что т.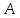
ни биссектрисе.
Найдём уравнение стороны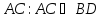
поэтому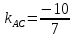
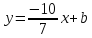
зная координаты т.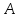
найдём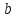
Итак,
уравнение
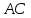
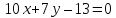
Рассмотрим
пучок с центром в т.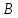
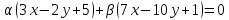
Пусть
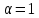
тогда уравнение пучка примет вид:
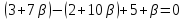
(1)
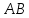
пучка, причём координаты т.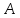
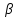
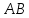
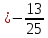
поэтому уравнение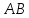
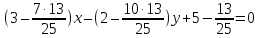
т.е.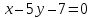
Найдём
угол между прямыми
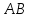
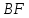
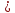
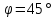
Тогда
угол
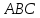
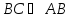
–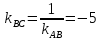
С другой стороны найдём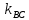
Итак,
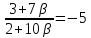
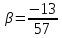
Найдём
уравнение стороны
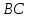
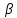
стороны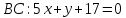
Ответ:
Образовательным
результатом после изучения данной темы
является сформированность компонент,
заявленных во введении, совокупности
компетенций (знать, уметь, владеть) на
двух уровнях: пороговый и продвинутый.
Пороговый уровень соответствует оценке
«удовлетворительно», продвинутый
уровень соответствует оценкам «хорошо»
или «отлично» в зависимости от результатов
защиты кейс-заданий.
Для
самостоятельной диагностики данных
компонент вам предлагаются следующие
задания.




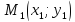
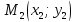


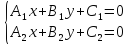
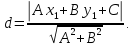

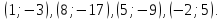
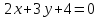 ,
,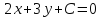 .
.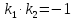 .
.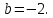
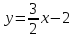
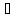
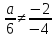 ;
;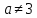
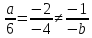 ;
;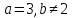 .
.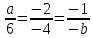 ;
;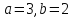 .
.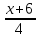
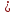
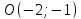
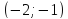
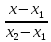
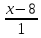
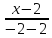
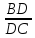
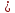
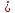
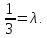
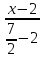
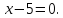
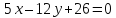 некоторую точку
некоторую точку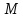 :
: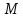 до прямой
до прямой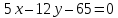 :
: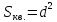 т.е.
т.е.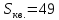 .
.