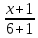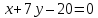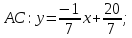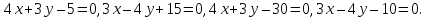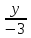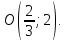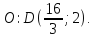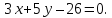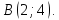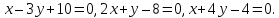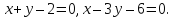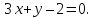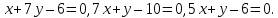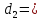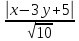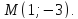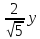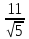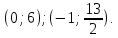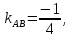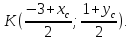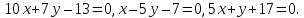Нахождение вектора, перпендикулярного данному вектору, примеры и решения
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Скалярное произведение двух ненулевых векторов a → и b → равном нулю для выполнения равенства a → , b → = 0 достаточно для их перпендикулярности.
Пусть заданные векторы a → и b → перпендикулярны, тогда выполним доказательство равенства a ⇀ , b → = 0 .
Из определения про скалярное произведение векторов мы знаем, что оно равняется произведению длин заданных векторов на косинус угла между ними. По условию a → и b → перпендикулярны, а, значит, исходя из определения, угол между ними 90 ° . Тогда имеем a → , b → = a → · b → · cos ( a → , b → ^ ) = a → · b → · cos 90 ° = 0 .
Вторая часть доказательства
При условии, когда a ⇀ , b → = 0 доказать перпендикулярность a → и b → .
По сути доказательство является обратным предыдущему. Известно, что a → и b → ненулевые, значит, из равенства a ⇀ , b → = a → · b → · cos ( a → , b → ) ^ найдем косинус. Тогда получим cos ( a → , b → ) ^ = ( a → , b → ) a → · b → = 0 a → · b → = 0 . Так как косинус равен нулю, можем сделать вывод, что угол a → , b → ^ векторов a → и b → равен 90 ° . По определению это и есть необходимое и достаточное свойство.
Условие перпендикулярности на координатной плоскости
Раздел скалярного произведения в координатах демонстрирует неравенство ( a → , b → ) = a x · b x + a y · b y , справедливое для векторов с координатами a → = ( a x , a y ) и b → = ( b x , b y ) , на плоскости и ( a → , b → ) = a x · b x + a y · b y для векторов a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид a x · b x + a y · b y = 0 , для трехмерного пространства a x · b x + a y · b y + a z · b z = 0 .
Применим на практике и рассмотрим на примерах.
Проверить свойство перпендикулярности двух векторов a → = ( 2 , — 3 ) , b → = ( — 6 , — 4 ) .
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
( a → , b → ) = a x · b x + a y · b y = 2 · ( — 6 ) + ( — 3 ) · ( — 4 ) = 0 . Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.
Ответ: да, заданные векторы a → и b → перпендикулярны.
Даны координатные векторы i → , j → , k → . Проверить, могут ли векторы i → — j → и i → + 2 · j → + 2 · k → быть перпендикулярными.
Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i → — j → и i → + 2 · j → + 2 · k → имеются соответствующие координаты ( 1 , — 1 , 0 ) и ( 1 , 2 , 2 ) . Подставляем числовые значения и получаем: i → + 2 · j → + 2 · k → , i → — j → = 1 · 1 + ( — 1 ) · 2 + 0 · 2 = — 1 .
Выражение не равно нулю, ( i → + 2 · j → + 2 · k → , i → — j → ) ≠ 0 , а это означает, что векторы i → — j → и i → + 2 · j → + 2 · k → не перпендикулярны, так как условие не выполнилось.
Ответ: нет, векторы i → — j → и i → + 2 · j → + 2 · k → не перпендикулярны.
Даны векторы a → = ( 1 , 0 , — 2 ) и b → = ( λ , 5 , 1 ) . Найти значение λ , при котором данные векторы перпендикулярны.
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · λ + 0 · 5 + ( — 2 ) · 1 = 0 ⇔ λ = 2
Ответ: векторы перпендикулярны при значении λ = 2 .
Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.
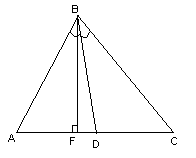
Дан треугольник А В С со сторонами А В = 8 , А С = 6 , В С = 10 см. проверить на перпендикулярность векторы A B → и A C → .
При перпендикулярности векторов A B → и A C → треугольник A B C считается прямоугольным. Тогда применим теорему Пифагора, где В С – гипотенуза треугольника. Равенство B C 2 = A B 2 + A C 2 должно выполниться. Отсюда следует, что 10 2 = 8 2 + 6 2 ⇔ 100 = 100 . Значит, А В и А С являются катетами треугольника А В С , следовательно, A B → и A C → перпендикулярны.
Нахождение вектора, перпендикулярного данному
Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Нахождение вектора, перпендикулярного данному в плоскости.
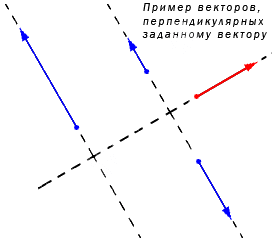
Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.
Задан ненулевой вектор a → , лежащий на прямой а. Тогда заданный b → , расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным и a → . Если вектору i → перпендикулярен вектор j → или любой из векторов λ · j → при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b → , перпендикулярному a → = ( a x , a y ) , сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a → = ( a x , a y ) . Для этого необходимо записать условие перпендикулярности векторов в такой форме a x · b x + a y · b y = 0 . Имеем b x и b y , являющиеся искомыми координатами перпендикулярного вектора. Когда a x ≠ 0 , значение b y является ненулевым, а b x вычислим из неравенства a x · b x + a y · b y = 0 ⇔ b x = — a y · b y a x . При a x = 0 и a y ≠ 0 присваиваем b x любое значение кроме нуля, а b y находим из выражения b y = — a x · b x a y .
Дан вектор с координатами a → = ( — 2 , 2 ) . Найти перпендикулярный данному вектор.
Обозначим искомый вектор как b → ( b x , b y ) . Найти его координаты можно из условия перпендикулярности векторов a → и b → . Тогда получим: ( a → , b → ) = a x · b x + a y · b y = — 2 · b x + 2 · b y = 0 . Присвоим b y = 1 и подставим: — 2 · b x + 2 · b y = 0 ⇔ — 2 · b x + 2 = 0 . Отсюда из формулы получим b x = — 2 — 2 = 1 2 . Значит, вектор b → = ( 1 2 , 1 ) является вектором, перпендикулярным a → .
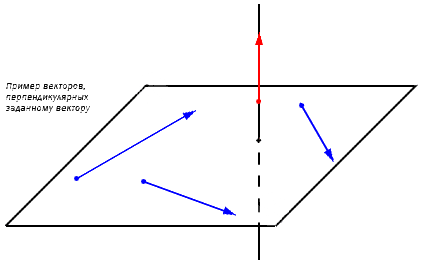
Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a → = ( a x , a y , a z ) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a → , лежащая на прямой a . Перпендикулярную прямой a плоскость обозначаем α . В этом случае любой ненулевой вектор b → из плоскости α перпендикулярен a → .
Необходимо найти координаты b → , перпендикулярного ненулевому вектору a → = ( a x , a y , a z ) .
Пусть задан b → с координатами b x , b y и b z . Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство a x · b x + a y · b y + a z · b z = 0 должно выполняться. Из условия a → — ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что a x ≠ 0 , ( a y ≠ 0 или a z ≠ 0 ). Следовательно, имеем право разделить на эту координату все неравенство a x · b x + a y · b y + a z · b z = 0 , получим выражение b x + a y · b y + a z · b z a x = 0 ⇔ b x = — a y · b y + a z · b z a x . Присваиваем координатам b y и b x любое значение, вычисляем значение b x , исходя из формулы, b x = — a y · b y + a z · b z a x . Искомый перпендикулярный вектор будет иметь значение a → = ( a x , a y , a z ) .
Рассмотрим доказательство на примере.
Дан вектор с координатами a → = ( 1 , 2 , 3 ) . Найти вектор, перпендикулярный данному.
Обозначим искомый вектор за b → = ( b x , b y , b z ) . Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.
a ⇀ , b ⇀ = 0 ⇔ a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · b x + 2 · b y + 3 · b z = 0 ⇔ b x = — ( 2 · b y + 3 · b z )
Если значение b y = 1 , b z = 1 , тогда b x = — 2 · b y — 3 · b z = — ( 2 · 1 + 3 · 1 ) = — 5 . Отсюда следует, что координаты вектора b → ( — 5 , 1 , 1 ) . Вектор b → является одним из перпендикулярных векторов заданному.
Ответ: b → = ( — 5 , 1 , 1 ) .
Нахождение координат вектора, перпендикулярного двум заданным векторам
Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторам a → ( a x , a y , a z ) и b → = ( b x , b y , b z ) . При условии коллинеарности векторов a → и b → в задаче достаточно будет найти вектор, перпендикулярный a → или b → .
При решении применяется понятие векторного произведения векторов.
Векторным произведением векторов a → и b → называют вектор, одновременно перпендикулярный и a → и b → . Для решения данной задачи применяется векторное произведение a → × b → . Для трехмерного пространства имеет вид a → × b → = a → j → k → a x a y a z b x b y b z
Разберем подробнее векторное произведение на примере задачи.
Заданы векторы b → = ( 0 , 2 , 3 ) и a → = ( 2 , 1 , 0 ) . Найти координаты любого перпендикулярного вектора данным одновременно.
Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :
a → × b → = i → j → k → 2 1 0 0 2 3 = i → · 1 · 3 + j → · 0 · 0 + k → · 2 · 2 — k → · 1 · 0 — j → · 2 · 3 — i → · 0 · 2 = 3 · i → + ( — 6 ) · j → + 4 · k →
Ответ: ( 3 , — 6 , 4 ) — координаты вектора, одновременно перпендикулярного заданным a → и b → .
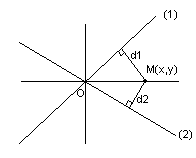
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Пусть дана некоторая точка М0 и вектор n. Проведем через точку М0 прямую l перпендикулярно вектору n (рис. 82).
Пусть M — произвольная точка. Точка M лежит на прямой l в том и только в том случае, когда вектор (overrightarrowM>) перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов n и (overrightarrowM>) равнялось нулю:
Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки M0 и M имеют координаты (x0 ; у0 ) и (x; у).
Тогда (overrightarrowM>) = (x — x0; у — у0). Обозначим координаты нормального вектора n через (А; В). Теперь равенство (1) можно записать так:
Уравнение (2) есть уравнение прямой l, проходящей через данную точку М0 (x0; у0) перпендикулярно данному вектору n = (А; В).
Задача 1. Составить уравнение прямой, проходящей через точку А (2; -3) перпендикулярно вектору n = (-1;5) (рис.83).
Пользуясь формулой (2), находим уравнение данной прямой:
— 1 • (x-2) + 5 • (у + 3) = 0
или, окончательно, x — 5у — 17 = 0.
Задача 2. Даны точки M1(2; -1) и M2(4; 5). Написать уравнение прямой, проходящей через точку М1 перпендикулярно вектору (overrightarrowM_<2>>).
Нормальный вектор искомой прямой n = (overrightarrowM_<2>>) имеет координаты (2; 6) (рис. 84).
Следовательно, по формуле (2) получим уравнение
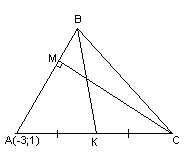
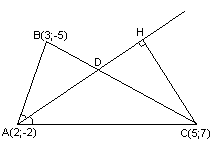
Задача 3. В треугольнике с вершинами в точках M1(-5; 2), M2(5; 6) и M3(1; -2) проведена медиана M1А1. Требуется составить уравнение прямой, проходящей через точку А1 перпендикулярно медиане M1A1 (рис. 85).
За нормальный вектор искомой прямой можно принять вектор n = (overrightarrowA_<1>>). Определим его координаты. Точка A1 — середина отрезка M2M3, поэтому, если (x1; y1) — ее координаты, то ( x_1 = frac<5+1><2>=3, ;;а ;; y_1=frac<6-2><2>=2 ).
Тогда нормальный вектор n = (overrightarrowA_<1>>) имеет координаты (8; 0). Следовательно, искомое уравнение прямой имеет вид
Задача 4. Дан треугольник с вершинами в точках А(-3; -1), В(2; 7) и С(5; 4). Требуется составить уравнение прямой, проходящей через вершину С перпендикулярно стороне AB (рис. 86).
За нормальный вектор искомой прямой можно взять вектор n = (overrightarrow).
Так как n = (2-(-3); 7 — (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим
или, окончательно, 5х + 8у — 57 = 0.
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением 

Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора 

Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».
источники:
http://razdupli.ru/teor/116_uravnenie-pryamoj-prohodyacshej-cherez-dannuyu-tochku-perpendikulyarno-dannomu-vektoru.php
http://mathter.pro/angem/2_2_5_normalnyi_vektor_pryamoy.html
Определение.
Любой ненулевой вектор, перпендикулярный
прямой называется её нормальным
вектором,
и обозначается
Теорема.
Алгебраическое уравнение 1-й степени
где
коэффициенты
одновременно не равные нулю, являетсяуравнением
прямой на плоскости
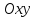
а вектор
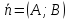
Верно
обратное:
на координатной плоскости
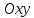
любой прямой с нормальным вектором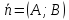
может быть записано в виде алгебраического
уравнения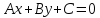
Определение.
Уравнение прямой вида
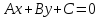
где
коэффициенты
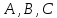
одновременно не равные нулю, называетсяобщим
уравнением прямой.
Известно,
что прямая определяется двумя точками.
Пусть
и
–
точки, лежащие на прямой
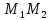
–
произвольная точка этой прямой. Тогда
векторы
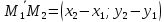
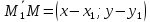
пропорциональны. Получаемуравнение
прямой, проходящей через две точки:
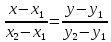
Определение.
Вектор,
параллельный прямой, называется
направляющим
вектором прямой.
Определение.
Пусть
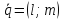
предыдущего уравнения получаемканоническое
уравнение прямой:
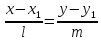
Определение.
В
тех же обозначениях, параметрическое
уравнение прямой
имеет вид:
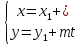
Определение.
Уравнение прямой вида
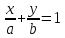
где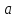
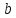
действительные числа, называетсяуравнением
прямой в отрезках.
Теорема.
Пусть
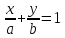
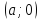
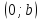
прямой с осями координат.
Определение.
Уравнение прямой вида

где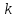
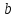
называетсяуравнением
прямой с угловым коэффициентом,
коэффициент
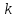
коэффициентом данной
прямой.
Теорема.
Пусть
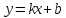
Тогда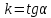
где угол
α
равен углу наклона данной прямой к оси
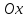
Если
известны угловые коэффициенты
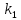
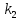
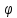
формуле:
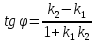
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:
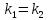
Признаком
перпендикулярности двух прямых является
соотношение:
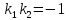
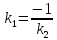
Теорема.
(Связь нормального вектора прямой с её
направляющим вектором и её угловым
коэффициентом.)
1)
Если
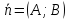
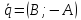
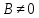
то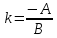
2)
Если
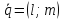
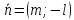
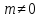
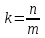
3)
Если
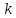
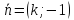
–
направляющий вектор.
Взаимное
расположение двух прямых на плоскости.
Две
прямые на плоскости могут пересекаться,
совпадать или быть параллельными.
Теорема.
Пусть прямые заданы общими уравнениями:
L1: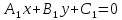
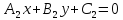
Тогда:
1)
если
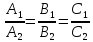
то прямые совпадают, и система уравнений
имеет
бесконечное множество решений;
2)
если
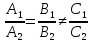
уравнений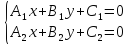
3)
если
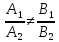
точки их пересечения являются единственным
решением системы уравнений
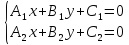
Определение.
Уравнение вида
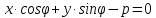
где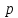
координат, называетсянормальным
уравнением прямой,
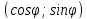
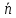
Чтобы
привести прямую к указанному виду,
разделим общее уравнение прямой на
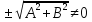
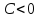
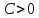
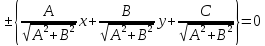
Теорема.
Орт нормального вектора
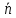
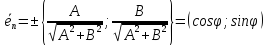
где
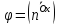
Теорема.
Расстояние от прямой до произвольной
точки
находится
по формуле:
Чтобы
найти расстояние
между двумя параллельными прямыми,
нужно взять произвольную точку на одной
из прямых и найти расстояние от нее до
другой прямой.
Чтобы
найти множество
точек, равноудаленных от двух прямых
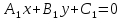
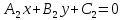
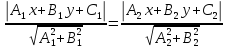
Раскрывая
модули в случае параллельных прямых,
получаем параллельную им прямую, лежащую
между данными прямыми, а в случае
пересекающихся прямых – биссектрисы
углов,
образованных пересечением прямых.
Определение.
Совокупность прямых, проходящих через
некоторую точку S,
называется пучком
прямых с центром S.
Теорема.
Если
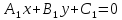
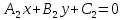
в точкеS,
то уравнение:
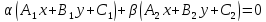
где
одновременно нулю, определяют прямую,
также проходящую через точкуS.
Более
того, в указанном уравнении числа всегда
возможно подобрать так, чтобы оно
определяло любую (заранее назначенную)
прямую, проходящую через точку S,
иначе говоря, любую прямую пучка с
центром S.
Поэтому уравнение вида называется
уравнением пучка с центром S.
Решение
типовых задач
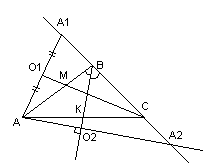
Задача
№1:
Даны
уравнения двух сторон параллелограмма
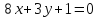
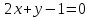
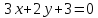
Определить координаты вершин этого
параллелограмма.
Решение:
Найдём
координаты т.
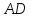
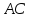
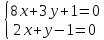
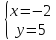
т.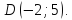
Подставим
координаты т.
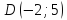
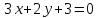
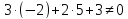
т.
следовательно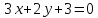
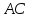
Найдём
координаты т.
как точки пересечения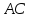
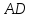
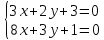
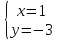
т.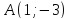
Найдём
координаты т.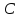
как точки пересечения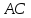
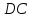
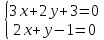

т.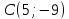
Найдём
координаты т.B:
в параллелограмме диагонали делят друг
друга пополам:
Найдём координаты т.
т.
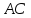
следовательно, т.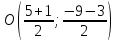
т.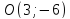
но т.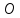
следовательно,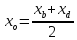
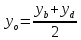
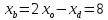
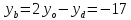
т.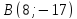
Ответ:
Задача
№2:
Дана
прямая
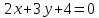
Составить уравнение прямой, проходящей
через точку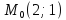
-
параллельно
данной прямой. -
перпендикулярно
к данной прямой.
Решение:
-
Искомая
прямая параллельна прямой
,
поэтому её уравнение имеет вид:.
Найдём
т.
точка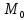
координаты удовлетворяют записанному
уравнению: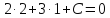
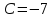
Итак, прямая принимает вид: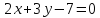
-
Т.к.
заданная и искомые прямые перпендикулярны,
то их угловые коэффициенты удовлетворяют
условию:
.
Найдём
угловой коэффициент прямой
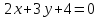
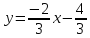
итак,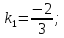
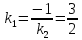
Запишем уравнение искомой прямой: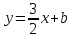
Точка
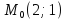
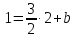
Уравнение
прямой принимает вид:
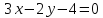
Ответ:
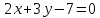
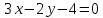
Задача
№3:
Определить,
при каких значениях a
и b
две прямые
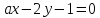
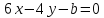
-
имеют
одну общую точку; -
параллельны;
-
совпадают.
Решение:
-
Прямые
имеют одну общую точку, когда они не
параллельны (их коэффициенты при x
и y
не пропорциональны):
;
-
Прямые
параллельны, когда коэффициенты при x
и y
пропорциональны:
;
.
-
Прямые
совпадают, когда все их коэффициенты
пропорциональны:
;
.
Задача
№4:
Найти
проекцию точки
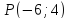
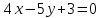
Решение:
Проведём
через т.
перпендикулярную прямой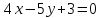
Точка
проекцией.
Прямая
её направляющим вектором служит
нормальный вектор прямой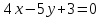
т.е.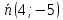
Запишем
уравнение прямой
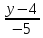
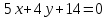
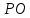
Найдём
координаты т.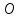
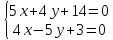
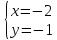
т.
Ответ:
Задача
№5:
Найти
точку
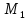
симметричную точке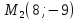
точки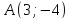
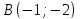
Решение:
Составим
уравнение
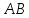
как прямой проходящей через 2 точки:
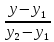
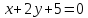
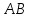
Найдём
уравнение прямой
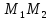
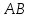
Нормальный
вектор
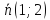
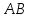
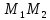
поэтому используем каноническое
уравнение прямой: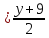
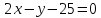
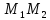
Найдём
координат т.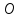
как точки пересечения прямых
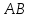
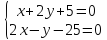
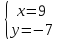
т.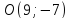
Так
как точка

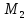
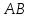
следовательно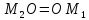
то есть т.
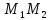
Найдём координаты точки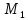
зная начало и середину отрезка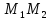
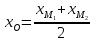
, тогда
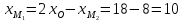
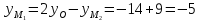
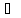
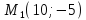
Ответ:
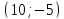
Задача
№6:
Даны
вершины треугольника
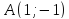
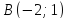
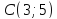
Составить уравнение перпендикуляра,
опущенного из вершины
Решение:
Найдём
координаты т.
как середины отрезка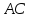
т.
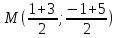
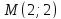
Запишем
уравнение медианы
как прямой, проходящей через две известные
точки:
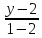
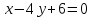
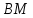
Нормальный
вектор для
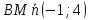
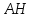
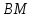
тогда уравнение примет вид:
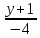
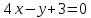
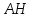
Ответ:
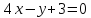
Задача
№7:
Даны
вершины треугольника

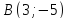
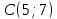
Составить уравнение перпендикуляра,
опущенного из вершины
вершине
Решение:
Пусть
Найдём
координаты т.
Тогда:
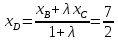
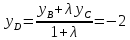
т.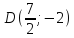
Уравнение
биссектрисы
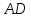
=
⇒
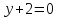
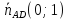
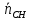
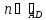
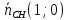
Точка
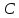
поэтому уравнение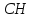
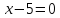
Ответ:
Задача
№8:
Две
стороны квадрата лежат на прямых
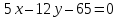
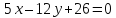
Вычислить его площадь.
Решение:
-
Выберем
на прямой
некоторую точку
:
пусть
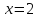
тогда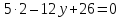
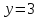
т.е.
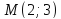
-
Найдём
расстояние от точки
до прямой
:
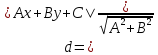
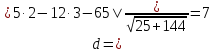
где
-
т.е.
.
Ответ:
Задача
№9:
Даны
две противоположные вершины квадрата
Составить уравнения его сторон.
Решение:
Зная
вершины
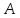

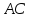
как прямой проходящей через две точки: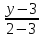
– уравнение прямой
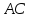
Т.к.
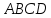
биссектрисами, поэтому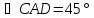
найдём угловой коэффициент
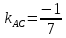
Зная
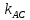

найдём угловой коэффициент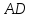
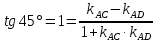
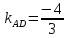
Уравнение
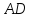
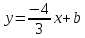
Найдём
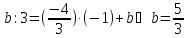
Тогда уравнение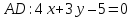
Т.к.
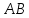
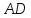
угловой коэффициент
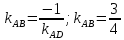
Уравнение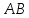
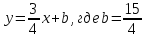
тогда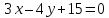
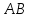
Т.к.
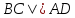
то уравнение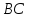
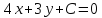
Зная,
что точка
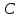
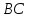
найдём свободный член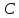
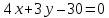
Аналогично
найдём уравнение стороны
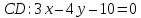
Ответ:
Задача
№10:
Вычислить
площадь треугольника, отсекаемого
прямой
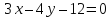
Решение:
Запишем
уравнение прямой
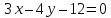
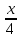
Из
этого уравнения следует, что длины
отрезков
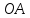
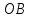
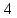
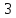
поэтому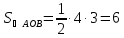
Ответ:
Задача
№11:
Составить
уравнения сторон треугольника, зная
одну из его вершин

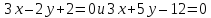
Решение:
Выясним,
что точка
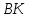
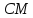
Найдём
координаты точки
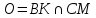
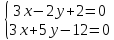
т.
Продолжим
медиану
и на её продолжении отложим отрезок
Соединим точку
Полученный четырёхугольник
пересекаясь в точке
делятся пополам).
Найдём
координаты точки
как конца отрезка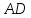

Найдём
уравнение прямой
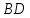
зная, что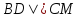

Найдём
координаты вершины
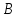
как точки пересечения прямых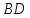
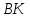
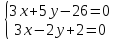
т.
Точка
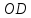
поэтому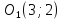
Найдём
координаты точки
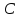
как конца отрезка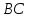
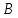
Зная
координаты всех вершин треугольника
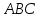
найдём уравнения его сторон, как прямых
проходящих через две точки.
Ответ:
Задача
№12:
Составить
уравнения сторон треугольника, зная
одну из его вершин
Решение:
Очевидно,
что точка

Найдём точку
симметричную точке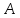
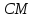
Можно доказать, что точка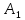
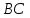
Опустим из т.
Т.к.
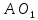
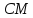
то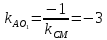
точка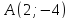
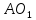
поэтому её уравнение примет вид:
Координаты
точки
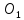
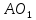
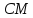
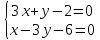
т.
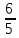
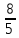
Найдём
координаты точки
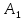
как конца отрезка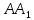
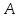
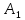
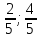
Аналогично
найдём точку
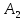
симметричную т.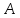
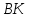
Точка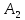
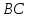
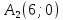
Тогда
уравнение стороны
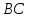
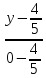
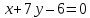
Найдём
координаты точек
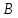
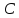
как точек пересечения прямой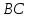
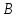
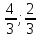
Зная
координаты вершин треугольника
найдём уравнения его сторон.
Ответ:
Задача
№13:
Составить
уравнения биссектрис углов, образованных
двумя пересекающимися прямыми:
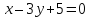
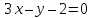
Решение:
Известно
свойство: биссектриса есть геометрическое
место точек, равноудалённых от сторон
угла.
Пусть
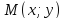
тогда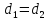
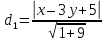
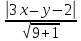
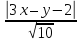
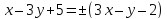
Тогда
уравнения биссектрис примут вид:
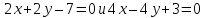
Ответ:
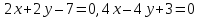
Задача
№14:
Составить
уравнение биссектрисы угла между прямыми
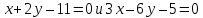
в котором лежит точка
Решение:
Найдём
отклонение точки
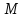
прямых, для этого приведём их уравнения
к нормальному виду: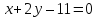
нормирующий множитель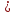
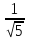
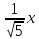
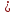
Найдём
отклонение
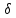
т.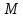
нормального уравнения подставим
координаты т.
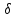
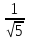
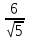
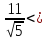
Аналогично
найдём отклонение
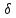
т.
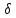
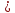
Отклонения имеют разные знаки, поэтому
при раскрытии модулей (см. решение
предыдущей задачи) справа ставим знак
«минус».
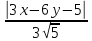
Уравнение
биссектрисы принимает вид:
Ответ:
Задача
№15:
На
прямой
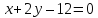
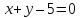
Решение:
Точки
равноудалённые от прямых
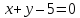
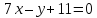
лежат на биссектрисах углов, образованных
этими прямыми. Аналогично решению
предыдущих задач найдём их:
Тогда
искомые точки являются точками пересечения
этих биссектрис и прямой
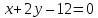
поэтому найдём их, решая системы: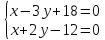
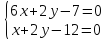
Ответ:
Задача
№16:
Составить
уравнения сторон треугольника, зная
одну из его вершин
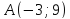
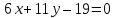
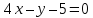
проведённых из различных вершин.
Решение:
Убедимся,
что точка
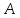
высоте.
Найдём
уравнение стороны
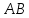
зная, что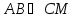
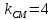
тогда уравнение примет вид:
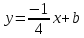
зная координаты т.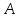
принадлежащей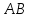
найдём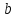
тогда уравнение примет вид: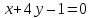
Найдём
координаты т.
как точки пересечения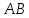
медианы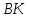
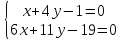
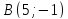
Пусть
точка
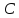
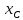
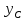
найдём их. Точка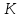
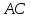
поэтому
Точка
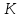
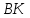
точка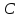
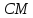
поэтому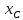
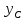
Откуда
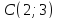
найдём уравнения всех его сторон.
Ответ:
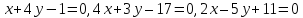
Задача
№17:
Через
точку
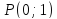
заключённый между прямыми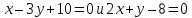
делился бы в точке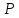
Решение:
Обозначим
через
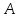
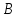
искомой прямой и пусть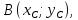
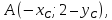
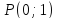
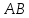
Координаты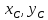
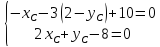
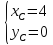
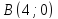
Составим
уравнение искомой прямой, которая
проходит через две точки, например,
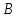
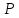
Ответ:
Задача
№18:
Составить
уравнения сторон треугольника
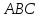
зная одну из его вершин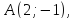
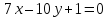
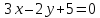
проведённых из одной вершины. Решить
задачу, не вычисляя координат вершин
Решение:
Можно
проверить, что т.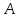
ни биссектрисе.
Найдём уравнение стороны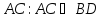
поэтому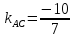
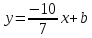
зная координаты т.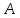
найдём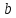
Итак,
уравнение
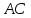
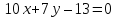
Рассмотрим
пучок с центром в т.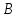
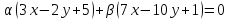
Пусть
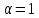
тогда уравнение пучка примет вид:
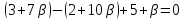
(1)
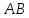
пучка, причём координаты т.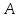
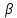
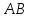
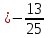
поэтому уравнение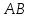
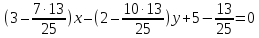
т.е.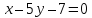
Найдём
угол между прямыми
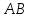
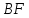
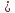
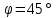
Тогда
угол
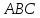
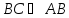
–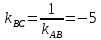
С другой стороны найдём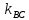
Итак,
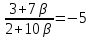
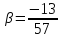
Найдём
уравнение стороны
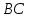
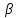
стороны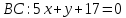
Ответ:
Образовательным
результатом после изучения данной темы
является сформированность компонент,
заявленных во введении, совокупности
компетенций (знать, уметь, владеть) на
двух уровнях: пороговый и продвинутый.
Пороговый уровень соответствует оценке
«удовлетворительно», продвинутый
уровень соответствует оценкам «хорошо»
или «отлично» в зависимости от результатов
защиты кейс-заданий.
Для
самостоятельной диагностики данных
компонент вам предлагаются следующие
задания.
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.
Замечание 1
Нормаль – синоним для слова перпендикуляр.
Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.
Можно выразить уравнение прямой и другим способом:
$y = kx + b$.
Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ – в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ
Нормальное уравнение прямой можно выразить и в тригонометрическом виде:
$x cdot cos{alpha} + y cdot sin{alpha} – p = 0$
где $alpha$ – угол между прямой и осью абсцисс, а $p$ – расстояние от начала координат до рассматриваемой прямой.
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:
- когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
- когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
- когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
- для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.
«Нормальный вектор прямой» 👇
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.
Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:
$y – y_0 = k cdot (x – x_0)$
Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой – самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.
Определение 1
Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.
Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.
Обозначив нормальный вектор прямой как $vec{n}(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как
$n_1 cdot (x – x_n) + n_2 cdot (y – y_0) = 0$
Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат
$Ax + By + C = 0$,
то нормальный вектор описывается формулой:
$bar{n}(A; B)$.
При этом говорят, что координаты нормального вектора “снимаются” с уравнения прямой.
Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar{p}(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar{p}(p_1; p_2)$ и точке $M_0(x_0; y_0)$:
$frac{x – x_0}{p_1} = frac{y – y_0}{p_2}$
В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:
$bar{p} cdot bar{n} = -B cdot A + A cdot B = 0 implies bar{p} perp bar{n}$
Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar{n}(A; B)$, можно выразить уравнение прямой в следующем виде:
$A(x – x_0) + B(y – y_0) = 0$
Пример 1
Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.
Для решения задействуем формулу $A cdot (x – x_0) + B cdot (y – y_0) = 0$
Подставив значения, получаем:
$3 cdot (x – (-1)) – (-1) cdot (y – (-3)) = 0$
$3 cdot (x + 1) – (y + 3) = 0$
$3x + 3 – y – 3 = 0$
$3x – y = 0$
Проверить правильность общего уравнения прямой можно “сняв” из него координаты для нормального вектора:
$3x – y = 0 implies A = 3; B = -1 implies bar{n}(A; B) = bar{n}(3; -1),$
Что соответствует числам исходных данных.
Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x – y = 0$:
$3 cdot (-1) – (-3) = 0$
Равенство верно. Осталось лишь найти формулу направляющего вектора:
$bar{p}(-B; A) implies bar{p}(1; 3)$
Ответ: $3x – y = 0; bar{p}(1; 3).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением в декартовой системе координат, то вектор
является вектором нормали данной прямой.
Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора приходилось аккуратно «вытаскивать» из уравнения, то координаты вектора нормали
достаточно просто «снять».
Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».


| Оглавление |
Автор: Aлeксaндр Eмeлин
Уравнения прямой, проходящей через точку перпендикулярно вектору
Общее уравнение прямой
Ненулевой вектор , перпендикулярный заданной прямой, называется нормальным вектором (или, короче, нормалью) для этой прямой.
Пусть на координатной плоскости (в прямоугольной системе координат) заданы точка
и ненулевой вектор
(рис. 3.5, а). Требуется составить уравнение прямой, проходящей через точку
перпендикулярно вектору
.
Выберем на плоскости произвольную точку . Обозначим
и
— радиус-векторы точек
и
. Точка
принадлежит заданной прямой тогда и только тогда, когда векторы
и
перпендикулярны (рис. 3.5, б). Условие ортогональности запишем при помощи скалярного произведения
. Учитывая, что
, получаем векторное уравнение прямой:
(3.5)
Это уравнение можно записать в другой форме. Преобразуем левую часть , используя свойства скалярного произведения. Обозначая
, получаем уравнение
(3.6)
выражающее постоянство проекций на нормаль радиус-векторов точек, принадлежащих прямой.
Получим координатную форму записи векторного уравнения прямой (3.5). Так как и
, по формуле (1.9) находим
или
(3.7)
Полученное соотношение (3.7) позволяет по координатам точки и координатам
нормали
записать уравнение прямой без промежуточных вычислений.
Обозначив , получим общее уравнение прямой на плоскости
(3.8)
Поскольку коэффициенты и
не равны нулю одновременно (это координаты ненулевого вектора
), уравнение (3.8) является алгебраическим уравнением первой степени, т.е. линейным уравнением с двумя неизвестными. Следовательно, прямая является алгебраической линией первого порядка.
Проводя рассуждения в обратном порядке, делаем вывод о том, что линейное уравнение (3.8) задает на координатной плоскости прямую. Полученные выводы сделаны для прямоугольной системы координат, но, учитывая теорему 3.1, они переносятся (без изменений) и на любую аффинную систему координат.
Теорема (3.2) об алгебраической линии первого порядка. Всякое уравнение первой степени с двумя неизвестными задает в аффинной системе координат прямую, и наоборот, всякая прямая в любой аффинной системе координат может быть задана уравнением первой степени с двумя неизвестными. Другими словами, алгебраическая линия первого порядка есть прямая.
Замечания 3.2
1. При составлении общего уравнения прямой нормаль выбирается неоднозначно: можно выбрать любую, отличную от нуля, длину нормали , а также одно из двух возможных направлений (противоположный вектор (
) также является нормалью). Например, вместо нормали
можно взять нормаль
, что соответствует умножению обеих частей уравнения (3.8) на число
.
2. Если один из коэффициентов уравнения прямой (3.8) равен нулю, общее уравнение прямой (3.8) принимает один из следующих частных видов:
а) если , уравнение (3.8) имеет вид
или
уравнение прямой, параллельной оси абсцисс (рис.3.6.a); при
прямая
совпадает с осью
;
б) если , уравнение (3.8) имеет вид
или
уравнение прямой, параллельной оси ординат (рис.3.6,б); при
прямая
совпадает с осью
;
в) если , уравнение (3.8) имеет вид
– уравнение прямой, проходящей через начало координат (рис.3.6,в).
3. Нормаль к прямой
совпадает с градиентом функции
:
В курсе математического анализа доказывается, что градиент направлен в сторону наискорейшего возрастания функции в данной точке.
4. Прямая разбивает плоскость на две полуплоскости (рис.3.7,а): положительную, координаты всех точек которой удовлетворяют неравенству
, и отрицательную, для точек которой
. Нормаль
, приложенная к любой точке прямой, принадлежит положительной полуплоскости. Другими словами, нормаль, приложенная к произвольной точке прямой, указывает на положительную полуплоскость (рис.3.7,а).
Действительно, обозначим через — многочлен первой степени от двух переменных
и
. Тогда для любой точки
, принадлежащей прямой (3.8), справедливо равенство
. Представим значение многочлена
в произвольной точке
плоскости в виде скалярного произведения:
где — нормаль к прямой
;
— точка, принадлежащая этой прямой. Знак выражения
определяется величиной угла
между нормалью
и вектором
. Например, для точки
угол
острый (рис.3.7,б), поэтому
, а для точки
угол
тупой (рис.3.7,б), поэтому
. Следовательно, координаты любой точки
, принадлежащей полуплоскости, на которую указывает нормаль, удовлетворяют неравенству
, а координаты точек
другой полуплоскости- неравенству
.
5. Абсолютное значение пропорционально расстоянию от точки
до прямой
, т.е. отношение расстояний от точек
и
до прямой
равно отношению
.
Действительно, в пункте 3 получено представление значений линейного трехчлена в виде скалярного произведения, которое можно выразить через алгебраическое значение длины ортогональной проекции:
Запишем отношение значений линейного трехчлена для двух точек
и
:
Учитывая, что абсолютная величина равна расстоянию от точки
до прямой, получаем искомое отношение
6. В аффинной системе координат линейное уравнение ах
задает, согласно теореме 3.2, прямую. Выводы, полученные в пунктах 2,3,4,5, остаются справедливыми с тем лишь исключением, что вектор
не является нормалью.
Пример 3.5. На координатной плоскости (в прямоугольной системе координат) заданы точки
и
. Составить уравнение серединного перпендикуляра к отрезку
(рис.3.8).
Решение. Серединный перпендикуляр, по определению, проходит перпендикулярно отрезку через его середину. Находим координаты середины
отрезка
:
то есть
.
Вектор можно взять в качестве нормали для серединного перпендикуляра. Находим координаты этого вектора, вычитая из координат его конца соответствующие координаты его начала:
Следовательно, уравнение (3.8) искомой прямой имеет вид . Осталось найти величину свободного члена
. Поскольку точка
принадлежит прямой, то ее координаты
должны удовлетворять уравнению этой прямой, следовательно,
. Отсюда
. Таким образом, серединный перпендикуляр задается уравнением
Уравнение этой прямой можно было получить в виде (3.7), подставляя координаты нормали и точки
.
Решение задачи получено аналитически без использования графического изображения (рис.3.8). Чертеж в аналитической геометрии служит, как правило, лишь иллюстрацией к решению.
Расстояние от точки до прямой
Пусть заданы на плоскости прямая, описываемая общим уравнением (3.8) , и точка
. Требуется найти расстояние
от точки до прямой.
Искомое расстояние равняется длине ортогональной проекции вектора на направление нормали
(рис.3.9):
, где
— любая точка на заданной прямой.
Запишем правую часть в координатной форме, выражая скалярное произведение и длину через координаты векторов ,
:
Поскольку координаты точки удовлетворяют уравнению (3.8), то
. Подставляя это выражение, получаем формулу расстояния от точки
до прямой
(3.9)
Пример 3.6. На координатной плоскости (в прямоугольной системе координат) заданы точки
и
. Требуется найти, в каком отношении прямая
делит отрезок
.
Решение. Найдем значения линейного трехчлена в точках
и
:
;
. Получили значения разных знаков. Следовательно, точки
и
лежат по разные стороны от прямой
(согласно пункту 4 замечаний 3.2, эти точки лежат в разных полуплоскостях), т.е. прямая
действительно пересекает отрезок
(в точке
на рис.3.10). Так как эти значения по абсолютной величине пропорциональны расстояниям от точек
и
до прямой
, то
Этот же результат можно получить по формуле (3.9). Находим расстояния и
от точек
и
до прямой
:
Следовательно, .
Нормированное уравнение прямой
Преобразуем общее уравнение прямой следующим образом. Если свободный член
, то разделим обе части на длину нормали
, а если
, то разделим на
. Получим уравнение
в котором свободный член , в силу описанного выбора знака, неположительный. Обозначим его через
. Коэффициенты при неизвестных являются координатами единичного вектора
или
, и равны направляющим косинусам:
Тогда уравнение принимает вид (3.10) и называется нормированное уравнение прямой
(3.10)
Замечания 3.3
1. Свободный член нормированного уравнения (3.10) равен расстоянию от начала координат до прямой.
Действительно, по формуле (3.9) находим расстояние от начала координат
до прямой, описываемой уравнением (3.10):
2. Нормированное уравнение прямой (3.10) можно записать в виде (3.7): , если в качестве нормали л выбрать единичный вектор
, так как
. Из двух возможных единичных нормалей условию
отвечает нормаль
, направленная к прямой (рис.3.11), если вектор
приложить к началу координат. При выборе противоположного вектора
получилось бы отрицательное значение
, которое не допускается в уравнении (3.10).
3. Коэффициенты общего уравнения прямой (3.8) определяются неоднозначно в силу неоднозначного выбора нормали. При составлении нормированного уравнения (3.10) прямой такого произвола нет. Здесь все коэффициенты определены однозначно (при ) или с точностью до знака (при
).
4. Нормированное уравнение прямой имеет смысл только в прямоугольной системе координат.
Пример 3.7. На координатной плоскости (в прямоугольной системе координат) заданы вершины
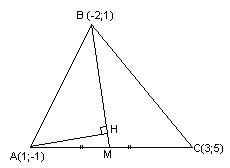
треугольника (рис.3.12). Требуется:
а) составить общее и нормированное уравнения прямой, содержащей высоту ;
б) найти расстояние от начала координат до прямой ;
в) найти расстояние от точки
до прямой
.
Решение. а) Вектор , перпендикулярный прямой
, является нормалью для этой прямой. Находим координаты вектора
, вычитая из координат конца координаты его начала:
Коэффициенты при неизвестных в общем уравнении прямой равны координатам нормали, поэтому
и
, т.е. уравнение имеет вид
. Подберем свободный член
так, чтобы прямая проходила через точку
. Для этого подставим координаты
и
точки
в уравнение:
. Отсюда
. Таким образом, искомое общее уравнение имеет вид:
.
Преобразуем общее уравнение . Поскольку в этом уравнении
, разделим его на
. Получим нормированное уравнение прямой
. Сравнивая с (3.10), находим направляющие косинусы
и параметр
.
б) Из пункта 1 замечаний 3.3 следует, что искомое расстояние от начала координат до прямой равно
.
в) Расстояние от точки
до прямой
находим по формуле (3.9):
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.







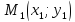
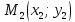
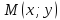


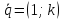
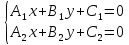
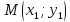
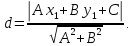

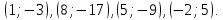
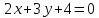 ,
,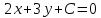 .
.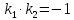 .
.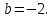
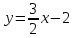
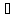
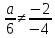 ;
;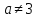
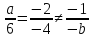 ;
;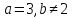 .
.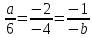 ;
;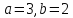 .
.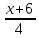
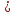
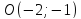
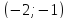
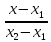
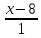
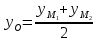
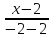
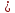
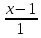
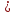
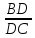
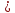
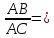
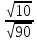
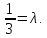
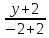
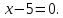
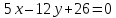 некоторую точку
некоторую точку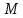 :
: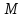 до прямой
до прямой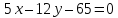 :
: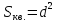 т.е.
т.е.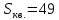 .
.