Как найти вектор шара
2018-05-14
Найти вектор напряженности электрического поля в центре шара радиуса $R$, объемная плотность заряда которого $rho = vec vec$, где $vec$ — постоянный вектор, $vec$ — радиус-вектор, проведенный из центра шара.
Рассмотрим элементарную сферическую оболочку толщины $dr$. Таким образом, поверхностная плотность заряда оболочки $sigma = rho dr = ( vec cdot vec ) dr$.
Таким образом, используя решение задачи 7315, напряженность поля, обусловленная этой оболочкой
Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Формула. Объём шара:
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
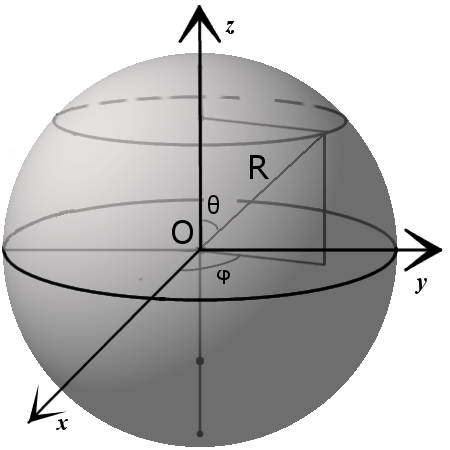
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2
Основные свойства сферы и шара
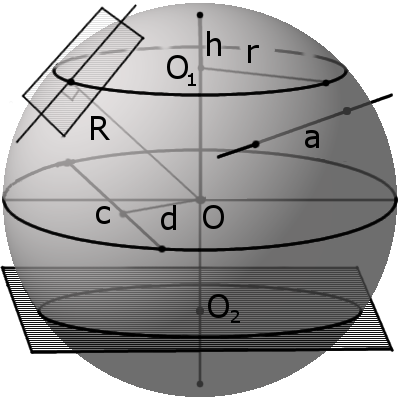
Секущая, хорда, секущая плоскость сферы и их свойства
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.
Касательная, касательная плоскость к сфере и их свойства
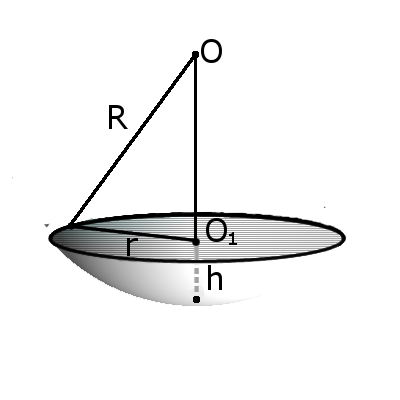
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
S = π R(2 h + √ 2 h R – h 2 )
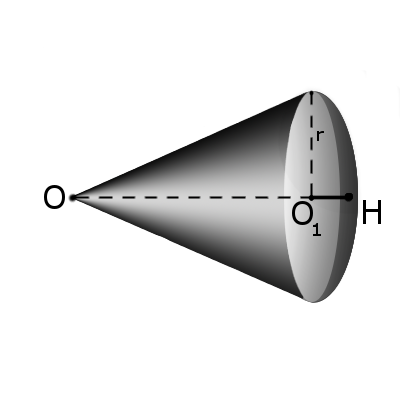
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/formula/sphere/
[/spoiler]
A tiny ball is placed in top of an ellipsoid $3x^2+2y^2+z^2=9$ at $(1,1,2)$. Find the three-dimensional vector $underline u$ in whose direction the ball will start moving after the ball is released.
I feel this problem involves usage of gradients but not sure how to tackle it.
EDIT the solution shouldn’t use physics knowledge and has to be based on directional derivatives and/or gradients.
EDIT 1 I’ve finally come up with the “no physics solution” however it is different from the accepted answer, I’d appreciate if other members confirm if the accepted answer is correct.
One potential flaw with the accepted answer is that it’s not using the $9$ from the original equation $3x^2+2y^2+z^2+mathbf{9}=0$.
Anyway this is my take:
The $xy$ direction in which the ball will fall is $-nabla f(1,1)$.
$f_x=-frac{3x}{sqrt{9-3x^2-2y^2}}stackrel{we.plug.in.x=1}{=}-frac{3}{2}$.
Similarly, $f_y=-1$ therefore $-nabla f(1,1)=langle 3/2,1 rangle$.
Let the 3d vector we’re after be $d=langle 3/2, 1, a rangle$. Notice that $d$ is perpendicular to the normal vector of the tangential plane $n=langle 6x,4x,-1 rangle=langle 6,4,-1 rangle$ so $dcdot n=0$ therefore $a=13$ so the final result is $d=langle frac{3}{2}, 1,13rangle$.
Теорема Гаусса и постулат Максвелла, представленные в интегральной форме, дают возможность решить ряд задач в тех случаях, когда условия симметрии таковы, что в каждой точке замкнутой поверхности интегрирования (поверхности симметрии), охватывающей заряды, вектор напряженности поля (или электрического смещения
)
имеет одно и то же значение и может быть вынесен из-под интеграла.
Пример 1. Точечный заряд q = 10-9 Кл помещен в начале сферической системы координат. Определить напряжение между точками а (Ra = 4см, qа = 45°, jа = 0°) и b (Rb = 8см, , qb = 180°, jb = 90°) и напряженность в тех же точках, если окружающей средой является воздух.
Решение.
Решение будем проводить с помощью теоремы Гаусса (1.9), так как среда однородна.
Поскольку поле точечного заряда характеризуется сферической симметрией, то, если в качестве поверхности интегрирования взять поверхность сферы с центром в точке, где расположен заряд (в нашем случае это начало системы координат), то в любой точке на поверхности этой сферы напряженность поля будет иметь одно и то же значение. Направление же вектора будет совпадать с направлением радиуса, то есть перпендикулярно к поверхности сферы. В связи с этим, интеграл по этой поверхности, составленный по теореме Гаусса, можно преобразовать следующим образом:
.
Поскольку данный интеграл (согласно теореме Гаусса) равен отношению заряда, помещенного внутри сферы, к диэлектрической проницаемости среды, то напряженность поля будет определяться соотношением
Еr = q/(4pe0r2).
Здесь индекс r у напряженности проставлен для того, чтобы показать, что напряженность поля имеет одну составляющую, направленную по радиусу.
Отметим, что данная формула полностью соответствует выражению (1.1), полученному из закона Кулона.
Поскольку напряженность электрического поля в данном случае имеет только радиальную составляющую, величина которой является функцией радиуса и не зависит от угловой координаты, то в указанных в исходном задании точках она будет равна:
E(ra)=q/(4pe0ra2)=10-9/(4p?8.85·10-12·0.042)=5.62кВ/м.
E(rв)=q/(4pe0rв2)=10-9/(4p8.85·10-12·0.082)=1.405кВ/м.
Разность потенциалов между точками а и в определяется при помощи выражения (1.6). Эта разность в потенциальном поле не зависит от пути интегрирования. Поэтому, если разбить путь интегрирования на две части и сначала проводить интегрирование вдоль радиуса от точки а до точки, которая является точкой пересечения продолжения этого радиуса с поверхностью воображаемой сферы с центром в начале координат и радиусом rв, а затем проводить интегрирование по любой линии, лежащей на поверхности этой серы от данной точки до точки в, то интеграл вдоль этой линии будет равен нулю, поскольку вектор напряженности поля имеет одну составляющую, направленную вдоль радиуса, а подинтегральным выражением в формуле (1.6) является скалярное произведение вектора напряженности поля и вектора dl, который совпадает с касательной к поверхности сферы.
Таким образом, разность потенциалов между точками а и в будет равна

Пример 2. Уединенный проводящий шар радиусом R0 = 6 см, поверхностная плотность заряда которого s = 0,1*10-6 Кл/м2, помещен в диэлектрик (er = 3).
Определить закон изменения напряженности поля и потенциала в функции расстояния r от центра шара, приняв потенциал равным нулю в бесконечности. Рассчитать напряжение между точками, одна из которых лежит на поверхности шара, а другая – на расстоянии 20 см от его поверхности. Вычислить емкость шара.
Решение.
Поле внутри проводящего шара отсутствует. Поле вне шара обладает сферической симметрией, поэтому рассчитывается с помощью теоремы Гаусса точно так же как и для точечного заряда.
Здесь в качестве поверхности интегрирования взята поверхность сферы радиуса r ?
R0 с центром, совпадающим с центром шара.
Заряд шара определяется через поверхностную плотность
q = s·4p·R02.
Таким образом, напряженность поля вне шара имеет только одну радиальную составляющую и равна
Еr = s·R02/(ere0r2) =
0,1·10-6·0,062/(3·8,85·10-12r2).
Потенциал в любой точке вне шара, находящейся на расстоянии r от его центра, определяется с помощью выражения (1.5), которое с учетом того, что напряженность поля направлена вдоль радиуса, будет иметь следующий вид:
Потенциал шара равен потенциалу любой точки, лежащей на поверхности шара (r = R0) U =
13,56/0,06 = 173,8 В.
Разность потенциалов между любыми точками А (r = RA) и В (r = RВ) определяется с помощью следующей формулы:
UA – UВ = 13,56· (1/RA – 1/RВ).
Таким образом, разность потенциалов между точкой, лежащей на поверхности шара, и точкой, отстоящей от поверхности на расстоянии 20 см, равна
UAВ = 13,56· (1/0,06 – 1/0,26) = 173,8 В.
Емкость шара можно определяется выражением (1.19)
С = 4·p·ere0·R0 = 4·p·3·8,85·10-12·0,06 = 2·10-11 Ф.
Пример 3.
Шар из диэлектрика (er = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: r = k*r,
где k = 0,05p [Кл/м4].
Радиус шара R = 2см. Рассчитать и построить графики изменения потенциала и напряженности поля вдоль радиуса.
Решение. В
данном случае поле также обладает сферической симметрией, но область не однородна. Поэтому здесь удобнее применять постулат Максвелла (1.10).
Так, при 0 ? r ? R где s – сферическая поверхность радиусом r с
центром, совпадающим с центром шара; v – объем, заключенный внутри этой поверхности.
Перепишем уравнение с учетом симметрии поля
Отсюда находим радиальную составляющую вектора электрического смещения:
Dr = 0,25·k·r2.
Напряженность электрического поля, которая также как и вектор электрического смещения направлена по радиусу, внутри шара будет равна
(1.8):
E1r = Dr/ere0 = 0,25·k·r2/ere0.
Вне шара (r ? R) электрическое смещение, исходя из постулата Максвелла, определяется следующим образом:
Следовательно, электрическое смещение и напряженность поля будут равны:
Dr = 0,25·k·R4/r2; Er = Dr/e0.
Графики изменения напряженности поля и вектора электрического смещения представлены на рис.1.4. Значения напряженности поля и вектора электрического смещения даны в относительных единицах. За базисные значения приняты значения этих величин на поверхности шара, которые для заданных исходных данных соответственно равны Erb = 4,435·105В/м; Drb = 1,571·10-5Кл/м2.
Потенциал поля внутри шара можно определить по формуле
,
где С1 – постоянная интегрирования.
Принимая потенциал бесконечно удаленной точки равным нулю, определим потенциал любой произвольной точки в области вне шара.

Постоянную интегрирования С1 можно определить из условия равенства потенциалов U1 и U2 на поверхности шара (при r = R)

Отсюда

График изменения потенциала вдоль радиуса также в относительных единицах показан на рис.1.4. За базисное значение потенциала принято значение потенциала на поверхности шара Ub = 35.5кВ.
Отметим, что если бы объемная плотность заряда r оставалась постоянной, то напряженность поля и потенциалы поля в соответствующих подобластях определялись бы следующими выражениями:
E1 = r·r/(3·ere0); U1 = – r·r2/(6·ere0) + C1;
E2 = r·R3/(3·e0·r2);
U2 = r·R3/(3·e0·r).
Постоянная С1 в этом случае определяется также из условия равенства потенциалов U1 и U2 на поверхности шара
С1 = r·R3· (1+2·er)/(6·e0·er).
Пример 4. Сферический конденсатор с двухслойным диэлектриком имеет радиус внутренней сферы r1=12 мм, внутренний радиус наружной сферы – r3=22 мм и радиус поверхности раздела диэлектриков – r2=16 мм.
Относительное значение диэлектрической проницаемости внутреннего слоя диэлектрика er1=5, наружного слоя – er2=3. Разрез конденсатора показан на рис.1.5. Заряд конденсатора q = 10-8Кл.
Определить и построить график изменения напряженности поля вдоль радиуса. Найти разность потенциалов между электродами. Вычислить емкость конденсатора. Изменяя радиус поверхности раздела диэлектриков r2 и значение диэлектрической проницаемости наружного слоя er2 получить конденсатор с наилучшим использованием двухслойного диэлектрика. Рассчитать емкость данного конденсатора и сопоставить ее с емкостью исходного конденсатора.
Решение. Используя постулат Максвелла для любой сферической поверхности радиусом r, построенной внутри k-го слоя (k=1,2) диэлектрика с диэлектрической проницаемостью erk, получим выражение для вектора электрического смещения и напряженности электрического поля
Dk = q/(4pr2); Ek = Dk/(erk·e0) = q/(4pr2·erk·e0).
Максимальное значение напряженности поля в первом слое, очевидно, будет на поверхности внутреннего электрода
E1max = q/(4p·r12·er1e0)=10-8/(4p·122·10-6·5·8,85·10-12) = 1,249·105 В/м.
Максимальное значение напряженности поля во втором слое на сферической поверхности раздела диэлектриков
E2max = q/(4pr22·er2·e0)=10-8/(4p162·10-6·3·8,85·10-12) =1,171*105 В/м.
Графики изменения напряженности поля в диэлектрике вдоль радиуса представлены на рис.1.6. Значения напряженности на графиках приведены в относительных единицах. За базисное значение принято максимальное значение напряженности в первом слое Eb= E2max.
Разность потенциалов между электродами определяется при помощи следующего выражения:
Емкость конденсатора равна (1.15)
C=q/U12 = 10-8/885,6 = 1,129·10-11Ф.
Отметим, что емкость сферического конденсатора с двухслойным диэлектриком можно определить и по такой формуле
С=С1С2/(С1+С2),
где С1 – емкость сферического конденсатора с однослойным диэлектриком с радиусами обкладок r1 и r2 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости первого слоя; С2 – емкость сферического конденсатора с однослойным диэлектриком с радиусами обкладок r2 и r3 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости второго слоя.
Поскольку емкость сферического конденсатора с однослойным диэлектриком определяется с помощью выражения (1.18), то емкости С1, С2 и С будут равны:
С1 = 4·p·8,85·10-12·5·0,012·0,016/(0,016-0,012) = 2,669·10-11Ф;
С2=4·p·8,85·10-12·3·0,016·0,022/(0,022-0,016) = 1,957·10-11Ф;
С=2,669·1,957·10-11(2,669+1,957) = 1,129·10-11Ф.
Для наилучшего использования диэлектриков в конденсаторе необходимо так подобрать толщину слоев, чтобы максимальное значение напряженности поля было одинаковым. Поскольку напряженность поля имеет максимальное значение у внутренней поверхности слоя, то для выполнения этого условия, необходимо, чтобы произведение квадрата внутреннего радиуса слоя на его диэлектрическую проницаемость было постоянным, то есть r12e1= r22e2=const.
Если значение диэлектрической проницаемости оставлять неизменным, а изменять толщину слоев, то с помощью данного выражения можно определить радиус поверхности раздела диэлектриков.
м.
Разность потенциалов U12 и емкость такого конденсатора будут равны: U12=910,13В; C=1,099*10-11Ф.
Пример 5.
Бесконечно длинная тонкая заряженная нить расположена в воздухе вдоль оси z цилиндрической системы координат (рис. 1.7). Линейная плотность заряда t=10-9Кл/м. Рассчитать и построить график изменения напряженности поля вдоль радиуса. Определить разность потенциалов между точками
m (rm=10cм; qm=270°) и n (rn=40cм; qn=180°).
Решение. В этом случае поле характеризуется цилиндрической симметрией, то есть во всех точках цилиндрической поверхности, охватывающей заряженную нить, произвольного радиуса r напряженность поля имеет одно и то же значение и направлена перпендикулярно к поверхности. Поэтому, если окружить нить цилиндрической поверхностью длиной l и радиусом r и использовать теорему Гаусса, то можно получить выражение для напряженности поля Е.
График изменения напряженности поля вдоль радиуса представлен на рис. 1.8.
Значение напряженности поля на графике даны в относительных единицах. За базисное значение принято значение напряженности на расстоянии одного миллиметра от начала координат (Еb=1,798·104 В/м).
Потенциал поля в любой точке m, расположенной на расстоянии rm от оси провода, равен:

Здесь rp – расстояние от оси провода до некоторой фиксированной точки пространства р, в которой потенциал принимается равным нулю.
Если за такую точку принять точку, расположенную на расстоянии одного метра от оси провода, то потенциал точки m будет равен:
.
Изменение потенциала вдоль радиуса представлено на рис. 1.8. Значения потенциала даны также в относительных единицах. За базисное значение потенциала принято значение потенциала в той же точке, что и базисное значение напряженности поля (Ub=124,226 В).
Разность потенциалов между точками, указанными в условии задачи, равна 24,931 В.
Пример 6.
Бесконечно длинный цилиндрический конденсатор с двухслойным диэлектриком имеет радиус внутреннего электрода r1=1 мм , внутренний радиус внешнего электрода – r3=4 мм и радиус поверхности раздела диэлектриков – r2=2 мм.
Относительное значение диэлектрической проницаемости внутреннего слоя диэлектрика er1=5, наружного слоя – er2=2,5. Поперечное сечение конденсатора показано на рис.1.9. Линейная плотность заряда конденсатора t = 10-8 Кл/м.
Определить и построить график изменения напряженности поля вдоль радиуса. Найти разность потенциалов между электродами.
Вычислить емкость конденсатора на единицу длины.
Решение. Для решения задачи используем обобщенную теорему Гаусса. В качестве поверхности интегрирования возьмем замкнутую цилиндрическую поверхность длиной l и радиусом r (r1?r?r3).
.
Ввиду цилиндрической симметрии (вектор электрического смещения на этой поверхности не изменяется по величине и направлен по радиусу) последнее уравнение можно переписать следующим образом:
D·2·p·r·l = t·l,
откуда
D = Dr = t/(2·p·r).
Напряженность поля в первом слое диэлектрика (r1 ?r ? r2) будет при этом равна:
E1 = D/(er1e0) = t/(2·p·er1e0·r).
Во втором слое (r2 ?r ? r3) –
E2 = D/(er2e0) = t/(2·p·er2e0·r).
График изменения напряженности поля представлен на рис.1.10. На графике значения напряженности поля представлены в относительных единицах. За базисное значение принято значение напряженности в первом слое при r = r1, ( Eb = 35,970 кВ/м).
Как видно из рис. 1.10, напряженность поля на границе раздела диэлектриков испытывает скачек. Для лучшего использования изоляции стараются подобрать толщину слоев диэлектрика и их диэлектрическую проницаемость таким образом, чтобы максимальное значение напряженности поля в обоих слоях было одинаково. Это будет соблюдаться при условии r1e1 = r2e2, как в данном примере.
Разность потенциалов между электродами определяется при помощи выражения (1.6), которое для цилиндрического конденсатора можно переписать в следующем виде:
74,792В.
Емкость конденсатора на единицу его длины будет равна:
С = t/U = 10-8/74,792 = 0,1337 нФ/м.
Отметим, что емкость цилиндрического конденсатора с двухслойным диэлектриком можно определить и по такой формуле
С=С1С2/(С1+С2),
где С1 – емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок r1 и r2 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости первого слоя; С2 – емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок r2 и r3 и диэлектрической проницаемостью диэлектрика, равной диэлектрическойпроницаемости второго слоя.
Поскольку емкость цилиндрического конденсатора с однослойным диэлектриком определяется с помощью выражения (1.23), то емкости С1, С2 и С будут равны:
С = С1·С2/(С1 + С2) = 0,1337 нФ/м.
Пример 7.
Бесконечно длинный цилиндр, выполненный из диэлектрика, относительное значение диэлектрической проницаемости которого er1 = 4, заряжен и находится в минеральном масле (er2 = 2,5).
Радиус цилиндра r0 = 5мм (рис. 1.11). Объемная плотность заряда является функцией расстояния от оси цилиндра r = r/10.

Решение. В
качестве поверхности интегрирования выбирается боковая поверхность цилиндра длиной один метр, радиусом r и с осью, совпадающей с осью исходного цилиндра. При 0 ? r ? r0 внутри этой поверхности будет находиться заряд, величина которого может быть определена с помощью следующего выражения:
Таким образом, с учетом цилиндрической симметрии поля,
получим
Отсюда
где А1=9.416·108 В/м3.
В области вне цилиндра (r0?r??)
Из этого выражения легко определяется напряженность поля вне цилиндра
где А2=183.432 В.
Потенциал электрического поля внутри цилиндра (при условии, что точка, в которой потенциал поля принимается равным нулю, лежит на оси цилиндра) можно определить следующим образом:
Потенциал поля в области вне цилиндра равен
Здесь В2 – постоянная интегрирования, которую можно найти из условия равенства потенциалов на поверхности цилиндра.
В.
Распределение напряженности электрического поля и потенциала представлено в относительных единицах на рис. 1.12. За базисные значения напряженности поля и потенциала приняты максимальное значение напряженности на границе раздела сред (Еmax=3.669·104 В/м) и значение потенциала при r=0.019 м (jв=-284 В).
В частном случае, когда объемная плотность заряда r является постоянной величиной, решение упрощается, и выражения для функции напряженности поля и потенциала будут иметь вид:
где

Рассчитать электростатическое поле, создаваемое зарядом, который равномерно распределен между двумя цилиндрическими бесконечно длинными поверхностями.
Объемная плотность заряда r=10-6 Кл/м3.
Радиус внешнего цилиндра R1=20 см, внутреннего – R2 =4 см, расстояние между осями цилиндров – а=10 см. Относительное значение диэлектрической проницаемости окружающей среды и обоих цилиндров равно er1=1.
Определить распределение составляющих напряженности электрического поля и потенциала вдоль осей Х и Y (рис. 1.13).
Решение.
Данная задача решается методом наложения. Сначала рассчитывается поле в любой точке М от заряда с объемной плотностью +r, равномерно распределенного по объему всего большого цилиндра. Затем в этой же точке рассчитывается поле от заряда, объемная плотность которого равна -r, равномерно распределенного по объему малого цилиндра. Результирующая напряженность поля Е в любой точке М определяется как векторная сумма напряженности Е1 и Е2. Потенциал любой точки определяется также как сумма потенциалов U1 и U2.
Так, в точке М, которая находится на расстоянии r1 от оси большого цилиндра и r2 от оси малого цилиндра и имеет координаты r1 и a (рис. 1.14) модули напряженности поля от соответствующих зарядов определяются согласно теореме Гаусса по следующим формулам:
Вектор напряженности Е1 направлен по радиусу r1 от оси О большого цилиндра, а вектор Е2 – по радиусу r2 к оси О1 малого цилиндра (рис. 1.14).
Потенциалы поля при этом будут равны:
Здесь С1 и С2 – постоянные интегрирования.
Потенциал поля в области между цилиндрами определяется следующим выражением:
Принимая потенциал равным нулю на оси большого цилиндра (r1=0; r2=a), найдем постоянную интегрирования С.
С учетом этого, выражение для потенциала в области между цилиндрами окончательно можно записать в следующем виде:
Если поле определяется в области, лежащей внутри малого цилиндра, то напряженность поля в произвольной точке этой области будет определяться при помощи следующего выражения:
Здесь i – единичный орт, направленный вдоль оси Х.
Таким образом, внутри малого цилиндра напряженность поля будет иметь только одну составляющую, направленную вдоль оси Х и являющуюся постоянной величиной.
Потенциал поля при этом будет равен
где В – постоянная интегрирования.
Эта постоянная определяется исходя из равенства потенциалов для точки, лежащей на поверхности малого цилиндра, один из которых рассчитывается по последнему уравнению, а второй – по выражению, справедливому для точек, находящихся в области между цилиндрами.
Определяя с помощью теоремы косинусов r2 через r1, выражения для потенциала и напряженности поля можно преобразовать.
.
Если точка, в которой определяется поле, лежит в области вне цилиндров (r1?R1), то модули напряженности поля будут определяться при помощи следующих выражений:
где t1 и t2 – линейная плотность зарядов большого и малого цилиндров.
Направление векторов напряженности поля определяется так же, как и для области, лежащей между цилиндрами.
Потенциал поля для области вне цилиндров будет равен
Постоянная интегрирования В1 определяется из условия равенства потенциалов на поверхности большого цилиндра (r1=R1, r2=R1-a), один из которых рассчитывается по последнему уравнению, а второй – по выражению, справедливому для точек, находящихся в области между цилиндрами.
Следовательно, окончательно можно записать следующее выражение для определения потенциала в данной области:
Построим графики изменения модуля напряженности поля и потенциала вдоль оси Y при х=0, для чего положим r1=y; r2=(y2+a2)0,5.
При этом выражения для напряженности поля и потенциала можно несколько преобразовать. Так, при 0?y?R1 они будут иметь следующий вид:
В области вне цилиндров (у?R1) эти выражения можно записать следующим образом:
Графики изменения данных функций представлены на рис. 1.15.
На графиках все величины даны в относительных величинах. За базисные значения потенциала и напряженности поля приняты значения соответствующих функций на поверхности цилиндра радиусом R1 (x=0; y=R1), которые оказались равными Uб=-1057 В,
Еб=10,94 кВ/м.
На рис. 1.16 представлены графики распределения потенциала и напряженности поля (в относительных единицах) вдоль оси Х (при Y=0).
Пример 9.
Рассчитать электростатическое поле от двух бесконечно длинных, равномерно заряженных, параллельных, тонких проводников, расположенных в воздухе на расстоянии 2d=6 м друг от друга. Проводники имеют одинаковые по величине, но противоположные по знаку заряды, линейная плотность которых равна t=4*10-9 Кл/м.
Построить график изменения напряженности поля вдоль оси Y (при х=0) и вывести уравнения для построения эквипотенциальных линий и линий поля.
Решение.
Поскольку среда линейна, то данную задачу можно решить методом наложения.
Вначале рассчитываем напряженность поля в любой точке М от правого провода (рис. 1.17), а затем в этой же точке от левого провода. Задача по расчету поля от бесконечно длинного заряженного провода решена в примере 5. Поэтому сразу запишем выражения для определения напряженности поля от правого и левого провода
Направление векторов напряженности поля показано на рис. 1.17. Результирующая напряженность поля определяется как векторная сумма этих векторов
Модуль данной результирующей напряженности поля рассчитывается по формуле
где
E1x, E2x,
E1y, E2y—
проекции векторов напряженности поля на соответствующие декартовы оси координат.
Здесь yм и xм – координаты произвольной точки М.
В частности, если точка М лежит на оси Y, то (r1=r2) результирующая напряженность поля будет направлена вдоль оси Х (Е=Ех). График распределения данной величины вдоль оси Y представлен на рис. 1.18. Значения напряженности поля на графике даны в относительных единицах, при этом за базисное значение принято значение напряженности в начале координат (x=0, y=0), которое оказалось равным 47,956 В/м.
Потенциал поля в любой точке М определяется также, как сумма потенциалов поля от одного и другого провода
Здесь С – постоянная интегрирования. Эта постоянная будет равна нулю, если принять потенциал точки, которая находится в начале координат, равным нулю.
В этом случае ось OY будет являться эквипотенциальной линией нулевого потенциала.
Все остальные линии равного потенциала являются окружностями с центрами, лежащими на оси ОХ. Координаты этих центров и радиусы окружностей определяются с помощью следующих формул:
Таким образом, если необходимо провести линию равного потенциала через точку, потенциал которой задан (например, 100 В), то надо определить k, используя формулу для потенциала
При построении картины поля, для того чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалось постоянным, должно соблюдаться условие
Здесь В – постоянная; n – порядковый номер линии равного потенциала.
Таким образом, число k при возрастании порядкового номера линии равного потенциала n должно изменяться в геометрической прогрессии.
Линиями поля данной системы заряженных проводников являются дуги окружностей, пересекающихся с проводниками. При этом, центры этих дуг лежат на оси OY и имеют координаты, которые определяются при помощи следующей формулы:
Чтобы при построении картины поля подразделить поле на трубки равного потенциала, необходимо при переходе от любой линии напряженности поля к соседней изменять угол J на постоянную величину.
Пример 10.
Два одинаковых бесконечно длинных проводящих цилиндра расположены в воздухе. Радиус цилиндров R=0.04 м, расстояние между геометрическими осями 2h=0.12 м (рис.1.19).
Напряжение, приложенное к цилиндрам U12=100 В.
Рассчитать электростатическое поле, построить графики изменения напряженности поля и потенциала вдоль оси х.
Найти емкость системы проводов на единицу длины.
Решение.
Поле внутри проводящих проводов отсутствует. Поле же в воздухе будет точно таким, как и поле от двух бесконечно тонких линейных проводников, проходящих через электрические оси данных проводов.
Таким образом, задача по расчету поля двух проводов круглого сечения сводится к нахождению электрических осей проводов, поскольку в дальнейшем расчет поля в воздухе будет аналогичным расчету поля, проведенному в предыдущем примере.
Поскольку поверхность проводящих проводов является поверхностью равного потенциала, то, используя выражения для координаты центра и радиуса линий равного потенциала, которые приведены в примере 9, можно получить формулу для определения координат центра электрических осей проводов b.
В условии задачи задана не линейная плотность зарядов, а разность потенциалов между проводами (разность потенциалов между точками m и n).
Поэтому, прежде всего, следует определить линейную плотность зарядов t. Для этого используем выражение для потенциалов, которое также приведено в предыдущем примере
Здесь r1 и r2 – расстояние от электрической оси первого (левого) и второго провода, соответственно, до точки m, которая находится на поверхности первого провода, а r1/ и r2/ – расстояние от электрической оси первого и второго провода, соответственно, до точки n, которая находится на поверхности второго провода.
С учетом последних соотношений, можно записать выражение для определения линейной плотности зарядов
После определения линейной плотности зарядов и расположения электрических осей проводов, выражения для расчета напряженности поля и потенциала в области вне проводов полностью аналогичны тем, которые приведены в примере 9.
Графики распределения напряженности поля и потенциала вдоль оси ОХ (при y=0) приведены на рис. 1.20. Все значения на графике даны в относительных единицах, причем, за базисные значения приняты значения напряженности поля и потенциала на поверхности правого провода, которые оказались равными Еб=2904 В/м, jб=-50 В.
С учетом того, что ось OY является осью симметрии для напряженности поля и осью антисимметрии для потенциала, графики построены только для положительных значений х.
Емкость между двумя проводниками на единицу их длины определяется при помощи следующего выражения:
Пример 11. Рассчитать
электростатическое поле от двух параллельных бесконечно длинных заряженных несоосных проводящих цилиндров, расположенных в воздухе. Радиусы цилиндров R1=0.02 м и R2=0.04 м. Расстояние между геометрическими осями D=0.08 м (рис. 1.21). Цилиндры имеют одинаковый по величине, но противоположный по знаку заряд, линейная плотность которого t1=-t2=t=10-8 Кл/м.
Определить разность потенциалов между цилиндрами, емкость системы на единицу длины.
Построить график изменения потенциала поля вдоль оси ОХ (при y=0).
Решение.
Расположим оси цилиндров (О1 и О2) так, чтобы их поверхности совпали с поверхностями равного потенциала. Обозначим через h1 и h2 расстояние от геометрических осей первого и второго цилиндра до плоскости постоянного (нулевого) потенциала, а через b – расстояние от электрических осей-до этой плоскости. После определения данных величин задача по расчету поля в области вне цилиндров сводится к расчету электростатического поля от двух заряженных бесконечно длинных линейных проводов, проходящих через центры зарядов, и оказывается, таким образом, полностью аналогичной задачам, рассмотренным в предыдущих примерах.
Используя выражение для определения координат центров зарядов, справедливое как для одного, так и для второго провода, составим следующее уравнение:
или
При заданном расположении цилиндров (рис. 1.21) имеем
h1+h2=D
и, следовательно,
.
В этом случае
Разность потенциалов между двумя цилиндрами можно определить по следующей формуле (как и в примере 10):
Здесь r1/ и r2/ – расстояние от центра электрических осей первого и второго цилиндра, соответственно, до точки n, лежащей на поверхности первого цилиндра; r1// и r2// – расстояние от центра электрических осей первого и второго цилиндра, соответственно, до точки m, лежащей на поверхности второго цилиндра
r1/ = (R1 + b – h1) = 0.0131м; r2/ = 2b – r1/ = 0.0381м;
r2// = (R2 + b – h2) = 0.0181м; r1// = 2b – r2// = 0.0331м.
Потенциал любой произвольной точки d будет равен
где r1 и r2 – расстояние от электрических осей первого и второго провода до точки d.
Если точка d лежит на оси ОХ между цилиндрами, то
r2 = b – x; r1 = b + x;
График изменения потенциала вдоль оси ОХ (при (R1 – h1) < x < (h2 – – R2)) показан на рис. 1.22.
Емкость системы цилиндров на единицу длины определяется по следующей формуле:
Построение линий равного потенциала и линий поля в области вне цилиндров проводится таким же образом, как и для линейных проводов, которые совпадают с электрическими осями (см. пример 9).
Пример 12. Бесконечно длинный проводящий цилиндр радиусом R1=2см расположен внутри другого бесконечно длинного проводящего цилиндра радиусом R2=6см.
Расстояние между геометрическими осями цилиндров D=3см (рис. 1.23). Область между цилиндрами заполнена диэлектриком с относительным значением диэлектрической проницаемости er=2.
Цилиндры имеют одинаковый по величине, но противоположный по знаку заряд, линейная плотность которого t1=-t2=t=10-8Кл/м.
Определить разность потенциалов между цилиндрами, емкость системы на единицу длины. Построить график изменения напряженности поля вдоль оси Х (при Y=0) между цилиндрами.
Решение.
Решение данной задачи, как и в предыдущих примерах, сводится к отысканию положения электрических осей.
Полагая, что оси проводов расположены так, что их поверхности совпадают с эквипотенциальными поверхностями электростатического поля, будем иметь:
где h1 и h2 – расстояние от геометрических осей цилиндров до плоскости постоянного (нулевого) потенциала; b – расстояние от электрических осей до этой же плоскости.
Последнее выражение можно переписать следующим образом:
Но, поскольку при расположении цилиндров один внутри другого, выполняется равенство
то
Таким образом, выражения для определения h1, h2, и b будут иметь следующий вид:
После нахождения положения электрических осей задача по расчету поля в диэлектрике между цилиндрами становится полностью аналогичной задаче по расчету поля от линейных проводов, совпадающих с электрическими осями цилиндров.
Так, потенциал любой точки М, находящейся в области между цилиндрами, будет равен
где r1 и r2 – расстояние от электрических осей первого и второго цилиндров соответственно до точки М.
Разность потенциалов между цилиндрами (между точками m и n) при этом будет равна
Здесь r1/ и r2/ – расстояние от электрических осей первого и второго цилиндров соответственно до точки m, а r1// и r2// – расстояние от электрических осей этих цилиндров до точки n.
При заданном расположении цилиндров указанные расстояния будут равны
Таким образом, разность потенциалов между цилиндрами Umn будет составлять величину, равную 67.1В.
Напряженность электрического поля в любой точке, лежащей на оси ОХ между цилиндрами (между точками m и n), находится методом наложения
График изменения данной величины вдоль оси ОХ представлен на рис. 1.24.
Для удобства изображения все величины на рисунке представлены в относительных единицах. За базисное значение напряженности поля принято значение напряженности поля на поверхности малого цилиндра в точке m (Eb =Еm=8020 В/м), а за базисное значение переменной х – абсолютное значение координаты этой же точки (хb=|хm|= 0.0183 м).
Емкость системы проводов на единицу их длины определяется с помощью следующей формулы:
Зная разность потенциалов между цилиндрами и линейную плотность зарядов t емкость С, согласно определению, можно найти и как отношение линейной плотности зарядов к разности потенциалов
Для построения силовых линий и линий равного потенциала можно воспользоваться рекомендациями, данными в предыдущих примерах.
Задача по физике – 7316
Пусть поверхностная плотность заряда на сфере радиуса $R$ зависит от полярного угла $theta$ как $sigma = sigma_{0} cos theta$ где $sigma_{0}$ — положительная постоянная. Показать, что такое распределение заряда можно представить как результат малого сдвига друг относительно друга двух равномерно заряженных шаров радиуса $R$, заряды которых одинаковы по модулю и противоположны по знаку. Воспользовавшись этим представлением, найти вектор напряженности электрического поля внутри данной сферы.
Подробнее
Задача по физике – 7317
Найти вектор напряженности электрического поля в центре шара радиуса $R$, объемная плотность заряда которого $rho = vec{a} vec{r}$, где $vec{a}$ — постоянный вектор, $vec{r}$ — радиус-вектор, проведенный из центра шара.
Подробнее
Задача по физике – 7318
Равномерно заряженная очень длинная нить, расположенная по оси круга радиуса $R$, упирается одним своим концом в его центр. Заряд нити на единицу длины равен $lambda$. Найти поток вектора $vec{E}$ через площадь круга.
Подробнее
Задача по физике – 7319
Два точечных заряда $q$ и $-q$ расположены на расстоянии $2l$ друг от друга (рис.). Найти поток вектора напряженности электрического поля через круг радиуса $R$.
Подробнее
Задача по физике – 7320
Шар радиуса $R$ равномерно заряжен с объемной плотностью $rho$. Найти поток вектора напряженности электрического поля через сечение шара, которое образовано плоскостью, отстоящей от центра шара на расстояние $r_{0} < R$.
Подробнее
Задача по физике – 7321
Две длинные параллельные друг другу нити равномерно заряжены так, что на единицу длины каждой из них приходится заряд $lambda$. Расстояние между нитями равно $l$. Найти максимальное значение напряженности электрического поля в плоскости симметрии этой системы, расположенной между нитями.
Подробнее
Задача по физике – 7322
Бесконечно длинная цилиндрическая поверхность круглого сечения заряжена равномерно по длине с поверхностной плотностью $sigma = sigma_{0} cos phi$, где $phi$ — полярный угол цилиндрической системы координат с осью z, совпадающей с осью данной поверхности. Найти модуль и направление вектора напряженности электрического поля на оси z.
Подробнее
Задача по физике – 7323
Напряженность электрического поля зависит только от координат х и у по закону $vec{E} = a(x vec{i} + y vec{j})/(x^{2} + y^{2})$, где $a$ — постоянная, $vec{i}$ и $vec{j}$ — орты осей х и у. Найти поток вектора $vec{E}$ через сферу радиуса $R$ с центром в начале координат.
Подробнее
Задача по физике – 7324
Шар радиуса $R$ имеет положительный заряд, объемная плотность которого зависит только от расстояния $r$ до его центра по закону $rho = rho_{0} (1 – r/R)$, где $rho_{0}$ — постоянная. Полагая диэлектрическую проницаемость шара и окружающего пространства равной единице, найти:
а) модуль вектора напряженности электрического поля внутри и вне шара как функцию расстояния $r$;
б) максимальное значение напряженности $E_{max}$ и соответствующее ему значение расстояния $r_{m}$.
Подробнее
Задача по физике – 7325
Система состоит из шара радиуса $R$, заряженного сферически симметрично, и окружающей среды, заполненной зарядом с объемной плотностью $rho = alpha /r$, где $alpha$ — постоянная, $r$ — расстояние от центра шара. Найти заряд шара, при котором модуль вектора напряженности электрического поля вне шара не будет зависеть от $r$. Чему равна эта напряженность? Диэлектрическая проницаемость шара и окружающей среды предполагается равной единице.
Подробнее
Задача по физике – 7326
Пространство заполнено зарядом с объемной плотностью $rho = rho_{0}e^{- alpha r^{3}}$, где $rho_{0}$ и $alpha$ — положительные константы, $r$ — расстояние от центра данной системы. Найти модуль вектора напряженности электрического поля как функцию $r$. Исследовать полученное выражение при малых и больших $r$, т. е. при $alpha r^{3} ll 1$ и $alpha r^{3} gg 1$.
Подробнее
Задача по физике – 7327
Внутри шара, заряженного равномерно с объемной плотностью $rho$, имеется сферическая полость. Центр полости смещен относительно центра шара на величину $a$. Найти напряженность $E$ поля внутри полости, полагая диэлектрическую проницаемость равной единице.
Подробнее
Задача по физике – 7328
Внутри бесконечно длинного круглого цилиндра, заряженного равномерно с объемной плотностью $rho$, имеется круглая цилиндрическая полость. Расстояние между осями цилиндра и полости равно $a$. Найти напряженность $E$ электрического поля в полости. Диэлектрическую проницаемость считать равной единице.
Подробнее
Задача по физике – 7329
Имеются два тонких проволочных кольца радиуса $R$ каждое, оси которых совпадают. Заряды колец равны $q$ и $-q$. Найти разность потенциалов между центрами колец, отстоящими друг от друга на расстояние $a$.
Подробнее
Задача по физике – 7330
Имеется бесконечно длинная прямая нить, заряженная равномерно с линейной плотностью $lambda = 0,40 мкКл/м$. Вычислить разность потенциалов точек 1 и 2, если точка 2 находится в $eta = 2,0$ раза дальше от нити, чем точка 1.
Подробнее