Содержание:
- Определение и формула силы трения
- Виды трения
- Единицы измерения силы трения
- Примеры решения задач
Определение и формула силы трения
Определение
Силой трения называют силу, которая возникает при относительном перемещении (или попытке перемещения) тел и
является результатом сопротивления движению окружающей среды или других тел.
Силы трения возникают тогда, когда соприкасающиеся тела (или их части) перемещаются относительно друг друга. При этом трение, которое появляется при относительном перемещении соприкасающихся тел, называют внешним. Трение, возникающее между частями одного сплошного тела (газ, жидкость) названо внутренним.
Сила трения – это вектор, который имеет направление вдоль касательной к трущимся поверхностям (слоям). При этом эта сила направлена в сторону противодействия относительному смещению этих поверхностей (слоев). Так, если два слоя жидкости перемещаются друг по другу, при этом движутся с различными скоростями, то сила, которая приложена к слою, перемещающемуся с большей скоростью, имеет направление в сторону, которая противоположна движению. Сила же, которая воздействует на слой, который движется с меньшей скоростью, направлена по движению.
Виды трения
Трение, которое возникает между поверхностями твердых тел, называют сухим. Оно возникает не только при скольжении поверхностей, но и при попытке вызвать перемещение поверхностей. При этом возникает сила трения покоя. Внешнее трение, которое появляется между движущимися телами, называют кинематическим.
Законы сухого трения говорят о том, что максимальная сила трения покоя и сила трения скольжения не зависят от площади поверхностей соприкосновения соприкасающихся тел, подверженных трению. Эти силы пропорциональны модулю силы нормального давления (N), которая прижимает трущиеся поверхности:
$$F_{t r}=mu N$$
где $mu$ – безразмерный коэффициент трения (покоя или скольжения).
Данный коэффициент зависит от природы и состояния поверхностей трущихся тел, например от наличия шероховатостей.
Если трение возникает как результат скольжения, то коэффициент трения является функцией скорости. Довольно часто
вместо коэффициента трения применяют угол трения, который равен:
$$operatorname{tg}varphi=mu ( 2 )$$
Угол $varphi_{0}=operatorname{arctg} mu_{0}$ равен минимальному углу наклона плоскости к горизонту,
при котором тело, лежащее на этой плоскости, начинает скользить, под воздействие силы тяжести.
Более точным считают закон трения, который принимает во внимание силы притяжения между молекулами тел, которые подвергаются трению:
$$F_{t r}=mu_{0}left(N+S p_{0}right)(3)$$
где S – общая площадь контакта тел, p0 – добавочное давление, которое вызывается силами молекулярного притяжения,
$mu_0$ – истинный коэффициент трения.
Трение между твердым телом и жидкостью (или газом) называют вязким (жидким). Сила вязкого трения становится равной нулю, если скорость относительного движения тел обращается в нуль.
При движении тела в жидкости или газе появляются силы сопротивления среды, которые могут стать существенно больше, чем силы трения. Величина силы трения скольжения зависит от формы, размеров и состояния поверхности тела, скорости движения тела относительно среды, вязкости среды. При не очень больших скоростях сила трения вычисляется при помощи формулы:
$$bar{F}_{t p}=-mu^{prime} bar{v}(4)$$
где знак минус означает, что сила трения имеет направление в сторону противоположную направлению вектора скорости. При увеличении скоростей движения тел в вязкой среде линейный закон (4) переходит в квадратичный:
$$bar{F}_{t p}=-mu^{prime prime} v^{2} frac{bar{v}}{v}(5)$$
Коэффициенты $mu^{prime}$ и
$mu^{prime prime}$ существенно зависимы от формы, размеров, состояния поверхностей
тел, вязкости среды.
Помимо этого выделяют трение качения.В первом приближении трение качения рассчитывают, применяя формулу:
$$F_{t r}=k frac{N}{r}(6)$$
где k – коэффициент трения качения, который имеет размерность длины и зависит от материала тел, подверженных контакту и качеств поверхностей и т.д. N – сила нормального давления , r – радиус катящегося тела.
Единицы измерения силы трения
Основной единицей измерения силы трения (как и любой другой силы) в системе СИ является: [P]=H
В СГС: [P]=дин.
Примеры решения задач
Пример
Задание. На горизонтальном диске лежит маленькое тело. Диск вращается вокруг оси,
которая проходит через его центр, перпендикулярно плоскости с угловой скоростью
$omega$. На каком расстоянии от центра диска может находиться в
состоянии равновесия тело, если коэффициент трения между диском и телом равен
$mu$?
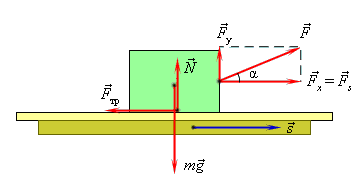
Решение. Изобразим на рис.1 силы, которые будут действовать на тело, положенное на вращающийся диск.
В соответствии со вторым законом Ньютона имеем:
$$m bar{g}+bar{F}_{t r}+bar{N}=m bar{a}(1.1)$$
В проекции на ось Yиз уравнения (1.1) получим:
$$-m g+N=0(1.2)$$
В проекции на ось X имеем:
$$-F_{t r}=m a_{n}=m frac{v^{2}}{r}(1.3)$$
где ускорение движения маленького тела равно по модуль нормальной составляющей полного ускорения. Силутрения покоя найдем как:
$$F_{t r}=mu N$$
примем во внимание выражение (1.2), тогда имеем:
$$F_{t r}=mu cdot m g(1.5)$$
приравняем правые части выражений (1.3) и (1.5):
$$m frac{v^{2}}{r}=mu cdot m g rightarrow frac{v^{2}}{r}=mu g rightarrow r=frac{v^{2}}{mu g}(1.6)$$
где маленькое тело (так как оно находится в состоянии покоя на диске) движется со скоростью, равной:
$$v=omega cdot r(1.7)$$
Следовательно:
$$r=frac{(omega cdot r)^{2}}{mu g} rightarrow r=frac{mu g}{omega^{2}}$$
Ответ. $r=frac{mu g}{omega^{2}}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. По наклонной поверхности равномерно движется тело. Угол наклона плоскости равен
$alpha$. Коков коэффициент трения между телом и наклонной плоскостью?
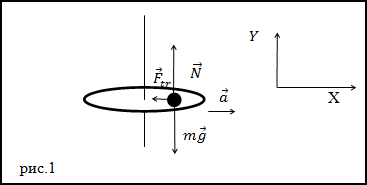
Решение. Сделаем рисунок.
В соответствии со вторым законом Ньютона, учитывая, что движение равномерное, имеем:
$$m bar{g}+bar{F}_{t r}+bar{N}=0(1.1)$$
В проекции на ось Y (данная ось параллельна силе реакции опоры) из уравнения (1.1) получим:
$$-m g cdot cos (alpha)+N=0 rightarrow N=m g cdot cos (alpha)(1.2)$$
В проекции на ось X имеем:
$$F_{t r}=m g cdot sin (alpha)(1.3)$$
Так как можно принять, что:
$$F_{t r}=mu N$$
то получаем:
$$m g cdot sin (alpha)=mu m g cdot cos (a) rightarrow mu=operatorname{tg}(alpha)$$
Ответ. $mu=operatorname{tg}(alpha)$
Читать дальше: Формула силы тяжести.
Содержание:
- Трение
- Трения скольжения
- Законы Амонтона-Кулона
- Угол и конус трения
- Трения нити по поверхности цилиндра
- Трения качения
- Примеры решения задач с учетом сил трения
Трение — это процесс механического взаимодействия соприкасающихся тел при их относительном смещении в плоскости касания (внешнее трение) либо при относительном смещении параллельных слоёв жидкости, газа или деформируемого твёрдого тела (внутреннее трение, или вязкость).
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Трение
Трение всегда, в одних случаях явно, а в других – скрыто, присутствует в практической деятельности человека и играет при этом как полезную, так и вредную роль. Основное свойство трения – сопротивляться любом перемещению тела, и это, как ни парадоксально, с одной стороны, помогает телу двигаться с определенной скоростью, а с другой – тратить
определенное количество энергии.
В зависимости от вида движения одного тела по поверхности другого различают трения скольжения, качения и верчения. Будем рассматривать первые два вида, еще называются трением первого рода и трением второго рода.
Трения скольжения
Пусть к телу весом Р, которое лежит на абсолютно гладкой горизонтальной поверхности и которая является связью для тела, приложенная активная сила  параллельная к поверхности (рис. 7.1). Реакция поверхности
параллельная к поверхности (рис. 7.1). Реакция поверхности в этом случае направлена по совместной нормали к поверхности и будет уравновешиваться силой
в этом случае направлена по совместной нормали к поверхности и будет уравновешиваться силой  а сила
а сила  а не уравновешена никакой другой силой, приведет тело в ускоренное движение по поверхности. Следует обратить внимание на то, что направление реакции
а не уравновешена никакой другой силой, приведет тело в ускоренное движение по поверхности. Следует обратить внимание на то, что направление реакции  в этом случае будет зависеть от направления действия активных сил. От активных сил будет зависеть только величина этой реакции.
в этом случае будет зависеть от направления действия активных сил. От активных сил будет зависеть только величина этой реакции.
Но в практике абсолютно гладких поверхностей практически не бывает. Все поверхности тел определенной степени шершавые.
Рассмотрим тело весом Р, которое лежит на шероховатой горизонтальной поверхности (рис. 7.2). Если к этому телу приложить горизонтальную силу то на тело, кроме двух уравновешенных сил
то на тело, кроме двух уравновешенных сил  и силы
и силы  будет действовать сила, возникающая между контактирующими поверхностями и которая будет направлена противоположно силы
будет действовать сила, возникающая между контактирующими поверхностями и которая будет направлена противоположно силы Обозначим эту силу
Обозначим эту силу  . Эта сила будет сопротивляться движения тела по шероховатой поверхности и в определенных пределах модуля силы
. Эта сила будет сопротивляться движения тела по шероховатой поверхности и в определенных пределах модуля силы  будет ее уравновешивать. Тело при этом будет находиться в состоянии покоя. силу
будет ее уравновешивать. Тело при этом будет находиться в состоянии покоя. силу называют силой трения скольжения. Будем рассматривать только так называемое сухое трение, то есть такое, когда между поверхностями что контактируют, нет масел, в отличие от вязкого трения, когда между этими поверхностями находятся тонкие слои масла.
называют силой трения скольжения. Будем рассматривать только так называемое сухое трение, то есть такое, когда между поверхностями что контактируют, нет масел, в отличие от вязкого трения, когда между этими поверхностями находятся тонкие слои масла.

Трения скольжения имеет двойственную механико-молекулярную природу. Оно обусловлено как сопротивлением, которое возникает при механической деформации микровыступов шероховатых поверхностей, так и преодолением межмолекулярных связей при достаточном сближении (на расстояние действия межмолекулярных сил) участков
контактирующих поверхностей (холодная сварка).
Итак, исходя из вышеизложенного, трение скольжения – это сопротивление, возникает при перемещении или попытке перемещения одного тела по поверхности другого.
Вернемся к детальному исследованию силы трения скольжения. Свойства сил трения скольжения можно исследовать на достаточно простом примере, схема которого приведена на рис. 7.3. Тело весом Р находится на горизонтальной шероховатой поверхности. К телу прикреплена нить, перекинута через блок, к концу которой подвешен груз весом  Вес тела и груза в процессе эксперимента можно менять.
Вес тела и груза в процессе эксперимента можно менять.

Натяжение нити, если пренебречь трением в оси блока, по модулю равен весу груза  а нормальная реакция
а нормальная реакция  Изменяя вес тела, можно менять модуль нормальной реакции
Изменяя вес тела, можно менять модуль нормальной реакции а изменяя вес груза, можно изменять модуль силы
а изменяя вес груза, можно изменять модуль силы  которая стремится двигать тело по поверхности. Очевидно, что когда
которая стремится двигать тело по поверхности. Очевидно, что когда  то тело находится в равновесии и сила трения
то тело находится в равновесии и сила трения отсутствует.
отсутствует.
Будем постепенно увеличивать вес груза  а значит, и силу
а значит, и силу  Сначала тело остается в состоянии покоя, то есть сила трения
Сначала тело остается в состоянии покоя, то есть сила трения  уравновешивает силу
уравновешивает силу увеличиваясь вместе с ней. Такое положение будет сохраняться до тех пор, пока сила трения не достигнет своего максимального значения
увеличиваясь вместе с ней. Такое положение будет сохраняться до тех пор, пока сила трения не достигнет своего максимального значения 
Этот момент характеризует предельный случай равновесия тела, когда тело находится на границе между состоянием покоя и движения.
Силу трения при отсутствии относительного движения между поверхностями тел называют силой трения покоя, или силой статического трения, или силой сцепления. Модуль этой силы может принимать различные значения, достигая максимального в момент начала относительного движения тел.
После достижения силой трения своего максимально возможного значения достаточно незначительного увеличения силы
достаточно незначительного увеличения силы чтобы началось движение тела. При этом, как показали опыты, после начала движения сила трения
чтобы началось движение тела. При этом, как показали опыты, после начала движения сила трения  сразу уменьшится, и для равномерного движения тела нужно уменьшить вес груза
сразу уменьшится, и для равномерного движения тела нужно уменьшить вес груза  В дальнейшем таким уменьшением
В дальнейшем таким уменьшением будем пренебрегать.
будем пренебрегать.
О первых исследованхия явления трения упоминается в работах Леонардо да Винчи (1452-1519). Однако впервые свойства сил трения сформулировали, основываясь на собственных исследованиях и работах, французский механик И. Амонтон (1663-1705) и французский физик Ш. Кулон (1736-1806).
Рассмотрим основные законы Амонтона-Кулона для сухого трения скольжения.
Законы Амонтона-Кулона
1. Вектор силы трения скольжения размещен в общей касательной плоскости контактирующих поверхностей тел и направлен в сторону, противоположную в направлении возможного движения тела под действием активных сил. Итак, направление силы трения зависит от активных сил, и ее модуль размещен между нулем и максимальным значением, которое достигается в момент нарушения состояния равновесия, то есть

2. Максимальная сила трения скольжения, при прочих равных условиях, не зависит от площади контактирующих поверхностей.
3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции):

где – безразмерный коэффициент пропорциональности, который называется коэффициентом трения скольжения (статический коэффициент трения, коэффициент сцепления).
– безразмерный коэффициент пропорциональности, который называется коэффициентом трения скольжения (статический коэффициент трения, коэффициент сцепления).
Коэффициент трения скольжения  зависит от материала и физического состояния поверхностей контактирующих тел (степени и характера обработки поверхностей, температуры, влажности и т.д.). Значение коэффициента трения скольжения устанавливаются экспериментально и приводятся в справочной литературе. Значение
зависит от материала и физического состояния поверхностей контактирующих тел (степени и характера обработки поверхностей, температуры, влажности и т.д.). Значение коэффициента трения скольжения устанавливаются экспериментально и приводятся в справочной литературе. Значение  для некоторых комбинаций материалов тел представлены в табл. 7.1.
для некоторых комбинаций материалов тел представлены в табл. 7.1.
Таблица 7.1
Коэффициент трения скольжения  для некоторых комбинаций материалов
для некоторых комбинаций материалов
Следует заметить, что приведенные значения коэффициентов трения являются приближенными, и их использование возможно только для предварительных расчетов.
Для точных расчетов необходимо каждый раз значение коэффициента трения определять экспериментально.
Закон Амонтона-Кулона о граничное значение силы трения справедлив и для движения одного тела по поверхности другого некоторой относительной скоростью. При скольжении тела по шероховатой поверхности в него, кроме других сил, приложенная сила трения, направленная в сторону, противоположную направлению скорости тела. Эту силу иногда называют динамической силой трения скольжения. Модуль этой силы

где  – коэффициент трения при движении (динамический коэффициент трения).
– коэффициент трения при движении (динамический коэффициент трения).
Опыты показали, что для большинства материалов  и
и  уменьшается с увеличением относительной скорости скольжения (за исключением трения кожи по металлу, где с ростом скорости
уменьшается с увеличением относительной скорости скольжения (за исключением трения кожи по металлу, где с ростом скорости  увеличивается). Однако для приближенных технических расчетов считают, что динамический коэффициент трения скольжения не зависит от относительной скорости и принимается в пределах, приведенных в справочной литературе.
увеличивается). Однако для приближенных технических расчетов считают, что динамический коэффициент трения скольжения не зависит от относительной скорости и принимается в пределах, приведенных в справочной литературе.
Замечания. Принимая во внимание зависимости (7.1) и (7.2), для силы трения в состоянии покоя тела можно записать неравенство

Случай строгого равенства в (7.2) соответствует максимальному значению силы трения. Это означает, что силу трения можно учесть с зависимостью  только в тех случаях, когда достоверно известно, что естьграничное состояние. Во всех остальных случаях силу трения необходимо определять из уравнений равновесия.
только в тех случаях, когда достоверно известно, что естьграничное состояние. Во всех остальных случаях силу трения необходимо определять из уравнений равновесия.
При движении тел по шероховатых поверхностях сила трения скольжения всегда однозначно определяется по зависимости (7.3).
Угол и конус трения
Пусть твердое тело под действием активных сил находится на шероховатой поверхности.
Полная реакция шероховатой поверхности (рис. 7.4) определяется по длине и направлению диагонали параллелограмма, построенного на нормальной реакции
(рис. 7.4) определяется по длине и направлению диагонали параллелограмма, построенного на нормальной реакции  и силы трения
и силы трения  то есть
то есть 
Полная реакция  отклонена от нормали к опорной поверхности на угол β в сторону, противоположную силе
отклонена от нормали к опорной поверхности на угол β в сторону, противоположную силе Как известно, с увеличением
Как известно, с увеличением  растет и сила трения
растет и сила трения 
и при этом полная реакция отклоняется от нормали на все более крупный угол. Это отклонение будет максимальным при  Наибольшее значение угла отклонения полной реакции
Наибольшее значение угла отклонения полной реакции  от нормали называется углом трения φ.
от нормали называется углом трения φ.

Из рис. 7.4 и зависимости (7.2) следует, что 
В зависимости от направления действия активных сил направление максимальной полной
реакции будет меняться. Геометрическое место всех возможных положений максимальной реакции  образует коническую поверхность – конус трения (Рис. 7.5). Если коэффициент трения
образует коническую поверхность – конус трения (Рис. 7.5). Если коэффициент трения  во всех направлениях шероховатой поверхности одинаковый, то по зависимости (7.6) конус трения будет круговым. Пространство внутри конуса трения имеет такое свойство, что какой бы большой по модулю не была равнодействующая всех активных сил
во всех направлениях шероховатой поверхности одинаковый, то по зависимости (7.6) конус трения будет круговым. Пространство внутри конуса трения имеет такое свойство, что какой бы большой по модулю не была равнодействующая всех активных сил  (рис. 7.6), линия действия которой размещена внутри конуса трения, она не выведет тело из состояния покоя.
(рис. 7.6), линия действия которой размещена внутри конуса трения, она не выведет тело из состояния покоя.


Для подтверждения этого свойства конуса трения запишем уравнение равновесия для тела, изображенного на рис. 7.6:

Из уравнений найдем  и, подставляя в неравенство (7.4), получим
и, подставляя в неравенство (7.4), получим  или, учитывая (7.6),
или, учитывая (7.6),
Следовательно, при равновесии тела  Это означает, что для возбуждения состояния
Это означает, что для возбуждения состояния
равновесия тела необходимо, чтобы равнодействующая активных сил  находилась
находилась
за конусом трения. Область, ограниченная конусом трения, называется областью равновесия. Наличием области равновесия объясняется явление самоторможения (заклинивания) деталей машин, а также величина максимального угла наклона боковой поверхности сыпучего тела к горизонту при насыпи плотины, так называемого угла естественного склона.
Покажем, что угол естественного склона равен углу трения между частицами сыпучего тела, из которого насыпается плотина (песок, земля тому подобное).

Рассмотрим частицу песка весом Р, которая лежит на боковой поверхности плотины (рис. 7.7). Очевидно, что  а используя зависимости (7.1) и (7.2), можно записать
а используя зависимости (7.1) и (7.2), можно записать 

По предельного равновесия  Учитывая, что равновесие возможна только при
Учитывая, что равновесие возможна только при  получим
получим  откуда
откуда  или
или 
Последнее равенство можно рассматривать как условие равновесия (самоторможения) частиц песка, лежащих на наклонной поверхности (поверхности плотины). Используя ее, можно рассчитать максимальный угол наклона боковой поверхности плотины при ее сооружении в зависимости от материала, из которого она строится.
Трения нити по поверхности цилиндра
До нитки, накинутой на круглый цилиндрический вал (рис. 7.8), приложена сила Найдем, какое наименьшее силу
Найдем, какое наименьшее силу  нужно приложить к второму концу нити, чтобы сохранить
нужно приложить к второму концу нити, чтобы сохранить
равновесие при заданном угле АОВ, равный  если коэффициент трения нити по поверхности вала
если коэффициент трения нити по поверхности вала 

Для этого рассмотрим равновесие элемента нити DЕ длиной  где R – радиус вала. Разница натяжения нити в точках D и Е равен
где R – радиус вала. Разница натяжения нити в точках D и Е равен  и уравновешивается силой трения
и уравновешивается силой трения  (dN – нормальная реакция), поскольку при малейшей силе
(dN – нормальная реакция), поскольку при малейшей силе  равновесие является граничной.
равновесие является граничной.
Следовательно 
Значение dN определим из уравнения равновесия в проекции на ось у.
Предполагая, что синус малого угла равен самому углу и пренебрегая малыми высшего порядка, найдем, что

Подставляя это значение dN в предварительное равенство, получим 
Поделим обе части последнего равенства на Т и возьмем интегралы справа в пределах от  до
до  а слева от
а слева от  до
до  (поскольку натяжение нити в точке, где
(поскольку натяжение нити в точке, где  равна
равна  а в точке, где
а в точке, где  равна
равна  ).
).
Получим  или
или 
Отсюда следует, что 
или
Из формулы (7.7), которая называется формулой Эйлера, видно, что сила  зависит только от коэффициента трения
зависит только от коэффициента трения  и угла
и угла  а от радиуса вала сила
а от радиуса вала сила  не зависит.
не зависит.
Для практики очень важным является тот факт, что, увеличивая угол (наматывая нить), можно значительно уменьшить силу  необходимую для уравновешивания силы
необходимую для уравновешивания силы 
Формула (7.7) определяет также отношение натяжения  (ведущей) и
(ведущей) и  (ведомой) веток паса, равномерно вращающего шкива, если проскальзывания паса по шкиву отсутствует. Считая, например,
(ведомой) веток паса, равномерно вращающего шкива, если проскальзывания паса по шкиву отсутствует. Считая, например,  и принимая
и принимая  для кожаного ремня и чугунного шкива, получим отношение натяжения
для кожаного ремня и чугунного шкива, получим отношение натяжения
Трения качения
Трением качения называется сопротивление, возникающее при качении или попытке качения одного тела по поверхности другого. Например, при качении цилиндрического катка по поверхности шероховатой горизонтальной плоскости, кроме трения скольжения, возникает трение качения. Это сопротивление возникает в результате деформаций поверхностей тел.
Рассмотрим каток весом  и радиусом r, который лежит на горизонтальной поверхности (рис. 7.9). К центру катка приложена горизонтальная сила
и радиусом r, который лежит на горизонтальной поверхности (рис. 7.9). К центру катка приложена горизонтальная сила  Под весом катка опорная поверхность деформируется и контакт происходит по некоторой площадке. При этом точка
Под весом катка опорная поверхность деформируется и контакт происходит по некоторой площадке. При этом точка
приложения реакций  и
и  перемещается из точки А в некоторую точку В.
перемещается из точки А в некоторую точку В.

При определенном значении модуля силы  каток будет находиться в равновесии. Запишем уравнение равновесия сил, приложенных к катку:
каток будет находиться в равновесии. Запишем уравнение равновесия сил, приложенных к катку:

Из первых двух уравнений получим  Это свидетельствует о то, что при равновесии катка к нему приложены две пары сил:
Это свидетельствует о то, что при равновесии катка к нему приложены две пары сил:  и
и  Первая пара стремится вернуть тело, то есть привести его в движение.
Первая пара стремится вернуть тело, то есть привести его в движение.
Вторая – сопротивляется этому повороту. Момент второй пары будем называть моментом трения качения и обозначим его  этот момент равен моменту силы
этот момент равен моменту силы относительно точки А
относительно точки А 
В любой момент равновесия катка обе пары уравновешиваются, что следует из третьего уравнения системы (7.8).
В начале движения момент трения качения достигнет своего максимального значение  которое по опытами пропорциональное нормальном давлении
которое по опытами пропорциональное нормальном давлении

Коэффициент пропорциональности  называется коэффициентом трения качения, или коэффициентом трения второго рода. Как видно из рисунка и зависимости (7.10),
называется коэффициентом трения качения, или коэффициентом трения второго рода. Как видно из рисунка и зависимости (7.10),
коэффициент трения качения  имеет размерность длины и является расстоянием от
имеет размерность длины и является расстоянием от
вертикальной прямой, проходящей через центр катка до точки приложения нормальной реакции  Это расстояние меняется в зависимости от модуля силы
Это расстояние меняется в зависимости от модуля силы  и достигает максимального значения за предельного состояния равновесия. Значение коэффициента
и достигает максимального значения за предельного состояния равновесия. Значение коэффициента  зависит от материала тел и определяется опытным путем. В состоянии равновесия катка момент трения качения
зависит от материала тел и определяется опытным путем. В состоянии равновесия катка момент трения качения  не превышает своего максимального значения, то есть
не превышает своего максимального значения, то есть 
Учитывая третье уравнение системы (7.8), а также (7.9) и (7.10), получим

откуда

Неравенство (7.12) определяет условие, при которой не происходит качения катка. С другой стороны, чтобы каток не скользил по поверхности, необходимо, чтобы сила была меньше максимальной силы трения
была меньше максимальной силы трения  то есть
то есть
Поскольку значение  в большинстве случаев значительно меньше коэффициента трения скольжения
в большинстве случаев значительно меньше коэффициента трения скольжения  то когда возрастает сила
то когда возрастает сила  всегда сначала будет происходить качения катка без проскальзывания. Практический вывод этого утверждения заключается в том, что в технике, если это возможно, необходимо заменять трения скольжения трением качения (колеса, катки, шарикоподшипники). Это уменьшает сопротивление трения.
всегда сначала будет происходить качения катка без проскальзывания. Практический вывод этого утверждения заключается в том, что в технике, если это возможно, необходимо заменять трения скольжения трением качения (колеса, катки, шарикоподшипники). Это уменьшает сопротивление трения.
Замечания. Исходя из физики процесса качения и используя лемму о параллельный перенос силы, при определении момента трения качения расчетную схему (рис. 7.9) можно заменить эквивалентной, изображенной на рис. 7.10.

Примеры решения задач с учетом сил трения
Задача 1. Лестница АВ весом P = 196 Н опирается на каменную стену и стоит на деревянном дубовом полу. Коэффициенты трения лестницы по полу и стене соответственно равны  под каким минимальным углом к полу нужно поставить лестницу, чтобы по ней мог подняться человек, вес которого
под каким минимальным углом к полу нужно поставить лестницу, чтобы по ней мог подняться человек, вес которого  (рис. 7.11).
(рис. 7.11).
Решение. Примем объектом равновесия лестницу АВ, к которой приложены силы: вес лестницы и вес человека
и вес человека 
Связями, наложенными на лестницу, будут шероховатые поверхности в точках А и В. Освободим объект равновесия от связей и заменим их действие реакциями
связей, которые разложим на составляющие: нормальные  и силы трения
и силы трения

Выберем систему координат, как показано на рис. 7.11, и запишем уравнения равновесия для плоской системы сил, приложенной к объекту равновесия в предельном состоянии покоя.

Принимаем  тогда в граничном состоянии лестницы:
тогда в граничном состоянии лестницы:

В полученной алгебраической системе есть пять неизвестных:
 и угол
и угол  Для получения статически обозначенной системы запишем еще два соотношения:
Для получения статически обозначенной системы запишем еще два соотношения:
Решая систему уравнений с учетом записанных соотношений, иметь

Задача 2. Определить соотношение между размерами механизма  показанного на рис. 7.12, при которых механизм был бы самотормозящей. Коэффициент трения между ползунами А и В и стенками равен
показанного на рис. 7.12, при которых механизм был бы самотормозящей. Коэффициент трения между ползунами А и В и стенками равен
Решение. Для того, чтобы механизм был самотормозящей, необходимо, чтобы линия действия силы давления стержней АС и ВС на ползуны А и В лежала внутри конуса трения, то есть чтобы выполнялось соотношение или
или 
В нашем случае
Если учесть, что АС> СD, то после преобразований получим 
Исходя из этого неравенства, можно спроектировать механизм, который был бы самотормозящей и который можно было бы использовать для временных, сменных опор.

Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Благодаря силе трения мы не скользим, отталкиваясь от поверхности, когда идем по тропинке.
Иногда силу трения увеличивают, разбрасывая песок на покрытую льдом поверхность ступеней крыльца.
В некоторых случаях силу трения стараются уменьшить, смазывая трущиеся поверхности, например, подшипники на оси колеса.
Трущиеся поверхности нагреваются, поэтому с помощью силы трения можно зажечь огонь.
Виды трения
Пусть одно тело лежит на поверхности другого тела. В этом случае между поверхностями действует сила трения покоя.
Она может быть практически равной нулю, когда поверхности расположены горизонтально. Но иногда трение покоя может быть достаточно большим.
К примеру, если толкнуть в бок тяжелый ящик, лежащий на горизонтальном полу, мы почувствуем сопротивление. Оно возникает благодаря тому, что между поверхностями ящика и пола действует сила трения покоя, которая, по третьему закону Ньютона равна силе, с которой мы толкаем ящик.
Примечание: Пока тело не сдвинулось с места, сила трения покоя ( overrightarrow{ F_{text{тр. покоя}}} ) равна силе ( vec{F} ), которая действует на тело!
[ large boxed{ left| overrightarrow{F_{text{тр. покоя}}} right| = left| vec{F} right| } ]
Чем больше становится приложенная нами сила, тем больше увеличивается трение покоя. Так будет происходить до тех пор, пока приложенную силу не увеличим настолько, что ящик сдвинется с места.
Как только ящик пришел в движение, сила трения покоя сменится силой трения скольжения.
Примечание: Сила трения скольжения меньше максимальной силы трения покоя.
Нам известно, что катить тележку с грузом по сухому асфальту легче, чем тянуть по асфальту волокуши с этим же грузом. Причина этого — сила трения.
Примечание: В местах соединения колес со ступицами присутствует трение, его называют трением качения, оно гораздо меньше трения скольжения.
Отличие между силами трения можно показать с помощью рисунка 1.
Трение покоя может изменяться от нуля до своего максимального значения (F_{max}). Это максимальное значение оказывается даже большим, чем сила трения скольжения.
Поэтому, с места столкнуть тело сложнее, чем подталкивать его, когда оно уже скользит по поверхности.
А сила трения качения будет незначительно отличаться от нуля. Катить всегда легче, чем тащить волоком.

Рис. 1. Шкала сил трения, трение качения меньше трения скольжения. А трение покоя может изменяться от нуля до величины, которая превышает трение скольжения
Сила трения имеет электромагнитную природу. Даже самая гладкая поверхность под микроскопом содержит бугры и впадины. Когда поверхности соприкасаются, тела взаимодействуют благодаря таким неровностям. Электронные оболочки атомов тел сближаются, образуется трение.
Формула для расчета силы трения
Рассмотрим тело, например, ящик (рис. 2), скользящий по горизонтальной поверхности со скоростью (vec{v}).
Ящик давит на поверхность своим весом, на рисунке он не обозначен. Вертикально вверх направлена сила реакции поверхности, на которую ящик давит.
А сила трения направлена против движения ящика.

Рис. 2. Сила трения скольжения направлена всегда против движения тела
Силу трения скольжения можно вычислить, используя такое выражение:
[ large boxed{ left| vec{F_{text{тр. сколь}}} right| = mu cdot N }]
( F_{text{тр. сколь}} left( H right) ) – сила трения, которая возникает при скольжении одного тела по поверхности другого;
( mu ) – коэффициент трения скольжения, это просто число, у него нет собственных единиц измерения;
( N left( H right) ) – сила реакции опоры. В каждом конкретном случае реакция опоры рассчитывается из соотношения, полученного при составлении векторных уравнений (ссылка).
Работа силы трения
Когда сила перемещает тело, физики говорят: «Сила совершает работу по перемещению тела».
Сила и перемещение – это векторы. Совершать работу может вектор силы, направленный по отношению к вектору перемещения под любым углом, кроме прямого!
Если же угол между направлением движения тела и силой будет прямым, то такая сила работу совершать не будет!
Сила трения может совершать работу. Но эта сила мешает телу двигаться, она направлена против движения. Поэтому, работу такой силы считаем отрицательной и записываем со знаком минус!
Примечание: Сила трения совершает работу, но эту работу мы записываем со знаком минус!
Работа любой силы — это скалярное произведение вектора силы на вектор перемещения.
В векторном виде выражение для работы можно записать так:
[ large boxed{ A_{text{тр}} = left( vec{F_{text{тр}}} cdot vec{S} right) }]
В школе формулу работы обычно записывают в скалярном виде:
[ large boxed{ A_{text{тр}} = left| vec{F_{text{тр}}} right| cdot left| vec{S} right| cdot cos(alpha) }]
( A_{text{тр}} left( text{Дж} right) ) – работа (силы трения), это скалярная величина;
( F_{text{тр}} left( H right) ) – сила трения;
( S left( text{м} right) ) – перемещение тела;
( alpha ) – угол между силой трения и перемещением тела;
Примечание: Трение относится к диссипативным силам. Когда диссипативная сила действует на систему, полная механическая энергия этой системы убывает (диссипирует). Убывающая энергия из механической переходит в другой вид энергии – к примеру, в тепловую энергию.
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении и направленная против движения
Ft = μ·N
Сила нормальной реакции опоры N=m·g, поэтому Ft = μ·m·g
Вектор силы трения скольжения всегда направлен противоположно вектору скорости движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел.
Сила трения скольжения зависит от силы давления тел друг на друга (силы нормальной реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. Это можно объяснить тем, что увеличивая площадь соприкосновения, мы уменьшаем удельное давление тел друг на друга.
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой μ. Обычно коэффициент трения меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки поверхностей. При скольжении сила трения направлена по касательной к соприкасающимся поверхностям в сторону, противоположную относительной скорости
Обозначения:
Ft – сила трения
μ – коэффициент трения
N – сила нормальной реакции опоры
m – масса тела
g – ускорение свободного падения
Глоссарий. Физика
Сила трения
Сила, возникающая на границе соприкосновения тел при отсутствии относительного движения тел, называется силой трения покоя.
Сила трения покоя Fтр равна по модулю внешней силе F, направленной по касательной к поверхности соприкосновения тел, и противоположна ей по направлению:

Прикрепим динамометр к бруску и заставим брусок двигаться равномерно по горизонтальной поверхности стола. Во время равномерного движения бруска динамометр показывает, что на брусок со стороны пружины действует постоянная сила упругости Fупр. При равномерном движении бруска равнодействующая всех сил равна нулю. Следовательно, кроме силы упругости, во время равномерного движения на брусок действует сила, равная по модулю силе упругости, но направленная в противоположную сторону. Эта сила называется силой трения скольжения Fтр.
Вектор силы трения скольжения Fтр всегда направлен противоположно вектору скорости движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел.
Силы трения возникают благодаря существованию сил взаимодействия между молекулами и атомами соприкасающихся тел. Последние обусловлены взаимодействием электрических зарядов, которыми обладают частицы, входящие в состав атомов. На основании опытов можно сделать вывод, что максимальное значение модуля силы трения покоя прямо пропорционально силе давления.
Взаимодействие тела и опоры вызывает деформацию и тела, и опоры. Силу упругости N, возникающую в результате деформации опоры и действующую на тело, называют силой реакции опоры.
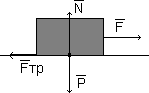
По третьему закону Ньютона сила давления и сила реакции опоры равны по модулю и противоположны по направлению.
Поэтому предыдущий вывод можно сформулировать так: модуль максимальной силы трения покоя пропорционален силе реакции опоры:
Fтрmax = μ · N
Греческой буквой μ (мю) обозначен коэффициент пропорциональности, называемый коэффициентом трения.
Модуль силы трения скольжения Fтр, как и модуль максимальной силы трения покоя, пропорционален модулю силы реакции опоры:
Fтр = μ · N
Максимальное значение силы трения покоя примерно равно силе трения скольжения, приближенно равны также коэффициенты трения покоя и скольжения.
Силы трения возникают так же и при качении тела. При одинаковой нагрузке сила трения качения значительно меньше силы трения скольжения. Поэтому для уменьшения сил трения в технике применяются колеса, шариковые и роликовые подшипники.
Другие заметки по физике