Как найти вектор скорости формула

Как найти вектор скорости формула

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Рисунок траектории движения материальной точки

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Радиус-вектор пример траектории

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

решение примера построения траектории

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

Решение задачи

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

формула вектора скорости

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

закон движения материальной точки

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Нахождение вектора скорости точки

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Формула вектора ускорения точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Пример решения задачи как найти вектор ускорения точки

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Как найти модуль вектора скорости

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Пример нахождения вектора ускорения

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Решение задач

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Источник

В прошлой статье мы немножко разобрались с тем, что такое механика  и зачем она нужна. Мы уже знаем, что такое система отсчета,  относительность движения и материальная точка. Что ж, пора двигаться дальше!  Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики  и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад  в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат  (или радиус-вектора точки) от времени.

Перемещение и путь

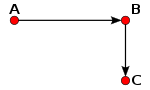
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

Перемещение и путь

 

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

Скорость и ускорение

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной  от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

Мгновенная скорость формула

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Мгновенное ускорение формула

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Тангенциальное ускорение формула

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Нормальное ускорение как найти

Здесь R – радиус окружности, по которой движется тело.

Векторы нормального, тангенциального и полного ускорения

 

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Закон равноускоренного движения

Здесь  – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Закон равноускоренного движения

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Кинематика пример решения задачи

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник
Скорость
{vec v}={frac {{mathrm {d}}{vec r}}{{mathrm {d}}t}}
Размерность LT−1
Единицы измерения
СИ м/с
СГС см/с
Примечания
вектор
Классическая механика
История…

Фундаментальные понятия

  • Пространство
  • Время
  • Масса
  • Скорость
  • Сила
  • Механическая работа
  • Энергия
  • Импульс

Формулировки

  • Ньютоновская механика
  • Лагранжева механика
  • Гамильтонова механика
  • Формализм Гамильтона — Якоби
  • Уравнения Рауса
  • Уравнения Аппеля
  • Теория Купмана — фон Неймана

Разделы

  • Прикладная механика
  • Небесная механика
  • Механика сплошных сред
  • Геометрическая оптика
  • Статистическая механика

Учёные

  • Галилей
  • Кеплер
  • Ньютон
  • Эйлер
  • Лаплас
  • Д’Аламбер
  • Лагранж
  • Гамильтон
  • Коши
См. также: Портал:Физика

Ско́рость (стандартное обозначение: {vec {v}}, от англ. velocity, исходно от лат. vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта. По определению, равна производной радиус-вектора точки по времени[1]. В СИ измеряется в метрах в секунду.

В русском языке этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, то есть проекцию вектора {vec {v}} на касательную к траектории точки[2]. В некоторых других языках для скалярной скорости имеются отдельные наименования, например англ. speed, лат. celeritas[значимость факта?].

Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.

Понятие «скорость» в классической механике[править | править код]

Случай материальной точки[править | править код]

Вектор скорости (мгновенной скорости) материальной точки в каждый момент времени определяется как производная по времени радиус-вектора {{vec r}} текущего положения этой точки, так что[3]:

{vec v}={{mathrm {d}}{{vec r}} over {mathrm {d}}t}equiv v_{{tau }}{{vec tau }},

где {{vec tau }}equiv {mathrm {d}}{{vec r}}/{mathrm {d}}s — единичный вектор касательной, проходящей через текущую точку траектории (он направлен в сторону возрастания дуговой координаты s движущейся точки), а v_{{tau }}equiv {dot {s}} — проекция вектора скорости на направление упомянутого единичного вектора, равная производной дуговой координаты по времени и именуемая алгебраической скоростью точки. В соответствии с приведёнными формулами, вектор скорости точки всегда направлен вдоль касательной, а алгебраическая скорость точки может отличаться от модуля v этого вектора лишь знаком[4]. При этом:

Пройденный точкой путь {tilde {s}} за промежуток времени от t_0 до t, находится как

{displaystyle {tilde {s}}=int _{t_{0}}^{t}|{dot {s}}|,mathrm {d} t;}.

Когда алгебраическая скорость точки всё время неотрицательна, путь совпадает с приращением дуговой координаты за время от t_0 до t (если же при этом начало отсчёта дуговой координаты совпадает с начальным положением движущейся точки, то {tilde {s}} будет просто совпадать с s).

Иллюстрация средней и мгновенной скорости

Если алгебраическая скорость точки не меняется с течением времени (или, что то же самое, модуль скорости постоянен), то движение точки называется[5] равномерным (алгебраическое касательное ускорение {ddot {s}} при этом тождественно равно нулю).

Предположим, что {{ddot {s}}}geqslant {0}. Тогда при равномерном движении скорость точки (алгебраическая) будет равна отношению пройденного пути {tilde {s}} к промежутку времени t-t_{0}, за который этот путь был пройден:

{{dot {s}}}^{{,{mathrm {cp}}}}={{tilde {s}} over t-t_{0}};.

В общем же случае аналогичные отношения

{{vec v}}^{{,,{mathrm {cp}}}}={{{vec r}}-{{vec r}}_{0} over t-t_{0}}equiv {Delta {{vec r}} over Delta {t}} и {{dot {s}}}^{{,{mathrm {cp}}}}={s-s_{0} over t-t_{0}}equiv {Delta {s} over Delta {t}}

определяют соответственно среднюю скорость точки[6] и её среднюю алгебраическую скорость; если термином «средняя скорость» пользуются, то о величинах {vec {v}} и {dot {s}} говорят (чтобы избежать путаницы) как о мгновенных скоростях.

Различие между двумя введёнными выше понятиями средней скорости состоит в следующем. Во-первых, {{vec v}}^{{,,{mathrm {cp}}}} — вектор, а {{dot {s}}}^{{,{mathrm {cp}}}} — скаляр. Во-вторых, эти величины могут не совпадать по модулю. Так, пусть точка движется по винтовой линии и за время своего движения проходит один виток; тогда модуль средней скорости этой точки будет равен отношению шага винтовой линии (то есть расстояния между её витками) ко времени движения, а модуль средней алгебраической скорости — отношению длины витка ко времени движения.

Случай тела конечных размеров[править | править код]

Для тела протяжённых размеров понятие «скорости» (тела как такового, а не одной из его точек) не может быть определено; исключение составляет случай мгновенно-поступательного движения. Говорят, что абсолютно твёрдое тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны[7]; тогда можно, разумеется, положить скорость тела равной скорости любой из его точек. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем же случае скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса модули скоростей точек на ободе относительно дороги принимают значения от нуля (в точке касания с дорогой) до удвоенного значения скорости центра колеса (в точке, диаметрально противоположной точке касания). Распределение скоростей точек абсолютно твёрдого тела описывается кинематической формулой Эйлера.

Начальная скорость[править | править код]

Начальная скорость ({displaystyle {vec {v}}_{0}}) — это скорость материальной точки в момент, принимаемый за нуль по шкале времени (то есть при t = 0)[8].

Истолкование {displaystyle {vec {v}}_{0}} как скорости, с которой тело начинает движение, не вполне корректно, поскольку покоившееся тело в принципе не может начать двигаться с отличной от нуля скоростью. При такой формулировке неявно подразумевается, что в короткий промежуток времени {displaystyle t=[-Delta tldots 0]} действовала большая по величине сила, на пренебрежимо малом участке разогнавшая тело до скорости {displaystyle {vec {v}}={vec {v}}_{0}} к моменту t = 0.

Запись скорости в разных системах координат[править | править код]

В декартовых координатах[править | править код]

В прямоугольной декартовой системе координат[9]:

{displaystyle mathbf {v} =v_{x}mathbf {i} +v_{y}mathbf {j} +v_{z}mathbf {k} .}

При этом {mathbf r}=x{mathbf i}+y{mathbf j}+z{mathbf k}, следовательно,

{displaystyle mathbf {v} ={frac {mathrm {d} (xmathbf {i} +ymathbf {j} +zmathbf {k} )}{mathrm {d} t}}={frac {mathrm {d} x}{mathrm {d} t}}mathbf {i} +{frac {mathrm {d} y}{mathrm {d} t}}mathbf {j} +{frac {mathrm {d} z}{mathrm {d} t}}mathbf {k} .}

Таким образом, компоненты вектора скорости — это скорости изменения соответствующих координат материальной точки[9]:

{displaystyle v_{x}={frac {mathrm {d} x}{mathrm {d} t}};v_{y}={frac {mathrm {d} y}{mathrm {d} t}};v_{z}={frac {mathrm {d} z}{mathrm {d} t}}.}

В цилиндрических координатах[править | править код]

Скорость в полярных координатах

В цилиндрических координатах R,varphi ,z[9]:

{displaystyle v_{R}={frac {mathrm {d} R}{mathrm {d} t}};v_{varphi }=R{frac {mathrm {d} varphi }{mathrm {d} t}};v_{z}={frac {mathrm {d} z}{mathrm {d} t}}.}

v_{varphi } носит название поперечной скорости, v_{R} — радиальной.

В сферических координатах[править | править код]

В сферических координатах R,varphi ,theta [9]:

{displaystyle v_{R}={frac {mathrm {d} R}{mathrm {d} t}};v_{varphi }=Rsin theta {frac {mathrm {d} varphi }{mathrm {d} t}};v_{theta }=R{frac {mathrm {d} theta }{mathrm {d} t}}.}

Для описания плоского движения иногда используются полярные координаты, которые можно рассматривать как частный случай цилиндрических (c {displaystyle z=} const) или сферических (с theta =pi /2).

Физическая и координатная скорости[править | править код]

В аналитической механике вышеприведённые и другие криволинейные координаты играют роль обобщённых координат; изменение положение тела описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями (они могут иметь размерность отличную от м/c). Физической же скоростью является производная радиус-вектора по времени, а её составляющие в каждом случае задаются всем стоящим перед соответствующим ортом выражением.

Некоторые связанные со скоростью понятия[править | править код]

Ряд величин в классической механике выражается через скорость.

Импульс, или количество движения, — это мера механического движения точки, которая определяется как произведение массы точки на её скорость

{vec p}=m{vec v}.

Импульс является векторной величиной, его направление совпадает с направлением скорости. Для замкнутой системы выполняется закон сохранения импульса.

От скорости также зависит кинетическая энергия механической системы. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения[10][11]:

{displaystyle T={frac {mv^{2}}{2}}+{frac {{mathcal {I}}{vec {omega }}^{2}}{2}},}

где m — масса тела, v — скорость центра масс тела, {mathcal {I}} — момент инерции тела, {vec omega } — угловая скорость тела.

Изменение скорости во времени характеризуется ускорением. Ускорение отражает изменение скорости как по величине (тангенциальное ускорение), так и по направлению (центростремительное ускорение)[12]:

{vec a}={frac {{mathrm {d}}{vec v}}{{mathrm {d}}t}}={vec a}_{tau }+{vec a}_{n}={frac {{mathrm {d}}|{vec v}|}{{mathrm {d}}t}}{vec e}_{tau }+{v^{2} over r}{vec e}_{n},

где r — радиус кривизны траектории точки.

Преобразования Галилея и Лоренца для скорости[править | править код]

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна {vec {v}}, а скорость системы отсчёта S' относительно системы отсчёта S равна vec u, то скорость тела при переходе в систему отсчёта S' будет равна[9]

{displaystyle {vec {v}}'={vec {v}}-{vec {u}}.}

Для скоростей, близких к скорости света, преобразования Галилея становятся несправедливы. При переходе из системы S в систему S' необходимо использовать преобразования Лоренца для скоростей[9]:

v_{x}'={frac {v_{x}-u}{1-(v_{x}u)/c^{2}}},v_{y}'={frac {v_{y}{sqrt {1-{frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},v_{z}'={frac {v_{z}{sqrt {1-{frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},

в предположении, что скорость vec u направлена вдоль оси x системы S. В пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Скорость в релятивистской механике[править | править код]

Четырёхмерная скорость[править | править код]

Одним из обобщений понятия скорости является четырёхмерная скорость (скорость в релятивистской механике[9]). В специальной теории относительности каждому событию ставится в соответствие точка пространства Минковского, три координаты которого представляют собой декартовы координаты трёхмерного евклидова пространства, а четвёртая ― временну́ю координату ct, где c ― скорость света, t ― время события. Компоненты четырёхмерного вектора скорости связаны с проекциями трёхмерного вектора скорости следующим образом[9]:

v_{0}={frac {c}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{1}={frac {v_{x}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{2}={frac {v_{y}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{3}={frac {v_{z}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}.

Четырёхмерный вектор скорости является времениподобным вектором, то есть лежит внутри светового конуса[9].

Существует также понятие четырёхимпульс, временна́я компонента которого равна E/c (где E — энергия). Для четырёхмерного импульса выполняется равенство[13]:

{displaystyle p_{i}=m,v_{i}},

где v_{i} — четырёхмерная скорость.

Понятие «быстрота»[править | править код]

В релятивистской механике угол между касательной к мировой линии частицы и осью времени в базовой системе отсчёта носит название быстроты (обозначается theta ). Быстрота выражается формулой

theta =c,{mathrm {Arth}},{frac {v}{c}}={frac {c}{2}}ln {frac {1+{dfrac {v}{c}}}{1-{dfrac {v}{c}}}},

где {mathrm {Arth}},x — ареатангенс, или гиперболический арктангенс. Быстрота стремится к бесконечности когда скорость стремится к скорости света. В отличие от скорости, для которой необходимо пользоваться преобразованиями Лоренца, быстрота аддитивна, то есть

theta '=theta +theta _{0},

где theta _{0} — быстрота системы отсчёта S' относительно системы отсчёта S.

Некоторые скорости[править | править код]

Космические скорости[править | править код]

Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос

Небесная механика изучает поведение тел Солнечной системы и других небесных тел. Движение искусственных космических тел изучается в астродинамике. При этом рассматривается несколько вариантов движения тел, для каждого из которых необходимо придание определённой скорости. Для вывода спутника на круговую орбиту ему необходимо придать первую космическую скорость (например, искусственный спутник Земли); преодолеть гравитационное притяжение позволит вторая космическая скорость (например, объект запущенный с Земли, вышедший за её орбиту, но находящийся в Солнечной системе); третья космическая скорость нужна чтобы покинуть звёздную систему, преодолев притяжение звезды (например, объект запущенный с Земли, вышедший за её орбиту и за пределы Солнечной системы); четвёртая космическая скорость позволит покинуть галактику.

В небесной механике под орбитальной скоростью понимают скорость вращения тела вокруг барицентра системы.

Скорости распространения волн[править | править код]

Скорость звука[править | править код]

Скорость звука — скорость распространения упругих волн в среде, определяется упругостью и плотностью среды. Скорость звука не является постоянной величиной и зависит от температуры (в газах), от направления распространения волны (в монокристаллах). При заданных внешних условиях обычно не зависит от частоты волны и её амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом. Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, поэтому при сжижении газа скорость звука возрастает.

Отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде называется числом Маха по имени австрийского учёного Эрнста Маха. Упрощённо, скорость, соответствующая 1 Маху при давлении в 1 атм (у земли на уровне моря), будет равна скорости звука в воздухе. Движение аппаратов со скоростью, сравнимой со скоростью звука, сопровождается рядом явлений, которые называются звуковой барьер. Скорости от 1,2 до 5 Махов называются сверхзвуковыми, скорости выше 5 Махов — гиперзвуковыми.

Скорость света[править | править код]

Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 секунды.

Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Традиционно обозначается латинской буквой «c» (произносится как [це]). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.

Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. Теперь ввиду современного определения метра скорость света считается равной точно 299792458 м/с[14].

Скорость гравитации[править | править код]

Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн. До сих пор остаётся не определённой экспериментально, но согласно общей теории относительности должна совпадать со скоростью света.

Единицы измерения скорости[править | править код]

Линейная скорость:

  • Метр в секунду, (м/с), производная единица системы СИ
  • Километр в час, (км/ч)
  • узел (морская миля в час)
  • Число Маха, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
  • Скорость света в вакууме (обозначается c)

Угловая скорость:

  • Радианы в секунду, принята в системах СИ и СГС. Физическая размерность 1/с.
  • Обороты в секунду (в технике)
  • градусы в секунду, грады в секунду

Соотношения между единицами скорости[править | править код]

  • 1 м/с = 3,6 км/ч
  • 1 узел = 1,852 км/ч = 0,514 м/c
  • Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
  • c = 299 792 458 м/c

Исторический очерк[править | править код]

Две стадии движения брошенного тела по теории Авиценны: отрезок АВ — период «насильственного стремления», отрезок ВС — период «естественного стремления» (падение вертикально вниз)

Автолик из Питаны в IV веке до н. э. определил равномерное движение так: «О точке говорится, что она равномерно перемещается, если в равные времена она проходит равные и одинаковые величины». Несмотря на то, что в определении участвовали путь и время, их отношение считалось бессмысленным[15], так как сравнивать можно было только однородные величины и скорость движения являлась чисто качественным, но не количественным понятием[16]. Живший в то же время Аристотель делил движение на «естественное», когда тело стремится занять своё естественное положение, и «насильственное», происходящее под действием силы. В случае «насильственного» движения произведение величины «двигателя» и времени движения равно произведению величины «движимого» и пройденного пути, что соответствует формуле Ft=ms, или F=mv[15]. Этих же взглядов придерживался Авиценна в XI веке, хотя и предлагал другие причины движения[17], а также Герард Брюссельский в конце XII —
начале XIII века. Герард написал трактат «О движении» — первый европейский трактат по кинематике — в котором сформулировал идею определения средней скорости движения тела (при вращении прямая, параллельная оси вращения, движется «одинаково с любой своей точкой», а радиус — «одинаково со своей серединой»)[18].

В 1328 году увидел свет «Трактат о пропорциях или о пропорциях скоростей при движении» Томаса Брадвардина, в котором он нашёл несоответствие в физике Аристотеля и связи скорости с действующими силами. Брадвардин заметил, что по словесной формуле Аристотеля если движущая сила равна сопротивлению, то скорость равна 1, в то время как она должна быть равна 0. Он также представил свою формулу изменения скорости, которая хоть и была не обоснована с физической точки зрения, но представляла собой первую функциональную зависимость скорости от причин движения. Брадвардин называл скорость «количеством движения»[19]. Уильям Хейтсбери, в трактате «О местном движении» ввёл понятие мгновенной скорости. В 1330—1340 годах он и другие ученики Брадвардина доказали так называемое «мертонское правило», которое означает равенство пути при равноускоренном движении и равномерном движении со средней скоростью[20].

Всякая широта движения, униформно приобретаемая или теряемая, соответствует своему среднему градусу, так что столько же в точности будет пройдено благодаря этой приобретаемой широте, сколько и благодаря среднему градусу, если бы тело двигалось всё время с этим средним градусом.

— «Мертонское правило» в формулировке Суайнсхеда[20]

В XIV веке Жан Буридан ввёл понятие импетуса[21], благодаря чему была определена величина изменения скорости — ускорение. Николай Орем, ученик Буридана, предложил считать, что благодаря импетусу ускорение остаётся постоянным (а не скорость, как полагал сам Буридан), предвосхитив, таким образом, второй закон Ньютона[22]. Орем также использовал графическое представление движения. В «Трактате о конфигурации качеств и движения» (1350) он предложил изображать отрезками перпендикулярных прямых количество и качество движения (время и скорость), иными словами, он нарисовал график изменения скорости в зависимости от времени[23].

По мнению Тартальи, только вертикальное падение тела является «естественным» движением, а все остальные — «насильственные», при этом у первого типа скорость постоянно возрастает, а у второго — убывает. Два этих типа движения не могут проистекать одновременно. Тарталья считал, что «насильственные» движения вызваны ударом, результатом которого является «эффект», определяемый скоростью[24]. С критикой работ Аристотеля и Тартальи выступал Бенедетти, который вслед за Оремом пользовался понятиями импетуса и ускорения[25].

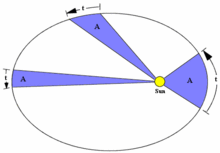
В 1609 году в работе «Новая астрономия» Кеплер сформулировал закон площадей, согласно которому секторная скорость планеты (площадь, описываемая отрезком планета — Солнце, за единицу времени) постоянна[26]. В «Началах философии» Декарт сформулировал закон сохранения количества движения, которое в его понимании есть произведение количества материи на скорость[27], при этом Декарт не принимал во внимание тот факт, что количество движения имеет не только величину, но и направление[28]. В дальнейшем понятие «количество движения» развивал Гук, который понимал его как «степень скорости, присущей в определённом количестве вещества»[29]. Гюйгенс, Валлис и Рен добавили к этому определению направление. В таком виде во второй половине XVII века количество движения стало важным понятием в динамике, в частности в работах Ньютона и Лейбница[30]. При этом Ньютон не определял в своих работах понятие скорости[31]. По-видимому, первая попытка явного определения скорости была сделана Валлисом в его трактате «Механика или геометрический трактат о движении» (1669—1671): «Скорость есть свойство движения, отражающееся в сравнении длины и времени; а именно, она определяет, какая длина в какое время проходится»[32].

В XVII веке были заложены основы математического анализа, а именно интегрального и дифференциального исчисления. В отличие от геометрических построений Лейбница, теория «флюксий» Ньютона строится на потребностях механики и имеет в своём основании понятие скорости. В своей теории Ньютон рассматривает переменную величину «флюенту» и её скорость изменения — «флюксию»[33].

Скорости в природе и технике[править | править код]

Основной источник: [34]

Метры в секунду
Скорость улитки {displaystyle 1{,}4times 10^{-2}}
Скорость черепахи {displaystyle 5{,}0times 10^{-2}}
Средняя скорость здорового человека (произвольный темп) {displaystyle 1{,}43}
Рекорд скорости человека в ходьбе на 50 км {displaystyle 3{,}4} ({displaystyle 3{,}92})
Рекорд скорости человека в беге на дистанции 100 м {displaystyle 1{,}0times 10^{1}} ({displaystyle 1{,}044times 10^{1}})
Скорость гепарда 31
Максимальная скорость полёта сокола 100
Максимальная скорость локомотива на железной дороге {displaystyle 110}
Максимальная скорость автомобиля {displaystyle 340}[35]
Средняя скорость молекулы азота при температуре 0 °C 500
Максимальная скорость пассажирского реактивного самолёта 700
Скорость движения Луны по орбите вокруг Земли 1000
Скорость искусственного спутника Земли {displaystyle 8000}
Скорость движения Земли по орбите вокруг Солнца {displaystyle 30000}
Скорость движения Солнца по орбите вокруг центра Галактики {displaystyle 230000}
Скорость электронов в кинескопе телевизора {displaystyle 1{,}0times 10^{8}}
Скорость движения самых далёких галактик {displaystyle 1{,}4times 10^{8}}
Максимальная скорость протонов в Большом адронном коллайдере 299 792 455
Скорость частицы Oh-My-God 299792457,9999999999999985310169558
Скорость безмассовых частиц (фотонов, глюонов, гравитонов) 299 792 458
Скорость тахионов и сверхбрадионов > 299792458

Скорости движения живых существ[править | править код]

  • Сапсан (самое быстрое животное): самая высокая зарегистрированная скорость — 389 км/ч[36];
  • Гепард (самое быстрое наземное животное): самая высокая зарегистрированная скорость — 98 км/ч[37];
  • Меч-рыба: от 100 до 130 км в час[37];
  • Чёрный марлин: самая высокая зарегистрированная скорость — 105 км/ч[36];
  • Вилорогая антилопа: самая высокая зарегистрированная скорость — 88,5 км/ч[36];
  • Лошадь (американский квортерхорс): 88 км/ч[36];
  • Человек: самая высокая зарегистрированная скорость — 44,72 км/ч (Усэйн Болт)[37].

Рекорды скорости транспортных средств[править | править код]

Самый быстрый рукотворный объект — Parker Solar Probe, 150 км/с (относительно Солнца) в 2021 году[38].

Абсолютный рекорд скорости в воздухе был поставлен в 1976 году американским самолетом-разведчиком Lockheed SR-71 Blackbird — 3529,56 км/ч.

Рекорд скорости на земле был установлен в 2003 году на ракетных санях и составил 10 325 км/ч или 2868 м/с (по другим данным, 10 430 км/ч)[39]

Самая высокая скорость на наземном управляемом транспортном средстве была достигнута на реактивном автомобиле Thrust SSC в 1997 году — 1228 км/ч.

Рекорд скорости на воде был поставлен в 1978 году австралийским судном с реактивным газотурбинным двигателем Spirit of Australia[en] — 511,11 км/ч[40]

См. также[править | править код]

  • Кинематика

Примечания[править | править код]

  1. ↑ Маркеев, 1990, с. 15.
  2. ↑ Старжинский, 1980, с. 154.
  3. ↑ Маркеев, 1990, с. 15—17.
  4. ↑ Старжинский, 1980, с. 154—155.
  5. ↑ Старжинский, 1980, с. 163.
  6. ↑ Старжинский, 1980, с. 152.
  7. ↑ Маркеев, 1990, с. 46—47.
  8. ↑ См. Всегда ли начальная скорость равна нулю? в справочнике «Студворк».
  9. ↑ 1 2 3 4 5 6 7 8 9 Скорость // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
  10. ↑ Главный редактор А. М. Прохоров. Кинетическая энергия // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
  11. ↑ Главный редактор А. М. Прохоров. Вращательное движение // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
  12. ↑ Главный редактор А. М. Прохоров. Ускорение // Физический энциклопедический словарь.. — 1983. Физическая энциклопедия
  13. ↑ Главный редактор А. М. Прохоров. Импульс // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
  14. ↑ Определение метра Архивная копия от 26 июня 2013 на Wayback Machine (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
  15. ↑ 1 2 Яковлев, 2001, с. 21.
  16. ↑ Яковлев, 2001, с. 34.
  17. ↑ Яковлев, 2001, с. 29.
  18. ↑ Яковлев, 2001, с. 31—32.
  19. ↑ Яковлев, 2001, с. 32—34.
  20. ↑ 1 2 Яковлев, 2001, с. 35.
  21. ↑ Яковлев, 2001, с. 35—36.
  22. ↑ Яковлев, 2001, с. 37.
  23. ↑ Яковлев, 2001, с. 37—38.
  24. ↑ Яковлев, 2001, с. 43.
  25. ↑ Яковлев, 2001, с. 45.
  26. ↑ Яковлев, 2001, с. 51—52.
  27. ↑ Яковлев, 2001, с. 59.
  28. ↑ Яковлев, 2001, с. 68.
  29. ↑ Яковлев, 2001, с. 77.
  30. ↑ Яковлев, 2001, с. 91.
  31. ↑ Яковлев, 2001, с. 96.
  32. ↑ Яковлев, 2001, с. 72—73.
  33. ↑ Яковлев, 2001, с. 64—66.
  34. ↑ Кабардин О.Ф., Орлов В.А., Пономарёва А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 44
  35. ↑ FIA World Land Speed Records (англ.). Federation Internationale de l’Automobile (10 июня 2012). Дата обращения: 3 декабря 2020. Архивировано 31 марта 2019 года.
  36. ↑ 1 2 3 4 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 29 июля 2021 года.
  37. ↑ 1 2 3 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 22 сентября 2020 года.
  38. ↑ Самый быстрый объект, созданный человеком. Зонд Parker Solar Probe развил скорость около 150 км/с. Дата обращения: 17 июня 2022. Архивировано 17 мая 2021 года.
  39. ↑ Test sets world land speed record. www.af.mil. Дата обращения: 19 апреля 2016.
  40. ↑ Назло рекордам: почему люди не хотят передвигаться очень быстро

Литература[править | править код]

  • Маркеев А. П.  Теоретическая механика. — М.: Наука, 1990. — 416 с. — ISBN 5-02-014016-3.
  • Старжинский В. М.  Теоретическая механика. — М.: Наука, 1980. — 464 с.
  • Яковлев В. И.  Предыстория аналитической механики. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 328 с. — ISBN 5-93972-063-3.
Источник

Для характеристики
быстроты движения вводится понятие
скорости.

Определение:
Средней
скоростью движения точки за интервал
времени от
доназывается
векторная величина равная отношению
приращения радиус-вектора точки за этот
промежуток времени к его продолжительности.

– средняя скорость.

Определение:
Скорость
(или мгновенная скорость) точки называется
векторная величина, равная первой
производной по времени от радиус-вектора.

Вектор скорости
характеризует движение, как по величине,
так и по направлению. Вектор скорости
всегда направлен по касательной к
траектории в сторону движения.

Определение:
Модуль
скорости равен первой производной по
времени от пройденного пути.

Разложим вектор
скорости по базису прямоугольной
декартовой системы координат:

, гдеVx,
Vy,
Vz
проекции вектора скорости на соответствующую
ось, которые соответственно равны:

где
– это иксовая проекция радиус-вектора
материальной точки.

В координатном
представлении вектор скорости имеет
вид:

Модуль вектора
скорости в координатном представлении:

Обратное соотношение.

Представим радиус
вектор скорости посредством определенного
и неопределенного интеграла:

где t,
t0
– начальный и конечный момент времени.

Представление
пройденного пути через модуль скорости
посредством определенного и неопределенного
интеграла.

§4. Вектор ускорения.

Для характеристики
быстроты изменения вектора скорости
точки в механике вводится понятие
ускорения.

Определение:
Среднее
ускорение за интервал времени от
доназывается векторная величина равная
отношению приращения вектора скорости
точки за данный интервал времени к его
величине.

Определение:
Ускорение
(или мгновенное ускорение) точки
называется векторная величина, численно
равная первой производной по времени
от скорости рассматриваемой точки или,
что то же самое, вторая производная по
времени от радиус-вектора этой точки:

Ускорение можно
ввести через предел от среднего ускорения:

Две введенные
записи ускорения являются эквивалентными.

Разложим вектор
ускорения по базису прямоугольной
декартовой системы координат:

где ax,
ay,
az
– проекции вектора ускорения на ось.

Координатное
представление модуля вектора ускорения:

Обратные соотношения:

;

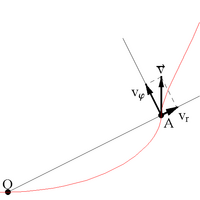
Рассмотрим движение
материальной точки вдоль плоской кривой.
Ускорение всегда направлено внутрь
вогнутости кривой или траектории. Введем
два единичных вектора:
,
который направлен по касательной к
траектории и– направлен перпендикулярно траектории
в центр кривой.

;

Разложим вектор
ускорения по заданным направлениям.

– касательное
ускорение.

Определение:
Касательное
ускорение – векторная величина,
характеризующая быстроту изменения
вектора скорости по модулю.

– векторное
представление.

– скалярное
представление.

– нормальное
ускорение.

Определение:
Нормальное
ускорение характеризует быстроту
изменения вектора скорости по направлению
и вычисляется по формуле:

-где R- радиус
кривизны траектории в точке М

Если траектория
– окружность, то R
– радиус окружности.

В скалярном
представлении:

Из свойств
составляющих полное ускорение следует,
что полное ускорение направленно в
сторону вогнутости траектории.

Модуль полного
ускорения равен:

Аналогично для
вектора полного ускорения:

Источник

Содержание:

  • Определение и формула скорости
  • Скорость в разных системах координат
  • Частные случаи формул для вычисления скорости
  • Единицы измерения скорости
  • Примеры решения задач

Определение и формула скорости

Определение

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
$bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

$$bar{v}=frac{d bar{r}}{d t}=dot{bar{r}}(1)$$

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения.
Модуль скорости можно определить как первую производную от длины пути (s) по времени:

$$v=frac{d s}{d t}=dot{s}(2)$$

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.

Скорость в разных системах координат

Проекции скорости на оси декартовой системы координат запишутся как:

$$v_{x}=dot{x} ; v_{y}=dot{y} ; v_{z}=dot{z}(3)$$

Следовательно, вектор скоростив декартовых координатах можно представить:

$$bar{v}=dot{x} bar{i}+dot{y} bar{j}+dot{z} bar{k}(4)$$

где $bar{i}, bar{j}, bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:

$$v=sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}}(5)$$

В цилиндрических координатах модуль скорости вычисляют при помощи формулы:

$$v=sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}}(6)$$

в сферической системе координат:

$$v=sqrt{(r)^{2}+(r dot{theta})^{2}+(r dot{varphi} sin theta)^{2}}(7)$$

Частные случаи формул для вычисления скорости

Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const).
При равномерном движении скорость можно вычислить, применяя формулу:

$$v=frac{s}{t}(8)$$

где s– длина пути, t – время, за которое материальная точка преодолела путь s.

При ускоренном движении скорость можно найти как:

$$bar{v}=int_{t_{1}}^{t_{2}} bar{a} d t(9)$$

где $bar{a}$ – ускорение точки,
$t_{1} leq t leq t_{2}$ – отрезок времени, в течение которого рассматривается скорость.

Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:

$$bar{v}=bar{v}_{0}+bar{a} t$$

где $bar{v}_0$ – начальная скорость движения,
$bar{a} = const$ .

Единицы измерения скорости

Основной единицей измерения скорости в системе СИ является: [v]=м/с2

В СГС: [v]=см/с2

Примеры решения задач

Пример

Задание. Движение материальной точки А задано уравнением:
$x=2 t^{2}-4 t^{3}$ . Точка начала свое движение при
t0=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для
этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

$$v=frac{d x}{d t}=4 t-12 t^{2}(1.1)$$

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент
времении сравним результат с нулем:

$$v(t=0,5)=4 cdot 0,5-12(0,5)^{2}=-1 lt 0$$

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Скорость материальной точки является функцией от времени вида:

$$v=10left(1-frac{t}{5}right)$$

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии
10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

$$x=int_{0}^{t} v d t=int_{0}^{t} 10left(1-frac{t}{5}right) d t=10 t-frac{10 t^{2}}{2 cdot 5}=10 t-t^{2}(2.1)$$

Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:

$$x=10 cdot 10-(10)^{2}=0(m)$$

Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат
приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:

$$
begin{array}{c}
10 t-t^{2}=10(2.2) \
t_{1}=5+sqrt{15} approx 8,8(c) ; t_{2}=5-sqrt{15} approx 1,13(c)
end{array}
$$

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:

$$10 t-t^{2}=-10(2.3)$$

При решении уравнения (2.3) нам подойдет корень равный:

$$t_{3}=5+6=11 (c)$$

Ответ. 1) $x=0 mathrm{~m}$ 2) $t_{1}=8,8 mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$

Читать дальше: Формула средней скорости.

Источник

Добавить комментарий