При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R→=F1→+F2→+F3→+…+Fn→=∑i=1nFi→.
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
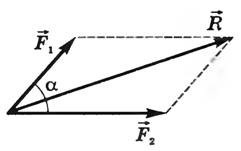
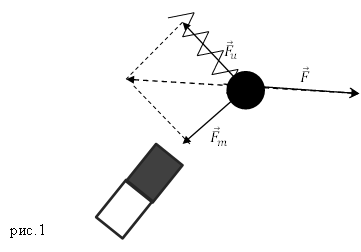
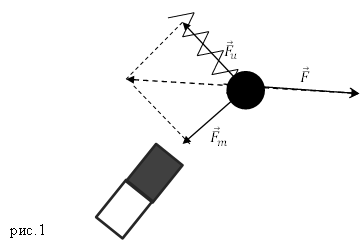
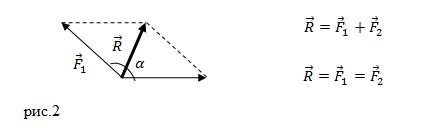
Для сложения 2-х сил используют правило параллелограмма (рисунок 1).
Рисунок 1. Сложение 2-х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R→=F1→2+F2→2+2F1→2F2→2cos α
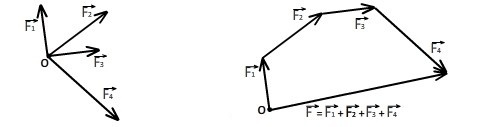
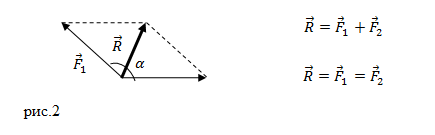
При необходимости сложения более 2-х сил используют правило многоугольника: от конца
1-й силы необходимо провести вектор, равный и параллельный 2-й силе; от конца 2-й силы необходимо провести вектор, равный и параллельный 3-й силе и т.д.
Рисунок 2. Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4-х сил: F1→, F2→, F3→, F4→. Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
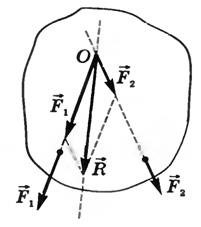
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3. Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0: ∑i=1nFi→=0→. В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2-мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2, приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2-х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2-х составляющих сил.
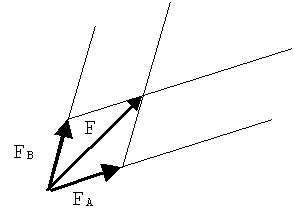
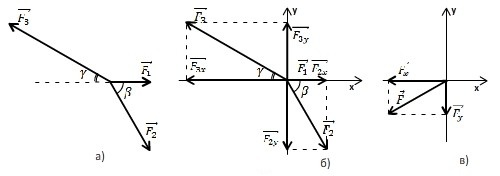
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b. Отрезок FA и отрезок FB изображают искомые силы.
Рисунок 4. Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2-й проекции (рисунок 5 а ).
Рисунок 5. Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F2→ силы F→.
Итак, 2-й способ решения: прибавим к силе силу, равную -F1→ (рисунок 5 в). В итоге получаем искомую силу F→.
Три силы F1→=1 Н; F2→=2 Н; F3→= 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а) и составляют углы с горизонталью α=0°; β=60°; γ=30° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6. Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси ОХ и OY таким образом, чтобы ось ОХ совпадала с горизонталью, вдоль которой направлена сила F1→. Сделаем проекцию данных сил на координатные оси (рисунок 6 б). Проекции F2y и F2x отрицательны. Сумма проекций сил на координатную ось ОХ равняется проекции на данную ось равнодействующей: F1+F2cosβ-F3cosγ=Fx=4-332≈-0,6 Н.
Точно также для проекций на ось OY: -F2sin β+F3sin γ=Fy=3-232≈-0,2 Н.
Модуль равнодействующей определим с помощью теоремы Пифагора:
F=Fx2+Fy2=0,36+0,04≈0,64 Н.
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в):
tg φ=FyFx=3-234-33≈0,4.
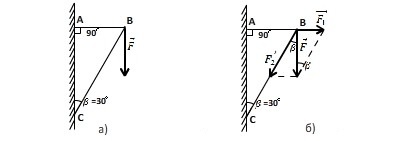
Сила F=1 кН приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7. Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F=1 кН=1000 Н
Пускай стержни прикручены к стене в точках А и С. На рисунке 7 б изображено разложение силы F→ на составляющие вдоль направлений АВ и ВС. Отсюда понятно, что
F1→=Ftg β≈577 Н;
F2→=Fcos β≈1155 Н.
Ответ: F1→=557 Н; F2→=1155 Н.
Законы сложения сил в механике
Вы будете перенаправлены на Автор24
При одновременном действии на одно тело нескольких сил тело движется с ускорением, являющимся векторной суммой ускорений, которые бы возникли под действием каждой силы в отдельности. Действующие на тело силы, приложенные к одной точке, складываются по правилу сложения векторов.
Векторная сумма всех сил, одновременно действующих на тело, называется равнодействующей силой и определяется правилом векторного сложения сил: $overrightarrow=<overrightarrow>_1+<overrightarrow>_2+<overrightarrow>_3+dots +<overrightarrow>_n=sum^n_<<overrightarrow>_i>$.
Равнодействующая сила оказывает на тело такое же действие, как сумма всех приложенных к нему сил.
Для сложения двух сил используется правило параллелограмма (рис.1):
Рисунок 1. Сложение двух сил по правилу параллелограмма
При этом модуль суммы двух сил находим по теореме косинусов:
Если нужно сложить более двух сил, приложенных в одной точке, то пользуются правилом многоугольника:
из конца первой силы проводят вектор, равный и параллельный второй силе; из конца второй силы — вектор, равный и параллельный третьей силе и так далее.
Рисунок 2. Сложение сил по правилу многоугольника
Замыкающий вектор, проведённый из точки приложения сил к концу последней силы, по величине и направлению равен равнодействующей. На рис.2 это правило проиллюстрировано на примере нахождения равнодействующей
четырёх сил $<overrightarrow>_1, <overrightarrow>_2,<overrightarrow>_3,<overrightarrow>_4$. Заметим, что при этом складываемые векторы не обязательно должны принадлежать одной плоскости.
Результат действия силы на материальную точку зависит только от ее модуля и направления. Твердое же тело имеет определенные размеры. Поэтому одинаковые по модулю и направлению силы вызывают различные движения твердого тела в зависимости от точки приложения. Прямая, проходящая через вектор силы, называется линией действия силы.
Рисунок 3. Сложение сил, приложенных к разным точкам тела
Если силы приложены к разным точкам тела и действуют не параллельно друг другу, то равнодействующая приложена к точке пересечения линий действия сил (рис.3).
Точка находится в равновесии, если векторная сумма всех сил, действующих на нее, равна нулю: $sum^n_<<overrightarrow>_i>=overrightarrow<0>$. В этом случае равна нулю и сумма проекций этих сил на любую ось координат.
Замену одной силы двумя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила, называют разложением сил. Разложение сил производят, как и их сложение, по правилу параллелограмма.
Задача разложения одной силы (модуль и направление которой известны) на две, приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, если известны:
- направления обеих составляющих сил;
- модуль и направление одной из составляющих сил;
- модули обеих составляющих сил.
Пусть, например, мы хотим разложить силу $F$ на две составляющие, лежащие в одной плоскости с F и направленные вдоль прямых а и b (рис.4). Для этого достаточно из конца вектора, изображающего F, провести две прямые, параллельные a и b. Отрезки $F_A$ и $F_B$ изобразят искомые силы.
Рисунок 4. Разложение вектора силы по направлениям
Другой вариант этой задачи – нахождение одной из проекций вектора силы по заданным векторам силы и второй проекции. (рис.5 а).
Рисунок 5. Нахождение проекции вектора силы по заданным векторам
Задача сводится к построению параллелограмма по диагонали и одной из сторон, известному из планиметрии. На рис.5б построен такой параллелограмм и указана искомая составляющая $<overrightarrow>_2$ силы $<overrightarrow>$.
Второй способ решения: прибавить к силе силу, равную – $<overrightarrow>_1$ (рис.5в).В результате получим искомую силу $<overrightarrow>_2$.
Готовые работы на аналогичную тему
$<overrightarrow>_1=1 Н;; <overrightarrow>_2=2 Н;; <overrightarrow>_3=3 Н$ приложены к одной точке , лежат в одной плоскости (рис.6 а) и составляют углы
горизонталью $alpha =0<>^circ ;;beta =60<>^circ ;;gamma =30<>^circ $соответственно. Найдите равнодействующую этих сил.
Проведём две взаимно перпендикулярные оси ОХ и OY так, чтобы ось ОХ совпадала с горизонталью, вдоль которой направлена сила $<overrightarrow>_1$. Спроецируем данные силы на оси координат (рис.6 б). Проекции $F_<2y>$ и $F_<2x>$ отрицательны. Сумма проекций сил на ось ОХ равна проекции на эту ось равнодействующей: $F_1+F_2-F_3=F_x=frac<4-3sqrt<3>><2>approx -0.6 H$. Аналогично, для проекций на ось OY: $-F_2+F_3frac<3-2sqrt<3>><2>approx -0.2 H$. Модуль равнодействующей определяется по теореме Пифагора: $F=sqrt=sqrt<0.36+0.04>approx 0,64 Н$. Направление равнодействующей определим с помощью угла между равнодействующей и осью (рис.6 в): $tgvarphi =frac= frac<3-2sqrt<3>><4-3sqrt<3>>approx 0.4$
Сила $F = 1kH$ приложена в точке В кронштейна и направлена вертикально вниз (рис.7а). Найдите составляющие этой силы по направлениям стержней кронштейна. Необходимые данные указаны на рисунке.
Пусть стержни прикреплены к стене в точках A и C. Разложение силы $<overrightarrow>$ на составляющие вдоль направлений АВ и ВС представлено на рис.7б. Откуда видно, что $left|<overrightarrow>_1right|=Ftgbeta approx 577 H; $
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 11 2022
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную – F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β – F 3 cos γ = F x = 4 – 3 3 2 ≈ – 0 , 6 Н .
Точно также для проекций на ось O Y : – F 2 sin β + F 3 sin γ = F y = 3 – 2 3 2 ≈ – 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 – 2 3 4 – 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline$ – это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (2) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60<>^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline$ можно найти, используя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<20>^2+<10>^2+2cdot 20cdot 10<cos (60<>^circ ) >>approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
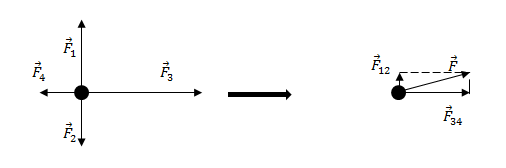
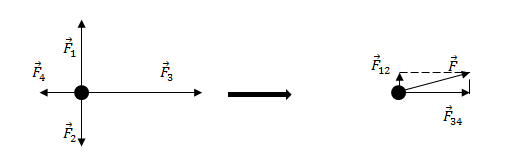
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
Найдем равнодействующую сил $<overline>_1$ и $<overline>_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
Так как $F_1>F_2$, то сила $<overline>_<12>$ направлена в туже сторону, что и сила $<overline>_1$.
Найдем равнодействующую сил $<overline>_3$ и $<overline>_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
Направление силы $<overline>_<34>$ совпадает с направлением вектора $<overline>_3$, так как $<overline>_3><overline>_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
Силы $<overline>_<12>$ и $<overline>_<34>$ взаимно перпендикулярны. Найдем длину вектора $overline$ по теореме Пифагора:
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/fizika/elementy-statiki/zakony-slozhenija-sil-v-mehanike/
http://www.webmath.ru/poleznoe/fizika/fizika_139_formula_ravnodejstvujushhej_vseh_sil.php
[/spoiler]
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ – это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ – масса тела, на которое действует сила $overline{F}$; $overline{a}$ – ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Сложение
сил,
операция определения векторной величины
R,
равной геометрической сумме векторов,
изображающих силы данной системы и
называется главным вектором этой системы
сил. С. с. производится по правилу сложения
векторов, в частности построением
многоугольника
сил.
Механический смысл величины R
определяется теоремами статики
и динамики.
Так, если система сил, действующих на
твёрдое тело, имеет равнодействующую,
то она равна главному вектору этих сил.
При движении любой механической системы
её центр масс движется так же, как
двигалась бы материальная точка, имеющая
массу, равную массе всей системы, и
находящаяся под действием силы, равной
главному вектору всех действующих на
систему внешних сил. Систе́ма
сходя́щихся сил —
это такая система сил, действующих на
абсолютно
твёрдое тело,
в которой линии действия всех сил
пересекаются в одной точке. Задачи с
системой сходящихся сил могут быть
решены как аналитически, так и графически
(методами графостатики).
Главный
вектор
F’гл представляет собой геометрическую
сумму всех сил,
составляющих систему
и перенесенных в центр приведения.
Модуль главного
вектора
можно определить через проекции на
координатные оси всех сил
системы.
4. Проекция силы на ось и проекция силы на плоскость. Аналитический способ задания сил. Аналитический способ сложения сил.
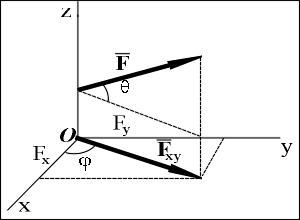
Проекцией
силы F
на ось
Ox называется скалярная величина Fx,
равная произведению ее модуля F на
косинус угла между силой и положительным
направлением оси: Fx=F·cos.Проекция силы на ось:
-
п
оложительна,
если угол-острый;
-
равна
нулю, если угол
–
прямой ( сила перпендикулярна оси ); -
отрицательна,
если угол
–
тупой.
Проекцией
силы F
на плоскость
Oxy называется вектор Fxy,
заключенный между проекциями начала и
конца силы F
на эту плоскость. В отличие от проекции
силы на ось, проекция силы на плоскость
является векторной величиной и
характеризуется не только числовым
значением, но и направлением в плоскости
Oxy. По модулю Fxy=F·cos, где
–
угол между векторамиF
и Fxy.
Проекция силы на плоскость используется,
например, для нахождения проекций силы
на оси, лежащие в этой плоскости (см.
рис.): Fx=Fxy·cos; Fy=Fxy·sin
.Аналитическое
сложение сил
основано на известной теореме векторной
алгебры: проекция вектора суммы на ось
равна алгебраической сумме проекций
слагаемых векторов на ту же ось:
Модуль
(численное значение) главного вектора
Действие силы на
твердое тело может вызвать вращательный
эффект, который для плоской системы сил
оценивается моментом силы относительно
какой-либо точки О на плоскости (рис.
13):
;
,
где
h1
и h2
плечи сил
и
относительно
точки О.
5. Равновесие системы сходящихся сил. Теорема о трех силах. Понятие о статической определимости системы сил.
Равновесие
системы сходящихся сил.Из
законов механики следует, что твердое
тело, на которое действуют взаимно
уравновешенные внешние силы, может не
только находиться в покое, но и совершать
движение, которое мы назовем движением
«по инерции». Таким движением будет,
например, поступательное равномерное
и прямолинейное движение тела.Отсюда
получаем два важных вывода: 1) Условиям
равновесия статики удовлетворяют силы,
действующие как на покоящееся тело, так
и на тело, движущееся «по инерции». 2)
Уравновешенность сил, приложенных к
свободному твердому телу, является
необходимым, но не достаточным условием
равновесия (покоя) самого тела; в покое
тело будет при этом находиться лишь в
том случае, если оно было в покое и до
момента приложения к нему уравновешенных
сил. Для равновесия приложенной к
твердому телу системы сходящихся сил
необходимо и достаточно, чтобы
равнодействующая этих сил была равна
нулю. Условия, которым при этом должны
удовлетворять сами силы, можно выразить
в геометрической или аналитической
форме.
-
Геометрическое
условие равновесия. Так как равнодействующая
R сходящихся сил определяется как
замыкающая сторона силового многоугольника,
построенного из этих сил, то R может
обратиться в нуль тогда и только тогда,
когда конец последней силы в многоугольнике
совпадает с началом первой, т. е. когда
многоугольник замкнется.
Следовательно,
для равновесия системы, сходящихся сил
необходимо и достаточно, чтобы силовой
многоугольник, построенный из этих сил,
был замкнут.
-
Аналитические
условия равновесия. Аналитически
равнодействующая системы сходящихся
сил определяется формулой
Теорема
о трех силах.
Если (абсолютно твердое) тело находится
в равновесии под действием плоской
системы трех непараллельных
сил
(т.е. сил, из которых хотя бы две
непараллельные), то линии их действия
пересекаются в одной точке. Доказательство.
Пусть из трех сил F1,
F2,
F3
, приложенных соответственно в точках
А, В и С (рис.3), непараллельными являются
F1 и
F2.
Продолжим линии их действия до пересечения
в точке О и перенесем в эту точку обе
силы. Очевидно, система {F1,
F2}
эквивалентна
,
а эта последняя уже имеет равнодействующую
R.
Таким образом, {F1,F2,F3}~{R,
F3,}.
(3) Но система двух сил находится в
равновесии только в том случае, если
они направлены вдоль одной прямой.
Следовательно, линия действия F3 должна
совпасть с линией действия R,
т.е. пройти через точку О.
|
|
Замечание.
Доказанное условие является
необходимым, но не достаточным условием
равновесия. Для достаточности нужно
еще равенство нулю геометрической суммы
приложенных сил (см. § 3.4).
Соседние файлы в папке механика
- #
- #
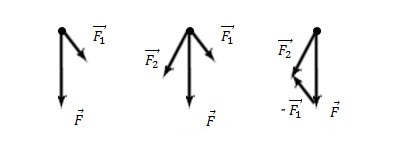
расставляешь векторы действующих сил на тело.
Потом складываешь их. Для этого есть определенные правила сложения:
1) Правило сложения векторов методом треугольника. Для сложения двух векторов .

Правило параллелограмма. Для сложения двух векторов по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
А модуль (длину) вектора суммы определяют по теореме косинусов 

К примеру вот так:
F1 – Сила реакции опоры
F2 – Сила тяги
F3 – Сила тяжести
F4 – Сила трения.
F’ – векторная сумма F4 и F1
F” – Векторная сумма F3 и F2







 оложительна,
оложительна,


