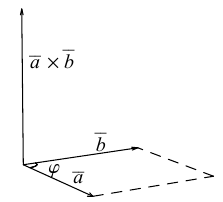
Как найти вектор коллинеарный вектору
Формула
Примеры нахождения коллинеарного вектора
Подставим координаты заданных векторов в это равенство и найдем значение $m$:
По пропорции имеем:
$$2 cdot m=(-1) cdot(-3) Rightarrow 2 cdot m=3 Rightarrow m=frac<3><2>=1,5$$

А тогда значения неизвестных параметров $m$ и $n$ находим из равенств
$$frac<3>=2 Rightarrow m=6$$ $$frac<1>=2 Rightarrow n=frac<1><2>=0,5$$
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!








Ищещь ответ на вопрос с которым нужна помощь?
Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
Решим эти уравнения:
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Условие коллинеарности векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R
Координатная форма условия коллинеарности векторов
Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .
По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ – произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Исходные данные: векторы a → = ( 3 – 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 – 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 – 2 2 ) = 1 3 2 – 4 + 3 – 2 2 = 1 2 – 1 b y = λ · a y ⇔ 2 + 1 = 1 2 – 1 · 1 ⇔ ( 2 + 1 ) · ( 2 – 1 ) = 1 ⇔ 1 ≡ 1
Т.е. b → = 1 2 – 1 · a → , следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 1 , 0 , – 2 ) и b → = ( – 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ – 3 = – 3 · 1 0 = – 3 · 0 6 = – 3 · ( – 2 ) , то верным будет равенство: b → = – 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 – 2 – 3 0 6 = i → · 0 · 6 + j → · ( – 2 ) · ( – 3 ) + k → · 1 · 0 – k → · 0 · ( – 3 ) – j → · 1 · 6 – i → · ( – 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Исходные данные: вектор a → = ( 2 , – 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 1 2 · a → = ( 1 , – 3 ) или вектор 3 · a → = ( 6 , – 18 ) .
Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , – 3 ) .
Исходные данные: вектор a → = ( 3 , 4 , – 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( – 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , – 1 2 )
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/library/vector/colinearity/
http://zaochnik.com/spravochnik/matematika/vektory/uslovie-kollinearnosti-vektorov/
[/spoiler]
$begingroup$
I have a question
Assume that there are 3 vectors x1,x2,x3 (each vector has the size 3*1 (3 dimension))
I want to find these vector that satisfy below conditions (the ininitial assumption x1 = [1 0 0] is ok)
x1’*x1 =1
x2’*x2 =1
x3’*x3 =1
x1’*x2 = 0.3
x1’*x3 = 0.2
x2’*x3 = 0.4
- upper values are cos(theta) between two vectors
In practice, I have large matrix(90*90) that has cos(theta) values therefore I want to know the general solution to solve this problem..
thank you!
user190080
3,6913 gold badges22 silver badges32 bronze badges
asked Jun 26, 2016 at 10:30
$endgroup$
3
$begingroup$
Regard $x_1, x_2, x_3$ as the columns of a 3×3 matrix $M$ and $x_1′, x_2′, x_3’$ as the rows of a second unknown matrix $M’$. The entries of the matrix product $N = M’M$ will be the values $x_i’ cdot x_j$ for various $i,j$. So to solve your problem fill in the matrix $N$ as needed, then multiply on the right by the matrix inverse of $M$ (so your original vectors need to be linearly independent) and read off your vectors $x_i’$ from the result $M’ = NM^{-1}$.
If your original vectors aren’t independent, the solution may or may not exist.
answered Jun 26, 2016 at 11:25
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Примеры решения задач

Задача 1.
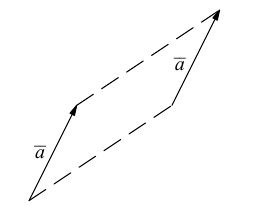
Определить длины диагоналей параллелограмма,
построенного на векторах
![]()
и
![]()
,
где
![]()
таковы, что
![]()
.
Решение.
Диагонали параллелограмма есть векторы
![]()
и
![]()
.
Вычислим длину вектора
:
![]()
.
Аналогично
вычисляется длина вектора
![]()
.
Задача 2.
Найдите вектор
,
коллинеарный вектору
![]()
и удовлетворяющий условию
![]()
.
Решение.
Обозначим вектор
![]()
,
тогда из условий задачи
![]()
или
![]()
,
тогда
![]()
.
Итак:
![]()
.
Задача 3.
Найти проекцию вектора
![]()
на направление вектора
![]()
.
Решение.
![]()
.
По формуле проекции вектора на ось будет
иметь место равенство
![]()
.
Задача 4.
Даны векторы:
![]()
.
П
роверить,
есть ли среди них коллинеарные. Найти
![]()
.
Решение.
Условие коллинеарности имеет вид
![]()
.
Этому условию удовлетворяют векторы
![]()
.
Следовательно, они коллинеарны. Найдем
длины
векторов
![]()
:
![]()
.
Угол между векторами
определяется по формуле
![]()
.
Т
огда
![]()
,
![]()
.
Используя формулу
![]()
,
получим
![]()
.
Задача 5.
На материальную точку действуют силы
![]()
.
Найти работу равнодействующей этих сил
при перемещении точки из положения
![]()
в положение
![]()
.
Решение.
Найдем силу
и вектор перемещения
![]()
.
![]()
,
тогда искомая работа
![]()
.
Задачи
1. Векторы
взаимно перпендикулярны, а вектор
образует с ними углы
![]()
.
Зная, что
![]()
,
найти: 1)
![]()
;
2)
![]()
.
2. Вычислить длину
диагоналей параллелограмма, построенного
на векторах
![]()
,
если известно, что
![]()
.
3. Доказать, что
вектор
![]()
перпендикулярен к вектору
.
4. Зная, что
![]()
,
определить, при каком значении коэффициента
векторы
![]()
окажутся перпендикулярными.
5. Даны вершины
четырехугольника:
![]()
.
Доказать, что его диагонали взаимно
перпендикулярны.
6. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах
![]()
.
7. Даны силы
![]()
.
Найти работу их равнодействующей при
перемещении точки из начала координат
в точку
![]()
.
8. Даны вершины
треугольника:
![]()
.
Найти проекцию вектора
на вектор
.
9. Найти вектор
![]()
,
перпендикулярный векторам
![]()
,
если известно, что его проекция на вектор
![]()
равна единице.
10. Сила, определяемая
вектором
![]()
,
разложена по трем направлениям, одно
из которых задано вектором
![]()
.
Найти составляющую силы
в направлении вектора
.
11. Даны вершины
треугольника:
![]()
.
Найти его внутренний угол при вершине
А и внешний угол при вершине В.
12. Даны три
последовательные вершины параллелограмма:
![]()
.
Найти его четвертую вершину D
и угол между векторами
![]()
.
13. На оси
![]()
найти точку, равноудаленную от точек
![]()
.
14. Доказать, что
треугольник с вершинами
![]()
![]()
прямоугольный.
Домашнее задание
1. Вычислить
скалярное произведение двух векторов
![]()
,
зная их разложение по трем единичным
взаимно перпендикулярным векторам
![]()
![]()
;
![]()
.
2. Найти длину
вектора
![]()
,
зная, что
![]()
– взаимно перпендику-
лярные орты.
3. Векторы
![]()
попарно образуют друг с другом углы,
каждый из которых равен
.
Зная, что
![]()
,
определить модуль вектора
![]()
.
4. Доказать, что
вектор
![]()
перпендикулярен к вектору
.
5. Даны векторы
![]()
,
совпадающие со сторонами треугольника
АВС. Найти разложение вектора, приложенного
к вершине В этого треугольника и
совпадающего с его высотой BD
по базису
![]()
.
6. Вычислить угол
между векторами
![]()
,
где
![]()
–
единичные взаимно перпендикулярные
векторы.
7. Даны силы
![]()
,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из положения
![]()
в положение
![]()
.
8. Даны вершины
треугольника
![]()
.
Определить его внутренний угол при
вершине В.
9. Вычислив
внутренние углы треугольника с вершинами
![]()
,
![]()
,
убедиться, что этот треугольник
равнобедренный.
10. Найти вектор
,
зная, что он перпендикулярен векторам
![]()
и
![]()
.
11. Найти вектор
,
коллинеарный вектору
![]()
и удовлетворяющий условию
![]()
,
где
![]()
.
12. Вычислить
проекцию вектора
![]()
на ось вектора
![]()
.
13. Даны векторы
![]()
.
Вычислить
![]()
.
14. Даны точки
![]()
.
Вычислить проекцию вектора
![]()
на ось вектора
![]()
.
Ответы к задачам
1) -7, 13. 2) 15,
![]()
.
4)
![]()
.
6)
![]()
.
7) 2. 8) -1/3.
9)
![]()
.
10)
![]()
.
11)
![]()
.
12)
![]()
.
13)
![]()
.
Ответы к домашнему
заданию
1) 9. 2) 5. 3) 10. 5)
![]()
.
6)
![]()
.
7) 13. 8)
.
10)
![]()
.
12) 6. 13) 5. 14) 3.
Занятие 3
Векторое
произведения векторов. Смешанное
произведение векторов
Определение1.
Тройка
некомпланарных векторов
называется правой (левой) если, находясь
внутри телесного угла, образованного
приведенными к общему началу векторами
и от него к
,
човершающимся против часовой стрелки
(по часовой стрелке)

![]()
Тройка правая
Тройка левая
Определение
2. Векторным
произведением вектора
на вектор
называется вектор
![]()
,
длина и направление которого определяются
условиями:
1.
![]()
,
где
– угол между
![]()
.
2.
![]()
.
3.
– правая тройка векторов.
Свойства
векторного произведения
1.
![]()
(свойство антиперестановочности
сомножителей);
2.
![]()
(распределительное относительно суммы
векторов);
3.
![]()
(сочетательное относиельно числового
множителя);
4.
![]()
(равенство нулю векторного произведения
означает коллинеарность векторов);
5.
![]()
,
т. е. момент сил равен векторному
произведению силы на плечо.
Если вектор
![]()
,
то
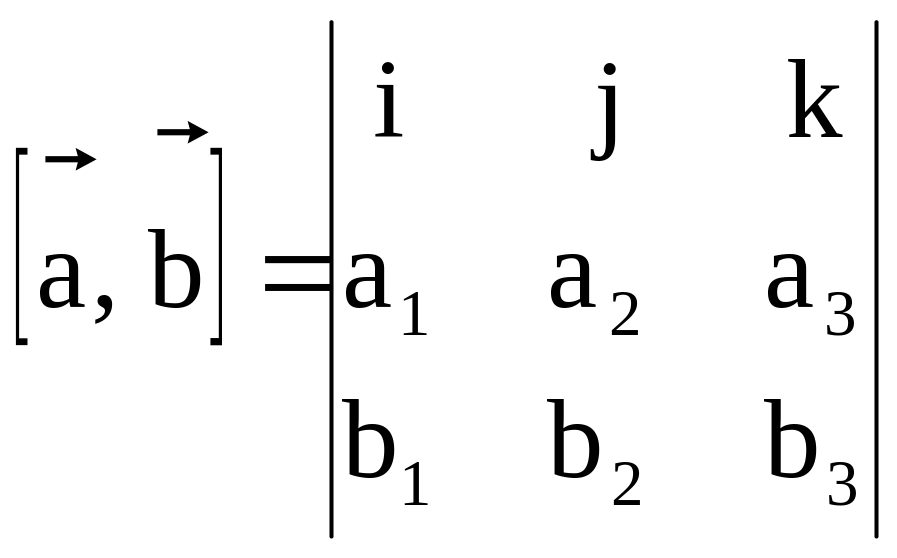
.
Определение
3. Смешанным
произведением
![]()
трех векторов называется число,
определяемое следующим образом:
![]()
.
Если векторы заданы своими координатами:
![]()
,
то
~

.
Свойства
смешанного произведения
1. Необходимым и
достаточным условием компланарности
векторов
является равенство
= 0.
2. Объем
параллелепипеда, построенного на
векторах
![]()
![]()
![]()
:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами 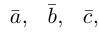
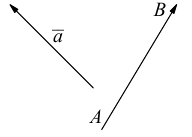
Длина отрезка, изображающего вектор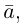 называется его длиной и обозначается через
называется его длиной и обозначается через 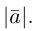 Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение
Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение 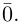
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
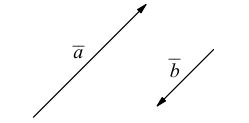
Два вектора 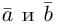 называются коллинеарными (обозначение
называются коллинеарными (обозначение 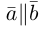 ), если отрезки их изображающие параллельны.
), если отрезки их изображающие параллельны.
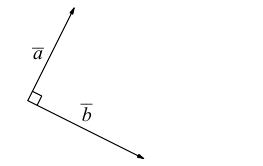
Аналогично, векторы а и b называются ортогональными (обозначение 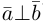 ), если соответствующие отрезки перпендикулярны.
), если соответствующие отрезки перпендикулярны.
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
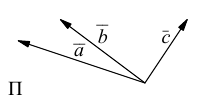
Углом между векторами 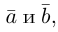 приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами
приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами 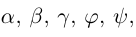 … или через
… или через 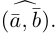
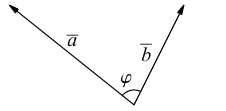
Два ненулевых вектора 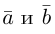 мы будем считать одинаково направленными, если
мы будем считать одинаково направленными, если 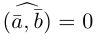 и противоположно направленными, если
и противоположно направленными, если 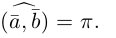
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 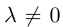 на вектор
на вектор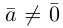 называется вектор
называется вектор 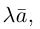 длина которого равна
длина которого равна 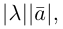 а направление его совпадает с направлением вектора
а направление его совпадает с направлением вектора 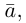 если
если 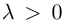 и имеет противоположное с ним направление, если
и имеет противоположное с ним направление, если 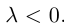 Если
Если 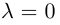 или
или 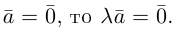
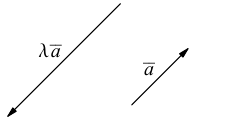
В частности, вектор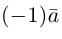 обозначается через
обозначается через 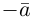 и называется вектором, противоположным вектору
и называется вектором, противоположным вектору 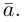
Если 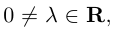 то произведение
то произведение 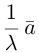 мы будем иногда записывать в виде
мы будем иногда записывать в виде 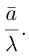
Из приведенного определения сразу же следует, что коллинеарные векторы 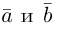 линейно связаны, т. е. существует константа
линейно связаны, т. е. существует константа 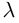 такая,что
такая,что 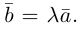 В качестве такой константы следует
В качестве такой константы следует
взять число 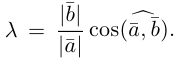 Если
Если 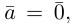 то
то 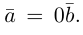 В частности, если
В частности, если 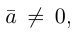 то вектором единичной длины с направлением данного вектора является вектор
то вектором единичной длины с направлением данного вектора является вектор 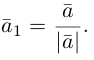
b) Сложение векторов.
Суммой двух векторов 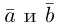 называется вектор
называется вектор 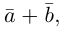 который находится по правилу треугольника
который находится по правилу треугольника
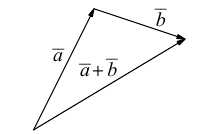
или по равносильному ему правилу параллелограмма
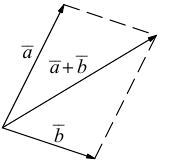
Вектор 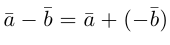 называется разностью векторов
называется разностью векторов 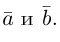
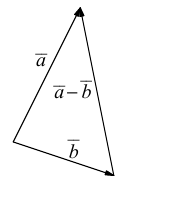
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 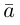 на вектор
на вектор 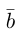 называется число
называется число
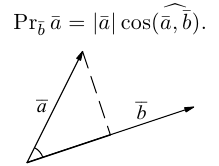
Геометрически очевидны следующие свойства проекции:
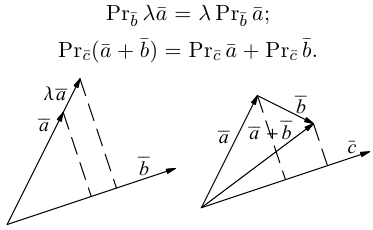
Пример №1
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
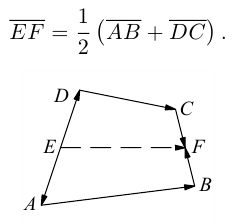
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
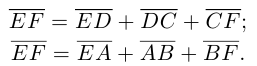
Сложив данные равенства и учитывая, что 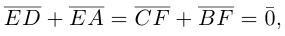 будем иметь:
будем иметь:
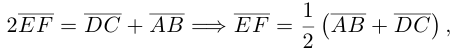
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 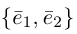 — базис на плоскости,
— базис на плоскости, 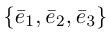 — базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора
— базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора 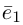 к вектору
к вектору 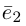 совершается против часовой стрелки, если наблюдение ведется со стороны вектора
совершается против часовой стрелки, если наблюдение ведется со стороны вектора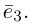 Сформулируем теперь фундаментальное свойство базиса.
Сформулируем теперь фундаментальное свойство базиса.
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 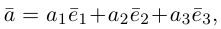 где действительные числа
где действительные числа 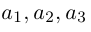 – координаты вектора
– координаты вектора 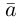 в базисе
в базисе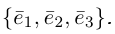
Приведем геометрическое доказательство этого утверждения.
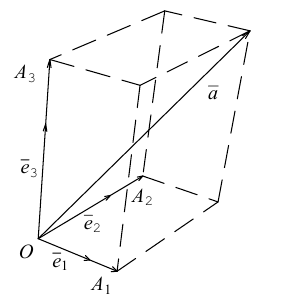
Вектор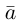 можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов
можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов 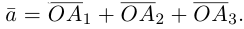 В виду коллинеарности векторов
В виду коллинеарности векторов 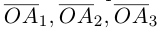 соответствующим базисным векторам, мы можем записать, что
соответствующим базисным векторам, мы можем записать, что 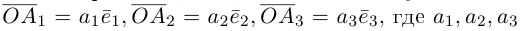 — некоторые действительные числа. Отсюда и следует искомое разложение.
— некоторые действительные числа. Отсюда и следует искомое разложение.
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 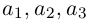 коротко записывается как
коротко записывается как 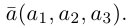
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 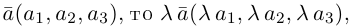 если
если 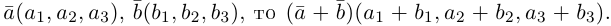 Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
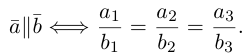
Рассмотрим теперь ортонормированный базис 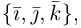 т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе
т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе 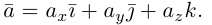
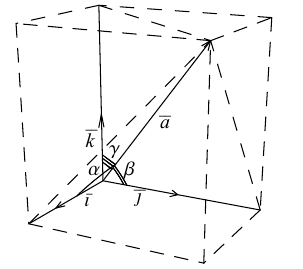
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
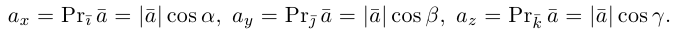
Величины 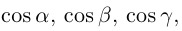 т. е. косинусы углов, которые образует данный вектор с ортами
т. е. косинусы углов, которые образует данный вектор с ортами 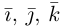 к соответственно, называются направляющими косинусами вектора
к соответственно, называются направляющими косинусами вектора 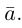 Единичный вектор
Единичный вектор 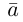 имеет координаты
имеет координаты 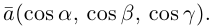
Очевидно также, что
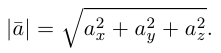
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 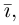 ось
ось 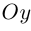 (ординат) — вдоль орта
(ординат) — вдоль орта 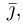 наконец, ось
наконец, ось 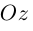 (аппликат) направим вдоль орта
(аппликат) направим вдоль орта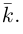

В выбранной системе координат координаты радиуса-вектора 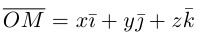 мы будем называть координатами точки М и записывать
мы будем называть координатами точки М и записывать 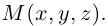
Если известны координаты начальной 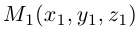 и конечной
и конечной 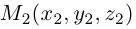 точек вектора, то из равенства
точек вектора, то из равенства 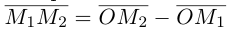 слезет, что его координаты равны
слезет, что его координаты равны
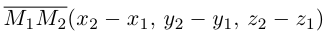 и, значит, расстояние между точками
и, значит, расстояние между точками 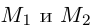 вычисляется по формуле
вычисляется по формуле
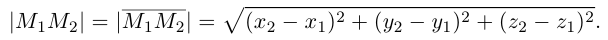
Найдем теперь координаты точки М, делящей отрезок с концами в точках 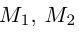 в данном
в данном
отношении 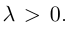 Так как
Так как 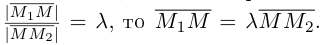 Отсюда, переходя к координатам получим:
Отсюда, переходя к координатам получим:
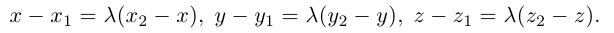
Следовательно, координаты искомой точки вычисляются по формулам:
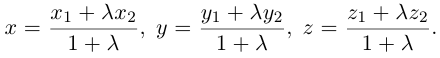
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
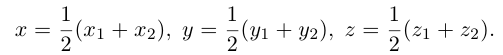
Пример №2
Треугольник задан координатами своих вершин 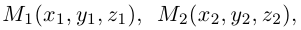
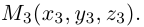 Найти координаты точки пересечения его медиан. Решение.
Найти координаты точки пересечения его медиан. Решение.
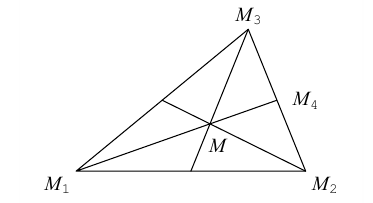
Пусть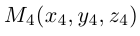 – середина отрезка
– середина отрезка 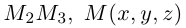 – точка пересечения медиан. Тогда
– точка пересечения медиан. Тогда
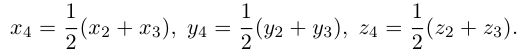
По известному свойству точки пересечения медиан 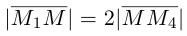 и потому
и потому
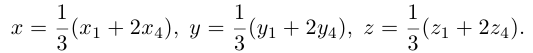
Подставив сюда найденные координаты точки 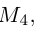 ползучим:
ползучим:
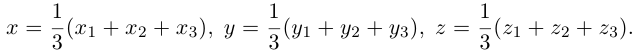
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 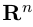 называется упорядоченная совокупность n векторов
называется упорядоченная совокупность n векторов

обладающая тем свойством, что любой вектор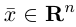 единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа
единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа 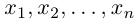 (координаты вектора
(координаты вектора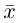 в базисе (1)) такие, что
в базисе (1)) такие, что

В качестве базиса в 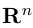 мы можем взять, например, векторы
мы можем взять, например, векторы
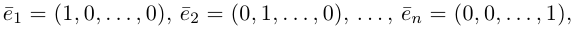
так как, очевидно, любой вектор 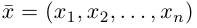 однозначно представляется в виде (2).
однозначно представляется в виде (2).
Скалярное произведение векторов
Определение: Скалярным произведением векторов 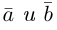 называется число
называется число
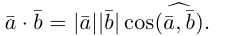
Из этого определения сразу же следует, что
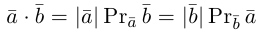
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
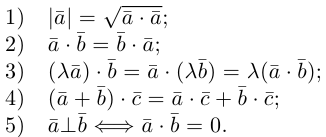
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 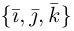 векторы
векторы 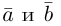 имеют координаты
имеют координаты 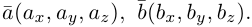 Заметив, что по свойствам 1) и 5) скалярного произведения
Заметив, что по свойствам 1) и 5) скалярного произведения
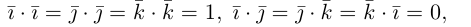
перемножим векторы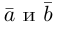 скалярно, используя свойства 2) – 4):
скалярно, используя свойства 2) – 4):
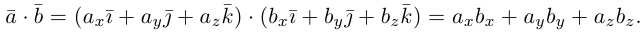
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 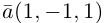 на две ортогональные составляющие, одна из которых коллинеарна вектору
на две ортогональные составляющие, одна из которых коллинеарна вектору 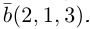
Решение.
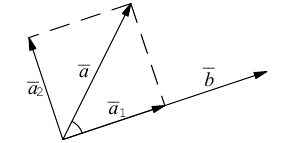
Из чертежа следует, что 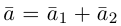 – искомое разложение. Найдем векторы
– искомое разложение. Найдем векторы 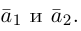 Составляющая
Составляющая 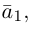 коллинеарная вектору
коллинеарная вектору 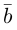 равна, очевидно, вектору проекции
равна, очевидно, вектору проекции 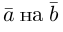 и, следовательно,
и, следовательно,
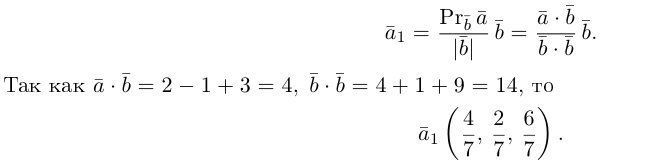
Тогда вторая ортогональная составляющая вектора 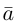 равна
равна
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 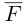 материальная тотп<а переместилась по прямой из положения В в положение С.
материальная тотп<а переместилась по прямой из положения В в положение С.
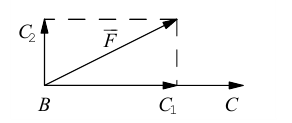
Найдем работу этой силы. Для этого разложим вектор силы 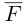 на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения
на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения 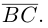 Тогда
Тогда
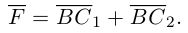
Составляющая 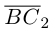 работы не совершает, следовательно, работа силы
работы не совершает, следовательно, работа силы 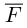 равна работе составляющей
равна работе составляющей 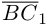 и, таким образом,
и, таким образом,
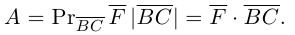
Окончательно, работа силы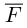 , под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
, под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
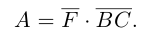
Замечание. Скалярным произведением векторов 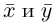 n-мерного пространства
n-мерного пространства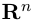 называется число
называется число 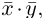 равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
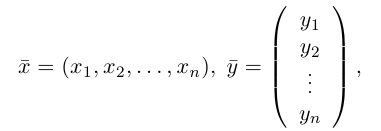
то
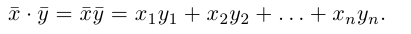
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 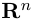 обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
Длиной вектора 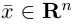 называется число
называется число
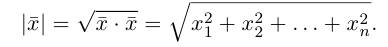
Векторы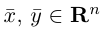 называются ортогональными, если
называются ортогональными, если 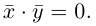 Векторы
Векторы
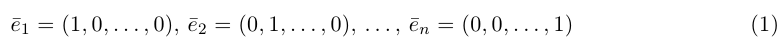
составляют ортонормированный базис пространства 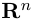 , так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
, так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
Любой вектор  мы можем рассматривать как точку
мы можем рассматривать как точку
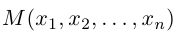
n-мерного пространства с координатами 
Взяв еще одну точку 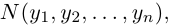 соответствующую вектору
соответствующую вектору 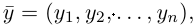 мы под расстоянием между точками М и N будем понимать длину вектора
мы под расстоянием между точками М и N будем понимать длину вектора 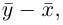 т. е. число
т. е. число
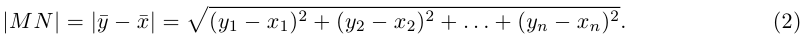
Таким образом переопределенное пространство 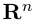 с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов 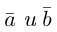 называется вектор
называется вектор  такой, что
такой, что
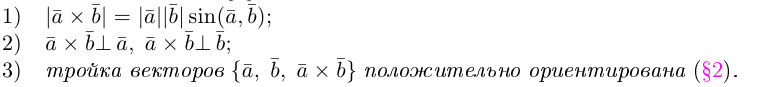
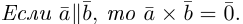
Из этого определения следует, что площадь параллелограмма, построенного на векторах 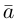 и
и 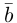 равна длине векторного произведения
равна длине векторного произведения  , т. е.
, т. е.
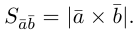
Сформулируем основные свойства векторного произведения.
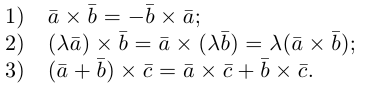
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 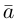 и
и 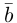 в ортонормированном базисе
в ортонормированном базисе 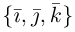 имеют координаты
имеют координаты 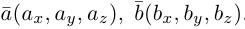 Учитывая, tito по определению векторного произведения
Учитывая, tito по определению векторного произведения
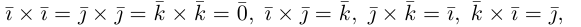
раскроем скобки в векторном произведении 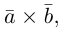 принимая во внимание свойства 1) – 3):
принимая во внимание свойства 1) – 3): 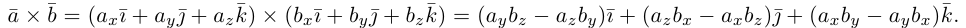
Полученный вектор мы можем записать в виде следующего символического определителя.
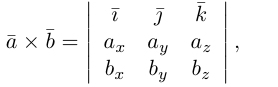
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 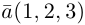 , ортогональную плоскости векторов
, ортогональную плоскости векторов 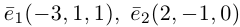 .
.
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 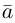 на векторное произведение
на векторное произведение и, следовательно.
и, следовательно.
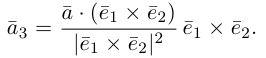
Переходим к вычислениям:
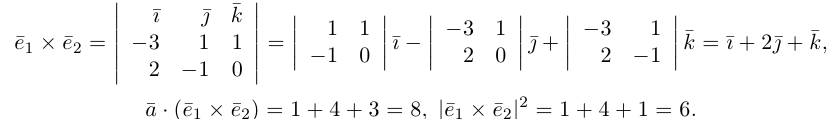
Тогда 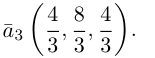
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
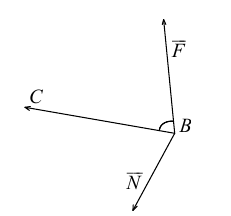
Итак, пусть сила 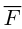 приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
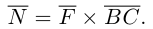
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 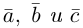 называется число
называется число
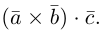
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
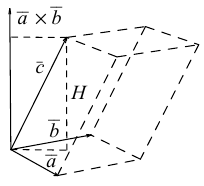
По определению смешанного произведения
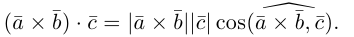
Поскольку 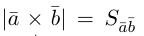 – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах 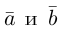 (§4)
(§4)
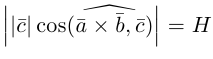 -высота параллелепипеда построенного на векторах
-высота параллелепипеда построенного на векторах 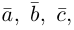 то
то
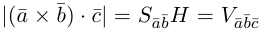
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 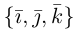 , т.е.
, т.е. 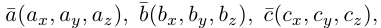 то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
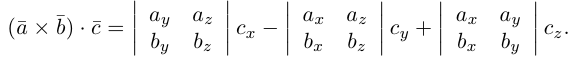
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
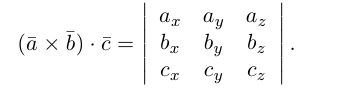
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
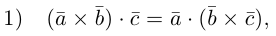
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 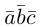 . которым мы и будем пользоваться в дальнейшем.
. которым мы и будем пользоваться в дальнейшем.
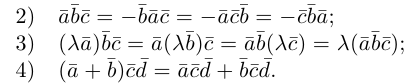
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 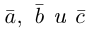 компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 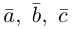 компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение
компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение 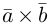 ортогонально вектору с и, следовательно,
ортогонально вектору с и, следовательно, 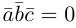 . Аналогично проверяется достаточность условия теоремы.
. Аналогично проверяется достаточность условия теоремы.
Следствие. Три вектора 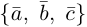 образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
Заметим, кроме того, что, если 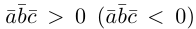 , то угол между векторами
, то угол между векторами 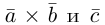 -острый (тупой) и, следовательно, базис
-острый (тупой) и, следовательно, базис 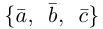 является положительно (отрицательно) ориентированным.
является положительно (отрицательно) ориентированным.
Пример №5
Доказать, что пять точек
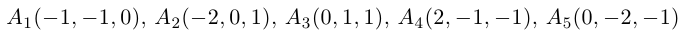
расположены в одной плоскости.
Решение. Рассмотрим векторы 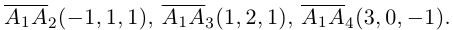 Так как
Так как
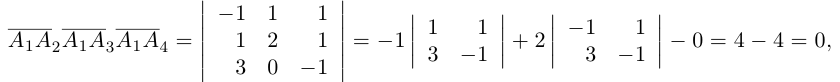
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 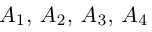 находятся в одной плоскости
находятся в одной плоскости 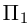 Аналогично покажем, что и точки
Аналогично покажем, что и точки 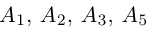 также принадлежат одной плоскости
также принадлежат одной плоскости 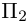 . Действительно,
. Действительно, 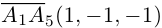
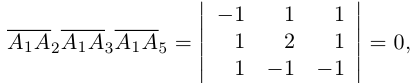
так как первая и третья строки в определителе пропорциональны. Плоскости 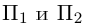 имеют три общие точки
имеют три общие точки 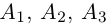 , следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
, следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
 А – начало, В – конец вектора
А – начало, В – конец вектора 
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 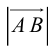 – расстояние между его началом и концом.
– расстояние между его началом и концом.
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
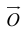 – нулевой вектор: его направление не определено, а длина
– нулевой вектор: его направление не определено, а длина 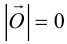 .
.
Определение: Векторы 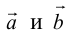 называются коллинеарными, если они лежат на параллельных прямых:
называются коллинеарными, если они лежат на параллельных прямых: 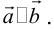
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 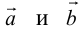 совмещаются в одной точке, и
совмещаются в одной точке, и 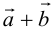 – диагональ параллелограмма, построенного на
– диагональ параллелограмма, построенного на  .
.
б) Правило треугольника (рис. 3): начало  совмещается с концом
совмещается с концом  направлен от начала
направлен от начала  к концу
к концу 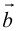 .
.
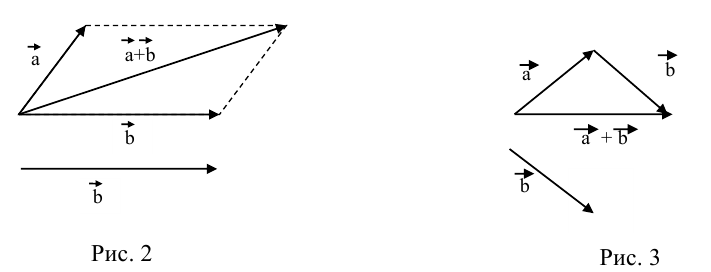
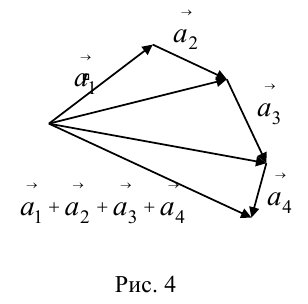
в) Правило сложения нескольких векторов (рис. 4).
Вектор 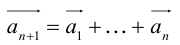 замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и
замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и 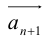 направлен от начала
направлен от начала 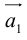 к концу
к концу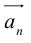 .
.
Умножение на число
Определение: Произведением вектора 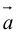 на число
на число 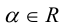 называется вектор
называется вектор 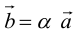 , aудовлетворяющий условиям:
, aудовлетворяющий условиям:
а) 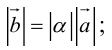
б) 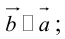
в)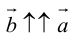 , если
, если 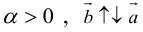 ,a если
,a если 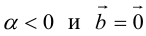 , если
, если 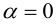 .
.
Произведение 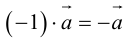 называется вектором, противоположным вектору
называется вектором, противоположным вектору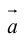 . Очевидно,
. Очевидно, 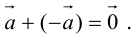 .
.
Определение: Разностью 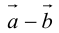 называется сумма вектора
называется сумма вектора 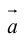 и вектора, противоположного
и вектора, противоположного 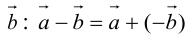 (рис. 5).
(рис. 5).

Начала 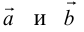 совмещаются в одной точке, и
совмещаются в одной точке, и 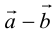 направлен от конца
направлен от конца 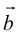 к концу
к концу 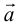 .
.
Свойства линейных операций
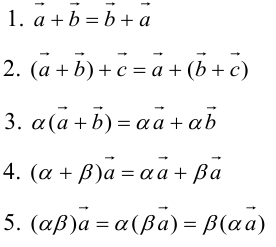
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: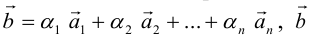 – линейная комбинация векторов
– линейная комбинация векторов 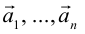 с коэффициентами
с коэффициентами 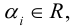
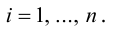
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 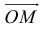 как линейную комбинацию
как линейную комбинацию
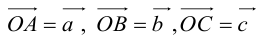 (рис. 6).
(рис. 6).
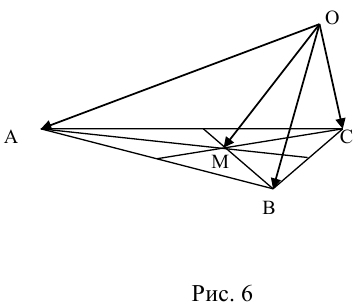
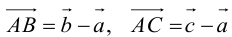 . Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что
. Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что 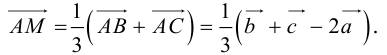
По правилу треугольника 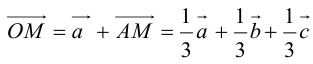 , то есть
, то есть 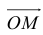 – линейная комбинация
– линейная комбинация 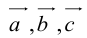 с коэффициентами
с коэффициентами 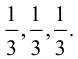
Теорема: Пусть 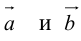 – неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
– неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
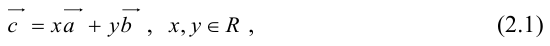
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 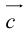 в виде (2.1) называется разложением его по двум неколлинеарным векторам.
в виде (2.1) называется разложением его по двум неколлинеарным векторам.
Доказательство:
- Пусть среди
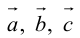 есть два коллинеарных, например:
есть два коллинеарных, например: 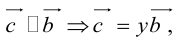
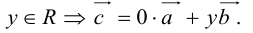
- Пусть среди
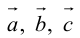 коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с 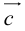 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 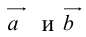 (рис. 7).
(рис. 7).
Тогда c 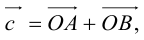 но
но 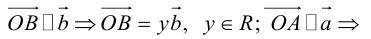
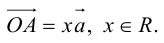 Поэтому
Поэтому 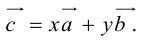
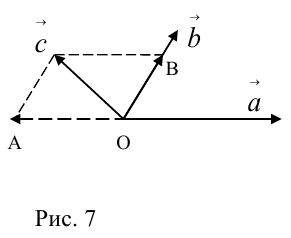
Докажем единственность разложения. Предположим, что 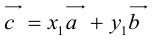 и
и 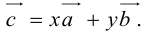 Тогда, вычитая одно равенство из другого, получим:
Тогда, вычитая одно равенство из другого, получим: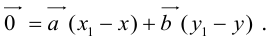
Если 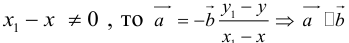 , что противоречит условию. Теорема доказана.
, что противоречит условию. Теорема доказана.
Теорема: Пусть 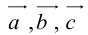 – некомпланарные векторы. Тогда любой вектор
– некомпланарные векторы. Тогда любой вектор 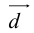 может быть представлен в виде
может быть представлен в виде
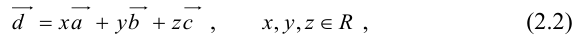
причем единственным образом.
Представление вектора 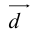 в виде (2.2) называется разложением его по трем некомпланарным.
в виде (2.2) называется разложением его по трем некомпланарным.
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 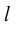 называется единичный вектор
называется единичный вектор 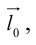
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 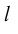 называется основание
называется основание 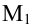 перпендикуляра, опущенного из М на
перпендикуляра, опущенного из М на 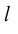 .
.
Определение: Ортогональной проекцией вектора 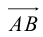 на ось
на ось 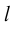 называется длина отрезка
называется длина отрезка 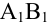 этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора
этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора 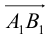 совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
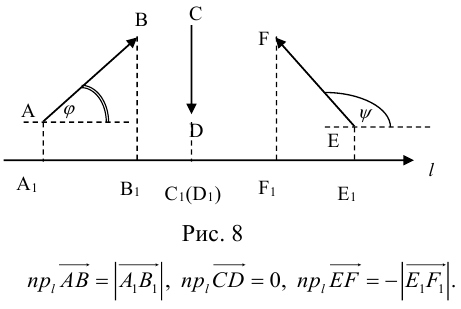
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
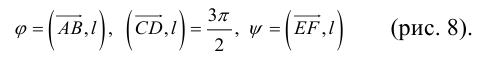
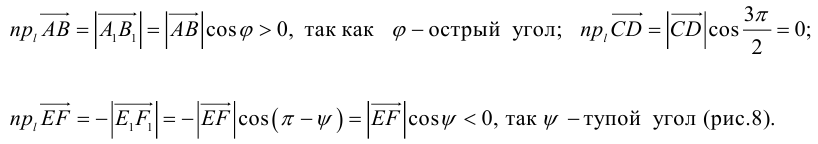
Очевидно, проекцию вектора на ось можно найти по формуле
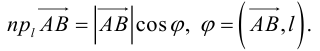
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
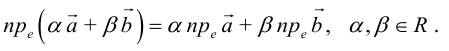
В частности, проекция суммы векторов равна сумме их проекций:
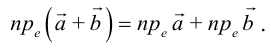
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 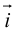 – орт оси ОХ,
– орт оси ОХ, 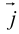 – орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).
– орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).

Аналогично в пространственной системе OXYZ 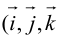 – орты координатных осей) (рис. 10):
– орты координатных осей) (рис. 10):
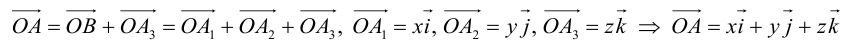
– разложение 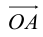 по ортам координатных осей (единственно по теореме 2).
по ортам координатных осей (единственно по теореме 2).
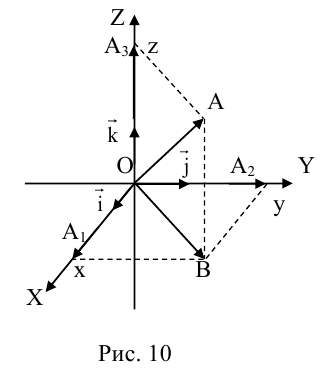
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 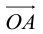 можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
Определение: Координатами вектора 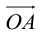 в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 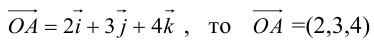 и наоборот, если
и наоборот, если
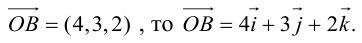
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
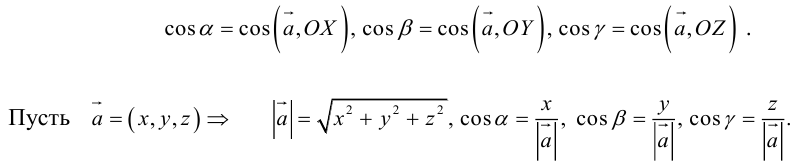
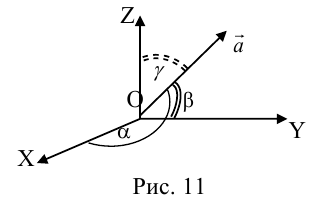
Из этих формул очевидно следует основное свойство направляющих косинусов:
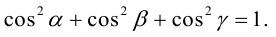
Если известны длина 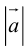 и направляющие косинусы вектора, то его координаты вычисляются по формулам:
и направляющие косинусы вектора, то его координаты вычисляются по формулам:
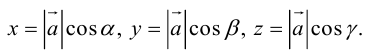
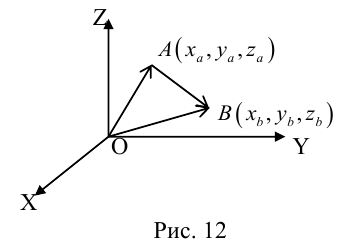
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
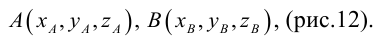
Тогда
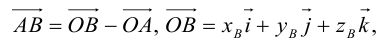
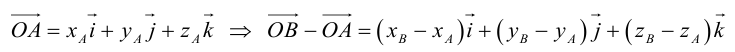 (см. свойства линейных операций над векторами). Таким образом,
(см. свойства линейных операций над векторами). Таким образом,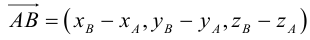 , то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
, то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
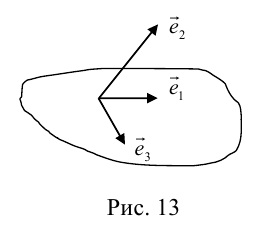
Если 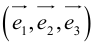 – базис, то
– базис, то 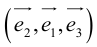 – другой базис, так как изменился порядок следования векторов.
– другой базис, так как изменился порядок следования векторов.
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать 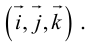
Из теоремы 2 следует, что всякий вектор 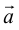 может быть разложен по базису
может быть разложен по базису 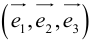 , то есть представлен в виде:
, то есть представлен в виде: 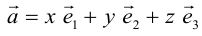 . Числа x,y,z называются координатами
. Числа x,y,z называются координатами 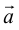 в базисе
в базисе 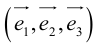 .
.
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 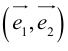 – базис, то представление вектора в виде
– базис, то представление вектора в виде 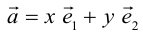 называется разложением
называется разложением 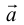 по базису
по базису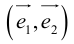 и x, y – координаты
и x, y – координаты 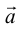 в этом базисе.
в этом базисе.
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 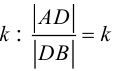 (рис. 14).
(рис. 14).
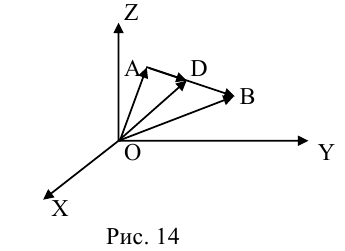
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
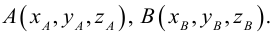
Обозначим
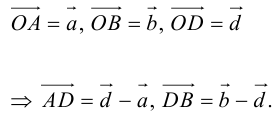
Так как 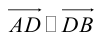 (лежат на одной прямой) и
(лежат на одной прямой) и 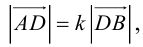 то
то

Переходя от этого векторного равенства к равенству соответствующих координат, получим:
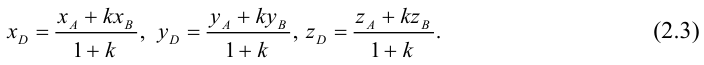
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
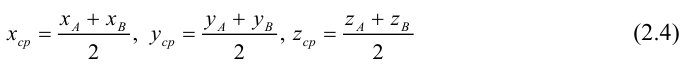
ЗАМЕЧАНИЕ 2. Если k < 0, 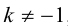 , то точка D лежит за пределами AB : так как
, то точка D лежит за пределами AB : так как 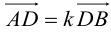 , то при
, то при 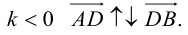
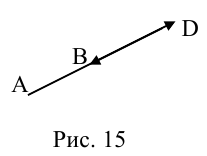
В этом случае 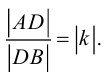
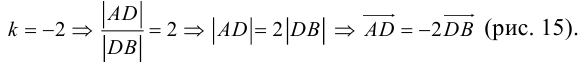
Скалярное произведение векторов
Определение: Скалярным произведением векторов 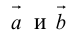 называется скаляр (число), равный
называется скаляр (число), равный 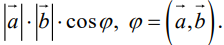
Скалярное произведение обозначается так: 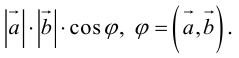 или
или 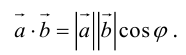
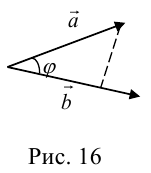
Так как 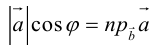 (рис. 16) или
(рис. 16) или 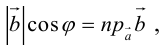 то
то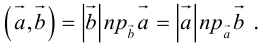
Свойства скалярного произведения
1.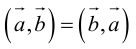 – очевидно из определения.
– очевидно из определения.
2.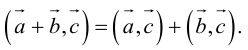
Доказательство:
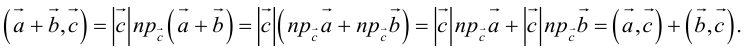
3.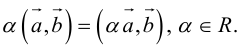
Доказательство:
а) 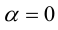 – очевидно.
– очевидно.
б) 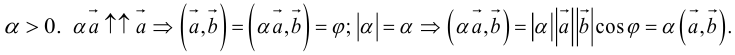
в) 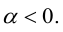 В этом случае
В этом случае
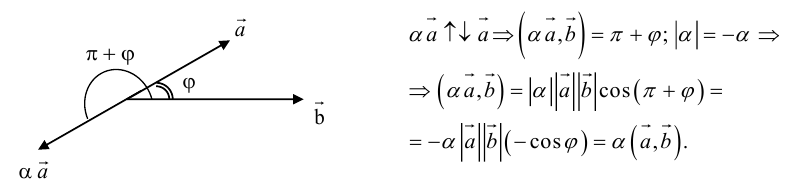
4.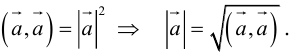
Отсюда следует, что 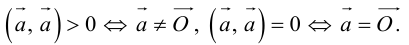
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.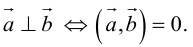
Доказательство:
а) пусть 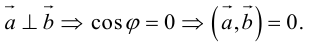
б) пусть 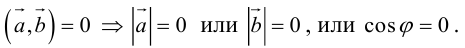
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 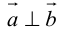 . В третьем случае
. В третьем случае 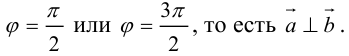
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов 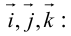
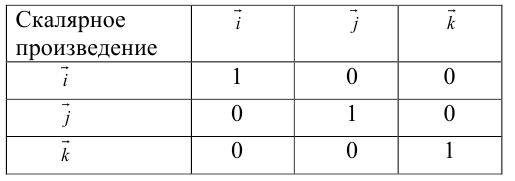
Пусть в некоторой пдск 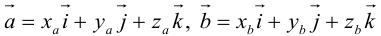 . Найдем скалярное произведение этих векторов:
. Найдем скалярное произведение этих векторов:
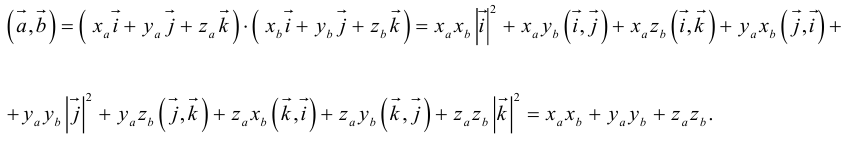
Таким образом, 
Пример №8
Найти, при каком значении x векторы 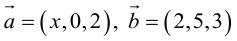 перпендикулярны.
перпендикулярны.
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5): 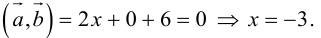
Пример №9
Найти угол между биссектрисой AD и медианой  если
если 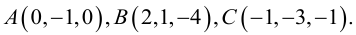
Так как 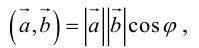
то 
Найдем координаты векторов 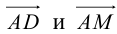 . Точка M – середина BC , поэтому по формулам (2.4)
. Точка M – середина BC , поэтому по формулам (2.4)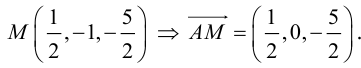
По теореме о биссектрисе внутреннего угла треугольника 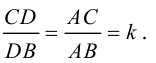
Чтобы найти k , вычислим длины AC и AB :
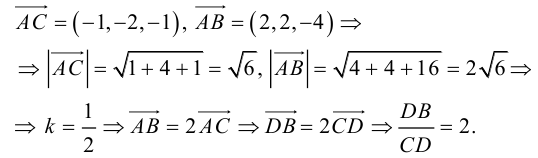
Разделим отрезок CB в данном отношении по формулам (2.3):
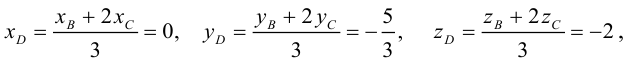
отсюда 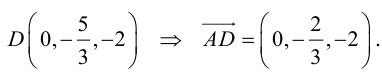
Заметим, что 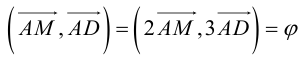 . Это замечание позволит нам не иметь дело с дробями, так как
. Это замечание позволит нам не иметь дело с дробями, так как
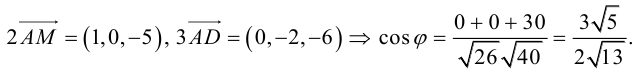
Пример №10
Найти 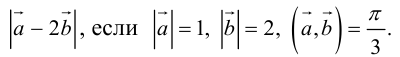
Воспользуемся свойствами 1–4 скалярного произведения:
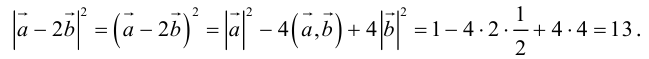
Отсюда 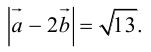
ЗАМЕЧАНИЕ. Так как работа силы 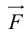 по перемещению материальной точки вдоль вектора
по перемещению материальной точки вдоль вектора 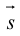 вычисляется по формуле
вычисляется по формуле 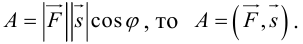
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 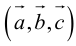 , имеющих общее начало, называется правой (левой), если
, имеющих общее начало, называется правой (левой), если 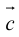 конца третьего вектора c вращение первого вектора
конца третьего вектора c вращение первого вектора 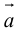 ко второму вектору
ко второму вектору 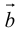 по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
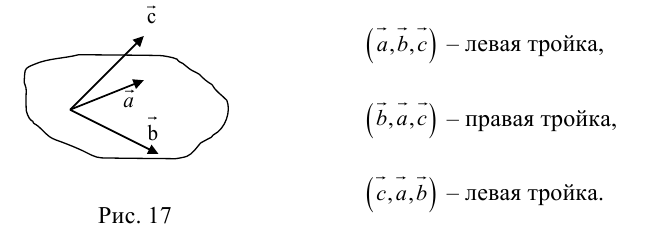
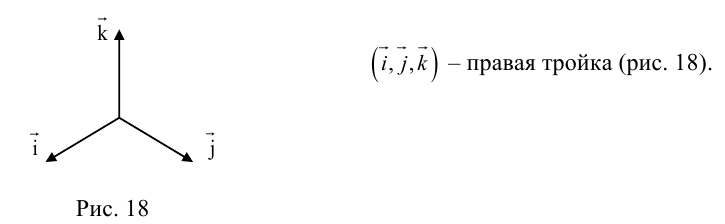
Определение: Векторным произведением вектора 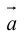 на вектор
на вектор 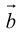 называется вектор
называется вектор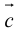 , удовлетворяющий условиям:
, удовлетворяющий условиям:
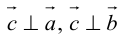 (
(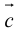 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 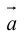 и
и 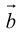 ).
). - Направление
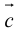 таково, что тройка
таково, что тройка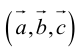 – правая.
– правая. 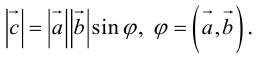
Векторное произведение обозначается так: 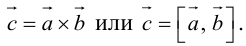
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
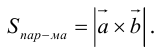
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
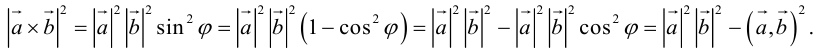
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
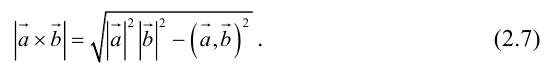
Пример №11
Найти площадь параллелограмма, построенного на векторах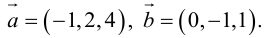
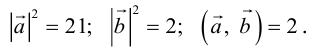
По формуле (2.7): 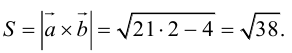
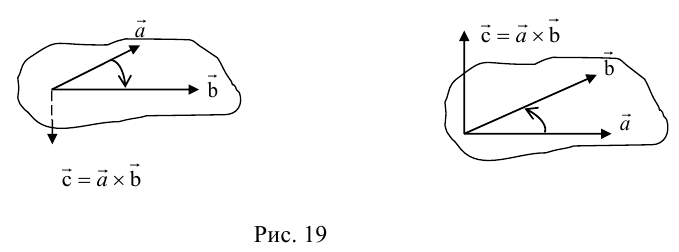
ЗАМЕЧАНИЕ 2. Направление вектора 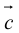 можно также (кроме п.2) определить по правилу винта: направление вектора
можно также (кроме п.2) определить по правилу винта: направление вектора 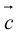 совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора
совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора 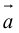 ко второму вектору
ко второму вектору  по кратчайшему пути (рис. 19).
по кратчайшему пути (рис. 19).
Свойства векторного произведения
1.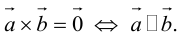
Доказательство:
а)пусть 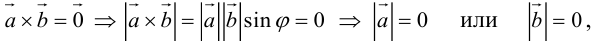 или
или 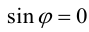 . В первом и втором случаях один из сомножителей – нулевой вектор.
. В первом и втором случаях один из сомножителей – нулевой вектор.
Его направление не определено, поэтому можно считать, что 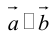 . Если
. Если 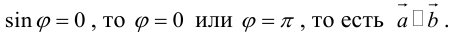
б)пусть 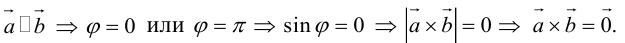
2. 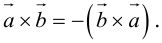
Доказательство: По определению направления векторов 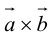 и
и 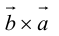 противоположны, а модули равны, значит, векторы отличаются лишь знаком.
противоположны, а модули равны, значит, векторы отличаются лишь знаком.
3.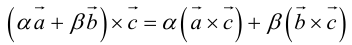 – свойство линейности векторного произведения по первому сомножителю (без доказательства).
– свойство линейности векторного произведения по первому сомножителю (без доказательства).
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 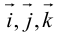 : векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
: векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
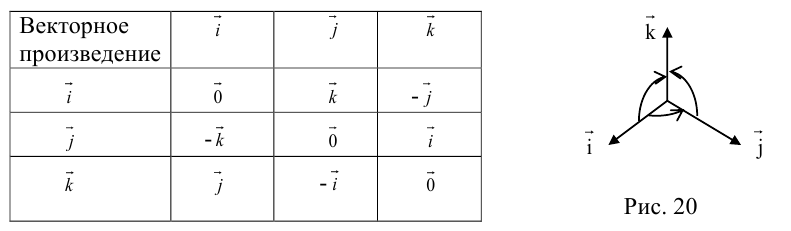
Пусть в некоторой пдск 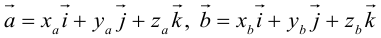 . Найдем векторное произведение этих векторов:
. Найдем векторное произведение этих векторов:
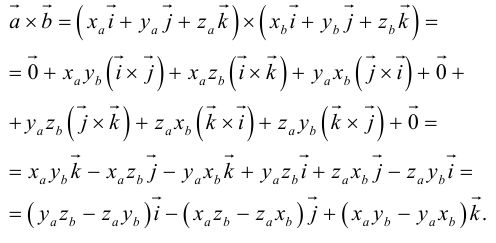
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
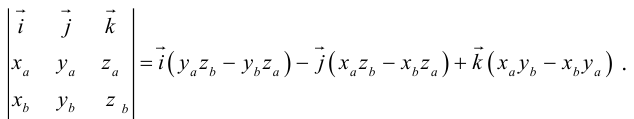
Таким образом,
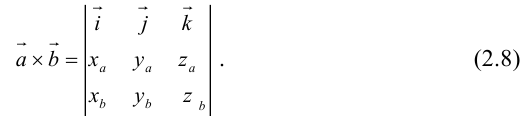
Пример №12
Вычислить векторное произведение векторов 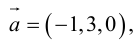
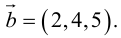
По формуле (2.8): 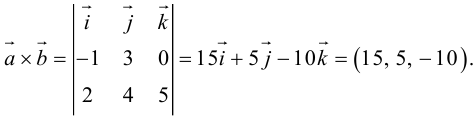
Заметим, что площадь треугольника, построенного на векторах 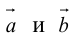 , можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что
, можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что 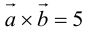
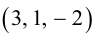
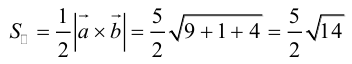
или
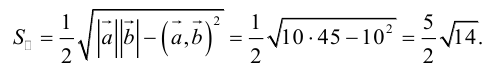
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 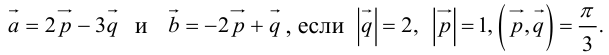
Так как 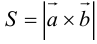 , то вычислим векторное произведение, используя его свойства:
, то вычислим векторное произведение, используя его свойства: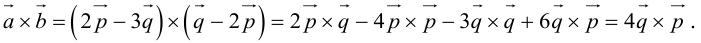
Отсюда 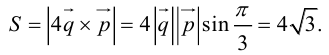
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 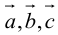 называется число
называется число 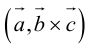 – скалярное произведение a на векторное произведение
– скалярное произведение a на векторное произведение 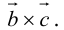
Смешанное произведение обозначается так: 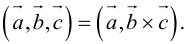
Пусть в некоторой пдск 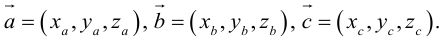
Обозначим
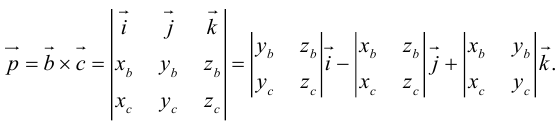
Тогда
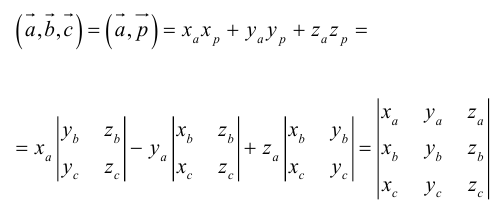
по 7 свойству определителей.
Таким образом,
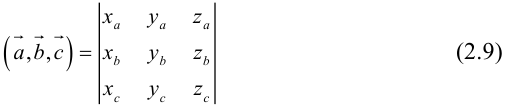
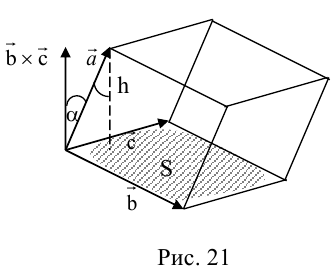
По определению скалярного произведения 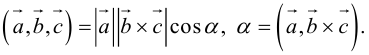
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
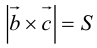 – площадь параллелограмма,
– площадь параллелограмма,
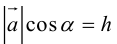 – высота параллелепипеда,
– высота параллелепипеда,
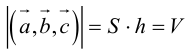 – объем параллелепипеда.
– объем параллелепипеда.
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 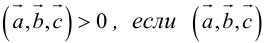 – правая тройка, и
– правая тройка, и 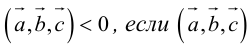 – левая тройка.
– левая тройка.
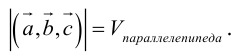
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 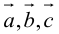 компланарны
компланарны
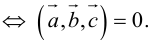
Доказательство: а) 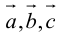 компланарны
компланарны 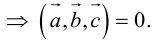
Если 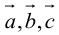 компланарны, то на них нельзя построить параллелепипед, а потому
компланарны, то на них нельзя построить параллелепипед, а потому 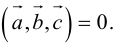
б)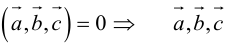 компланарны.
компланарны.
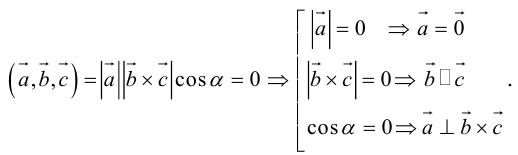
Во всех трех случаях 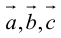 компланарны: в частности, если
компланарны: в частности, если 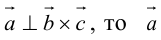 параллелен плоскости векторов
параллелен плоскости векторов 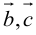 , что означает их компланарность.
, что означает их компланарность.
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
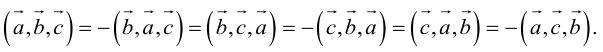
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами: 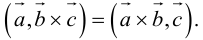
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим: 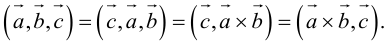
4. Смешанное произведение линейно по каждому из трех сомножителей.
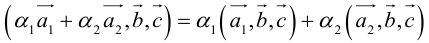 – линейность по первому сомножителю.
– линейность по первому сомножителю.
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
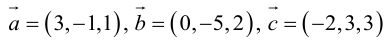 , и его высоту, перпендикулярную плоскости векторов
, и его высоту, перпендикулярную плоскости векторов 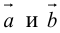 .
.
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому 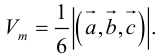
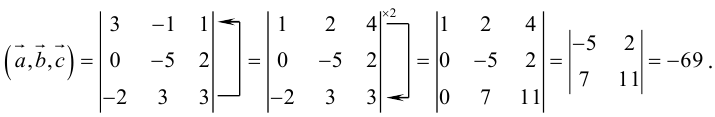
Отсюда 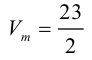 (заметим, что
(заметим, что  – левая тройка, так как смешанное произведение отрицательно).
– левая тройка, так как смешанное произведение отрицательно).
Чтобы найти высоту, воспользуемся формулой
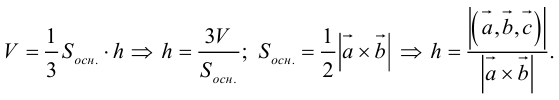
По формуле (2.7) 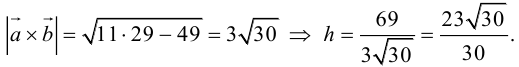
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
|
0 / 0 / 0 Регистрация: 14.09.2021 Сообщений: 13 |
|
|
1 |
|
|
24.10.2021, 15:24. Показов 868. Ответов 4
Найти вектор x, удовлетворяющий указанным условиям: Помогите, пожалуйста.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
24.10.2021, 15:24 |
|
Ответы с готовыми решениями:
Найти вектор удовлетворяющий условиям Найти вектор х, удовлетворяющий данным условиям Найти вектор, удовлетворяющий условию
4 |
|
2662 / 1726 / 175 Регистрация: 05.06.2011 Сообщений: 4,956 |
|
|
24.10.2021, 16:26 |
2 |
|
Ну, например, распишите покомпонентно.
0 |
|
1446 / 916 / 249 Регистрация: 05.10.2014 Сообщений: 4,544 |
|
|
24.10.2021, 16:49 |
3 |
|
Помогите, пожалуйста. можно со скалярного произведения начать, выпишите его определение и примените ко 2 равенству
1 |
|
0 / 0 / 0 Регистрация: 14.09.2021 Сообщений: 13 |
|
|
24.10.2021, 18:15 [ТС] |
4 |
|
можно со скалярного произведения начать, выпишите его определение и примените ко 2 равенству Из второго выражения получил первую координату вектора 3. Из первого выражения вторую координату 6. А для чего дано 3 выражение и как ним воспользоваться?
0 |
|
418 / 306 / 79 Регистрация: 14.03.2021 Сообщений: 1,202 |
|
|
24.10.2021, 20:05 |
5 |
|
А для чего дано 3 выражение и как ним воспользоваться? Модуль вектора, который записывается, как определитель 3-го порядка. В строчках – орты и координаты перемножаемых.
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
24.10.2021, 20:05 |
|
Помогаю со студенческими работами здесь Составить уравнение линии, точки которой удовлетворяют указанным условиям Найти вектор, удовлетворяющий заданным свойствам есть вектор, допустим, о нем известно -… Найти решение уравнения, удовлетворяющее указанным условиям Объясните пожалуйста как решать, с… Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям Заранее спасибо
Дать геометрическое описание множества точек комплексной плоскости, удовлетворяющих указанным условиям Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 5 |

 Найти вектор x , удовлетворяющий указанным условиям
Найти вектор x , удовлетворяющий указанным условиям
