Как найти вектор ускорения кориолиса – Сайт, где вы сможете решить свои вопросы

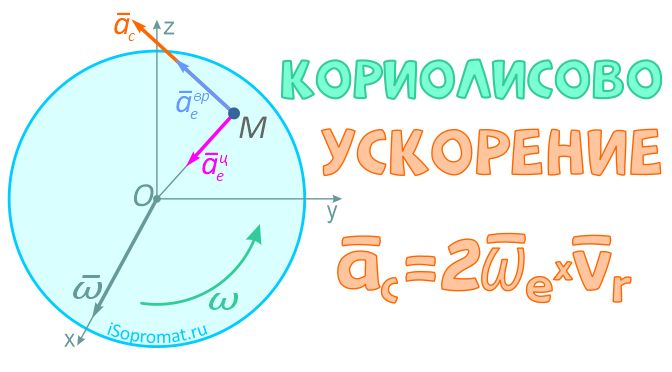
Ускорение Кориолиса

Ускорение Кориолиса (Кориолисово ускорение) характеризует изменение относительной скорости по направлению за счет переносного вращения и изменение величины переносной скорости за счет относительного движения.

Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3)

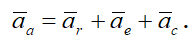
Теорема Кориолиса
Направление ускорения Кориолиса

Рис. 3

Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение a_r направлено вдоль этой прямой и определяется выражением

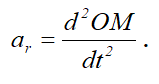
Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением

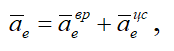
Переносное ускорение

где a_e^вр= ε ⋅ OM — вращательное ускорение точки M, направленное перпендикулярно отрезку OM;
a_e^цс= ω²⋅ OM — центростремительное ускорение точки M, направленное к центру диска.

Ускорение Кориолиса или поворотное ускорение определяется по формуле

где ω_e — переносная угловая скорость,
ν_r — относительная скорость точки.

Направление Кориолисова ускорения определяется по правилу векторного произведения или по правилу Жуковского.

Величина ускорения Кориолиса определяется выражением

Величина Кориолисова ускорения

где α – угол между векторами ω_e и ν_r.

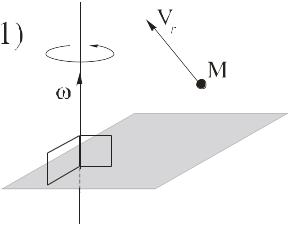
Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка M движется относительно диска с постоянной относительной скоростью (рис.4).

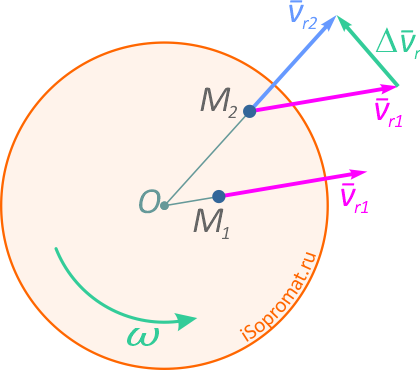
Рис. 4

Пусть в момент времени t₁ точка M занимала положение M₁ и имела относительную скорость ν_r1. За промежуток времени Δt точка M переместится в положение M₂, при этом направление скорости ν_r изменится вследствие вращения диска. Вектор ν_r получит приращение Δν_r.

Отношение 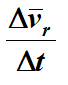определяет среднее ускорение точки за промежуток времени Δt. Предел отношения 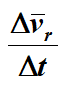при Δt→ 0 есть производная 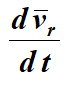как производная от вектора постоянного по величине.

Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t₁ и t₂ переносная скорость определяется выражениями

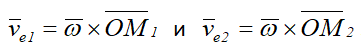
Тогда приращение вектора ν_e за счет относительного движения будет равно

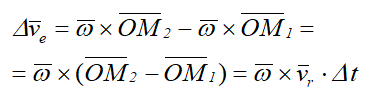
Отношение 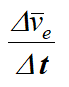в пределе при Δt→ 0 дает производную

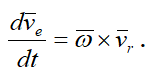
Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

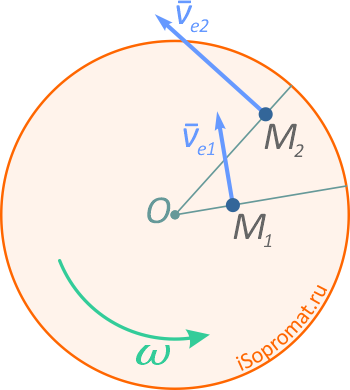
Изменение величины переносной скорости

Рис. 5

Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых

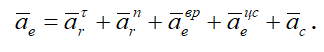
Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:

Аналитический метод сложения векторов

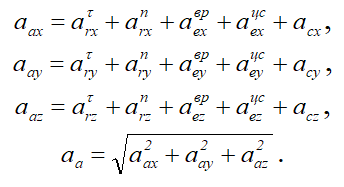
Примеры решения задач >
Сферическое движение и способы его задания >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Запрос «Эффект Кориолиса» перенаправляется сюда; см. также другие значения.

Рис. 1. При вращении диска более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Переместить тело вдоль радиуса так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б») можно, увеличив скорость тела, то есть придав ему ускорение. Если система отсчёта вращается вместе с диском, то видно, что тело «не хочет» оставаться на радиусе, а «пытается» уйти влево — с точки зрения наблюдателя во вращающейся системе отсчёта, это результат действия силы Кориолиса.

Рис. 2. Траектории шарика при движении без трения по поверхности вращающейся тарелки в разных системах отсчёта (вверху — в инерциальной по прямой, внизу — в неинерциальной, вращающейся вместе с тарелкой).

Си́ла Кориоли́са — одна из сил инерции, использующаяся при рассмотрении движения материальной точки относительно вращающейся системы отсчёта. Добавление силы Кориолиса к действующим на материальную точку физическим силам позволяет учесть влияние вращения системы отсчёта на такое движение^[1].

Названа по имени французского учёного Гаспа́ра-Гюста́ва де Кориоли́са, впервые описавшего её в статье, опубликованной в 1835 году^[2]^[3]. Иногда высказываются мнения, что первым математическое выражение для силы получил Пьер-Симон Лаплас в 1775 году^[4], а эффект отклонения движущихся объектов во вращающихся системах отсчёта был описан Джованни Баттиста Риччоли и Франческо Мария Гримальди в 1651 году^[5].

Часто под термином «эффект Кориолиса» подразумевается наиболее важный случай проявления силы Кориолиса — который возникает в связи с суточным вращением Земли.
Так как угловая скорость вращения Земли мала (1 оборот в день), эта сила, как правило, мала по сравнению с другими силами.
Эффекты обычно становятся заметными только для движений, происходящих на больших расстояниях при длительных периодах времени, таких как крупномасштабное движение воздуха атмосферы (вихреобразные циклоны) или воды в океане (Гольфстрим). Такие движения, как правило, происходят вдоль поверхности Земли, поэтому для них часто важна только горизонтальная составляющая силы Кориолиса. Она заставляет движущиеся вдоль поверхности Земли объекты (от полюсов к экватору) отклоняться вправо (по отношению к направлению движения) в северном полушарии и влево в южном. Эффект горизонтального отклонения сильнее близ полюсов, так как эффективная скорость вращения вокруг локальной вертикальной оси значительнее там и уменьшается до нуля у экватора^[⇨].

Предварительное рассмотрение[править | править код]

Пусть в какой-либо инерциальной системе отсчёта (ИСО) имеется радиус, равномерно вращающийся вокруг перпендикулярной к нему оси. Если вдоль этого радиуса в направлении от центра вращения с постоянной относительно радиуса скоростью движется материальная точка (МТ), то вместе с увеличением расстояния от центра вращения, в ИСО возрастает и компонента скорости тела, направленная перпендикулярно радиусу. Значит, в данном случае компонента ускорения точки, перпендикулярная радиусу, отлична от нуля. Эта компонента ускорения МТ в инерциальной системе отсчёта и представляет собой ускорение Кориолиса.

При рассмотрении того же самого движения в неинерциальной системе отсчёта (НИСО), вращающейся вместе с радиусом, наблюдаемая картина будет другой. Действительно, в этой системе отсчёта скорость МТ не изменяется и, соответственно, компонента её ускорения, перпендикулярная радиусу, равна нулю. Значит, движение выглядит так, как будто во вращающейся системе отсчёта на МТ действует дополнительная сила, направленная противоположно ускорению Кориолиса и компенсирующая его. Эта дополнительная «сила», вводимая для удобства описания движения, но в действительности отсутствующая, и есть сила Кориолиса. Понятно, что данная «сила» позволяет учесть влияние вращения подвижной системы отсчёта на относительное движение МТ, но при этом никакому реальному взаимодействию МТ с другими телами не соответствует^[6].

Более строго — ускорение Кориолиса есть удвоенное векторное произведение вектора угловой скорости вращения системы координат на вектор скорости движения МТ относительно вращающейся системы координат^[7]. Соответственно, сила Кориолиса равна произведению массы МТ на её ускорение Кориолиса, взятому со знаком минус^[1].

Определение[править | править код]

Пусть имеются две системы отсчёта, одна из которых $(S)$ инерциальная, а другая ${displaystyle left(S,'right)}$ движется относительно первой произвольным образом и в общем случае является неинерциальной. Будем также рассматривать движение произвольной материальной точки массы $m$ . Её ускорение по отношению к первой системе отсчёта обозначим ${vec a}_{a}$ , а по отношению ко второй — ${vec a}_{r}$ .

Связь между ускорениями ${vec a}_{a}$ и ${vec a}_{r}$ следует из теоремы Кориолиса (см. ниже)^[8]:

${vec a}_{a}={vec a}_{r}+{vec a}_{e}+{vec a}_{K},$

где ${vec a}_{e}$ — перено́сное ускорение, а ${vec a}_{K}$ — ускорение Кориолиса (кориолисово ускорение, поворотное ускорение). Напомним, что переносным ускорением называют ускорение той точки системы $S,'$ относительно системы $S$ , в которой в данный момент находится рассматриваемая материальная точка^[9].

После умножения на массу точки и учёта второго закона Ньютона $m{vec a}_{a}={vec F}$ , данное соотношение можно представить в виде

$m{vec a}_{r}={vec F}+(-m{vec a}_{e})+(-m{vec a}_{K}).$

Величину $(-m{vec a}_{e})$ называют переносной силой инерции, а величину ${displaystyle (-m{vec {a}}_{K})}$ — силой Кориолиса (кориолисовой силой). Обозначив их ${vec F}_{e}$ и ${vec F}_{K}$ соответственно, можно записать

$m{vec a}_{r}={vec F}+{vec F}_{e}+{vec F}_{K}.$

Полученное выражение выражает основной закон динамики для неинерциальных систем отсчёта.

Из кинематики известно, что

${vec a}_{K}=2left[{vec omega }times {vec v}_{r}right],$

где ${vec {omega }}$ — угловая скорость вращения неинерциальной системы отсчёта $S,'$ , ${vec v}_{r}$ — скорость движения рассматриваемой материальной точки в этой системе отсчёта; квадратными скобками обозначена операция векторного произведения.
С учётом этого для силы Кориолиса выполняется

${vec F}_{K}=-2,m,left[{vec omega }times {vec v}_{r}right].$

Замечания

Согласно принятой в русскоязычной литературе терминологии, кориолисово ускорение материальной точки — это часть её ускорения в инерциальной системе отсчёта $S$ ^[7]^[10]. Этим оно отличается, например, от центробежного ускорения, возникающего в неинерциальной системе отсчёта $S,'$ .
В иноязычной литературе встречается альтернативное определение кориолисового ускорения с противоположным знаком: ${vec a}_{K}equiv -2left[{vec omega }times {vec v}_{r}right]$ . В таком случае кориолисово ускорение и кориолисова сила оказываются связаны соотношением: ${vec a}_{K}={frac {F_{K}}{m}}$ ^[11]^[12]^[13]^[14]. В рамках такого определения кориолисово ускорение является частью ускорения тела в неинерциальной системе отсчёта $S,'$ .

Теорема Кориолиса[править | править код]

Пусть точка совершает сложное движение: движется относительно неинерциальной системы отсчёта $S,'$ со скоростью ${vec {v}}_{r}$ ; система $S,'$ при этом сама движется относительно инерциальной системы координат $S$ , причём линейная скорость движущегося в трёхмерном пространстве произвольным образом мгновенного центра скоростей $O$ равна $vec {v}_0$ , а угловая скорость вращения системы $S,'$ относительно мгновенного центра скоростей равна $vecomega$ . Мгновенный центр скоростей находится с помощью теоремы вращения Эйлера.

Тогда абсолютная скорость рассматриваемой точки (то есть её линейная скорость в инерциальной системе координат) будет такой:

${vec v}={vec {v}}_{0}+left[{vec omega }times {vec R}right]+{vec {v}}_{r}$ , причём ${frac {d}{dt}}{vec R}=left[{vec omega }times {vec R}right]+{vec {v}}_{r}$ ,

где $vec R$ — радиус-вектор точки относительно мгновенного центра скоростей $O$ . Первые два слагаемых в правой части равенства представляют собой переносную скорость точки, а последнее — её относительную скорость.

Продифференцируем это равенство по времени:

${frac {d}{dt}}{vec v}={frac {d}{dt}}{vec {v}}_{0}+{frac {d}{dt}}left[{vec omega }times {vec R}right]+{frac {d}{dt}}{vec {v}}_{r}.$

Найдём значение каждого слагаемого в инерциальной системе координат:

$frac{d}{dt} vec {v}_0 = vec {a}_0 ,$

${displaystyle {frac {d}{dt}}left[{vec {omega }}times {vec {R}}right]=left[{vec {varepsilon }}times {vec {R}}right]+left[{vec {omega }}times {frac {d}{dt}}{vec {R}}right]=left[{vec {varepsilon }}times {vec {R}}right]+{biggl [}{vec {omega }}times left[{vec {omega }}times {vec {R}}right]{biggr ]}+left[{vec {omega }}times {vec {v}}_{r}right],}$

${frac {d}{dt}}{vec {v}}_{r}=left[{vec omega }times {vec {v}}_{r}right]+{frac {{stackrel {~}{d_{r}}}{vec {v}}_{r}}{dt}},$

где ${vec {a}}_{r}={frac {{stackrel {~}{d_{r}}}{vec {v}}_{r}}{dt}}$ — линейное ускорение точки относительно системы $S,'$ , ${vec varepsilon }={frac {d{vec omega }}{dt}}$ — угловое ускорение системы $S,'$ .

Таким образом, имеем:

${displaystyle {frac {d}{dt}}{vec {v}}={vec {a}}={vec {a}}_{0}+left[{vec {varepsilon }}times {vec {R}}right]+{biggl [}{vec {omega }}times left[{vec {omega }}times {vec {R}}right]{biggr ]}+{vec {a}}_{r}+2left[{vec {omega }}times {vec {v}}_{r}right].}$

Полученное равенство служит математическим выражением теоремы Кориолиса: Абсолютное ускорение точки в сложном движении равно геометрической сумме её переносного ускорения (сумма первых трёх слагаемых в правой части), относительного ускорения (четвёртое слагаемое) и добавочного кориолисова ускорения (последнее слагаемое), равного $2left[{vec omega }times {vec {v}}_{r}right]$ .

Используя обозначения
${displaystyle {vec {a}}_{e}={vec {a}}_{0}+left[{vec {varepsilon }}times {vec {R}}right]+{biggl [}{vec {omega }}times left[{vec {omega }}times {vec {R}}right]{biggl ]}}$ и ${vec a}_{K}=2left[{vec omega }times {vec {v}}_{r}right]$ , получим запись теоремы Кориолиса в более сжатом виде:

${vec a}_{a}={vec a}_{e}+{vec a}_{r}+{vec a}_{K}.$

Сам Кориолис выражал в 1835 г. свои результаты в иной форме, вводя в рассмотрение переносную и кориолисову силы инерции; общепринятая же ныне чисто кинематическая формулировка теоремы Кориолиса предложена в 1862 г. Анри Эме Резалем^[15].

В частном случае вращательного движения инерциальной системы отсчёта относительно начала координат для того, чтобы точка относительно неинерциальной системы отсчёта двигалась прямолинейно по радиусу к оси вращения (см. рис.), необходимо приложить к ней силу, которая будет противодействующей суммы силы Кориолиса $-2mleft[{vec omega }times {vec {v}}_{r}right]$ , переносной вращательной силы $-mleft[{vec varepsilon }times {vec R}right]$ и переносной силы инерции поступательного движения системы отсчёта $-m{vec {a}}_{0}$ . Составляющая же ускорения $left[{vec omega }times left[{vec omega }times {vec R}right]right]$ не отклонит тело от этой прямой, так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение ${displaystyle left[{vec {omega }}times left[{vec {omega }}times {vec {R}}right]right]+{vec {a}}_{r}=0}$ , которое если умножить векторно на ${vec R}$ , то с учётом $left[{vec R}times left[{vec omega }times left[{vec omega }times {vec R}right]right]right]=0$ получим относительно ${vec {v}}_{r}$ дифференциальное уравнение $left[{vec R}times {frac {{stackrel {~}{d_{r}}}{vec {v}}_{r}}{dt}}right]equiv 0$ , имеющее при любых ${vec R}$ и ${vec {v}}_{r}$ общим решением $left[{vec R}times {vec {v}}_{r}right]={vec {Const}}$ , которое и является уравнением такой прямой — $left[{vec R}times {vec {v}}_{r}right]={vec {0}}$ .

Обсуждение[править | править код]

Правило Жуковского[править | править код]

Н. Е. Жуковский предложил удобный способ нахождения кориолисова ускорения:

Ускорение Кориолиса ${vec a}_{K}$ можно получить, спроецировав вектор относительной скорости точки ${vec {v}}$ на плоскость, перпендикулярную вектору переносной угловой скорости ${vec {omega }}$ , увеличив полученную проекцию в $2omega$ раз и повернув её на 90 градусов в направлении переносного вращения.

Физический смысл[править | править код]

Пусть точка движется со скоростью ${vec {v}}$ вдоль прямой к центру координат инерциальной системы отсчёта (см. рис.).

Тогда данное движение приведёт к изменению расстояния до центра вращения $R$ и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой — её переносной скорости.

Как мы знаем, эта скорость движения равна

${vec {v}}_{e}=left[{vec omega }times {vec R}right].$

Данное изменение будет равно:

$d{vec {v}}_{e}=left[{vec omega }times d{vec R}right].$

Проведя дифференцирование по времени, получим

${displaystyle {vec {a}}=left[{vec {omega }}times {vec {v}}right].}$

(Направление данного ускорения перпендикулярно ${vec {omega }}$ и ${vec {v}}$ ).

С другой стороны, вектор ${vec {v}}$ для точки, остающейся неподвижной относительно инерциального пространства, повернётся относительно неинерциального на угол $omega dt$ . Или приращение скорости будет

${displaystyle d{v}_{r}=vsin omega dt=vtimes omega dt.}$

При ${displaystyle trightarrow 0,}$ соответственно, второе ускорение будет:

${displaystyle {vec {a}}=left[{vec {omega }}times {vec {v}}right].}$

Общее ускорение будет

${displaystyle {vec {a}}_{k}=2left[{vec {omega }}times {vec {v}}right].}$

Как видно, система отсчёта не претерпела изменения угловой скорости ${vec omega }.$
Линейная скорость относительно неё не меняется и остаётся ${vec v}.$ Тем не менее, ускорение не равно нулю.

Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным.
Ускорение из-за поворота вектора скорости останется

${vec a}=left[{vec omega }times {vec v}right],$

а также прибавляется ускорение в результате изменения центростремительного ускорения точки.

Введение в рассмотрение силы Кориолиса производится для того, чтобы иметь возможность описывать движение тел в неинерциальных системах отсчёта с помощью уравнений, по форме совпадающих с уравнением второго закона Ньютона. В то же время сила Кориолиса никак не связана с каким-либо взаимодействием рассматриваемого тела с другими телами, а все её свойства определяются только обстоятельствами кинематического характера, обусловленными выбором конкретной неинерциальной системы отсчёта. В связи с этим о силе Кориолиса говорят, что она не является физической силой, и называют её псевдосилой^[16].

Сила Кориолиса не инвариантна относительно перехода из одной системы отсчёта в другую. Она не подчиняется закону действия и противодействия. Движение тела под действием силы Кориолиса аналогично движению во внешнем силовом поле. Сила Кориолиса всегда является внешней по отношению к любому движению системы материальных тел.

Сила Кориолиса и закон сохранения момента импульса[править | править код]

Если вращающаяся лаборатория, принимаемая за неинерциальную систему отсчёта, имеет конечный момент инерции, то в соответствии с законом сохранения момента импульса при движении тела по радиусу, перпендикулярному оси вращения, угловая скорость вращения будет увеличиваться (при движении тела к центру) или уменьшаться (при движении тела от центра). Рассмотрим эту ситуацию с точки зрения неинерциальной системы.

Хорошим примером может быть человек, который перемещается в радиальном направлении по вращающейся карусели (например, держась за ведущий к центру поручень). При этом с точки зрения человека он при движении к центру будет совершать работу против центробежной силы (эта работа пойдёт на увеличение энергии вращения карусели). На него также будет действовать сила Кориолиса, которая стремится отклонить его движение от радиального направления («сносит» его вбок), и противодействуя сносу (прилагая поперечное усилие к поручню), он будет раскручивать карусель.

При движении от центра центробежная сила будет совершать работу над человеком (за счёт уменьшения энергии вращения), а противодействие силе Кориолиса будет тормозить карусель.

Сила Кориолиса в природе и технике[править | править код]

Самый важный случай действия силы Кориолиса связан с суточным вращением Земли.
Поскольку Земля вращается, для правильного анализа движения объектов в системах, привязанных к Земле, необходимо учитывать силу Кориолиса.
Сила Кориолиса, вызванная вращением Земли, может быть замечена при наблюдении за движением маятника Фуко^[17].

В Северном полушарии приложенная к движущемуся поезду сила Кориолиса направлена перпендикулярно рельсам, имеет горизонтальную составляющую и стремится сместить поезд вправо по ходу движения. Из-за этого реборды колёс, расположенных по правой стороне поезда, оказываются прижаты к рельсам.
Кроме того, поскольку сила Кориолиса приложена к центру масс каждого вагона, то она создаёт момент силы, из-за которого возрастает нормальная сила реакции, действующая на колёса со стороны правого рельса в направлении, перпендикулярном поверхности рельса, и уменьшается аналогичная сила, действующая со стороны левого рельса. Понятно, что в силу 3-го закона Ньютона сила давления вагонов на правый рельс также больше, чем на левый^[18].
На одноколейных железных дорогах поезда обычно ходят в обоих направлениях, поэтому последствия действия силы Кориолиса оказываются одинаковыми для обоих рельсов. Иначе обстоят дела на двухколейных дорогах. На таких дорогах по каждой колее поезда движутся только в одном направлении, вследствие чего действие силы Кориолиса приводит к тому, что правые по ходу движения рельсы изнашиваются сильнее, чем левые. Очевидно, что в Южном полушарии из-за изменения направления силы Кориолиса больше изнашиваются левые рельсы^[19]. На экваторе эффект отсутствует, поскольку в этом случае сила Кориолиса направлена по вертикали (при движении вдоль экватора) или равна нулю (при движении вдоль меридиана).

Кроме того, сила Кориолиса проявляется и в глобальных масштабах.
Вместо того чтобы течь непосредственно из области высокого давления в низкое, как это было бы в невращающейся системе, ветры и течения, как правило, текут вправо от этого направления в Северном полушарии и влево от этого направления в Южном. Поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы^[20] (см. Закон Бэра). В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов^[21] (см. геострофический ветер): в Северном полушарии вращение воздушных масс происходит в циклонах против часовой стрелки, а в антициклонах — по часовой стрелке; в Южном — наоборот: по часовой стрелке в циклонах и против — в антициклонах. Отклонение ветров (пассатов) при циркуляции атмосферы — также проявление силы Кориолиса.

Силу Кориолиса необходимо учитывать при рассмотрении планетарных движений воды в океане. Она является причиной возникновения гироскопических волн^[22], волн Россби.

При идеальных условиях сила Кориолиса определяет направление закручивания воды — например, при сливе в раковине (феномен «обратного закручивания воды при стоке»). На практике зависимость направления закручивания воды от полушария проявляется лишь в тщательно спланированных экспериментах, проведённых вдали от экватора, в которых используются строго симметричные сосуды, многочасовой отстой жидкости перед измерением, контроль внешних условий (стабильность температуры и отсутствие потоков воздуха)^[23]. Отклонения от таких идеальных условий оказывают на направление закручивания воды большее влияние, чем сила Кориолиса.

См. также[править | править код]

Сила Кориолиса в гидроаэромеханике
Центростремительное ускорение
Кориолисов расходомер
Увлечение инерциальных систем отсчёта

Примечания[править | править код]

↑ ¹ ² Тарг С. М. Кориолиса сила // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 461. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ Фрейман Л. С. К истории доказательства теоремы Кориолиса // Труды института истории естествознания и техники / Гл. ред. Н. А. Фигуровский. — М.: АН СССР, 1956. — Т. 10. — С. 213—244.
↑ Coriolis G. Sur les équations du mouvement relative des systèmes de corps (фр.) // Journ. Ecole polytechn. — 1835. — Vol. 15, n^o 24. — P. 142—154. Архивировано 21 января 2018 года.
↑ Manuel López-Mariscal. Further Coriolis correlation considerations (англ.) // Physics Today. — 2012. — Vol. 65. — P. 8. — doi:10.1063/PT.3.1764. (недоступная ссылка)
↑ Christopher M. Graney. Coriolis effect, two centuries before Coriolis (англ.) // Physics Today. — 2011. — Vol. 64. — P. 8. — doi:10.1063/PT.3.1195. (недоступная ссылка)
↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 70. — 320 с.
↑ ¹ ² Тарг С. М. Кориолиса ускорение // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 461. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ Маркеев А. П. Теоретическая механика: Учебник для университетов. — М.: ЧеРО, 1999. — С. 74. — 572 с.
↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 156. — 416 с. — ISBN 5-06-003117-9.
↑ Хайкин С. Э. Силы инерции и невесомость. — М.: «Наука», 1967. — С. 163—164.
↑ N. de Nevers. Air Pollution Control Engeneering. — 2. — The MkGraw-Hill Companies, Inc., 1999. — С. 88. — 586 с. — ISBN 0-07-039367-2.
↑ Bela G. Liptak. Flow Measurement. — CRS Press, 1993. — С. 51. — 211 с. — ISBN 0-8019-8386-X.
↑ A. Berthoz, Werner Graf, Pierre Paul Vidal. The Head-neck Sensory Motor System. — 1. — Oxford University Press, 1992. — С. 216. — 748 с. — ISBN 0-19-506820-3.
↑ E. Brinckmann. Biology in Space and Life on Earth: Effects of Spaceflight on Biological Systems. — 1. — Heppenheim: Wiley-VCH, 2007. — С. 30. — ISBN 978-3-527-40668-5.
↑ Веселовский И. Н. Очерки по истории теоретической механики. — М.: Высшая школа, 1974. — 287 с. — С. 203—204.
↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 69—70. — 320 с.
↑ Сила Кориолиса. Дата обращения: 7 декабря 2009. Архивировано 16 ноября 2012 года.
↑ Матвеев А. Н. Механика и теория относительности. — Издание 2-е, переработанное. — М.: Высш. шк., 1986. — С. 167. — 320 с. — 28 000 экз.
↑ Хайкин С. Э. Силы инерции и невесомость. — М.: «Наука», 1967. — С. 161—163.
↑ Краткая географическая энциклопедия. Закон Бэра. Дата обращения: 7 декабря 2009. Архивировано 7 декабря 2010 года.
↑ Сурдин В. Ванна и закон Бэра // Квант. — 2003. — № 3. — С. 13. Архивировано 3 июля 2009 года.
↑ Научная Сеть. Колебания и волны. Лекции. Дата обращения: 7 декабря 2009. Архивировано 12 февраля 2007 года.
↑ Can somebody finally settle this question: Does water flowing down a drain spin in different directions depending on which hemisphere you’re in? And if so, why?, Scientific American. Архивировано 5 ноября 2016 года. Дата обращения: 4 ноября 2016.

Литература[править | править код]

Persson, A. The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885 // History of Meteorology 2 (2005): 1-24. (англ.)

Источник

Вектор
находится по формуле (9):

Модуль
ускорения равен

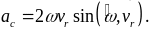
1414* MERGEFORMAT ()

Из
равенства (13) следует, что ускорение
Кориолиса равно нулю в трёх случаях:

(подвижная система движется либо
поступательно, либо в данный момент не
вращается);

(точка покоится в подвижной системе
координат);

(в подвижной системе координат точка
движется параллельно оси вращения
системы).

Направление
вектора ускорения Кориолиса определяется
либо по общему для векторных произведений
правилу (перпендикулярно плоскости

туда, откуда поворот первого сомножителя
ко второму на наименьший угол происходит
против хода часовой стрелки), либо по
правилу
Н.Е.Жуковского.

Правило Жуковского для определения направления кориолисова ускорения.

Для определения
направления ускорения Кориолиса надо:

1) выбрать плоскость,
перпендикулярную к оси переносного
вращения;

2) спроектировать
вектор относительной скорости на
выбранную плоскость;

3) повернуть
полученную проекцию на угол 90
по направлению
переносного вращения.

Полученное
направление и будет направлением
кориолисова ускорения. В этом направлении
следует отложить вычисленный ранее по
формуле (13) модуль ускорения.

В
некоторых практических задачах
применение правила Жуковского упрощается:
вектор относительной скорости точки
сразу расположен в плоскости,
перпендикулярной к оси переносного
вращения. Тогда для определения
направления ускорения Кориолиса надо
просто повернуть вектор относительной
скорости на угол 90
по направлению
переносного вращения.
Примеры.

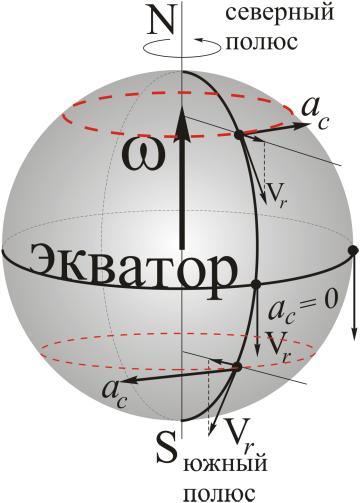
Более
сложный пример: движение точки по
поверхности Земли с севера на юг вдоль
меридиана.

В
северном полушарии кориолисово ускорение
точки будет направлено к востоку. В
момент пересечения точкой экватора
ускорение Кориолиса обратится в нуль
(вектор относительной скорости параллелен
оси вращения Земли). При движении с
севера на юг в южном полушарии кориолисово
ускорение направлено к западу.

Физический
смысл кориолисова ускорения:
согласно равенству (9) ускорение Кориолиса
состоит из двух слагаемых.

Первое
слагаемое определяет изменение
относительной скорости за счёт
переносного движения точки.
Действительно

Второе
слагаемое определяет изменение
переносной скорости за счёт относительного
движения точки.

Согласно
равенству (10) абсолютное ускорение
точки в общем случае равно сумме трёх
ускорений. Поэтому для определения
модуля абсолютного ускорения следует
использовать общий приём: выбрать
какую-либо систему координат,
спроектировать формулу (10) на эти оси
и найти проекции абсолютного ускорения

1515* MERGEFORMAT ()

Тогда
модуль ускорения будет равен

1616* MERGEFORMAT ()

Рассмотрим
примеры.

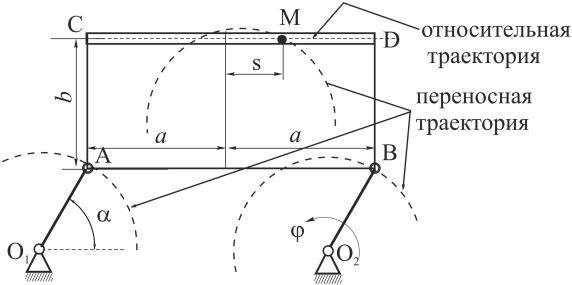
Пример
1.
Прямоугольная пластина прикреплена
шарнирами в точках А и В к двум одинаковым
кривошипам длины r
= 10 см. Кривошипы вращаются вокруг осей
О₁
и О₂
по закону

рад. По каналу CD пластины движется груз
М по закону

см.

В
момент, когда кривошипы наклонены к
горизонтали на угол 60,
найти абсолютные скорость и ускорение
груза.

Решение.
Относительное
движение груза
– движение по пластинке. Относительная
траектория – прямая CD.

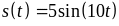
– это закон относительного движения
(относительное движение задано
естественным способом: траектория,
начало отсчёта, положительное направление
и закон движения по траектории).

Переносное
движение –
движение вместе с пластиной. Пластина
движется поступательно, т.к. кривошипы
одинаковы. Следовательно, переносное
движение – поступательное. Переносные
траектории – окружности радиуса r.

Абсолютное
движение – движение груза относительно
неподвижной плоскости, связанной с
основаниями кривошипов. Абсолютные
траектории – сложные кривые.

Примеры
абсолютных траекторий.

Так
как переносное движение поступательное
(
),
то, выбирая в качестве полюса «о» точку
В, будем искать абсолютные скорость и
ускорение согласно равенствам

Относительная
скорость

Относительное
ускорение

Легко
установить, что, когда кривошипы
составляют с горизонталью угол

,
момент времени t будет равен

.

Тогда
при

получим

см/с.

см/с².

Знаки
показывают, что вектор

направлен от центра О (в сторону
возрастания s), а вектор

– к точке О (модуль относительной
скорости уменьшается).

Так
как переносное движение поступательное,
то переносными скоростью и ускорением
точки М будут скорость и ускорение
точки В пластины. Находим угловую
скорость и угловое ускорение кривошипа
( не путать
с угловыми скоростью и ускорением
пластины – они равны 0!)

Модуль
скорости точки В

см/с.

Модуль
ускорения точки В

Модули

не зависят от времени. Так как

,
то кривошипы вращаются против часовой
стрелки (в сторону возрастания угла

В
результате получаем картинки.

С
помощью этих рисунков можем получить

Аналогичные
результаты можно получить, если
воспользоваться «универсальным»
способом. Выберем координатные оси:
ось x – горизонтально вправо; ось y –
вертикально вверх. Тогда

Для
ускорения получим

Пример
2. Круглая
пластина радиуса R = 20 см вращается
вокруг оси О, перпендикулярной плоскости
пластины и расположенной на её краю,
по закону

рад. По краю пластины, начиная от точки
О, движется груз по закону

см.

В
момент времени t = 1 с найти абсолютные
скорость и ускорение груза.

Решение.
Относительное
движение –
движение по краю пластины. Относительная
траектория
– окружность радиуса R с центром в О₁.
s(t)
– это закон относительного движения.
Относительное движение задано, таким
образом, естественным способом.

Переносное
движение –
это вращение вместе с пластиной по
закону

,
т.е. переносное движение вращательное.
Переносные траектории – окружности с
центрами в точке О.

Абсолютное
движение – движение относительно
неподвижной плоскости, связанной с
основанием шарнира О. Абсолютные
траектории – сложные кривые, зависящие
от законов движения s и .
Рассмотрим ряд примеров абсолютного
движения для заданных в условии задачи
законов, а также для

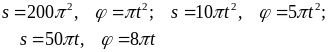
Находим
положение груза на пластине при t = 1 с:
s(1) = 10
см, что составляет четверть длины
окружности пластины (2R
= 40
см). Положение можно также установить,
вычислив центральный угол: 
= s(1)/R = /2
рад.

Следовательно,
при t = 1 с переносной траекторией груза
будет окружность с центром в О и радиуса

см.

Находим
относительную скорость: т.к. относительное
движение задано естественным способом,
то

см//с.

Для
определения переносной скорости найдём
угловую скорость пластины (переносную
угловую скорость)

Тогда

см/с.

Изображаем
векторы

и
,согласно равенству

,
– вектор абсолютной скорости. Из рисунка
следует

Через
проекции на оси O₁xy
:

Тогда

Определяем
относительное ускорение:

Находим
переносное ускорение точки: угловое
ускорение пластины равно

Тогда

Определяем
модуль кориолисова ускорения

Изображаем
направления всех векторов на рисунке:

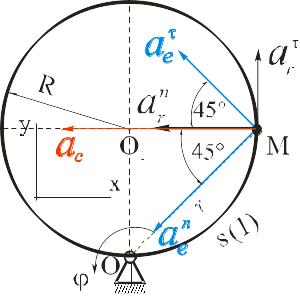
Согласно
формуле

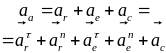
находим
абсолютное ускорение груза: вычисляем
проекции вектора на оси координат

Тогда

см/с² .

КОНЕЦ

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Ускорение и сила Кориолиса – что это?

Опубликовано 19 Фев 2014
Рубрика: Механика | 2 комментария

Гаспар-Гюстав де Кориолис на фоне спиральной галактики Из этой статьи вы не узнаете ничего нового о крутых правых берегах рек северного полушария, о направлениях вращения атмосферных циклонов и антициклонов, о пассатах и о закручивании воды в сливном отверстии ванны или раковины. Эта статья расскажет вам об…

…истоках понятий «ускорение Кориолиса» и «сила Кориолиса».

Прежде чем начать отвечать на вопрос заголовка статьи я хочу напомнить несколько определений. Для упрощения понимания при изучении сложных движений тел в теоретической механике были введены понятия относительного движения и переносного, а так же присущих им скоростей и ускорений.

Относительное движение характеризуется относительной траекторией, относительной скоростью v_отн и относительным ускорением a_отн и представляет собой движение материальной точки относительно подвижной системы координат.

Переносное движение, характеризующееся переносной траекторией, переносной скоростью v_пер и переносным ускорением a_пер, представляет собой движение подвижной системы координат вместе со всеми жестко связанными с ней точками пространства по отношению к неподвижной (абсолютной) системе координат.

Абсолютное движение, характеризующееся абсолютной траекторией, абсолютной скоростью v и абсолютным ускорением a, это — движение точки относительно неподвижной системы координат.

Далее в тексте статьи для отличия векторных величин от абсолютных значений приняты следующие обозначения:

a^— — вектор

a — абсолютное значение (модуль)

Приношу извинения за отступление от использования общепринятых символов в обозначении векторов.

Основные формулы сложного движения материальной точки в векторной форме:

v^—= v_отн^—+ v_пер^—

a^—= a_отн^—+ a_пер^—+ a_кор^—

Если со скоростью все понятно и логично, то с ускорением все не так очевидно. Что это за третий вектор a_кор^—? Откуда он взялся? Именно ему – третьему слагаемому векторного уравнения ускорения материальной точки при сложном движении – ускорению Кориолиса — и посвящена эта статья.

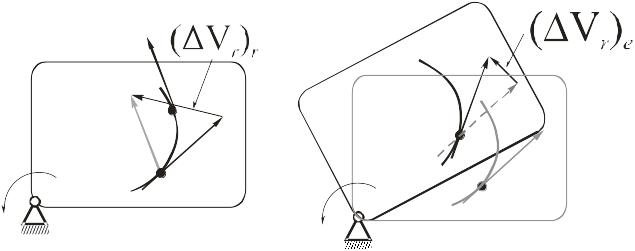
Если относительное ускорение является параметром изменения относительной скорости в относительном движении материальной точки, переносное ускорение – параметром изменения переносной скорости в переносном движении, то ускорение Кориолиса характеризует изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении. Непонятно? Разберемся, как обычно, на примере!

Как возникает ускорение Кориолиса

1. На рисунке, расположенном ниже, изображен механизм, состоящий из кулисы, вращающейся с постоянной угловой скоростью ω_первокруг точки O и ползун, перемещающийся по кулисе с постоянной линейной скоростью v_отн. Следовательно, угловое ускорение кулисы и связанной с ней подвижной системы координат (ось x) ε_перравно нулю. Так же равно нулю и линейное ускорение точки C ползуна a_отн относительно кулисы (подвижной системы координат – оси х).

ω_пер= const ε_пер= 0

v_отн= const a_отн= 0

2. Как можно догадаться по аббревиатурам – относительное движение в нашем примере – это прямолинейное движение ползуна — точки C — по кулисе, а переносное движение – это вращение ползуна вместе кулисой вокруг центра – точки О. Ось x₀ – ось неподвижной системы координат.

3. То, что ускорения ε_пер= 0 и a_отн= 0 выбрано в примере не случайно. Это облегчит и упростит восприятие и понимание сути и природы возникновения кориолисова ускорения и рождаемой этим ускорением – силы Кориолиса.

Ускорение Кориолиса и сила Кориолиса - схема возникновения

4. При переносном движении (вращении кулисы) вектор относительной линейной скорости v_отн1^— повернется за малый промежуток времени dt на весьма незначительный угол dφ и получит при этом приращение (изменение) в виде вектора dv_отн^—_.

dφ = ω_пер* dt

dv_отн^—= v_отн2^—— v_отн1^—

dv_отн= v_отн* dφ = v_отн* ω_пер* dt

5. Вектор относительной скорости точки C v_отн2^—в положении №2 сохранил свой размер и направление относительно подвижной системы координат – оси x. Но в абсолютном пространстве этот вектор повернулся за счет переносного движения на угол dφ и переместился за счет относительного движения на расстояние dS!

6. При стремящемся к нулю угле поворота dφ вектор изменения относительной скорости dv_отн^— будет перпендикулярен вектору относительной скорости v_отн2^—.

7. Изменение скорости может быть вызвано только наличием ненулевого ускорения, которое и приобретет точка С. Направление вектора этого ускорения a₁^— совпадает с направлением вектора изменения относительной скорости dv_отн^—.

a₁= dv_отн/ dt = v_отн* ω_пер

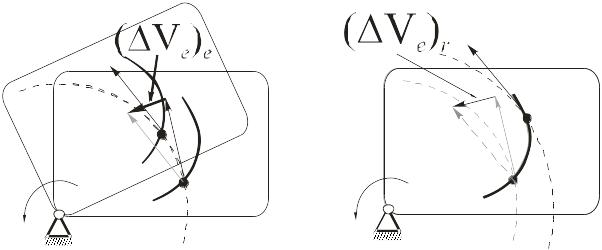
8. При относительном движении (прямолинейном перемещении точки C ползуна по кулисе) вектор переносной линейной скорости v_пер^— за незначительный промежуток времени dt переместится на расстояние dS и получит приращение (изменение) — вектор dv_пер^—_.

dS = v_отн* dt

dv_пер^—= v_пер2^—— v_пер1^—— dv^ц_пер^—

dv_пер= ω_пер* dS = ω_пер* v_отн* dt

9. Вектор переносной скорости точки C v_пер2^—в положении №2 увеличил свой размер и сохранил направление относительно подвижной системы координат – оси x. В неподвижной системе координат (ось x₀) этот вектор повернулся за счет переносного движения на угол dφ и переместился на расстояние dS благодаря переносному движению!

10. По аналогии с относительной скоростью дополнительное изменение переносной скорости может быть вызвано только наличием ненулевого ускорения, которое приобретет точка С в этом движении. Направление вектора этого ускорения a₂^— совпадает с направлением вектора изменения переносной скорости dv_пер^—.

a₂= dv_пер/ dt = ω_пер* v_отн

11. Появление вектора изменения переносной скорости dv^ц_пер^—вызвано переносным движением (вращением)! На точку C действует переносное ускорение a_пер – в нашем случае центростремительное, вектор которого направлен к центру вращения точке O.

a_пер2= ω_пер²* S₂

В нашем примере это ускорение действует и в начальный момент времени (в положении №1), его значение равно:

a_пер1= ω_пер²* S₁

12. Векторы a₁^—и a₂^— имеют одинаковое направление! На рисунке это визуально не совсем так по причине невозможности начертить понятную схему при близком к нулю угле поворота dφ. Чтобы найти полное добавочное ускорение точки C, которое она получила из-за изменения вектора относительной скорости v_отн1^—в переносном движении и вектора переносной скорости v_пер1^— в относительном движении необходимо сложить векторы a₁^—и a₂^—. Это и есть ускорение Кориолиса точки C.

a_кор^—= a₁^—+ a₂^—

a_кор= a₁+ a₂= 2 * ω_пер* v_отн

13. Основные зависимости скорости и ускорения точки C в неподвижной системе координат в векторной и абсолютной формах для нашего примера выглядят так:

v^—= v_отн^—+ v_пер^—

v = (v_отн²+ ω_пер²* S²)^0,5

a^—= a_пер^—+ a_кор^—

a = (ω_пер⁴* S²+ a_кор²)^0,5= (ω_пер⁴* S²+ 4 * ω_пер²* v_отн²)^0,5

Итоги и выводы

Ускорение Кориолиса возникает при сложном движении точки только при одновременном выполнении трех независимых условий:

1. Переносное движение должно быть вращательным. То есть угловая скорость переносного движения должна быть не равна нулю.

2. Направление относительного движения не должно быть параллельно оси переносного вращения.

3. Относительное движение должно быть поступательным. То есть линейная скорость относительного движения не должна быть равна нулю.

Для определения направления вектора ускорения Кориолиса необходимо повернуть вектор линейной относительной скорости на 90° в сторону переносного вращения.

Если точка обладает массой, то согласно второму закону Ньютона кориолисово ускорение совместно с массой создадут силу инерции, направленную в сторону противоположную вектору ускорения. Это и есть сила Кориолиса!

Именно сила Кориолиса, действуя на некотором плече, создает момент, который называется гироскопическим моментом!

О гироскопических явлениях можно прочитать в целом ряде других статей этого блога.

В этой статье мне, как всегда, хотелось кратко и доходчиво рассказать о весьма непростых понятиях – об ускорении и силе Кориолиса. Удалось это или нет с интересом прочту в Ваших комментариях, уважаемые читатели!

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Источник

Макеты страниц

Вычисление и построение ускорения Кориолиса

Для определения величины и направления кориолисова ускорения прежде всего следует вычислить и направить относительную скорость . Далее строится вектор переносной угловой скорости и переносится параллельно себе в точку М. После этого остается воспользоваться правилом векторной алгебры для определения векторного произведения.

Ускорение направлено перпендикулярно плоскости, в которой лежат векторы и , в ту сторону, из которой кратчайший поворот от вектора к вектору виден происходящим против часовой стрелки (рис. 114).

Рис. 113.

Модуль ускорения Кориолиса определяется по формуле

где – угол между векторами и .

Ускорение Кориолиса равно нулю в следующих случаях.

1. Когда один из векторных сомножителей равен нулю ( или ).

2. Когда векторы и коллинеарны. В этом случае угол равен либо 0 (рис. 115, а), либо 180° (рис. 115,5), поэтому , а вместе с ним и , равны нулю.

3. Когда переносное движение является поступательным. В этом случае движение подвижных осей не имеет вращательной составляющей, поэтому переносная угловая скорость равна нулю в любой момент времени: . В любой момент времени будет равно нулю и кориолисово ускорение, и теорема сложения ускорений при поступательном переносном движении принимает такой же вид, как и теорема сложения скоростей:

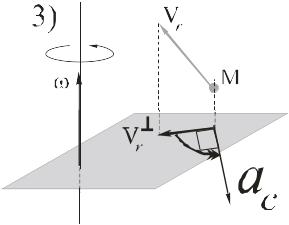
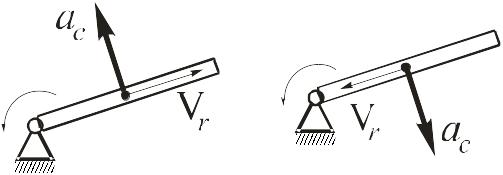
Так обстоит дело, например, при сложном движении точки М, показанном на рис. 116. Переносным движением является движение стержня АВ (спарника), которое при условии является поступательным. Ускорение Кориолиса в данном случае отсутствует.

Рис. 114

Рис. 115

Рис. 116.

Пример.

Жесткая рамка в виде прямоугольного треугольника ОАВ вращается вокруг неподвижной оси с угловой скоростью (рис. 117). По гипотенузе ОВ движется точка М согласно уравнению . Найти абсолютную скорость и абсолютное ускорение точки момент времени .

Рис. 117.

Точка М совершает сложное движение- одновременно движется относительно рамки (подвижная система координат) и окружающих неподвижных предметов (неподвижная система координат). Переносным движением является вращательное движение рамки, относительным – прямолинейное движение точки М вдоль прямой ОВ. Пусть М – положение точки в текущий момент в расчетный момент .

Переносная скорость точки М найдется как линейная скорость точки М рамки, совпадающей в данный момент с движущейся точкой М. (При определении переносной скорости можно пользоваться следующим приемом: мысленно остановить относительное движение и найти скорость в оставшемся движении). Так как рамка вращается, переносную скорость вычисляем по формуле

Подставляя данные из условия задачи, находим:

Примем, что в расчетный момент плоскость рамки совпадает с плоскостью рисунка. Тогда вектор будет направлен перпендикулярно к плоскости рисунка “от нас”.

Величину относительной скорости находим, дифференцируя закон относительного движения