Векторы — это наборы чисел, расположенные горизонтально (вектор-строка) или вертикально (вектор-столбец).
здесь i — номер компоненты вектора.
Упражнение 6.1.1. Сложить два вектора:
Иллюстрация к примеру – рис. 14.
Рис. 14. Иллюстрация к упражнению 6.1.1.
Задача 6.1.1 . Умножить вектор на число.
Умножение вектор-столбца на вектор-строку.
В блоке (вектор-столбце) А2:А5 записаны числа: 1,2,3,4. Требуется получить в блоке B2:D5 три вектор-столбца, каждый из которых представляет собой результат умножения исходного вектор-столбца на вектор-строку: 2, -3, 4 (B1:D1). Рис.15. К упр. 6.1.2.
1-й способ: записать в ячейку В2 формулу =$А2*В$1 и скопировать ее в остальные ячейки диапазона B2:D5.
2 -й способ (более экономный): выделить блок B2:D5. Запишем в него формулу массива <=А2:А5*B1:D1>.
Анализ решения. Табличный массив <2;-3;4>- вектор-строка, а блок А2:А5 – вектор-столбец. Значит, матрица B2:D5 размерностью 4Х3 является результатом умножения вектор-столбца А2:А5 (4Х1) на вектор-строку B1:D1 (1Х3).
Примечание. Если ввести формулу <=B1:D1* А2:А5>, то получится тот же результат, хотя с позиций матричной алгебры вектор-строку (1х3) нельзя умножать на вектор-столбец (4х1) из-за несогласованности размеров (число столбцов в первом сомножителе должно равняться числу строк во втором сомножителе).
У
пражнение 6.1.3. Вычислить скалярное произведение двух векторов.
Примечание. Тот же результат можно получить с помощью обычной функции: =СУММПРОИЗВ (А5:А12, В5:В12).
Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы.
Упражнение 6.2.1. Сложение матриц.
Задание. Сложить матрицы М и N, где
Решение.
M= и N=
Примечание. Выделен блок, имеющий те же размеры, что и исходные матрицы.
Упражнение 6.2.2 . Вычислить линейную комбинацию матриц 2*М – N (матрицы М.и N из упражнения 6.2.1.).
Решение. В блок А7:С8 ввести табличную формулу <= 2*М – N >.
Задача 6.2.1. Осмысленные результаты (не имеющие ничего общего с матричной алгеброй) получаются при сложении матриц разных размеров. Придумать примеры и попытаться выявить правила, по которым Excel выполняет такое сложение.
Для матричных операций в Excel предусмотрены функции, входящие в категорию “Математические”:
Примечание. Первая из этих функций возвращает число, поэтому вводится как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы.
Упражнение 6.2.3. Вычислить определитель и обратную матрицу для матрицы:
Решение. Разместить исходную матрицу в блоке А1 :СЗ.
Рис. 16. Иллюстрация к упражнению 6.2.3.
У
Решение:
пражнение 6.2.4. Вычислить абсолютные отклонения величин в матрицах.
В блок А9:С11 ввести табличную формулу <= abs (A-AО)>.
Пример вычисления определителя матрицы
А, введенной в формулу как массив констант: =МОПРЕД(<-73; 78; 24:
Задача 6.2.2 . При каком значении элемента а33 определитель матрицы А обратится в нуль.
Задача 6.2.3. Дана матрица S = . Вычислить матрицу 2SS Т – Е, где Т — операция транспонирования,
Е — единичная матрица.
Задача 6.2.4. Вычислить обратную матрицу для
и применить форматирование, чтобы элементы матрицы представляли собой правильные дроби. Выбрать формат на основе величины определителя матрицы.
Набор матричных операций в Excel беден.
Если нужно серьезно работать с матрицами, лучше прибегнуть к помощи таких математических пакетов, как MatLAB (Matrix LABoratory), Mathematica, Derive .
Вычисление длины (модуля) вектора в EXCEL
history 14 декабря 2015 г.
-
Группы статей
- Пользовательский формат
- Векторы
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 .
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
2. Нахождение длины вектора через координаты точек
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
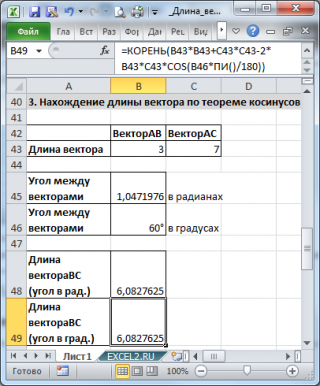
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 – угол между ними в радианах (в долях числа ПИ() ).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL
4. Нахождение длины вектора через координаты точек треугольника
Пусть заданы 3 точки треугольника, образованного векторами.
Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) .
Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).
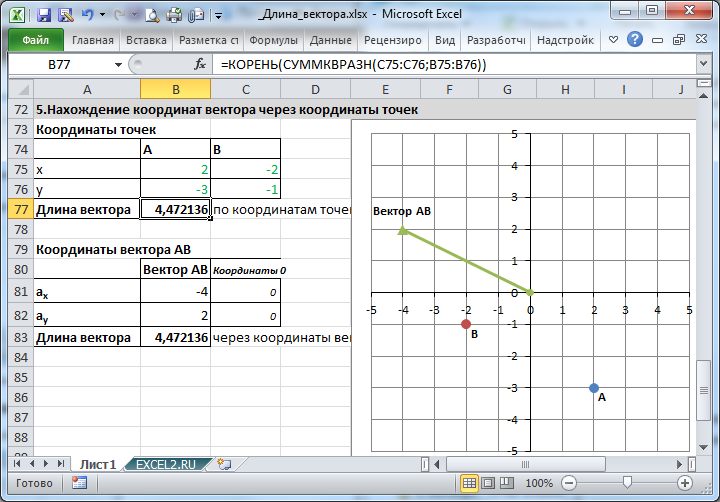
5. Нахождение координат вектора через координаты точек
Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.
Векторы и матрицы в Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Векторы и матрицы в Excel
C овокупность n чисел , заданных в определенном порядке, называется n -мерным вектором. Числа a i – компонент s или координат s вектора, n —размерностью вектора.
Два n -мерных вектора и называются равными, если все их соответствующие компоненты равны: .
Суммой двух n -мерных векторов и называется n -мерный вектор
.
Операция сложения векторов обладает свойствами коммутативности и ассоциативности .
Вектор , все компоненты которого равны нулю, называется нуль-вектором. Нуль-вектор ведет себя при сложения векторов аналогично числу нуль в арифметике.
Вектор называется противоположным вектору . Очевидно,
Операция вычитания векторов определяется как сложение с противоположным вектором .
Под произведением вектора на число понимают вектор .
Умножение вектора на число обладает свойством ассоциативности и свойством дистрибутивности относительно векторного и числового сомножителей .
Модуль (норма, длина) вектора .
Пример вычисления модуля вектора (2, 5, 3, -4) приведен на рисунке 1.
Р
исунок 1 – Вычисление длины вектора
Здесь применены функция = КОРЕНЬ ( число ), где аргументом функции может быть либо конкретное число, либо адрес ячейки, в которой оно записано, и функция = СУММКВ ( число1 ; число2 ;…), где аргументами функции являются адреса ячеек (адрес массива) с координатами вектора.
В общем случае скалярное произведение двух векторов , где – угол между векторами. Скалярным произведение двух n -мерных векторов и может быть определено как сумма произведений одноименных координат данных векторов:
.
Операция скалярного умножения векторов обладает следующими свойствами:
.
В Excel скалярное произведение векторов вычисляется с помощью функции = СУММПРОИЗВ ( массив1 ; массив2;… ), где массив1 ; массив2;…- от 2 до 30 массивов, чьи компонент нужно перемножить, а затем сложить полученные произведения. Все массивы должны иметь одну и то же размерность (пример на рисунке 2).
Векторным произведением вектора на вектор называется вектор , длина которого численно равна площади параллелограмма построенного на векторах и , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от к вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора (рисунок 3).
Треугольник, стороны которого есть стороны параллелограмма и его диагонали имеет площадь, равную половине величины векторного произв
едения двух векторов.
Р
исунок 2 – Определение скалярного произведения двух векторов
Значение векторного произведения определяется следующим образом:
На рисунке 4 приведен пример вычисления векторного произведения векторов, площади параллелограмма, треугольника. Проверка правильности вычисления векторного произведения заключается в проверке соответствия нулю величины скалярных произведений векторов и
Р
исунок 4 – Вычисление векторного произведения векторов
Перейдем к рассмотрению основных операций матричного исчисления.
Числа, расположенные в виде прямоугольной таблицы, состоящей из m строк и n столбцов, образуют матрицу размера m х n :
Две матрицы A и B одного и того же размера m × n являются равными, если равны все их соответствующие элементы:
Матрица, состоящая из одного столбца (т. е. если n = 1) или из од- ной строки (т. е. если m = 1), называется вектором — столбцом или, соответственно, вектором — строкой.
Матрица называется нулевой, если все ее элементы равны нулю. Нулевая матрица обозначается
При n = m матрица называется квадратной, а число ее строк (столбцов) – порядком матрицы. Элементы квадратной матрицы образуют ее главную диагональ.
Квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю:
Квадратная матрица называется единичной, если все элементы ее главной диагонали равны единице, а остальные — нулю:
Если в матрице А заменить строки столбцами, сохранив их порядок, то получится новая матрица
называемая транспонированной по отношению к матрице А.
Если А=А Т , то такая матрица называется симметричной.
В Excel для транспонирования матриц используется функция =ТРАНСП(массив) – рисунок 5.
Р
исунок 5 – Вызов функции ТРАНСП
Пример. Имеем исходную матрицу
.
Из определения ясно, что транспонированной будет матрица А Т :
.
Решение задачи в Excel представлено на рисунке 6
Рисунок 6 – Транспонирование матрицы
Порядок решения следующий:
– определить место для транспонированной матриц (в рассматриваемом примере это G2:I4);
– в ячейку размещения первого элемента транспонированной матрицы ввести формулу =ТРАНС(С2:E5);
– выделить массив ячеек, в которых будут размещаться все элементы транспонированной матрицы;
– нажать Shit + Ctrl + Enter .
Суммой матриц А и В одинакового размера является матрица С , элементы которой равны сумме соответствующих элементов суммируемых матриц:
Произведение матрицы на число – то матрица, элементы которой получаются умножением всех элементов исходной матрицы на данное число:
Умножение матрицы на матрицу определяется только при условии, что число столбцов первого сомножителя А равно числу строк второго сомножителя В . Под произведением матрицы размером m x k на матрицу размером k x n понимают матрицу размером m x n , элемент которой равен скалярному произведению i -й строки матрицы на j -й столбец матрицы :
В Excel для вычисления произведения матриц используется функция
= МУМНОЖ ( массив1 ; массив2 ), где массивы – совокупности элементов перемножаемых матриц (рисунок 7).
Р
исунок 7 – Умножение матриц
Формула для расчета произведения матриц должна быть введена как формула массива!
Пусть даны матрицы
Вычислим их произведение в Excel (рисунок 8).
– шаг1 – определение области размещения результата (на рисунке 8 выделена пункитом);
– шаг 2 – ввод в начальную ячейку результирующего массива формулы умножения матриц;
–
шаг 3 – выделить результирующий массив и нажать F2;
–
шаг 3 – нажать Shift+Ctrl+Enter.
Рисунок 8 – Вычисление произведения матриц
Действие умножения матрицы на матрицу обладает свойствами:
Отметим, что в общем случае
Если условие равенства произведения матриц при изменении их последовательности выполняется, то матрицы называются перестановочными между собой.
При умножении квадратной матрицы саму на себя получаем квадратную матрицу второй степени, при n -кратном умножении получим квадратную матрицу n -го порядка ( n -й степени).
Определитель (или детерминант) матрицы – одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы, – определитель равен нулю.
Для матрицы первого порядка значение определителя равно единственному элементу этой матрицы.
Для матрицы 2х2 определитель вычисляется как
Для матриц более высоких порядков n x n определитель можно вычислить, применив следующую рекурсивную формулу:
, где – дополнительный минор к элементу .
Возможно разложение как по строкам, так и по столбцам.
В
Excel определитель вычисляется с помощью функции = МОПРЕД ( массив ), где массив есть совокупность элементов матрицы (рисунок 9).
Рисунок 9 – Расчет определителя матрицы
Квадратная матрица называется неособенной ( невырожденной ), если ее определитель не равен нулю. В противном случае она называется особенной ( вырожденной ) или сингулярной .
Детерминант треугольной матрицы равен произведению ее диагональных элементов
Обратной матрицей к матрице называют такую матрицу, для которой
А А -1 = E
Обратную матрицу можно найти по следующей формуле:
, где – определитель матрицы, – транспонированная матрица.
Н
а рисунке 10 приведен пример определения обратной матрицы с помощью функции Excel = МОБР ( массив ).
Рисунок 10 – Расчет обратной матрицы
Заметим, что функция применяется к массиву как в ранее приведенных примерах.
Проверим выполнение условия А А -1 = E (рисунок 11)
Р
исунок 11- Произведение матрицы на обратную матрицу
Собственным числом квадратной матрицы
называется такое число , которое обращает определитель матрицы в 0: .
Или, по-другому, собственными числами матрицы А являются корни уравнения и только они.
Матрица называется характеристической матрицей матрицы А , многочлен называется характеристическим многочленом матрицы А , уравнение называется характеристическим уравнением матрицы А.
Для вычисления собственных чисел существуют классические приемы, сводящиеся к решению полиномиальных уравнений. Собственные числа определяют системы компьютерной математики. Найдем все собственные числа произвольной квадратной матрицы с помощью Excel на примере квадратной матрицы размерностью 3х3:
Необходимо найти такие значения , при котором
Оформим лист Excel следующим образом (рисунок 12):
Рисунок 12 – Вычисление собственного числа матрицы
В ячейку B2 введено =2-F2; в ячейку С3 – =-6-F2; в ячейку D4 – =1-F2.
Из рисунка 12 видно, что при =0 определитель также равен 0, т.е. =0 есть первое собственное число матрицы.
Д
ля определения других собственных числе воспользуемся поиском (Меню Сервис-Поск решения …) – рисунок 13, установив целевую ячейку $E$2, в которой вычисляется значение определителя матрицы. Требуемое значение определителя – 0. Поиск осуществляется путем подбора значения , отображаемом в ячейке $F$2.
Рисунок 13 – Вычисление собственного числа матрицы
О щелчку на кнопке Выполнить, появляется окно Результат поиска решения (рисунок 14).
Рисунок 14 – Результат поиска решения
Выбираем Сохранить найденное решение и Тип отчета – Результаты . Щелкаем на Ок. Получаем ожидаемый результат =0.
П
овторим выполненные действия, введя в окне Поиск решения ограничение $F$2>=1 (рисунок 15):
Рисунок 15 – Ввод ограничения
В результате поиска получаем второе значение собственного числа: =3.
Повторим поиск при ограничении.
Если установить в ограничениях >=4, то поиск не находит решения. Ищем отрицательное собственное число и устанавливаем в ограничениях
П
ри добавлении в систему ограничений Е1>=-10 (рисунок 16) поиск нашел третье собственное число, равное -6 (рисунок 17)
Р
исунок 16 – Поиск собственного числа при двухстороннем ограничении
Рисунок 17 – Результат поиска третьего собственного числа
Собственным вектором соответствующим собственному числу λ называют такой вектор , который удовлетворяет матричному равенству:
Найдем собственный вектор матрицы
Данная матрица имеет собственные числа: λ1 = 0 λ2 = 3 λ3 = -6.
1. Заносим содержимое ячеек матрицы в ячейки таблицы (B2:D4).
2. В ячейку (B6) вводим λ для которого необходимо найти собственный вектор. Пусть λ = 3.
3. В ячейки (F2:F4) поместим любые числа: F2 = 1; F3 = 1; F4 = 1.
4. В ячейки (G2:G4) заносим произведение матрицы (ячейки В2:В4) на вектор (ячейки F2:F4).
5. В ячейки (H2:H4) заносим умножение столбца на собственное число λ находящийся в ячейки (B6).
6. В ячейки (I2:I4) заносим разность столбцов (F2:F4) и (H2:H4).
7. В главном меню открываем Сервис – Поиск решения . Вводим следующие данные: Целевая ячейка $I$2, Равной значению (0); Изменяя ячейки $F$2:$F$4; Ограничения $I$3=0; $I$4=0.
Нажать кнопку « Выполнить ».
В
ячейках (F2:F4) появятся числа, эти это и есть собственный вектор для данного собственного числа (рисунок 18).
Рисунок 18 – Определение собственного вектора матрицы
Последовательно выполнить операции п.п. 2, 3, 7 при остальных значениях собственных чисел матрицы.
Задания для самостоятельной работы
Повторить решение всех примеров, приведенных в Лекции №5.
Сформировать случайным образом два вектора, состоящих из 5 элементов. Элементы векторов должны быть в диапазоне -5…+15
Определить длину векторов.
Вычислить сумму и разность векторов.
Определить скалярное произведение этих векторов.
Определить угол между векторами.
Определить векторное произведение двух векторов.
Проверить правильность вычисления векторного произведения путем определения скалярного произведения каждого из исходных векторов с результатом вычисления векторного произведения.
Сформировать случайным образом матрицу размером 4х4 и матрицу 4х3. Элементы матрицы должны быть в диапазоне -10…+20.
Получить транспонированные матрицы исходных матриц.
Проверить правильность решения путем умножения исходной матрицы на транспонированную.
Определить произведение исходных матриц.
Найти матрицу 3-го порядка для исходной квадратной матрицы.
Определить детерминант исходной квадратной матрицы.
[spoiler title=”источники:”]
http://excel2.ru/articles/vychislenie-dliny-modulya-vektora-v-ms-excel
http://infourok.ru/vektori-i-matrici-v-ecel-1119397.html
[/spoiler]
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор
– это направленный отрезок прямой.
Длина этого отрезка определяет числовое значение вектора и называется
длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a
x
и a
y
, то длину вектора можно найти по формуле
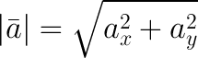
В случае вектора в пространстве добавляется третья координата
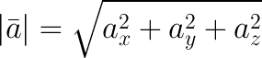
В MS EXCEL выражение
=КОРЕНЬ(СУММКВ(B8:B9))
позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки
B8:B9
, см.
файл примера
).
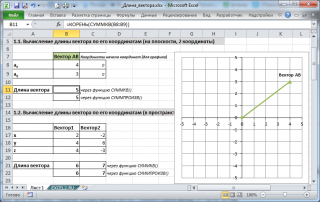
Функция
СУММКВ()
возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =
B8*B8+B9*B9
.
В
файле примера
также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение
=КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9))
.
2. Нахождение длины вектора через координаты точек
Если вектор
задан через координаты точек его начала и конца, то формула будет другой
=КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны
C28:C29
и
B28:B29
соответственно.
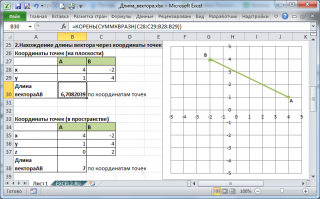
Функция
СУММКВРАЗН()
в
озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
![]()
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу
=КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках
B43:B43
содержатся длины векторов а и b, а в ячейке
В45
– угол между ними в радианах (в долях числа
ПИ()
).
Если угол задан в градусах, то формула будет немного отличаться
=КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание
: для наглядности в ячейке со значением угла в градусах можно применить
пользовательский формат
, см. например, статью
Отображение широты и долготы в MS EXCEL
4. Нахождение длины вектора через координаты точек треугольника
Пусть заданы 3 точки треугольника, образованного векторами.
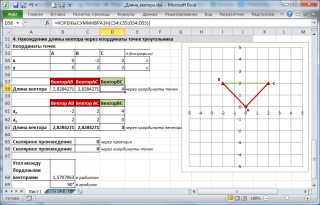
Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле
=КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55))
.
Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).
5. Нахождение координат вектора через координаты точек
Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.
Министерство
образования и науки Российской Федерации
Саратовский
государственный технический университет
имени Гагарина Ю.А.
Методические
указания и задания для студентов
Саратов
2012
Введение
Методические
указания представлены в виде набора
практических и лабораторных работ для
развития навыков моделирования и
реализации решения инженерных задач.
Задачи сопровождаются инструкциями
выполнения. Предлагаемые упражнения и
задания помогут усвоить технику
использования MS Excel и найти эффективные
способы решения практических задач.
Основные понятия Массивы
Массив
данных – это совокупность однотипных
элементов. Тип элементов в MS Excel
определяется с помощью Формат Ячейки.
В MS Excel можно работать с одномерными
и двумерными массивами.
Одномерные
массивы (векторы), состоят из элементов
строк или столбцов, например, B2:B5, C9:G9
(рис. 1).

Рис. 1
Двумерные
массивы (матрицы) состоят из элементов,
располагающихся в прямоугольном
диапазоне, например, A2:C3,
B8:C12 (рис.
2).
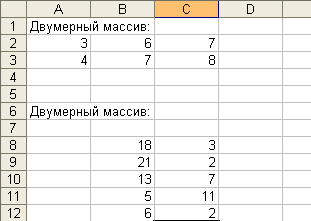
Рис. 2
Формулы массивов
Формулы
массивов используются для того, чтобы
производить вычисления над несколькими
значениями (массивом значений), не
производя копирования и заполнения.
П
ример.
Выполним сложение и вычитание двух
векторов А=(а1,а2,…аn)
и B=(b1,b2,…bn),
где n = 4, например, (рис.
3).
Рис. 3
Инструкция
для сложения элементов двух векторов
(рис. 3):
-
Выделить
диапазон (строка) D3:G3,
где будет результат сложения; -
Ввести
знак равенства в строку формул; -
Выделить
первый массив D1:G1; -
Вставить
знак «плюс»; -
Выделить
второй массив D2:G2; -
Нажать
комбинацию клавиш Ctrl+Shift+Enter. -
Просмотреть
содержимое ячеек полученного вектора.
В каждой ячейке будет отображена одна
и та же формула
{=D1:G1+
D2:G2}.
Инструкция
для вычитания элементов двух векторов
(рис. 3):
-
Выделить диапазон (строка) D4:G4.
-
Ввести
знак равенства. -
Выделить
первый массив D1:G1. -
Вставить
знак «минус». -
Выделить
второй массив D2:G2. -
Нажать
комбинацию клавиш Ctrl+Shift+Enter. -
Просмотреть
содержимое ячеек полученного вектора.
В каждой ячейке будет отображена одна
и та же формула
{=D1:G1-
D2:G2}.
Изменить
содержимое ячеек полученных строк
(векторов) невозможно. Нельзя вставить
столбец в вектор. При таких попытках
будет выдано сообщение, что нельзя
изменить часть массива.
Если
при выполнении пункта 6 инструкций,
нажать на клавиатуре клавишу Enter вместо
клавиш Ctrl+Shift+Enter, то в этом случае формула
вычислит только одно, первое значение
вектора. Перейти в режим редактирования
нужно нажатием клавиши F2. Затем
одновременно нажать Ctrl+Shift+Enter.
Ошибки в формулах
При
наборе формул могут быть допущены
ошибки, например:
Набраны
две арифметические операции подряд,
пропущен оператор, например, (рис. 4 а)
вод формулы =(A1+A2-/A4), при наборе допущена
элементарная ошибка или пропущен адрес
ячейки или ошибочно введены подряд две
арифметические операции вычитания и
деления (рис. 4 б–4 г).
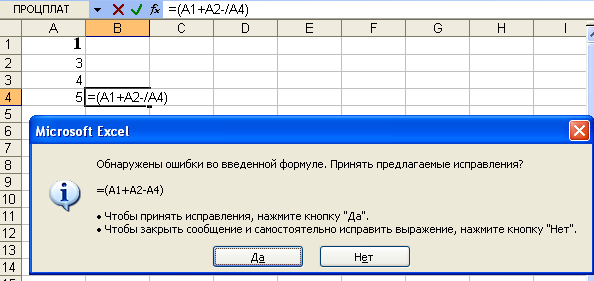
Рис. 4 а
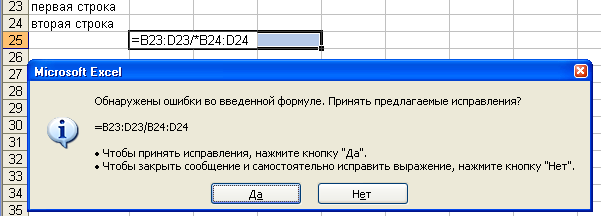
Рис. 4 б
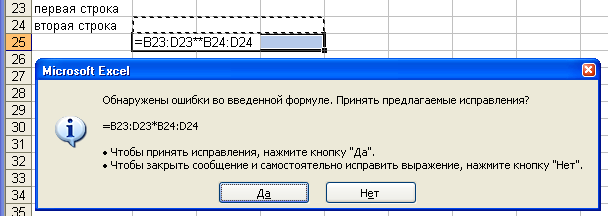
Рис. 4 в
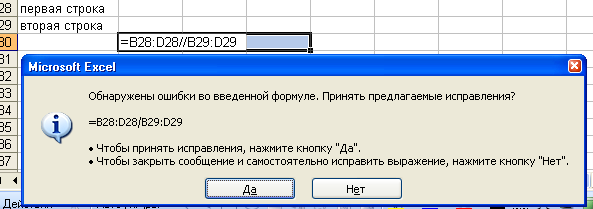
Рис. 4 г
Если
при выполнении сложения элементов двух
строк, ошибочно введены в формулу два
знака арифметических операций подряд,
сначала «+», а затем «–», то не будет
ошибки, выполнится операция вычитания
(рис. 5).
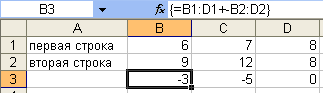
Рис. 5
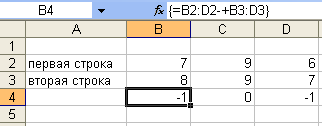
Рис. 6
Если
при выполнении сложения элементов двух
строк, ошибочно введены в формулу два
знака арифметических операций подряд,
сначала «–», а затем «+», то не будет
ошибки, опять выполнится операция
вычитания (рис. 6).
Пробел
между вектором А1:D1 и
В2:D2 означает пересечение
диапазонов (рис. 7). Пересечения ячеек
#ПУСТО!
Точка
с запятой – это объединение диапазонов
(рис. 8). В формуле ошибка.
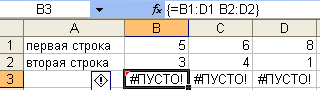
Рис. 7
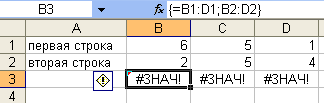
Рис. 8
Могут
возникать ошибки в формулах при попытках
деления на 0

Рис. 9
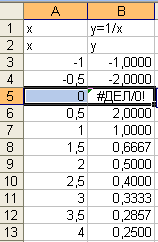
Рис. 10
Ошибки
могут быть связаны с неопределенными
именами ячеек, использованных в формулах:
ошибка #ИМЯ? – не распознается имя,
используемое в формуле (рис. 11–12).
Имя адреса ячейки qod не
было присвоено;
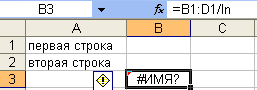
Рис. 11
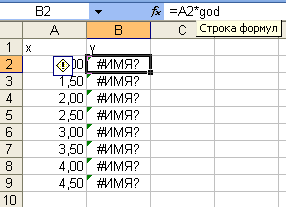
Рис. 12
Ошибка
#ЗНАЧ! – используются операторы или
аргументы недопустимого типа (рис. 13).
В ячейке B12 возникла ошибка
#ЗНАЧ! В этом случае это значит, что
складываются содержимое ячеек А12 и А13
разного типа. A13 определено
как тип дата, а A12 – как
число.
Ошибка
#Н/Д возникла в C6
неопределенных данных, т.е. не определены
значения ячеек A6 и B6
(рис. 14).
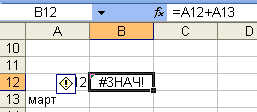
Рис.13
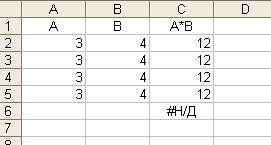
Рис. 14
В этом
примере ошибка #ПУСТО! возникает при
пересечении двух диапазонов, которые
в действительности не имеют общих ячеек
(рис. 15).

Рис. 15
Ошибка
#ЧИСЛО! На рис. 16, 17 возникает при вычислении
натурального логарифма от нуля, что
невозможно.
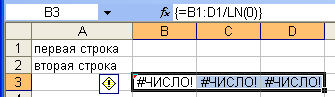
Рис. 16
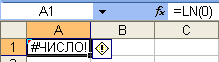
Рис. 17
Такого
рода ошибка, как на рис. 18, происходит
при «переполнении», когда числовое
значение вычисляемой формулы слишком
велико или слишком мало для используемого
формата.
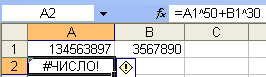
Рис. 18
Ошибка
#ССЫЛКА! – неправильная ссылка на
ячейку. В ячейке В8 (рис. 19) вычислена
сумма элементов массива A1:B7.
При попытке скопировать содержимое
ячейки В8 в ячейку С1 и произошла ошибка.
При копировании часто возникает ошибка
#ССЫЛКА.
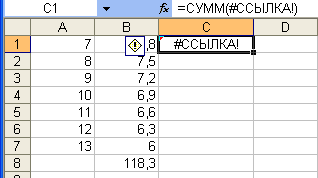
Рис.19
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Автор:
Laura McKinney
Дата создания:
1 Апрель 2021
Дата обновления:
11 Май 2023
Содержание
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6

Microsoft Excel – одна из самых мощных программ для работы с электронными таблицами на рынке, которая полезна для самых разных задач, от финансового анализа до научных проектов. Однако большинство людей думают, что Excel ограничивает манипуляции с сетками формул, то есть функциональность традиционной электронной таблицы. Однако сценарии Visual Basic в Excel упрощают это, даже более того. С помощью Visual Basic вы можете нарисовать любую фигуру в электронной таблице и использовать ее для создания рисунков, диаграмм и другой графики, помогающей визуализировать электронную таблицу.
Шаг 1
Откройте Microsoft Excel. Если у вас Excel 2007 или новее, перейдите на вкладку «Просмотр» на ленте и нажмите «Макросы», в противном случае нажмите меню «Инструменты» и выберите «Макросы». Появится диалоговое окно макроса.
Шаг 2
Введите имя макроса и нажмите «Создать». Это должно открыть редактор приложения Visual Basic с новой пустой подпрограммой, отображаемой на экране.
Шаг 3
Определите координаты «X» и «Y», которые вы хотите использовать для начала и конца вашего вектора. Левый верхний угол рабочего листа находится в позиции (0, 0), а «X» и «Y» будут увеличиваться при перемещении вправо и вниз соответственно. Поместите эти значения в переменные, например:
start_x = 0 start_y = 0 end_x = 100 end_y = 100
Эти значения будут рисовать диагональную линию в верхнем левом углу рабочего листа. Возможно, вам придется поэкспериментировать с разными числами, чтобы получить линию именно там, где вы хотите.
Шаг 4
Добавьте код для рисования самой линии:
line = Sheet1.Shapes.AddLine (начало_x, начало_y, конец_x, конец_y)
Шаг 5
Введите код, чтобы добавить стрелку в конец строки, чтобы она выглядела как вектор:
line.Line.EndArrowheadStyle = MsoArrowheadStyle.msoArrowheadTriangle
Закройте редактор Visual Basic и откройте диалоговое окно макроса (см. Шаг 1). Щелкните макрос и нажмите «Выполнить». Вы должны увидеть свою линию.
Используйте функцию ПРОСМОТР, одну из функций поиска и работы со ссылками, когда нужно взять одну строку или столбец и найти значение, находящееся в той же позиции в другой строке или столбце.
Предположим, что вы знаете артикул детали автомобиля, но не знаете ее цену. Тогда, используя функцию ПРОСМОТР, вы сможете вернуть значение цены в ячейку H2 при вводе артикула в ячейку H1.

Используйте функцию ПРОСМОТР для поиска в одной строке или одном столбце. В приведенном выше примере рассматривается поиск цен в столбце D.
Советы: Рассмотрим одну из новых функций подстановки в зависимости от используемой версии.
-
Используйте функцию ВПР для поиска данных в одной строке или столбце, а также для поиска в нескольких строках и столбцах (например, в таблице). Это расширенная версия функции ПРОСМОТР. Посмотрите видеоролик о том, как использовать функцию ВПР.
-
Если вы используете Microsoft 365, используйте функцию XLOOKUP — это не только быстрее, но и в любом направлении (вверх, вниз, влево, вправо).
Функцию ПРОСМОТР можно использовать двумя способами: в векторной форме и в форме массива.
-
Векторная форма: используйте эту форму LOOKUP для поиска значения в одной строке или в одном столбце. Используйте векторную форму, если нужно указать диапазон, содержащий значения, которые необходимо сопоставить. Например, если вы хотите найти значение в столбце A, вниз до строки 6.
-
Форма массива. Мы настоятельно рекомендуем использовать ВПР или ГПР вместо формы массива. Посмотрите это видео об использовании ВПР. Форма массива предоставляется для совместимости с другими программами электронной таблицы, но ее функциональные возможности ограничены.
Массив — это набор значений в строках и столбцах (например, в таблице), в которых выполняется поиск. Например, если вам нужно найти значение в первых шести строках столбцов A и B, это и будет поиском с использованием массива. Функция ПРОСМОТР вернет наиболее близкое значение. Чтобы использовать форму массива, сначала необходимо отсортировать данные.
Векторная форма
При использовании векторной формы функции ПРОСМОТР выполняется поиск значения в пределах только одной строки или одного столбца (так называемый вектор) и возврат значения из той же позиции второго диапазона.
Синтаксис
ПРОСМОТР(искомое_значение; просматриваемый_вектор; [вектор_результатов])
Функция ПРОСМОТР в векторной форме имеет аргументы, указанные ниже.
-
Искомое_значение. Обязательный аргумент. Значение, которое функция ПРОСМОТР ищет в первом векторе. Искомое_значение может быть числом, текстом, логическим значением, именем или ссылкой на значение.
-
Просматриваемый_вектор Обязательный аргумент. Диапазон, состоящий из одной строки или одного столбца. Значения в аргументе просматриваемый_вектор могут быть текстом, числами или логическими значениями.
Важно: Значения в аргументе просматриваемый_вектор должны быть расположены в порядке возрастания: …, -2, -1, 0, 1, 2, …, A-Z, ЛОЖЬ, ИСТИНА; в противном случае функция ПРОСМОТР может возвратить неправильный результат. Текст в нижнем и верхнем регистрах считается эквивалентным.
-
result_vector Необязательный. Диапазон, содержащий только одну строку или столбец. Размер result_vector должен совпадать с размером lookup_vector. Он должен иметь одинаковый размер.
Замечания
-
Если функции ПРОСМОТР не удается найти искомое_значение, то в просматриваемом_векторе выбирается наибольшее значение, которое меньше искомого_значения или равно ему.
-
Если искомое_значение меньше, чем наименьшее значение в аргументе просматриваемый_вектор, функция ПРОСМОТР возвращает значение ошибки #Н/Д.
Примеры векторов
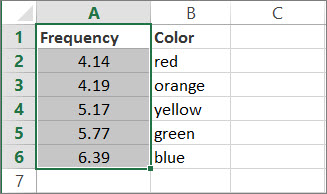
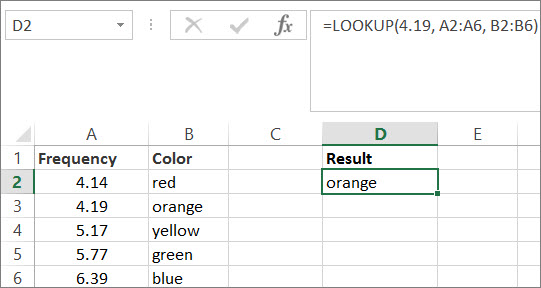
Чтобы лучше разобраться в работе функции ПРОСМОТР, вы можете сами опробовать рассмотренные примеры на практике. В первом примере у вас должна получиться электронная таблица, которая выглядит примерно так:
-
Скопируйте данные из таблицы ниже и вставьте их в новый лист Excel.
Скопируйте эти данные в столбец A
Скопируйте эти данные в столбец B
Частота
4,14
Цвет
красный
4,19
оранжевый
5,17
желтый
5,77
зеленый
6,39
синий
-
Теперь скопируйте формулы ПРОСМОТРА из приведенной ниже таблицы в столбец D своего листа.
Скопируйте эту формулу в столбец D
Ниже описано, что эта формула означает
Предполагаемый результат
Формула
=ПРОСМОТР(4,19; A2:A6; B2:B6)
Поиск значения 4,19 в столбце A и возврат значения из столбца B, находящегося в той же строке.
оранжевый
=ПРОСМОТР(5,75; A2:A6; B2:B6)
Поиск значения 5,75 в столбце A, соответствующего ближайшему наименьшему значению (5,17), и возврат значения из столбца B, находящегося в той же строке.
желтый
=ПРОСМОТР(7,66; A2:A6; B2:B6)
Поиск значения 7,66 в столбце A, соответствующего ближайшему наименьшему значению (6,39), и возврат значения из столбца B, находящегося в той же строке.
синий
=ПРОСМОТР(0; A2:A6; B2:B6)
Поиск значения 0 в столбце A и возврат значения ошибки, так как 0 меньше наименьшего значения (4,14) в столбце A.
#Н/Д
-
Чтобы эти формулы выводили результат, может потребоваться выделить их на листе Excel и нажать клавишу F2, а затем — ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Форма массива
Совет: Мы настоятельно рекомендуем использовать ВПР или ГПР вместо формы массива. См. это видео о функции ВПР. В нем приведены примеры. Форма поиска массива предоставляется для обеспечения совместимости с другими программами электронной таблицы, но ее функциональные возможности ограничены.
Форма массива функции ПРОСМОТР просматривает первую строку или первый столбец массив, находит указанное значение и возвращает значение из аналогичной позиции последней строки или столбца массива. Эта форма функции ПРОСМОТР используется, если сравниваемые значения находятся в первой строке или первом столбце массива.
Синтаксис
ПРОСМОТР(искомое_значение, массив)
Функция ПРОСМОТР в форме массива имеет аргументы, указанные ниже.
-
Искомое_значение. Обязательный аргумент. Значение, которое функция ПРОСМОТР ищет в массиве. Аргумент искомое_значение может быть числом, текстом, логическим значением, именем или ссылкой на значение.
-
Если функции ПРОСМОТР не удается найти искомое_значение, то в массиве выбирается наибольшее значение, которое меньше искомого_значения или равно ему.
-
Если искомое_значение меньше, чем наименьшее значение в первой строке или первом столбце (в зависимости от размерности массива), то функция ПРОСМОТР возвращает значение ошибки #Н/Д.
-
-
массив. Обязательный аргумент. Диапазон ячеек, содержащих текст, числа или логические значения, которые требуется сравнить с искомым значением.
Форма массива функции ПРОСМОТР очень похожа на функции ГПР и ВПР. Различие заключается в том, что функция ГПР ищет искомое_значение в первой строке, функция ВПР — в первом столбце, а функция ПРОСМОТР выполняет поиск в соответствии с размерностями массива.
-
Если ширина массива больше его высоты (т. е. есть массив имеет больше столбцов чем строк), то функция ПРОСМОТР ищет искомое_значение в первой строке.
-
Если высота массива больше его ширины (т. е. массив имеет больше строк, чем столбцов), то функция ПРОСМОТР выполняет поиск в первом столбце.
-
Используя функции ГПР и ВПР, можно указывать индекс по направлению вниз и вправо, а функция ПРОСМОТР всегда выбирает последнее значение в строке или столбце.
Важно: Значения в массиве должны быть расположены в порядке возрастания: …, -2, -1, 0, 1, 2, …, A-Z, ЛОЖЬ, ИСТИНА; в противном случае функция ПРОСМОТР может возвратить неправильный результат. Текст в нижнем и верхнем регистрах считается эквивалентным.
-
