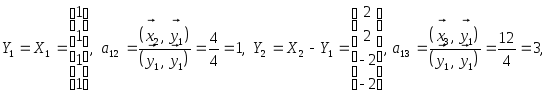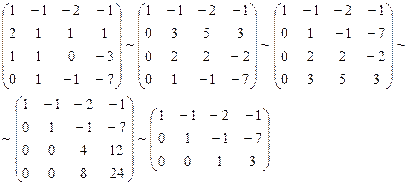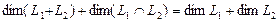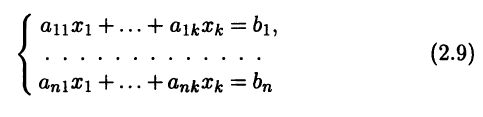Как найти вектор в линейной оболочке векторов - Сайт, где вы сможете решить свои вопросы

Определение
1.
Линейной
оболочкой
заданной
конечной совокупности

элементов векторного пространства
ⁿ
над полем К называется множество всех
линейных комбинаций этих элементов с
коэффициентами из поля К. При этом сама
совокупность

называется порождающей
системой
данной линейной оболочки, а сама линейная
оболочка обозначается символом
.

Линейные оболочки
обладают следующими свойствами:

.
Линейная оболочка элементов векторного
пространства
ⁿ
является подпространством М векторного
пространства
ⁿ.

Данный
результат следует из определения
линейной оболочки: сумма
двух векторов из линейной оболочки
будет принадлежать линейной оболочки
(одна из линейных комбинаций), произведение
вектора из линейной оболочки также
будет принадлежать линейной оболочки.

.
Линейная оболочка может совпадать со
всем пространством Rⁿ
(если образующая
система является базисом
в пространстве Rⁿ
)

.
Линейная оболочка

является наименьшим подпространством,
содержащим элементы
.
Все остальные подпространства могут
только содержать вектора порождающей
системы или их возможные комбинации.

.
Если какой-нибудь элемент из порождающей
системы элементов

есть линейная комбинация остальных
элементов этой системы, то его можно
удалить из порождающей системы, не
изменив при этом линейной оболочки.

.
Если координатная матрица системы
образующих

имеет ранг р, где
,
то любая линейно независимая система
,
является базисом линейной оболочки
,
а сама линейная оболочка будет
подпространством размерности р,
.

Примеры.

Если
a,
b,
с – геометрические векторы, лежащие
на одной прямой. В этом случае линейная
оболочка L(а,b,c)=
L(a).Здесь
линейная оболочка является одномерным
пространством, которое состоит из всех
вектор, лежащих на прямой, причем вектор
а
–является базисом.
Пусть
a,
b,
с – геометрические векторы, причем a,
b
не коллинеарны, с = а + b.
В этом случае линейная оболочка L(а,b,c)=
L(a,b).Здесь
линейная оболочка является двумерным
пространством, состоящем из всех
векторов, компланарных с векторами a
и b.
Вектора а,b
составляют базис в L(a,b).
Любой вектор из L
представляется в виде линейной комбинации
векторов а
и b.

Вообще,
в конечномерном пространстве R
всякое подпространство L

является линейной
оболочкой некоторой системы векторов.

Рассмотри
следующую задачу.
В евклидовом пространстве Eⁿ
задана линейная оболочка
,
где k

n.
Требуется:

1)Найти
размерность и базис линейной оболочки
;
2)Выделить в линейной оболочке

ортогональный базис и

достроить
его до
ортонормированного базиса евклидова

пространства
Eⁿ.

Если
схема решения первой задачи нам знакома,
то решение второй задачи строится на
следующем теоретическом результате.

Теорема
(Грама
– Шмидта)

Пусть

– система линейно независимых векторов
в евклидовом пространстве, где k

n,
являющихся образующей системой линейной
оболочки
.
Система векторов
,
описываемая формулами

,
. . .

где
коэффициенты

,
,

образует
ортогональный
базис
линейной оболочки
.

Доказательство.
Для
доказательства теоремы достаточно
доказать следующее утверждение: вектор

ортогонален вектору
.

Действительно,
умножая скалярно вектор

на вектор
,
получим

==0

Следствие.
Результат теоремы дает
алгоритм последовательной ортогонализации
системы линейно независимых элементов
( так
называемый
метод Грама – Шмидта).

Пример

В
евклидовом пространстве E⁴
линейная оболочка

задана образующей системой векторов

с координатами

Требуется:

а)
найти размерность и базис линейной
оболочки

б)
указать в линейной оболочке

ортонормированный базис

и
достроить его до ортонормированного
базиса евклидова

пространства
E⁴.

Решение.
Рассмотрим координатную матрицу
.
Так как

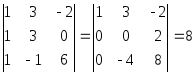
то
,
элементы

линейно независимы в E⁴
и образуют базис данной линейной
оболочки, являющейся подпространством
в E⁴.

Для
построения ортонормированного базиса
в E⁴
применим метод
ортогонализации
Грама-Шмидта. Получим

,

.

Записывая векторы
столбцами их координат, последовательно
найдем

Легко
проверить, что полученные элементы

попарно ортогональны. Найдем ортогональный
им вектор
.

Пусть
,
то неизвестные координаты

вектора Y₄
найдутся из условий

,,.

Так
как
,
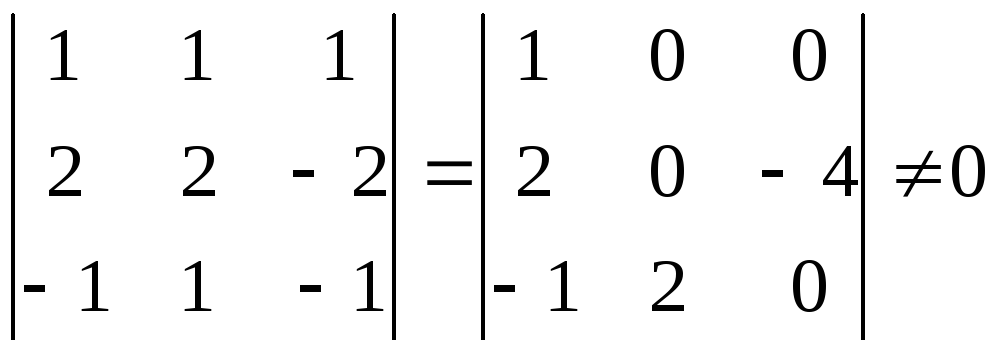
в последней системе неизвестные

можно взять в качестве базисных
неизвестных.

Если
для свободной (небазисной) неизвестной
,
то
.

Нормировав
найденные векторы
,
построим ортонормированный базис в E⁴:

Задача
решена.

В
завершении параграфа введем важное
определение.

Пусть

– – базис в Eⁿ
и векторы

представлены в этом базисе своими
разложениями

Тогда
скалярное произведение этих векторов
имеет вид

или в матричной форме
,
где

– столбцы координат векторов

в базисе

а симметричная матрица

составлена из скалярных произведений
базисных векторов:

В
общем случае в качестве элементов
матрицы А рассматривают скалярные
произведения произвольной системы
векторов а₁,
а₂,…,
а_n

Определение
3.
Определитель
матрицы А
скалярных произведений заданной системы
векторов
называют определителем
Грама.

Теорема
Произвольная
система
векторов,
заданных в ортонормированном
базисе,
будет линейно
независимой,
если ее определитель
Грама отличен от нуля.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 – 2 1 – 1 1 2 – 2 A = 3 – 2 1 2 1 2 3 – 1 – 2 = 3 · 1 · ( – 2 ) + ( – 2 ) · 2 · 3 + 1 · 2 · ( – 1 ) – 1 · 1 · 3 – ( – 2 ) · 2 · ( – 2 ) – 3 · 2 · ( – 1 ) = = – 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , – 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , – 1 , – 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 – 1 1 0 1 – 2 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 – 2 – 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , – 1 , – 2 ) a ( 2 ) = ( 0 , 2 , 1 , – 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства – e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n – некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 – x 1 ) · e ( 1 ) + ( x

2 – x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 – x 2 ) , . . . , ( x

n – x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , – 1 , 1 ) e ( 2 ) = ( 3 , 2 , – 5 ) e ( 3 ) = ( 2 , 1 , – 3 ) x = ( 6 , 2 , – 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 – 1 1 3 2 – 5 2 1 – 3

1 – 1 1 0 5 – 8 0 3 – 5

1 – 1 1 0 5 – 8 0 0 – 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 – 1 2 1 1 – 5 – 3 = – 1 ∆ x

1 = 6 3 2 2 2 1 – 7 – 5 – 3 = – 1 , x

1 ∆ = – 1 – 1 = 1 ∆ x

2 = 1 6 2 – 1 2 1 1 – 7 – 3 = – 1 , x

2 ∆ = – 1 – 1 = 1 ∆ x

3 = 1 3 6 – 1 2 2 1 – 5 – 7 = – 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) – координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

Линейные оболочки и подпространства

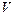
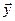
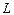
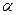
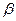
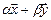
Определение. Подпространством линейного пространства называется множество векторов из такое, что для любых двух векторови из и любых двух вещественных чисел и линейная комбинация также принадлежит .

Утверждение. Подпространство само является линейным пространством.

Определение. Линейной оболочкой системы векторов называется множество всех линейных комбинаций векторов . Обозначается .

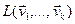
Утверждение. Линейная оболочка системы векторов является подпространством.

Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .

Определение. Суммой двух подпространств и называется множество всех векторов , представимых в виде , где , . Обозначается .

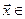
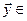
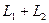
Утверждение. Сумма и пересечение подпространств и являются линейными пространствами, и их размерности связаны равенством

+ = + .

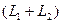
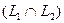
Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.

Примеры

1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами .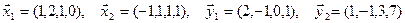

Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства , порождённого векторами , равенство нулю линейной комбинации , эквивалентное системе уравнений , достигается лишь при условии . Следовательно, векторы линейно

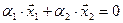
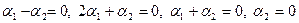
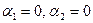
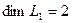
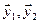
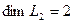
независимы и размерность подпространства равна 2: . Для подпространства , порождённого векторами , проводя аналогичный анализ, получим .

Вычислим теперь размерность пересечения подпространств и . По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор подпространства является линейной комбинацией базисных векторов : . Аналогично для подпространства имеем , тогда условие принадлежности пересечению есть или .

Это условие представляет собой систему уравнений относительно коэффициентов . Составим матрицу системы и упростим её с помощью элементарных преобразований:

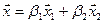
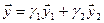
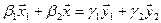
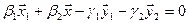
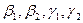
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим ,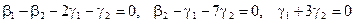

откуда .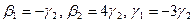

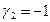
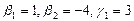
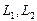
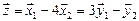
Полагая свободное неизвестное , для остальных имеем

. Итак, пересечение подпространств имеет один базисный вектор

Размерность пересечения 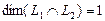. Следовательно, в соответствии с равенством

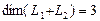
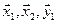
размерность суммы подпространств . В качестве базиса суммы подпространств можно взять, например, векторы , дополненные вектором . В линейной независимости векторов убедиться нетрудно.

Задачи

3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами , , , , .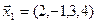

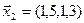
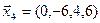
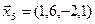
3.40. Найти размерность и какой-либо базис линейной оболочки векторов , , , , .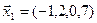

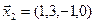
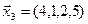
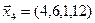
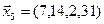
3.41. Является ли подпространством в указанном пространстве множество

а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;

б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;

в) сходящихся к числу последовательностей в пространстве сходящихся последовательностей;

г) диагональных матриц в пространстве квадратных матриц того же порядка;

д) невырожденных матриц в пространстве симметричных матриц того же порядка;

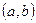
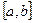
е) дифференцируемых на интервале функций в пространстве функций, непрерывных на отрезке .

3.42. Почему не является подпространством в указанном пространстве множество

а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;

б) векторов из пространства R n , координаты которых удовлетворяют уравнению ;

в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;

г) вырожденных матриц в пространстве квадратных матриц того же порядка;

д) монотонно возрастающих и ограниченных на множестве 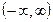функций в пространстве функций, ограниченных на том же множестве.

3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:

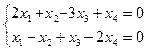
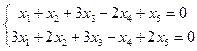
а) ; б) ;

в) .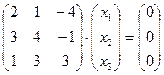

3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:

а) все n-мерные векторы, координаты которых удовлетворяют уравнению ;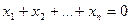

б) все n-мерные векторы, у которых первая координата равна нулю;

в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;

г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;

д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.

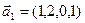
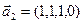
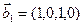
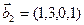
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами , и , . Является ли эта сумма прямой суммой?

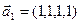
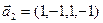
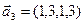
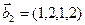
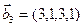
3.46. Найти размерность суммы и пересечения линейных оболочек векторов , , и , , . Является ли их cумма прямой?

3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами и , если

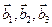
а) , , , , , ;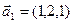

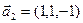
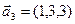
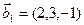
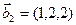
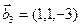
б) , , , , , .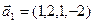

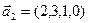
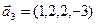
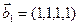
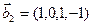
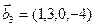
3.48. Найти базис суммы и пересечения линейных оболочек и , если

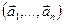
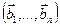
а) , , , ;

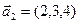
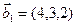
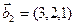
б) , , , , , .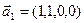

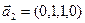
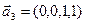
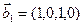
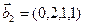
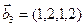
Является ли прямой сумма этих подпространств?

[spoiler title=”источники:”]

http://lektsii.org/10-6017.html

[/spoiler]

Источник

Пусть L – n-мерное линейное пространство, в котором фиксирован некоторый базис е = (e₁ … е_n) и выбраны векторы a₁, …, a_k, b. Запишем разложение выбранных векторов по базису е:

a_j = ea_j, j = 1,k, b = eb,

где a_j = (a_1j … a_nj)^T , j = 1,k, b = (b₁ … b_n)^T – столбцы координат соответствующих векторов
. Пусть А – матрица типа n × k, составленная из координатных столбцов векторов a₁, …, а_k, а (A|b) – матрица, полученная из матрицы А добавлением справа еще одного столбца b.

Для вектора b возможны два случая:

1) вектор b принадлежит линейной оболочке span{a₁,…, a_k};

2) вектор b не принадлежит span{a₁,…,a_k}.

В первом случае добавление к системе векторов a₁, …, a_k вектора b не приводит к расширению линейной оболочки системы и, следовательно,

dimspan{a₁,… ,а_k} = dimspan{a₁,… ,а_k,b}.

По теореме 2.6 заключаем, что RgA = Rg(A|b).

Во втором случае, наоборот, добавление вектора b к системе векторов a₁, …, а_k приводит к расширению линейной оболочки, причем по теореме 2.5

dimspan{a₁,… ,а_k,b} = dimspan{a₁,… ,а_k} + 1,

так как

span{a₁,…, a_k, b} = span{a₁,…, a_k} ⊕ span{b}.

Следовательно, Rg(A|b) = RgA + 1.

Выясним теперь, что означают эти два случая “на координатном уровне”. В первом случае условие b ∈ span{a₁,… ,a_k} означает существование разложения

х₁а₁ +… + x_ka_k = b (2.8)

с некоторыми действительными коэффициентами x₁, …, x_k.
Записывая это векторное равенство в координатной форме, получаем систему линейных алгебраических уравнений (СЛАУ)

относительно переменных х = (х₁ … x_k)^T, которая в матричной форме имеет вид Ах = b. Существование разложения (2.8) означает, что полученная система имеет решение. Во втором случае представление (2.8) невозможно, т.е. система (2.9) не имеет решений.

Итак, следующие четыре утверждения эквивалентны между собой:

– b ∈ span{a₁,…,a_k};

– dimspan{a₁,… ,а_k,b} = dimspan{a₁,…,а_k};

– Rg(A|b) = RgA;

– система Ах = b из n линейных алгебраических уравнений относительно k неизвестных совместна.

Эквивалентность последних двух утверждений составляет содержание теоремы Кронекера – Капелли [III], которая верна для произвольных СЛАУ. Отметим, что любая система из п ли-нейных алгебраических уравнений относительно к неизвестных может быть получена как результат проведенных рассуждений. Для этого достаточно в качестве векторов a₁, …, a_k рассмотреть столбцы коэффициентов при неизвестных, а в качестве вектора b – столбец свободных членов. Все эти столбцы могут рассматриваться как n-мерные векторы в линейном арифметическом пространстве Rⁿ.

Таким образом, теорему Кронекера – Капелли можно переформулировать следующим образом: для того чтобы линейная оболочка системы векторов a₁, …, а_k совпадала с линейной оболочкой расширенной системы a₁, …, а_k, b, необходимо и достаточно, чтобы были равны размерности этих линейных оболочек.

Предположим, что квадратная СЛАУ Ах = b имеет решение при любом столбце b правых частей. Рассматривая столбцы матрицы А и столбец b как элементы a₁, …, a_n, b n-мерного линейного арифметического пространства и записывая СЛАУ в векторной форме

x₁a₁ + x₂a₂ + … + x_na_n = b,

заключаем, что линейная оболочка системы векторов a₁, …, а_n совпадает со всем линейным пространством Rⁿ. Из этого следует, что ранг этой системы векторов равен размерности линейного пространства n, а так как в системе ровно n векторов, то она, согласно теореме 2.6, линейно независима. Другими словами, столбцы матрицы А линейно независимы, а матрица А является невырожденной (см. теорему о базисном миноре [III]).

Таким образом, если квадратная СЛАУ Ах = b имеет решение при любой правой части, то матрица А системы невырождег на, а решение системы при любой правой части единственно.

Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ

Источник

Все курсы > Линейная алгебра > Занятие 2

Продолжим работать в том же ноутбуке⧉

Определение

С понятием вектора тесно связано понятие векторного или линейного пространства (vector space, linear space).

По большому счету, векторное пространство — это множество векторов, которые мы можем складывать (vector addition) и умножать на число или скаляр (scalar multiplication).

В частности, сложение и умножение на число двумерных (состоящих из двух компонентов) векторов дает нам двумерный вектор, трехмерных — трехмерный и так далее.

$$ begin{bmatrix} 3 \ 4 end{bmatrix} + 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} = begin{bmatrix} 5 \ 8 end{bmatrix} $$

При этом сложить, например, двумерный и трехмерный вектор нельзя

$$ begin{bmatrix} 3 \ 4 end{bmatrix} + begin{bmatrix} 4 \ 3 \ 3 end{bmatrix} = ? $$

Также нельзя сформировать векторное пространство из двумерных векторов, лежащих только в первой четверти координатной плоскости. Хотя для таких векторов будет задана операция сложения, при умножении на отрицательный скаляр мы можем выйти за пределы первой четверти.

Поэтому говорят, что векторное пространство должно быть замкнуто относительно операций сложения и умножения на скаляр (closed under vector addition and scalar multiplication).

Двумерное пространтсво вещественных чисел принято обозначать $R^2$, трехмерное $R^3$, n-мерное — $R^n$.

Отметим, что вектор $begin{bmatrix} 1 \ 2 \ 0 end{bmatrix}$ — это вектор в $R^3$ с нулевым третьим компонентом.

Линейная комбинация векторов

Любой вектор внутри одного пространства (например, $R^2$) можно представить как линейную комбинацию конечного числа векторов (linear combination of a finite set of vectors).

$$ 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} + 3 cdot begin{bmatrix} 2 \ 1 end{bmatrix} = begin{bmatrix} 8 \ 7 end{bmatrix} $$

Под линейной комбинацией, как вы видите, понимается опять же сложение векторов и их умножение на число.

Аксиомы векторных пространств

Операции в векторных пространствах должны отвечать следующим правилам:

$ mathbf u + (mathbf v + mathbf w) = (mathbf u + mathbf v) + mathbf w $
$ mathbf v + mathbf w = mathbf w + mathbf v $
Существует нулевой вектор $ mathbf 0 Rightarrow mathbf 0 + mathbf v = mathbf v, forall mathbf v $
Для каждого $ mathbf v $ существует $ -mathbf v Rightarrow mathbf v + (-mathbf v) $
$ a(b mathbf v) = (ab) mathbf v $
$ 1 mathbf v = mathbf v $
$ a(mathbf v + mathbf w) = a mathbf v + a mathbf w $
$ (a + b) mathbf v = a mathbf v + b mathbf v $

Этим правилам могут отвечать не только векторы действительных чисел в пространстве $R^n$ (Евклидово пространство), но и, в частности, векторы функций. В этом случае речь идет о функциональных пространствах (function spaces).

Видео про абстрактные векторные пространства⧉.

Примечание. Некоторые понятия, упомянутые в видео выше, в частности, линейные преобразования (linear transformations), ядро матрицы (null space) и собственные векторы и значения (eigenvectors and eigenvalues) будут рассмотрены на более поздних занятиях.

Серия видео про алгебраические структуры⧉.

Внутреннее произведение

Скалярное произведение (dot product) является частным случаем внутреннего произведения (inner product) для евклидового пространства.

Приведем простой пример того, почему скалярное произведение может не подойти для векторов, состоящих, например, из комплексных чисел $mathbb C$. Ранее мы сказали, что скалярное произведение вектора самого на себя есть квадрат длины этого вектора, т.е. $mathbf x^T mathbf x = || mathbf x ||^2 $, и нам бы хотелось, чтобы квадрат длины был положителен.

Для действительных векторов это условие выполняется всегда, так как мы возводим в квадрат каждый компонент (вещественное число) такого вектора. Теперь рассмотрим комплексный вектор

$$ mathbf z = begin{bmatrix} 1 \ i end{bmatrix} in mathbb C^2 $$

По правилам скалярного произведения квадрат его длины был бы равен

$$ mathbf z^T mathbf z = begin{bmatrix} 1 & i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + i cdot i = 1-1 = 0 $$

Для того чтобы квадрат ненулевого вектора не был равен нулю в векторных пространствах комплексных чисел скалярное (а точнее внутреннее) произведение задано как $overline{mathbf z}^T mathbf z$, где $overline{mathbf z}$ является комплексно сопряженным (complex conjugate) к $mathbf z$ вектором. Тогда,

$$ overline{mathbf z}^T mathbf z = begin{bmatrix} 1 & -i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + (-i) cdot i = 1+1 = 2 $$

Векторное подпространство

Определение

Подпространством (subspace) векторного пространства $K$ называется множество $S$ его элементов, само являющееся векторным пространством относительно введенных в $K$ операций сложения и умножения на число.

Другими словами, чтобы $S$ было подпространством $K$ для каждого $mathbf v, mathbf w in S, K$ и $a in mathbb{R}$ должно выполняться ${ mathbf v + mathbf w, a mathbf v } in S, K$.

Например, выше мы сказали, что векторы $R^2$ первой четверти координатной плоскости не могут образовывать векторное пространство, потому что мы не можем задать для них операцию умножения на число, результатом которой был бы вектор только в этой четверти.

При этом, если мы возьмем на пространстве $R^2$ подпространство всех векторов, лежащих на прямой линии и проходящих через начало координат, то такое подпространство будет отвечать аксиомам векторных пространств.

Примечание. $R^1$ нельзя назвать подпространством $R^2$, потому что у векторов $R^1$ только один компонент, а у векторов $R^2$, даже тех, которые лежат на одной линии, их два.

Пересечение подпространств

Если $S$ и $T$ — подпространства, то $S cap T$ тоже подпространство. Возьмем $mathbf v, mathbf w in S, T$. Тогда $mathbf v + mathbf w in S, T$ и $a mathbf v in S,T$, так как $S$ и $T$ отвечают свойствам подпространств.

Ортогональные подпространства

Подпространство $S$ будет ортогонально подпространству $T$, если каждый вектор в $S$ ортогонален каждому вектору в $T$.

$$ forall mathbf v in S perp forall mathbf w in T $$

Ортогональное дополнение

Если внутри некоторого пространства $K$ существует подпространство $S$, и внутри этого же пространства $K$ можно найти другое ортогональное ему подпространство $S^{perp}$, то такое подпространство называется ортогональным дополнением (orthogonal complement) подпространства $S$.

Более формально, пусть $S$ — подпространство $K$. Тогда ортогональным дополнением $S^{perp}$ будет множество всех векторов $mathbf w in K$, для которых скалярное произведение $mathbf w cdot mathbf v = 0$ для любого $mathbf v in S$.

$$ S^{perp} = { mathbf w in K hspace{5pt} | hspace{5pt} mathbf w cdot mathbf v = 0, hspace{5pt} forall mathbf v in S hspace{2pt} } $$

Покажем, что $S^{perp}$ также является подпространством. Возьмем два вектора $mathbf a, mathbf b in S^{perp} $. Для того чтобы $S^{perp}$ было подпространством, нам нужно продемонстрировать замкнутость относительно сложения и умножения на скаляр.

$$ mathbf a + mathbf b underset{mathord{?}}{in} S^{perp} $$

$$ c cdot mathbf a underset{mathord{?}}{in} S^{perp} $$

Начнем со сложения. По определению ортогонального дополнения

$$ mathbf a cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$

$$ mathbf b cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$

Тогда,

$$ (mathbf a + mathbf b) cdot mathbf v = mathbf a cdot mathbf v + mathbf b cdot mathbf v = mathbf 0 + mathbf 0 = mathbf 0 $$

Другими словами, мы показали, что сумма векторов принадлежащих $ S^{perp} $ также ортогонально вектору $mathbf v in S$, а значит принадлежит $ S^{perp} $, $ mathbf a + mathbf b in S^{perp} $. Перейдем к умножению на скаляр.

$$ c cdot mathbf a cdot mathbf v = c cdot ( mathbf a cdot mathbf v) = c cdot mathbf 0 = mathbf 0 $$

Это доказывает, что $ c cdot mathbf a in S^{perp} $.

Таким образом, ортогональное дополнение подпространства само является векторным подпространством.

Отметим, что нулевой вектор всегда принадлежит ортогональному дополнению, поскольку при $c = 0$

$$ c cdot mathbf a = 0 cdot mathbf a = mathbf 0 rightarrow mathbf 0 in S^{perp} $$

Обратите внимание, что нулевой вектор также присутствует в подпространстве $S$, $mathbf 0 in S$.

Более того, $S cap S^{perp} = { mathbf 0 } $. Это легко доказать. Возьмем некоторый вектор $mathbf x$, который одновременно принадлежит $ S $ и $ S^{perp} $, $mathbf x in S, S^{perp}$.

Тогда по определению ортогонального дополнения должно выполняться $mathbf x cdot mathbf x = 0 $. Такому условию отвечает только нулевой вектор.

Линейная независимость векторов

Когда один вектор можно выразить через умножение другого вектора на число говорят, что эти векторы линейно зависимы (linearly dependent). С двумя линейно независимыми (linearly independent) векторами $ mathbf v_1, mathbf v_2 $ такого сделать не получится.

$$ mathbf v_2 neq k mathbf v_1 $$

где k — некоторое число.

Рассмотрим пример трех векторов. Чтобы эти три вектора были линейно независимы, не должно быть возможности выразить третий вектор через линейные комбинации (сложение и умножение на скаляр) первых двух.

$$ mathbf v_3 neq k_1 mathbf v_1 + k_2 mathbf v_2 $$

Если так сделать нельзя, мы попадаем в трехмерное пространство, если можно — останемся на плоскости.

Линейная оболочка

Линейная оболочка (linear span) — это множество всех возможных линейных комбинаций с помощью данного набора векторов.

Если у нас два линейно независимых (двумерных) вектора, то оболочка — $R^2$ (плоскость), если три (трехмерных) вектора, но один из них линейно зависим, то по-прежнему $R^2$.

Оболочка — это ответ на вопрос, какие векторы можно построить с помощью сложения и умножения на скаляр $n$ n-мерных векторов. Линейно зависимый вектор находится внутри оболочки, создаваемой комбинациями других линейно независимых векторов.

Базис пространства

Имея два двумерных линейно независимых вектора (например, $begin{bmatrix} 1 \ 2 end{bmatrix}$ и $begin{bmatrix} 3 \ 1 end{bmatrix}$), мы можем представить любой другой вектор в пространстве $ R^2 $, сложив эти два вектора и умножив их на скаляр. Такие векторы называются базисом пространства (basis of a vector space) $ R^2 $, по сути его координатами.

В целом, базисом называется такое множество линейно независимых векторов внутри векторного пространства, с помощью которых можно выразить любой другой вектор этого пространства.

Базис можно представить как некоторую систему координат, которой пользуются все векторы данного пространства.

Повторим пример с единичными векторами $mathbf i$ и $mathbf j$.

i = np.array([1, 0])

j = np.array([0, 1])

ax = plt.axes()

plt.xlim([–0.07, 3])

plt.ylim([–0.07, 3])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

plt.show()

Приведенный выше базис называется стандартным (standard, natural basis). Это самый «экономный» или удобный способ представить все остальные векторы этого пространства.

При этом выбор такого базиса конечно условен, ничто не мешает мне перейти к другой системе координат, то есть другому базису.

Можно сказать, что координаты вектора имеют смысл только если мы знаем в какой системе координат (каком базисе) они выражены. При этом верно и то, что вектор существует в пространстве вне зависимости от системы координат или базиса.

Смена базиса

Предположим, что у нас есть два вектора исходного стандартного базиса $ mathbf g_1 $ и $ mathbf g_2 $ (на рисунке ниже изображены зеленым цветом). Кроме этого, у нас есть вектор $mathbf r$ (красный). Эти векторы имеют следующие координаты

$$ mathbf g_1 = begin{bmatrix} 1 \ 0 end{bmatrix}, mathbf g_2 = begin{bmatrix} 0 \ 1 end{bmatrix}, mathbf r_g = begin{bmatrix} 3 \ 4 end{bmatrix} $$

Если векторы нового базиса ортогональны (это важно), то мы можем выразить координаты вектора $mathbf r$ в новом базисе. Новым базисом будут следующие векторы $ mathbf b_1 $ и $ mathbf b_2 $ (черные):

$$ mathbf b_1 = begin{bmatrix} 2 \ 1 end{bmatrix}, mathbf b_2 = begin{bmatrix} -2 \ 4 end{bmatrix} $$

Посмотрим на эти векторы на графике.

g1 = np.array([1, 0])

g2 = np.array([0, 1])

r = np.array([3, 4])

b1 = np.array([2, 1])

b2 = np.array([–2, 4])

ax = plt.axes()

plt.xlim([–2.5, 4.5])

plt.ylim([–0.07, 4.5])

plt.grid()

ax.arrow(0, 0, g1[0], g1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, g2[0], g2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’)

ax.arrow(0, 0, b1[0], b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’)

ax.arrow(0, 0, b2[0], b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’)

plt.show()

Убедимся, что векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $ перпендикулярны (ортогональны).

Найдем скалярные и векторные проекции красного вектора $ mathbf r $ на векторы $ mathbf b_1 $ и $ mathbf b_2 $.

scalar_proj_r_on_b1 = np.dot(r, b1) / np.linalg.norm(b1)

vector_proj_r_on_b1 = scalar_proj_r_on_b1 * (b1 / np.linalg.norm(b1))

scalar_proj_r_on_b1.round(1), vector_proj_r_on_b1

scalar_proj_r_on_b2 = np.dot(r, b2) / np.linalg.norm(b2) ** 2

vector_proj_r_on_b2 = scalar_proj_r_on_b2 * b2

scalar_proj_r_on_b2.round(1), vector_proj_r_on_b2

Посмотрим на векторные проекции.

plt.figure(figsize = (6, 6))

ax = plt.axes()

plt.xlim([–2, 4.5])

plt.ylim([–0.07, 4.5])

plt.grid()

ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’)

ax.arrow(0, 0, vector_proj_r_on_b1[0], vector_proj_r_on_b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’)

ax.arrow(0, 0, vector_proj_r_on_b2[0], vector_proj_r_on_b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’)

plt.show()

В сумме векторные проекции должны дать вектор $ mathbf r_g $ в исходном базисе.

vector_proj_r_on_b1 + vector_proj_r_on_b2

В новом же базисе вектор $ mathbf r_b $ можно выразить, как скалярные проекции вектора $ mathbf r $ на векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $.

np.array([scalar_proj_r_on_b1, scalar_proj_r_on_b2]).round(1)

Другими словами,

$$ mathbf r_b approx begin{bmatrix} 4,5 \ 2,2 end{bmatrix} $$

Ортонормированный базис

Если угол между векторами базиса равен 90 градусов, то такой базис называют ортогональным (orthogonal). Если одновременно это единичные (нормализованные) векторы, то такой базис называется ортонормированным (orthonormal).

Ортонормированный базис называют стандартным базисом пространства $R^n$.

$$ forall { mathbf q_1, …, mathbf q_k } in R^n $$

$$ mathbf q_i^T cdot mathbf q_j = begin{cases} 0, i not= j \ 1, i=j end{cases} $$

Хотя векторы базиса не обязательно должны быть ортогональными и иметь единичную норму, во многих случаях это удобно.

Видео про линейную оболочку⧉.

Подведем итог

Мы ввели понятие векторного пространства, подпространства, линейной комбинации векторов, понятия базиса, линейной независимости векторов и линейной оболочки.

Перейдем к изучению матриц и начнем этот путь с рассмотрения линейных преобразований.

Источник

Рассмотрим L – линейное пространство.

– Сколько в L линейно независимых векторов.

– Какой из смысл.

Определение: Линейное пространство L называется N-мерным, а число N – размерностью, если в L существует N линейно независимых векторов, причём любые N+1 векторов линейно зависимы.

Определение: В N-мерном линейном пространстве L любая совокупность(система) N линейно независимых векторов называется базисом.

, – базисные векторы.

Определение: если – базис в , то для любого существуют числа : . Это разложение вектора по базису.

Теорема 8: В данном базисе координаты вектора определены однозначно

Доказательство(от противного): Пусть в базисе два набора чисел для вектора

Так как линейно независимы, то все

Если в L существует любое число линейно независимых векторов, то L называется бесконечномерным линейным пространством.

Примеры базисов:

Базис Вейля

Подпространство и линейная оболочка

Пусть

L – множество

M – подмножество

Кроме того

L – линейное пространство

Тогда M – подпространство в L, если

Рассмотрим систему векторов .

Определение: Линейной оболочкой системы векторов называется множество всевозможных линейных комбинаций этих векторов. То есть: . Очевидно, что и является подпространством.