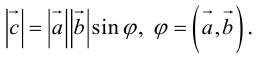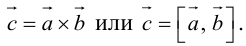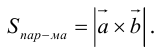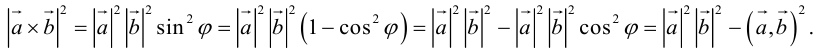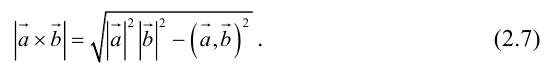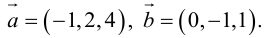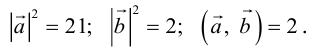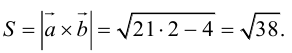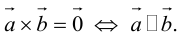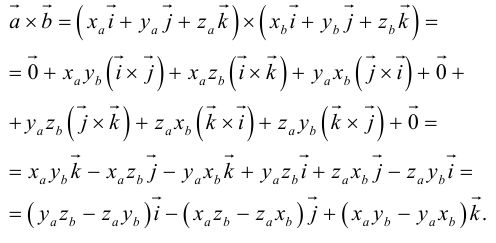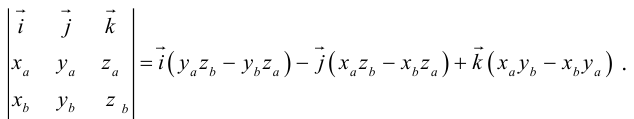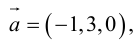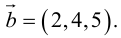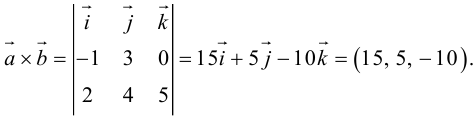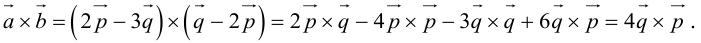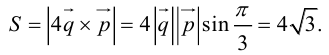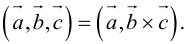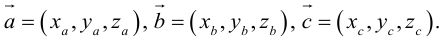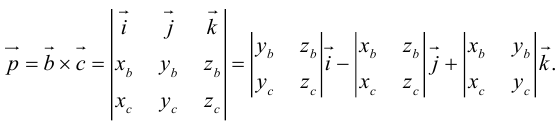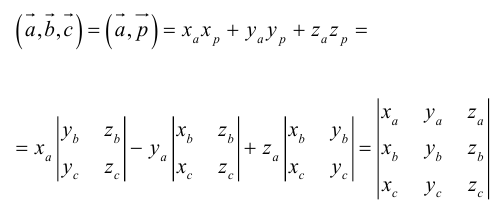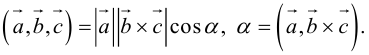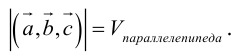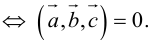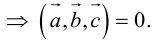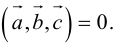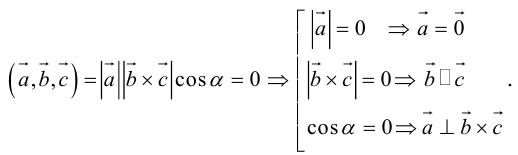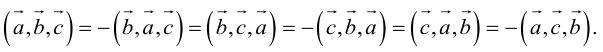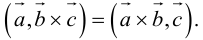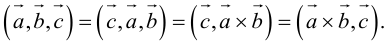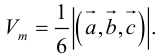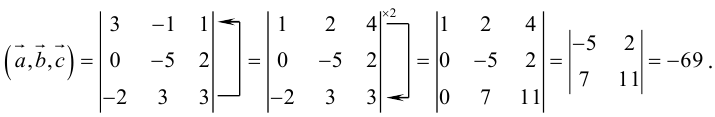Лекция №3
Длина вектора в
ортонормированном базисе. Угол между
векторами.
Скалярное
произведение векторов
При решении задач,
связанных с вычислением длин отрезков
(векторов) или величин углов удобнее
рассматривать так называемые
ортонормированные базисы.
Определение
3.1.
Базис
называется ортонормированным, если его
векторы удовлетворяют двум условиям:
;
.
Т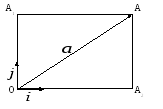
3.2. Длина
вектора
,
заданного координатами в ортонормированном
базисе
вычисляется по формуле
Доказательство.
-
Пусть
и
.
Отложим векторы
от некоторой точки О плоскости. Построим
прямоугольник
так, чтобы лучи
и
содержали бы векторы
,
а
.
-
По теореме Пифагора
имеем:
,
-
Так как
и
,
то
.
Значит,
.
Пусть векторы
и
– ненулевые векторы. Отложим от
произвольной точки О векторы
,
и рассмотрим лучи
и
.
О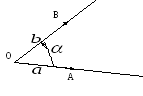
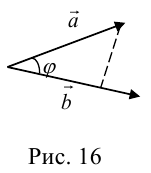
3.3. Углом
между векторами
и
называется угол между лучами их
содержащими
и
,
если эти лучи не совпадают.
Если лучи
и
совпадают,
то угол между ними считается равным
нулю.
Угол между векторами
и
обозначается
так:
.
Так как два угла,
стороны которых сонаправлены, равны,
то угол между векторами не зависит от
выбора точки О.
Определение
3.4. Скалярное
произведение векторов равно произведению
длин этих векторов на косинус угла между
ними:
.
Из формулы заключаем,
что
тогда и только тогда, когда векторы
и
перпендикулярны. Это утверждение
справедливо и в том случае, когда хотя
бы один из векторов
и
– нулевой. Скалярное произведение
.
Число
называется скалярным квадратом вектора
и обозначается через
.
Таким образом,
.
Теорема 3.5.
Скалярное произведение двух векторов
и
,
заданных в ортонормированном базисе,
есть число, равное сумме произведений
соответствующих координат, т.е.
.
Доказательство.
I
Пусть векторы
и
не нулевые и не коллинеарные.
1. Рассмотрим
треугольник
:
-
по определению
разности векторов имеем:
;
-
по теореме косинусов
имеем:
-
Значит,
или
-
Так как
,
то
и
(*)
2. Распишем равенство
(*) в координатах:
Таким образом,
II.
Пусть векторы
и
ненулевые и коллинеарные.
-
По теореме о
коллинеарных векторах существует такое
,
что
,
следовательно
-
Найдем скалярное
произведение векторов
и
по определению 3.4:
Следствие 3.6.
Векторы
и
,
заданные в ортонормированном базисе,
взаимно перпендикулярны тогда и только,
когда
.
Следствие 3.7.
Косинус
угла между ненулевыми векторами
и
,
заданными
в ортонормированном базисе, вычисляется
по формуле:
Свойства
скалярного умножения 3.8.
Для
любого действительного числа
и произвольных векторов
,
и
справедливы следующие равенства:
3.8.1.
3.8.2.
и
3.8.3.
3.8.4.
Ограничимся
доказательством свойства 3.8.3. Остальные
доказываются аналогично.
Доказательство
свойства 3.8.3.
Так как вектор
имеет координаты
,
то по формуле скалярного произведения
в ортонормированном базисе имеем:
=
=
=
.
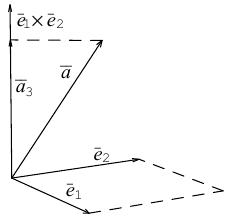
Геометрический
смысл координат вектора.
-
Пусть в
ортонормированном базисе задан некоторый
вектор
.
Его можно разложить по базису:
2
Умножим обе части разложения вектора
скалярно на
,
.
Имеем:
.
3. Учитывая, что
,
имеем:
Определение
3.5
Косинусы
углов
между вектором
и базисными векторами
,
называются направляющими косинусами
вектора
в ортонормированном базисе.
Если
,
то
Соседние файлы в папке вопрос 1
- #
- #
- #
Как найти координаты вектора в базисе
Решение:
Записываем матрицу перехода А:
и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f1 , f2 , f3 линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:
Обратная матрица А -1
Находим координаты вектора х относительно нового базиса.
Пример №1 . Даны векторы a<1;2;1>, b<2;-2;1>, c <1;-2;0>и d <0;3;1>. Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 – β*2 – γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b – 3/2c
Пример №2 . Даны векторы 


Пример №3 . Даны два линейных преобразования:
х’1 = a11x1 + a12x2 + a13x3, х”1 = b11x’1 + b12x’2 + b13x’3,
х’2 = a21x1 + a22x2 + a23x3, х”2 = b21x’1 + b22x’2 + b23x’3,
х’3 = a31x1 + a32x2 + a33x3, х”3 = b31x’1 + b32x’2 + b33x’3,
Средствами матричного исчисления найти преобразование, выражающее х”1, x”2, x”3 через х1, х2, х3.
х’1 = 4x1 + 3x2 + 5x3, х”1 = – x’1 + 3x’2 – 2x’3,
х’2 = 6x1 + 7x2 + x3, х”2 = – 4x’1 + x’2 + 2x’3,
х’3 = 9x1 + x2 + 8x3, х”3 = 3x’1 – 4x’2 + 5x’3,
Решение. Используя калькулятор, получаем:
Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 – 1*1) – 6*(3*8 – 1*5) + 9*(3*1 – 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .
| A -1 = -1/182 |
|
Матрицу Х ищем по формуле:
| X = A -1 ·B = -1/182 |
|
* | = |
|
Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e 1= AB , e 2= AC , e 3= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e 1, e 2, e 3)
Решение. Пункты (а-д) решаются через онлайн калькулятор.
Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид 
Решим полученную систему уравнений.
Ортогональные векторы и условие ортогональности
В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.
Ортогональные векторы: определение и условие
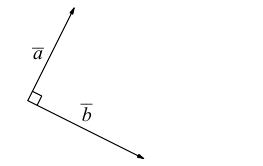
Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .
Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.
Примеры решения задач на ортогональность векторов
Плоские задачи на ортогональность векторов
Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:
a ¯ × b ¯ = a x × b x + a y × b y = 0
Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; – 1 >ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) = 2 – 2 = 0
Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.
Задача 2. Докажем, что векторы a ¯ = < 3 ; – 1 >и b ¯ = < 7 ; 5 >ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 3 × 7 + ( – 1 ) × 5 = 21 – 5 = 16
Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.
Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.
Как решить?
Найдем скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = – 4 n = – 2
Ответ: векторы являются ортогональными при значении n = 2 .
Примеры пространственных задач на ортогональность векторов
При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .
Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >являются ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) + 0 × 10 = 2 – 2 = 0
Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.
Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; – 8 >будут являться ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( – 8 ) = 2 n + 4 – 8 = 2 n – 4 2 n – 4 = 0 2 n = 4 n = 2
Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .
Ортогональный и ортонормированный базисы евклидова пространства
Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.
Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортогональным , если все образующие его векторы попарно ортогональны, т.е.
Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортонормированным , если его векторы попарно ортогональны и длина каждого из них равна единице:
Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.
В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.
Выражение скалярного произведения через координаты сомножителей
Пусть [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf[/math] и [math]mathbf[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.
Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:
Преобразуем это выражение, используя операции с матрицами:
y=begin y_1&cdots& y_n end^T[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] , a [math]G(mathbf_1,mathbf_2,ldots, mathbf_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений
которая называется матрицей Грама системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] .
Преимущества ортонормированного базиса
Для ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)[/math] ортонормированной системы [math]mathbf_1, mathbf_2,ldots, mathbf_n[/math] равна единичной матрице: [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)=E[/math] .
1. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] находится по формуле: [math]langle mathbf,mathbfrangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] , а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf[/math] .
2. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] длина вектора [math]mathbf[/math] вычисляется по формуле [math]|mathbf|= sqrt[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] .
3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf[/math] относительно ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf,mathbf_1rangle,ldots, x_n=langle mathbf,mathbf_nrangle[/math] .
В самом деле, умножая обе части равенства [math]mathbf= x_1 mathbf_1+ldots+x_n mathbf_n[/math] на [math]mathbf_1[/math] , получаем
Аналогично доказываются остальные формулы.
Изменение матрицы Грама при переходе от одного базиса к другому
Пусть [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] и [math](mathbf)= (mathbf_1,ldots,mathbf_n)[/math] — два базиса евклидова пространства [math]mathbb[/math] , a [math]S[/math] — матрица перехода от базиса [math](mathbf)[/math] к базису [math](mathbf)colon, (mathbf)=(mathbf)S[/math] . Требуется найти связь матриц Грама систем векторов [math](mathbf)[/math] и [math](mathbf)[/math]
По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] в разных базисах:
где [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] и [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>,[/math] [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>[/math] , получаем тождество
Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :
Записав это равенство для ортонормированных базисов [math](mathbf)[/math] и [math](mathbf)[/math] , получаем [math]E=S^TES[/math] , так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf_1,ldots,mathbf_n)= G(mathbf_1,ldots,mathbf_n)=E[/math] . Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^<-1>=S^T[/math] .
Свойства определителя Грама
Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.
1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.
Действительно, если система [math]mathbf_1, mathbf_2, ldots,mathbf_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math] , не равные нулю одновременно, что
Умножая это равенство скалярно на [math]mathbf_1[/math] , затем на [math]mathbf_2[/math] и т.д. на [math]mathbf_k[/math] , получаем однородную систему уравнений [math]G(mathbf_1,mathbf_2,ldots,mathbf_k)x=o[/math] , которая имеет нетривиальное решение [math]x=beginx_1&cdots&x_k end^T[/math] . Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.
Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.
Главный минор матрицы Грама системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.
2. Определитель Грама [math]det_1,mathbf_2, ldots, mathbf_k)>[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] . Другими словами, если в процессе ортогонализации векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] получены векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , то
Действительно, в процессе ортогонализации по векторам [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] последовательно строятся векторы
После первого шага определитель Грама не изменяется
Выполним с определителем [math]det G(mathbf_1, mathbf_2, ldots,mathbf_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_<21>)[/math] , а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_<21>)[/math] . Получим определитель
Так как при этих преобразованиях определитель не изменяется, то
Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:
Вычислим правую часть этого равенства. Матрица [math]G(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] Грама ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов является диагональной, так как [math]langle mathbf_i,mathbf_jrangle=0[/math] при [math]ine j[/math] . Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:
3. Определитель Грама любой системы [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] векторов удовлетворяет двойному неравенству
Докажем неотрицательность определителя Грама. Если система [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , для которых по свойству 2:
Оценим теперь скалярный квадрат [math]langle mathbf_j,mathbf_jrangle[/math] . Выполняя процесс ортого-1нализации, имеем [math]mathbf_j= mathbf_j+ alpha_mathbf_1+ ldots+ alpha_mathbf_[/math] . Отсюда
Следовательно, по свойству 2 имеем
1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.
2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.
3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара :
Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math] , элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math] . Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb^n[/math] . По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:
4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).
Изоморфизм евклидовых пространств
Два евклидовых пространства [math]mathbb[/math] и [math]mathbb'[/math] называются изоморфными [math](mathbbleftrightarrow mathbb’)[/math] , если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:
где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb[/math] и [math]mathbb'[/math] соответственно.
Напомним, что для изоморфизма конечномерных линейных пространств необходимо и достаточно, чтобы их размерности совпадали (см. теорему 8.3). Покажем, что это условие достаточно для изоморфизма евклидовых пространств (необходимость следует из определения). Как и при доказательстве теоремы 8.3, установим изоморфизм n-мерного евклидова пространства [math]mathbb[/math] с вещественным арифметическим пространством [math]mathbb^n[/math] со скалярным произведением (8.27). В самом деле, взяв в пространстве [math]mathbb[/math] какой-нибудь ортонормированный базис [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] , поставим в соответствие каждому вектору [math]mathbfin mathbb[/math] его координатный столбец [math]xin mathbb^n
(mathbfleftrightarrow x)[/math] . Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbbleftrightarrow mathbb^n[/math] . В ортонормированном базисе скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] пространства [math]mathbb[/math] находится по формуле
(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math] , т.е. скалярные произведения соответствующих элементов равны
Следовательно, евклидовы пространства [math]mathbb[/math] и [math]mathbb^n[/math] изоморфны.
Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb^n[/math] со стандартным скалярным произведением (8.27).
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/ortogonalnye-vektory-i-uslovie-ortogonalnosti/
http://mathhelpplanet.com/static.php?p=ortogonalnyi-i-ortonormirovannyi-bazisy-evklidova-prostranstva
[/spoiler]
Оглавление — Линейная алгебра
Ортогональный и ортонормированный базисы евклидова пространства
Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.
Базис [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е.
[math]langle mathbf{e}_i,mathbf{e}_jrangle=0[/math] при [math]ine j,~~ i=1,2,ldots,n,~~ j=1,2,ldots,n.[/math]
Базис [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] евклидова пространства называется ортонормированным, если его векторы попарно ортогональны и длина каждого из них равна единице:
[math]langle mathbf{e}_i,mathbf{e}_jrangle= begin{cases}1,&i=j,\ 0,&ine j end{cases}i=1,2,ldots,n,~~ j=1,2,ldots,n.[/math]
(8.31)
Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.
В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.
Выражение скалярного произведения через координаты сомножителей
Пусть [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf{x}[/math] и [math]mathbf{y}[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.
[math]mathbf{x}= x_1 mathbf{e}_1+x_2 mathbf{e}_2+ldots+ x_n mathbf{e}_n,qquad mathbf{y}= y_1 mathbf{e}_1+y_2 mathbf{e}_2+ldots+ y_n mathbf{e}_n.[/math]
Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:
[math]langle mathbf{x},mathbf{y}rangle= langle x_1 mathbf{e}_1+x_2 mathbf{e}_2+ldots+ x_n mathbf{e}_n,, y_1 mathbf{e}_1+y_2 mathbf{e}_2+ldots+ y_n mathbf{e}_n rangle= sum_{i=1}^{n}sum_{i=1}^{n}x_iy_jlangle mathbf{e}_i,mathbf{e}_jrangle.[/math]
Преобразуем это выражение, используя операции с матрицами:
[math]langle mathbf{x},mathbf{y}rangle= x^Tcdot G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)cdot y,[/math]
(8.32)
где [math]x=begin{pmatrix}x_1&cdots x_nend{pmatrix}^T,~ y=begin{pmatrix} y_1&cdots& y_n end{pmatrix}^T[/math] — координатные столбцы векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math], a [math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений
[math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)= begin{pmatrix} langle mathbf{e}_1,mathbf{e}_1rangle& langle mathbf{e}_1,mathbf{e}_2rangle &cdots&langle mathbf{e}_1, mathbf{e}_nrangle\ langle mathbf{e}_2,mathbf{e}_1rangle& langle mathbf{e}_2, mathbf{e}_2rangle &cdots&langle mathbf{e}_2,mathbf{e}_nrangle\ vdots&vdots&ddots&vdots\ langle mathbf{e}_n,mathbf{e}_1rangle& langle mathbf{e}_n,mathbf{e}_2rangle &cdots&langle mathbf{e}_n,mathbf{e}_nrangle end{pmatrix}!.[/math]
(8.33)
которая называется матрицей Грама системы векторов [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math].
Преимущества ортонормированного базиса
Для ортонормированного базиса [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf{e}_1, mathbf{e}_2,ldots,mathbf{e}_n)[/math] ортонормированной системы [math]mathbf{e}_1, mathbf{e}_2,ldots, mathbf{e}_n[/math] равна единичной матрице: [math]G(mathbf{e}_1, mathbf{e}_2,ldots,mathbf{e}_n)=E[/math].
1. В ортонормированном базисе [math]mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n[/math] скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] находится по формуле: [math]langle mathbf{x},mathbf{y}rangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math], где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf{x}[/math], а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf{y}[/math].
2. В ортонормированном базисе [math]mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n[/math] длина вектора [math]mathbf{x}[/math] вычисляется по формуле [math]|mathbf{x}|= sqrt{x_1^2+x_2^2+ldots+x_n^2}[/math], где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf{x}[/math].
3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf{x}[/math] относительно ортонормированного базиса [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf{x},mathbf{e}_1rangle,ldots, x_n=langle mathbf{x},mathbf{e}_nrangle[/math].
В самом деле, умножая обе части равенства [math]mathbf{x}= x_1 mathbf{e}_1+ldots+x_n mathbf{e}_n[/math] на [math]mathbf{e}_1[/math], получаем
[math]langle mathbf{x},mathbf{e}_1rangle= x_1underbrace{langlemathbf{e}_1, mathbf{e}_1 rangle}_{1}+ x_2underbrace{langle mathbf{e}_1,mathbf{e}_2 rangle}_{0}+ldots+ x_nunderbrace{langle mathbf{e}_n, mathbf{e}_n rangle}_{0}quad Leftrightarrowquad x_1=langle mathbf{x},mathbf{e}_1rangle.[/math]
Аналогично доказываются остальные формулы.
Изменение матрицы Грама при переходе от одного базиса к другому
Пусть [math](mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)[/math] и [math](mathbf{f})= (mathbf{f}_1,ldots,mathbf{f}_n)[/math] — два базиса евклидова пространства [math]mathbb{E}[/math], a [math]S[/math] — матрица перехода от базиса [math](mathbf{e})[/math] к базису [math](mathbf{f})colon, (mathbf{f})=(mathbf{e})S[/math]. Требуется найти связь матриц Грама систем векторов [math](mathbf{e})[/math] и [math](mathbf{f})[/math]
По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] в разных базисах:
[math]langle mathbf{x},mathbf{y}rangle= {mathop{x}limits_{(mathbf{e})}}^Tcdot, G(mathbf{e}_1,ldots,mathbf{e}_n)cdot mathop{mathbf{y}}limits_{(mathbf{e})}= {mathop{x}limits_{(mathbf{f})}}^Tcdot, G(mathbf{f}_1,ldots,mathbf{f}_n)cdot mathop{mathbf{y}}limits_{(mathbf{f})},[/math]
где [math]mathop{x}limits_{(mathbf{e})},, mathop{x}limits_{(mathbf{f})}[/math] и [math]mathop{y}limits_{(mathbf{e})},, mathop{y}limits_{(mathbf{f})}[/math] — координатные столбцы векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathop{x}limits_{(mathbf{e})}= S mathop{x}limits_{(mathbf{f})},[/math] [math]mathop{y}limits_{(mathbf{e})}= S mathop{y}limits_{(mathbf{f})}[/math], получаем тождество
[math]{mathop{x}limits_{(mathbf{f})}}^Tcdot S^Tcdot, G(mathbf{e}_1,ldots,mathbf{e}_n)cdot Scdot mathop{mathbf{y}}limits_{(mathbf{f})}= {mathop{x}limits_{(mathbf{f})}}^Tcdot, G(mathbf{f}_1,ldots,mathbf{f}_n)cdot mathop{mathbf{y}}limits_{(mathbf{f})}.[/math]
Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому:
[math]G(mathbf{f}_1,ldots,mathbf{f}_n)= S^Tcdot G(mathbf{e}_1,ldots,mathbf{e}_n)cdot S.[/math]
Записав это равенство для ортонормированных базисов [math](mathbf{e})[/math] и [math](mathbf{f})[/math], получаем [math]E=S^TES[/math], так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf{e}_1,ldots,mathbf{e}_n)= G(mathbf{f}_1,ldots,mathbf{f}_n)=E[/math]. Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^{-1}=S^T[/math].
Свойства определителя Грама
Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.
1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.
Действительно, если система [math]mathbf{v}_1, mathbf{v}_2, ldots,mathbf{v}_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math], не равные нулю одновременно, что
[math]x_1cdot mathbf{v}_1+x_2cdot mathbf{v}_2+ldots+ x_kcdot mathbf{v}_k= mathbf{o}.[/math]
Умножая это равенство скалярно на [math]mathbf{v}_1[/math], затем на [math]mathbf{v}_2[/math] и т.д. на [math]mathbf{v}_k[/math], получаем однородную систему уравнений [math]G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)x=o[/math], которая имеет нетривиальное решение [math]x=begin{pmatrix}x_1&cdots&x_k end{pmatrix}^T[/math]. Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.
Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.
Главный минор матрицы Грама системы [math]mathbf{v}_1, mathbf{v}_2,ldots,mathbf{v}_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.
2. Определитель Грама [math]det{G (mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k)}[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k[/math]. Другими словами, если в процессе ортогонализации векторов [math]mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k[/math] получены векторы [math]mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k[/math], то
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots,mathbf{w}_k)= langle mathbf{w}_1,mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldotscdot langle mathbf{w}_k,mathbf{w}_krangle.[/math]
Действительно, в процессе ортогонализации по векторам [math]mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k[/math] последовательно строятся векторы
[math]mathbf{w}_1=mathbf{v}_1,quad mathbf{w}_2= mathbf{v}_2- alpha_{21} mathbf{w}_1,quad ldots,quad mathbf{w}_k= mathbf{v}_k- sum_{j=1}^{k-1}alpha_{kj} mathbf{w}_j.[/math]
После первого шага определитель Грама не изменяется
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{v}_2, ldots,mathbf{v}_k).[/math]
Выполним с определителем [math]det G(mathbf{w}_1, mathbf{v}_2, ldots,mathbf{v}_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_{21})[/math], а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_{21})[/math]. Получим определитель
[math]det G(mathbf{w}_1,mathbf{v}_2-alpha_{21}mathbf{w}_1,ldots,mathbf{v}_k)= det G(mathbf{w}_1,mathbf{w}_2, mathbf{v}_3, ldots,mathbf{v}_k).[/math]
Так как при этих преобразованиях определитель не изменяется, то
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2,mathbf{v}_3, ldots,mathbf{v}_k).[/math]
Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots,mathbf{w}_k).[/math]
Вычислим правую часть этого равенства. Матрица [math]G(mathbf{w}_1,mathbf{w}_2,ldots, mathbf{w}_k)[/math] Грама ортогональной системы [math]mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k[/math] векторов является диагональной, так как [math]langle mathbf{w}_i,mathbf{w}_jrangle=0[/math] при [math]ine j[/math]. Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:
[math]det G(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k)= langle mathbf{w}_1, mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldots langle mathbf{w}_k, mathbf{w}_krangle.[/math]
3. Определитель Грама любой системы [math]mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k[/math] векторов удовлетворяет двойному неравенству
[math]0leqslant det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k) leqslant langle mathbf{v}_1, mathbf{v}_1ranglecdot langle mathbf{v}_2,mathbf{v}_2ranglecdot ldots langle mathbf{v}_k, mathbf{v}_krangle.[/math]
Докажем неотрицательность определителя Грама. Если система [math]mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf{w}_1,mathbf{w}_2, ldots, mathbf{w}_k[/math], для которых по свойству 2:
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots, mathbf{w}_k)= |mathbf{w}_1|^2cdot |mathbf{w}_2|^2cdot ldotscdot |mathbf{w}_k|^2>0.[/math]
Оценим теперь скалярный квадрат [math]langle mathbf{v}_j,mathbf{w}_jrangle[/math]. Выполняя процесс ортого-1нализации, имеем [math]mathbf{v}_j= mathbf{w}_j+ alpha_{j,1}mathbf{w}_1+ ldots+ alpha_{j,j-1}mathbf{w}_{j-1}[/math]. Отсюда
[math]langle mathbf{v}_j,mathbf{w}_jrangle= langle mathbf{w}_j,mathbf{w}_jrangle+ sum_{i=1}^{j-1}alpha_{i,i}^2 langle mathbf{w}_j,mathbf{w}_jrangle geqslant langle mathbf{w}_j, mathbf{w}_jrangle.[/math]
Следовательно, по свойству 2 имеем
[math]langle mathbf{v}_1,mathbf{v}_1ranglecdot langle mathbf{v}_2,mathbf{v}_2 ranglecdot ldotscdot langle mathbf{v}_k,mathbf{v}_kranglegeqslant langle mathbf{w}_1, mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldotscdot langle mathbf{w}_k, mathbf{w}_krangle= det G(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k).[/math]
Замечания 8.12
1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.
2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.
3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара:
[math](det{A})^2leqslant prod_{i=1}^{n}Bigl(a_{i,1}^2+ a_{i,2}^2+ldots+ a_{i,n}^2Bigr).[/math]
Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math], элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math]. Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb{R}^n[/math]. По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:
[math]begin{aligned} (det{A})^2&= det{A}cdotdet{A}= det{A^T}cdotdet{A}= det(A^TA)= det G(a_1,a_2,ldots,a_n)leqslant\[2pt] &leqslant |a_1|^2cdot |a_2|^2cdot ldotscdot |a_n|^2= prod_{i=1}^{n}Bigl(a_{i,1}^2+ a_{i,2}^2+ldots+ a_{i,n}^2Bigr). end{aligned}[/math]
4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).
Изоморфизм евклидовых пространств
Два евклидовых пространства [math]mathbb{E}[/math] и [math]mathbb{E}'[/math] называются изоморфными [math](mathbb{E}leftrightarrow mathbb{E}’)[/math], если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:
[math]left.{begin{matrix}mathbf{u}leftrightarrow mathbf{u}’\ mathbf{v}leftrightarrow mathbf{v}’end{matrix}}right}quad Rightarrowquad langle mathbf{u},mathbf{v}rangle= langle mathbf{u}’,mathbf{v}’rangle’.[/math]
‘
где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb{E}[/math] и [math]mathbb{E}'[/math] соответственно.
Напомним, что для изоморфизма конечномерных линейных пространств необходимо и достаточно, чтобы их размерности совпадали (см. теорему 8.3). Покажем, что это условие достаточно для изоморфизма евклидовых пространств (необходимость следует из определения). Как и при доказательстве теоремы 8.3, установим изоморфизм n-мерного евклидова пространства [math]mathbb{E}[/math] с вещественным арифметическим пространством [math]mathbb{R}^n[/math] со скалярным произведением (8.27). В самом деле, взяв в пространстве [math]mathbb{E}[/math] какой-нибудь ортонормированный базис [math](mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)[/math], поставим в соответствие каждому вектору [math]mathbf{x}in mathbb{E}[/math] его координатный столбец [math]xin mathbb{R}^n~ (mathbf{x}leftrightarrow x)[/math]. Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbb{E}leftrightarrow mathbb{R}^n[/math]. В ортонормированном базисе скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] пространства [math]mathbb{E}[/math] находится по формуле
[math]langle mathbf{x},mathbf{y}rangle= x_1cdot y_1+x_2cdot y_2+ldots+x_ncdot y_n[/math]
(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math], т.е. скалярные произведения соответствующих элементов равны
[math]langle mathbf{x},mathbf{y}rangle= x_1cdot y_1+x_2cdot y_2+ldots+x_ncdot y_n=x^Tcdot y.[/math]
Следовательно, евклидовы пространства [math]mathbb{E}[/math] и [math]mathbb{R}^n[/math] изоморфны.
Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb{R}^n[/math] со стандартным скалярным произведением (8.27).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Определение 3. Базис 



Если, кроме того,

то базис называется ортонормированным.
Лемма. Попарно ортогональные и отличные от нуля векторы линейно независимы.
Доказательство. Пусть векторы 



Умножая обе части этого равенства скалярно на 

откуда, поскольку 




Теорема 1. Во всяком евклидовом пространстве 
Доказательство. Пусть 




откуда

Так как 



Допустим теперь, что попарно ортогональные и отличные от нуля векторы 

и подберем числа 




откуда

Знаменатель 




Это построение мы будем продолжать до тех пор, пока не найдем последнего (ненулевого) вектора

ортогонального всем предыдущим векторам 


линейно независимы и, значит, образуют (ортогональный) базис. Если теперь каждый из векторов 

Легко видеть, что если первые 



Примененный здесь способ получения ортонормированной системы векторов из заданной линейно независимой системы носит название процесса ортогонализации.
Замечание. Если 




Для доказательства достаточно дополнить 


Пример. Найти ортогональный базис в пространстве многочленов степени не выше 4, определенных на отрезке 
Решение. В качестве исходного базиса возьмем

Положим

Далее, положим 




Пусть 




Положим, наконец, 





и

откуда 


Полученные многочлены

— это (с точностью до множителей) первые пять из так называемых многочленов Лежандра, играющих важную роль в математической физике.
Найдем выражение скалярного произведения векторов в координатах. Пусть ей 
базис пространства 


Тогда

где 






Легко видеть, что, и обратно, если в базисе 

и

равно

то этот базис ортонорм и рованный, так как в этом случае 

Пусть 






Пусть 




и поставить в соответствие каждому вектору х из 






(и значит,

то скалярное произведение

Таким образом, пространства 



Таким образом, 

Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор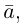
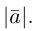
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 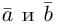
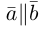
Аналогично, векторы а и b называются ортогональными (обозначение 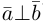
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
Углом между векторами 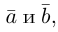
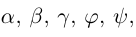
Два ненулевых вектора 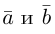
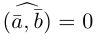
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 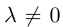
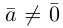
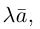
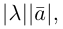
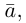
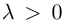
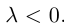
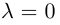
В частности, вектор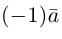
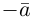
Если 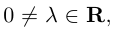
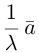
Из приведенного определения сразу же следует, что коллинеарные векторы 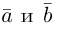
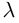
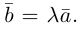
взять число 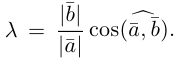
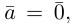
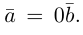
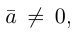
b) Сложение векторов.
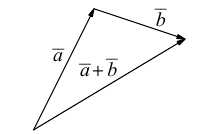
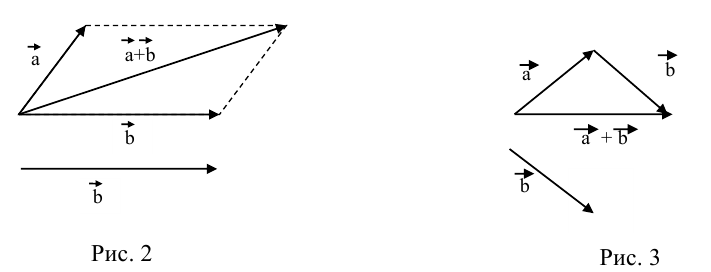
Суммой двух векторов 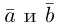
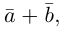
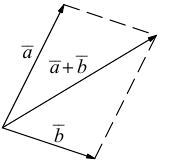
или по равносильному ему правилу параллелограмма
Вектор 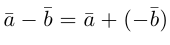
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
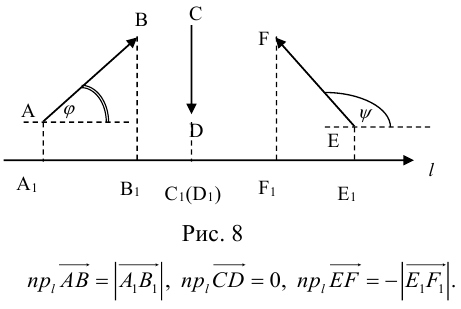
Проекцией вектора 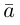
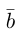
Геометрически очевидны следующие свойства проекции:
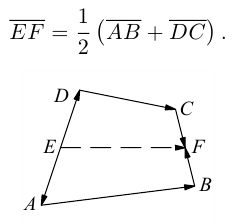
Пример №1
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 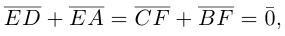
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 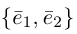
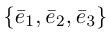
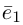
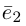
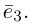
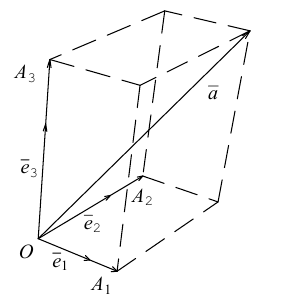
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 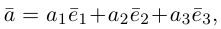
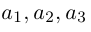
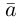
Приведем геометрическое доказательство этого утверждения.
Вектор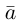
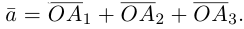
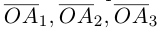
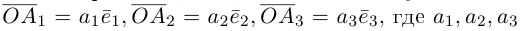
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 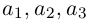
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 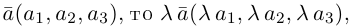
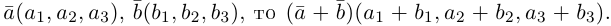
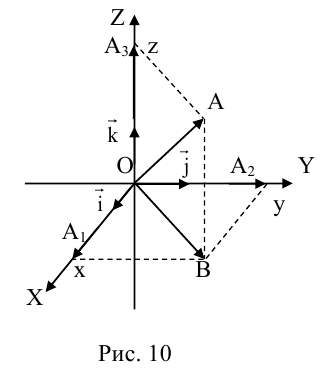
Рассмотрим теперь ортонормированный базис 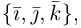
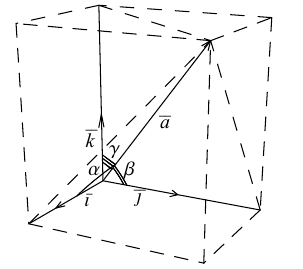
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 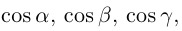
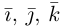
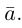
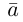
Очевидно также, что
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 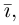
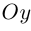
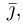
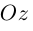
В выбранной системе координат координаты радиуса-вектора 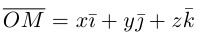
Если известны координаты начальной 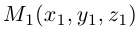
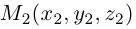
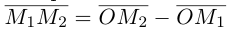
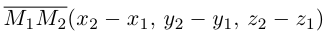
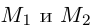
Найдем теперь координаты точки М, делящей отрезок с концами в точках 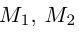
отношении 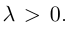
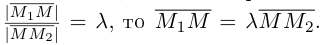
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
Пример №2
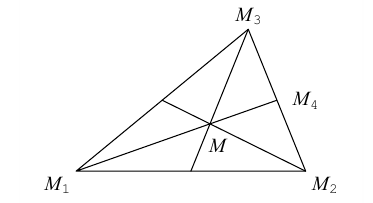
Треугольник задан координатами своих вершин 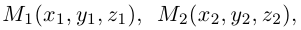
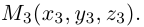
Пусть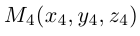
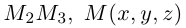
По известному свойству точки пересечения медиан 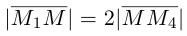
Подставив сюда найденные координаты точки 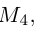
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 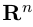
обладающая тем свойством, что любой вектор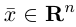
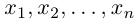
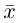
В качестве базиса в 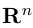
так как, очевидно, любой вектор 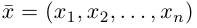
Скалярное произведение векторов
Определение: Скалярным произведением векторов 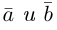
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 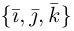
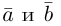
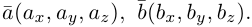
перемножим векторы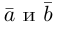
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
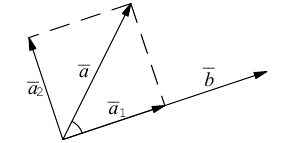
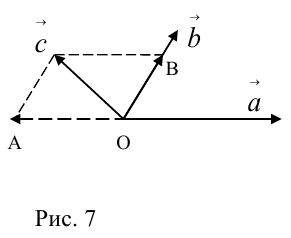
Разложить вектор 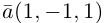
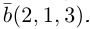
Решение.
Из чертежа следует, что 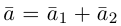
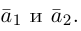
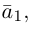
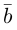
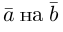
Тогда вторая ортогональная составляющая вектора 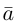
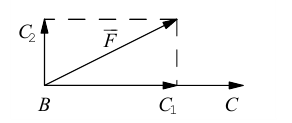
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 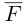
Найдем работу этой силы. Для этого разложим вектор силы 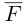
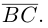
Составляющая 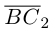
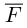
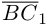
Окончательно, работа силы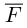
Замечание. Скалярным произведением векторов 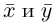
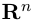
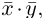
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 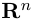
Длиной вектора 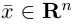
Векторы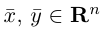
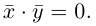
составляют ортонормированный базис пространства 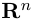
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 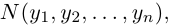
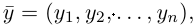
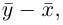
Таким образом переопределенное пространство 
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
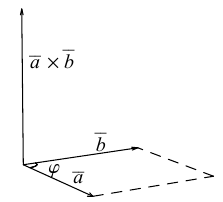
Определение: Векторным произведением некоялинеарных векторов 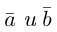

Из этого определения следует, что площадь параллелограмма, построенного на векторах 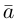
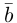

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 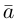
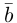
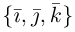
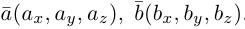
раскроем скобки в векторном произведении 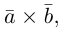
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 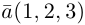
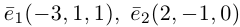
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 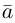

Переходим к вычислениям:
Тогда
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 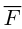
Смешанное произведение векторов
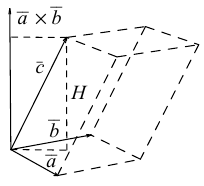
Определение: Смешанным произведением трех векторов 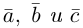
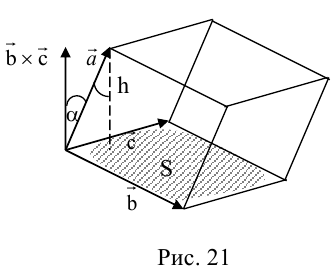
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 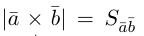
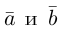
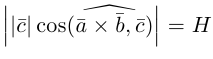
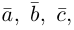
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 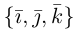
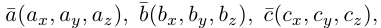
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 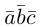
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 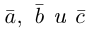
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 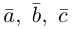
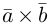
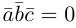
Следствие. Три вектора 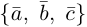
Заметим, кроме того, что, если 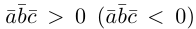
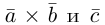
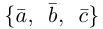
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 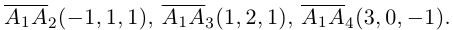
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 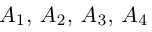
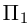
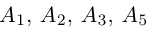
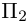
так как первая и третья строки в определителе пропорциональны. Плоскости 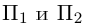
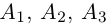
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
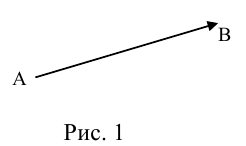
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 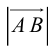
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
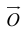
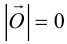
Определение: Векторы 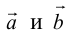
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 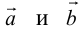
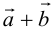
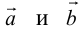
б) Правило треугольника (рис. 3): начало 
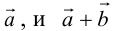
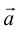
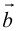
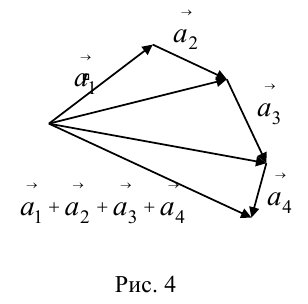
в) Правило сложения нескольких векторов (рис. 4).
Вектор 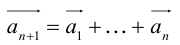
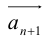
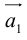
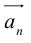
Умножение на число
Определение: Произведением вектора 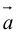
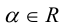
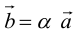
а) 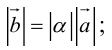
б) 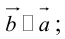
в)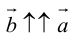
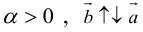
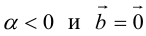
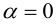
Произведение 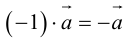
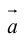
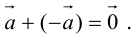
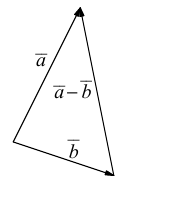
Определение: Разностью 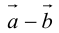
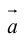
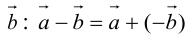
Начала 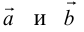
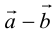
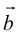
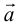
Свойства линейных операций
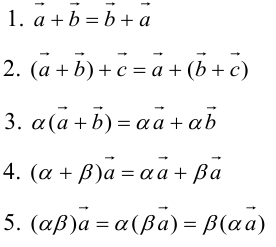
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: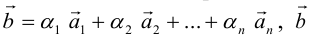
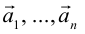
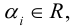
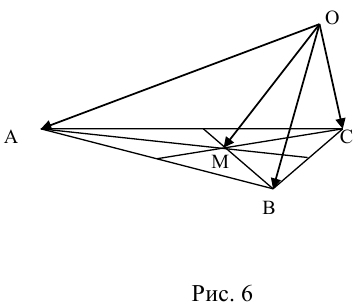
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 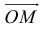
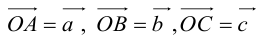
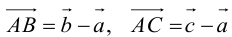
По правилу треугольника 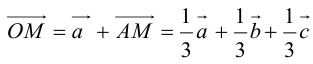
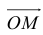
Теорема: Пусть 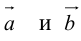
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 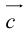
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 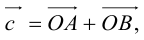
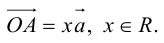
Докажем единственность разложения. Предположим, что 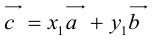
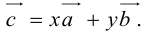
Если 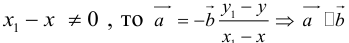
Теорема: Пусть 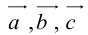
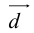
причем единственным образом.
Представление вектора 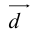
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 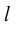
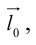
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 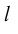
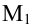
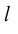
Определение: Ортогональной проекцией вектора 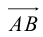
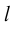
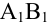
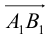
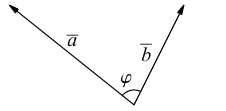
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
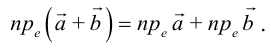
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 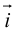
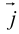

Аналогично в пространственной системе OXYZ 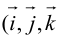
– разложение 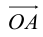
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 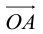
Определение: Координатами вектора 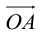
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 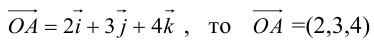
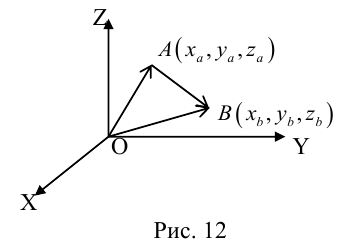
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
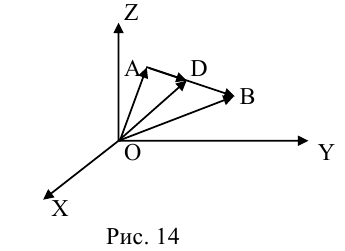
Если известны длина 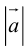
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
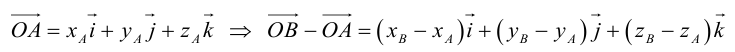
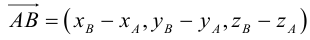
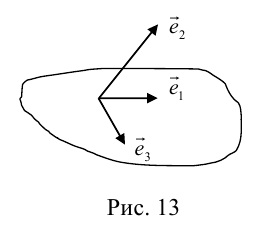
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 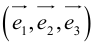
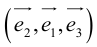
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 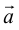
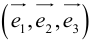
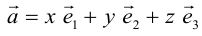
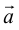
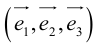
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 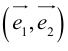
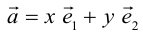
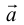
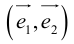
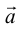
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
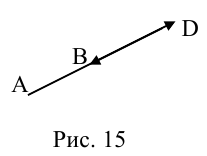
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 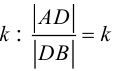
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
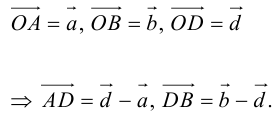
Так как 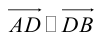
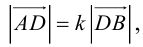
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
ЗАМЕЧАНИЕ 2. Если k < 0, 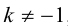
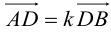
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 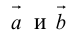
Скалярное произведение обозначается так: 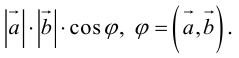
Так как 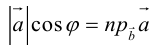
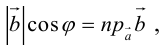
Свойства скалярного произведения
1.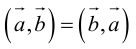
2.
Доказательство:
3.
Доказательство:
а) 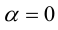
б)
в) 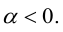
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 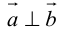
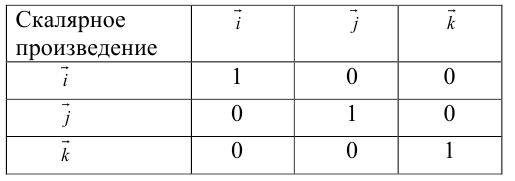
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 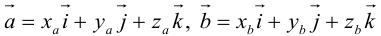
Таким образом,
Пример №8
Найти, при каком значении x векторы 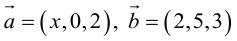
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 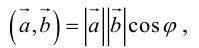
то
Найдем координаты векторов 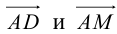
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 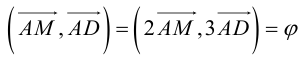
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 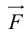
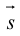
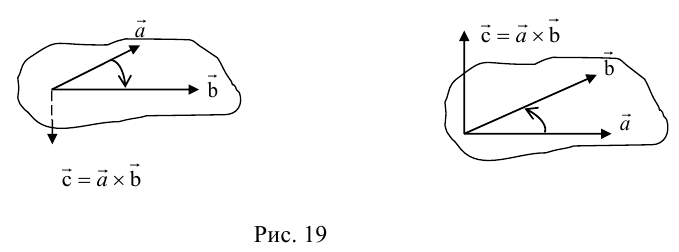
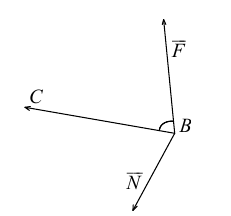
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 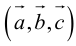
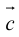
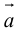
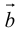
Определение: Векторным произведением вектора 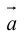
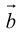
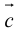
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 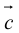
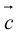
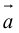
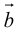
Свойства векторного произведения
1.
Доказательство:
а)пусть 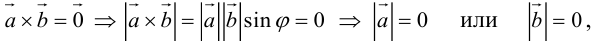
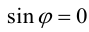
Его направление не определено, поэтому можно считать, что 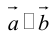
б)пусть
2. 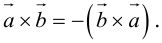
Доказательство: По определению направления векторов 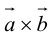
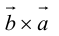
3.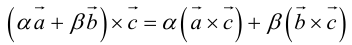
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 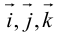
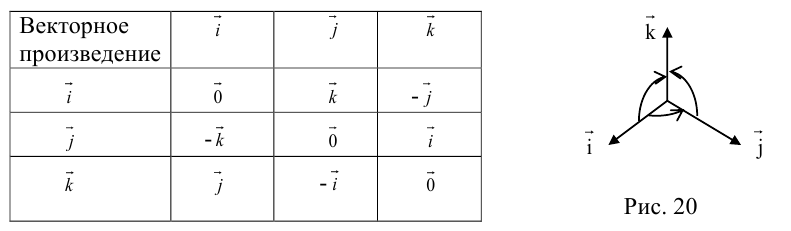
Пусть в некоторой пдск 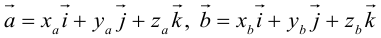
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
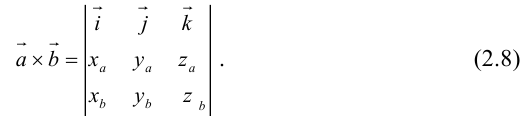
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 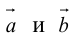
или
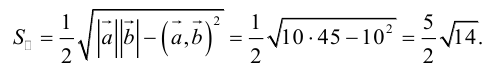
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 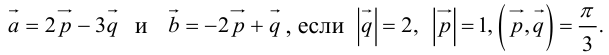
Так как 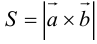
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 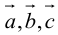
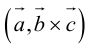
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
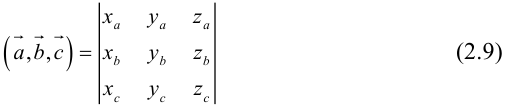
По определению скалярного произведения
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
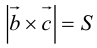
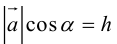
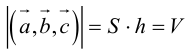
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 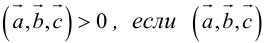
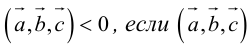
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 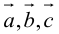
Доказательство: а) 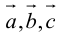
Если 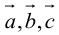
б)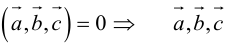
Во всех трех случаях 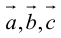
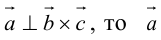
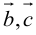
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
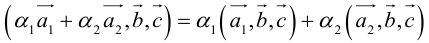
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
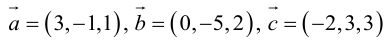
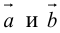
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 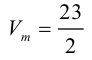

Чтобы найти высоту, воспользуемся формулой
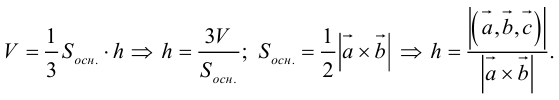
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика

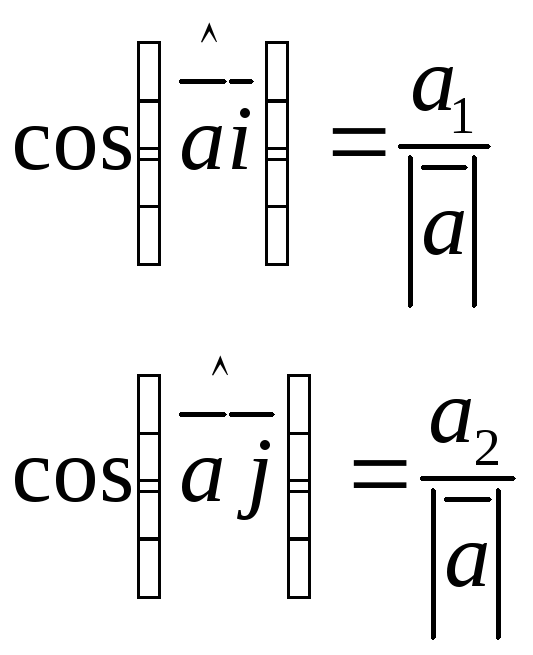
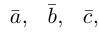
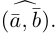
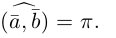
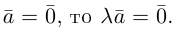
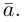
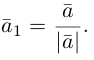
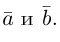
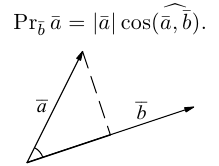
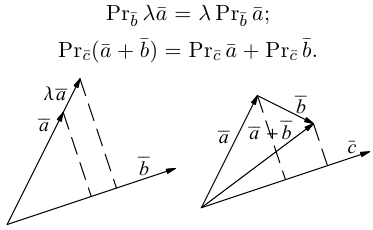
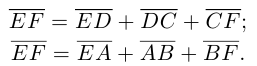
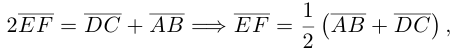
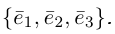
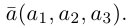
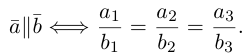
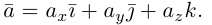
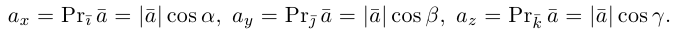
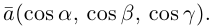
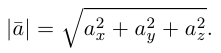
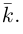

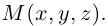
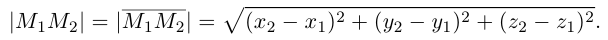
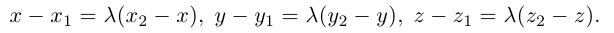
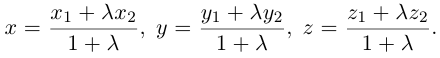
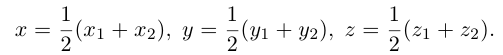
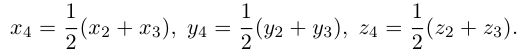
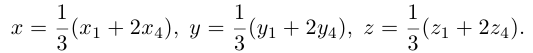
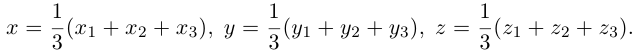


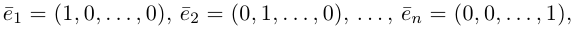
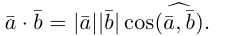
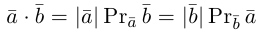
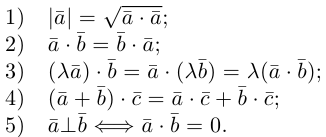
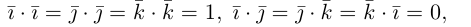
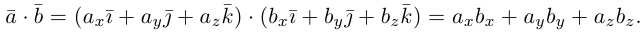
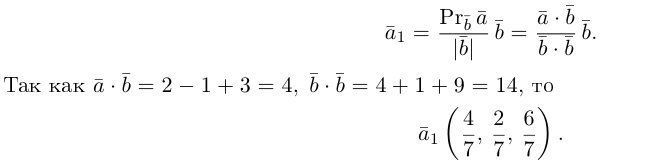
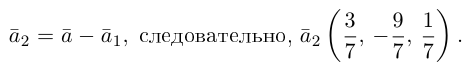
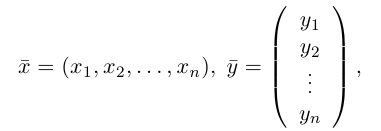
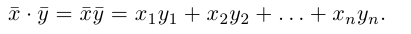
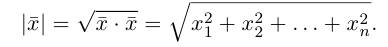
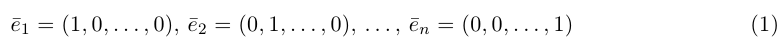

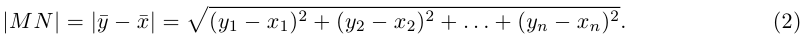
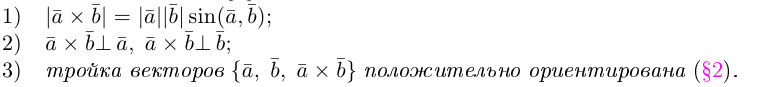
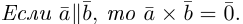
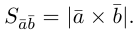
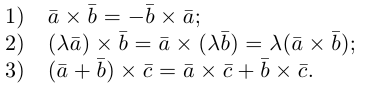
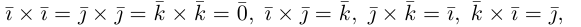
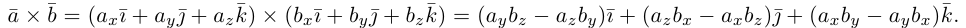
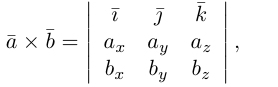
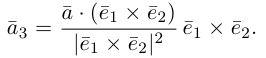
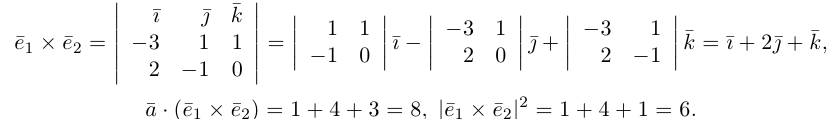
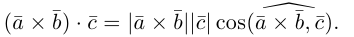
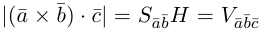
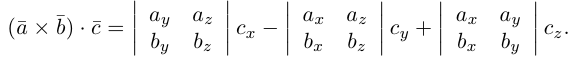
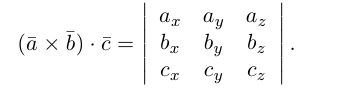
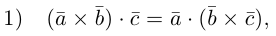
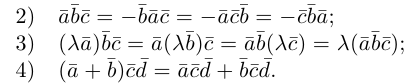
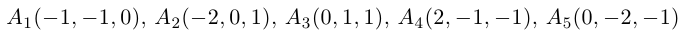
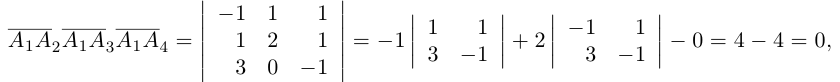
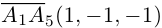
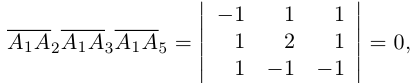
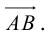
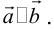

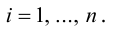
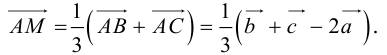
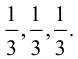
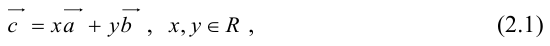
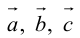 есть два коллинеарных, например:
есть два коллинеарных, например: 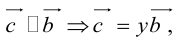
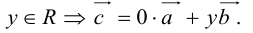
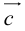 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат  (рис. 7).
(рис. 7). 
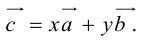
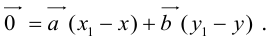
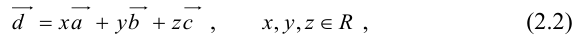
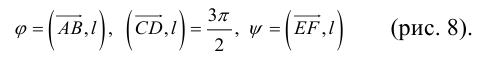
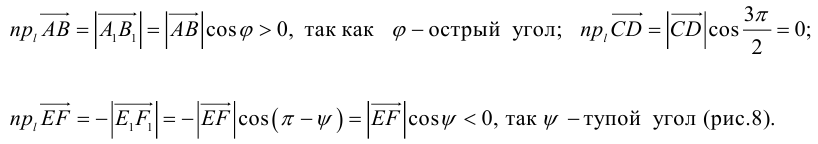
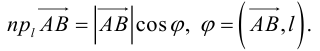
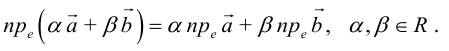
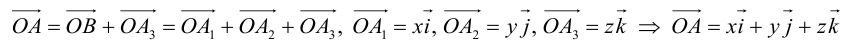
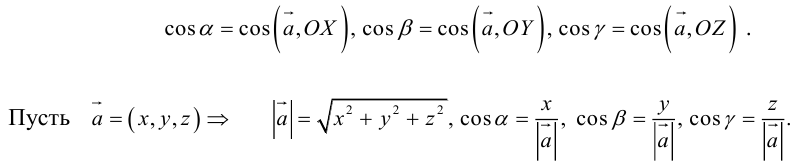
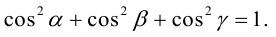
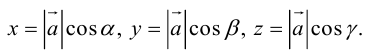
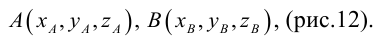
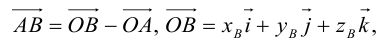
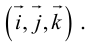
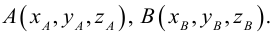

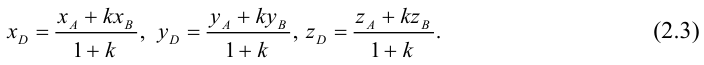
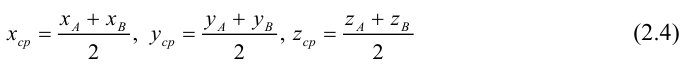
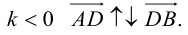
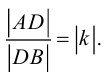
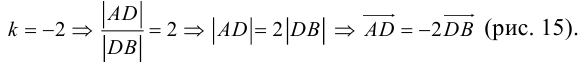
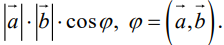
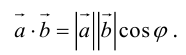
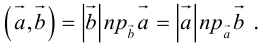
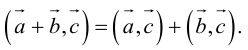
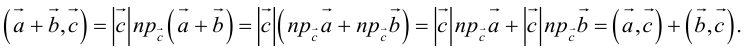
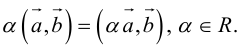
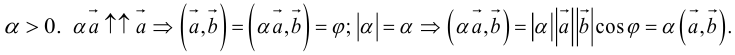
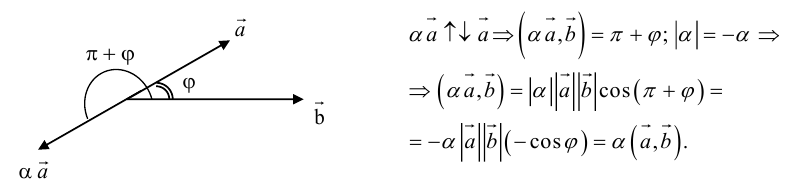
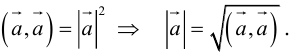
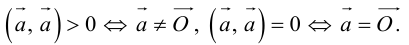
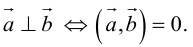
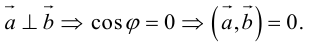
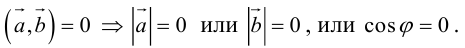
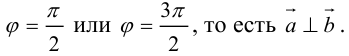
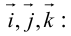
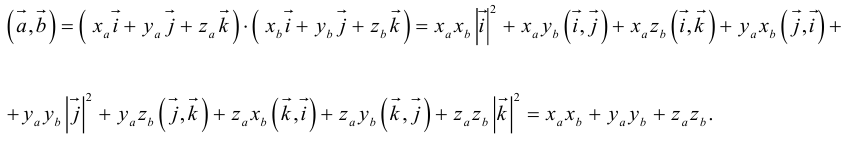

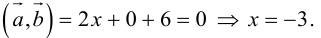
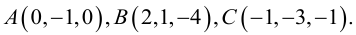

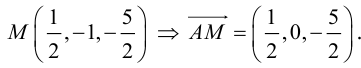
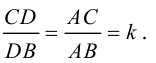
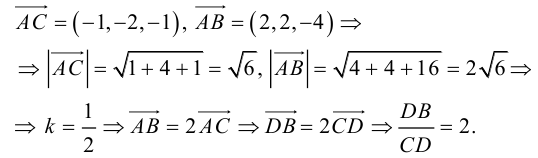
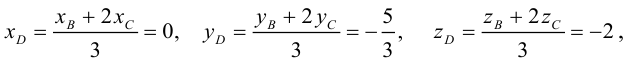
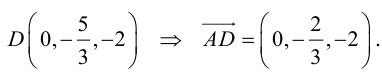
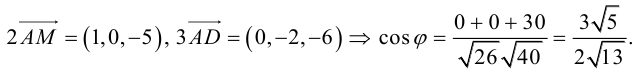
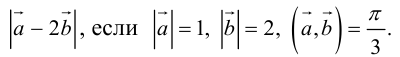
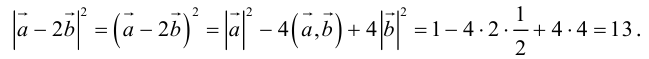
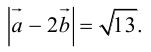
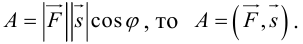
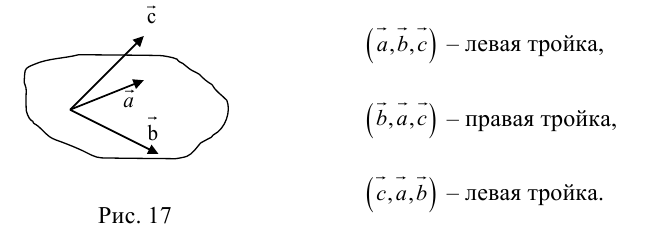
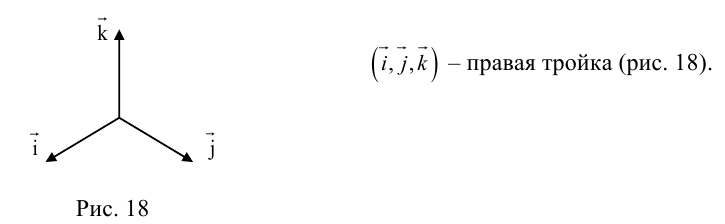
 (
(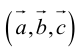 – правая.
– правая.