Задача
Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках
и векторе объемов конечного использования
.
Требуется:
Указание:
При вычислениях производить округление с точностью до тысячных.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Матрица прямых затрат
Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора
:
Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:
Подставляя
числовые значения, получаем:
Матрица «Затраты – выпуск»
Найдем матрицу
«Затраты – выпуск»
Вектор конечного использования Y для валового объема выпуска X
Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения:
Для этого выполним умножение двух матриц
Матрица полных затрат
Найдем
матрицу коэффициентов полных материальных затрат
-она будет равна обратной матрице
:
Определитель матрицы
:
Алгебраические
дополнения:
Обратная матрица:
Вектор валового объема выпуска X для конечного использования Y
Вектор валового объема выпуска
для конечного продукта
определим формуле:
Приросты валовых объемов выпуска
Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на
по сравнению с
:
Матрица полных затрат ресурсов S
Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:
Суммарная потребность в ресурсах
Суммарная потребность в ресурсах для вектора Y0:
Суммарная потребность в ресурсах для вектора Yn:
Матрицы косвенных затрат и сумма затрат
Найдем
матрицы косвенных затрат первого, второго и третьего порядка
Сумма затрат:
Разность
матриц:
Вектор потребности в продукции
Найдем
вектор потребности в продукции всех отраслей материального производства bij
для получения единицы конечного продукта bj вида. Для этого
просуммируем столбцы матрицы полных затрат:
Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.
Балансовый анализ. Математическая модель многоотраслевой экономики (метод Леонтьева)
Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объём производства каждой из п отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а сдругой – как потребитель продукции и своей, и произведённой, другими отраслями.
Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В.Леонтьевым
Предположим, что рассматривается п отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени (например, год).
Введём следующие обозначения: хi – общий (валовой) объём продукции i – й отрасли (i= 1,2. n);
xij – объём продукции i – й отрасли, потребляемой j-й отраслью в процессе производства (i, j = 1,2. n);
уi – объём конечного продукта i – й отрасли для непроизводственного потребления.
Так как валовой объём продукции любой i – й отрасли равен суммарному объёму продукции, потребляемой п отраслями, и конечного продукта, то
 (1.15)
(1.15)
Уравнения (1.15) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (1.15), имеют стоимостное выражение.
Введём коэффициенты прямых затрат  :
:
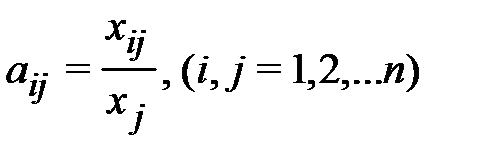 (1.16)
(1.16)
показывающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли.
Можно полагать, что в некотором промежутке времени коэффициенты aij будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
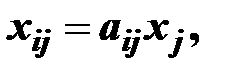
 (1.17)
(1.17)
вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной. Теперь соотношения баланса (1.15) примут вид:
 (1.18)
(1.18)
Обозначим 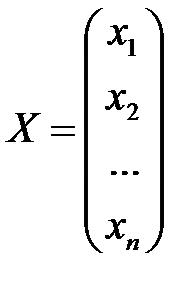 ,
, 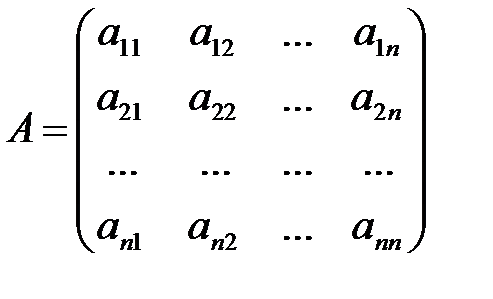 ,
,  ,
,
где Х – вектор валового выпуска, Y – вектор конечного продукта,А – матрица прямых затрат (технологическая или структурная матрица).
Тогда систему (1.15) можно записать в матричном виде:
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.
Перепишем уравнение (1.19) в виде:
Если матрица (Е – А) невырожденная, т.е. |Е – А|≠0, то
Матрица S = (Е – А) -1 называется матрицей полных затрат.
Каждый элемент sij матрицы S есть величина валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли  (j=1,2. n).
(j=1,2. n).
В соответствии с экономическим смыслом задачи значения хi должны быть неотрицательны при неотрицательных значениях
 и
и  , где i, j = 1, 2,…,n.
, где i, j = 1, 2,…,n.
Определение. Матрица А ≥ 0 называется продуктивной, если для любого вектора Y ≥ 0 существует решение X ≥ 0 уравнения (Е-А)Х=Y. В этом случае и модель Леонтьева называется продуктивной.
Существует несколько критериев продуктивности матрицы А.
Первый критерий продуктивности. Матрица А продуктивна, если максимум сумм элементов её столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица А продуктивна, если  для любых i, j = 1,2. n и
для любых i, j = 1,2. n и  , и существует номер j такой, что
, и существует номер j такой, что  .
.
Второй критерий продуктивности. Матрица A ≥ 0 продуктивна тогда и только тогда, когда матрица (Е – А) – 1 существует и неотрицательна.
Пример 9. В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.:
| Отрасль | Потребление | Конеч-ный продукт | Валовой выпуск |
| энергетика | машиностроение | ||
| Производство | Энергетика Машиностроение |
Вычислить необходимый объём валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроение сохранится на прежнем уровне.
Решение. Имеем 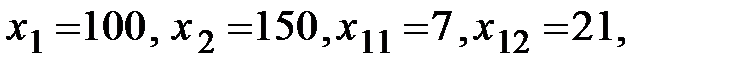
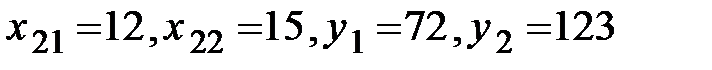 .
.
По формуле (1.16) находим коэффициенты прямых затрат: 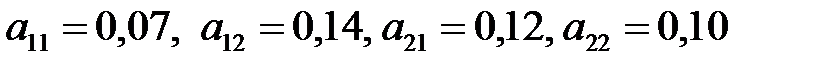 , т.е матрица прямых затрат
, т.е матрица прямых затрат
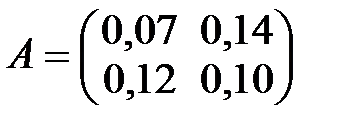 имеет неотрицательные элементы и удовлетворяет первому критерию продуктивности:
имеет неотрицательные элементы и удовлетворяет первому критерию продуктивности:  .
.
Поэтому для любого вектора конечного продукта Y можно найти необходимый объём валового выпуска Х по формуле (1.21):
Найдём матрицу полных затрат S = (E – A) -1 :
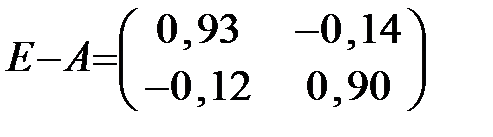 . Так как |Е – А|=0,8202 ≠ 0, то по формуле (1.14) для вычисления обратной матрицы имеем:
. Так как |Е – А|=0,8202 ≠ 0, то по формуле (1.14) для вычисления обратной матрицы имеем: 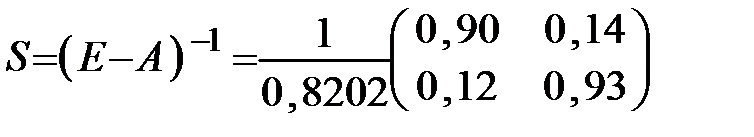 .
.
По условию вектор конечного продукта должен быть равен 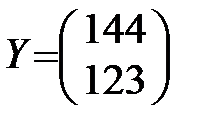 . Тогда по формуле (1.21) получаем вектор валового выпуска:
. Тогда по формуле (1.21) получаем вектор валового выпуска:
 , т.е. валовой выпуск в энергетической отрасли надо увеличить до 179, 0 усл. ед., а в машиностроительной – до 160,5 усл. ед.
, т.е. валовой выпуск в энергетической отрасли надо увеличить до 179, 0 усл. ед., а в машиностроительной – до 160,5 усл. ед.
Ответ:  (усл. ед.),
(усл. ед.),  (усл. ед.).
(усл. ед.).
Векторная алгебра
Основные понятия векторной алгебры
Определение. Вектором называется направленный отрезок АВ, в котором
точка А рассматривается как начало, а точка В – как конец.
Вектор обозначается  или
или  , и изображается следующим образом:
, и изображается следующим образом:
В Модуль (длина) вектора обозначается  или
или 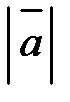 .
.
А или 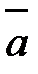
Определение. Векторы называются коллинеарными, если они расположены
на одной или на параллельных прямых, и компланарными,
если они лежат на одной или на параллельных плоскостях.
Определение. Векторы называются равными, если: а) равны их длины;
б) они коллинеарны; с) направлены в одну сторону.
Определение. Координатами 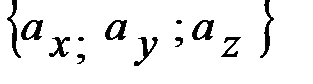 вектора
вектора  в системе ХОУ
в системе ХОУ
называются проекции этого вектора на оси Ох, Оу, Оz.
В этом случае пишут : 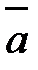 =
= 
Определение. Базисными ортами называются единичные векторы 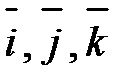 , направленные соответственно по координатным осям Ох, Оу, Оz.
, направленные соответственно по координатным осям Ох, Оу, Оz.
Координаты вектора являются коэффициентами его разложения по ортам:

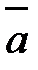 = ах ·
= ах ·  + ау ·
+ ау · 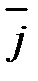 + аz ·
+ аz · 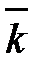 . (2.1)
. (2.1)
координаты вектора  равны разностям соответсвующих координат его
равны разностям соответсвующих координат его
конца В и начала А, т.е.

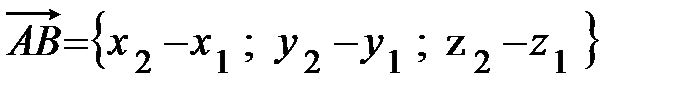 . (2.2)
. (2.2)
Длина вектора , заданного своими координатами 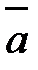 =
=  , вычисляется по формуле:
, вычисляется по формуле:
 . (2.3)
. (2.3)
При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются), а при умножении вектора на число каждая его координата умножается на это число.
Пример 10. Вектор  задан координатами начала А и конца В: А (-2;3;-5 ),
задан координатами начала А и конца В: А (-2;3;-5 ),
В ( 2; -3; 1 ). Найти координаты вектора и его длину.
Решение. По формуле (2.2) найдём координаты вектора  :
:  =
=
По формуле (2.3) определяем его длину:  .
.
Ответ:  =
= 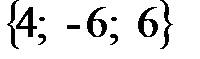 ;
; 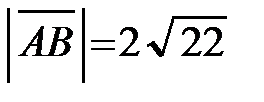 .
.
Пример 11. Даны три вектора: 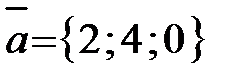 ,
, 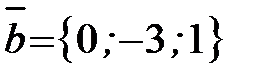 ,
,  .
.
Найти координаты вектора 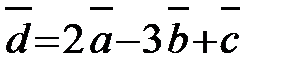 .
.
Решение. Имеем  ,
,  ,
,  .
.
Тогда 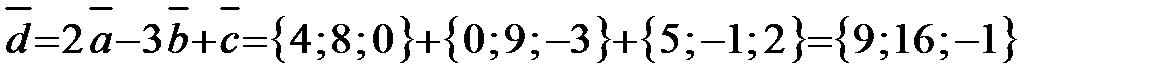 .
.
Ответ:  .
.
Межотраслевой баланс
С помощью сервиса в онлайн режиме можно:
- найти коэффициенты полных материальных затрат, определить вектор валовой продукции;
- составить межотраслевой баланс, составить схему межотраслевого баланса труда;
- проверить продуктивность матрицы.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.
Система уравнений X = AX + Y называется экономико-математической моделью межотраслевого баланса (МОБ) или моделью «затраты – выпуск». C помощью нее можно выполнить следующие расчеты:
- подставив в модель объемы валовой продукции каждой отрасли Xi, можно определить объем конечной продукции отрасли Yj: Y = (E – A)X
- задав величины конечной продукции всех отраслей Yj, можно определить величины валовой продукции каждой отрасли Xi: X = (E – A) -1 Y
- установив для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти объемы конечной продукции первых отраслей и объемы валовой продукции вторых.
Здесь A – матрица прямых затрат, коэффициенты которой, aij показывают затраты i-й отрасли на производство единицы продукции j-й отрасли. Введем обозначение B = (E – A) -1 . Матрица B называется матрицей полных материальных затрат, коэффициенты которой, bij показывают полный объем продукции i-й отрасли, используемой для производства единицы продукции j-й отрасли. С учетом линейности соотношений эффект распространения спроса ΔX, вызванный изменением конечного спроса на величину ΔY рассчитывается как: ΔX = B·ΔY
Через C=A-B обозначают матрицу косвенных затрат.
Пример №1 . Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y .
Пример №2 . Дан межотраслевой баланс трехотраслевой модели хозяйства:
| № отрасли потребления | 1 | 2 | 3 | Конечный продукт | Валовый продукт | Y’ | |
| № отрасли | 1 | 20 | 20 | 60 | 100 | 200 | 150 |
| отрасли | 2 | 20 | 40 | 60 | 80 | 200 | 100 |
| производства | 3 | 20 | 0 | 10 | 70 | 100 | 100 |
Определить:
1) технологическую матрицу;
2) матрицу коэффициентов полных затрат;
3) дать экономический анализ каждого столбца матрицы коэффициентов полных затрат;
4) определить валовый выпуск X’ на новый ассортимент конечной продукции Y’;
Решение.
Находим валовой объем продукции xi;
x1 = 20 + 20 + 60 + 100 = 200
x2 = 20 + 40 + 60 + 80 = 200
x3 = 20 + 0 + 10 + 70 = 100
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | 20 | 20 | 60 | 100 | 200 |
| 20 | 40 | 60 | 80 | 200 | |
| 20 | 0 | 10 | 70 | 100 |
По формуле aij = xij / xj находим коэффициенты прямых затрат:
a11 = 20/200 = 0.1; a12 = 20/200 = 0.1; a13 = 60/100 = 0.6; a21 = 20/200 = 0.1; a22 = 40/200 = 0.2; a23 = 60/100 = 0.6; a31 = 20/200 = 0.1; a32 = 0/200 = 0; a33 = 10/100 = 0.1;
| 0.1 | 0.1 | 0.6 |
| 0.1 | 0.2 | 0.6 |
| 0.1 | 0 | 0.1 |
Определим матрицу коэффициентов полных затрат с помощью формул обращения невырожденных матриц.
а) Находим матрицу (E-A):
| (E-A) = |
|
б) Вычисляем обратную матрицу (E-A) -1 :
| 0,9 | -0,1 | -0,6 |
| -0,1 | 0,8 | -0,6 |
| -0,1 | 0 | 0,9 |
Найдем величины валовой продукции трех отраслей
| X’ = (B -1 *Y’) = |
|
* | = |
Пример №3 . В модели межотраслевого баланса
| Производство | Потребление | Конечная продукция | Валовая продукция | ||
| 1 | 2 | 3 | |||
| 1 | 10 | 5 | 15 | 70 | 100 |
| 2 | 20 | … | … | … | … |
| 3 | 30 | … | … | … | … |
| Оплата труда | 30 | … | … | … | … |
| Прибыль D | D | … | … | … | … |
прибыль D равна:
D = Валовая продукция – Затраты на производство – Оплата труда = 100 – (10+20+30) – 30 = 10.
Как найти вектор валового выпуска
МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ
ИНСТИТУТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА
Кафедра «Моделирование в экономике и управлении»
МАТЕМАТИЧЕСКИЕ МОДЕЛИ В УПРАВЛЕНИИ
Методическое пособие по проведению лабораторных работ.
Тема «Балансовые экономико-математические модели и их моделирование на Excel»:
Тема 1. Экономико-математическая модель межотраслевого баланса (модель Леонтьева).
Тема 2. Экономико-математическая модель международной торговли.
Лабораторная работа №5
Курс “Математические модели в управлении” читается студентам второго курсов дневной и вечерней форм обучения факультета управления по специальностям: 061000 – “Государственное и муниципальное управление”, 061100 – “Менеджмент”. Курс читается два семестра и охватывает основные темы исследования операций, теории массового обслуживания и теории игр.
Предметом изучения дисциплины “Математические модели в управлении” являются математические модели и методы решения исследования операций, теории массового обслуживания и теории игр.
Цель курса – сформировать у студентов комплекс знаний необходимых для:
· анализа современных проблем в области производства, торговли, финансов, денежного обращения и кредитов;
· оптимальному решению тактических и стратегических задач организационного управления;
Задачи курса научить студентов:
· владеть приемами постановки задач организационного управления;
· на основе описательных задач строить математические модели;
· умению выбрать соответствующий метод решения задачи;
· проведению численных исследований математических моделей;
· умению проведения анализа результатов вычислений;
· умению выбрать наиболее эффективное управляющее решение.
Особенностью программы для студентов факультета управления является:
· рассмотрение актуальных проблем организационного управления в различных структурах – производственных, торговых, финансово – кредитных;
· применение математических методов при анализе и выработки управляющих решений.
Изучив курс, студент:
должен владеть моделями математического программирования, теории игр и массового обслуживания;
уметь использовать математические методы при решении задач организационного управления;
должен уметь использовать в своей работе средства вычислительной техники и современных информационных технологий.
Лабораторные работы призваны, на практике, помочь студентам применить знания полученные на лекциях и при самостоятельной работе. В качестве программной среды используются средства Microsoft Offis Excel (электронные таблицы MS Offis ).
Программные средства Excel – Поиск решения является мощным инструментом решения вычислительных и оптимизационных задач.
Порядок выполнения работы
На лабораторную работу каждый студент приносит тетрадь для выполнения лабораторных работ, в которой будут содержаться математические модели и результаты решения задач на Excel.
Задание . Получить вариант задачи у преподавателя. Составить математическую модель задачи. Найти решение задачи в Excel и показать результаты поиска решения преподавателю на экране компьютера.
Отчет. Отчет по лабораторной работе представляется в тетради студента и должен содержать все полученные результаты. Отчет демонстрируется преподавателю на данном лабораторном занятии.
Лабораторная работа № 5
Лабораторная работы №5 состоит из двух тем: Тема 1. Экономико-математическая модель межотраслевого баланса (модель Леонтьева), и Тема 2. Экономико-математическая модель международной торговли.
Тема 1. Экономико-математическая модель межотраслевого баланса (модель Леонтьева). Моделирование средствами Excel .
Программное обеспечение: Microsoft Excel
Рассмотрим модель межотраслевого баланса, называемую еще моделью Леонтьева или моделью «затраты-выпуск».
Предположим, что производственный сектор народного хозяйства разбит на n отраслей (энергетика, машиностроение, сельское хозяйство и т.д.).
Рассмотрим отрасль i , i = 1, 2,…, n . Она выпускает некую продукцию за данный промежуток времени (например, за год) в объеме xi, который еще называют валовым выпуском. Часть объема продукции xi , произведенная i-ой отраслью используется для собственного производства в объеме xi i , часть – поступает в остальные отрасли j = 1, 2,…, n для потребления при производстве в объемах xij , и некоторая часть объемом y i – для потребления в непроизводственной сфере, так называемый объем конечного потребления. Перечисленные сферы распределения валового продукта i-ой отрасли приводят к соотношению баланса
, i = 1, 2,…, n .
Введем коэффициенты прямых затрат a ij , которые показывают, сколько единиц продукции i-ой отрасли затрачивается на производство одной единицы продукции в отрасли j. Тогда можно записать, что количество продукции, произведенной в отрасли i в объеме xij и поступающей для производственных нужд в отрасль j, равно
Считаем сложившуюся технологию производства во всех отраслях неизменной (за рассматриваемый период времени), означающую, что коэффициенты прямых затрат a ij постоянны. Тогда получаем следующее соотношение баланса, называемого моделью Леонтьева
, i = 1, 2,…, n . (1)
Введя вектор валового выпуска X, матрицу прямых затрат A и вектор конечного потребления Y
модель Леонтьева (1) можно записать в матричном виде
Матрица A ≥ 0, у которой все элементы a ij ≥ 0 (неотрицательны), называется продуктивной матрицей, если существует такой неотрицательный вектор X ≥ 0, для которого выполняется неравенство
Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором продукции выпускается больше, чем затрачивается на ее производство. Другими словами, при этом режиме создается конечный (прибавочный) продукт Y = X – AX > 0.
Модель Леонтьева с продуктивной матрицей A называется продуктивной моделью.
Для проверки продуктивности матрицы A достаточно существования обратной матрицы B = ( E – A ) -1 с неотрицательными элементами, где матрица E – единичная матрица
.
С помощью модели Леонтьева (2) можно выполнить три вида плановых расчетов, при условии соблюдения условия продуктивности матрицы A:
1) Зная (или задавая) объемы валовой продукции всех отраслей X можно определить объемы конечной продукции всех отраслей Y
2) Задавая величины конечной продукции всех отраслей Y можно определить величины валовой продукции каждой отрасли
X = ( E – A ) -1 Y (3)
3) Задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.
называется матрицей полных материальных затрат. Ее смысл следует из матричного равенства (3), которое можно записать в виде X = BY . Элементы матрицы B показывают, сколько всего необходимо произвести продукции в i-ой отрасли, для выпуска в сферу конечного потребления единицы продукции отрасли j.
Пример с использованием технологии Excel
Задача . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
1) Матрицу коэффициентов полных материальных затрат B
2) Проверить продуктивность матрицы A
2) Вектор валового выпуска X
3) Межотраслевые поставки продукции xij
Математическая модель и последовательность расчетов
Модель Леонтьева имеет вид
Матрица полных материальных затрат B равна
Продуктивность матрицы A проверяется, по вычисленной матрице B. Если эта матрица существует и все ее элементы неотрицательны, то матрица A продуктивна.
Вектор валового выпуска X рассчитывается по формуле
Межотраслевые поставки продукции xij вычисляются по формуле
Процесс решения задачи средствами Microsoft Excel
Для решения задачи межотраслевого баланса необходимо уметь выполнять с помощью Excel следующие операции над матрицами:
– Умножение матрицы на вектор
– Умножение двух матриц
– Транспонирование матрицы или вектора
– Сложение двух матриц
1. Задание Исходных данных задачи
Вызовите Microsoft Excel.
Введите матрицу A в ячейки с адресами А2:С4 и вектор Y в ячейки с адресами Е2:Е4 (рис. 1).
Рис. 1. Задание исходных данных и последовательное выполнение плановых расчетов
2. Вычисление матрицы коэффициентов полных материальных затрат B.
2.1. Введите единичную матрицу Е в ячейки с номерами А7:С9.
2.2. Вычислите матрицу Е – А. Матрица Е – А является разностью двух матриц Е и А. Для вычисления разности двух матриц необходимо проделать следующее:
– установите курсор мыши в левый верхний угол (это ячейка с адресом А12) результирующей матрицы Е – А, которая будет расположена в ячейках с адресами А12:С14;
– введите формулу =А7-А2 для вычисления первого элемента результирующей матрицы Е – А, предварительно установив английскую раскладку клавиатуры;
– введенную формулу скопируйте во все остальные ячейки результирующей матрицы. Для этого, установите курсор мыши в ячейку А12; наведите указатель мыши на точку в правом нижнем углу ячейки, так чтобы указатель мыши принял вид крестика; при нажатой левой кнопке мыши протяните указатель до ячейки С12, а затем так же протяните указатель мыши до ячейки С14.
В результате в ячейках А12:С14 появится искомая матрица, равная разности двух исходных матриц Е и А.
2.3. Вычислите матрицу B = ( E – A ) -1 , являющейся обратной по отношению к матрице Е – А. Матрица Е – А расположена в ячейках с адресами А12:С14. Для вычисления матрицы В необходимо проделать следующее:
– выделите диапазон ячеек А17:С19 для размещения матрицы В;
– нажмите на панели инструментов кнопку Вставка, а затем кнопку Функция. В появившемся окне в поле Категория выберите Математические, а в поле Выберите функцию – имя функции МОБР. Щелкните на кнопке ОК;
– появившееся диалоговое окно МОБР мышью отодвиньте в сторону от исходной матрицы Е – А и введите диапазон матрицы Е – А (диапазон ячеек А12:С14) в рабочее поле Массив (протащив указатель мыши при нажатой левой кнопке от ячейки А12 до ячейки С14);
– нажмите комбинацию клавиш Ctrl+Shift+Enter. Обратите внимание, что нажимать надо не клавишу ОК(!), а именно комбинацию клавиш Ctrl+Shift+Enter.
В диапазоне ячеек А17:С19 появится искомая обратная матрица ( E – A ) -1 , равная матрице B.
3. Проверка продуктивности матрицы А.
Поскольку матрица В найдена, следовательно она существует. Все элементы матрицы В неотрицательны, поэтому матрица В – продуктивна.
4. Вычисление вектора валового выпуска X .
Вычисление вектора валового выпуска X находим по матричной формуле X = BY , в которой матрица В вычислена, а вектор Y задан.
Вычисление вектора X = BY производится с помощью операции умножения матриц, а в данном случае – умножения матрицы В на вектор Y. Для этого необходимо:
– выделить диапазон ячеек Е7:Е9, где будет расположен вектор Х. Обратите внимание, что по правилам умножения матриц, размерность результирующей матрицы Х должна быть равна количеству строк матрицы В на количество столбцов матрицы Y. В нашем случае, размерность вектора Х равна: три строки на один столбец;
– нажать на панели инструментов кнопку Вставка, а затем кнопку Функция. В появившемся окне в поле Категория выберите Математические, а в поле Выберите функцию – имя функции МУМНОЖ. Щелкните на кнопке ОК;
– появившееся диалоговое окно МУМНОЖ мышью отодвиньте в сторону от исходных матриц В и Y и введите диапазон матрицы В (диапазон ячеек А17:С19) в рабочее поле Массив 1 (протащив указатель мыши при нажатой левой кнопке от ячейки А17 до ячейки С19), а диапазон вектора Y (ячейки Е2:Е4) в рабочее поле Массив 2 (рис. 2);
Рис. 2. Диалоговое окно умножения матриц МУМНОЖ
– нажмите комбинацию клавиш Ctrl+Shift+Enter. Обратите внимание, что нажимать надо не клавишу ОК(!), а именно комбинацию клавиш Ctrl+Shift+Enter.
В диапазоне ячеек Е7:Е9 появится искомый вектор Х.
5. Вычисление межотраслевых поставок продукции xij
Межотраслевые поставки продукции xij вычисляются по формуле
где a ij – элементы исходной матрицы А, расположенной в ячейках А2:С4, xj – элементы вектора Х, найденного выше в п. 4 и расположенные в ячейках Е7:Е9.
Для проведения вычислений xij необходимо проделать следующее.
5.1. Вычислить транспонированный вектор Х т относительно вектора Х. При этом вектор-столбец Х станет вектором-строкой Х т . Это необходимо для согласования размерностей дальнейшего умножения элементов векторов.
– выделить указателем мыши при нажатой левой кнопке ячейки Е12:G12, в которых будет располагаться транспонированный вектор Х т ;
– нажать на панели инструментов кнопку Вставка, а затем кнопку Функция. В появившемся окне в поле Категория выберите Ссылки и массивы, а в поле Выберите функцию – имя функции ТРАНСП (рис. 3). Щелкните на кнопке ОК;
– появившееся диалоговое окно ТРАНСП мышью отодвиньте в сторону от исходного вектора Х и введите диапазон вектора Х (диапазон ячеек Е7:Е9) в рабочее поле Массив (протащив указатель мыши при нажатой левой кнопке от ячейки Е7 до ячейки Е9);
– нажмите сочетание клавиш Ctrl+Shift+Enter.
Рис. 3. Диалоговое окно транспонирования матрицы
В результате в поле ячеек Е12:G12 расположится транспонированный вектор Х т .
5.2. Вычислить межотраслевые поставки продукции xij . Для этого проделать следующие операции:
– поставить курсор мыши в ячейку А22, в которой будет расположено значение x11. В этой ячейке набрать формулу =A2*E12, которая означает, что x11 = a 11 x1 .
– введенную формулу скопируйте во все остальные ячейки первой строки (в ячейки А22:С22, протащив мышью крестик в правом нижнем углу от ячейки А22 при нажатой левой кнопке мыши, до ячейки С22. При этом будут вычислены x12 = a 12 x2 и x13 = a 13 x3 .
Затем в ячейке А23 наберите формулу =A3*E12 и повторяя аналогичную процедуру, получите значения x21 = a 21 x1 , x22 = a 22 x2 и x23 = a 23 x3 . Повторите аналогичные действия для ячеек А24:С24.
В результате все межотраслевые поставки продукции будут найдены и расположатся в матрице с ячейками А22:С24.
Тема 2. Экономико-математическая модель международной торговли (линейная модель обмена). Моделирование средствами Excel
Рассмотрим бюджеты n стран, которые обозначим как x1, x2, … , x n .
Предположим, что национальный доход x j страны j затрачивается на закупку товаров внутри страны и на импорт из других стран.
Обозначим через xij количество средств страны j расходуемое на закупку товаров из страны i, при этом x j j – затраты на закупку товаров внутри страны j. Тогда сумма всех затрат страны j, идущее на закупку товаров как внутри страны, так и на импорт из других стран должна равняться национальному доходу страны x j , т.е.
, j = 1, 2,…, n . (4)
Разделив обе части равенства (4) на x j и введя коэффициенты получим
, j = 1, 2,…, n (5)
Коэффициенты равны доли национального дохода страны j расходуемую на закупку товаров у страны i.
Матрица A коэффициентов
(6)
называется структурной матрицей торговли. Понятно, что сумма элементов каждого столбца равна единице.
С другой стороны, количество средств страны j расходуемое на закупку товаров из страны i и равное xij, является выручкой для страны i за свой товар, который у нее закупила страна j. Суммарная выручка i-ой страны равна
, i = 1, 2,…, n (7)
Так как , то и равенство (7) можно записать в виде
, i = 1, 2,…, n . (8)
Международная торговля называется сбалансированной, если сумма платежей (затрат) каждого государства равна его суммарной выручке от внешней и внутренней торговли.
В сбалансированной системе международной торговли не должно быть дефицита, другими словами, у каждой страны выручка от торговли должна быть не меньше ее национального дохода, т.е.
, i = 1, 2,…, n .
Одновременное выполнение этих неравенств может иметь место только в том случае, если
, i = 1, 2,…, n , (9)
т.е. у всех торгующих стран выручка от внешней и внутренней торговли должна совпадать с национальным доходом.
Равенства (9), с использованием (8), можно записать в матричном виде
где А – структурная матрица (6) международной торговли; Х – вектор национальных доходов стран
.
Матричное уравнение (10) соответствует задаче на собственное значение и собственный вектор матрицы А. Очевидно, что собственное значение матрицы А, согласно уравнению (10), равно 1, а собственный вектор, соответствующий этому собственному значению, равен Х.
Таким образом, баланс в международной торговле достигается тогда, когда собственное значение структурной матрицы международной торговли равно единице, а вектор национальных доходов торгующих стран является собственным вектором, соответствующим этому единичному собственному значении.
С помощью линейной модели международной торговли можно, зная структурную матрицу международной торговли А найти такие величины национальных доходов торгующих стран (вектор Х), чтобы международная торговля была сбалансированной.
Моделирование с использованием технологии Excel.
Определение собственного вектора X матрицы А с помощью средств Micro so ft Excel невозможно.
Поэтому математическую модель международной торговли сводят к задаче линейного программирования. Для этого, систему уравнений
где Е – единичная матрица
которая получается из уравнений (10) переносом правой части в левую, трактуют как ограничения-равенства.
Кроме того, вводят новое ограничение-неравенство
,
отражающее условие, по которому сумма бюджетов всех стран должна быть не больше заданной величины S.
В качестве целевой функции вводится сумма бюджетов всех стран, которая должна достигать максимума:
Итак, математическая модель сбалансированной международной торговли сводится к следующей оптимизационной задаче линейного программирования. Необходимо найти максимум целевой функции
Пример с использованием технологии Excel
Задача . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 7680 млн.ден.ед.
Решение задачи средствами Excel
Методика решения задачи линейного программирования с помощью средств Поиска решения Excel подробно рассматривалась в Лабораторной работе №1 и поэтому здесь уже рассматриваться не будет.
Рис. 4. Исходные данные в Excel
Задание исходных данных на рабочем листе Excel приведено на рис.4.
В ячейки В2:Е6 занесены коэффициенты при системе ограничений, в ячейках G2:G6 содержатся ограничения в правых частях, в ячейки I2:I6 занесены формулы левых частей ограничений, ячейки В9:Е9 содержат изменяемые переменные . Например, в ячейке I2 записана формула ограничений =СУММПРОИЗВ(В2:Е2;В9:Е9). Аналогичные формулы записаны в ячейках I3:I6. Формула целевой функции =СУММ(В9:Е9) занесена в ячейку С10.
Рис. 5.Решение задачи средствами Excel
Процесс решения – занесение в окно Поиск решения ячейки с формулой целевой функции, занесение изменяемых ячеек, внесение ограничений приведено на рис. 5. В окне Параметры необходимо отметить: Линейная модель, Неотрицательные значения, Автоматическое масштабирование.
На рис. 5 приведены также результаты решения, согласно которым национальные доходы четырех стран равны соответственно 1015.359, 1458.228, 3251.308, 1955.105 млн.ден.ед. Из содержимого ячеек I2:I6 видно, что все ограничения выполнены. Значение целевой функции (ячейка С10) равно 7680 млн.ден.ед.
Индивидуальные задания по Теме 1
Задание 1 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 2 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 3 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 4 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 5 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 6 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 7 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 8 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 9 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 10 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 11 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Задание 12 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:
.
Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции xij
Индивидуальные задания по Теме 2
Задание 1 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 4590 млн.ден.ед.
Задание 2 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 15055 млн.ден.ед.
Задание 3 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 9000 млн.ден.ед.
Задание 4 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 59550 млн.ден.ед.
Задание 5 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 15590 млн.ден.ед.
Задание 6 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 51503 млн.ден.ед.
Задание 7 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 25590 млн.ден.ед.
Задание 8 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна
,
а сумма бюджетов стран не превышает 83355 млн.ден.ед.
1. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – М.: Вузовский учебник, 2004
[spoiler title=”источники:”]
http://axd.semestr.ru/econ/balans.php
http://meu.rsuh.ru/madera/HTML-LR5.htm
[/spoiler]
Модель
Леонтьева характеризует связи между
выпуском продукции в одной отрасли и
затратами, расходованием продукции
всех участвующих отраслей, необходимым
для обеспечения этого выпуска.
Обозначим:
![]() –общий валовый
–общий валовый
объём продукции i–й
отрасли,![]()
![]() –объём продукции
–объём продукции
i–й отрасли,
потребляемыйj–й
отраслью в процессе производства при
выпуске объёма продукции![]()
![]() –объём конечного
–объём конечного
продукта i–й
отрасли для непроизводственного
потребления,![]() .
.
Так
как валовый объём продукции любой i–й
отрасли равен суммарному объёму
продукции, потребляемойпотраслями
и конечного продукта, то получаем
уравнение:
![]() ,
,
![]() .
.
В
стоимостном межотраслевом балансе все
величины, входящие в это уравнение,
имеют стоимостное выражение. Межотраслевой
баланс может быть составлен в денежной
и натуральной форме.
Технология
производства остается на одном и том
же уровне довольно длительное время,
и, следовательно, объём потребления j–й
отраслью продукцииi–й
отрасли при производстве своей продукции
в объеме![]() единиц
единиц
есть технологическая константа:
![]() ,
,
![]() ,
,
![]()
это
коэффициенты прямых затрат. Показывают
затраты продукции i–й
отрасли на производство единицы продукцийj–й отрасли.
Этот
важный факт был установлен В. Леонтьевым
на основании анализа экономики США в
период перед Второй мировой войной: в
течение длительного времени величины
![]() –
–
коэффициенты прямых затрат меняются
очень незначительно и потому могут
рассматриваться как постоянные числа.
Согласно
этой гипотезе выразим:
![]() .
.
Тогда
уравнения межотраслевого баланса можно
переписать в виде системы уравнений:

Введем в
рассмотрение соответственно:
 –вектор-столбец
–вектор-столбец
объемов производственной продукции
(вектор валового выпуска);
 –вектор-столбец
–вектор-столбец
объемов продукции конечного потребления
(вектор конечного потребления);
 –матрица
–матрица
коэффициентов прямых затрат (технологическая
или структурная матрица).
Тогда
система уравнений в матричной форме
примет вид:
![]()
Это
соотношение называют уравнением
линейного межотраслевого баланса или
модели Леонтьева.
Уравнение
межотраслевого баланса можно использовать
в двух целях, а именно:
Рассмотрим
решение задачи первого типа.
Известен
вектор объемов валового выпуска
![]() .
.
Требуется вычислить вектор объемов
конечного потребления![]()
Пример
10. Пусть вектор![]() выпуска
выпуска
продукции отрасли и матрица внутреннего
потребленияAдля трех
различных отраслей производства имеют
соответственно вид
 ,
,

Требуется
вычислить вектор объемов конечного
потребления
![]()
Решение.
Из
матричного уравнения межотраслевого
баланса
![]() получим для вектора объемов конечного
получим для вектора объемов конечного
потребления выражение в виде:
![]() .
.
Находим
матрицы:
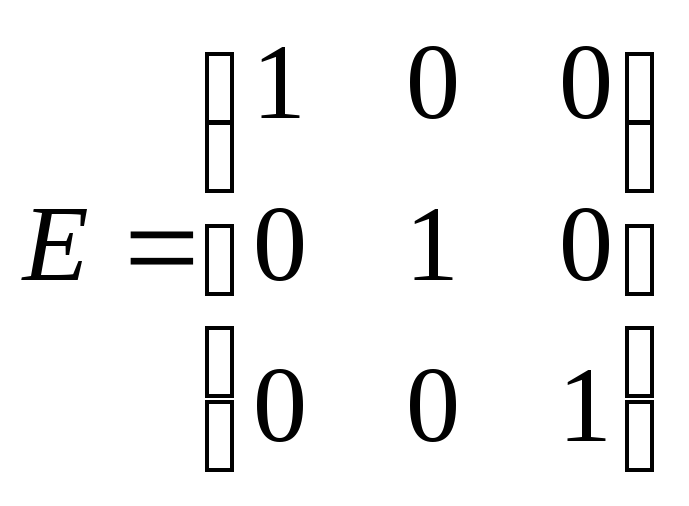
 .
.
Тогда
по формуле получим:

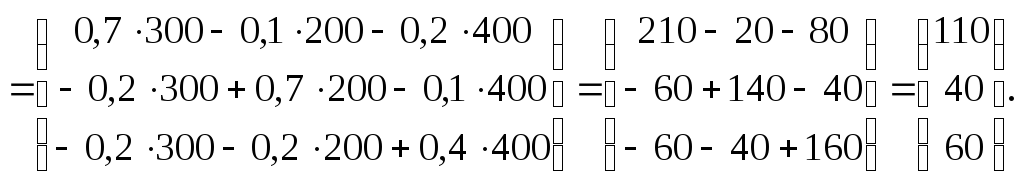
Ответ: ,
,
то есть объемы конечного продукта
составляют для: первой отрасли – 110
ед.;
второй
отрасли – 40 ед.;
третьей
отрасли – 60 ед.
Рассмотрим
решение задачи второго типа.
Для
некоторого периода времени известен
вектор конечного потребления
![]() и
и
матрица коэффициентов прямых затратA. Требуется определить
вектор валового выпуска![]() .
.
Решение
этой задачи в общем виде:
1.
![]()
2.
![]()
![]()
![]()
Однако
такая система в силу прикладного
характера данной задачи имеет особенности:
все элементы матрицы A,
и векторов![]() и
и![]() должны
должны
быть неотрицательными.
Матрица
A, все элементы которой
неотрицательны, называетсяпродуктивной,
если для любого вектора![]() с неотрицательными компонентами
с неотрицательными компонентами
существует решение уравнения вектор![]() ,
,
все элементы которого неотрицательны.
В таком случае и модель Леонтьева
называется продуктивной.
Матрица
![]() называется матрицейполных затрат.
называется матрицейполных затрат.
Существует
несколько критериев продуктивности
матрицы A. Используем
два из них.
Первый
критерий продуктивности. МатрицаAпродуктивна тогда и только тогда, когда
матрица![]() существует и ее элементы неотрицательны.
существует и ее элементы неотрицательны.
Второй
критерий продуктивности. МатрицаAс неотрицательными элементами продуктивна,
если сумма элементов по любому ее столбцу
(строке) не превосходит единицы:
![]() ,
,
причем
хотя бы для одного столбца (строки) эта
сумма строго меньше единицы.
Пример 11.Таблица 11 содержит данные баланса трех
отраслей промышленности за некоторый
период.
Таблица 11
|
№ п/п |
Отрасль |
Потребление |
Конечный |
Валовой выпуск |
||
|
1 |
2 |
3 |
||||
|
1 |
Добыча |
5 |
35 |
20 |
40 |
100 |
|
2 |
Энергетика |
10 |
10 |
20 |
60 |
100 |
|
3 |
Машиностроение |
20 |
10 |
10 |
10 |
50 |
Требуется найти
объем валового выпуска продукции, если
конечное потребление по отраслям
увеличить соответственно до 60, 70 и 30.
Решение.
Выпишем
векторы валового выпуска
![]() и
и
конечного потребления![]() :
:
 ,
,
 ,
,
Согласно
формулам для коэффициентов прямых
затрат
![]() ,
,
вычислим![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
В результате
получаем матрицу коэффициентов прямых
затрат:
 .
.
Требования
к неотрицательности элементов всех
матриц выполнены:
![]() неотрицателен;
неотрицателен;![]() неотрицателен;A– из неотрицательных
неотрицателен;A– из неотрицательных
элементов.
Проверим,
что матрица Aудовлетворяет второму критерию
продуктивности, т.е. найдем суммы ее
элементов по всем строчкам и столбцам
соответственно.
0,05 + 0,35 +
0,4 = 0,8 < 1;
0,1 + 0,1 +
0,4 = 0,6 < 1;
0,2 + 0,1 +
0,2 = 0,5 < 1;
0,05 + 0,15 +
0,2 = 0,4 < 1;
0,35 + 0,1 +
0,1 = 0,55 < 1;
0,4 + 0,4 +
0,2 = 1.
Поскольку
сумма элементов по любому ее столбцу
(строке) не превосходит единицы и хотя
бы для одного столбца (строки) эта сумма
строго меньше единицы, то второй критерий
выполнен.
Для
проверки первого критерия продуктивности
найдем матрицу
![]() ,
,
это есть матрица полных затрат.
1.
По условию:
 ;
; ;
;
 .
.
2.
Найдем определитель этой матрицы,
разложив по первой строке:
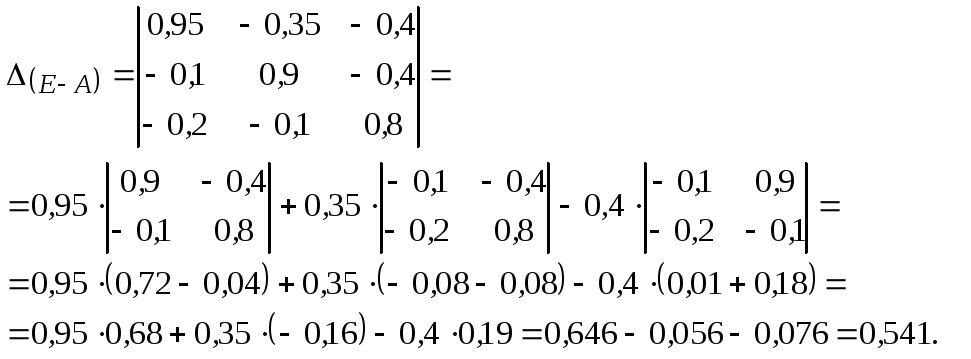
3. Вычисляем
алгебраические дополнения.
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В результате
вычислений, по формуле обратной матрицы,
составим матрицу полных затрат (для
вычислений обратной матрицы можно
использовать функции программы EXCEL,
см.приложение 2):
 .
.
Поскольку
существует обратная матрица
![]() и ее элементы неотрицательны, то и первый
и ее элементы неотрицательны, то и первый
критерий продуктивности выполнен.
Вывод.Все условия продуктивности выполнены.
Следовательно, существует и единственное
решение уравнения![]()
Компоненты
![]() неизвестного
неизвестного![]() можно найти из системы уравнений, которая
можно найти из системы уравнений, которая
имеет вид:

Новый
вектор конечного продукта должен иметь
вид:
 .
.
Новое
значение валового выпуска находим по
формуле
![]() .
.

Ответ:чтобы обеспечить заданное увеличение
компонент вектора конечного продукта
с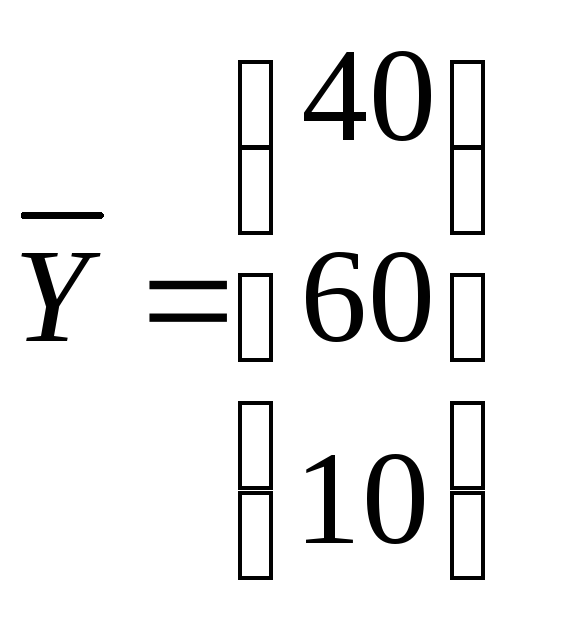 до
до ,
,
необходимо увеличить соответствующие
валовые выпуски:
добычу и переработку
углеводородов со 100 до 152,14, то есть на
52,14%,
уровень
энергетики со 100 до 135,8, то есть на 35,8%,
выпуск
машиностроения с 50 до 92,51, то есть на
42,51%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лекция 9. Линейные экономические модели
Модель Леонтьева многоотраслевой экономики
Эффективное ведение народного хозяйства предполагает наличие баланса между отдельными отраслями.
Предположим, что вся производящая сфера народного хозяйства разбита на некоторое число n отраслей, каждая из которых производит свой однородный продукт, причем разные отрасли производят разные продукты. Разумеется, такое представление об отрасли является в значительной мере абстракцией, так как в реальной экономике отрасль определяется не только названием выпускаемого продукта, но и ведомственной принадлежностью своих предприятий (например, данному министерству, тресту и т.п.). Однако представление об отрасли в указанном выше смысле (как «чистой» отрасли) все же полезно, так как оно позволяет провести анализ сложившейся технологической структуры народного хозяйства, изучить функционирование народного хозяйства «в первом приближении».
Итак, предполагаем, что имеется n различных отраслей O1,…,On, каждая из которых производит свой продукт. В дальнейшем отрасль Оi , будем называть «i-я отрасль». В процессе производства своего продукта каждая отрасль нуждается в продукции других отраслей (производственное потребление). Будем вести речь о некотором определенном промежутки времени [Т0, T1], (обычно таким промежутком служит плановый год) и введем следующие обозначения:
хi – общий объем продукции отрасли i за данный промежуток времени – так называемый валовой выпуск отрасли i.
xij – объем продукции отрасли i, расходуемый отраслью j в процессе производства;
уi – объем продукции отрасли i, предназначенный к потреблению в непроизводственной сфере – объем конечного потребления. Этот объем составляет обычно более 75% всей производственной продукции. В него входят создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.
Рекомендуемые материалы
В течение отчетного года были произведены и реализованы изделия А, В, С в количестве 5 000 шт. каждое. Цены изделий А, В, С – 700, 550, 350 д. е. соответственно. При этом прямые переменные материальные затраты на изделие составили по А – 300, по В –
Домашнее задание вариант 7
FREE
Основные макроэкономические показатели
Черная масса вала руля – 8,5 кг. Чистая масса – 7 кг. Цена заготовки – 1,15 д.е. Цена отходов – 7,01 д.е. за тонну. Заработная плата на всех опера-циях вала составила 0,28 д.е. Расходы по цеху составляют 250%, общеза-водские расходы – 130% от заработ
Вариант 7 – ДЗ №1 – Микроэкономика
Указанные величины можно свести в таблицу.
Таблица 9
Показатели работы отраслей
|
Производственное потребление |
Конечное потребление |
Валовой выпуск |
|
|
|
|
Балансовый характер этой таблицы выражается в том, что при любом i= l, …, n должно выполняться соотношение
xi = xi1 + xi2 +…+ xin + yi, (14)
означающее, что валовой выпуск xi расходуется на производственное потребление, равное xi1 + xi2 +…+ xin, и непроизводственное потребление, равное уi. Будем называть (14) соотношениями баланса.
Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки, киловатт-часы и т.п.), или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевой балансы. Для определенности в дальнейшем будем иметь в виду (если не оговорено противное) стоимостной баланс.
В. Леонтьев, рассматривая развитие американской экономики в предвоенный период, обратил внимание на важное обстоятельство. А именно, величины  остаются постоянными в течение ряда лет. Это обуславливается примерным постоянством используемой технологии.
остаются постоянными в течение ряда лет. Это обуславливается примерным постоянством используемой технологии.
В соответствии со сказанным сделаем такое допущение: для выпуска любого объема хj продукции отрасли j необходимо затратить продукцию отрасли i в качестве aijxj , где аij – постоянный коэффициент. Проще говоря, материальные издержки пропорциональны объему производимой продукции. Это допущение постулирует, как говорят, линейность существующей технологии. Принцип линейности распространяется и на другие виды издержек. Например, на оплату труда, а также на нормативную прибыль. Итак, согласно гипотезе линейности имеем
xij = aij xj(i, j =1, …, n). (15)
Коэффициенты аij называют коэффициентами прямых затрат (коэффициент материалоемкости).
В предположении линейности соотношения (14) принимают вид:
x1 = a11x1 + a12x2 + … +a1n xn + y1
x2 = a21x1 + a22x2 + … +a2n xn + y2
…………………………………..
xn = an1x1 + an2x2 + … +ann xn + yn,
или, в матричной записи,
 , (16)
, (16)
где

Вектор  называется вектором валового выпуска, вектор
называется вектором валового выпуска, вектор  – вектором конечного потребления, а матрица А – матрицей прямых затрат. Соотношение (16) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов
– вектором конечного потребления, а матрица А – матрицей прямых затрат. Соотношение (16) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов  и
и  это соотношение называют также моделью Леонтьева.
это соотношение называют также моделью Леонтьева.
Уравнения межотраслевого баланса можно использовать для целей планирования. В этом случае задача ставится так: для предстоящего планового периода [T0,T1] задается вектор  конечного потребления. Требуется определить вектор
конечного потребления. Требуется определить вектор  валового выпуска. Проще говоря, нужно решить задачу: сколько следует произвести продукции различных видов, чтобы обеспечить заданный уровень конечного потребления? В этом случае необходимо решить систему линейных уравнений (16) с неизвестным вектором
валового выпуска. Проще говоря, нужно решить задачу: сколько следует произвести продукции различных видов, чтобы обеспечить заданный уровень конечного потребления? В этом случае необходимо решить систему линейных уравнений (16) с неизвестным вектором  при заданных матрице А и вектору
при заданных матрице А и вектору  . При этом нужно иметь в виду следующие особенности системы (16):
. При этом нужно иметь в виду следующие особенности системы (16):
1. Все компоненты матрицы А и вектора  неотрицательны (это вытекает из экономического смысла А и
неотрицательны (это вытекает из экономического смысла А и  ). Для краткости будем говорить о неотрицательности самой матрицы А и вектора
). Для краткости будем говорить о неотрицательности самой матрицы А и вектора  и записывать это так:
и записывать это так:  .
.
2. Все компоненты вектора  также должны быть неотрицательными:
также должны быть неотрицательными:  .
.
Замечание. Обратим внимание на смысл коэффициентов аij прямых затрат в случае стоимостного (а не натурального) баланса. В этом случае из (16) видно, что aij совпадает со значением хij при xj = 1 (1 руб.).
Таким образом, аij есть стоимость продукции отрасли i, вложенной в 1 руб. продукции отрасли j. Отсюда, между прочим, видно, что стоимостной подход по сравнению с натуральным обладает более широкими возможностями, при таком подходе уже необязательно рассматривать «чистые», т. е. однопродуктовые, отрасли. Ведь и в случае многопродуктовых отраслей тоже можно говорить о стоимостном вкладе одной отрасли в выпуск 1 руб. продукции другой отрасли; скажем, о вкладе промышленной сферы в выпуск 1 руб. сельскохозяйственной продукции или о вкладе промышленной группы А (производство предметов потребления). Вместе с тем надо понимать, что планирование исключительно в стоимостных величинах может легко привести к дисбалансу потоков материально-технического снабжения.
Пример 31. Таблица 10 содержит данные баланса трех отраслей промышленности за некоторый период времени. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить, соответственно, до 60, 70и 30 условных денежных единиц.
Таблица 10
Показатели работы 3 отраслей
|
№ п/п |
Отрасль |
Потребление |
Конечный продукт |
Валовый выпуск |
||
|
1 |
2 |
3 |
||||
|
1 2 3 |
Добыча и переработка углеводородов Энергетика Машиностроение |
5 10 20 |
35 10 10 |
20 20 10 |
40 60 10 |
100 100 50 |
Решение. Выпишем векторы валового выпуска и конечного потребления и матрицу коэффициентов прямых затрат. Согласно формуле (9.1), имеем:
 ,
,  ,
,  .
.
Матрица А удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь
 . (9.2)
. (9.2)
Требуется найти новый вектор валового выпуска  , удовлетворяющий соотношениям баланса в предположении, что матрица А не изменяется. В таком случае компоненты
, удовлетворяющий соотношениям баланса в предположении, что матрица А не изменяется. В таком случае компоненты  неизвестного вектора
неизвестного вектора  находятся из системы уравнений, которая в матричной форме имеет следующий вид:
находятся из системы уравнений, которая в матричной форме имеет следующий вид:
 , или
, или  . (9.3)
. (9.3)
Матрица этой системы
 .
.
Решение системы линейных уравнений (9.3) при заданном векторе правой части (9.12) (например, методом Гаусса) дает новый вектор  как решение уравнений межотраслевого баланса:
как решение уравнений межотраслевого баланса:
 .
.
Таким образом, для того чтобы обеспечить заданное увеличение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и переработку углеводородов на 52,2 %, уровень энергетики – на 35,8 % и выпуск машиностроения – на 85 % – по сравнению с исходными величинами, указанными в табл. 9.2.
Продуктивные модели Леонтьева
Определение. Матрица А ³ 0 называется продуктивной, если для любого вектора  ³ 0 существует решение
³ 0 существует решение  ³ 0 уравнения (9.1)
³ 0 уравнения (9.1)
 (13)
(13)
В этом случае модель Леонтьева, определяемая матрицей А, тоже называется продуктивной.
Итак, модель Леонтьева продуктивна, если любой вектор  ³ 0 конечного потребления можно получить при валовом выпуске
³ 0 конечного потребления можно получить при валовом выпуске  ³ 0.
³ 0.
Нижеследующая теорема 1 показывает, что нет необходимости требовать существования решения  ³ 0 уравнения (9.1) для любого вектора
³ 0 уравнения (9.1) для любого вектора  ³ 0. Достаточно, чтобы такое решение существовало хотя бы для одного вектора
³ 0. Достаточно, чтобы такое решение существовало хотя бы для одного вектора  ³ 0.
³ 0.
Условимся в дальнейшем писать  ³ 0 и называть вектор
³ 0 и называть вектор  положительным, если все компоненты этого вектора строго положительны.
положительным, если все компоненты этого вектора строго положительны.
Теорема 9.1 (первый критерий продуктивности.) Если А ³ 0 и для некоторого положительного вектора  * уравнение (7.3) имеет решение
* уравнение (7.3) имеет решение  * ³ 0, то матрица А продуктивна.
* ³ 0, то матрица А продуктивна.
Заметим, что на самом деле  > 0, что следует из
> 0, что следует из  * = А
* = А * +
* +  * и А ³ 0,
* и А ³ 0,  *³ 0,
*³ 0,  * ³ 0.
* ³ 0.
Уравнение Леонтьева (9.1) можно записать следующим образом:
(Е – А)  =
=  , (9.4)
, (9.4)
где Е – единичная матрица.
Возникает, естественно, вопрос об обращении матрицы Е – А.
Понятно, что если обратная матрица (Е – А)-1 существует, то из (9.4) вытекает
 (Е – А)-1
(Е – А)-1 (9.5)
(9.5)
Следующая теорема дает более эффективное условие продуктивности, чем теорема 9.1
Теорема 9.2 (второй критерий продуктивности). Матрица А ³ 0 продуктивна тогда и только тогда, когда матрица (Е – А)-1 существует и неотрицательна.
Доказательство. Если (Е – А)-1 существует и ³ 0, то из формулы (9.5) следует продуктивность матрицы А.
Обратно, пусть матрица А продуктивна, Рассмотрим следующие системы уравнений:
(Е – А) 
 , (Е – А)
, (Е – А)  ,…, (Е – А)
,…, (Е – А)  , где е1, е2,…, еn – столбцы единичной матрицы. Каждая из этих систем в силу продуктивности матрицы А имеет неотрицательное решение, т.е. существуют такие векторы (столбцы)
, где е1, е2,…, еn – столбцы единичной матрицы. Каждая из этих систем в силу продуктивности матрицы А имеет неотрицательное решение, т.е. существуют такие векторы (столбцы)  ³ 0,
³ 0,  ³ 0,…,
³ 0,…,  ³ 0, что
³ 0, что
(Е – А)  =
=  , (Е – А)
, (Е – А) =
=  ,…, (Е – А)
,…, (Е – А)  =
=  . (9.6)
. (9.6)
Обозначим через С матрицу, составленную из столбцов с1,с2,…,сп. Тогда вместо п равенств (9.6) можно написать одно: (Е – А)С = Е.
Следовательно, матрица (Е – А) имеет обратную С, причем С ³ 0. Теорема доказана.
Пример 32. Исследуем на продуктивность матрицу

В данном случае

Необходимые вычисления предоставим читателю провести самостоятельно. Получаем матрицу (Е – А)-1, которая существует и равна

Мы видим, что эта матрица неотрицательна. Следовательно, А продуктивна.
Теорема 3. (третий критерий продуктивности). Матрица А ³ 0 продуктивна тогда и только тогда, когда сходиться бесконечный ряд.
Е + А + А2 + … (9.7)
Полученный нами критерий продуктивности матрицы А (сходимость ряда (9.7)) в ряде случаев может быть использован для проверки матрицы А на продуктивность. Покажем, например, что если сумма элементов любого столбца неотрицательной матрицы А меньше 1*, то А продуктивна. Действительно, пусть q – наибольшая из указанных сумм, q <1. Ясно, что тогда все элементы матрицы А не превосходят q. Из правила перемножения матриц легко вывести, что любой элемент матрицы А2 не превосходит q2:
(A2)ij = ai1ajl + ai2aj2 +…+ ainanj £ q (ai1 +…+ anj) < q2 <1.
Точно так же получим, что элементы матрицы А3 не превосходит q3 и т.д. Отсюда следует сходимость ряда (9.7), а значит, и продуктивность матрицы А.
Например для матрицы

сумма элементов каждого столбца меньше единицы. Следовательно, А продуктивна.
Аналогично доказывается, что если в неотрицательной матрице А сумма элементов любой строки меньше 1, то матрица А продуктивна. Впрочем, то же самое можно вывести и из следующего предложения: если продуктивна матрица А, то продуктивна и матрица Ат ,что следует из теоремы 2.
Пусть А  0 – продуктивная матрица. Запасом продуктивности матрицы А назовем такое число
0 – продуктивная матрица. Запасом продуктивности матрицы А назовем такое число  , что все матрицы
, что все матрицы  , где 1<
, где 1< <1 +
<1 +  , продуктивны, а матрица (1+
, продуктивны, а матрица (1+ )А – не продуктивна.
)А – не продуктивна.
Пример 33. Выяснить, какой запас продуктивности имеет матрица А из примера 30.
Решение. Будем руководствоваться критерием продуктивности из теоремы 2 (существование неотрицательной матрицы (Е – А)-1). В данном случае

Определитель этой матрицы
 .
.
Обратной матрицей будет
 .
.
Для продуктивности  нужно, чтобы все элементы обратной матрицы были неотрицательны, т.е.
нужно, чтобы все элементы обратной матрицы были неотрицательны, т.е.  ,
,  ,
,  . Имеем
. Имеем  при
при  ,
,  . Отсюда матрица
. Отсюда матрица  продуктивной при
продуктивной при  , т.е.
, т.е.  . Запас продуктивности матрицы А равен 0,015.
. Запас продуктивности матрицы А равен 0,015.
Задания для самостоятельной работы
Задача 1. Отрасль состоит из четырех предприятий: вектор выпуска продукции и матрица коэффициентов прямых затрат имеют вид
 ,
,  .
.
Найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.
Задача 2. Предприятие выпускает три вида продукции с использованием трех видов сырья, характеристики производства указаны в табл. 9.3.
Таблица 9.3
Данные по выпуску продукции
|
Вид сырья |
Расход сырья по видам продукции, вес. ед./изд. |
Запас сырья, вес. ед. |
||
|
1 |
2 |
3 |
||
|
1 2 3 |
5 10 9 |
12 6 11 |
7 8 4 |
2350 2060 2270 |
Найти объем выпуска продукции каждого вида при заданных запасах сырья.
Задача 3. В условиях примера 2 из 2.3.3 определить прирост объемов валовых выпусков по каждой отрасли (в процентах), если конечное потребление увеличить по отраслям, соответственно, на 30, 10 и 50 %. Решить задачу методом обратной матрицы и методом Гаусса.
Задача 4. Исследовать на продуктивность матрицу
 .
.
Найти запас продуктивности.
Лекция 10. Линейные экономические модели:
модель равновесных цен, модель международной торговли
Модель равновесных цен
Рассмотрим теперь балансовую модель, двойственную к модели Леонтьева – так называемую модель равновесных цен. Пусть, как и прежде, А – матрица прямых затрат,  (xl, x2,…,xn) – вектор валового выпуска. Обозначим через
(xl, x2,…,xn) – вектор валового выпуска. Обозначим через  (р1, р2, …рn – вектор цен, i-я координата которого равна цене единицы продукции i-й отрасли; тогда, например, первая отрасль получит доход, равный p1, х1.
(р1, р2, …рn – вектор цен, i-я координата которого равна цене единицы продукции i-й отрасли; тогда, например, первая отрасль получит доход, равный p1, х1.
Часть своего дохода эта отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции ей необходима продукция первой отрасли в объеме a11, второй отрасли в объеме а21, n-й отрасли в объеме an1 т. д. На покупку этой продукции ею будет затрачена сумма, равная a11 p1 + a21 p2 +…+ anl pn. Следовательно, для выпуска продукции в объеме х1 первой отрасли необходимо потратить на закупку продукции других отраслей сумму равную x1(a11p1 + a21p2 +…+ an1pn). Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим V1 (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
Таким образом, имеет место следующее равенство:
x1 p1 = x1 (a11 p1 +a21 p2 +… +an1 pn) + V1.
Разделив это равенство на х1 получаем
p1 = (a11 p1 +a21 p2 +… +an1 pn) + v1,
где v1  – норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
– норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
Подобным же образом получаем для остальных отраслей
p2 = a12 p1 + a22 p2 + … + an2 pn +v2
……………………………………
pn = a1n p1 + a2n p2 +…+ ann pn +v2
Найденные равенства могут быть записаны в матричной форме следующим образом:
 , (9.8)
, (9.8)
где  – вектор норм добавленной стоимости.
– вектор норм добавленной стоимости.
Как мы видим, полученные уравнения очень похожи на уравнения модели Леонтьева с той лишь разницей, что  заменен на
заменен на ,
, – на
– на , А – на Ат.
, А – на Ат.
Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукцию отраслей. Она также позволяет прогнозировать изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.
Пример 34. Рассмотрим экономическую систему, состоящую из трех отраслей. Назовем их условно: топливно-энергетическая отрасль, промышленность и сельское хозяйство. Пусть

– транспонированная матрица прямых затрат,  = (4;10;4)
= (4;10;4)
– вектор норм добавленной стоимости.
Определим равновесные цены. Для этого, как и в модели Леонтьева, воспользуемся формулой (9.8):
 ,
,
где СТ = (Е – АТ)-1 транспонированная матрица полных затрат.
После необходимых вычислений имеем

Отсюда получаем, что  .
.
Допустим теперь, что в топливно-энергетической отрасли произойдет увеличение нормы добавленной стоимости на 1,11. Определим равновесные цены в этом случае. Принимая во внимание, что  (5,11;10;4), находим, что
(5,11;10;4), находим, что

Таким образом, продукция первой отрасли подорожала на 14,5 %, второй – на 3,5% третьей отрасли – на 4,17%. Нетрудно также, зная объемы выпуска, подсчитать вызванную этим повышением инфляцию.
Модель международной торговли.
Собственные векторы и собственные значения матриц
Модель международной торговли (кратко: модель обмена) служит для ответа на следующий вопрос: какими должны быть соотношения между государственными бюджетами стран, торгующих между собой, чтобы торговля была взаимовыгодной, т.е. не было значительного дефицита торгового баланса для каждой из стран- участниц.
Проблема достаточно важна, так как дефицит в торговле между странами порождает такие явления, как лицензии, квоты, таможенные пошлины и даже торговые войны.
Для простоты изложения рассмотрим три страны-участницы торговли с государственными бюджетами Х1, Х2, Х3, которые условно назовем США, Германия, и Кувейт. Будем считать, что весь госбюджет каждой страны тратится на закупки товаров либо внутри страны, либо на импорт из других стран. Пусть, скажем, США тратят половину своего бюджета на закупку товаров внутри страны,  бюджета – на товары из Германии, оставшуюся
бюджета – на товары из Германии, оставшуюся  бюджета – на товары из Кувейта. Кувейт, в свою очередь, тратит
бюджета – на товары из Кувейта. Кувейт, в свою очередь, тратит  бюджета на закупки в Германии и ничего не закупает внутри страны.
бюджета на закупки в Германии и ничего не закупает внутри страны.
Введем структурную матрицу торговли:
США Германия Кувейт

Вообще, пусть аij – часть госбюджета, которую j-я стана тратит на закупки товаров i-й страны. Заметим, что сумма элементов матрицы А в каждом столбце равна единице.
После подведения итогов торговля за год страна под номером i получит выручку pi = ai1X1 + ai2X2 + ai3X3. Например, США будут иметь выручку

доля США доля Германии доля Кувейта
Для того чтобы торговля была сбалансированной, необходимо потребовать бездефицитность торговли для каждой страны:
 для всех i
для всех i
Предложение 1. Условием бездефицитной торговли являются равенства p = Xi, i = 1,2,3.
В матричной форме утверждение, содержащееся в предложении 1, выглядит следующим образом:
АХ = Х, (9.9)
где

Обобщая равенства (9.9) рассмотрим следующее.
Определение 10.1. Ненулевой вектор  называется собственным вектором квадратной матрицы А порядка n, если
называется собственным вектором квадратной матрицы А порядка n, если
 (9.10)
(9.10)
где  – некоторое число.
– некоторое число.
При этом число  называется собственным значением матрицы А. Говорят так:
называется собственным значением матрицы А. Говорят так:  есть собственный вектор матрицы А, принадлежащий ее собственному значению
есть собственный вектор матрицы А, принадлежащий ее собственному значению  .
.
Пример 35. Найдем собственные векторы и собственные значения следующей матрицы порядка 2:

Положим  – вектор – столбец. Тогда из соотношения (9.10) следует, что
– вектор – столбец. Тогда из соотношения (9.10) следует, что

т.е.
 ,
,
или
 , (9.11)
, (9.11)
Если вектор  – собственный, то это означает, что однородная система уравнений (9.11) имеет ненулевое решение. Согласно последней теореме это условие эквивалентно тому, что определитель системы (9.11) равен нулю.
– собственный, то это означает, что однородная система уравнений (9.11) имеет ненулевое решение. Согласно последней теореме это условие эквивалентно тому, что определитель системы (9.11) равен нулю.
 ,
,
или  . Таким образом, собственными значениями матрицы А будут числа 2 и 3.
. Таким образом, собственными значениями матрицы А будут числа 2 и 3.
Найдем соответствующие собственные векторы. Подставим  =2 и
=2 и  =3 в систему (9.11)
=3 в систему (9.11)
 =2
=2  =3
=3




Однородная система уравнений  тогда и только тогда имеет ненулевое решение, когда ее определитель равен нулю:
тогда и только тогда имеет ненулевое решение, когда ее определитель равен нулю:

Если раскрыть данный определитель, как в рассмотренном примере (9.11), то получится многочлен степени п относительно  , называемый характеристическим многочленом матрицы А.
, называемый характеристическим многочленом матрицы А.
Определение 10.2. Уравнение

называется характеристическим уравнением матрицы А.
Таким образом, собственные значения матрицы А являются корнями ее характеристического уравнения.
Пример 36. Найти собственные значения собственные векторы матрицы.

Запишем характеристическое уравнение:

или  . Следовательно,
. Следовательно,  – единственное собственное значение матрицы А. Система уравнений для отыскания собственных векторов сводиться к единственному уравнению:
– единственное собственное значение матрицы А. Система уравнений для отыскания собственных векторов сводиться к единственному уравнению:
х1 + х2=0,
т.е. собственный вектор х = (–а, а, b) представляется в виде линейной комбинации

двух линейно независимых векторов  и
и  .
.
Вернемся к отысканию собственного вектора X в модели международной торговли. Система уравнений для нахождения X имеет вид (9.9) т.е.

 = 0.
= 0.
Нетрудно найти общее решение этой системы:

поэтому в качестве собственного вектора можно взять вектор
 (4; 3; 2)
(4; 3; 2)
В частности, это означает, что сбалансированность торговли этих трех стран может быть достигнута только в том случае, когда госбюджеты находятся в отношении
X1: X2: X3 = 4: 3: 2
Определение. Максимальное по модулю собственное значение неотрицательной матрицы А называется числом Фробениуса матрицы А, а соответствующий ему неотрицательный собственный вектор – вектором Фробениуса для А.
Понятие собственного значения, а также понятие вектора Фробениуса неотрицательной матрицы А позволяют по- новому подойти к вопросу о продуктивности модели Леонтьева.
Теорема. Неотрицательная квадратная матрица А продуктивна тогда и только тогда, когда ее число Фробениуса меньше единицы.
Люди также интересуются этой лекцией: 8 Приложения.
Задания для самостоятельной работы
Экономическая система состоит из 3 отраслей: топливно-энергетическая, промышленность, сельское хозяйство. Пусть
 –
–
– транспонированная матрица прямых затрат,  – вектор норм добавленной стоимости.
– вектор норм добавленной стоимости.
1. Определить равновесные цены.
2. Определить равновесные цены, если произойдет увеличение нормы добавленной стоимости на 1,1 в топливно-энергетической отрасли.



