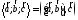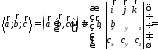Содержание:
Векторное и смешанное произведения векторов в векторной алгебре
Векторное произведение
Определение: Тройка векторов
Пример:
Рис. 13. Правая (а) и левая (б) тройки векторов.
Определение: Векторным произведением векторов 
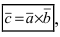
- по модулю численно равен площади параллелограмма, построенного на векторах
- перпендикулярен плоскости, в которой лежат вектора
- тройка векторов
является правой.
Замечание: Из определения векторного произведения следует, что направление вектора 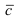
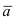
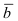
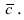
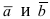
Рис. 14. Площадь параллелограмма, определяющего длину вектора 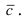
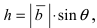
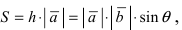
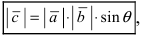
Векторное произведение векторов обладает следующими свойствами:
Замечание: Свойство 4. определяет второе условие коллинеарности векторов.
Формула для векторного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть 
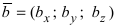
Доказательство: Запишем вектора 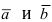
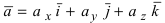
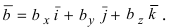
Используя эту таблицу, вычислим векторное произведение векторов
Отсюда следует, что 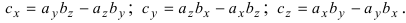
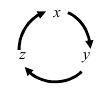
Рис. 15. Циклический переход от одной координаты к другой.
Для нахождения, например проекции 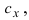
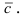
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, то есть окончательно можно записать, что
Пример:
Найти, при каком значении параметра m вектор 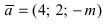
Решение:
Согласно свойству 4. для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов
Так как вектор 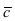
- Заказать решение задач по высшей математике
Пример:
Найти векторное произведение векторов
Решение:
Пример:
Найти векторное произведение векторов
Решение:
Приложения векторного произведения
1. Физика. Пусть точка начала вектора 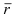
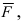
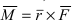
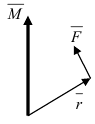
2. Геометрия. Пусть даны три разные точки 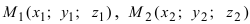
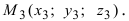
Введем в рассмотрение вектора 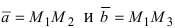
Рис. 17. Площадь треугольника
Проекции этих векторов равны:
Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов 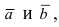
Пример:
Даны три точки 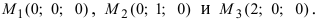
Решение:
Введем в рассмотрение вектора 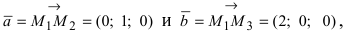
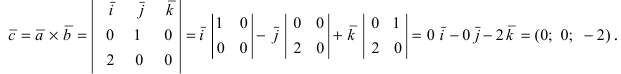
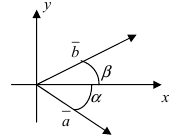
3. Тригонометрия. Выведем формулу для
Пусть в плоской декартовой системе координат даны векторы 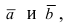
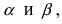
Рис. 18. Синус суммы двух углов.
Проекции векторов равны 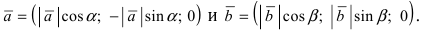
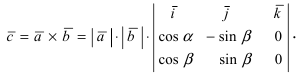
Длина этого вектора равна 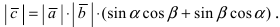
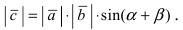
Смешанное произведение векторов
Определение: Смешанным произведением векторов 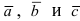
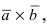
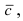
Получим формулу для вычисления смешанного произведения
Обменяв местами первую строку со второй, а затем и с третьей, получим окончательную формулу
Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
1. 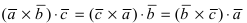
2. Смешанное произведение векторов 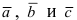
Рис. 19. Объем параллелепипеда, построенного на векторах
Так как
3. Если вектора 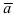
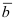
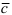
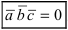
Замечание: Свойство 3. определяет условие компланарности трех векторов, т.е. если 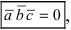
Пример:
Доказать, что вектора 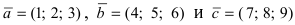
Решение:
Согласно формуле, определяющей смешанное произведение векторов, имеем
Пример:
Даны 4 точки 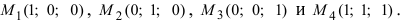
Решение:
Составим векторы 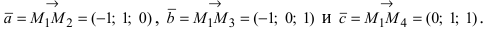
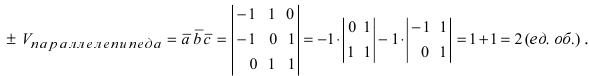
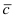
Пример:
Чему равен объём пирамиды с вершинами А, В, С и D (координаты точек А, В, С и D взять из VIII.). Найти длину высоту, которая опущена из точки А на основание BCD.
Решение:
Объём пирамиды равен 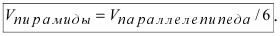
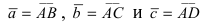
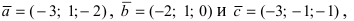
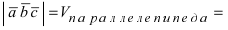
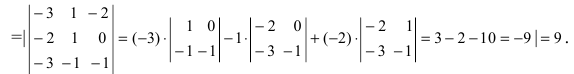
С другой стороны, её объём по формуле из средней школы равен
Вычислим площадь треугольника BCD, лежащего в основании пирамиды: 
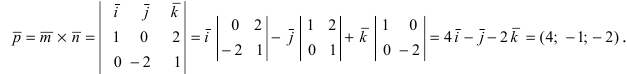
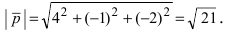
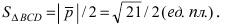
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Матричный метод
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
Содержание:
- Векторы
- Действия над векторами
- Умножение вектора на число
- Скалярное произведение векторов
- Векторное произведение
- Смешенное произведение векторов
- Разложение вектора по базису
- Действия над векторами, заданными своими координатами
- Проекция вектора на ось
- Проекции вектора на оси координат
- Направляющие косинусы вектора
- Разложение вектора по ортам
- Действия над векторами, заданными в координатной форме
- Вектор – основные определения
- Операции над векторами и их свойства
- Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
- Координаты вектора
- Скалярное произведение векторов и его свойства
- Векторы и их решение
- Собственные числа и собственные векторы
- Векторная алгебра
- Векторы: основные определения, линейные операции
- Линейные операции над векторами
- Умножения вектора на скаляр
- Основные свойства проекции вектора на ось
- Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
- Скалярное, векторное, смешанное произведения векторов
- Векторное произведение двух векторов
- Смешанное произведение векторов, заданных в координатной форме
- Простейшие задачи аналитической геометрии
- Задача об определении площади треугольника
- Задача о деление отрезка в заданном отношении
Векторы
В математике вектором называют величину, которая характеризуется только числом и направлением. Так определённые векторы ещё называют свободными векторами. Примером физических величин, которые имеют векторный характер являются скорость, сила, ускорение. Геометрически вектор — это направленный отрезок, хотя правильней говорить про целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковые длину и направление.
Векторы обозначают малыми латинскими буквами с чертой сверху 


Действия над векторами
Рассмотрим основные действия, определённые над векторами.
1. Сложение векторов. Суммой векторов 





Учитывая, что 

Вычитание векторов сводится к сложению противоположного вектора
Запишем основные свойства действий сложения векторов:
Заметим, что сумма нескольких векторов находится последовательным сложением двух из них, например:
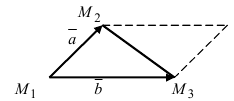
Геометрически сумма нескольких векторов находится их последовательным отложением один за одним так, чтоб начало следующего совпадало с концом предыдущего. Суммой является вектор, который будет соединять начало первого с концом последнего (рис. 4). Если такая последовательность векторов даёт замкнутую ломаную то суммой векторов является 
Умножение вектора на число
Произведением вектора 


а) 
б) 




Запишем основные свойства действий умножения вектора на число:
Скалярное произведение векторов
Скалярным произведением 






Очевидно, что скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда когда эти вектора перпендикулярны (ортогональны). Действительно, если 

Наоборот, если 

Например, скалярное произведение 
Запишем основные свойства действий скалярного умножения векторов:
Векторное произведение
Векторным произведением 



1) модуль вектора 


2) вектор 


3) вектор 





Модуль векторного произведения равен площади параллелограмма, построенного на векторах 







Приведём основные свойства векторного произведения:
1) векторное произведение 


2) от перестановки местами векторов-сомножителей векторное произведение меняет знак на противоположный: 
3) 
4) 
Физическое содержание векторного произведения такое. Если 







Смешенное произведение векторов
Смешенным произведением векторов 



Как результат скалярного произведения векторов 


Действительно, 




Объём V параллелепипеда, построенного на векторах 
Однако, знак смешенного произведения совпадает со знаком 




Из геометрического содержания смешенного произведения выходит, что
1) смешанное произведение равно нулю тогда и только тогда, когда перемноженные вектора копланарные (условие компланарных векторов);
2)
Учитывая коммутативность скалярного произведения и антикоммутативность векторного, для произвольных векторов 
Пример 1.
Доказать, что когда М — точка АВС и О — произвольные точки пространства, то выполняется равенство:
Решение.
Пусть 



тогда
Пример 2.
У прямоугольного параллелепипеда рёбра 




Решение.
Пусть 

рис. 9.
Далее,
Этим закончен “перевод” условия задачи на “язык” векторов.
Теперь произведём вычисления с векторами:
Наконец “переводим” полученные вектора равенства снова на “геометрический язык”. Поскольку 

Далее поскольку 




Разложение вектора по базису
Базисом на площади называют упорядоченную пару неколлинеарных векторов и точку отсчёта.
Теорема. Любой вектор 



Доказательство.
Пусть векторы 





Тогда по правилу параллелограмма 
Но 

Числа, которые стоят при базисных векторах в разложении вектора за двумя неколлинеарными векторами называют координатами вектора в данном базисе и обозначают 
Соответственно в пространстве базисом называется упорядоченная тройка некомпланарных векторов и точки отсчёта. Для четырёх некомпланарных векторов справедлива следующая теорема.
Теорема. Любой вектор 




Доказательство.
От точки О отложим векторы 


в котором вектор 
Числа х,у,z которые стоят при базисных векторах в разложении вектора по трём некомпланарным векторам называют координатами вектора в пространстве и обозначают 






Отсюда легко установить длину вектора как расстояние между двумя точками:
Действия над векторами, заданными своими координатами
1. При сложении двух, или более векторов их соответствующие координаты складываются:
Действительно:
2. При вычитании векторов соответствующие координаты вычитаются:
Доказательство аналогично предыдущему.
3. При умножении вектора на число все координаты умножаются на это число.
Правда, для вектора 

4. Скалярное произведение двух векторов 
Правда:
Поскольку 

5. Векторное произведение векторов 
6. Смешенное произведение трёх векторов 
Пример 1.
Зная координаты векторов 

Решение:
Ответ: 
Пример 2.
Зная координаты векторов 

Решение.
Ответ: 
Пример 3.
Зная координаты векторов 
а) скалярное произведение векторов
б) векторное произведение векторов
в) смешенное произведение векторов 
Решение.
Ответ:
На основании приведённых выше формул действий над векторами можно установить следующие условия и соотношения для нулевых векторов
1. Угол между векторами.
2. Условие перпендикулярности двух векторов:
(векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю).
3. Условие коллинеарности двух векторов: 
4. Условие компланарности трёх векторов.
(три вектора компланарны тогда и только тогда, когда их смешенное произведение равно нулю).
5. Деление отрезка АВ в заданном отношении.
Если точка 

Если точка М делит отрезок АВ на пополам то 
Действия над векторами (теория)
а) Произведение вектора на число.
Определение 1. Произведением вектора 

который имеет длину 

Рис. 12.
Условие 
является условием коллинеарности двух векторов.
б) Сложение векторов.
Определение 2. Суммой двух векторов 






Рис. 13.
Понятно, что вектор 


Для векторной суммы справедливый переместительный закон
Легко убедиться, что для векторной суммы имеет место соединительный
закон 
Исходя из определения 2, легко находим сумму, например, четырех векторов 
Рис. 14.
Вектор 


в) Вычитание векторов.
Действие вычитание векторов можно рассматривать как обратное действие относительно сложения векторов.
Определение. Разностью 



Рис. 15.
Как видно из рис. 15, одна диагональ 




Дадим еще одно определение разности векторов.
Определение. Разностью двух векторов 


Проекция вектора на ось
Пусть имеем произвольную ось l на плоскости и некоторый вектор 
Рис. 16.
Опустим из начала A вектора и из конца B перпендикуляры на ось l. Основаниями перпендикуляров будут точки A1 и B1, которые называются проекциями точек A и B.
Величина A1B1 называется проекцией вектора 


Определение 1. Проекцией вектора 
Из точки A проведем прямую, параллельную оси l, которая пересечет отрезок BB1 в точке C. Вектор 


Определение 2. Проекция вектора на любую ось равна произведению длины этого вектора на косинус угла между осью и вектором.
Если угол φ острый, то проекция 

Свойства проекций.
1. Если векторы 


2. Проекция суммы векторов на любую ось равна сумме проекций слагаемых на ту же ось, то есть:
3. Проекция разности двух векторов на ось l равна разности величин проекций на ту же ось, то есть:
4. Если вектор 

Проекции вектора на оси координат
Рассматривается прямоугольная система координат Oxyz в пространстве и произвольный вектор 
Пусть 
Проекции x, y, z вектора 

Если заданы две точки A (x1; y1; z1) и B (x2; y2; z2), то координаты вектора 
x = x2 – x1, y = y2 – y1, z = z2 – z1 .
Рис. 17
Действительно, проведем через точки A и B плоскости, перпендикулярные оси Ox и обозначим точки их пересечения соответственно A1 и B1 (рис.17). Точки A1 и B1 имеют на оси Ox координаты x1 и x2 , но 
x = x2 – x1 . Аналогично доказывается, что y = y2 – y1, z = z2 – z1 .
Направляющие косинусы вектора
Пусть имеем вектор 
Рис. 18
Через точку M проведем плоскости, перпендикулярные к осям координат, и вместе с координатными плоскостями они образуют параллелепипед, диагональ которого — отрезок OM (рис.18). Через α, β, γ обозначим углы, которые образует вектор 


Квадрат диагонали прямоугольного параллелепипеда равна сумме квадратов длин трех его измерений.
Поэтому


Формула (2.8) выражает длину вектора через его координаты. Тогда на основе формул (2.7) и (2.8) получим
Отсюда для направляющих косинусов получаем

Для направляющих косинусов справедливо равенство 
Разложение вектора по ортам
Рассмотрим прямоугольную систему координат в пространстве и вектор, начало которого в точке O (рис.19) .
Рис. 19.
Обозначим орты осей координат Ox, Oy, Oz соответственно через 
Спроецируем вектор 
Из прямоугольника ODMC видно, что вектор 

Тогда

Вектор 
Векторы 




Подставляя эти значения в равенство (2.10), учитывая, что 

Слагаемые 

Тройка векторов 

Пример 1. Построить вектор 
Рис. 20.
Решение. Компоненты вектора 


соответствует прямоугольный параллелепипед, диагональ которого является искомый вектор (рис. 20).
Действия над векторами, заданными в координатной форме
Если векторы заданы в координатной форме, то действия сложения, вычитания, умножения вектора на число можно заменить простыми арифметическими операциями над координатами этих векторов по таким правилам.
Правило 1. При сложении векторов их одноименные координаты складываются
Пусть имеем векторы 





Сложив эти равенства, получим

Итак, координаты вектора 
Правило 2. Чтобы отнять от вектора 



Правило 3. Чтобы умножить вектор 


Пример 1. Найти вектор 
Решение. Выполним действия последовательно и найдем

Значит,
Вектор – основные определения
Определение вектора в пространстве ничем не отличается от определения вектора на плоскости.
Определение 1. Вектором называется направленный отрезок, т.е. отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Так же как и на плоскости, векторы обозначаются 
Определение 2. Длиной (или модулем) вектора 


Длина вектора 


Любая точка пространства также считается вектором, который называется нулевым. Начало такого вектора совпадает с его концом, а длина равна нулю. Обозначения нулевого вектора:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Определение 3. Векторы 

Если ненулевые векторы 







Ясно, что сонаправленные векторы, в силу их определения, коллинеарны. Если два коллинеарных вектора не сонаправлены, то они называются противоположно направленными. Обозначения остаются обычными: 





Определение 4. Векторы 



Теорема 1. От любой тонки пространства можно отложить вектор, равный данному, и притом только один.
Доказательство этой теоремы аналогично доказательству соответствующей планиметрической теоремы.
Возможно вам будут полезны данные страницы:
Операции над векторами и их свойства
Операции над векторами в пространстве аналогичны соответствующим операциям на плоскости.
Пусть даны два вектора 








Теорема 2. Сумма 




Правило треугольника можно сформулировать и так: для любых трёх точек 
Кроме того, сумму двух неколлинеарных векторов с общим началом можно построить и по правилу параллелограмма: 




Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве:
1)
2) 
3) 
Здесь 
Определение 5. Два ненулевых вектора называются противоположными, если их длины равны и эти векторы противоположно направлены.
Вектор, противоположный данному ненулевому вектору 
Определение 6. Разностью двух векторов 



Разность векторов 



Разность векторов 



Из законов сложения векторов следует, что сумма нескольких векторов не зависит от порядка слагаемых.
Умножение (произведение) вектора на число и его свойства, так же как и свойства операции сложения, не претерпевают изменений и в пространстве.
Определение 7. Произведением ненулевого вектора 








Таким образом, по определению, 






Свойства умножения вектора на число не отличаются от аналогичных свойств на плоскости:
-
— ассоциативность (сочетательный закон);
-
—дистрибутивность относительно сложения векторов (1-й распределительный закон);
-
— дистрибутивность относительно сложения чисел (2-й распределительный закон).
Здесь 


Справедлива также и лемма о коллинеарных векторах: если векторы 


что 

Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
Теорема 3. Пусть 



Доказательство
1. Из равенства 





2. Пусть 




З. Компланарные и некомпланарные векторы
Следующее понятие уже не имеет аналога в планиметрии.
Определение 8. Векторы называются компланарными, если лучи, задающие их направления, параллельны некоторой плоскости.
Замечание. Из определения 8 следует, что при откладывании от одной точки векторов, равных нескольким данным компланарным векторам, получим векторы, лежащие в одной плоскости. Таким образом, компланарные векторы лежат либо в одной плоскости, либо в параллельных плоскостях.
Очевидно, что любые два вектора компланарны и любые три вектора, два из которых коллинеарны, также являются компланарными (поясните). Рассмотрим теперь условия, при которых три вектора, из которых никакие два не коллинеарны, являются компланарными.
Теорема 4. Векторы 




Доказательство
1. Пусть векторы 
точки 
















Докажем, что векторы 






Отложим от произвольной точки 







Если векторы 






Следующая теорема, называемая теоремой о разложении вектора по трём некомпланарным векторам, является основной во всей элементарной (школьной) векторной алгебре.
Теорема 5. Любой вектор 




2. Пусть векторы 





















3. Докажем теперь, что разложение вектора 



Тогда
отсюда
– т. е. векторы
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
по данным векторам
единственно. Теорема доказана.
Итак, любой вектор 





Координаты вектора
Так же как и на плоскости, в пространстве помимо координат точки вводятся координаты вектора. Рассмотрим три попарно перпендикулярных вектора 












Свойства векторов пространства, заданных своими координатами, аналогичны соответствующим свойствам векторов на плоскости:
- Два вектора равны в том и только том случае, если равны их координаты.
- Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат этих векторов, т.е. для векторов
получаем
- При умножении вектора на число каждая его координата умножается на это число, т.е. для вектора
и действительного числа
получаем
Докажем, например, свойство 2. Так как 



Скалярное произведение векторов и его свойства
Определение скалярного произведения векторов 

Определение 11. Скалярным произведением векторов 

Теорема 8. Два ненулевых вектора 

Доказательство этой теоремы вытекает из формулы (9).
Определение 12. Скалярным квадратом вектора 


Так как 
Таким образом, длина вектора равна квадратному корню из его скалярного квадрата.
Замечание. Скалярное произведение есть число, поэтому грубой ошибкой явилась бы запись:
Если векторы 


Теорема 9. Скалярное произведение векторов равно сумме произведений их соответственных координат, т. е.
Доказательство. Отложим от произвольной точки 







итак как 


поэтому
Решение любой геометрической задачи на вычисление сводится, в сущности, к нахождению величин двух типов: расстояний и углов. Если в пространстве задан некоторый базис (в частности, прямоугольный), т. е. тройка некомпланарных векторов, то на основании теоремы 5 любой вектор пространства можно разложить по векторам этого базиса, причём единственным образом.
Если известны длины векторов, образующих базис, углы между ними и разложение некоторого вектора по векторам этого базиса, то, используя свойства скалярного произведения, можно определить длину такого вектора и угол, образуемый им с любым другим вектором, разложение которого по векторам этого базиса известно.
Таким образом, векторы позволяют находить решения довольно широкого класса геометрических задач, а умение определять разложение вектора по базисным векторам является важнейшим фактором их решения.
Для решения задач о разложении вектора по трём данным некомпланарным векторам, разумеется, необходимо, помимо теоремы 5, знание предшествующего ей материала.
Примеры с решением
Задача 1.
Основанием четырёхугольной пирамиды 






Решение (см. рис. 14).
1. 

2. Так как 


Ответ:
Заметим, что в разложении вектора 








Задача 2.
Пусть 


Решение (см. рис. 15). Пусть 






Ответ:
Векторы и их решение
Вектором называется направленный отрезок. Направление отрезка показывается стрелкой. Различают начало и конец отрезка.
Два вектора называются равными между собой, если каждый из них можно получить параллельными перенесениями другого.
Равные векторы являются параллельными (колинеарными), имеют одно и то же направление и одинаковую длину. Длина вектора 
Вектор называется нулевым (ноль- вектором), если он имеет нулевую длину, то есть его конец сходится с началом.
Чтобы найти сумму двух векторов 



Суммой 






Для складывания векторов имеют место такие законы:
1) переставной (коммутативный)
2) связующий
3) для каждого вектора 

4)
5) для некоторых двух векторов 

Если вектор 



Пусть вектор имеет начало в точке 





Если вектор 
Произведением вектора 






Любой вектор 
где 



Пример 1.73
Даны два вектора: 

Найти вектор
Решение
Признаком колинеарности двух векторов 

Скалярным произведением двух векторов 


Скалярное произведение можно записать в таком виде:
Если векторы 

Учитывая формулы (1.18) и (1.19), можно найти косинус угла между векторами 

Отсюда получается условие перпендикулярности двух векторов: если 

Среди свойств скалярного произведения отметим так:
Векторным произведением вектора 


1) длина вектора 
2) вектор 

3) из конца вектора 


Заметим, что 


В координатной форме векторное произведение векторов 

Смешанным или скалярно – векторным произведением трех векторов 



Если векторы 
Если известные координаты сомножителей 
Если три ненулевых 
Следует, в координатной форме условие компланарности трех ненулевых векторов имеет вид:
Решение примеров:
Пример 1.74
Заданы координатами точек 


1) вектор 
2) угол между векторами 
3) координаты вектора
4) объем пирамиды с вершинами в точках
Решение
1) По формуле (1.14) находим
тогда
2) Косинус угла между векторами 

Поскольку косинус угла отрицательный, то угол 
3) Координаты векторного произведения находим по формуле (1.22):
4) Чтобы найти объем пирамиды, найдем сначала смешанное произведение векторов, что выходят из одной вершины пирамиды:
Тогда объем пирамиды
Собственные числа и собственные векторы
Вектор – столбец 




Тут 



Координаты собственного вектора 

Собственный вектор обозначаются с точностью к постоянному множителю.
Решение примеров:
Пример 1.90.
Обозначить собственные определения и собственные векторы матрицы
Решение. Характеристические уравнения данной матрицы имеет вид (1.24):

отсюда получается, что матрица 





которое приводится к одному уравнению
Возьмем 
Следует, первый собственный вектор является
Второй вектор 

Эта система уравнений так же приводится к одному уравнению 


Таким образом, матрица 




Пример 1.91
Найти собственные векторы и собственные значения матрицы
Решение. Характеристическое уравнение
Раскрыв определитель получим:
Корень 


Система уравнений для определения собственных векторов имеет вид:
Последовательно подставим 

Фундаментальная система уравнений получается, если свободным переменным 
Получили два линейно независимые собственные векторы. Вся совокупность векторов, что соответствуют собственному значению 
Фундаментальная система решений получается, если взять
Векторная алгебра
Понятие «вектор» (от лат. vector – носитель), как отрезка, имеет определенную длину и определенное направление, впервые появилось в работах по построению числовых систем в ирландского математика Уильяма Гамильтона (1805-1865). Это понятие связано с объектами, которые характеризуются величиной и направлением, например, скорость, сила, ускорение. При этом скорость можно понимать в широком смысле: скорость изменения издержек производства, доходов, спроса, потребления и предложения и др. Вектор может указывать направление наибольшего возрастания или убывания функции, описывающей различные экономические процессы. Векторы, рассмотренные в данном разделе, является частным случаем 
Для графического изображения решения экономических задач на плоскости и в пространстве применяются средства аналитической геометрии. Аналитическая геометрия – математическая наука, объектом изучения которой являются геометрические фигуры, а предметом – установление их свойств средствами алгебры с помощью координатного метода. Теоретической базой этой науки является частично известна из школы векторная алгебра.
Основателем метода координат и, вместе с тем, аналитической геометрии является Рене Декарт (1596-1650) – французский философ, математик, физик и физиолог. Его именем и названа известная «декартова прямоугольная система координат», которая позволяет определить положение фигуры на плоскости и тела в пространстве.
После изучения данной темы вы сможете:
● использовать инструмент векторной алгебры для геометрического изображения и анализа объектов экономических процессов;
● применять уравнение прямой линии на плоскости для геометрической интерпретации зависимости между функциональному признаку и аргументом, что на нее влияет;
● применять уравнение кривых второго порядка при построении нелинейных математических моделей экономических задач;
● осуществлять геометрическую интерпретацию решений экономических задач с помощью поверхностей и плоскостей.
Векторы: основные определения, линейные операции
Выберем на произвольной прямой (в 






алфавита с чертой: 
Рис. 6.1
В применимых задачах естественных наук существенным является обстоятельство – где, в какой точке находится начало вектора. Например, результат действия силы зависит не только от ее величины и направления действия, но и от того, в какой точке она прикладывается.
Вектор, для которого фиксированная (не фиксирована) начальная точка называется связанным (свободным). Векторы, которые применяются в экономических задачах, как правило, не являются связанными, поэтому в дальнейшем будем рассматривать преимущественно свободные векторы
Длиной, или модулем, вектора называется длина соответствующего отрезка и обозначается одним из символов:
Нулевым вектором 0, или ноль-вектором, называется вектор, длина которого равна нулю, а направление его считается произвольным (неопределенным).
Единичным вектором 
Равными векторами называются векторы, которые принадлежат одной прямой или параллельным прямым, одинаково направлены и имеют равные длины.
Взаимно противоположными называются векторы, которые принадлежат одной прямой или параллельным прямым, имеют равные длины, но противоположно направлены. Вектор, противоположный вектору 

Коллинеарными называют векторы, которые принадлежат одной прямой или параллельным прямым.
Компланарными называются векторы, которые принадлежат одной плоскости или параллельным плоскостям.
Линейные операции над векторами
Будем считать, что векторы 



1. Суммой векторов 


Параллельный перенос можно осуществить и так, что объединятся начала векторов 

Рис. 6.2
Правило треугольника обобщается на произвольное конечное число векторов. Если параллельным переносом расположить векторы так, что конец предыдущего вектора (начиная с первого) является началом следующего, то результирующим будет вектор, соединяющий начало первого вектора слагаемого с концом последнего (рис. 6.3):
Рис. 6.3
Соответствующее правило называют правилом многоугольника.
Свойства суммы векторов:
1) переставная, или коммутативна:
2) соединительная, или ассоциативная:
3)
4)
Разницу 

Умножения вектора на скаляр
Пусть 










Рис. 6.4
При


Свойства умножения вектора на скаляр:
1) переставной или коммутативных закон:

2) соединительный, или ассоциативный закон:

3) распределительный или дистрибутивный закон:

4)
5)
Из определения умножения вектора на скаляр следует необходимое и достаточное условие коллинеарности двух векторов: вектора 

Известно, что три ненулевые векторы 


Рассмотрим понятие, имеет очень важное значение в теории векторов – проекции вектора на ось (прямую, имеет направление; заданное направление считать положительным, противоположное направление – отрицательным).
Компонентой вектора 





Рис. 6.5
Проекцией вектора 






Основные свойства проекции вектора на ось
1. Проекция вектора на ось 

2. Проекция суммы двух векторов на эту ось равна сумме их проекций на эту ось:
Это свойство обобщается на любое конечное число векторов.
3. Проекция на ось произведения вектора со скаляром равна произведению со скаляром проекции самого вектора на ось:
Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
Пусть в трехмерном векторном пространстве 


Рис. 6.6
Выберем в пространстве произвольную точку 





Под декартовыми прямоугольными координатами точки 

Точка 





Измерениями параллелепипеда есть модули координат точки 
Углы 


откуда:
Косинусы направляющих углов называются направляющими косинусами радиус-вектора 
1) направляющие косинусы являются координатами единичного радиус-вектора:
2) сумма квадратов направляющих косинусов вектора 
Понятие «координата», «направляющие углы», «направляющие косинусы» без изменений переносятся на любые свободные векторы, потому начало каждого из них параллельным переносом можно поместить в начало 
Координатами любого вектора 



Задача вектора тройкой его координат 
Для единичных векторов 

Длина произвольного вектора 
Найти длину и направляющие косинусы вектора
По формулам (6.5) имеем:
Установим связь между координатами вектора – числами – и его компонентами – векторами – с помощью единичных векторов 
Рис. 6.7
Компонентами вектора 


Следовательно, любой вектор 
Изображение вектора с 
Согласно свойствами операций над векторами, алгебраическая форма задания дает возможность установить результаты действий над векторами, заданными в координатной форме.
1. При добавлении (вычитании) двух векторов с 


Действительно, по свойствам ассоциативности и дистрибутивности имеем:
2. При умножении вектора 

Действительно, согласно распределительным свойствам умножения скаляра на сумму векторов имеем:
Скалярное, векторное, смешанное произведения векторов
Скалярным произведением двух векторов 



Вместо 


Для определения угла 







Основные свойства скалярного произведения векторов вытекают из его определения (6.7).
1. Скалярное произведение 
2. Скалярный квадрат вектора равен квадрату его модуля, то есть
3. Скалярное произведение подчиняется всем законам арифметики чисел относительно линейных операций:
4. Скалярное произведение двух векторов равно произведению модуля одного из них с проекцией второго на ось, направление которого определяется первым вектором:
Доказательство этого свойства основывается на определении (6.3).
Скалярное произведение векторов 

1. Вычислим скалярные произведения единичных векторов 

2. Находим произведение 
Раскрываем скобки и получаем:
Скалярное произведение двух векторов равно сумме произведений одноименных координат. Это полностью совпадает с определением скалярного произведения 
Как следствие из (6.12) при 
Определим угол между двумя ненулевыми векторами 

Следовательно, косинус угла между двумя векторами определяется формулой:
Отсюда
В результате с соотношением (6.13) получим критерий ортогональности двух векторов, заданных в координатной форме:
Критерием коллинеарности векторов 

Векторное произведение двух векторов
Пусть 








1) модуль его численно равен площади параллелограмма, построенного на векторах 

2) он перпендикулярный плоскости параллелограмма 



Рис. 6.9
Векторное произведение обозначается символами: 
Следовательно,
где 




Основные свойства векторного произведения вытекают из его определения.
1. Векторное произведение ненулевых векторов равно ноль-вектору тогда и только тогда, когда векторы 

Еще одним критерием коллинеарности векторов является равенство нулевому вектору их векторного произведения.
2. Векторные произведения с разным порядком сомножителей являются взаимно противоположными векторами:
Это означает, что векторное произведение не подчиняется переставному (коммутативному) закону.
3. Векторное произведение подчиняется ассоциативному закону относительно скалярного множителя и дистрибутивному закону относительно сложения:
где
Векторное произведение векторов 

1. Определяем векторные произведения ортов 
Векторное произведение одноименных векторов по свойству 1 дает ноль вектор:
Однако все векторные произведения разноименных единичных векторов будут давать единичные векторы:
Рис. 6.10
Рассмотрим, например, произведение 




2. Находим произведение 
Множители при 
Коэффициенты при единичных векторах в соотношении (6.20) являются координатами вектора 


Если символы 

Найдем векторное произведение векторов 
Модуль векторного произведения 

Смешанным произведением трех векторов 


Смешанное произведение можно обозначать тройкой векторов 





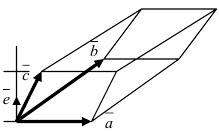
Геометрическая интерпретация смешанного произведения. Пусть 

Рис. 6.11
Вектор 





Согласно (6.11) скалярное произведение 



где 




Модуль смешанного произведения трех векторов численно равен объему параллелепипеда 
Основные свойства смешанного произведения вытекают из его определения и геометрической интерпретации.
1. Смешанное произведение ненулевых векторов равно нулю, если по крайней мере два из трех векторов коллинеарны или все три – компланарны, и наоборот.
Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения:

Свяжем с изображенными на плоскости векторами 
2. Циклическая перестановка трех сомножителей смешанного произведения не меняет его величины, а отрицательное перестановки меняет его знак на противоположный:
Смешанное произведение векторов, заданных в координатной форме
Пусть имеем три ненулевые векторы 
Полученная сумма произведений является расписанием определителя 3-го порядка, составленный из координат векторов, по элементам его третьей строки, то есть:
Векторы 

С помощью смешанного произведения векторов легко определить, относятся ли четыре точки 
Простейшие задачи аналитической геометрии
Задача об определении длины отрезка. Найти длину отрезка 

1. Введем в рассмотрение вектор 



2. Определим координаты вектора 


3. Находим модуль вектора 

Задача об определении площади треугольника
Найдем площадь треугольника, заданного координатами вершин:
По аксиомой стереометрии известно, что три точки в пространстве определяют плоскость и притом только одну. Для упрощения изложения, не нарушает общего подхода к решению задачи, договоримся рассматривать треугольник 



1. Введем в рассмотрение векторы:
и найдем их векторное произведение
По соотношению (6.20) имеем:
2. Вычислим модуль вектора 


Тогда для площади треугольника 
Знак 

Если треугольник принадлежит не плоскости 
Найдем площадь треугольника с вершинами 

Введем в рассмотрение векторы: 


Тогда

Задача о деление отрезка в заданном отношении
Пусть в пространстве заданы две точки 







Рис. 6.15
Число 
называется отношением, в котором точка 



Задача о деление отрезка в заданном отношении формулируется так: найти координаты точки 




Пусть точкам 




С этого векторного равенства найдем вектор
или в координатах:
Отсюда, если отрезок разделить на две равные части точкой 

Можно доказать, что координаты точки пересечения медиан треугольника, заданного координатами его вершин 
Лекции:
- Объем конуса
- Разложение на множители
- Деление многочлена на многочлен
- Правила дифференцирования
- Теорема Пифагора
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Прямая линия на плоскости
- Выпуклость и вогнутость графика функции
- Матанализ для чайников
- Производные некоторых элементарных функций
1.
Упорядоченная тройка некомпланарных
векторов называется правой,
если при приведении этих векторов к
общему началу ближайший поворот от
первого вектора ко второму виден с конца
третьего вектора совершающимся против
часовой стрелки. В противном случае
тройка называется левой.
Замечание.
Стандартный
ортонормированный базис
пространства
V3
задается
правой тройкой ортов.
2.
Векторным произведением векторов
и
называется вектор
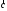
направление и длина которого определяются
следующими условиями:
1.
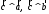
2
,
,

и
не коллинеарны);
3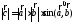
Векторное
произведение векторов
и
обозначается
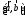
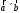
3.Геометрический
смысл векторного произведения двух
векторов. Длина
векторного произведения векторов
и
равна площади параллелограмма,
построенного на этих векторах.
4.
Механический смысл векторного произведения
двух векторов. Если
к точке А приложена сила
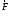
то момент этой силы относительно точки
О равен
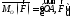
5.
Свойства
векторного произведения двух векторов.
1.
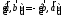
(антикоммутативность)
2.
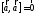
3.
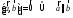
4.
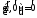
5.
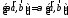
6.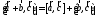
Данные
свойства векторного произведения
инвариантны
относительно выбора системы координат.
6.
Векторное произведение векторов
ортонормированного базиса.
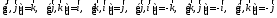
Все
эти равенства удобно запоминать с
помощью диаграммы. Произведение двух
ортов взятых подряд по кругу дает третий
орт, а в обратном направлении – третий
со знаком «–».
7.
Выражение векторного произведения двух
векторов, заданных в ортонормированном
базисе.
Координаты
векторного произведения векторов
и
равны алгебраическим дополнениям
элементов первой строки символического
определителя
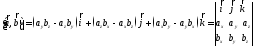
8.
Двойное векторное произведение. Вектор
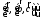
векторным произведением
векторов
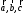
Справедливо равенство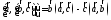
Именно в таком виде формулу для вычисления
двойного векторного произведения и
запоминают. Для этого есть у нее название
«бац минус
цаб».
5. Смешанное произведение векторов
1.
Смешанным
произведением трех векторов
называется число, равное скалярному
произведению векторного произведения
первых двух векторов на третий вектор.
Смешанное произведение векторов
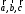
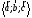
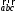
2.
Геометрический смысл смешанного
произведения трех векторов. Модуль
смешанного произведения векторов
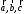
на этих векторах. Смешанное произведение
положительно, если тройка векторов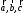
– левая (если векторы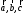
равно нулю).
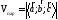
Следствие.
Объем
тетраэдра, построенного на трех векторах,
равен одной шестой модуля их смешанного
произведения
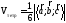
3. Свойства смешанного произведения.
1.
Если один из трех сомножителей равен
нулю-вектору, то их смешанное произведение
равно нулю 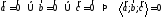
2.
Критерий компланарности трех векторов:
для того,
чтобы три вектора были компланарными,
необходимо и достаточно, чтобы их
смешанное произведение было равно нулю;
3.
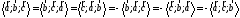
4.
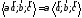
5.
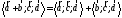
4.Выражение
смешанного произведения двух векторов,
заданных в ортонормированном базисе.
Смешанное
произведение трех векторов в
ортонормированном базисе равно
определителю, строками которого являются
координаты этих векторов данном базисе.
Пусть
векторы
,
и

разложения
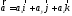
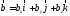
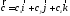
Тогда
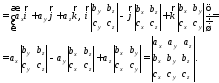
Три
вектора компланарны тогда и только
тогда, когда определитель, строками
которого являются координаты этих
векторов в ортонормированном базисе,
равен нулю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
Макеты страниц
1. Векторным произведением векторов 

1) длина вектора 


2) вектор 

3) вектор 
Векторное произведение векторов х и у обычно обозначается через 
Оно обладает следующими свойствами:

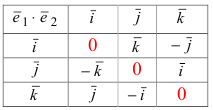
Найдем теперь таблицу векторных произведений векторов ортонормироваппого базиса пространства 

В этих таблицах векторы, стоящие слева, считаются первыми, а векторы, стоящие сверху, — вторыми сомножителями векторного произведения.
Чтобы записать векторные произведения базисных векторов в одной форме для любого ортонормированного базиса, введем величину 


правый, 


и равные нулю, если какие-нибудь два из индексов 
При помощи величин векторные произведения базисных векторов всегда, при любой ориентации базиса, могут быть записаны в виде

где в правой части, как обычно, производится суммирование по индексу 

Но первые два члена этой суммы равны нулю, 

Отсюда для правой системы мы получим

а для левой

что соответствует нашим таблицам.
Пусть 


Пользуясь вторым и третьим свойствами векторного произведения, мы получим отсюда

где в правой части суммирование происходит по всем трем индексам 
отбросить равные нулю слагаемые, может быть записана в виде

или, как обычно, в виде определителя третьего порядка:

Если обозначить векторное произведение 




(так как 

При 
Заметим, что введенное нами определение векторного произведения несколько отличается от определения этого понятия, принятого во многих книгах по аналитической геометрии и векторному исчислению (см., например, [10], стр. 44). Это отличие состоит в том, что в пашем определении векторное произведение не зависит от ориентации системы координат, а в упомянутых книгах оно меняет знак при изменении этой ориентации. Поэтому там векторное произведение не является обычным вектором, а является так называемым аксиальным вектором. У нас же векторное произведение определено однозначно, независимо от выбора базиса, и поэтому оно является обычным вектором. Тем самым мы избавляемся от необходимости рассмотрения аксиальных векторов.
2. Смешанное произведение векторов определяется формулой

и равно объему параллелепипеда, построенного на векторах 

Смешанное произведение векторов обладает следующими свойствами:

Легко проверить, что для смешанных произведений базисных векторов имеют место формулы

В самом деле,

В правой части этого равенства производится суммирование по индексу I. Но скалярное произведение будет отлично от нуля только тогда, когда 

Пусть теперь даны три произвольных вектора 

Пользуясь третьим и четвертым свойствами смешанного произведения, мы можем раскрыть скобки, стоящие в правой части этого равенства. Тогда мы получим

где индексы 


примет вид

Это выражение может быть обычным образом записано в виде определителя третьего порядка:

3. Рассмотрим двойное векторное произведение х 


Если векторы у и 






Обозначим через 






С другой стороны,

Положим 






(здесь 


Теперь

и, сравнивая это соотношение с равенством (3), мы получаем 
Но если умножить соотношение (2) скалярно на вектор 

откуда 
ЗАДАЧИ И УПРАЖНЕНИЯ
(см. скан)
(см. скан)
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ЛИНЕЙНОЕ ПРОСТРАНСТВО
- § 1. Понятие линейного пространства
- § 2. Линейная зависимость векторов
- § 3. Размерность и базис линейного пространства
- § 4. Прямоугольный базис в трехмерном пространстве. Скалярное произведение векторов
- § 5. Векторное и смешанное произведения векторов
- § 6. Преобразования ортонормированного базиса. Основная задача тензорного исчисления
- § 7. Некоторые вопросы аналитической геометрии в пространстве
- ГЛАВА II. ПОЛИЛИНЕЙНЫЕ ФОРМЫ И ТЕНЗОРЫ
- § 2. Билинейные формы
- § 3. Полилинейные формы. Общее определение тензора
- § 4. Алгебраические операции над тензорами
- § 5. Симметричные и антисимметричные тензоры
- ГЛАВА III. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ВЕКТОРНОГО ПРОСТРАНСТВА И ТЕНЗОРЫ ВТОРОЙ ВАЛЕНТНОСТИ
- § 2. Матрица линейного преобразования
- § 3. Определитель матрицы линейного преобразования. Ранг матрицы
- § 4. Линейные преобразования и билинейные формы
- § 5. Умножение линейных преобразований и умножение матриц
- § 6. Обратное линейное преобразование и обратная матрица
- § 7. Группа линейных преобразований и ее подгруппы
- ГЛАВА XIV. ПРИВЕДЕНИЕ К ПРОСТЕЙШЕМУ ВИДУ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 1. Собственные векторы и собственные значения линейного преобразования
- § 2. Приведение к простейшему виду матрицы линейного преобразования в случае различных собственных значений
- § 3. Многочлены от матриц и теорема Гамильтона—Кэли
- § 4. Свойства собственных векторов и собственных значений симметричного линейного прейбразования
- § 5. Приведение к диагональному виду матрицы симметричного линейного преобразования
- § 6. Приведение квадратичной формы к каноническому виду
- § 7. Представление невырожденного линейного преобразования в виде произведения симметричного и ортогонального преобразований
- ГЛАВА V. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Общее уравнение поверхности второго порядка. Его инварианты
- § 2. Приведение к простейшему виду общего уравнения поверхности второго порядка
- § 3. Определение типа поверхности второго порядка при помощи инвариантов
- § 4. Классификация поверхностей второго порядка
- § 5. Приложение теории инвариантов к классификации поверхностей второго порядка
- § 6. Центральные и нецентральные поверхности второго порядка
- § 7. Примеры
- ГЛАВА VI. ПРИЛОЖЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К НЕКОТОРЫМ ВОПРОСАМ МЕХАНИКИ И ФИЗИКИ
- § 2. Некоторые свойства кристаллов, связанные с тензорами второй валентности
- § 3. Тензоры напряжений и деформации
- § 4. Дальнейшие свойства кристаллов
- ГЛАВА VII. ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА
- § 1. Тензорное поле и его дифференцирование
- § 2. Механика деформируемой среды
- § 3. Ортогоналыше криволинейные системы координат
- § 4. Подвижной репер ортогональной криволинейной системы координат и тензорные поля
- § 5. Дифференцирование тензорного поля в криволинейных координатах
- ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И УПРАЖНЕНИЙ
- ЛИТЕРАТУРА
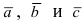
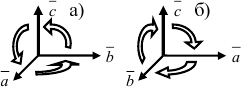
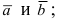
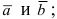
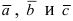 является правой.
является правой.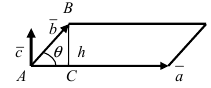
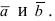
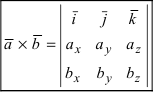
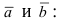
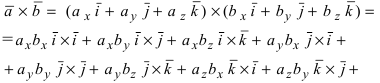
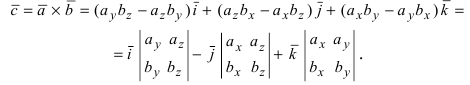
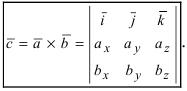
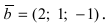
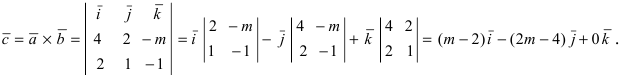
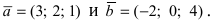
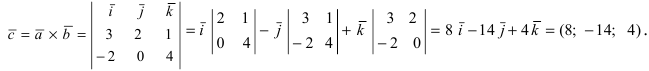
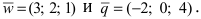
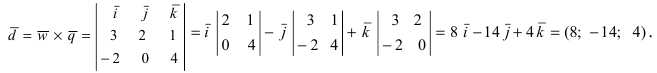
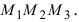
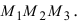
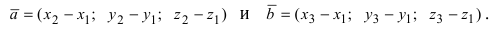

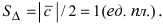
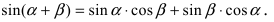
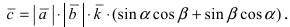
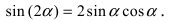
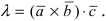
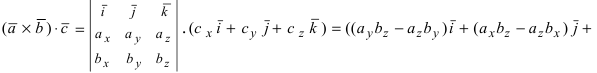
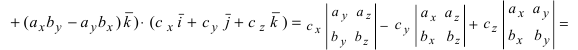
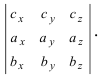
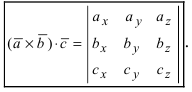
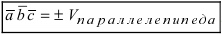
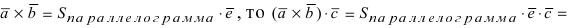
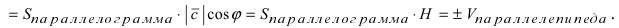
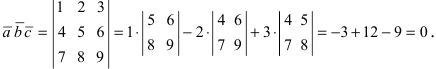
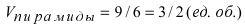
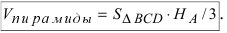
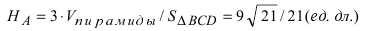























































































 — ассоциативность (сочетательный закон);
— ассоциативность (сочетательный закон); —дистрибутивность относительно сложения векторов (1-й распределительный закон);
—дистрибутивность относительно сложения векторов (1-й распределительный закон); — дистрибутивность относительно сложения чисел (2-й распределительный закон).
— дистрибутивность относительно сложения чисел (2-й распределительный закон).











 отсюда
отсюда 
 – т. е. векторы
– т. е. векторы  компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора  по данным векторам
по данным векторам  единственно. Теорема доказана.
единственно. Теорема доказана.

 получаем
получаем 
 и действительного числа
и действительного числа  получаем
получаем