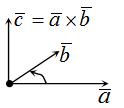Как найти векторное произведение через матрицу

Как найти векторное произведение через матрицу

Определение векторного произведения

Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.

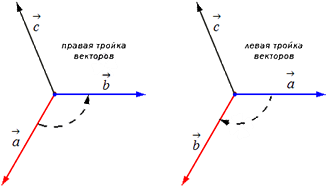
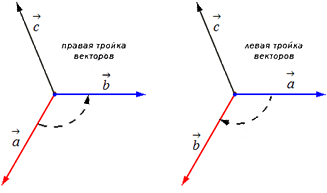
Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.

Определение векторного произведения

Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

Определение векторного произведения

Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.

Определение 1

Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

  • если векторы a→ и b→ коллинеарны, он будет нулевым;
  • он будет перпендикулярен и вектору a→​​​​ и вектору b→ т.е. ∠a→c→=∠b→c→=π2 ;
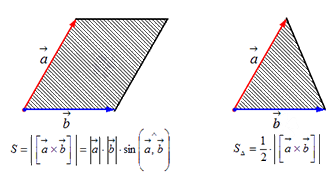
  • его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
  • тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.

Координаты векторного произведения

Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

Определение 2

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz) называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz

Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

  1. антикоммутативность a→×b→=-b→×a→;
  2. дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
  3. ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ – произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

Доказательство антикоммутативности

По определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .

Пример 1

Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.

Решение

С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.

Ответ: 1522.

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов  a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

Пример 2

В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.

Решение

По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.

Ответ: a→×b→=-2i→-2j→-2k→.

Пример 3

Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ – орты прямоугольной декартовой системы координат.

Решение

Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.

Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0)  и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.

Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.

Ответ: i→-j→×i→+j→+k→=6..

Пример 4

В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.

Решение

Векторы  AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к  AB→​​​​​ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.

Ответ: -6i→+j→-4k→. – один из перпендикулярных векторов.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Пример 5

Векторы  a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.

Решение

По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→

Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→..

Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..

Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.

По условию векторы  a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.

Ответ: 3·a→-b→×a→-2·b→=60.

Геометрический смысл векторного произведения

Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма – удвоенного треугольника, а именно произведению сторон в виде векторов  a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.

Это и есть геометрический смысл векторного произведения.

Геометрический смысл векторного произведения

Физический смысл векторного произведения

В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.

Определение 3

Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.

Источник

Векторное произведение в трёхмерном евклидовом пространстве

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой[⇨]. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Таким образом, для определения векторного произведения двух векторов необходимо задать ориентацию пространства, то есть сказать, какая тройка векторов является правой, а какая — левой. При этом не является обязательным задание в рассматриваемом пространстве какой-либо системы координат. В частности, при заданной ориентации пространства результат векторного произведения не зависит от того, является ли рассматриваемая система координат правой или левой. При этом формулы выражения координат векторного произведения через координаты исходных векторов в правой и левой ортонормированной прямоугольной системе координат отличаются знаком.

Векторное произведение не обладает свойствами коммутативности и ассоциативности. Оно является антикоммутативным и, в отличие от скалярного произведения векторов, результат является опять вектором.

Полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы коллинеарны.

Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения.

История[править | править код]

Векторное произведение было введено У. Гамильтоном в 1846 году[1] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[2].

Определение[править | править код]

Векторным произведением вектора {vec {a}} на вектор {vec {b}} в трёхмерном евклидовом пространстве называется вектор {vec {c}}, удовлетворяющий следующим требованиям:

Обозначения:

{displaystyle {vec {c}}=[{vec {a}}{vec {b}}]=[{vec {a}},;{vec {b}}]={vec {a}}times {vec {b}}={vec {a}}wedge {vec {b}}.}

Замечания[править | править код]

В качестве определения можно использовать описанное далее выражение векторного произведения в координатах в правой (или левой) прямоугольной системе координат.

Также в качестве исходного определения может быть взят набор алгебраических свойств векторного произведения.

Правые и левые тройки векторов в трёхмерном евклидовом пространстве[править | править код]

Рассмотрим упорядоченную тройку некомпланарных (линейно независимых) векторов {vec {a}},{vec {b}},{vec {c}} в трёхмерном евклидовом пространстве. В ориентированном пространстве такая тройка векторов будет либо «правой», либо «левой».

Геометрическое определение[править | править код]

Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов {vec {a}},{vec {b}},{vec {c}} в трёхмерном пространстве называется правой, если с конца вектора {vec {c}} кратчайший поворот от вектора {vec {a}} к вектору {vec {b}} виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.

Определение с помощью руки[править | править код]

Другое определение связано с правой рукой человека, откуда и берётся название. На рисунке тройка векторов {vec {a}}, {vec {b}}, {displaystyle {vec {a}}times {vec {b}}} является правой.

Алгебраическое определение[править | править код]

Существует также аналитический способ определения правой и левой тройки векторов, который требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора {vec {a}}, второй — вектора {vec {b}}, третьей — вектора {vec {c}}. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

  • Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
  • Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
  • Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Замечания[править | править код]

Определения «правой» и «левой» тройки векторов зависят от ориентации пространства, но не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого определение самого векторного произведения. При этом формулы выражения координат векторного произведения через координаты исходных векторов будут отличаться знаком в правой и левой прямоугольной системе координат.

Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.

При заданной ориентации пространства система координат называется правой (левой), если тройка из векторов с координатами {displaystyle (1,0,0)}, {displaystyle (0,1,0)}, {displaystyle (0,0,1)} является правой (левой).

Геометрическое определение и определение с помощью руки сами задают ориентацию пространства. Алгебраическое определение задаёт способ разбить тройки некомпланарных векторов на два класса одинаково ориентированных векторов, но оно не задаёт ориентацию пространства, а использует уже заданную — ту, на основании которой данная система координат считается правой или левой. При этом, если ориентация системы координат неизвестна, можно сравнивать знак определителя со знаком определителя другой тройки некомпланарных векторов, ориентация которой известна — если знаки совпадают, то тройки одинаково ориентированы, если знаки противоположны — тройки ориентированы противоположно.

Свойства[править | править код]

Геометрические свойства векторного произведения[править | править код]

Рисунок 1: Площадь параллелограмма равна модулю векторного произведения

Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на

a × b и вектора

b × c на

a, первым шагом является нахождение векторного произведения (модуль которого равен площади одной из сторон), а вторым — нахождение скалярного произведения (которое равно объёму параллелепипеда)

{displaystyle [{vec {a}},;{vec {b}}]=Scdot {vec {e}}.}
{displaystyle [{vec {a}},;{vec {c}}]=mathrm {Pr} _{vec {e}}{vec {a}}cdot |{vec {c}}|cdot {vec {g}}.}
  • При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
{displaystyle V=|langle {vec {a}},;[{vec {b}},;{vec {c}}]rangle |.}

На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:

{displaystyle V=langle [{vec {a}},;{vec {b}}],;{vec {c}}rangle =langle {vec {a}},;[{vec {b}},;{vec {c}}]rangle .}

Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов так же, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.

Алгебраические свойства векторного произведения[править | править код]

Далее {displaystyle [{vec {a}},;{vec {b}}]} и {displaystyle langle {vec {a}},;{vec {b}}rangle } обозначают соответственно векторное и скалярное произведение векторов {vec {a}} и {vec {b}}.

Представление Описание
{displaystyle [{vec {a}},;{vec {b}}]=-[{vec {b}},{vec {a}}]} Антикоммутативность.
{displaystyle [alpha cdot {vec {a}},;{vec {b}}]=[{vec {a}},;alpha cdot {vec {b}}]=alpha cdot [{vec {a}},;{vec {b}}]} Ассоциативность умножения на скаляр.
{displaystyle [{vec {a}}+{vec {b}},;{vec {c}}]=[{vec {a}},;{vec {c}}]+[{vec {b}},;{vec {c}}]} Дистрибутивность по сложению.
{displaystyle [[{vec {a}},;{vec {b}}],;{vec {c}}]+[[{vec {b}},;{vec {c}}],;{vec {a}}]+[[{vec {c}},{vec {a}}],;{vec {b}}]={vec {0}}} Тождество Якоби.
{displaystyle [{vec {a}},;{vec {a}}]={vec {0}}}
{displaystyle [{vec {a}},;[{vec {b}},;{vec {c}}]]={vec {b}}cdot langle {vec {a}},;{vec {c}}rangle -{vec {c}}cdot langle {vec {a}},;{vec {b}}rangle } Формула «БАЦ минус ЦАБ», тождество Лагранжа.
{displaystyle |[{vec {a}},,{vec {b}}]|^{2}+langle {vec {a}},,{vec {b}}rangle ^{2}=|{vec {a}}|^{2}cdot |{vec {b}}|^{2}} Частный случай мультипликативности нормы кватернионов.
{displaystyle langle [{vec {a}},,{vec {b}}],,{vec {c}}rangle =langle {vec {a}},,[{vec {b}},,{vec {c}}]rangle } Значение этого выражения называют смешанным произведением векторов a, b, c.

Выражение в координатах[править | править код]

В правом ортонормированном базисе[править | править код]

Если два вектора vec a и {displaystyle {vec {b}}} представлены в правом ортонормированном базисе координатами

{displaystyle {vec {a}}=(a_{x},;a_{y},;a_{z}),}
{displaystyle {vec {b}}=(b_{x},;b_{y},;b_{z}),}

то их векторное произведение имеет координаты

{displaystyle [{vec {a}},;{vec {b}}]=(a_{y}b_{z}-a_{z}b_{y},;a_{z}b_{x}-a_{x}b_{z},;a_{x}b_{y}-a_{y}b_{x}).}

Для запоминания этой формулы удобно использовать мнемонический определитель:

{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}},}

где {displaystyle mathbf {i} =(1,0,0)}, {displaystyle mathbf {j} =(0,1,0)}, {displaystyle mathbf {k} =(0,0,1)}, или

{displaystyle [{vec {a}},;{vec {b}}]_{i}=sum _{j,k=1}^{3}varepsilon _{ijk}a_{j}b_{k},}

где varepsilon _{{ijk}} — символ Леви-Чивиты.

В левом ортонормированном базисе[править | править код]

Если базис левый ортонормированный, то векторное произведение в координатах имеет вид

{displaystyle [{vec {a}},;{vec {b}}]=(a_{z}b_{y}-a_{y}b_{z},;a_{x}b_{z}-a_{z}b_{x},;a_{y}b_{x}-a_{x}b_{y}).}

Для запоминания, аналогично:

{displaystyle [{vec {a}},;{vec {b}}]=-{begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}},}

или

{displaystyle [{vec {a}},;{vec {b}}]_{i}=-sum _{j,k=1}^{3}varepsilon _{ijk}cdot a_{j}cdot b_{k}.}

Формулы для левой системы координат можно получить из формул правой системы координат, записав те же векторы vec a и {displaystyle {vec {b}}} во вспомогательной правой системе координат ({mathbf i}'={mathbf i},{mathbf j}'={mathbf j},{mathbf k}'=-{mathbf k}):

{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}mathbf {i} '&mathbf {j} '&mathbf {k} '\a'_{x}&a'_{y}&a'_{z}\b'_{x}&b'_{y}&b'_{z}end{vmatrix}}={begin{vmatrix}mathbf {i} &mathbf {j} &-mathbf {k} \a_{x}&a_{y}&-a_{z}\b_{x}&b_{y}&-b_{z}end{vmatrix}}=-{begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}}.}

В произвольной аффинной системе координат[править | править код]

Векторное произведение в произвольной аффинной системе координат {displaystyle O{vec {e}}_{1}{vec {e}}_{2}{vec {e}}_{3}} имеет координаты

{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}[{vec {e}}_{2},;{vec {e}}_{3}]&[{vec {e}}_{3},;{vec {e}}_{1}]&[{vec {e}}_{1},;{vec {e}}_{2}]\a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}}.}

Вариации и обобщения[править | править код]

Кватернионы[править | править код]

Координаты векторного произведения в правом ортонормированном базисе можно также записать в кватернионной форме, поэтому буквы {mathbf i}, {mathbf j}, {mathbf k} — стандартные обозначения для ортов в mathbb {R} ^{3}: они рассматриваются как воображаемые кватернионы.

Заметим, что соотношения через векторное произведение между {mathbf i}, {mathbf j} и {mathbf k} соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор (a_{1},;a_{2},;a_{3}) как кватернион a_{1}i+a_{2}j+a_{3}k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.

Преобразование к матричной форме[править | править код]

Векторное произведение двух векторов в координатах в правом ортонормированном базисе можно записать как произведение кососимметрической матрицы и вектора:

{displaystyle [{vec {a}},;{vec {b}}]=[{vec {a}}]_{times }{vec {b}}={begin{bmatrix},0&!-a_{3}&,,a_{2}\,,a_{3}&0&!-a_{1}\-a_{2}&,,a_{1}&,0end{bmatrix}}{begin{bmatrix}b_{1}\b_{2}\b_{3}end{bmatrix}},}
{displaystyle [{vec {b}},;{vec {a}}]={vec {b}}^{T}[{vec {a}}]_{times }={begin{bmatrix}b_{1}&b_{2}&b_{3}end{bmatrix}}{begin{bmatrix},0&!-a_{3}&,,,a_{2}\,,,a_{3}&,0&!-a_{1}\-a_{2}&,,a_{1}&,0end{bmatrix}},}

где

{displaystyle [{vec {a}}]_{times }{stackrel {rm {def}}{=}}{begin{bmatrix},,0&!-a_{3}&,,,a_{2}\,,,a_{3}&0&!-a_{1}\!-a_{2}&,,a_{1}&,,0end{bmatrix}}.}

Пусть {vec {a}} равен векторному произведению:

{displaystyle {vec {a}}=[{vec {c}},;{vec {d}}],}

тогда

{displaystyle [{vec {a}}]_{times }=({vec {c}}{vec {d}}^{T})^{T}-{vec {c}}{vec {d}}^{T}.}

Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь n(n-1)/2 независимых компонент в n-мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.

С такой формой записи также зачастую проще работать (например, в эпиполярной геометрии[en]).

Из общих свойств векторного произведения следует, что

{displaystyle [{vec {a}}]_{times },{vec {a}}={vec {0}}} и {displaystyle {vec {a}}^{T},[{vec {a}}]_{times }={vec {0}},}

а так как {displaystyle [{vec {a}}]_{times }} кососимметрична, то

{displaystyle {vec {b}}^{T},[{vec {a}}]_{times },{vec {b}}=0.}

В такой форме записи легко доказывается тождество Лагранжа (правило «БАЦ минус ЦАБ»).

Распространение на матрицы[править | править код]

В трёхмерном случае можно определить в координатах в произвольном базисе векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу A как столбец векторов, тогда

{displaystyle {begin{bmatrix}{vec {a}}_{1}\{vec {a}}_{2}\{vec {a}}_{3}end{bmatrix}}times {vec {b}}={begin{bmatrix}{vec {a}}_{1}times {vec {b}}\{vec {a}}_{2}times {vec {b}}\{vec {a}}_{3}times {vec {b}}end{bmatrix}},}
{displaystyle {begin{bmatrix}{vec {a}}_{1}\{vec {a}}_{2}\{vec {a}}_{3}end{bmatrix}}cdot {vec {b}}={begin{bmatrix}{vec {a}}_{1}cdot {vec {b}}\{vec {a}}_{2}cdot {vec {b}}\{vec {a}}_{3}cdot {vec {b}}end{bmatrix}}.}

Умножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот.
Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (A — матрица, {vec x}, {displaystyle {vec {y}}} — векторы):

{displaystyle Acdot ({vec {x}}times {vec {y}})=(Atimes {vec {x}})cdot {vec {y}},}
{displaystyle Atimes ({vec {x}}times {vec {y}})={vec {x}}(Acdot {vec {y}})-{vec {y}}(Acdot {vec {x}}).}

После этого можно изменить форму записи для векторного произведения:

{displaystyle {vec {x}}times {vec {y}}=Ecdot ({vec {x}}times {vec {y}})=(Etimes {vec {x}})cdot {vec {y}},}

E — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в mathbb {R} ^{3} примет вид:

int limits _{{Sigma }}operatorname {rot},{mathbf {A^{T}}},{mathbf {dSigma }}=int limits _{{partial Sigma }}{mathbf {A}}cdot ,d{mathbf {r}},

где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева (базис считается правым ортонормированным). В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:

int limits _{{Sigma }}operatorname {grad},utimes ,{mathbf {dSigma }}=int limits _{{partial Sigma }}u,d{mathbf {r}},
int limits _{{Sigma }}left[{mathbf {dSigma }};left[nabla ;{mathbf a}right]right]=int limits _{{partial Sigma }}{mathbf a}times d{mathbf {r}}.

Размерности, не равные трём[править | править код]

Пусть n — размерность пространства.

Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение {mathbb {R}}^{n}times {mathbb {R}}^{n}to {mathbb {R}}^{n}, можно ввести только для размерностей 3 и 7.

Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (n-1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в n-мерном пространстве на операцию с n сомножителями. Используя символ Леви-Чивиты varepsilon _{{i_{1}i_{2}i_{3}ldots i_{n}}} с n индексами, можно явно записать такое (n-1)-валентное векторное произведение как

{displaystyle P_{i}(mathbf {a} ,mathbf {b} ,mathbf {c} ,dotsc )=sum _{j,k,m,dotsc =1}^{n}varepsilon _{ijkldots }a_{j}b_{k}c_{m}ldots =det left({begin{pmatrix}mathbf {e_{1}} \vdots \mathbf {e_{n}} end{pmatrix}},mathbf {a} ,mathbf {b} ,mathbf {c} ,ldots right)cdot mathbf {e_{i}} ,}

{displaystyle mathbf {P} (mathbf {a_{1}} ,mathbf {a_{2}} ,ldots ,mathbf {a_{n-1}} )=det left({begin{pmatrix}mathbf {e_{1}} \vdots \mathbf {e_{n}} end{pmatrix}},mathbf {a_{1}} ,mathbf {a_{2}} ,ldots ,mathbf {a_{n-1}} right)={begin{vmatrix}mathbf {e_{1}} &mathbf {e_{2}} &cdots &mathbf {e_{n}} \a_{1_{1}}&a_{1_{2}}&cdots &a_{1_{n}}\a_{2_{1}}&a_{2_{2}}&cdots &a_{2_{n}}\vdots &vdots &ddots &vdots \a_{n-1_{1}}&a_{n-1_{2}}&cdots &a_{n-1_{n}}end{vmatrix}}.}

Такое обобщение дает гиперплощадь размерности n-1.

Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при nneq 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:

P_{{ij}}({mathbf {a,b}})=a_{i}b_{j}-a_{j}b_{i}.

Эта конструкция называется внешним произведением.

Для двумерного случая операция

P({mathbf {a,b}})=a_{1}b_{2}-a_{2}b_{1}.

называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению.)

Алгебра Ли векторов[править | править код]

Векторное произведение вводит на {mathbb {R}}^{{3}} структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению mathbb {R} ^{3} с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.

См. также[править | править код]

Произведения векторов

Другое

  • Ротор
  • Дивергенция

Примечания[править | править код]

  1. ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101.
  2. ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.

Литература[править | править код]

    1. Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. АН СССР: Изд-во «НАУКА», М. 1965.

Ссылки[править | править код]

  • Многомерное векторное произведение Архивная копия от 5 сентября 2015 на Wayback Machine
  • Векторное произведение и его свойства. Примеры решения задач Архивная копия от 23 февраля 2011 на Wayback Machine
  • В. И. Гервидс. Правое и левое вращение. НИЯУ МИФИ (10 марта 2011). — Физические демонстрации. Дата обращения: 3 мая 2011. Архивировано 23 декабря 2015 года.
Источник

Содержание:

  • Формула
  • Примеры вычисления векторного произведения векторов

Формула

Для того чтобы найти векторное произведение
$[bar{a}, bar{b}]$ двух векторов, заданных своими координатами
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и
$bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, необходимо
вычислить следующий определитель

$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$

Обычно такой определитель вычисляют разложением по первой строке. Отметим также, что результатом векторного произведения является вектор.

Примеры вычисления векторного произведения векторов

Пример

Задание. Найти векторное произведение векторов
$bar{a}=(1 ; 0 ; 0)$ и $bar{b}=(0 ; 1 ; 0)$

Решение. Для вычисления векторного произведения заданных векторов воспользуемся формулой

$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$

Подставляя координаты заданных векторов, получим:

$$[bar{a}, bar{b}]=left|begin{array}{lll}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|$$

Раскладываем определитель по первой строке:

$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|=$$
$$=bar{i} cdotleft|begin{array}{cc}0 & 0 \ 1 & 0end{array}right|-bar{j} cdotleft|begin{array}{cc}1 & 0 \ 0 & 0end{array}right|+bar{k} cdotleft|begin{array}{cc}1 & 0 \ 0 & 1end{array}right|=$$
$$=0 cdot bar{i}-0 cdot bar{j}+1 cdot k$$

Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляем
как определитель второго порядка: от произведения элементов главной диагонали отнимаем произведение элементов побочной.

Итак, координаты искомого вектора равны коэффициентам при ортах, то есть

$$[bar{a}, bar{b}]=(0 ; 0 ; 1)$$

Ответ. $[bar{a}, bar{b}]=(0 ; 0 ; 1)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Даны векторы
$bar{a}=(5 ; 3 ;-4)$ и $bar{b}=(6 ; 7 ;-8)$ . Найти координаты векторного произведения
$[bar{a}, bar{b}]$

Решение. Координаты векторного произведения
$[bar{a}, bar{b}]$ вычисляются по формуле

$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$

Подставляя координаты заданных векторов, получим:

$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 5 & 3 & -4 \ 6 & 7 & -8end{array}right|$$

Раскладываем полученный определитель по первой строке:

$$=bar{i} cdotleft|begin{array}{cc}3 & -4 \ 7 & -8end{array}right|-bar{j} cdotleft|begin{array}{cc}5 & -4 \ 6 & -8end{array}right|+bar{k} cdotleft|begin{array}{cc}5 & 3 \ 6 & 7end{array}right|=$$
$$=[3 cdot(-8)-7 cdot(-4)] cdot bar{i}-[5 cdot(-8)-6 cdot(-4)] cdot bar{j}+$$
$$+[5 cdot 7-6 cdot 3] cdot bar{k}=(-24+28) bar{i}-(-40+24) bar{j}+(35-18) bar{k}=$$
$$=4 cdot bar{i}+16 cdot bar{j}+17 cdot bar{k}$$

Тогда

$$[bar{a}, bar{b}]=(4 ; 16 ; 17)$$

Ответ. $[bar{a}, bar{b}]=(4 ; 16 ; 17)$

Читать дальше: как найти смешанное произведение векторов.

Источник

Векторное произведение векторов и его свойства

Геометрическая интерпретация векторного произведения векторов

Вектор vec{c} называется векторным произведением неколлинеарных векторов vec{a} и vec{b}, если:

1) его длина равна произведению длин векторов vec{a} и vec{b} на синус угла между ними: |vec{c}|=|vec{a}|cdot|vec{b}|cdotsinvarphi (рис.1.42);

2) вектор vec{c} ортогонален векторам vec{a} и vec{b};

3) векторы vec{a}, vec{b}, vec{c} (в указанном порядке) образуют правую тройку.

Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Векторное произведение обозначается mathop{vec{c}=bigl[vec{a},vec{b}bigr]}limits_{{.}} (или vec{a}timesvec{b}).

Алгебраические свойства векторного произведения

Для любых векторов vec{a}, vec{b}, vec{c} и любого действительного числа lambda:

1. bigl[vec{a},vec{b}bigr]=-bigl[vec{b},vec{a}bigr];

2. bigl[vec{a}+vec{b},vec{c}bigr]=bigl[vec{a},vec{c}bigr]+bigl[vec{b},vec{c}bigr];

3. bigl[lambdacdotvec{a},vec{b}bigr]=lambdacdotbigl[vec{a},vec{b}bigr].

Первое свойство определяет антисимметричность векторного произведения, второе и третье — аддитивность и однородность по первому множителю. Эти свойства аналогичны свойствам произведения чисел: первое свойство “противоположно” закону коммутативности умножения чисел (закон антикоммутативности), второе свойство соответствует закону дистрибутивности умножения чисел по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является вектор, то такое произведение векторов называется векторным.

Поворот вектора к вектору

Докажем первое свойство, предполагая, что векторы vec{a} и vec{b} не коллинеарны (в противном случае обе части доказываемого равенства равны нулевому вектору). По определению векторы vec{c}=[vec{a},vec{b}] и vec{c}=[vec{b},vec{a}] имеют равные длины left(|vec{c}|=|vec{a}|cdot|vec{b}|cdotsinvarphi=|vec{d}|right) и коллинеарны (так как оба вектора перпендикулярны одной плоскости). По определению тройки векторов vec{a},vec{b},vec{c} и vec{b},vec{a},vec{d} — правые, т.е. вектор vec{c} направлен так, что кратчайший поворот от vec{a} к vec{b} происходит в положительном направлении (против часовой стрелки), если смотреть из конца вектора vec{c}, а вектор vec{d} направлен так, что кратчайший поворот от vec{b} к vec{a} происходит в положительном направлении, если смотреть из конца вектора vec{d} (рис. 1.43). Это означает, что векторы vec{c} и vec{d} противоположно направлены. Следовательно, vec{c}=-vec{d}, что и требовалось доказать. Доказательство остальных свойств приведено ниже (см. пункт 1 замечаний 1.13).

Замечания 1.12

1. Свойства аддитивности и однородности векторного произведения означают линейность векторного произведения по первому множителю:

bigl[alphacdotvec{a}+betacdotvec{b},,vec{c}bigr],=alphacdot[vec{a},vec{c}]+betacdot[vec{b},vec{c}]

для любых векторов vec{a},vec{b},vec{c} и любых действительных чисел alpha и beta.

2. В силу антисимметричности векторное произведение линейно и по второму множителю, т.е. линейно по любому множителю.

Геометрические свойства векторного произведения

1. Модуль векторного произведения численно равен площади параллелограмма, построенного на множителях (рис. 1.42,6).

2. Векторное произведение равняется нулевому вектору тогда и только тогда, когда множители коллинеарны, т.е.

[vec{a},vec{b}]=vec{o}~Leftrightarrow~vec{a}parallelvec{b}, в частности, [vec{a},vec{a}]=vec{o}.

Первое свойство следует из определения. Докажем второе свойство. Равенство |vec{a}|cdot|vec{b}|cdotsinvarphi=0 возможно в трех случаях: vec{a}=vec{o}, или vec{b}=vec{o}, или sinvarphi=0. В каждом из этих случаев векторы vec{a} и vec{b} коллинеарны (см. разд. 1.1).

Треугольник, построенный на векторах

Пример 1.19. Вычислить площади параллелограмма и треугольника, построенных на векторах vec{p}=vec{m}+2vec{n},~vec{q}=vec{m}-3vec{n}, где |vec{m}|=3,~|vec{n}|=2, угол между векторами vec{m} и vec{n} равен pi/6 (рис. 1.44).

Решение. Используя алгебраические свойства, найдем сначала векторное произведение

begin{aligned}{[vec{p},vec{q}]}&=[vec{m}+2vec{n},vec{m}-3vec{n}]=[vec{m},vec{m}-3vec{n}]+[2vec{n},vec{m}-3vec{n}]=\[3pt]&=[vec{m},vec{m}-3vec{n}]+2[n,vec{m}-3vec{n}]=[vec{m},vec{m}]-3[vec{m},vec{n}]+2left({[vec{n},vec{m}]-3[vec{n},vec{n}]}right)=\[3pt] &=underbrace{[vec{m}, vec{m}]}_{vec{o}}-3[vec{m},vec{n}]+2underbrace{[vec{n},vec{m}]}_{-[vec{m},vec{n}]}-6underbrace{[vec{n},vec{n}]}_{vec{o}}=-5[vec{m},vec{n}],end{aligned}

а затем его модуль bigl|[vec{p},vec{q}]bigl|= |-5|cdot bigl|vec{m}, vec{n}bigl|=5cdot|vec{m}|cdot|vec{n}|cdotsinfrac{pi}{6}=5cdot3cdot2cdotfrac{1}{2}=15.

По первому геометрическому свойству векторного произведения искомая площадь параллелограмма равна S_{*}=15, а площадь треугольника в 2 раза меньше: S_{triangle}=frac{1}{2}cdot S_{*}=frac{15}{2}.

Выражение векторного произведения через координаты векторов

Пусть в пространстве задан ортонормированный (стандартный) базис vec{i},vec{j},vec{k}. Векторные произведения базисных векторов находятся по определению:

Ортонормированный базис в пространстве

begin{aligned}&[vec{i},vec{j}]=vec{k};qquad phantom{-}[vec{j},vec{k}]=vec{i};qquad phantom{-}[vec{k}, vec{i}]= vec{j};\[2pt]&[vec{j},vec{i}]=-vec{k};qquad [vec{k},vec{j}]=-vec{i};qquad [vec{i},vec{k}]=-vec{j};\[2pt]&[vec{i},vec{i}]=[vec{j},vec{j}]=[vec{k},vec{k}]=vec{o}.end{aligned}

(1.14)

Формулы (1.14) можно получить, используя диаграмму (рис. 1.45): если на этой схеме кратчайший поворот от первого множителя ко второму совершается в положительном направлении (указанном стрелкой), то произведение равно третьему вектору, а если — в отрицательном направлении, то произведение равно третьему вектору, взятому со знаком минус (противоположному вектору).

Найдем выражение векторного произведения через координаты множителей. Пусть в стандартном базисе vec{i},vec{j},vec{k} векторы vec{a} и vec{b} имеют координаты x_a,y_a,z_a и x_b,y_b,z_b соответственно. Тогда, используя линейность векторного произведения по любому множителю (см. пункт 2 замечаний 1.12) и формулы (1.14), получаем

begin{aligned}bigl[vec{a},vec{b}bigr],=,&bigl[x_a{cdot}vec{i},+,y_a{cdot}vec{j},+z_a{cdot}vec{k},,x_b{cdot}vec{i},+,y_b{cdot}vec{j},+z_b{cdot}vec{k}bigr],=\[3pt] =,&x_ax_b{cdot}bigl[vec{i},vec{i}bigr],+,x_ay_b{cdot}bigl[vec{i},vec{j}bigr],+,x_az_b{cdot}bigl[vec{i},vec{k}bigr],+,y_ax_b{cdot}bigl[vec{j},vec{i}bigr],+,y_ay_b{cdot}bigl[vec{j},vec{j}bigr]+\[3pt] &phantom{=x_ax_b},+,y_az_b{cdot}bigl[vec{j},vec{k}bigr],+,z_ax_b{cdot}bigl[vec{k},vec{i}bigr],+,z_ay_b{cdot}bigl[vec{k},vec{j}bigr],+,z_az_b{cdot}bigl[vec{k},vec{k}bigr],=\[3pt] =,&bigl(y_az_b-y_bz_abigl)cdotvec{i}-bigl(x_az_b-x_bz_abigl)cdotvec{j}+bigl(x_ay_b-x_by_abigl)cdotvec{k}.end{aligned}

Запишем это равенство при помощи определителей второго порядка:

bigl[vec{a}, vec{b}bigr],= ,vec{i}cdot begin{vmatrix} y_a&z_a\y_b&z_bend{vmatrix},-,vec{j}cdot begin{vmatrix} x_a&z_a\x_b&z_b end{vmatrix}+ vec{k}cdot begin{vmatrix} x_a&y_a\x_b&y_bend{vmatrix}.

(1.15)

Правую часть (1.15) можно представить как результат разложения символического определителя третьего порядка по первой строке

vec{i}cdotbegin{vmatrix}y_a&z_a\y_b&z_bend{vmatrix},-,vec{j}cdotbegin{vmatrix}x_a&z_a\x_b&z_bend{vmatrix},+,vec{k}cdotbegin{vmatrix}x_a&y_a\x_b&y_bend{vmatrix}=begin{vmatrix}vec{i}&vec{j}&vec{k}\x_a&y_a&z_a\x_b&y_b&z_bend{vmatrix}.

Формула вычисления векторного произведения

Теорема 1.8 (формула вычисления векторного произведения). Если векторы vec{a} и vec{b} в правом ортонормированием базисе vec{i},vec{j},vec{k} имеют координаты x_a,y_a,z_a и x_b,y_b,z_b соответственно, то векторное произведение этих векторов находится по формуле (1.15), которую принято записывать в виде

bigl[vec{a}, vec{b}bigr],= begin{vmatrix} vec{i}& vec{j}&vec{k}\x_a&y_a&z_a\x_b&y_b&z_bend{vmatrix}.

(1.16)

Если a=begin{pmatrix}x_a&y_a&z_aend{pmatrix}^T и b=begin{pmatrix}x_b&y_b&z_bend{pmatrix}^T — координатные столбцы векторов vec{a} и vec{b} в стандартном базисе, то координатный столбец c=begin{pmatrix}x_c&y_c&z_cend{pmatrix}^T векторного произведения vec{c}=[vec{a},vec{b}] находится по формуле

Параллелограмм построен на векторах

begin{pmatrix} x_c\y_c\z_c end{pmatrix}= begin{pmatrix}0&-z_a&y_a\z_a&0&-x_a\-y_a&x_a&0 end{pmatrix}!cdot !begin{pmatrix} x_b\y_b\z_bend{pmatrix}.

В самом деле, выполняя умножение матрицы на столбец, получаем

begin{pmatrix}x_c\y_c\z_cend{pmatrix}=begin{pmatrix}y_acdot z_b-y_bcdot z_a\x_bcdot z_a-x_acdot z_b\x_acdot y_b-x_bcdot y_aend{pmatrix}.

Тогда vec{c}=[vec{a},vec{b}]=(y_az_b-y_bz_a){cdot}vec{i}+(x_bz_a-x_az_b){cdot}vec{j}+(x_ay_a-x_by_a){cdot}vec{k}, что совпадает с (1.15).

Пример 1.20. Параллелограмм ABCD построен на векторах overrightarrow{AB}=vec{i}+2vec{j}+2vec{k},~overrightarrow{AD}=3vec{i}-2vec{j}+vec{k} (рис. 1.46). Найти:

а) векторные произведения bigl[overrightarrow{AB}, overrightarrow{AD}bigr] и bigl[overrightarrow{AC}, overrightarrow{BD}bigr];
б) площадь параллелограмма ABCD;
в) направляющие косинусы такого вектора vec{n}, перпендикулярного плоскости параллелограмма ABCD,

для которого тройка overrightarrow{AB}, overrightarrow{AD}, vec{n} — левая.

Решение. а) Векторное произведение bigl[overrightarrow{AB},overrightarrow{AD}bigr] находим по формуле (1.16):

bigl[overrightarrow{AB},overrightarrow{AD}bigr]=begin{vmatrix},vec{i}&vec{j}&vec{k}\1&2&2\3&-2&1,end{vmatrix}=vec{i}begin{vmatrix}2&2\-2&1end{vmatrix}-vec{j}begin{vmatrix}1&2\3&1end{vmatrix}+vec{k}begin{vmatrix}1&2\3&-2end{vmatrix}=6,vec{i}+5,vec{j}-8,vec{k}.

Для нахождения векторного произведения можно использовать матричную запись формулы (1.15) (см. теорему 1.8). Векторам vec{a}=overrightarrow{AB} и vec{b}=overrightarrow{AD} соответствуют координатные столбцы a=begin{pmatrix} 1&2&2 end{pmatrix}^T,~~ b=begin{pmatrix} 3&-2&1 end{pmatrix}^T.

По указанной формуле получаем координатный столбец c вектора vec{c}=[vec{a},vec{b}]:

begin{pmatrix}x_c\[2pt]y_c\[2pt]z_cend{pmatrix}=begin{pmatrix}0&-2&2\[2pt]2&0&-1\[2pt]-2&1&0end{pmatrix}!!cdot!!begin{pmatrix}3\[2pt]-2\[2pt]1end{pmatrix}=begin{pmatrix}0cdot3+(-2)cdot(-2)+2cdot1\[2pt]2cdot3+0cdot(-2)+(-1)cdot1\[2pt](-2)cdot3+1cdot(-2)+0cdot1end{pmatrix}=begin{pmatrix}6\[2pt]5\[2pt]-8end{pmatrix}!.

то есть vec{c}=[vec{a},vec{b}]= 6,vec{i}+ 5vec{j}- 8,vec{k}. Результаты совпадают.

Векторное произведение bigl[overrightarrow{AC}, overrightarrow{BD}bigr] находим, используя алгебраические свойства:

bigl[overrightarrow{AC},overrightarrow{BD}bigr],=!bigl[overrightarrow{AB}+overrightarrow{AD},overrightarrow{AD}-overrightarrow{AB}bigr],=!bigl[overrightarrow{AB},overrightarrow{AD}bigr]-underbrace{bigl[overrightarrow{AB},overrightarrow{AB}bigr]}_{vec{o}}+underbrace{bigl[overrightarrow{AD},overrightarrow{AD}bigr]}_{vec{o}}-underbrace{bigl[overrightarrow{AD},overrightarrow{AB}bigr]}_{-[overrightarrow{AB},overrightarrow{AD}]}=2bigl[overrightarrow{AB},overrightarrow{AD}bigr]

Следовательно, bigl[overrightarrow{AC},overrightarrow{BD}bigr]=2bigl(6,vec{i}+5,vec{j}-8,vec{k}bigl),=12,vec{i}+10,vec{j}-16,vec{k}.

б) Площадь параллелограмма ABCD находим как модуль векторного произведения bigl[overrightarrow{AB},overrightarrow{AD}bigr]:

S_{*}=Bigl|bigl[overrightarrow{AB},overrightarrow{AD}bigr]Bigl|,=Bigl|6,vec{i}+5,vec{j}-8,vec{k}Bigl|,=sqrt{6^2+5^2+(-8)^2}=sqrt{125}=5sqrt{5}.

в) Вектор, противоположный вектору bigl[overrightarrow{AB},overrightarrow{AD}bigr], удовлетворяет перечисленным в условии требованиям, поэтому

vec{n}=-[overrightarrow{AB},overrightarrow{AD}]=-(6,vec{i}+5,vec{j}-8,vec{k})=-6,vec{i}-5,vec{j}+8,vec{k}.

Разделив этот вектор на его длину |vec{n}|=Bigl|[overrightarrow{AB},overrightarrow{AD}]Bigl|,=5sqrt{5}, получим единичныи вектор:

frac{vec{n}}{|vec{n}|}=frac{-6,vec{i}-5,vec{j}+8,vec{k}}{5sqrt{5}}=-frac{6}{5sqrt{5}},vec{i}-frac{1}{sqrt{5}},vec{j}+frac{8}{5sqrt{5}},vec{k}.

Согласно его координатами служат направляющие косинусы

cosalpha=-frac{6}{5sqrt{5}},qquad cosbeta=-frac{1}{sqrt{5}},qquad cosgamma=frac{8}{5sqrt{5}}.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Векторное произведение векторов

Определение

Определение

Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $.

векторное произведение векторов

Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.

Формула

Формула 1

Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле:

$$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$
Формула 2

В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$

где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $.

Определитель во второй формуле можно раскрыть по первой строке:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 – a_3 b_2) – overline{j} (a_1 b_3 – a_3 b_1) + overline{k} (a_1 b_2 – a_2 b_1) $$

Итого вторая формула приобретает окончательный короткий вид:

$$ overline{a} times overline{b} = (a_2 b_3 – a_3 b_2; a_3 b_1 – a_1 b_3; a_1 b_2 – a_2 b_1) $$

Свойства

  1. При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
  2. Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
  3. $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$

Примеры решений

Пример 1

Найти векторное произведение векторов, заданных координатами

$$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$
Решение

Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) – overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} – overline{j} + 3overline{k} $$

Полученный ответ можно записать в удобном виде:

$$ overline{a} times overline{b} = (5, -1, 3) $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ overline{a} times overline{b} = (5, -1, 3) $$

Геометрический смысл

  • Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
  • Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
  • Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.

 

    Пример 2
    Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$
    Решение

    Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов.

    Находим определитель:

    $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) – overline{j}(2+3) + overline{k}(4+1) = -5overline{i} – 5overline{j} + 5overline{k} $$

    Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора:

    $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$

    По формуле нахождения площади треугольника имеем:

    $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$
    Ответ
    $$ S_Delta = 4.33 $$
    Источник

    Добавить комментарий