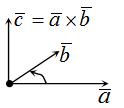Векторное произведение векторов
Определение
| Определение |
|
Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $. |
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.
Формула
| Формула 1 |
|
Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$ |
| Формула 2 |
|
В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $. |
Определитель во второй формуле можно раскрыть по первой строке:
$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 – a_3 b_2) – overline{j} (a_1 b_3 – a_3 b_1) + overline{k} (a_1 b_2 – a_2 b_1) $$
Итого вторая формула приобретает окончательный короткий вид:
$$ overline{a} times overline{b} = (a_2 b_3 – a_3 b_2; a_3 b_1 – a_1 b_3; a_1 b_2 – a_2 b_1) $$
Свойства
- При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
- Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
- $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$
Примеры решений
| Пример 1 |
|
Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$ |
| Решение |
|
Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) – overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} – overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a} times overline{b} = (5, -1, 3) $$ |
Геометрический смысл
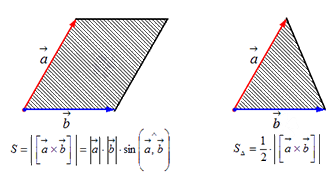
- Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
- Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
- Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.
| Пример 2 |
| Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$ |
| Решение |
|
Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) – overline{j}(2+3) + overline{k}(4+1) = -5overline{i} – 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$ |
| Ответ |
| $$ S_Delta = 4.33 $$ |
Определение векторного произведения
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.
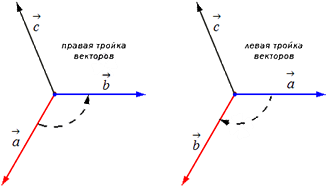
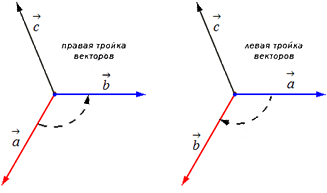
Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.
Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a→ и b→ коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a→ и вектору b→ т.е. ∠a→c→=∠b→c→=π2 ;
- его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
- тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.
Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz) называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz
Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a→×b→=-b→×a→;
- дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
- ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ – произвольное действительное число.
Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
По определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .
Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.
Решение
С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.
Ответ: 1522.
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.
Рассмотрим следующие примеры.
В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.
Решение
По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.
Ответ: a→×b→=-2i→-2j→-2k→.
Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ – орты прямоугольной декартовой системы координат.
Решение
Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.
Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0) и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.
Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.
Ответ: i→-j→×i→+j→+k→=6..
В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.
Решение
Векторы AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к AB→ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.
Ответ: -6i→+j→-4k→. – один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Векторы a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.
Решение
По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→
Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→..
Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..
Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.
По условию векторы a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.
Ответ: 3·a→-b→×a→-2·b→=60.
Геометрический смысл векторного произведения
Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма – удвоенного треугольника, а именно произведению сторон в виде векторов a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.
Это и есть геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.
Содержание:
- Формула
- Примеры вычисления векторного произведения векторов
Формула
Для того чтобы найти векторное произведение
$[bar{a}, bar{b}]$ двух векторов, заданных своими координатами
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и
$bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, необходимо
вычислить следующий определитель
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Обычно такой определитель вычисляют разложением по первой строке. Отметим также, что результатом векторного произведения является вектор.
Примеры вычисления векторного произведения векторов
Пример
Задание. Найти векторное произведение векторов
$bar{a}=(1 ; 0 ; 0)$ и $bar{b}=(0 ; 1 ; 0)$
Решение. Для вычисления векторного произведения заданных векторов воспользуемся формулой
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Подставляя координаты заданных векторов, получим:
$$[bar{a}, bar{b}]=left|begin{array}{lll}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|$$
Раскладываем определитель по первой строке:
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|=$$
$$=bar{i} cdotleft|begin{array}{cc}0 & 0 \ 1 & 0end{array}right|-bar{j} cdotleft|begin{array}{cc}1 & 0 \ 0 & 0end{array}right|+bar{k} cdotleft|begin{array}{cc}1 & 0 \ 0 & 1end{array}right|=$$
$$=0 cdot bar{i}-0 cdot bar{j}+1 cdot k$$
Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляем
как определитель второго порядка: от произведения элементов главной диагонали отнимаем произведение элементов побочной.
Итак, координаты искомого вектора равны коэффициентам при ортах, то есть
$$[bar{a}, bar{b}]=(0 ; 0 ; 1)$$
Ответ. $[bar{a}, bar{b}]=(0 ; 0 ; 1)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны векторы
$bar{a}=(5 ; 3 ;-4)$ и $bar{b}=(6 ; 7 ;-8)$ . Найти координаты векторного произведения
$[bar{a}, bar{b}]$
Решение. Координаты векторного произведения
$[bar{a}, bar{b}]$ вычисляются по формуле
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Подставляя координаты заданных векторов, получим:
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 5 & 3 & -4 \ 6 & 7 & -8end{array}right|$$
Раскладываем полученный определитель по первой строке:
$$=bar{i} cdotleft|begin{array}{cc}3 & -4 \ 7 & -8end{array}right|-bar{j} cdotleft|begin{array}{cc}5 & -4 \ 6 & -8end{array}right|+bar{k} cdotleft|begin{array}{cc}5 & 3 \ 6 & 7end{array}right|=$$
$$=[3 cdot(-8)-7 cdot(-4)] cdot bar{i}-[5 cdot(-8)-6 cdot(-4)] cdot bar{j}+$$
$$+[5 cdot 7-6 cdot 3] cdot bar{k}=(-24+28) bar{i}-(-40+24) bar{j}+(35-18) bar{k}=$$
$$=4 cdot bar{i}+16 cdot bar{j}+17 cdot bar{k}$$
Тогда
$$[bar{a}, bar{b}]=(4 ; 16 ; 17)$$
Ответ. $[bar{a}, bar{b}]=(4 ; 16 ; 17)$
Читать дальше: как найти смешанное произведение векторов.
Любовь Петровна Гаврилюк
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Угол между векторами
Для того чтобы мы могли ввести понятие векторного произведения двух векторов, нужно сначала разобраться с таким понятие, как угол между этими векторами.
Пусть нам даны два вектора $overline{α}$ и $overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $overline{α}=overline{OA}$ и $overline{β}=overline{OB}$, тогда угол $AOB$ будет называться углом между этими векторами (рис. 1).
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Причем мы будем считать, что если векторы $overline{α}$ и $overline{β}$ будут сонаправленными, или один или оба из них нулевой, то угол между этими векторами будет равен $0^circ$.
Обозначение: $∠(overline{α},overline{β})$
Понятие векторного произведения векторов и формула нахождения
Определение 1
Векторным произведением двух векторов называется вектор, перпендикулярный обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $overline{α}хoverline{β}$.
Математически это выглядит следующим образом:
- $|overline{α}хoverline{β}|=|overline{α}||overline{β}|sin∠(overline{α},overline{β})$
- $overline{α}хoverline{β}⊥overline{α}$, $overline{α}хoverline{β}⊥overline{β}$
- $(overline{α}хoverline{β},overline{α},overline{β})$ и $(overline{i},overline{j},overline{k})$ одинаково ориентированы (рис. 2)
«Как найти векторное произведение векторов» 👇
Рисунок 2. Произведение векторов. Автор24 — интернет-биржа студенческих работ
Очевидно, что внешнее произведение векторов будет равняться нулевому вектору в двух случаях:
- Если длина одного или обоих векторов равняется нулю.
- Если угол между этими векторами будет равняться $180^circ$ или $0^circ$ (так как в этом случае синус равняется нулю).
Чтобы наглядно увидеть, как находится векторное произведение векторов, рассмотрим следующие примеры решения.
Пример 1
Найти длину вектора $overline{δ}$, который будет являться результатом векторного произведения векторов, с координатами $overline{α}=(0,4,0)$ и $overline{β}=(3,0,0)$.
Решение.
Изобразим эти векторы в декартовом координатном пространстве (рис. 3):
Рисунок 3. Векторы в декартовом координатном пространстве. Автор24 — интернет-биржа студенческих работ
Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^circ$. Найдем длины этих векторов:
$|overline{α}|=sqrt{0+16+0}=4$
$|overline{β}|=sqrt{9+0+0}=3$
Тогда, по определению 1, получим модуль $|overline{δ}|$
$|overline{δ}|=|overline{α}||overline{β}|sin90^circ=4cdot 3cdot 1=12$
Ответ: $12$.
Вычисление векторного произведения по координатам векторов
Из определения 1 сразу же вытекает и способ нахождения векторного произведения для двух векторов. Поскольку вектор кроме значения имеет еще и направление, находить его только при помощи скалярной величины невозможно. Но помимо него существует еще способ нахождения с помощью координат данных нам векторов.
Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые будут иметь координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$
Иначе, раскрывая определитель, получим следующие координаты
$overline{α}хoverline{β}=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Пример 2
Найти вектор векторного произведения коллинеарных векторов $overline{α}$ и $overline{β}$ с координатами $(0,3,3)$ и $(-1,2,6)$.
Решение.
Воспользуемся формулой, приведенной выше. Получим
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\0&3&3\-1&2&6end{vmatrix}=(18-6)overline{i}-(0+3)overline{j}+(0+3)overline{k}=12overline{i}-3overline{j}+3overline{k}=(12,-3,3)$
Ответ: $(12,-3,3)$.
Свойства векторного произведения векторов
Для произвольных смешанных трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$, а также $r∈R$ справедливы следующие свойства:
-
$overline{α}хoverline{β}=-(overline{β}хoverline{α})$
Верность этого свойства будет следовать из третьего пункта определения 1.
-
$(roverline{α})хoverline{β}=r(overline{α}хoverline{β})$ и $overline{α}х(roverline{β})=r(overline{α}хoverline{β})$
Из формулы для нахождения векторного произведения будем получать:
$(roverline{α})overline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\rα_1&rα_2&rα_3\β_1&β_2&β_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$
$overline{α}х(roverline{β})=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\rβ_1&rβ_2&rβ_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$
-
$overline{α}х(overline{β}+overline{γ})=overline{α}overline{β}+overline{α}overline{γ}$ и $(overline{α}+overline{β})overline{γ}=overline{α}overline{γ}+overline{β}overline{γ}$.
Данное свойство векторного произведения векторов также можно проверить с помощью формулы.
Следующее свойство называют геометрическим смыслом векторного произведения:
-
Длина вектора векторного произведения равняется площади параллелограмма, который нужно было построить между ними (рис. 4)
Рисунок 4. Длина вектора векторного произведения. Автор24 — интернет-биржа студенческих работ
Пример 3
Найдите площадь параллелограмма, вершины которого имеют координаты $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ и $(3,8,0)$.
Решение.
Вначале изобразим данный параллелограмм в координатном пространстве (рис.5):
Рисунок 5. Параллелограмм в координатном пространстве. Автор24 — интернет-биржа студенческих работ
Видим, что две стороны этого параллелограмма построены с помощью коллинеарных векторов с координатами $overline{α}=(3,0,0)$ и $overline{β}=(0,8,0)$. Используя четвертое свойство, получим:
$S=|overline{α}хoverline{β}|$
Найдем вектор $overline{α}хoverline{β}$:
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\3&0&0\0&8&0end{vmatrix}=0overline{i}-0overline{j}+24overline{k}=(0,0,24)$
Следовательно
$S=|overline{α}хoverline{β}|=sqrt{0+0+24^2}=24$
Ответ: $24$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В данной публикации мы рассмотрим, каким образом можно найти векторное произведение двух векторов, приведем геометрическую интерпретацию, алгебраическую формулу и свойства этого действия, а также разберем пример решения задачи.
- Геометрическая интерпретация
- Формула векторного произведения
- Свойства векторного произведения
- Пример задачи
Геометрическая интерпретация
Векторное произведение двух ненулевых векторов a и b – это вектор c, который обозначается как [a, b] или a x b.
Длина вектора c равна площади параллелограмма, построенного с помощью векторов a и b.
При этом c перпендикулярен плоскости, в которой расположены a и b, и расположен так, чтобы наименьшее вращение от a к b выполнялось против часовой стрелки (с точки зрения конца вектора).
Формула векторного произведения
Произведение векторов a = {ax; ay, az} и b = {bx; by, bz} вычисляется с помощью одной из формул ниже:
Свойства векторного произведения
1. Векторное произведение двух ненулевых векторов равняется нулю тогда и только тогда, когда эти векторы являются коллинеарными.
[a, b] = 0, если
a || b
.
2. Модуль векторного произведения двух векторов равняется площади параллелограмма, образованного этими векторами.
Sпарал. = |a x b|
3. Площадь треугольника, образованного двумя векторами, равняется половине их векторного произведения.
SΔ = 1/2 · |a x b|
4. Вектор, являющийся векторным произведением двух других векторов, перпендикулярен им.
c ⟂ a, c ⟂ b.
5. a x b = –b x a
6. (m a) x a = a x (m b) = m (a x b)
7. (a + b) x c = a x c + b x c
Пример задачи
Вычислим векторное произведение a = {2; 4; 5} и b = {9; -3; 1}.
Решение:
Ответ: a x b = {19; 43; -42}.