Как найти векторное произведение векторов в пространстве

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой^[⇨]. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Таким образом, для определения векторного произведения двух векторов необходимо задать ориентацию пространства, то есть сказать, какая тройка векторов является правой, а какая — левой. При этом не является обязательным задание в рассматриваемом пространстве какой-либо системы координат. В частности, при заданной ориентации пространства результат векторного произведения не зависит от того, является ли рассматриваемая система координат правой или левой. При этом формулы выражения координат векторного произведения через координаты исходных векторов в правой и левой ортонормированной прямоугольной системе координат отличаются знаком.

Векторное произведение не обладает свойствами коммутативности и ассоциативности. Оно является антикоммутативным и, в отличие от скалярного произведения векторов, результат является опять вектором.

Полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы коллинеарны.

Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения.

История[править | править код]

Векторное произведение было введено У. Гамильтоном в 1846 году^[1] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю^[2].

Определение[править | править код]

Векторным произведением вектора на вектор в трёхмерном евклидовом пространстве называется вектор , удовлетворяющий следующим требованиям:

Обозначения:

Замечания[править | править код]

В качестве определения можно использовать описанное далее выражение векторного произведения в координатах в правой (или левой) прямоугольной системе координат.

Также в качестве исходного определения может быть взят набор алгебраических свойств векторного произведения.

Правые и левые тройки векторов в трёхмерном евклидовом пространстве[править | править код]

Рассмотрим упорядоченную тройку некомпланарных (линейно независимых) векторов в трёхмерном евклидовом пространстве. В ориентированном пространстве такая тройка векторов будет либо «правой», либо «левой».

Геометрическое определение[править | править код]

Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если с конца вектора кратчайший поворот от вектора к вектору виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.

Определение с помощью руки[править | править код]

Другое определение связано с правой рукой человека, откуда и берётся название. На рисунке тройка векторов , , является правой.

Алгебраическое определение[править | править код]

Существует также аналитический способ определения правой и левой тройки векторов, который требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора , второй — вектора , третьей — вектора . Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

• Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
• Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
• Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Замечания[править | править код]

Определения «правой» и «левой» тройки векторов зависят от ориентации пространства, но не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого определение самого векторного произведения. При этом формулы выражения координат векторного произведения через координаты исходных векторов будут отличаться знаком в правой и левой прямоугольной системе координат.

Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.

При заданной ориентации пространства система координат называется правой (левой), если тройка из векторов с координатами , , является правой (левой).

Геометрическое определение и определение с помощью руки сами задают ориентацию пространства. Алгебраическое определение задаёт способ разбить тройки некомпланарных векторов на два класса одинаково ориентированных векторов, но оно не задаёт ориентацию пространства, а использует уже заданную — ту, на основании которой данная система координат считается правой или левой. При этом, если ориентация системы координат неизвестна, можно сравнивать знак определителя со знаком определителя другой тройки некомпланарных векторов, ориентация которой известна — если знаки совпадают, то тройки одинаково ориентированы, если знаки противоположны — тройки ориентированы противоположно.

Свойства[править | править код]

Геометрические свойства векторного произведения[править | править код]

• При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.

На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:

Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов так же, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.

Алгебраические свойства векторного произведения[править | править код]

Далее и обозначают соответственно векторное и скалярное произведение векторов и .

Представление	Описание
	Антикоммутативность.
	Ассоциативность умножения на скаляр.
	Дистрибутивность по сложению.
	Тождество Якоби.
	Формула «БАЦ минус ЦАБ», тождество Лагранжа.
	Частный случай мультипликативности нормы кватернионов.
	Значение этого выражения называют смешанным произведением векторов , , .

Выражение в координатах[править | править код]

В правом ортонормированном базисе[править | править код]

Если два вектора и представлены в правом ортонормированном базисе координатами

то их векторное произведение имеет координаты

Для запоминания этой формулы удобно использовать мнемонический определитель:

где , , , или

где  — символ Леви-Чивиты.

В левом ортонормированном базисе[править | править код]

Если базис левый ортонормированный, то векторное произведение в координатах имеет вид

Для запоминания, аналогично:

или

Формулы для левой системы координат можно получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():

В произвольной аффинной системе координат[править | править код]

Векторное произведение в произвольной аффинной системе координат имеет координаты

Вариации и обобщения[править | править код]

Кватернионы[править | править код]

Координаты векторного произведения в правом ортонормированном базисе можно также записать в кватернионной форме, поэтому буквы , ,  — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.

Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.

Преобразование к матричной форме[править | править код]

Векторное произведение двух векторов в координатах в правом ортонормированном базисе можно записать как произведение кососимметрической матрицы и вектора:

где

Пусть равен векторному произведению:

тогда

Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.

С такой формой записи также зачастую проще работать (например, в эпиполярной геометрии^[en]).

Из общих свойств векторного произведения следует, что

и

а так как кососимметрична, то

В такой форме записи легко доказывается тождество Лагранжа (правило «БАЦ минус ЦАБ»).

Распространение на матрицы[править | править код]

В трёхмерном случае можно определить в координатах в произвольном базисе векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда

Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот.
Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, ,  — векторы):

После этого можно изменить форму записи для векторного произведения:

 — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:

где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева (базис считается правым ортонормированным). В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:

Размерности, не равные трём[править | править код]

Пусть  — размерность пространства.

Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.

Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как

Такое обобщение дает гиперплощадь размерности .

Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:

.

Эта конструкция называется внешним произведением.

Для двумерного случая операция

.

называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению.)

Алгебра Ли векторов[править | править код]

Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.

См. также[править | править код]

Произведения векторов

Другое

• Ротор
• Дивергенция

Примечания[править | править код]

Литература[править | править код]

• 1. Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. АН СССР: Изд-во «НАУКА», М. 1965.

Ссылки[править | править код]

• Многомерное векторное произведение Архивная копия от 5 сентября 2015 на Wayback Machine
• Векторное произведение и его свойства. Примеры решения задач Архивная копия от 23 февраля 2011 на Wayback Machine
• В. И. Гервидс. Правое и левое вращение. НИЯУ МИФИ (10 марта 2011). — Физические демонстрации. Дата обращения: 3 мая 2011. Архивировано 23 декабря 2015 года.

Векторное произведение векторов

Определение

Определение

Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $.

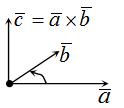
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.

Формула

Формула 1

Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$

Формула 2

В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $.

Определитель во второй формуле можно раскрыть по первой строке:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 – a_3 b_2) – overline{j} (a_1 b_3 – a_3 b_1) + overline{k} (a_1 b_2 – a_2 b_1) $$

Итого вторая формула приобретает окончательный короткий вид:

$$ overline{a} times overline{b} = (a_2 b_3 – a_3 b_2; a_3 b_1 – a_1 b_3; a_1 b_2 – a_2 b_1) $$

Свойства

1. При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
2. Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
3. $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$

Примеры решений

Пример 1

Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$

Решение

Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) – overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} – overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a} times overline{b} = (5, -1, 3) $$

Геометрический смысл

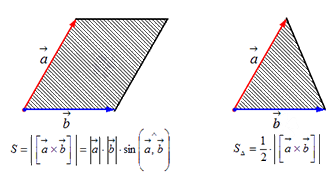
• Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
• Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
• Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.

 

Пример 2

Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$

Решение

Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) – overline{j}(2+3) + overline{k}(4+1) = -5overline{i} – 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$

Ответ

$$ S_Delta = 4.33 $$

Определение векторного произведения

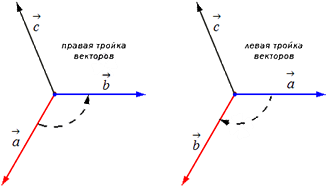
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.

Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.

Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

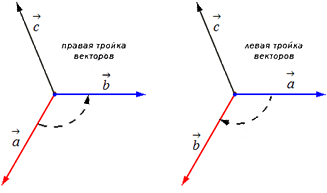
Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.

Координаты векторного произведения

Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz) называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz

Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

1. антикоммутативность a→×b→=-b→×a→;
2. дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
3. ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ – произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

По определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов  a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Геометрический смысл векторного произведения

Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма – удвоенного треугольника, а именно произведению сторон в виде векторов  a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.

Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.

Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.

Угол между векторами

Для того чтобы мы могли ввести понятие векторного произведения двух векторов, нужно сначала разобраться с таким понятие, как угол между этими векторами.

Пусть нам даны два вектора $overline{α}$ и $overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $overline{α}=overline{OA}$ и $overline{β}=overline{OB}$, тогда угол $AOB$ будет называться углом между этими векторами (рис. 1).

Причем мы будем считать, что если векторы $overline{α}$ и $overline{β}$ будут сонаправленными, или один или оба из них нулевой, то угол между этими векторами будет равен $0^circ$.

Обозначение: $∠(overline{α},overline{β})$

Понятие векторного произведения векторов и формула нахождения

Обозначение: $overline{α}хoverline{β}$.

Математически это выглядит следующим образом:

1. $|overline{α}хoverline{β}|=|overline{α}||overline{β}|sin⁡∠(overline{α},overline{β})$
2. $overline{α}хoverline{β}⊥overline{α}$, $overline{α}хoverline{β}⊥overline{β}$
3. $(overline{α}хoverline{β},overline{α},overline{β})$ и $(overline{i},overline{j},overline{k})$ одинаково ориентированы (рис. 2)

«Как найти векторное произведение векторов» 👇

Очевидно, что внешнее произведение векторов будет равняться нулевому вектору в двух случаях:

1. Если длина одного или обоих векторов равняется нулю.
2. Если угол между этими векторами будет равняться $180^circ$ или $0^circ$ (так как в этом случае синус равняется нулю).

Чтобы наглядно увидеть, как находится векторное произведение векторов, рассмотрим следующие примеры решения.

Вычисление векторного произведения по координатам векторов

Из определения 1 сразу же вытекает и способ нахождения векторного произведения для двух векторов. Поскольку вектор кроме значения имеет еще и направление, находить его только при помощи скалярной величины невозможно. Но помимо него существует еще способ нахождения с помощью координат данных нам векторов.

Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые будут иметь координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

Иначе, раскрывая определитель, получим следующие координаты

$overline{α}хoverline{β}=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

Свойства векторного произведения векторов

Для произвольных смешанных трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$, а также $r∈R$ справедливы следующие свойства:

1. $overline{α}хoverline{β}=-(overline{β}хoverline{α})$

   Верность этого свойства будет следовать из третьего пункта определения 1.

2. $(roverline{α})хoverline{β}=r(overline{α}хoverline{β})$ и $overline{α}х(roverline{β})=r(overline{α}хoverline{β})$

   Из формулы для нахождения векторного произведения будем получать:

   $(roverline{α})overline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\rα_1&rα_2&rα_3\β_1&β_2&β_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$

   $overline{α}х(roverline{β})=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\rβ_1&rβ_2&rβ_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$

3. $overline{α}х(overline{β}+overline{γ})=overline{α}overline{β}+overline{α}overline{γ}$ и $(overline{α}+overline{β})overline{γ}=overline{α}overline{γ}+overline{β}overline{γ}$.

   Данное свойство векторного произведения векторов также можно проверить с помощью формулы.

   Следующее свойство называют геометрическим смыслом векторного произведения:

4. Длина вектора векторного произведения равняется площади параллелограмма, который нужно было построить между ними (рис. 4)

   

   Рисунок 4. Длина вектора векторного произведения. Автор24 — интернет-биржа студенческих работ

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.

Векторное Произведение Векторов. Свойства, определение

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

• Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
• Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
• Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Координаты векторного произведения

• Рассмотрим векторное произведение векторов в координатах.
• Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
• В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

1. , где
2. →i, →j, →k — координатные векторы.
3. Это определение показывает нам векторное произведение в координатной форме.
4. Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
5. Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

1. Антикоммутативность
2. Свойство дистрибутивностиили
3. Сочетательное свойствоили, где λ произвольное действительное число.

• Для большей ясности докажем свойство антикоммутативности векторного произведения.
• По определению
• и
• Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
• что доказывает свойство антикоммутативности векторного произведения.
• Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
• Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна. А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F]. Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до векторов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!

Смешанное произведение векторов: свойства примеры и решения, геометрический смысл смешанного произведения векторов

Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение.

В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.

Термин

Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.

Определение 1

Смешанным произведением a→, b→ и d→ является та величина, которая равняется скалярному произведению a→×b→ и d→ , где a→×b→ — умножение a→ и b→ . Операцию умножения a→, b→ и d→ зачастую обозначают a→·b→·d→ . Можно преобразовать формулу так:a→·b→·d→=(a→×b→,d→) .

Умножение в системе координат

• Мы можем умножить вектора, если они указаны на координатной плоскости.
• Возьмем i→, j→, k→
• Произведение векторов в данном конкретном случае будет иметь следующий вид:a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→

Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.

1. Из этого следует:
2. a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→
3. Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
4. a→×b→=( ayazbybz·i→-axazbxbz·j→+axaybxby·k→, dx·i→+dy·j→+dz·k→)==ayazbybz·dx-axazbxbz·dy+axaybxby·dz=axayazbxbybzdxdydz
5. Таким образом, можно сделать вывод, что:
6. a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz

Определение 3

Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz .

Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.

1. (λ·a→)·b→·d→=a→·(λ·b→)·d→=a→·b→·(λ·d→)=λ·a→·b→·d→    λ∈R ;
2. a→·b→·d→=d→·a→·b→=b→·d→·a→;   a→·d→·b→=b→·a→·d→=d→·b→·a→ ;
3. (a(1)→+a(2)→)·b→·d→=a(1)→·b→·d→+a(2)→·b→·d→a→·(b(1)→+b(2)→)·d→=a→·b(1)→·d→+a→·b(2)→·d→a→·b→·(d(1)→+d(2)→)=a→·b→·d(2)→+a→·b→·d(2)→

Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль. Результатом умножения также будет нуль в том случае, если два или больше множителей равны.

Действительно, если a→=b→ , то, следуя определению векторного произведения [a→×b→]=a→·b→·sin 0 =0 , следовательно, смешанное произведение равно нулю, так как ([a→×b→], d→)=(0→, d→)=0 .

Если же a→=b→ или b→=d→ , то угол между векторами [a→×b→] и d→ равен π2 . По определению скалярного произведения векторов ([a→×b→], d→)=[a→×b→]·d→·cosπ2=0 .

Свойства операции умножения чаще всего требуются во время решения задач. Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.

Пример 1

Докажите равенство ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→) , где λ — некоторое действительное число.

Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:

• ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→) Мы разобрали, что (([a→×b→], b→)=0. Из этого следует, что ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→)==([a→×b→], d→)+([a→×b→], λ·a→)+0=([a→×b→], d→)+([a→×b→], λ·a→)

Согласно первому свойству ([a⇀×b⇀], λ·a→)=λ·([a⇀×b⇀],a→) , а ([a⇀×b⇀], a→)=0 . Таким образом, ([a⇀×b⇀], λ·a→) . Поэтому,
([a⇀×b⇀], d→+λ·a→+b→)=([a⇀×b⇀], d→)+([a⇀×b⇀], λ·a→)==([a⇀×b⇀], d→)+0=([a⇀×b⇀], d→)

Равенство доказано.

Пример 2

Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.

Решение

Исходя из условия, можно представить пример в виде неравенства a→×b→, d→≤a→·b→·d→ .

По определению, преобразуем неравенство a→×b→, d→=a→×b→·d→·cos(a→×b→^, d→)==a→·b→·sin(a→, b→^)·d→·cos([a→×b→^], d)

Используя элементарные функции, можно сделать вывод, что 0≤sin(a→, b→^)≤1,  0≤cos([a→×b→^], d→)≤1 .

Из этого можно сделать вывод, что
(a→×b→, d→)=a→·b→·sin(a→, b→)^·d→·cos(a→×b→^, d→)≤≤a→·b→·1·d→·1=a→·b→·d→

Неравенство доказано.

Разбор типовых задач

Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz .

Пример 3

В прямоугольной системе координат представлены 3 вектора с такими координатами: a→=(1, -2, 3),  b→(-2, 2, 1),  d→=(3,-2, 5) . Необходимо определить, чему равно произведение указанных векторов a→·b→·d→ .

Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz=1-23-2213-25==1·2·5+(-1)·1·3+3·(-2)·(-2)-3·2·3-(-1)·(-2)·5-1·1·(-2)=-7

Пример 4

Необходимо найти произведение векторовi→+j→, i→+j→-k→, i→+j→+2·k→ , где i→,j→, k→ — орты прямоугольной декартовой системы координат.

Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i→+j→=(1, 1, 0)i→+j→-k→=(1, 1, -1)i→+j→+2·k→=(1, 1, 2)

Используем формулу, которая использовалась выше
i→+j→×(i→+j→-k→, (i→+j→+2·k→)=11011-1112=0i→+j→×(i→+j→-k→, (i→+j→+2·k→)=0

Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.

Пример 5

В прямоугольной системе координат расположены три вектора a→,b→ и d→ , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4, 2 и 3. Необходимо умножить вектора.

Обозначим c→=a→×b→ .

Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a→·b→·d→=([a→×b→], d→)=c→,d→=c→·d→·cos(c→, d→^) .

Используем длину вектора d→ , указанную в условии примера: a→·b→·d→=c→·d→·cos(c→, d→^)=3·c→·cos(c→, d→^) . Необходимо определить с→и с→, d→^ . По условию a→,b→^=π2, a→=4, b→=2 .

Вектор c→ найдем с помощью формулы: c→=[a→×b→]=a→·b→·sina→, b→^=4·2·sinπ2=8 Можно сделать вывод, что c→ перпендикулярен a→ и b→ . Вектора a→, b→, c→ будут являться правой тройкой, так использована декартовая система координат.

Векторы c→ и d→ будут однонаправленными, то есть, c→,d→^=0 . Используя выведенные результаты, решаем пример a→·b→·d→=3·c→·cos(c→, d→^)=3·8·cos 0=24 .

a→·b→·d→=24 .

Геометрический смысл

Используем множители a→, b→ и d→ .

Вектора a→, b→ и d→ исходят от одной точки. Используем их как стороны для построения фигуры.

Обозначим, что c→=[a→×b→]. Для данного случая можно определить произведение векторов как a→·b→·d→=c→·d→·cos(c→, d→^)=c→·npc→d→ , где npc→d→ — числовая проекция вектора d→ на направление вектора c→=[a→×b→] .

Абсолютная величина npc→d→ равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a→, b→ и d→ в качестве сторон. Исходя из этого, следует уточнить, что c→=[a→×b→] перпендикулярен a→ и вектору и вектору согласно определению умножения векторов. Величина c→=a→xb→ равняется площади параллелепипеда, построенного на векторах a→ и b→ .

Делаем вывод, что модуль произведения a→·b→·d→=c→·npc→d→ равен результату умножения площади основания на высоту фигуры, которая построена на векторах a→, b→ и d→ .

Определение 4

Абсолютная величина векторного произведения является объемом параллелепипеда: Vпараллелепипида=a→·b→·d→ .

Данная формула и является геометрическим смыслом.

Определение 5

Объем тетраэдра, который построен на a→,b→ и d→ , равняется 1/6 объема параллелепипеда Получаем, Vтэтраэда=16·Vпараллелепипида=16·a→·b→·d→ .