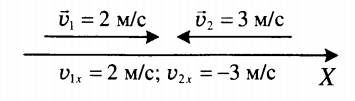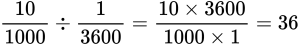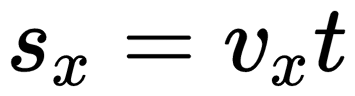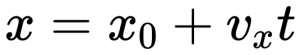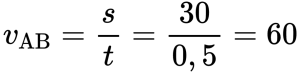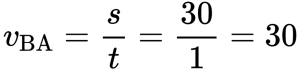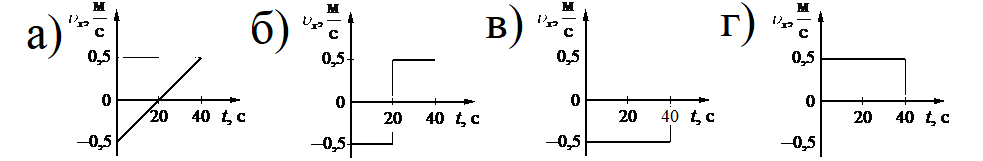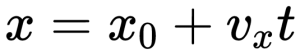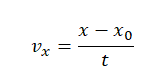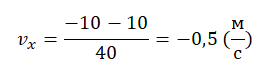Как найти векторное время

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

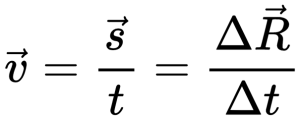
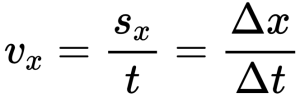
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Дополнительные единицы измерения

• 1 км/ч (километр в час) = 1000 м/3600 с.
• 1 км/мин (километр в минуту) = 1000 м/60 с.
• 1 км/с (километр в секунду) = 1000 м/с.
• 1 м/мин (метр в минуту) = 1 м/60 с.
• 1 см/с (сантиметр в секунду) = 0,01 м/с.

Спидометр — прибор для измерения модули скорости тела.

График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Определение направления движения по графику скорости

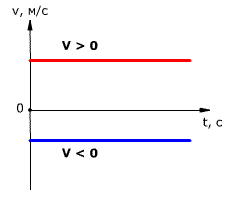
• Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
• Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
• Если график скорости совпадает с осью времени, тело покоится.

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

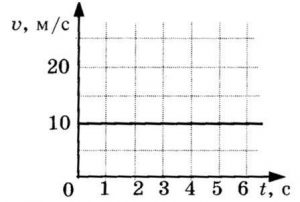
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

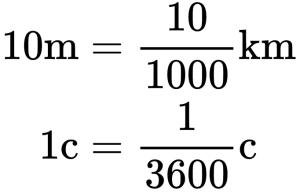
Перемещение и координаты тела при равномерном прямолинейном движении

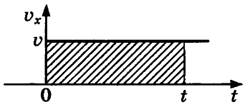
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

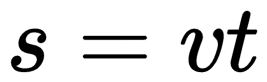
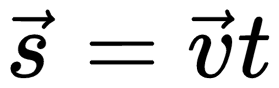
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Определение направления движения по графику проекции перемещения

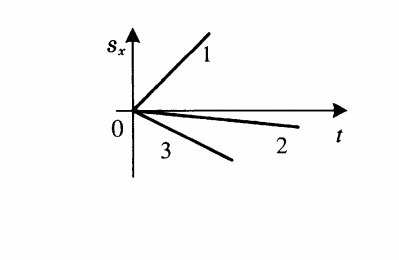
• Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
• Если луч лежит ниже оси времени, тело движется против оси ОХ.
• Если луч совпадает с этой осью, тело покоится.

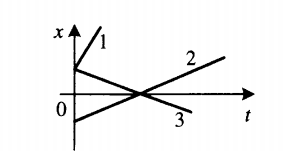
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:

Определение направления движения тела по графику координаты

• Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
• Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ. На картинке выше этому соответствует график тела 3.
• Если координата не изменяется, тело покоится.

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

1. На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
2. Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
3. На участке 1 тело движется равномерно, а на участке 2 оно покоится.
4. На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.
5. Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

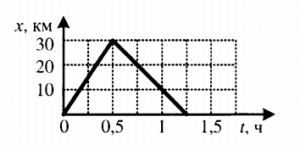
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

1. Выбрать любой временной интервал.
2. Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
3. Записать формулу скорости и вычислить ее для 1 и 2 тела.
4. Найти n — отношение скорости второго тела к скорости первого тела

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

• Для графика 1: начальный путь s₁₀ = 0 м. Конечный путь равен s₁ = 80 м.
• Для графика 2: начальный путь s₂₀ = 0 м. Конечный путь равен s₂ = 120 м.

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Какой из графиков соответствует зависимости от времени для проекции υ x скорости этого тела на ось Ox ?

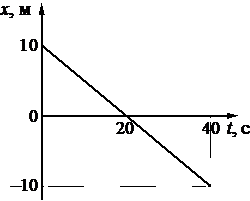
Алгоритм решения

1. Записать уравнение координаты при равномерном прямолинейном движении.
2. Выразить из уравнения проекцию скорости.
3. Определить начальную и конечную координаты, а также время, в течение которого двигалось тело.
4. Вычислить проекцию скорости.
5. Выбрать соответствующий график.

Решение

Уравнение координаты при равномерном прямолинейном движении имеет вид:

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Охарактеризовать движение тела на различных участках графика.
2. Выделить участки движения, над которыми нужно работать по условию задачи.
3. Записать исходные данные.
4. Записать формулу определения искомой величины.
5. Произвести вычисления.

Решение

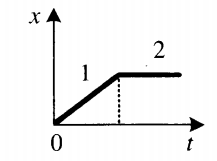
Весь график можно поделить на 3 участка:

1. От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
2. От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
3. От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

1. От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
2. От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

• Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
• Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Векторное время

Скалярные часы не являются строго непротиворечивыми и не позволяют зафиксировать параллелизм событий. События, которые могли бы происходить одновременно, могут получить различные отметки времени как будто они происходили в каком-то определенном порядке. Для некоторых задач, например, рассмотренных в п. 3.2.2, такое ограничение не является существенным. Однако, к примеру, при отладке распределенных программ (англ, distributed debugging) информация о том, оказывают ли события потенциальное влияние друг на друга или нет, становится важной.

Параллелизм событий можно зафиксировать, если часовые отметки времени параллельных событий оказываются несравнимыми. Другими словами, выявление параллельных событий возможно только тогда, когда множество Т допустимых значений логического времени оказывается упорядоченным частично, но не линейно. Чтобы понять, из каких элементов может состоять такое множество, предположим, что в каждом процессе работают логические локальные часы, увеличивающие свои показания на единицу перед наступлением каждого события. Тогда для стороннего наблюдателя, которому одномоментно доступна вся картина происходящего, ход выполнения распределенной системы будет определяться совокупностью показаний локальных часов всех процессов. Подходящей структурой данных для представления такого глобального времени будет являться Димерный вектор, в котором /-й компонент содержит текущее значение локального времени процесса P?. Пример изменения глобального векторного времени V с точки зрения стороннего наблюдателя приведен на рис. 3.5.

Рис. 3.5. Пример изменения глобального векторного времени.

Процессам же текущее значение глобального времени недоступно. Каждый процесс может лишь сформировать свое собственное представление о ходе выполнения процессов распределенной системы через поступающие ему сообщения. Для этого каждый процесс Р_; должен локально поддерживать работу с вектором У,[1..Л^]. В компоненте У,Vj содержит последние сведения, полученные процессом Р, о локальном времени процесса Pj. Другими словами, если V,[/‘] = х, то процесс Pi “знает” о том, что локальное время процесса Р, достигло значения лс. Стоит отметить, что к настоящему моменту локальные часы процесса Pj могли уйти вперед, т.е. текущее локальное время процесса Pj может превышать значение jc, однако, процесс Р, не получал об этом никакой информации через направляемые ему сообщения. Весь вектор V, можно рассматривать как локальное представление процесса Р, о глобальном векторном времени, отражающем ход выполнения всех процессов в распределенной системе.

Таким образом, областью значений часовой функции 0 является множество TV-мерных векторов неотрицательных целых чисел, где N – количество процессов в распределенной системе. Поэтому такие часы называют векторными часами. Отметка времени события e_h происходящего в процессе Р„ определяется всеми компонентами вектора Vj на момент наступления е,. Такую отметку часто называют векторной отметкой времени события е, и обозначают через У(е).

Для сравнения двух векторных отметок времени V(ej) и V(ej r ) событий еi и е/ введем следующие отношения:

Очевидно, что введенное выше отношение 2. Например, вектора У <е,)= [2, 3, 0] и V(ej r ) = [0, 4, 1J являются несравнимыми. Для обозначения этого факта будем использовать запись У(е,) II У(е/):

Для выполнения условия непротиворечивости логических часов каждый процесс Р, использует следующие правила продвижения своего векторного времени.

Правило 1: перед выполнением любого события процесс Р, увеличивает показания своих локальных часов V,[/]:

Как и для случая скалярного времени, каждый раз d может принимать любые значения. Однако обычно d всегда полагают равным единице.

Перед выполнением события получения сообщения процесс вынужден произвести немного другие действия согласно следующему правилу.

Правило 2: в каждое передаваемое сообщение добавляется значение векторного времени V/ процесса-отправителя Р, на момент отправки этого сообщения. Когда процесс Pj получает сообщение с отметкой времени У,_тп, он выполняет следующие шаги:

1. обновляет свое логическое глобальное время по правилу:

• 2. исполняет Правило 1;
• 3. доставляет сообщение и приступает к его обработке.

[spoiler title=”источники:”]

http://ozlib.com/847793/informatika/vektornoe_vremya

[/spoiler]

Соседние файлы в папке Lit

• #
• #
• #

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Определение:

Векторные часы — это функция $VC(e) colon E to mathbb R^n$ (из событий в вектор константного размера) такая, что для любых двух событий $e$ и $f$ следующие утверждения равносильны: $e to f$ ($e$ произошло-до $f$) $VC(e) < VC(f)$ (все компоненты $VC(e)$ меньше всех компонент $VC(f)$)

Алгоритм векторных часов можно построить из логических часов Лампорта, если попросить каждый процесс помнить счётчики всех процессов, а не только свой:

• каждый поток имеет целочисленный $n$-мерный вектор ($n$ — количество потоков), проинициализированный нулями.
• в случае внутреннего события счётчик текущего процесса увеличивается на 1;
• перед отправкой сообщения внутренний счётчик, соответствующий текущему процессу, увеличивается на 1, и вектор целиком прикрепляется к сообщению;
• при получении сообщения счётчик текущего процесса увеличивается на 1, далее значения в текущем векторе выставляются в покомпонентный максимум от текущего и полученного.

Значением вышеупомянутой функции на событии является значение переменной, принадлежащей тому же потоку, что и событие. Стоит заметить, что векторное время уникально для каждого события.

Оказывается, что если в распределенной системе ввести частичный порядок предшествования на событиях, то имеет место следующее утверждение:
a предшествует b, тогда и только тогда, когда логическое время векторных часов события a меньше логического времени события b (при этом вектор x меньше вектора y покомпонентно с одной строгостью, т.е если для каждой компоненты выполяется и ).

Важным свойством векторных часов в распределенных системах с введенным частичным порядком предшествования оказывается то, что при сравнении векторов времени двух событий достаточно сравнивать только компоненты процессов, которым эти события принадлежат.