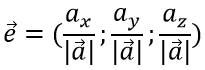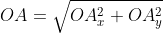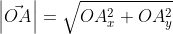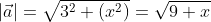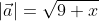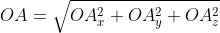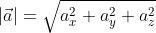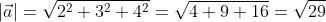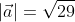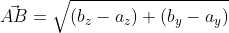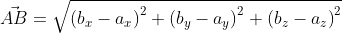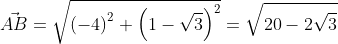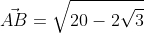1.5.5. Как найти единичный вектор?
Единичный вектор – это вектор, длина которого в ортонормированном базисе равна единице. Таковыми являются сами
координатные векторы 
и 
, 
и противоположно направленные им векторы, например:
То, что их длина равна единице, элементарно видно не только по чертежам, но и по формулам 
.
А теперь рассмотрим произвольный вектор 
либо
и поставим задачу найти
единичный вектор 
, коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора 
разделить на его длину:
либо 
,
или, что то же самое – умножить каждую координату вектора 
на 
. То
есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный
вектор очевиден:
либо 
Задача 10
Найти единичные векторы, коллинеарные векторам а) 
, б) 
. Выполнить проверку.
Решение: а) вычислим длину вектора 
и найдём
сонаправленный единичный вектор:
, от иррациональности в знаменателе (корня) тут
обычно не избавляются. Проверка состоит в нахождении длины полученного вектора:
, что и требовалось проверить.
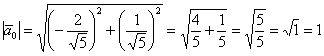
Второй вектор очевиден: 
, как очевидна и его
длина 
.
Ответ: 
Потребность найти единичный вектор возникает не только в геометрических задачах, и поэтому обязательно прорешайте пункт б)
самостоятельно.
1.5.6. Деление отрезка в данном отношении
1.5.4. Действия с векторами в координатах
| Оглавление |
Автор: Aлeксaндр Eмeлин
Единичный вектор
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
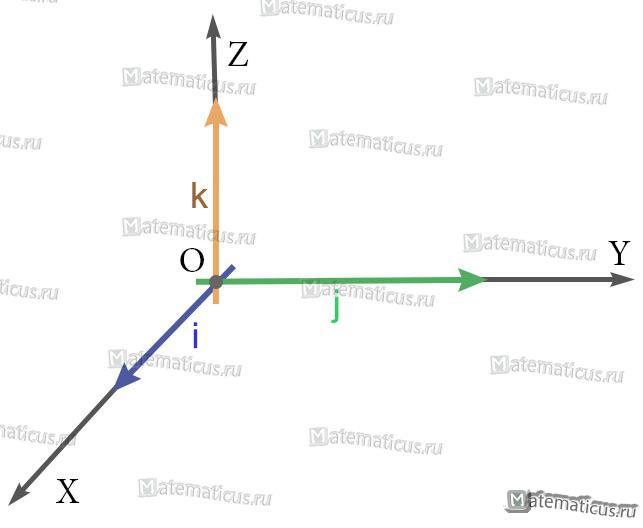
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0), j(0;1;0), k(0;0;1)
Единичные векторы являются некомпланарными.
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Находим длину вектора a
затем вычисляем единичный вектор e
Векторное произведения единичных векторов
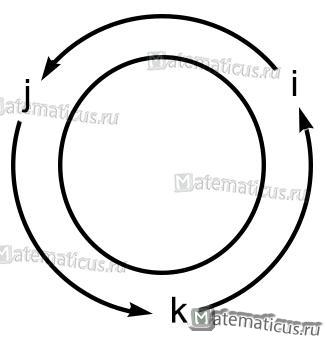
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.
На основании схемы получаем таблицу векторного произведения единичных векторов
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
Решение
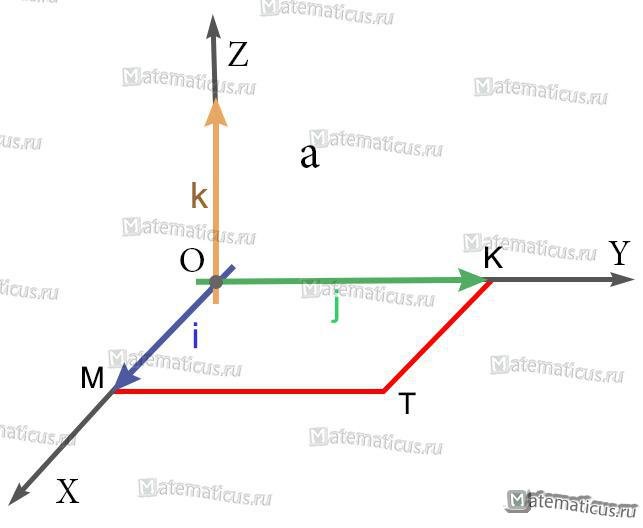
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.5 / 5. Количество оценок: 4
Нахождение длины вектора, примеры и решения
Длина вектора – основные формулы
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
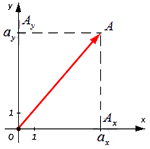
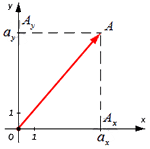
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e
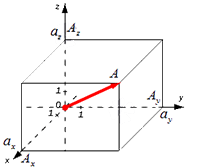
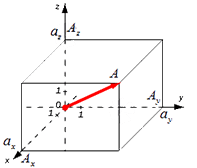
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Вычислить длину вектора a → = 4 · i → – 3 · j → + 5 · k → , где i → , j → , k → – орты прямоугольной системы координат.
Дано разложение вектора a → = 4 · i → – 3 · j → + 5 · k → , его координаты равны a → = 4 , – 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( – 3 ) 2 + 5 2 = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x – a x ; b y – a y ) значит, его длина может быть определена по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2
А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B – 3 , 1 .
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x – a x ) 2 + ( b y – a y ) 2 : A B → = ( – 3 – 1 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( – 3 – 1 ; 1 – 3 ) = ( – 4 ; 1 – 3 ) ; A B → = ( – 4 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 . –
Ответ: A B → = 20 – 2 3 .
Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .
Для начала распишем длину вектора A B → по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 = ( 5 – 0 ) 2 + ( 2 – 1 ) 2 + ( λ 2 – 2 ) 2 = 26 + ( λ 2 – 2 ) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :
26 + ( λ 2 – 2 ) 2 = 30 26 + ( λ 2 – 2 ) 2 = 30 ( λ 2 – 2 ) 2 = 4 λ 2 – 2 = 2 и л и λ 2 – 2 = – 2 λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 – 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 – 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x – a x ) 2 + ( b y – a y ) 2 или A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 , в некоторых случаях следует использовать теорему косинусов.
Длина вектора — основные формулы
Время чтения: 16 минут
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора – отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать 
.
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор 
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.
На взятой системе координат, от её начала отложим вектор
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
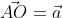
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора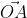 
получаем
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:
Когда вектор дан в формате разложения по координатным векторам 
, то вычислить его можно по той же формуле , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат , в данной системе координат.
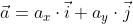
Чтобы рассчитать длину = (3, √x), расположенного в прямоугольной системе координат.
Чтобы найти модуль вектора используем ранее приведённую формулу
Ответ: 
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор =(aₓ ; aᵧ ; a 
)
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО – диагональ прямоугольного параллелепипеда), поэтому
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
Ответ: 
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор 
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
При этом формула вычисления длины вектора для трёхмерного пространства, с координатами 
и 
), будет следующей:
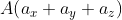
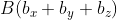
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
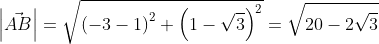
Существует второй вариант решения, где формулы применяются по очереди:
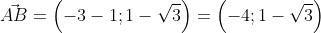
Ответ: 
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
длина вектора формула для трёхмерного пространства;
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/dlina_vectora/
http://www.napishem.ru/spravochnik/matematika/dlina-vektora-osnovnye-formuly.html
[/spoiler]
Download Article
Learn how to calculate a unit vector and pass your math test with flying colors
Download Article
- Unit Vector Formula
- How to Calculate a Unit Vector
- Vectors
- Unit Vectors
- Magnitude
- Example Problems
- Solutions
|
|
|
|
|
|
At some point in your algebra course, you might have to learn about vectors, including unit vectors and magnitude. While your teacher or tutor may have taught a whole class on calculating a unit vector, you might still have some questions about the process. That’s why we’ve broken it down for you, below! Check out our guide to finding a unit vector, including a refresher on what vectors are and the formula for calculating magnitude, so you can ace your next pop quiz.
Things You Should Know
-
The formula to find unit vector is
. You can calculate the unit vector of any vector by dividing the vector by its magnitude . For instance, to calculate the unit vector of vector , you would follow this equation: .[1]
Advertisement
-
1
-
2
Divide the vector by its magnitude. Once you’ve determined the magnitude of the vector, take the vector and divide it by its magnitude. So if vector
is , then = = (, ). The unit vector, then, is ().[3]
Advertisement
-
A vector is an object that contains both direction and magnitude. A vector is represented as a line on the Cartesian coordinate system, and it is denoted as a set of numbers representing its relationship to the x-axis (the vertical line on the graph) and the y-axis (the horizontal line). A vector’s magnitude refers to the size of the vector and is represented by a line with an arrow on the end. The length of the line denotes the length of the vector, while the direction of the arrow denotes the direction of the vector. Vectors possess both a starting point (the tail) and an ending point (the head, where the arrow is).[4]
-
A unit vector is a vector with a magnitude of 1. Unit vectors, also called direction vectors, are used to describe the direction of a given vector—or, the angle the vector makes on an x-axis. Unit vectors are marked with a cap symbol, which looks like a little arrow pointing upward: ^.[5]
Advertisement
-
The magnitude is the length or size of the vector. A vector’s magnitude, also called its norm, denotes its length on an x-axis (or the vertical line on the graph on which the vector appears), giving it numeric value. The magnitude on summarizes the length of the vector on the x-axis, y-axis (the horizontal line), and z-axis. Magnitude is denoted as 2 vertical lines, one on each side of the vector:
. To calculate the magnitude of a given vector with the direction of the x-axis, y-axis, or z-axis, follow the Pythagorean Theorem: add the squares of the vector’s direction ratios. Then, calculate the square root of that sum.[6]
- The magnitude of would be , the magnitude of would be , and the magnitude of would be .
- To find the magnitude of vector , where = (and where , , and represent the x-axis, y-axis, and z-axis, respectively), use the following equation: = √.
- For example, if and and , then , and = √ = √ = . Thus, the magnitude of vector would be 3 units.
- The magnitude of
-
1
Given vector
= + + , find . -
2
Given vector
= + , find .
Advertisement
-
1
Answer #1:
=. In this problem, we’re asked to find the unit vector of a 3-dimensional vector; hence, the inclusion of the z-axis in the equation. To find the unit vector, we identified the magnitude of the vector and then divided the vector by its magnitude:[7]
-
2
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Thanks to all authors for creating a page that has been read 1,184 times.
Did this article help you?
Все курсы > Линейная алгебра > Занятие 1
Материалы по линейной алгебре используют определения и примеры следующих курсов:
- 3Blue1Brown⧉
- Khan Academy: Linear Algebra⧉
- Linear Algebra⧉, PCA⧉, ICL
- Linear Algebra⧉, MIT
- Matrix Methods for Data Analysis and Machine Learning⧉, MIT
- Matrix Algebra for Engineers⧉
На первом занятии мы более подробно рассмотрим понятие вектора и векторного пространства.
Ноутбук к сегодняшнему занятию⧉
Понятие вектора
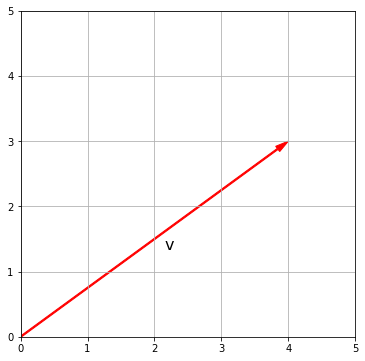
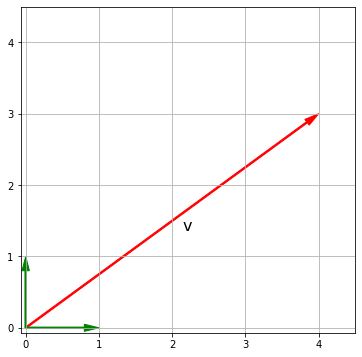
Вектор (vector) — это направленный отрезок, и для нас будет важно, что любой вектор обладает длиной (magnitude) и направлением (direction). Например, возьмем вот такой двумерный вектор $textbf{v}$
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix} $$
На курсе мы будем обозначать векторы полужирной строчной буквой, например $textbf{v}$, а матрицы заглавной буквой, например, А.
Вектор $textbf{v}$ удобно изобразить на координатной плоскости, исходящим из начала координат.
|
v = np.array([4, 3]) ax = plt.axes() plt.xlim([0, 5]) plt.ylim([0, 5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Добавлю, что вектор — частный случай матрицы. В случае вектор-столбца речь идет о матрице размерностью n x 1. В случае вектор-строки — 1 x n. Вектор $textbf{v}$ — это матрица 2 х 1.
Операции над векторами
Сложение векторов
Складывать векторы очень несложно. Достаточно сложить их компоненты или координаты.
$$ begin{bmatrix} 4 \ 3 end{bmatrix} + begin{bmatrix} 2 \ -1 end{bmatrix} = begin{bmatrix} 6 \ 2 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([2, –1]) a_plus_b = a + b a_plus_b |
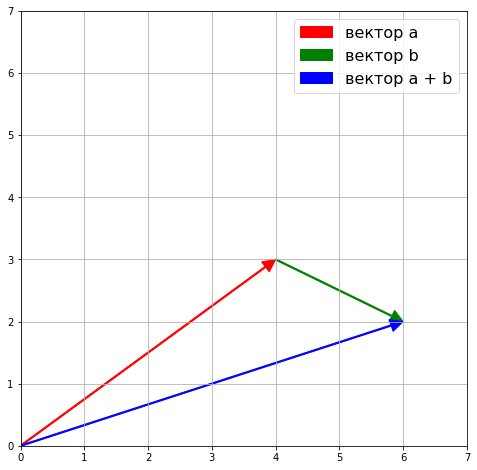
Графически, если поставить начало второго вектора в конец первого, сложение можно представить как расстояние от начала первого вектора до конца второго. Своего рода путь, пройденный двумя векторами.
|
ax = plt.axes() plt.xlim([0, 7]) plt.ylim([0, 7]) plt.grid() arrow_a = ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b = ax.arrow(a[0], a[1], b[0], b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) arrow_a_plus_b = ax.arrow(0, 0, a_plus_b[0], a_plus_b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.legend([arrow_a, arrow_b, arrow_a_plus_b], [‘вектор a’, ‘вектор b’, ‘вектор a + b’], prop = {‘size’: 16}) plt.show() |
Сложение векторов ассоциативно $textbf{a} + textbf{b} = textbf{b} + textbf{a}$.
Умножение на скаляр
Умножение на скаляр просто удлиняет или укорачивает вектор.
$$ 2 cdot textbf{v} = 2 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} 8 \ 6 end{bmatrix} $$
|
v = np.array([4, 3]) double_v = 2 * v double_v |
|
ax = plt.axes() plt.xlim([0, 10]) plt.ylim([0, 10]) plt.grid() ax.arrow(0, 0, double_v[0], double_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘2v’, xy=(double_v[0], double_v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Умножение на отрицательное число не только удлиняет или укорачивает вектор, но и переворачивает его направление.
$$ -0,5 cdot textbf{v} = -0,5 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} -2 \ -1,5 end{bmatrix} $$
|
v = np.array([4, 3]) neg_half_v = –0.5 * v neg_half_v |
|
ax = plt.axes() plt.xlim([–5, 5]) plt.ylim([–5, 5]) plt.grid() ax.arrow(0, 0, neg_half_v[0], neg_half_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘-0.5v’, xy=(neg_half_v[0], neg_half_v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Очевидно, что умножение на −1 просто переворачивает направление вектора, но не меняет его длины.
$$ -1 cdot textbf{v} = -1 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} -4 \ -3 end{bmatrix} $$
|
v = np.array([4, 3]) neg_one_v = –1 * v neg_one_v |
|
ax = plt.axes() plt.xlim([–5, 5]) plt.ylim([–5, 5]) plt.grid() ax.arrow(0, 0, neg_one_v[0], neg_one_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘-v’, xy=(neg_one_v[0], neg_one_v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Вычитание и деление на число
Вычитание векторов можно представить как сумму первого вектора со вторым вектором, умноженным на −1.
$$ begin{bmatrix} 4 \ 3 end{bmatrix} + left( -1 cdot begin{bmatrix} 2 \ -1 end{bmatrix} right) = begin{bmatrix} 2 \ 4 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([2, –1]) b_neg = –1 * b a_minus_b = a + b_neg b_neg, a_minus_b |
|
(array([-2, 1]), array([2, 4])) |
Графически мы сначала находим вектор $textbf{-b}$ (зеленая стрелка), а затем прибавляем его к вектору $textbf{a}$ (красная стрелка).
|
plt.figure(figsize = (8, 8)) ax = plt.axes() plt.xlim([0, 7]) plt.ylim([0, 7]) plt.grid() arrow_a = ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b_neg = ax.arrow(a[0], a[1], b_neg[0], b_neg[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) arrow_b = ax.arrow(a[0], a[1], b[0], b[1], width = 0.0001, head_width = 0.1, head_length = 0.1, length_includes_head = True, fc = ‘black’, ec = ‘black’, linestyle = ‘–‘) arrow_a_minus_b = ax.arrow(0, 0, a_minus_b[0], a_minus_b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.legend([arrow_a, arrow_b_neg, arrow_b, arrow_a_minus_b], [‘вектор a’, ‘вектор -b’, ‘вектор b’, ‘вектор a+(-b)’], prop = {‘size’: 16}) plt.show() |
Остается добавить, что деление вектора на число, это всего лишь умножение на обратное число (multiplicative inverse). Разделим вектор $textbf{v}$ на семь.
$$ frac{textbf{v}}{7} = begin{bmatrix} 4 \ 3 end{bmatrix} cdot frac{1}{7} = begin{bmatrix} frac{4}{7} \ frac{3}{7} end{bmatrix} $$
|
v = np.array([4, 3]) v * (1/7) |
|
array([0.57142857, 0.42857143]) |
Тот факт, что мы выразили вычитание через сложение и умножение на скаляр, а деление через умножение на обратное число позволило нам остаться в пределах операций сложения и умножения на скаляр.
Видео про векторы⧉.
Длина вектора
Длину или норму вектора (norm, length, magnitude or size of a vector) рассчитать не сложно, достаточно вспомнить теорему Пифагора. Снова возьмем вектор $textbf{v}$
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix} $$
|
v = np.array([4, 3]) ax = plt.axes() plt.xlim([0, 5]) plt.ylim([–0.01, 5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.hlines(y = 0, xmin = 0, xmax = 4, linewidth = 3, color = ‘b’, linestyles = ‘–‘) ax.vlines(x = 4, ymin = 0, ymax = 3, linewidth = 3, color = ‘g’, linestyles = ‘–‘) plt.show() |
Как видно на графике, вектор $textbf{v}$, смещение вдоль оси x и смещение вдоль оси y образуют прямоугольный треугольник. Значит, длина вектора (гипотенуза) равна квадратному корню из суммы квадратов смещений (катетов или в нашем случае координат).
$$ ||textbf{v}|| = sqrt{4^2 + 3^2} = sqrt{25} = 5 $$
Для n-мерного вектора ничего не меняется.
$$ ||textbf{v}|| = sqrt{v_1^2 + v_2^2 + dots + v_n^2} $$
Например, найдем длину трехмерного вектора $textbf{w}$.
$$ textbf{w} = begin{bmatrix} 6 \ 3 \ 2 end{bmatrix} rightarrow ||textbf{w}|| = sqrt{6^2 + 3^2 + 2^2} = sqrt{49} = 7 $$
Единичный вектор
Вектор с длиной, равной единице, называют единичным вектором (unit vector). Примерами единичных векторов, с которыми мы будем часто встречаться в пространстве $ R^2 $, являются следующие два вектора
$$ hat{i} = begin{bmatrix} 1 \ 0 end{bmatrix}, hat{j} = begin{bmatrix} 0 \ 1 end{bmatrix} $$
Единичный вектор принято обозначать строчной буквой с знаком циркумфлекса, «крышечки» (hat).
Проверим, равна ли их длина единице.
$$ ||hat{i}|| = sqrt{1^2 + 0^2} = sqrt{1} = 1, ||hat{j}|| = sqrt{0^2 + 1^2} = sqrt{1} = 1 $$
Интересно, что с помощью векторов $ hat{i}, hat{j} $ можно выразить любой другой вектор в $ R^2 $. Например, вектор $textbf{v}$ можно представить как
$$ 4 begin{bmatrix} 1 \ 0 end{bmatrix} + 3 begin{bmatrix} 0 \ 1 end{bmatrix} = begin{bmatrix} 4 \ 3 end{bmatrix} rightarrow 4hat{i} + 3 hat{j} $$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
v = np.array([4, 3]) i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([–0.07, 4.5]) plt.ylim([–0.07, 4.5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Это обстоятельство нам пригодится в будущем.
Нормализация вектора
Длина нормализованного вектора равна единице. Для того чтобы нормализовать вектор, достаточно разделить вектор на его длину. Создадим единичный вектор $hat{v}$ для вектора $textbf{v}$.
$$ hat{v} = frac{textbf{v}}{||textbf{v}||} = frac{1}{5} cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} frac{4}{5} \ frac{3}{5} end{bmatrix} $$
|
v = np.array([4, 3]) v * (1/np.linalg.norm(v)) |
Скалярное произведение
Важной операцией над векторами является уже знакомое нам скалярное произведение (dot product). В качестве напоминания того, как работает скалярное произведение приведем несложный пример. Пусть даны два вектора $textbf{v}$ и $textbf{w}$.
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix}, textbf{w} = begin{bmatrix} 2 \ 1 end{bmatrix} $$
Найдем их скалярное произведение.
$$ textbf{v} cdot textbf{w} = 4 cdot 2 + 3 cdot 1 = 11 $$
Как вы видите, мы перемножаем компоненты векторов и складываем получившиеся произведения.
Скалярное произведение как длина вектора
Интересно, что корень из скалярного произведения вектора на самого себя есть его длина.
$$ sqrt{ textbf{v} cdot textbf{v} } = sqrt{4 cdot 4 + 3 cdot 3 } = sqrt{ 4^2 + 3^2 } = sqrt{25} = 5 $$
|
v = np.array([4, 3]) np.sqrt(v.dot(v)) |
Угол между векторами
Помимо этого скалярное произведение определяется как произведение длин векторов на косинус угла между ними.
$$ mathbf a cdot mathbf b = ||a|| cdot ||b|| cdot cos(theta) $$
Именно это свойство привело нас к расчету косинусного расстояния между векторами.
$$ cos(theta) = frac{mathbf a cdot mathbf b}{||a|| cdot ||b||} $$
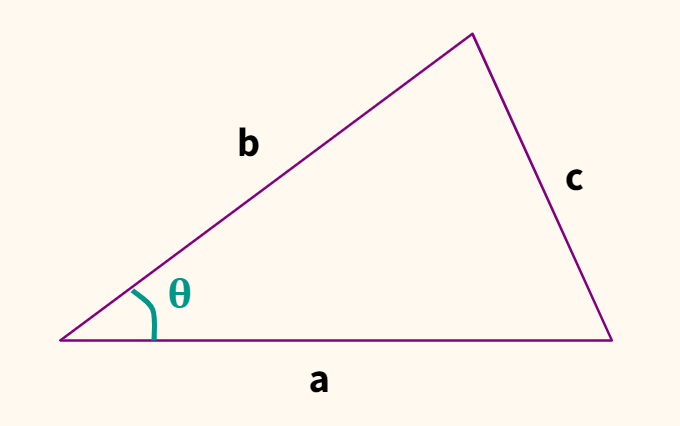
Выведем эту формулу. Для начала вспомним теорему косинусов.
$$ c^2 = a^2 + b^2-2ab cdot cos(theta) $$
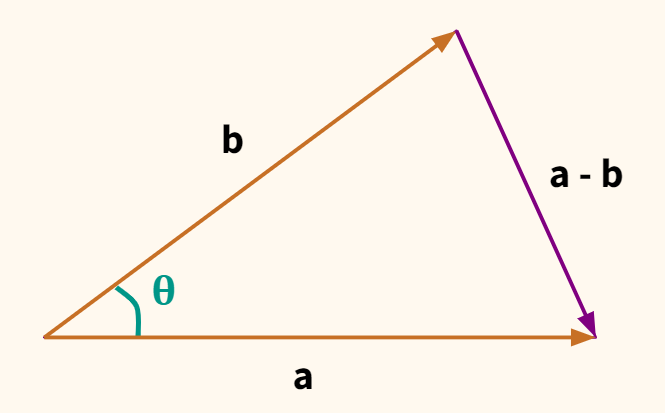
Теперь представим, что у нас не стороны треугольника, а векторы. Если сторону а обозначить как вектор $ textbf{a} $, сторону b — как вектор $ textbf{b} $, то сторона с станет разностью между $ textbf{a} $ и $ textbf{b} $. Чтобы убедиться в этом, найдите $ textbf{-b} $ и приставьте его к окончанию $ textbf{a} $.
Выразим теорему косинусов через длины векторов.
$$ || a-b ||^2 = ||a||^2 + ||b||^2-2 cdot ||a|| cdot ||b|| cdot cos(theta) $$
Помня, что длина есть скалярное произведение вектора на самого себя, мы можем выразить левую часть $ || a-b || $ как
$$ (a-b)(a-b) = a cdot a-a cdot b-b cdot a + (-b) cdot (-b) = ||a||^2-2ab + ||b||^2 $$
Поместим результат в исходное выражение.
$$ ||a||^2-2ab + ||b||^2 = ||a||^2 + ||b||^2-2 cdot ||a|| cdot ||b|| cdot cos(theta) $$
Сократив подобные члены получим
$$ a cdot b = ||a|| cdot ||b|| cdot cos(theta) $$
Выводы. Из тригонометрии мы помним, что косинус 90 градусов равен нулю. Как следствие, скалярное произведение перпендиклярных (правильнее сказать ортогональных (orthogonal)) векторов $ textbf{a} perp textbf{b} $ равно нулю.
$$ a cdot b = ||a|| cdot ||b|| cdot cos(90) = 0 $$
Очевидно, что если угол между двумерными векторами меньше 90 градусов, косинус, а значит и скалярное произведение положительны. В противном случае — отрицательны. Для n-мерных векторов положительное скалярное произведение говорит, что они в целом смотрят в одну строну, отрицательное — противоположные.
Для коллинеарных (сонаправленных) векторов скалярное произведение равно произведению их длин, потому что косинус нуля равен единице.
$$ a cdot b = ||a|| cdot ||b|| cdot cos(0) = ||a|| cdot ||b|| $$
Добавлю, что если $ textbf{a} $ и $ textbf{b} $ — единичные векторы, то косинус угла между векторами просто равен его их скалярному произведению.
$$ cos(theta) = a cdot b $$
Рассчитаем косинусное расстояние для векторов
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix}, textbf{w} = begin{bmatrix} 1 \ 7 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([1, 7]) numerator = np.dot(a, b) aLen = np.linalg.norm(a) bLen = np.linalg.norm(b) denominator = aLen * bLen cosine = numerator / denominator angle = np.arccos(cosine) * 360/2/np.pi cosine, angle |
|
(0.7071067811865475, 45.00000000000001) |
|
from scipy.spatial import distance 1 – distance.cosine([4, 3], [1, 7]) |
Внешнее произведение
Под внешним произведением (outer product) понимается умножение вектор-столбца на вектор-строку по обычным правилам матричного умножения. Результатом такого произведения будет матрица, а не число, как в случае скалярного произведения.
Ортогональность векторов
Еще раз продемонстрируем, почему если векторы ортогональны, их скалярное произведение будет равно нулю. Возьмем три вектора, образовывающих прямоугольный треугольник.
Тогда, по теореме Пифагора,
$$ || mathbf x ||^2 + || mathbf y ||^2 = || mathbf x + mathbf y ||^2 $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = (mathbf x + mathbf y)^T (mathbf x + mathbf y) $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = mathbf x^T mathbf x + mathbf y^T mathbf y + mathbf x^T mathbf y + mathbf y^T mathbf x $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = mathbf x^T mathbf x + mathbf y^T mathbf y + 2 mathbf x^T mathbf y $$
$$ mathbf 0 = 2 mathbf x^T mathbf y $$
$$ mathbf x^T mathbf y = mathbf 0 $$
Проекция вектора на вектор
Подойдем к скалярному произведению с другой стороны. Рассмотрим два вектора $ textbf{a} $ и $ textbf{b} $ и найдем проекцию первого вектора на второй.
Проекция через угол между векторами
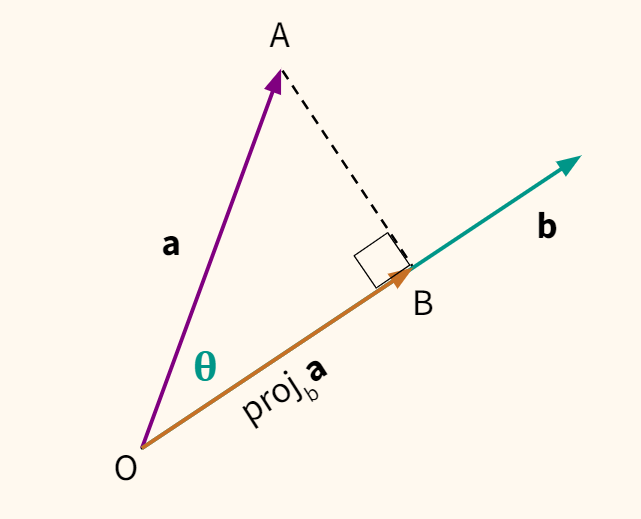
Говоря неформально, проекцией вектора $ textbf{a} $ на вектор $ textbf{b} $ будет такой участок вектора $ textbf{b} $, что расстояние от точки A до точки B минимально. Минимальным оно будет, если угол OAB будет равен 90 градусов. Получается прямоугольный треугольник. Найдем отрезок OB.
$$ cos(theta) = frac {OB}{OA} = frac {OB}{||a||} rightarrow OB = ||a|| cdot cos(theta) $$
Выразим то же самое через формулу скалярного произведения, заменив $||a|| cdot cos(theta) $ на OB.
$$ b cdot a = ||b|| cdot ||a|| cdot cos(theta) rightarrow b cdot a = ||b|| cdot OB $$
Так мы нашли длину проекции OB. Ее называют числовой или скалярной проекцией (scalar projection).
$$ frac{b cdot a}{||b||} = ||a|| cdot cos(theta) = OB $$
Более того, если длина вектора $ textbf{b} $ равна единице, то длина проекции OB просто равна скалярному произведению.
$$ ||b|| = 1 rightarrow b cdot a = OB $$
Это объясняет, почему скалярное произведение еще называют projection product.
Очевидное и тем не менее интересное примечание. Обратите внимание на связь понимания скалярного произведения как проекции одного вектора на другой и произведения длин векторов на косинус угла между ними. Если векторы перпендикулярны, проекция одного вектора на другой равна нулю, а значит и произведение проекции второго вектора на первый равно нулю.
Предположим, нас интересует не только длина проекции, но и ее направление. В этом случае говорят про векторную проекцию (vector projection).
Она выражается как произведение нормализованного вектора $ textbf{b} $ на длину проекции (то есть скалярную проекцию) OB.
$$ proj_mathbf{b} textbf{a} = OB cdot hat{b} $$
Перепишем OB через скалярное произведение, а $hat{b}$ через частное вектора $ textbf{b} $ на его длину.
$$ proj_mathbf{b} textbf{a} = frac{b cdot a}{||b||} cdot frac{b}{||b||} $$
Таким образом, можно сказать, что векторная проекция показывает, длину вектора $ textbf{a} $ в направлении вектора $ textbf{b} $.
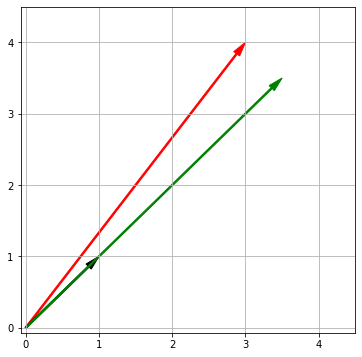
Пример. Возьмем два вектора a и b и найдем вначале скалярную, затем векторную проекцию вектора a на вектор b.
|
a = np.array([3, 4]) b = np.array([1, 1]) scalar_proj_a_on_b = np.dot(a, b) / np.linalg.norm(b) scalar_proj_a_on_b |
|
vector_proj_a_on_b = scalar_proj_a_on_b * (b / np.linalg.norm(b)) vector_proj_a_on_b |
|
a = np.array([3, 4]) b = np.array([1, 1]) proj = np.array([3.5, 3.5]) ax = plt.axes() plt.xlim([–0.07, 4.5]) plt.ylim([–0.07, 4.5]) plt.grid() ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b[0], b[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, proj[0], proj[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Матрица проекции
Векторную проекцию можно выразить с помощью матрицы проекции $P$.
$$ proj_mathbf{b} textbf{a} = P cdot mathbf a = frac{mathbf b mathbf b^T}{mathbf b^T mathbf b} cdot mathbf a $$
В знаменателе находится скалярное произведение и результатом умножения будет число. В числителе — внешнее произведение и результатом будет матрица. Найдем внешнее произведение из примера выше.
|
b_bT = np.outer(b, b) b_bT |
Найдем скалярное произведение.
Создадим матрицу проекции $P$ и умножим ее на вектор $mathbf a$.
Симметрия скалярного произведения
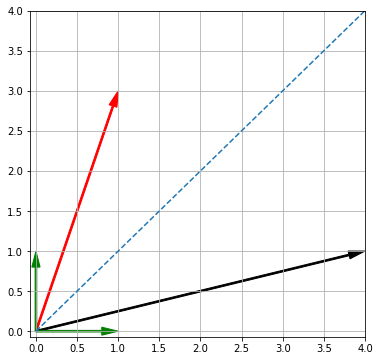
Продемонстрируем с точки зрения проекции, почему $a cdot b = b cdot a $. Возьмем два вектора a и b.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
a = np.array([1, 3]) b = np.array([4, 1]) i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([–0.07, 4]) plt.ylim([–0.07, 4]) plt.grid() ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b[0], b[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.plot([0, 4], [0, 4], linestyle = ‘dashed’) plt.show() |
Выше мы сказали, что $ a cdot b = OB cdot ||b|| $. То есть скалярное произведение вектора a на вектор b равно произведению проекции a на b, умноженной на длину вектора b.
Продемонстрируем, что произведение проекции вектора a на вектор b, умноженное на длину вектора b, равно произведению проекции вектора b на вектор a, умноженному на длину вектора a.
$$ proj_ba times || b || = proj_ab times || a || $$
|
scalar_proj_a_on_b = np.dot(a, b) / np.linalg.norm(b) scalar_proj_a_on_b * np.linalg.norm(b) |
|
scalar_proj_b_on_a = np.dot(b, a) / np.linalg.norm(a) scalar_proj_b_on_a * np.linalg.norm(a) |
|
np.dot(a, b), np.dot(b, a) |
Видео про скалярное произведение векторов⧉.
Векторное произведение
Векторное произведение (cross product) задано только в трехмерном пространстве. Результатом такого произведения будет вектор, перпендикулярный каждому из исходных векторов. Приведем иллюстрацию из Википедии⧉.
Математически векторное произведение задается формулой
$$ a times b = || a || || b || sin(theta) $$
Геометрически — это площадь параллелограмма, сформированного из исходных векторов a и b.
Приведем пример.
|
a = [1, 2, 3] b = [4, 5, 6] np.cross(a, b) |
Подведем итог
Сегодня мы ввели понятие вектора, познакомились с базовыми операциями с векторами, в частности, изучили скалярное произведение векторов и научились находить скалярную и векторную проекцию одного вектора на другой.
Перейдем к рассмотрению векторного пространства.
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0);j(0;1;0); k(0;0;1);
Замечание 1
Единичные векторы являются некомпланарными.
Замечание 2
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
Пример
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Решение
Находим длину вектора a
$left| {vec a} right| = sqrt {{1^2} + {2^2} + {{left( { — 2} right)}^2}} = 3$
затем вычисляем единичный вектор e
$vec e = left( {frac{1}{3};frac{2}{3}; — frac{2}{3}} right)$
Векторное произведения единичных векторов
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус». Смотрите схему 1.
Схема 1
На основании схемы получаем таблицу векторного произведения единичных векторов
i×i=0 i×j=k i×k=-j
j×i=-k j×j=0 j×k=i
k×i=j k×j=-i k×k=0
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
20687
