Найти медиану треугольника по координатам вершин
Как найти медиану если даны координаты вершин треугольника?
Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.
Рассмотрим нахождение медианы на конкретном примере.
Дано: ΔABC,
1) Так как AF — медиана треугольника ABC, то F — середина BC.
Вычислить медиану значений, хранящихся в Vector-c++?
Я студент-программист, и для проекта, над которым я работаю, из того, что мне нужно сделать, это вычислить медианное значение вектора значений int. Я должен сделать это, используя только функцию сортировки из STL и векторных функций-членов, таких как .begin() , .end() и .size() .
Я также должен убедиться, что нахожу медиану, имеет ли вектор нечетное число значений или четное число значений.
и я штука ниже я включил моя попытка. Так где же я ошибаюсь? Я был бы признателен, если бы вы дали мне несколько советов или ресурсов, чтобы двигаться в правильном направлении.
код:
спасибо!!
6 ответов
Вы делаете дополнительное разделение и в целом делаете его немного более сложным, чем это должно быть. Кроме того, нет необходимости создавать делитель, когда 2 на самом деле более значим в контексте.
нет необходимости полностью сортировать вектор: std::nth_element может сделать достаточно работы, чтобы поставить медиану в правильное положение. См. мой ответ на этот вопрос для примера.
конечно, это не поможет, если ваш учитель запрещает использовать правильный инструмент для работы.
следующая простая функция, которая возвращает медиану набора значений с помощью итераторов ввода. Он не будет изменять исходный набор данных за счет выделения памяти.
Если вы хотите избежать затрат на выделение копии набора данных и хотите изменить базовый набор данных, вы можете использовать это вместо:
не делай этого. Это просто делает ваш код более запутанным. Вы, вероятно, читали рекомендации о том, чтобы не использовать магические числа, но четность против странности чисел является фундаментальным свойством, поэтому абстрагирование этого не дает никакой пользы, но затрудняет читаемость.
вы берете итератор в конец вектора, беря другой итератор, который указывает на один конец вектора, добавляя итераторы вместе (что не является операцией, которая имеет смысл), и затем делим полученный итератор (что также не имеет смысла). Это более сложный случай; сначала я объясню, что делать с вектором нечетного размера, а четный случай оставлю вам в качестве упражнения.
опять же, вы делите итератор. Вместо этого вы хотите увеличить итератор до начала вектора на hWScores.size() / 2 элементы:
и обратите внимание, что вы должны разыменования итераторы для получения значений из них. Было бы проще, если бы вы использовали индексы:
я приведу ниже пример программы, которая несколько похожа на ту, что в ответе Макса С. Чтобы помочь ОП продвигать свои знания и понимание, я внес ряд изменений. У меня:
a) изменил вызов по ссылке const на вызов по значению, так как сортировка захочет изменить порядок элементов в вашем векторе (EDIT: я только что видел, что Роб Кеннеди также сказал это, когда я готовил свой пост)
b) заменил size_t на более подходящий вектор >:: size_type (собственно, удобный синоним последнего),
c) сохраненный размер / 2 в промежуточную переменную,
d) выбрасывается исключение, если вектор пуст, и
e) я также ввел условный оператор (? :).
На самом деле, все эти исправления прямо из главы 4 “ускоренного C++” Кенига и Му.
Я не совсем уверен, каковы ваши ограничения на пользователя функций-членов vector, но индексируйте доступ с [] или at() упростит доступ к элементам:
вы также можете работать с итераторами типа begin() + offset как вы сейчас делаете, но затем вам нужно сначала вычислить правильное смещение с size()/2 и добавить, что до begin() , а не наоборот. Также вам нужно разыменовать результирующий итератор, чтобы получить доступ к фактическому значению при этом точка:
Мой любимый алгоритм: нахождение медианы за линейное время
Нахождение медианы за O(n log n)
Самым прямолинейным способом нахождения медианы является сортировка списка и выбор медианы по её индексу. Самая быстрая сортировка сравнением выполняется за O(n log n) , поэтому от неё зависит время выполнения 1 , 2 .
У этого способа самый простой код, но он определённо не самый быстрый.
Нахождение медианы за среднее время O(n)
Следующим нашим шагом будет нахождение медианы в среднем за линейное время, если нам будет везти. Этот алгоритм, называемый «quickselect», разработан Тони Хоаром, который также изобрёл алгоритм сортировки с похожим названием — quicksort. Это рекурсивный алгоритм, и он может находить любой элемент (не только медиану).
- Выберем индекс списка. Способ выбора не важен, на практике вполне подходит и случайный. Элемент с этим индексом называется опорным элементом (pivot).
- Разделим список на две группы:
- Элементы меньше или равные pivot, lesser_els
- Элементы строго большие, чем pivot, great_els
- Мы знаем, что одна из этих групп содержит медиану. Предположим, что мы ищем k-тый элемент:
- Если в lesser_els есть k или больше элементов, рекурсивно обходим список lesser_els в поисках k-того элемента.
- Если в lesser_els меньше, чем k элементтов, рекурсивно обходим список greater_els . Вместо поиска k мы ищем k-len(lesser_els) .
Вот пример алгоритма, выполняемого для 11 элементов:
Чтобы найти с помощью quickselect медиану, мы выделим quickselect в отдельную функцию. Наша функция quickselect_median будет вызывать quickselect с нужными индексами.
В реальном мире Quickselect отлично себя проявляет: он почти не потребляет лишних ресурсов и выполняется в среднем за O(n) . Давайте докажем это.
Доказательство среднего времени O(n)
В среднем pivot разбивает список на две приблизительно равных части. Поэтому каждая последующая рекурсия оперирует с 1 ⁄2 данных предыдущего шага.
Существует множество способов доказательства того, что этот ряд сходится к 2n. Вместо того, чтобы приводить их здесь, я сошлюсь на замечательную статью в Википедии, посвящённую этому бесконечному ряду.
Quickselect даёт нам линейную скорость, но только в среднем случае. Что, если нас не устраивает среднее, и мы хотим гарантированного выполнения алгоритма за линейное время?
Детерминированное O(n)
В предыдущем разделе я описал quickselect, алгоритм со средней скоростью O(n) . «Среднее» в этом контексте означает, что в среднем алгоритм будет выполняться за O(n) . С технической точки зрения, нам может очень не повезти: на каждом шаге мы можем выбирать в качестве pivot наибольший элемент. На каждом этапе мы сможем избавляться от одного элемента из списка, и в результате получим скорость O(n^2) , а не O(n) .
С учётом этого, нам нужен алгоритм для подбора опорных элементов. Нашей целью будет выбор за линейное время pivot, который в худшем случае удаляет достаточное количество элементов для обеспечения скорости O(n) при использовании его вместе с quickselect. Этот алгоритм был разработан в 1973 году Блумом (Blum), Флойдом (Floyd), Праттом (Pratt), Ривестом (Rivest) и Тарьяном (Tarjan). Если моего объяснения вам не хватит, то можете изучить их статью 1973 года. Вместо того, чтобы описывать алгоритм, я подробно прокомментирую мою реализацию на Python:
Давайте докажем, что медиана медиан является хорошим pivot. Нам поможет, если мы представим визуализацию нашего алгоритма выбора опорных элементов:
Красным овалом обозначены медианы фрагментов, а центральным кругом — медиана медиан. Не забывайте, мы хотим, чтобы pivot разделял список как можно ровнее. В худшем возможном случае каждый элемент в синем прямоугольнике (слева вверху) будет меньше или равен pivot. Верхний правый прямоугольник содержит 3 ⁄5 половины строк — 3/5*1/2=3/10 . Поэтому на каждом этапе мы избавляемся по крайней мере от 30% строк.
Но достаточно ли нам отбрасывать 30% элементов на каждом этапе? На каждом этапе наш алгоритм должен выполнять следующее:
- Выполнять работу O(n) по разбиению элементов
- Для рекурсии решать одну подзадачу размером в 7 ⁄10 от исходной
- Для вычисления медианы медиан решать одну подзадачу размером с 1 ⁄5 от исходной
В результате мы получаем следующее уравнение полного времени выполнения T(n) :
Не так уж просто доказать, почему это равно O(n) . Быстрое решение заключается в том, чтобы положиться на основную теорему о рекуррентных соотношениях. Мы попадаем в третий случай теоремы, при котором работа на каждом уровне доминирует над работой подзадач. В этом случае общая работа будет просто равна работе на каждом уровне, то есть O(n) .
Подводим итог
У нас есть quickselect, алгоритм, который находит медиану за линейное время при условии наличия достаточно хорошей опорного элемента. У нас есть алгоритм медианы медиан, алгоритм O(n) для выбора опорного элемента (который достаточно хорош для quickselect). Соединив их, мы получили алгоритм нахождения медианы (или n-ного элемента в списка) за линейное время!
Медианы за линейное время на практике
В реальном мире почти всегда достаточно случайного выбора медианы. Хотя подход с медианой медиан всё равно выполняется за линейное время, на практике его вычисление длится слишком долго. В стандартной библиотеке C++ используется алгоритм под названием introselect, в котором применено сочетание heapselect и quickselect; предел его выполнения O(n log n) . Introselect позволяет использовать обычно быстрый алгоритм с плохим верхним пределом в сочетании с алгоритмом, который медленнее на практике, но имеет хороший верхний предел. Реализации начинают с быстрого алгоритма, но возвращаются к более медленному, если не могут выбрать эффективные опорные элементы.
В завершение приведу сравнение элементов, используемых в каждой из реализаций. Это не скорость выполнения, а общее количество элементов, которые рассматривает функция quickselect. Здесь не учитывается работа по вычислению медианы медиан.
Именно этого мы и ожидали! Детерминированный опорный элемент почти всегда рассматривает при quickselect меньшее количество элементов, чем случайный. Иногда нам везёт и мы угадываем pivot с первой попытки, что проявляется как впадины на зелёной линии. Математика работает!
- Это может стать интересным применением поразрядной сортировки (radix sort), если вам нужно найти медиану в списке целых чисел, каждое из которых меньше 2 32 .
- На самом деле в Python используется Timsort, впечатляющее сочетание теоретических пределов и практической скорости. Заметки о списках в Python.
[spoiler title=”источники:”]
http://askdev.ru/q/vychislit-medianu-znacheniy-hranyaschihsya-v-vector-c-96101/
http://habr.com/ru/post/346930/
[/spoiler]
Найти медиану треугольника по координатам вершин
Как найти медиану если даны координаты вершин треугольника?
Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.
Рассмотрим нахождение медианы на конкретном примере.
 Дано: ΔABC,
Дано: ΔABC,
A(-11;12), B(3;8), C(-1;6),
AF — медиана.
Найти: AF
Решение:
1) Так как AF — медиана треугольника ABC, то F — середина BC.
По формулам координат середины отрезка:
![]()
![]()
Итак, F(1;7).
2) По формуле расстояния между точками
![]()
![]()
![]()
Ответ: 13.
Ответ на первый ответ постой:
Скалярное произведение есть скаляр, равный произведению модулей на косинус угла между ними:
А=|p|*|q|*cos(p, q) = 3 *1* cos (pi/3) = 3*0,5=1,5..
Со вторыми заданиями немного сложнее:
Сначала установим условно вектор q на оси х, тогда получим, что оба вектора начинаются в 0 и имеют между собой заданный угол..
Разложим оба вектора p и q на взаимно ортогональные составляющие:
px=|p|cos (п/3)=3*0,5=1,5
py=|p|sin (п/3)=3*0,86=2,6
qx=|q|=1
qy=0
Далее согласно заданным выражениям AB = 2p – q; AC = 3p + 2q произведём вычисления для каждой спроецированной компоненты..
AB = 2p – q; AC = 3p + 2q
АВх=2*1,5-1=2
АВу=2*2,6=5,2
АСх=3*1,5+2=6,5
АСу=3*1,5=4,5
Итак, мы задали точку А(0;0), получили точки В(2;5,2) С(6,5;4,5)..
Вектор ВС задаётся точкой А и В..
Теперь всё просто: находим длину отрезка ВС по известным координатам:
|BC|=sqrt((6,5-2)^2+(5,2-4,5)^2)= 4,5..
отношение cos a=(5,2-4,5)/4,5 есть угол относительно оси абсцисс, относительно которой мы и отсчитываем угол а=81 град=1,41 рад..
Модуль и угол задают вектор ВС..
Чтобы найти длину медианы нужно найти точку М, которая делит ВС напополам 4,5/2 = 2,25..
Из подобия прямоугольного треугольника, построенного на точек М стороны
(6,5-2)/2+2 = 4,25..
(5,2-4,5)/2+4,5= 4,85..
Это координаты точки М (4,25;4,85)..
Теперь находим АМ=sqrt((4,25)^2+(4,85)^2)=6,45..
Это и есть искомая длина медианы..
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given two vectors, a and b of different sizes, where array a has m number of elements and array b has n number of elements. The task is to find the median of two vectors. This problem is an extension of the Median of two sorted arrays of different sizes problem.
Example:
Input: a = {1, 4}
b = {2}Output: The median is 2.
Explanation:
The merged vector = {1, 2, 4}
So, the median is 2.Input: a = {1, 2}
b = {3, 5}Output: The median is 2.50000
Explanation:
The merged vector = {1, 2, 3, 5}
So, the median is (2 + 3) / 2 = 2.5.
Approach:
- Initialize vector a.
- Initialize vector b.
- Create a new vector of size a + b.
- Iterate using a loop the first vector and store the data into a newly created vector and similarly for the second vector after iterating the first vector.
- Merged both sorted vectors in the newly created vector by using the merge() STL function.
- Find the median for even and odd sizes and return it.
Below is the C++ implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double findMedianSortedVectors(vector<int>& a,
vector<int>& b)
{
vector<int> c(a.size() + b.size());
int k = 0;
double median = 0;
int size_a = a.size();
int size_b = b.size();
for (int i = 0; i < size_a; i++)
{
c[k++] = a[i];
}
for (int i = 0; i < size_b; i++)
{
c[k++] = b[i];
}
merge(a.begin(), a.end(),
b.begin(), b.end(), c.begin());
int n = c.size();
if (n % 2 == 0)
{
median = c[(n / 2) - 1] + c[n / 2];
median = median / 2;
}
else
{
median = c[(n - 1) / 2];
}
return median;
}
int main()
{
vector<int> v1;
vector<int> v2;
v1.push_back(1);
v1.push_back(4);
v2.push_back(2);
double median_vectors =
findMedianSortedVectors(v1, v2);
cout << median_vectors << endl;
return 0;
}
Java
import java.io.*;
import java.util.Collections;
import java.util.Vector;
class GFG {
public static double
findMedianSortedVectors(Vector<Integer> a,
Vector<Integer> b)
{
Vector<Integer> c = new Vector<Integer>();
double median = 0;
int size_a = a.size();
int size_b = b.size();
for (int i = 0; i < size_a; i++) {
c.add(a.get(i));
}
for (int i = 0; i < size_b; i++) {
c.add(b.get(i));
}
Collections.sort(c);
int n = c.size();
if (n % 2 == 0) {
median = c.get((n / 2) - 1) + c.get(n / 2);
median = median / 2;
}
else {
median = c.get((n - 1) / 2);
}
return median;
}
public static void main(String[] args)
{
Vector<Integer> v1 = new Vector<Integer>();
Vector<Integer> v2 = new Vector<Integer>();
v1.add(1);
v1.add(4);
v2.add(2);
double median_vectors
= findMedianSortedVectors(v1, v2);
System.out.println(median_vectors);
}
}
Python3
def findMedianSortedVectors(a, b):
c = []
for i in range(0, len(a)):
c.append(0)
for i in range(0, len(b)):
c.append(0)
k = 0
median = 0
size_a = len(a)
size_b = len(b)
for i in range(0, size_a):
c[k] = a[i]
k += 1
for i in range(0, size_b):
c[k] = b[i]
k += 1
c.sort()
n = len(c)
if (n % 2 == 0):
median = c[(n // 2) - 1] + c[n // 2]
median = median / 2
else:
median = c[(n - 1) // 2]
return median
v1 = [1, 4]
v2 = [2]
median_lists = findMedianSortedVectors(v1, v2)
print(median_lists)
C#
using System;
using System.Collections;
using System.Collections.Generic;
class GFG
{
public static double
findMedianSortedVectors(ArrayList a,
ArrayList b)
{
ArrayList c = new ArrayList();
double median = 0;
int size_a = a.Count;
int size_b = b.Count;
for (int i = 0; i < size_a; i++) {
c.Add(a[i]);
}
for (int i = 0; i < size_b; i++) {
c.Add(b[i]);
}
c.Sort();
int n = c.Count;
if (n % 2 == 0) {
median = (int)c[(n / 2) - 1] + (int)c[n / 2];
median = median / 2;
}
else {
median = (int)c[(n - 1) / 2];
}
return median;
}
public static void Main()
{
ArrayList v1 = new ArrayList();
ArrayList v2 = new ArrayList();
v1.Add(1);
v1.Add(4);
v2.Add(2);
double median_vectors
= findMedianSortedVectors(v1, v2);
Console.WriteLine(median_vectors);
}
}
Javascript
<script>
function findMedianSortedVectors(a, b)
{
let c = new Array(a.length + b.length);
let k = 0;
let median = 0;
let size_a = a.length;
let size_b = b.length;
for (let i = 0; i < size_a; i++)
{
c[k++] = a[i];
}
for (let i = 0; i < size_b; i++)
{
c[k++] = b[i];
}
c.sort(function (a, b) { return a - b })
let n = c.length;
if (n % 2 == 0)
{
median = c[(Math.floor(n / 2) - 1)] + c[(Math.floor(n / 2))];
median = Math.floor(median / 2);
}
else
{
median = c[(Math.floor((n - 1) / 2))];
}
return median;
}
let v1 = [];
let v2 = [];
v1.push(1);
v1.push(4);
v2.push(2);
let median_vectors =
findMedianSortedVectors(v1, v2);
document.write(median_vectors + '<br>');
</script>
Complexity:
Time Complexity: O(m + n) as to merge both the vectors O(m+n) time is needed.
Space Complexity: O(1) as no extra space is required.
Last Updated :
24 Mar, 2023
Like Article
Save Article

информация о
следующих вебинарах и чатах на сайте ИДО

2. Даны вершины треугольника
Составить:
а) уравнение стороны АВ и найти ее длину,
b) уравнение медианы BM и найти ее длину,
с) уравнение высоты СН и найти ее длину,
d) косинус угла между медианой ВМ и высотой СН.
78
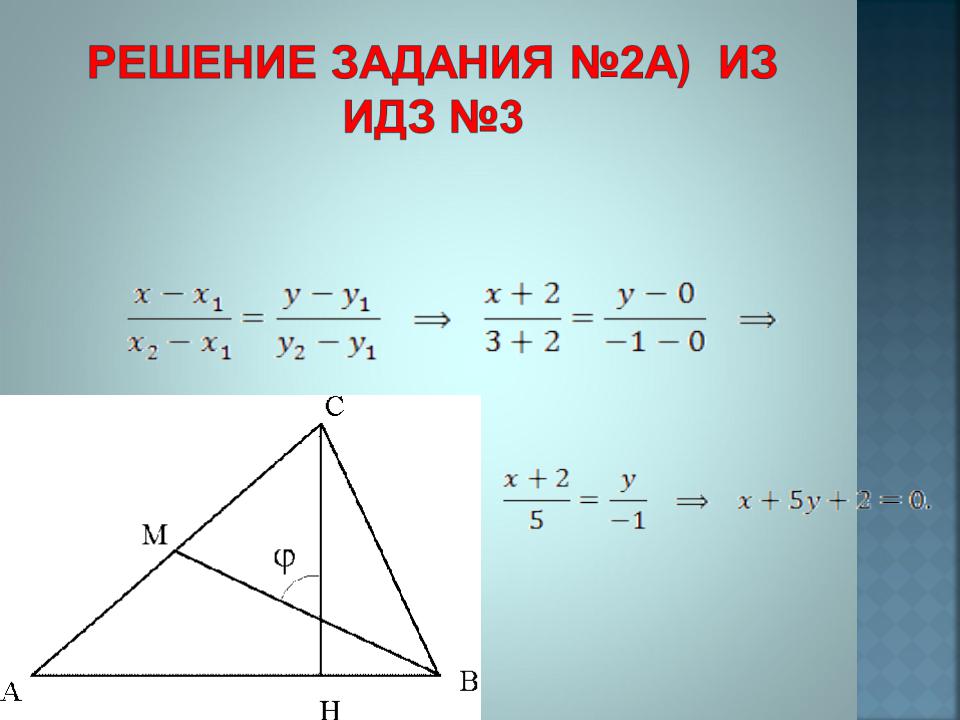
а) Для составления уравнения стороны АВ воспользуемся уравнением прямой, проходящей через две точки:
79
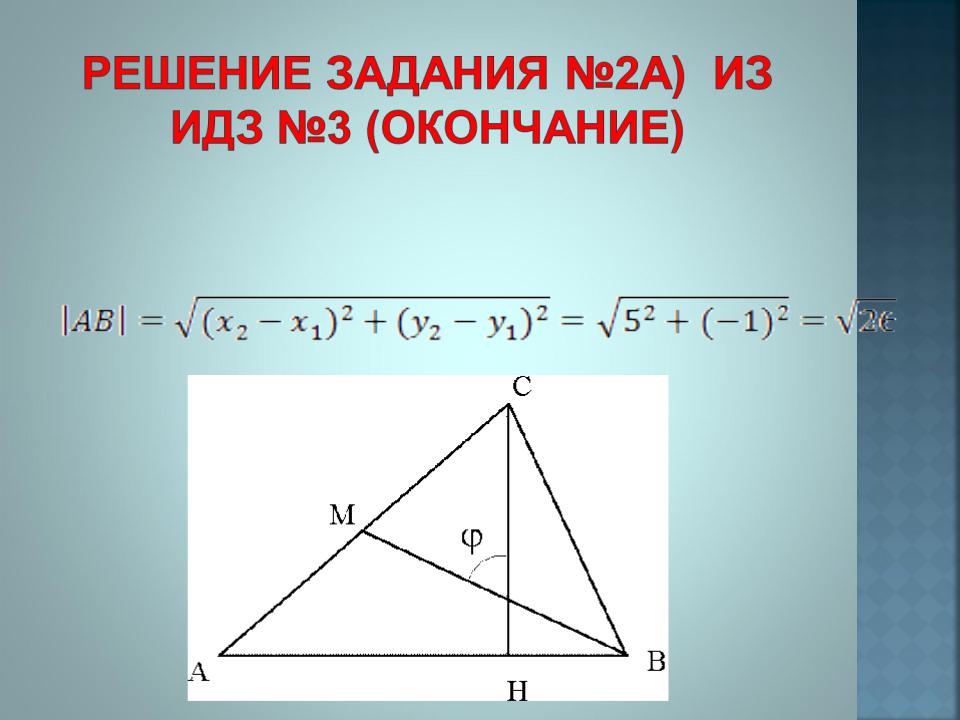
Длину стороны АВ найдем как расстояние между двумя точками
80

b) Вектор медианы треугольника равен полусумме векторов его сторон, т.е.
Длина медианы есть модуль вектора
81
