Как найти велечину углов

Математика

5 класс

Урок № 27

Углы. Измерение углов

Перечень рассматриваемых вопросов:

– понятие «угол», «величина угла»;

– виды углов;

– построение углов;

– измерение величины угла.

Тезаурус

Угол – геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки, которая называется вершиной угла.

Градус – единица измерения углов, составляющая часть развёрнутого угла.

Градусная мера угла – число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия», – сказал в своё время французский архитектор Ле Корбюзье, и трудно с ним не согласиться. Геометрические фигуры постоянно встречаются в творениях природы и человека.

Сегодня мы рассмотрим ещё одну геометрическую фигуру – угол, разберём его виды и опишем процесс построения и измерения углов.

Для начала определим, что называют углом.

Углом называют геометрическую фигуру, образованную двумя лучами, выходящими из одной точки.

Построим угол. Для этого отметим на плоскости точку О и проведём два луча – ОК и ОМ. Получим геометрическую фигуру, образованную точкой О и двумя лучами, исходящими из этой точки. Такую геометрическую фигуру и называют углом.

Лучи ОК и ОМ называют сторонами угла, точку О – общее начало этих лучей – называют вершиной угла.

Обозначается угол чаще всего тремя буквами. Например, ∠КОМ или ∠МОК. В середине пишется буква, которой обозначена вершина угла. Также угол можно обозначать и одной буквой, поставленной у вершины угла. Например, ∠О.

Начертим два луча, исходящих из точки О и принадлежащих одной прямой.

Лучи ОС и OК вместе с точкой О дополняют друг друга до прямой – это дополнительные лучи. Угол называют развёрнутым, если его стороны являются дополнительными лучами.

Угол СОК – развёрнутый.

Построим развёрнутый угол АОВ и полуокружность с центром в точке О. Полуокружность разделим на 180 равных частей. Если построим углы с вершиной в точке О, стороны которых проходят через точки деления полуокружности, то таких углов будет 180. Один такой угол будет составлять часть развёрнутого угла.

рисунок

Меру угла, составляющего часть развёрнутого угла, принимают за единицу измерения углов и называют градусом. Обозначают: 1º.

Градусной мерой угла называют число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.

Например, градусная мера угла КOВ равна 25 градусам, так как в нём единица измерения градус содержится двадцать пять раз. Записывают: ∠КОВ = 25º.

рисунок

Стоит отметить, что для более точного измерения угла используют доли градуса:

– минуты, которые обозначают одной чёрточкой сверху над цифрой справа,

– секунды, которые обозначаются двумя чёрточками над цифрой справа.

В одном градусе содержится 60 минут, а в одной минуте – 60 секунд.

Например, если угол А равен 10 градусам 5 минутам, записывают: ∠А = 10º5′.

Градусная мера развёрнутого угла равна 180º.

Для измерения углов в градусах пользуются прибором, который называется транспортиром. На транспортире имеется шкала – полуокружность, разделённая на 180 равных частей. На линейке транспортира чёрточкой отмечен центр полуокружности транспортира.

Чтобы найти градусную меру угла, например, угла АВС, нужно совместить центр транспортира с вершиной угла, в данном случае точкой В; расположить линейку транспортира так, чтобы одна из сторон угла прошла через начало отсчёта шкалы транспортира – ноль градусов (в данном случае сторона АВ), и найти на шкале транспортира деление, через которое проходит другая сторона угла – в данном случае сторона ВС.

Это деление шкалы покажет градусную меру угла. В нашем случае – это 120º.

Транспортир применяется также для построения угла, мера которого известна. Построим, например, угол KNM, равный 60º. Для этого:

– проведём луч NM;

– совместим центр транспортира с точкой N;

– расположим линейку транспортира так, чтобы луч NM прошёл через начало отсчёта шкалы транспортира;

– найдём на шкале транспортира деление, соответствующее шестидесяти градусам, и отметим напротив него точку К;

– проведём луч NK. Мы построили угол KNM, равный 60º.

Ответить на вопрос, равны ли углы, и, если не равны, то какой из них больше или меньше, можно, сравнивая их градусные меры. Углы с равными градусными мерами равны. Из двух углов больше тот, который имеет большую градусную меру; а меньше тот, который имеет меньшую градусную меру.

Углы можно сравнить также наложением. Если при этом они совпадают, то равны.

Помимо развёрнутого, углы можно разделить на следующие виды: прямой, острый и тупой.

Угол называют прямым, если его градусная мера равна 90º.

Острым – если его градусная мера меньше 90º.

Тупым – если его градусная мера больше 90º и меньше 180º.

Рассмотрим ещё два вида углов, которые встречаются в геометрических задачах: это вертикальные углы, то есть пара углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Например, угол один и два.

И смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.

Например, угол САВ и угол САD.

Вместе смежные углы составляют развёрнутый угол. Следовательно, сумма величин смежных углов составляет 180º.

Итак, сегодня мы познакомились с разными видами углов и научились строить их с помощью транспортира.

Для определения величины углов используется прибор, который называют транспортир. Но существуют и более высокоточные приборы.

Так, гониометр использовался для определения положения судна в море или океане.

Теодолит – прибор для измерения горизонтальных и вертикальных углов при геодезических работах, в строительстве и т. п.

Секстант применялся для измерения высоты Солнца над горизонтом с целью определения географических координат той местности, в которой производится измерение, и на судах.

Посох Якова, служащий для измерения углов, – один из первых инструментов для астрономических наблюдений.

Была ли эта статья полезной?

Как найти величину угла треугольника

Плоский треугольник в евклидовой геометрии составляют три угла, образованные его сторонами. Величины этих углов можно рассчитать несколькими способами. В силу того, что треугольник – одна из простейших фигур, существуют несложные формулы расчета, которые еще более упрощаются, если их применять к правильным и симметричным многоугольникам этого рода.

Инструкция

Если известны величины двух углов произвольного треугольника (β и γ), то величину третьего (α) можно определить исходя из теоремы о сумме углов в треугольнике. Она гласит, что эта сумма в евклидовой геометрии всегда равна 180°. То есть для нахождения единственного неизвестного угла в вершинах треугольника отнимайте от 180° величины двух известных углов: α=180°-β-γ.

Если речь идет о прямоугольном треугольнике, то для нахождения величины неизвестного острого угла (α) достаточно знать величину другого острого угла (β). Так как в таком треугольнике угол, лежащий напротив гипотенузы, всегда равен 90°, то для нахождения величины неизвестного угла отнимайте от 90° величину известного угла: α=90°-β.

В равнобедренном треугольнике тоже достаточно знать величину одного из углов, чтобы вычислить два других. Если известен угол (γ) между сторонами равной длины, то для вычисления обоих остальных углов найдите половину от разницы между 180° и величиной известного угла – эти углы в равнобедренном треугольнике будут равны: α=β=(180°-γ)/2. Из этого вытекает, что если известна величина одного из равных углов, то угол между равными сторонами можно определить как разницу между 180° и удвоенной величиной известного угла: γ=180°-2*α.

Если известны длины трех сторон (A, B, C) в произвольном треугольнике, то величину угла можно найти по теореме косинусов. Например, косинус угла (β), лежащего напротив стороны B, можно выразить как сумму возведенных в квадрат длин сторон A и C, уменьшенную на возведенную в квадрат длину стороны B и поделенную на удвоенное произведение длин сторон A и C: cos(β)=(A²+C²-B²)/(2*A*C). А чтобы найти величину угла, зная чему равен его косинус, надо найти его арк-функцию, то есть арккосинус. Значит β=arccos((A²+C²-B²)/(2*A*C)). Аналогичным способом можно найти величины углов, лежащих напротив остальных сторон в этом треугольнике.

Источники:

• величины углов

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Содержание страницы:

Понятие угла

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B  или ∠ B O A ,  но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O .

Величину угла измеряют в градусах. ∠ A O B = 24 ° .

Виды углов:

Биссектриса угла

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Или

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла.

∠ A O D = ∠ B O D = ∠ A O B 2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B .

Углы, образованные при пересечении двух прямых

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180 ° .

Пример:

Пары углов

( 1 ) и ( 3 )
( 2 ) и ( 4 )

называются вертикальными.

По свойству вертикальных углов:

∠ C O D = ∠ A O B
∠ B O D = ∠ A O C

Пары углов

( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )

называются смежными.

По свойству смежных углов:

∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °

Углы, образованные при пересечении двух прямых секущей

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

Пары углов:

( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )

называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

Пары углов:

( 3 ) и ( 5 )
( 4 ) и ( 6 )

называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

Пары углов:

( 1 ) и ( 7 )
( 2 ) и ( 8 )

называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

Пары углов:

( 3 ) и ( 6 )
( 4 ) и ( 5 )

называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

Пары углов:

( 1 ) и ( 8 )
( 2 ) и ( 7 )

называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:

• Соответственные углы равны.
• Внутренние накрест лежащие углы равны.
• Внешние накрест лежащие углы равны.
• Сумма внутренних односторонних углов равна 180 ° .
• Сумма внешних односторонних углов равна 180 ° .

Сумма углов многоугольника

Сумма углов произвольного n -угольника вычисляется по формуле:

S n = 180 ° ⋅ ( n − 2 )

где n – это количество углов в n -угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.

Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °

Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °

Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n -угольника, необходимо сумму углов этого многоугольника разделить на количество углов.

α n = 180 ° ⋅ ( n − 2 ) n

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с углами

Скачать домашнее задание к уроку 2.

Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

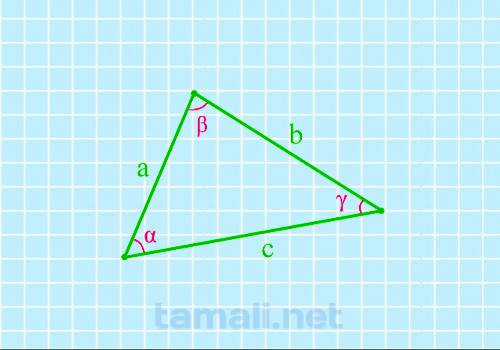
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

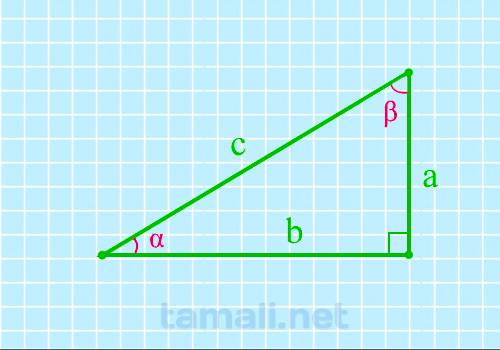
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

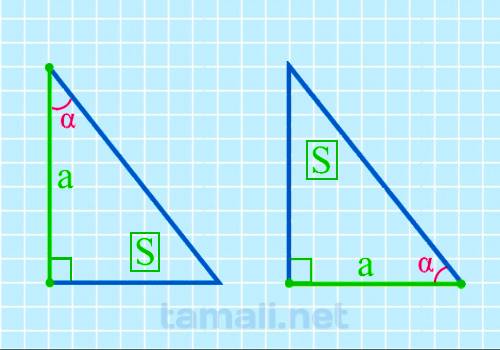
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

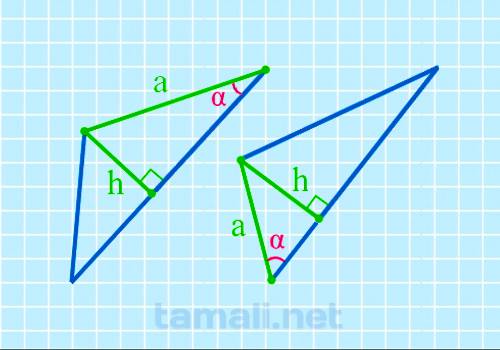
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

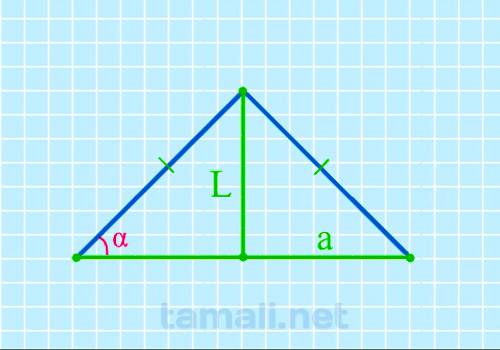
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

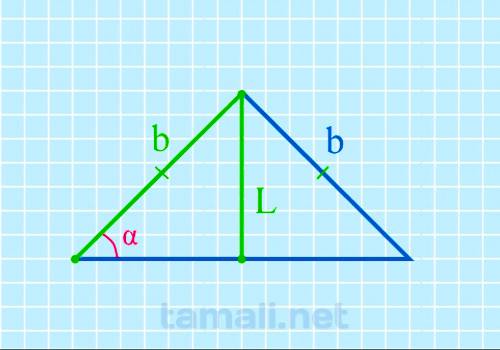
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

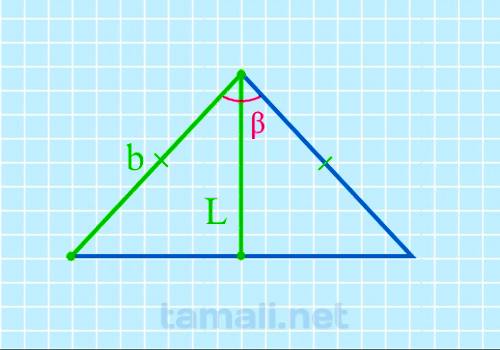
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

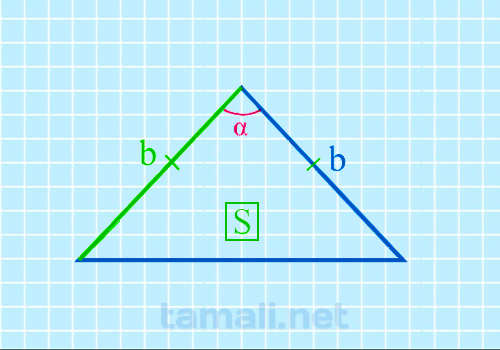
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.