Как найти величину допускаемой нагрузки

Как найти величину допускаемой нагрузки

Р
е ш е н и е

Определяем наибольшую допускаемую
нагрузку. Для этого сначала строим эпюру
моментов (рис. 3.10) и находим значение
изгибающего момента в опасном сечении,
.
Балку располагаем таким образом, чтобы
нагрузка была приложена в плоскостиХOY.

Рис. 3.10.

Величину Рможно определить из
условия прочности по нормальным
напряжениям

; .

отсюда

кН,

где
– допускаемое напряжение;Wz
– момент сопротивления (ч. I,
п. 4.1).

Расчетно-графическая
работа № 4

РАСЧЕТ
ПРОЧНОСТИ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК

Общие указания

Задание состоит из двух частей. В первой
части необходимо рассчитать консольную
балку и подобрать из условия прочности
сечение в виде круга и прямоугольника.
Во второй части предлагается рассчитать
двухопорную шарнирную балку, из условия
прочности подобрать сечение в виде
двутавра и сделать полную проверку его
прочности. Перед выполнением работы
необходимо вспомнить раздел: «Плоский
изгиб прямого бруса». Далее приведены
основные теоретические сведения.

Основные
теоретические сведения

Для того чтобы определить внутренние
силовые факторы в произвольном сечении,
необходимо мысленно рассечь балку (рис.
4.1,а) и рассмотреть равновесие одной из
ее частей (рис. 4.1,б).

a

б

Рис. 4.1.

При плоском поперечном изгибе вся
нагрузка расположена в главной плоскости
хOу, поэтому
она не дает проекций сил на осиzих,и моментов относительно осейхиу. Следовательно, отличными
от нуля остаются только величиныQ
yиMz.
Итак, при изгибе в сечении балки действуют
два внутренних силовых фактора:поперечная
силаQyиизгибающий моментМz.

Поперечная сила Qy
равна сумме проекций всех сил,
расположенных по одну сторону от сечения,
на осьу, перпендикулярную оси балки.
Изгибающий моментМzравен сумме моментов всех сил, расположенных
по одну сторону от сечения, относительно
центра тяжести этого сечения. Правило
знаков установлено следующее: поперечная
сила считается положительной, если она
стремится повернуть вырезанный из балки
элемент бесконечно малой длины по ходу
часовой стрелки; изгибающий момент
считается положительным, если он
вызывает растяжение нижних волокон
(рис. 4.2).

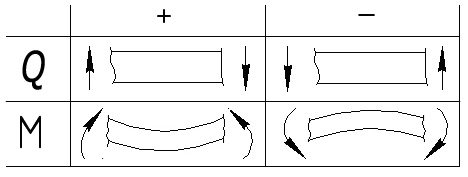
Рис. 4.2.

Примечание:
Необходимо
отметить, что правило знаков для Q
и М не совпадает с правилом знаков для
уравнений статики.

Порядок построения эпюр Qy и мz

  1. Составляются
    уравнения статики, из которых определяются
    величины и направления опорных реакций.

  2. Балка
    разбивается на участки. Участок –
    отрезок стержня, в пределах которого
    нагрузка монотонна, а площадь поперечного
    сечения постоянна.

  3. Для
    каждого участка составляются аналитические
    выражения поперечных сил Qy(х)
    и изгибающихся моментов Мz(х).

  4. По
    полученным выражениям вычисляются
    ординаты эпюр на границах участков.

  5. Определяются
    сечения, в которых действуют моменты
    и вычисляются значения этих моментов.

  6. По
    ординатам и формулам строятся эпюры.
    Анализ дифференциальных зависимостей
    между
    ипозволяет установить некоторые
    особенности эпюр поперечных сил и
    изгибающих моментов.

  7. Участок
    балки – это часть её, в пределах которой
    функции Qy
    и Mz
    непрерывны. Участок ограничен
    сосредоточенными силами или моментами,
    а также началом и концом распределённой
    нагрузки.

  8. На
    участках, где нет распределённой
    нагрузки, поперечная сила Qy
    постоянна, а изгибающий момент Мz
    меняется по линейному закону.

  9. На
    участках, где к балке приложена равномерно
    распределённая нагрузка q,
    поперечная сила Qy
    меняется по линейному закону, а изгибающий
    момент Мz
    – по закону квадратной параболы.

  10. Изгибающий
    момент достигает максимума или минимума
    в сечениях, в которых график Qy
    пересекает нулевую (базисную) линию.
    При этом выпуклость параболы обращена
    в сторону, противоположную направлению
    действия нагрузки q
    –правило «зонтика» (рис. 4.3).

  11. На
    участках, где Qy
    = 0, Мz
    = const – имеет место чистый изгиб.

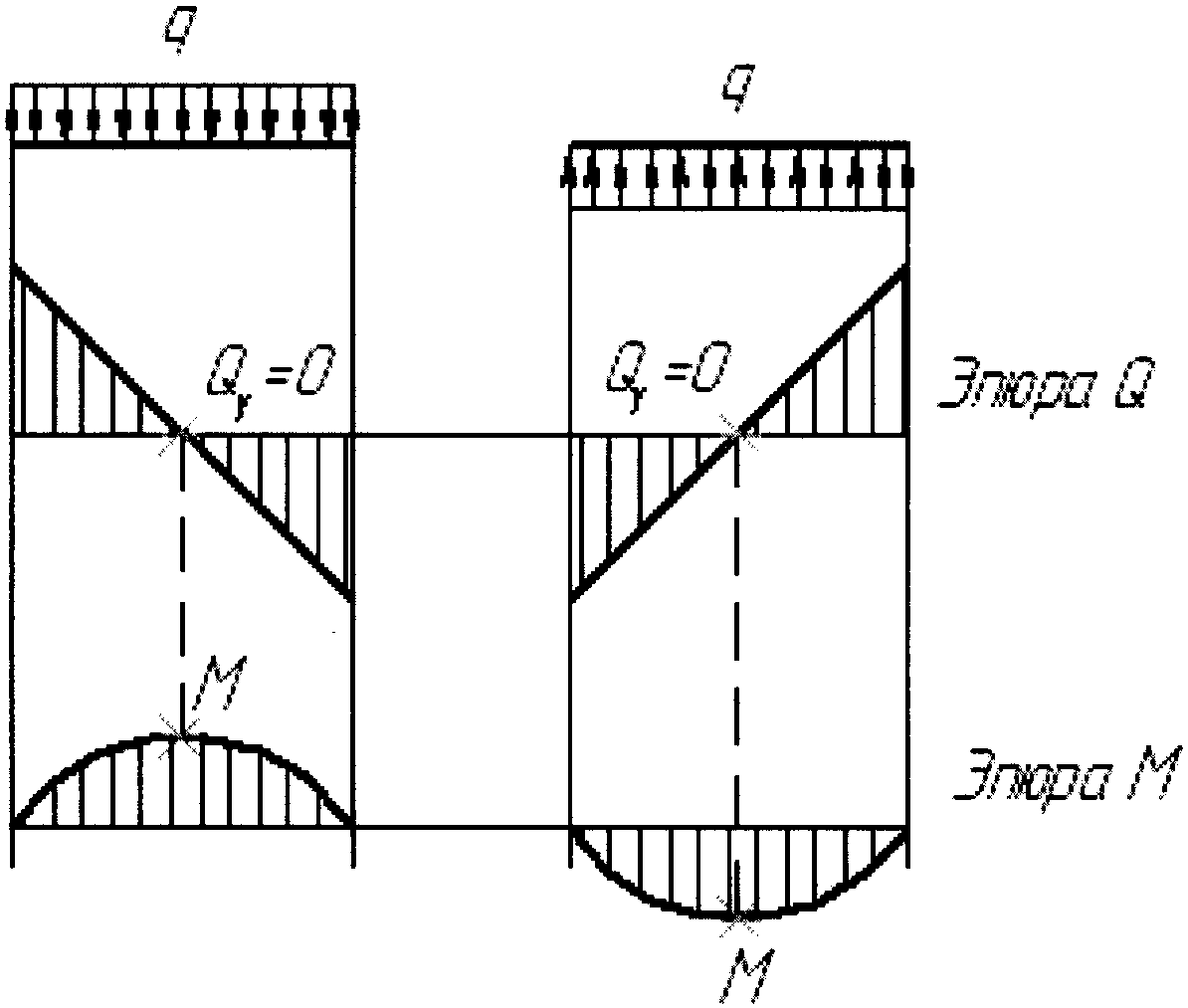
Рис.
4.3.

  1. При
    движении по балке слева направо на
    участках, где Qy
    > 0, изгибающий момент Мz
    возрастает; на участках, где Qy
    < 0, Mz
    – убывает.

  2. В
    сечениях, где к балке приложены
    сосредоточенные силы, на эпюре Q
    будут скачки на величину и в направлении
    приложенных сил, а на эпюре Мz
    будут переломы, причем остриё перелома
    направлено против действия силы.

  3. В
    сечениях, где к балке приложены
    сосредоточенные моменты, на эпюре М
    будут скачки на величину этих моментов
    (на эпюре Q
    изменений не будет). Направление скачка
    зависит от направления внешнего момента.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Для стержневой системы, показанной на рис. 1, из условий прочности и жесткости определить допускаемое значение силы P. Расчетное сопротивление материала стержней R=200Мпа, модуль упругости E=210000Мпа, допускаемое удлинение каждого из стержней [Δ]=2мм, площадь сечения стержня AB , стержня АС .

Решение.

Рассмотрим равновесие узла А. На него действует плоская сходящаяся система сил, для которой можно записать два уравнения равновесия

Из первого уравнения выразими подставим во второе уравнение

Отсюда выразим усилия в стержнях системы через силу P

Оба стержня растянуты. Запишем условия прочности и жесткости для стержня АВ

Длины стержней найдем по теореме синусов

Подставим (3) в (4)

Из этих соотношений найдем два значения для силы P

Аналогично, записывая условия прочности и жесткости для стержня АС,

найдем еще два значения для силы P

Из полученных четырех значений в качестве допускаемой нагрузки следует принять наименьшее значение

Проверим выполнения условий прочности и жесткости. Для стержня АВ:

Для стержня АС:

Все условия выполняются.

Ответ:

Решение этой задачи в среде Mathcad можно посмотреть ЗДЕСЬ

Источник

Определить грузоподъемность (допускаемую нагрузку [F]) шарнирно-стержневой системы для двух случаев:

  1. Если материал стержней пластичный (сталь – 3, [σ]=160 МПа),
  2. Если материал стержней хрупкий (чугун — [σр]=20 МПа, [σс]=80МПа).

2014-09-01 22-25-28 Скриншот экрана

Сначала необходимо найти усилия в стержнях, оставляя нагрузку в общем (буквенном) виде. Начинаем с использования метода сечений: делаем сквозной (замкнутый) разрез и рассматриваем равновесие средней части (неизвестные усилия при этом предполагаем положительными, т.е. растягивающими): 2014-09-01 22-30-21 Скриншот экрана

∑х = Н = 0,       (1)

∑у = R+N1— F–N2=0,    (2)

∑М(А)= N1·1 — F·2 – N2·3=0, (3)

В этих трёх уравнениях статики содержатся 4 неизвестных, следовательно, задача один раз статически неопределима. Для раскрытия статической неопределимости придётся составить одно дополнительное уравнение, но уже не статическое, а геометрическое, которое выражало бы условие совместности деформаций всех упругих элементов системы. С этой целью следует рассмотреть систему в деформированном состоянии с тем, чтобы «связать» друг с другом абсолютные деформации первого и второго стержней. Картина возможной деформации системы:

2014-09-01 22-37-38 Скриншот экрана

Очевидно, что ВВ1 – удлинение первого стержня (∆ℓ1), а СС1 – укорочение второго (∆ℓ2). Из подобия треугольников

2014-09-01 22-40-13 Скриншот экрана

или

2014-09-01 22-44-30 Скриншот экрана

По формуле Гука:

2014-09-01 22-49-05 Скриншот экрана

(знак «плюс» соответствует деформации удлинения), а

2014-09-01 22-50-46 Скриншот экрана

(знак «минус» соответствует деформации укорочения). После подстановки получим необходимое нам дополнительное уравнение:

2014-09-01 22-52-19 Скриншот экрана      (4)

Т.к. ℓ1=2ℓ, ℓ2=ℓ, А1= 2см2, А2= 4см2, то

2014-09-01 22-53-58 Скриншот экрана ,

откуда N2=-12N1. Подставляя это соотношение в уравнение (3), имеем: N1·1- F·2 — (-12N1) 3=0, откуда

2014-09-01 23-03-38 Скриншот экрана(растяжение), и тогда

2014-09-01 23-05-33 Скриншот экрана (сжатие).

Напряжения в стержнях будут:

2014-09-01 23-17-50 Скриншот экрана

Для определения допускаемой нагрузки используем условия прочности при растяжении-сжатии.

Случай 1. Оба стержня из пластичного материала, который одинаково сопротивляется как растяжению, так и сжатию. Для него достаточно одного условия прочности:

|maxσ| ≤ [σ].

Наибольшим по абсолютной величине оказывается напряжение во втором стержне. Его и вводим в условие прочности. Допускаемая нагрузка (или грузоподъёмность) – это такая величина нагрузки, при которой напряжение в точности равно допускаемому значению (т.е. в условии прочности необходимо оставить знак равенства) 2014-09-01 23-20-01 Скриншот экрана

Случай 2. Оба стержня из хрупкого материала. В этом случае требуется выполнение двух условий прочности: а) по растяжению: maxσр ≤ [σр],

б) по сжатию |maxσс| ≤ [σс].

Начинать можно с любого из них. Например, из первого условия: 2014-09-01 23-23-11 Скриншот экрана

найдём одно значение допускаемой нагрузки (по растяжению): 2014-09-01 23-24-37 Скриншот экрана

Если принять это значение за допускаемую нагрузку, то во втором стержне возникает напряжение

2014-09-01 23-26-57 Скриншот экрана

Это напряжение превышает допускаемое значение по сжатию: |σII| =120МПа > [σр]=80МПа, следовательно, нагрузка [Fр] не является допускаемой для всей конструкции. Поэтому будем определять допускаемую нагрузку из второго условия прочности: 2014-09-01 23-28-31 Скриншот экрана Остается лишь убедиться, что при такой нагрузке в первом стержне условие прочности будет выполнено.2014-09-01 23-29-43 Скриншот экрана

что меньше допускаемого по растяжению напряжения [σр]=20МПа. Итак, для варианта стержней из хрупкого материала допускаемая нагрузка [F]=49,333 кН.

Источник

Макеты страниц

Основной задачей расчета конструкции является обеспечение ее прочности в условиях эксплуатации.

Прочность конструкции, выполненной из хрупкого металла, считается обеспеченной, если во всех поперечных сечениях всех ее элементов фактические напряжения меньше предела прочности материала. Величины нагрузок, напряжения в конструкции и предел прочности материала нельзя установить совершенно точно (в связи с приближенностью методики расчета, способов определения предела прочности и т. д.).

Поэтому необходимо, чтобы наибольшие напряжения, полученные в результате расчета конструкции (расчетные напряжения), не превышали некоторой величины, меньшей предела прочности, называемой допускаемым напряжением. Значение допускаемого напряжения устанавливается путем деления предела прочности на величину, большую единицы, называемую коэффициентом запаса.

В соответствии с изложенным условие прочности конструкции, выполненной из хрупкого материала, выражается в виде

где — наибольшие расчетные растягивающие и сжимающие напряжения в конструкции; и [-допускаемые напряжения при растяжении и сжатии соответственно.

Допускаемые напряжения зависят от пределов прочности материала на растяжение и сжатие ствс и определяются выражениями

где – нормативный (требуемый) коэффициент запаса прочности по отношению к пределу прочности.

В формулы (39.2) и (40.2) подставляются абсолютные значения напряжений

Для конструкций из пластичных материалов (у которых пределы прочности на растяжение и сжатие одинаковы) используется следующее условие прочности:

где а — наибольшее по абсолютной величине сжимающее или растягивающее расчетное напряжение в конструкции.

Допускаемое напряжение для пластичных материалов определяется по формуле

где — нормативный (требуемый) коэффициент запаса прочности по отношению к пределу текучести.

Использование при определении допускаемых напряжений для пластичных материалов предела текучести (а не предела прочности, как для хрупких материалов) связано с тем, что после достижения предела текучести деформации могут весьма резко увеличиваться даже при незначительном увеличении нагрузки и конструкции могут перестать удовлетворять условиям их эксплуатации.

Расчет прочности, выполняемый с использованием условий прочности (39.2) или (41.2), называется расчетом по допускаемым напряжениям. Нагрузка, при которой наибольшие напряжения в конструкции равны допускаемым напряжениям, называется допускаемой.

Деформации ряда конструкций из пластичных материалов после достижения предела текучести не возрастают резко даже при существенном увеличении нагрузки, если она не превышает величины так называемой предельной нагрузки. Такими, например, являются статически неопределимые конструкции (см. § 9.2), а также конструкции с элементами, испытывающими деформации изгиба или кручения.

Расчет этих конструкций производят или по допускаемым напряжениям, т. е. с использованием условия прочности (41.2), или по так называемому предельному состоянию. В последнем случае допускаемую нагрузку называют предельно допускаемой нагрузкой, а ее величину определяют путем деления предельной нагрузки на нормативный коэффициент запаса несущей способности. Два простейших примера расчета конструкции по предельному состоянию приведены ниже в § 9.2 и примере расчета 12.2.

Следует стремиться к тому, чтобы допускаемые напряжения были полностью использованы, т. е. удовлетворялось условие если это по ряду причин (например, в связи с необходимостью стандартизации размеров элементов конструкции) не удается, то расчетные напряжения должны как можно меньше отличаться от допускаемых. Возможно незначительное превышение расчетных допускаемых напряжений и, следовательно, некоторое снижение фактического коэффициента запаса прочности (по сравнению с нормативным).

Расчет центрально растянутого или сжатого элемента конструкции на прочность должен обеспечить выполнение условия прочности для всех поперечных сечений элемента. При этом большое значение имеет правильное определение так называемых опасных сечений элемента, в которых возникают наибольшие растягивающие и наибольшие сжимающие напряжения. В тех случаях, когда допускаемые напряжения на растяжение или сжатие одинаковы, достаточно найти одно опасное сечение, в котором имеются наибольшие по абсолютной величине нормальные напряжения.

При постоянной по длине бруса величине продольной силы опасным является поперечное сечение, площадь которого имеет наименьшее значение. При брусе постоянного сечения опасным является то поперечное сечение, в котором возникает наибольшая продольная сила.

При расчет конструкций на прочность встречаются три вида задач, различающихся формой использования условий прочности:

а) проверка напряжений (проверочный расчет);

б) подбор сечений (проектный расчет);

в) определение грузоподъемности (определение допускаемой нагрузки). Рассмотрим эти виды задач на примере растянутого стержня из пластичного материала.

При проверке напряжений площади поперечных сечений F и продольные силы N известны и расчет заключается в вычислении расчетных (фактических) напряжений а в характерных сечениях элементов.

Полученное при этом наибольшее напряжение сравнивают затем с допускаемым:

При подборе сечений определяют требуемые площади поперечных сечений элемента (по известным продольным силам N и допускаемому напряжению ). Принимаемые площади сечений F должны удовлетворять условию прочности, выраженному в следующем виде:

При определении грузоподъемности по известным значениям F и допускаемому напряжению вычисляют допускаемые величины продольных сил: По полученным значениям затем определяются допускаемые величины внешних нагрузок [Р].

Для этого случая условие прочности имеет вид

Величины нормативных коэффициентов запаса прочности устанавливаются нормами. Они зависят от класса конструкции (капитальная, временная и т. п.), намечаемого срока ее эксплуатации, нагрузки (статическая, циклическая и т. п.), возможной неоднородности изготовления материалов (например, бетона), от вида деформации (растяжение, сжатие, изгиб и т. д.) и других факторов. В ряде случаев приходится снижать коэффициент запаса в целях уменьшения веса конструкции, а иногда увеличивать коэффициент запаса — при необходимости учитывать износ трущихся частей машин, коррозию и загнивание материала.

Величины нормативных коэффициентов запаса для различных материалов, сооружений и нагрузок имеют в большинстве случаев значения: — от 2,5 до 5 и — от 1,5 до 2,5.

Коэффициенты запаса прочности, а следовательно, и допускаемые напряжения для строительных конструкций регламентированы соответствующими нормами их проектирования. В машиностроении обычно выбирают требуемый коэффициент запаса прочности, ориентируясь на опыт проектирования и эксплуатации машин аналогичных конструкций. Кроме того, ряд передовых машиностроительных заводов имеет внутризаводские нормы допускаемых напряжений, часто используемые и другими родственными предприятиями.

Ориентировочные величины допускаемых напряжений при растяжении и сжатии для ряда материалов приведены в приложении II.

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
  • § 2.1. РАСЧЕТНАЯ СХЕМА. НАГРУЗКИ
  • § 3.1. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ
  • § 4.1. НАПРЯЖЕНИЯ
  • § 5.1. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ
  • § 6.1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
  • Вопросы для самопроверки
  • Глава 2. РАСТЯЖЕНИЕ И СЖАТИЕ
  • § 1.2. ПРОДОЛЬНАЯ СИЛА
  • § 2.2. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ И НАКЛОННЫХ СЕЧЕНИЯХ БРУСА
  • § 3.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ
  • § 4.2. ДИАГРАММЫ РАСТЯЖЕНИЯ И СЖАТИЯ
  • § 5.2. ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ
  • § 6.2. РАБОТА СИЛЫ ПРИ ЕЕ СТАТИЧЕСКОМ ДЕЙСТВИИ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
  • § 7.2. СОБСТВЕННЫЙ ВЕС БРУСА
  • § 8.2. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. РАСЧЕТЫ НА ПРОЧНОСТЬ
  • § 9.2. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
  • § 10.2. МЕСТНЫЕ НАПРЯЖЕНИЯ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 3. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ
  • § 1.3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ
  • § 2.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
  • § 3.3. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ
  • § 4.3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ
  • § 5.3. ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ С ПОМОЩЬЮ КРУГА МОРА
  • § 6.3. ПОНЯТИЕ О ПРОСТРАНСТВЕННОМ НАПРЯЖЕННОМ СОСТОЯНИИ
  • § 7.3. ОБОБЩЕННЫЙ ЗАКОН ГУКА
  • § 8.3. ОБЪЕМНАЯ ДЕФОРМАЦИЯ
  • § 9.3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 4. СДВИГ
  • § 1.4. ЧИСТЫЙ СДВИГ
  • § 2.4. ДЕФОРМАЦИЯ ПРИ СДВИГЕ. ЗАКОН ГУКА ПРИ СДВИГЕ
  • § 3.4. ОБЪЕМНАЯ ДЕФОРМАЦИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ E, G и «мю»
  • § 4.4. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НЕКОТОРЫХ ПРОСТЕЙШИХ КОНСТРУКЦИЙ, РАБОТАЮЩИХ НА СДВИГ
  • Расчет заклепочных соединений
  • Расчет сварных соединений
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
  • § 2.5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ
  • § 3.5. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЙ
  • § 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЕЧЕНИЙ ПРОСТОЙ ФОРМЫ
  • § 5.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ
  • § 6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
  • § 7.5. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ. ГЛАВНЫЕ ОСИ ИНЕРЦИИ
  • § 8.5. ИССЛЕДОВАНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ С ПОМОЩЬЮ КРУГА МОРА
  • § 9.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 6. КРУЧЕНИЕ
  • § 1.6. ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЙ МОМЕНТ
  • § 2.6. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
  • § 3.6. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
  • § 4.6. РАСЧЕТ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ
  • § 5.6. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ВИНТОВЫХ ПРУЖИН
  • § 6.6. КРУЧЕНИЕ ПРЯМОГО БРУСА НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
  • § 7.6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 7. ПРЯМОЙ ИЗГИБ
  • § 1.7. ВНУТРЕННИЕ УСИЛИЯ
  • § 3.7. ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ
  • § 4.7. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ
  • § 5.7. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ, ПОПЕРЕЧНОЙ СИЛОЙ И ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ
  • § 6.7. ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ
  • § 7.7. ПРЯМОЙ ЧИСТЫЙ ИЗГИБ
  • § 8.7. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ
  • § 9.7. ГЛАВНЫЕ НАПРЯЖЕНИЯ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ
  • § 10.7. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
  • § 11.7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
  • § 12.7. ПОНЯТИЕ О ЦЕНТРЕ ИЗГИБА
  • § 13.7. ПОНЯТИЕ О РАСЧЕТЕ СОСТАВНЫХ БАЛОК
  • § 14.7. ПОНЯТИЕ О БАЛКАХ РАЗНОРОДНОЙ УПРУГОСТИ
  • § 15.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ
  • § 16.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ
  • § 17.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В БАЛКАХ ГРАФО-АНАЛИТИЧЕСКИМ МЕТОДОМ
  • § 18.7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 8. ТЕОРИИ ПРОЧНОСТИ
  • § 1.8. КЛАССИЧЕСКИЕ И ЭНЕРГЕТИЧЕСКАЯ ТЕОРИИ ПРОЧНОСТИ
  • § 2.8. ТЕОРИЯ ПРОЧНОСТИ МОРА
  • § 3.8. ЕДИНАЯ ТЕОРИЯ ПРОЧНОСТИ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 9. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
  • § 1.9. КОСОЙ ИЗГИБ
  • § 2.9. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ БРУСЬЕВ БОЛЬШОЙ ЖЕСТКОСТИ
  • § 3.9. ЯДРО СЕЧЕНИЯ
  • § 4.9. ИЗГИБ С КРУЧЕНИЕМ БРУСЬЕВ КРУГЛОГО СЕЧЕНИЯ
  • § 5.9. ОБЩИЙ СЛУЧАЙ ДЕЙСТВИЯ СИЛ НА БРУС КРУГЛОГО СЕЧЕНИЯ
  • § 6.9. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ ПРОСТРАНСТВЕННЫХ БРУСЬЕВ С ЛОМАНОЙ ОСЬЮ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 10. РАСЧЕТ КРИВЫХ БРУСЬЕВ
  • § 2.10. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ
  • § 3.10. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА БОЛЬШОЙ КРИВИЗНЫ
  • § 4.10. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ ПРИ ЧИСТОМ ИЗГИБЕ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ
  • § 1.11. РАБОТА ВНЕШНИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
  • § 2.11. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ
  • § 3.11. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЯ
  • 4.11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ. ИНТЕГРАЛ МОРА
  • § 5.11. ПРАВИЛО ВЕРЕЩАГИНА
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 12. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ
  • § 1.12. СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ
  • § 2.12. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ
  • § 3.12. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
  • § 4.12. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ
  • § 5.12. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ
  • § 6.12. ПРОВЕРКА ПРАВИЛЬНОСТИ ЭПЮР М, Q И N
  • § 7.12. НЕРАЗРЕЗНЫЕ БАЛКИ
  • ПРИМЕРЫ РАСЧЕТА
  • Вопросы для самопроверки
  • Глава 13. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ
  • § 1.13. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ УПРУГИХ ТЕЛ
  • § 2.13. ПРОДОЛЬНЫЙ ИЗГИБ
  • § 3.13. ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАПРЯЖЕНИЯХ, ПРЕВЫШАЮЩИХ ПРЕДЕЛ ПРОПОРЦИОНАЛЬНОСТИ
  • § 4.13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ
  • § 5.13. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 14. ДИНАМИЧЕСКАЯ НАГРУЗКА
  • § 2.14. ДИНАМИЧЕСКИЕ ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ СТАТИЧЕСКОГО РАСЧЕТА СИСТЕМ
  • § 3.14. УДАР
  • § 4.14. ЧАСТНЫЕ СЛУЧАИ УДАРНОГО ДЕЙСТВИЯ НАГРУЗКИ
  • § 5.14. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 15. НАПРЯЖЕНИЯ, ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ
  • § 1.15. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ. УСТАЛОСТЬ
  • § 2.15. ПРЕДЕЛ ВЫНОСЛИВОСТИ
  • § 3.15. ДИАГРАММЫ ПРЕДЕЛЬНЫХ АМПЛИТУД И ПРЕДЕЛЬНЫХ НАПРЯЖЕНИИ
  • § 4.1. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЕЛИЧИНУ ПРЕДЕЛА ВЫНОСЛИВОСТИ
  • § 5.15. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
  • Примеры расчета
  • Вопросы для самопроверки
  • Глава 16. ТОНКОСТЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ОБОЛОЧКИ И ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ
  • § 1.16. РАСЧЕТ ТОНКОСТЕННЫХ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК
  • § 2.16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • Глава 17. РАСЧЕТ КОНСТРУКЦИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ
  • § 2.17. РАСТЯЖЕНИЕ И СЖАТИЕ
  • § 3.17. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
  • § 4.17. ИЗГИБ БАЛОК
  • § 5.17. МЕТОД РАСЧЕТА КОНСТРУКЦИЙ ПО РАСЧЕТНЫМ ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
  • Примеры расчета
  • Задачи для самостоятельного решения
  • Вопросы для самопроверки
  • ПРИЛОЖЕНИЯ
Источник

Определение – допускаемая нагрузка

Cтраница 2

Данные для определения допускаемой нагрузки. При переменной нагрузке ее режим задается в виде относительных величин крутящих моментов в процентах от номинального крутящего момента, который является искомым.
 [16]

Данные для определения допускаемой нагрузки. Те же данные, что и при проверочном расчете, за исключением величины крутящего момента, которая является искомой. При переменной нагрузке ее режим задается в виде относительных величин крутящих моментов в процентах номинального крутящего момента, который является искомым.
 [17]

Поскольку при определении допускаемой нагрузки размеры поперечного сечения бруса известны, этот расчет следует рассматривать как разновидность проверочного расчета.
 [18]

Таким образом, для определения допускаемой нагрузки необходимо сначала найти величину опасной ( разрушающей) нагрузки Ят. Это можно сделать, воспользовавшись формулой (19.67) или (19.78), если предположить, что предел пропорциональности и предел текучести совпадают. Применяя формулу (19.78), результат можно найти скорее.
 [19]

Таким образом, для определения допускаемой нагрузки необходимо сначала найти величину опасной ( разрушающей) нагрузки Рт. Это можно сделать, воспользовавшись формулой (19.67) или (19.78), если предположить, что предел пропорциональности и предел текучести совпадают. Применяя формулу (19.78), результат можно найти скорее.
 [20]

Таким образом, для определения допускаемой нагрузки необходимо сначала найти величину опасной ( разрушающей) нагрузки / V Это можно сделать, воспользовавшись формулой (20.67) или (20.78), если предположить, что предел пропорциональности и предел текучести совпадают. Применяя формулу (20.78), результат можно найти скорее.
 [21]

Методика и формулы для определения допускаемых нагрузок кабелей с резиновой изоляцией в свинцовой оболочке не отличаются от принятых в расчетах для кабелей с бумажной пропитанной изоляцией в свинцовой оболочке. Удельное тепловое сопротивление резиновой изоляции принимается равным в пределах 500 – 750 тепл. Веред-нем обычно принимают значение удельного теплового сопротивления резины равным 650 тепл.
 [22]

Здесь ставится задача об определении допускаемой нагрузки для бруса двутаврового поперечного сечения. Очень поучительным представляется вопрос об определении опасного поперечного сечения бруса – оно не совпадает с тем, в котором суммарный изгибающий момент максимален.
 [23]

Первый метод дан для случая определения допускаемой нагрузки, когда известны размеры и материалы зубчатых колес и относительный режим нагрузки, но им можно пользоваться и при проектировании новой передачи. Проверочный расчет при использовании этого метода сводится к сравнению фактически действующей нагрузки с допускаемой.
 [25]

Опыт применения теории упругости к определению допускаемых нагрузок на грунт на основе экспериментальных работ ( 1930 г.) и знаменитые Основы динамики грунтовой массы ( 1931 – 1937 гг.); обширная монография Н. П. Пузыревского Фундаменты ( 1934 г.), содержавшая много новых идей и методов расчета; первые в мире учебники Н. А. Цы-товича Основы механики грунтов ( 1934 г.), Н. Н. Иванова и В. В. Охотина Дорожное почвоведение и механика грунтов ( 1934 г.) и И. В. Попова Механика грунтов ( 1937 г.); серия статей Н. Н. Маслова в 1934 – 1936 гг. по вопросам геотехнических исследований, опубликованная в сборниках Свирьстроя; работы в области грунтоведения М. М. Филатова Почвы и грунты в дорожном деле ( 1932 г.) и Основы дорожного грунтоведения ( 1936 г.) и А. Ф. Лебедева Почвенные и грунтовые воды ( 1930 г.) и, наконец, многочисленные исследования их учеников.
 [26]

Предварительный упругий расчет системы при определении допускаемой нагрузки в рассматриваемом методе не обязателен.
 [27]

Многие преподаватели не решают задачи на определение допускаемой нагрузки, так как, вероятно, опыт подсказывает им, что для учащихся задачи этого типа труднее других. Конечно, идти по линии наименьшего сопротивл ения в ущерб знаниям и навыкам учащихся непозволительно. Определение допускаемой нагрузки целесообразно отрабатывать на стержневых системах, при их решении надо составить условие прочности для каждого из двух-четырех стержней, входящих в систему. Продольные силы, возникающие в поперечных сечениях стержней, должны быть на основе метода сечений выражены через внешнюю силу, действующую на систему. Из условий прочности будут определены два ( три или четыре) допускаемых значения силы. Необходимо проверить, что правильный ответ не случаен, учащиеся должны ясно и логично его обосновать.
 [28]

Многие преподаватели не решают задачи на определение допускаемой нагрузки, так как, вероятно, опыт подсказывает им, что для учащихся: задачи этого типа труднее других. Конечно, идти по линии наименьшего сопротивления в ущерб знаниям и навыкам учащихся непозволительно. Определение допускаемой нагрузки целесообразно отрабатывать на стержневых системах, при их решении надо составить условие прочности для каждого из двух-четырех стержней, входящих в систему. Продольные силы, возникающие в поперечных сечениях стержней, должны быть на основе метода сечений выражены через внешнюю силу, действующую на систему. Из условий прочности будут определены два ( три или четыре) допускаемых значения силы. Необходимо проверить, что правильный ответ не случаен, учащиеся должны ясно и логично его обосновать.
 [29]

Статический коэффициент работоспособности подшипника служит для определения допускаемой нагрузки на подшипник при его неподвижном состоянии. Им пользуются для расчета подшипников, оба кольца которых вращаются в одном направлении с одинаковым числом оборотов, для подшипников с качательным движением, а также для подшипников, которые вращаются с очень небольшим числом оборотов. Статический коэффициент работоспособности следует применять и в таких случаях, когда на вращающийся подшипник действуют непродолжительные, но очень большие динамические нагрузки.
 [30]

Страницы:  

   1

   2

   3

   4

Источник

Добавить комментарий