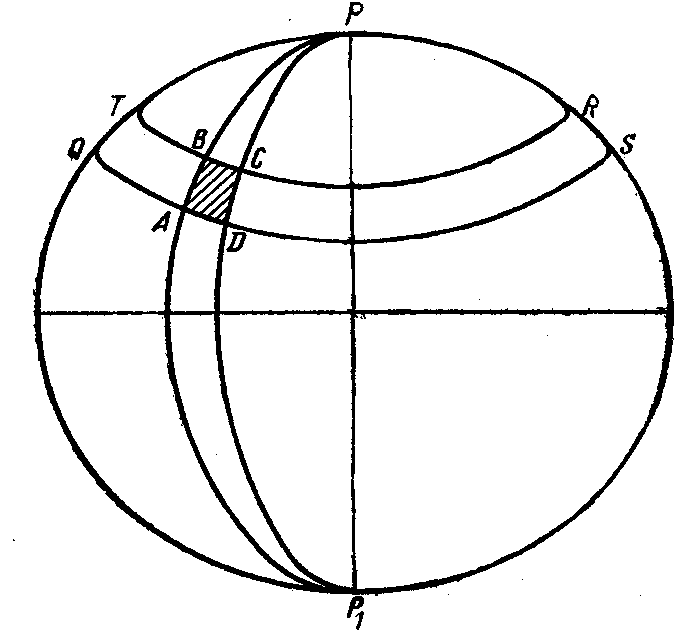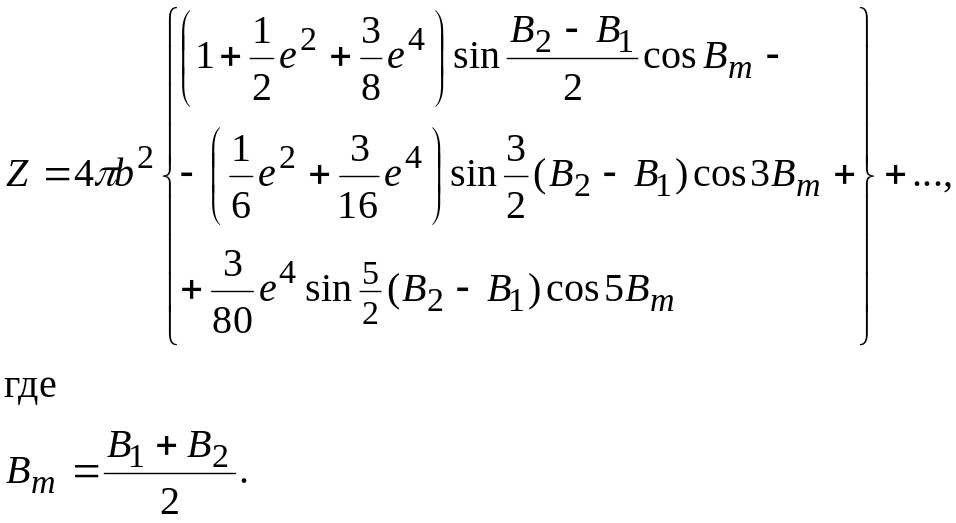Как найти величину дуги меридиана

§ 18.Градусная сетка. Географические координаты

Вы узнаете

•Что такое географическая широта и долгота.

•Как определять географические координаты точки по градусной сетке.

Вспомните

•Одинаковую ли длину имеют параллели и меридианы?

•В каких единицах измеряют углы и дуги окружностей?

Обратитесь к электронному приложению

Градусная сетка. Пересекающиеся параллели и меридианы образуют на глобусах и картах сетку (рис. 53). Каждая «ячейка» сетки состоит из дуг окружностей. Дуги окружностей, как и углы, можно измерять в градусах, поэтому систему параллелей и меридианов называют градусной сеткой. Градусная мера окружности составляет 360°. (Вспомните компас!) Полуокружность — это дуга величиной 180°.

Градусная сетка — это система пересекающихся линий — параллелей и меридианов, которые нанесены на глобус или географическую карту.

С помощью градусной сетки определяют географические координаты точек на земной поверхности: географическую широту и географическую долготу.

Географическая широта. Все параллели, нанесённые на глобус и карты, имеют обозначения в градусах (0°, 10°, 20° и т. д.). На глобусе они подписаны вдоль начального меридиана, на карте полушарий — на круглой рамке карты. Эти числа указывают географическую широту параллелей (рис. 54).

Географическая широта — это величина дуги меридиана в градусах от экватора до заданной точки.

Все точки, лежащие на одной параллели, имеют одинаковую широту. Поскольку географическую широту отсчитывают от экватора, его широта — 0° ш. Значения широты на полюсах — 90° ш.

Все точки, лежащиев Северном полушарии, имеют северную широту (с. ш.), а точки, лежащие в Южном полушарии, — южную широту (ю. ш.).

Географическая долгота. Чтобы определить местоположение какого-либо пункта, недостаточно знать только его широту. Ведь на одной и той же параллели много разных объектов! Поэтому приходится определять географическую долготу (рис. 55).

Географическая долгота — это величина дуги параллели в градусах от начального меридиана до заданной точки.

Все точки, лежащие на одном меридиане, имеют одинаковую долготу. Поскольку географическую долготу отсчитывают от начального (Гринвичского) меридиана, его долгота — 0° д. Поэтому этот меридиан часто называют нулевым. Значения долготы изменяются от 0 до 180°.

Все точки, находящиеся к востоку от начального (нулевого) меридиана, имеют восточную долготу (в. д.), а точки, лежащие к западу от него, — западную долготу (з. д.). Значения долготы в градусах на глобусе и карте полушарий подписывают вдоль экватора у его пересечения с меридианами.

Определение географических координат. Чтобы определить географическую широту объекта, нужно определить параллель, на которой он находится. Например, Санкт-Петербург расположен в Северном полушарии на параллели 60°, поэтому его широта 60° с. ш. А как определить широту, если объект расположен между параллелями? Для этого нужно определить широту ближайшей к объекту параллели со стороны экватора и к ней прибавить число градусов дуги меридиана от этой параллели до объекта. Например, Москва располагается севернее параллели 50°. Число градусов по меридиану между этой параллелью и Москвой равно шести. Значит, географическая широта Москвы будет 56° с. ш.

Так же нужно поступать при определении географической долготы объекта. Если он располагается между двумя меридианами, то сначала узнают долготу ближайшего к объекту меридиана со стороны Гринвича. Затем к ней прибавляют число градусов дуги параллели между этим меридианом и самим пунктом. Например, Москва находится восточнее меридиана 30°. Дуга параллели между меридианом 30° и Москвой составляет 8°. Это значит, что географическая долгота Москвы 38°. Так как город расположен к востоку от нулевого меридиана, его долгота восточная — 38° в. д.

Определение расстояний по градусной сетке. С помощью градусной сетки на географической карте можно определять расстояния. Все меридианы имеют одинаковую длину. Поэтому длины дуг меридианов величиной 1° равны примерно 111 км. А вот длины дуг величиной 1° для разных параллелей неодинаковы — они уменьшаются по направлению от экватора к полюсам. Поэтому для расчётов расстояний используют таблицу значений длин дуг 1° параллелей для разных широт.

Широта, °	0	10	20	30	40	50	60	70	80
Длина 1°, км	111,4	109,6	104,6	96,4	85,4	71,6	55,8	38,2	19,4

ВОПРОСЫ И ЗАДАНИЯ

1.Какие линии составляют градусную сетку? Для чего она служит?

2.Что такое географическая широта; географическая долгота?

3.По рисункам 54 и 55 определите географические координаты Владивостока и Лондона.

4.Определите по карте:

— какие горы протягиваются в Евразии вдоль параллели 30° с. ш.; вдоль меридиана 60° в. д.;

— какие объекты имеют географические координаты 78° с. ш. и 104° в. д.; 35° ю. ш. и 20° в. д.; 66° с. ш. и 170° з. д.; 52° с. ш. и 0° д.; 5° с. ш. и 10° в. д. Нанесите эти объекты на контурную карту;

— географические координаты Лондона, Нью-Йорка, Рио-де-Жанейро.

5.С помощью градусной сетки по карте полушарий определите:

— расстояние (в градусах и километрах) от экватора до места впадения реки Нил в Средиземное море;

— ширину Южной Америки (в градусах и километрах) по параллели 20° ю. ш.

Длина дуги параллели

Этот онлайн калькулятор вычисляет переводит длину дуги параллели на определенной широте из градусов в метры.

Есть у нас калькулятор, вычисляющий длину дуги меридиана в зависимости от широты, а точнее, длину дуги меридиана размером в одну минуту, более известной как морская миля. Для полноты решил написать калькулятор, рассчитывающий размер длины дуги параллели в зависимости от широты. Из достаточно очевидных соображений, чем больше широта, то есть, чем ближе мы к тому или иному полюсу, тем меньше размер дуги, скажем, в 1 градус, в метрах. Калькулятор ниже и считает размер этой дуги на заданной широте по заданному угловому размеру дуги. Для справки, на экваторе размер дуги параллели в один градус будет максимальным (широта равна нулю) и составит 111 км 319 метров (приближенно). Как это считается, описано под калькулятором.

Длина дуги параллели

Длина дуги параллели

Длина дуги параллели

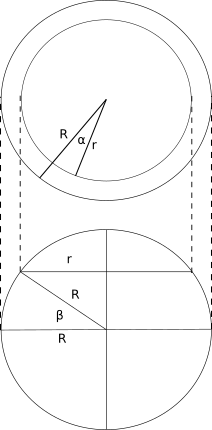
Расчет достаточно простой, и выполняется из общих геометрических соображений. Землю мы конечно приближенно представляем сферой (хотя она геоид).
Чтобы найти длину дуги окружности по углу дуги α, достаточно радиус окружности r умножить на угол дуги в радианах

Для длины дуги в 360 градусов, или 2π радиан, формула превращается в известную всем формула длины окружности

Как видно из рисунка, на определенной широте нас интересует радиус окружности r, полученной при отсечении части сферы плоскостью, параллельной плоскости экватора. На самом экваторе радиус совпадает с радиусом земли R. Выразим интересующий нас радиус через радиус Земли R и заданную широту β:

Соответственно, финальная формула

Ну и в качестве радиуса Земли берем значение, определенное в стандарте WGS-84, а именно, 6378137м. Вот и всё.

Источник

12. Вычисление длины дуги параллели

Параллель на эллипсоиде вращения является окружностью, поэтому вычисление дуги параллели сводится к определению дуги окружности с центральным углом, равным разности долгот конечных точек дуги.

Радиус параллели r определяется по формуле (9.9), которая имеет вид:

. (12.1)

Длина дуги параллели s΄, имеющей широту В и разность долгот конечных точек дуги l, очевидно, дается формулой:

. (12.2)

Отсюда легко получаем разность долгот двух точек параллели под широтой В, расположенных на расстоянии s’,

В табл. 3 приводятся для справок длины дуг параллелей для широт от 30 до 70° на эллипсоиде Красовского.

Длина дуги параллели (м)

П р и м е р. Вычислить длину дуги параллели между точками, лежащими на одной параллели, если даны долготы этих точек и широта параллели.

13. Вычисление площадей съемочных трапеций

Вычисление площади съемочной трапеции или листа карты сводится к определению части поверхности эллипсоида, ограниченной линиями меридианов и параллелей.

Возьмем на эллипсоиде (рис. 13.1) два бесконечно близко расположенных меридиана РВАР₁ и PCDP₁ с долготами l и 1 + dl и две бесконечно близко расположенные параллели TBCR и QADS с широтами В и B+dB, пересечения которых образуют бесконечно малую трапецию АВСD.

Стороны этой трапеции как элементы дуг меридианов и параллелей будут равны:

Площадь элементарной трапеции ABCD выразится формулой:

Площадь dZ всего пояса, ограниченного указанными параллелями, получится, если в формуле для dT величину dl заменить через 2π, т. е

. (13.2)

Площадь поверхности пояса эллипсоида, расположенного между параллелями с широтами B₁ и В₂, будет:

. (13.3)

Для вычисления интеграла (13.3) разложим подинтегральную функцию в ряд по биному Ньютона (интеграл берется и в конечном виде, однако получаемое при этом выражение мало пригодно для вычислений):

Для приведения этой формулы к виду, удобному для практического применения, воспользуемся формулами, дающими выражения синусов нечетных степеней в функции синусов кратных дуг(эти формулы получаются на основе общей формулы:

(13.6)

Заменяя в формуле (13.5) синусы нечетных степеней согласно выражениям (13.6) и подставляя пределы интегрирования, будем иметь:

(13.7)

Заменяя разности синусов по известным формулам тригонометрии, получим:

При разложении выражения (13.4) в ряд члены с е 6 , е 8 и т. д. не были приняты во внимание. Более точная формула для площади пояса, с учетом членов с е 6 , е 8 , будет иметь следующий вид:

Для эллипсоида Красовского эти коэффициенты имеют следующие численные значения:

Формула (13.8) выражает площадь пояса эллипсоида, ограниченного параллелями с широтами В₁ и В₂. Чтобы получить формулы для вычисления площадей трапеций данного масштаба и номенклатуры, берут разность широт северной и южной рамок трапеций B₂ — B₁ и определяют, какую долю площади всего пояса составляет площадь трапеции данного масштаба, причем, очевидно, эта доля определится в зависимости от разности долгот меридианов западной и восточной рамок трапеции.

Например, для государственной карты масштаба 1: 1 000 000 B₂ — B₁ = 4°; разность долгот восточной и западной рамок карты Δl = 6°, т. е. равна 1: 60 от полной окружности пояса. Поэтому рабочая формула для вычисления площадей трапеции масштаба 1: 1 000 000 будет:

(13.10)

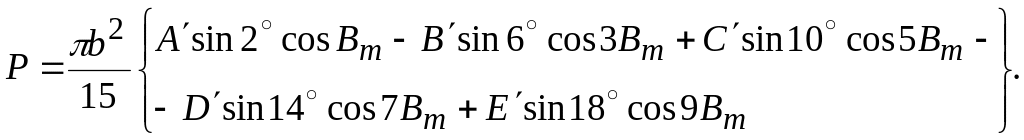
Положив в формуле (13.7) B₁ = 0, B₂ = 90° и удвоив полученное выражение, получим формулу для вычисления площади ∑ всей поверхности эллипсоида с удержанием любого числа членов, так как закон построения членов ряда совершенно ясен:

(13.11)

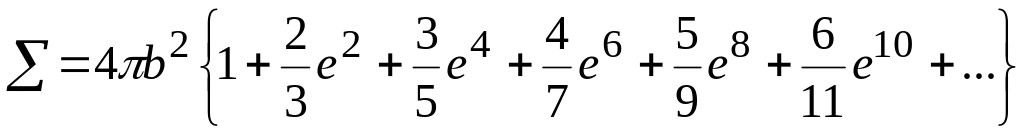
Рассмотрим пример на вычисление площади трапеции масштаба 1: 100 000.

П р и м е р. Вычислить площадь трапеции карты масштаба 1:100 000 N-36-14.

Для площади трапеции карты этого масштаба формула будет иметь следующий вид:

Источник

Чему равен 1 градус по меридиану?

Чему равен 1 градус по параллели?

Длина дуги параллели в 1° по долготе

Принято определение экватора как нулевой параллели. Северный полюс имеет широту +90 градусов, Южный полюс — −90°. Расстояние между двумя параллелями (фактически — дуга меридиана), которые отличаются на 1° по широте, — примерно 111 км.

Как определить длину дуги одного градуса параллели?

Для определения длины одного градуса дуги произвольной параллели нужно умножить 111,3 км (длину дуги экваториальной параллели в 1 градус) на косинус угла, соответствующего искомой параллели.

Сколько километров в одном градусе широты?

Тут все просто: длина окружности (меридиана) постоянна — 40 008,55 км, разделим на 360°, получим: 111,134861111 км в одном градусе, делим на 60 минут: 1,85224768519 км в одной минуте, делим на 60 секунд: 0,0308707947531 км (30,8707947531 м) в одной секунде.

Чему равен 1 градус долготы?

Географическая миля определяется как длина одной минуты дуги вдоль экватора, поэтому длина градуса долготы вдоль экватора составляет ровно 60 географических миль или 111,3 километра.

Чему равен 1 градус на 60 параллели?

Сколько метров в 1 градусе широты? Таким образом, 1 минута широты соответствует 1/21 600 части большой окружности Земли и принимается за 1 морскую (или воздушную) милю. Следовательно, в 1 градусе 60 морских миль. При измерениях на суше расстояние в 1 градус соответствует 69 уставным милям, или 111 км.

Какая длина в километрах 1 градуса дуги экватора?

На картах и глобусах проводят самую большую окружность – экватор, плоскость которого перпендикулярна земной оси. Экватор делит Землю на северное и южное полушария. Длина дуги 1° экватора : 360° = 111,3км.

Сколько метров в 1 градусе долготы?

При измерениях на суше расстояние в 1 градус соответствует 69 уставным милям, или 111 км. Легко рассчитать расстояние между экватором и любой точкой с известной широтой.

Как рассчитать длину дуги меридиана?

Длина дуги меридиана и параллели

Если необходимо вычислить длину дуги меридиана ΔХ =Х2-Х1 , заключенную между двумя точками с широтами, соответственно В2 и В1, то ее получают как разность длин дуг меридианов от экватора до этих точек.

Какое расстояние между двумя меридианами?

Нумерация идет от 0 градусов гринвичского меридиана до 180 градусов — меридиана, проходящего с противоположной стороны Земного шара. В областях близких к экватору расстояние между двумя меридианами, отстоящими друг от друга на один градус, равно 111,1 км.

Сколько градусов в широте?

Широта любой точки экватора равна 0°, северного полюса — +90°, южного полюса — −90°. У всех точек одной параллели широта одинакова. Широты, близкие к экватору, называют «низкими», а близкие к полюсам — «высокими».

Сколько минут в одном географическом градусе?

Окружность разделяется на 360° или 400 градов. Каждый градус делится на 60 минут, каждая из которых состоит из 60 секунд. Географическая система координат состоит из линий широты и долготы.

Сколько метров в одной географической секунде?

Одна секунда вдоль меридиана соответствует примерно 31 м Одна десятая секунды вдоль меридиана соответствует примерно 3,1 м

Сколько минут и секунд в градусе?

Минуты и секунды По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″.

Как определить долготу и широту места?

Значения широты и долготы, как правило, измеряются либо в десятичных градусах, либо в градусах, минутах, секундах (DMS). Значения широты отсчитываются относительно экватора и могут изменяться от 90° на Южном полюсе до +90° на Северном полюсе. Значения долготы отсчитываются относительно нулевого меридиана.

Что такое широта и долгота простыми словами?

Широта обозначает расположение места к северу или югу от экватора, а долгота указывает его положение к западу или востоку. . Отсчет широты оказалось удобно начинать от экватора – самой широкой параллели. Нумерация идет от 0 градусов на экваторе, до 90 градусов на южном и северном полюсах.

Источник

Как определить длину дуги одного градуса параллели?

Чему равна длина дуги одного градуса параллели?

Длина дуги параллели в 1° по долготе

Расстояние между двумя параллелями (фактически — дуга меридиана), которые отличаются на 1° по широте, — примерно 111 км.

Чему равен 1 градус долготы?

Географическая миля определяется как длина одной минуты дуги вдоль экватора, поэтому длина градуса долготы вдоль экватора составляет ровно 60 географических миль или 111,3 километра.

Чему равен 1 градус на карте?

Следовательно, в 1 градусе 60 морских миль. При измерениях на суше расстояние в 1 градус соответствует 69 уставным милям, или 111 км.

Какое расстояние между двумя меридианами?

Нумерация идет от 0 градусов гринвичского меридиана до 180 градусов — меридиана, проходящего с противоположной стороны Земного шара. В областях близких к экватору расстояние между двумя меридианами, отстоящими друг от друга на один градус, равно 111,1 км.

Как можно узнать по карте полушарий длину дуги 1 градуса параллели?

Для определения длины одного градуса дуги произвольной параллели нужно умножить 111,3 км (длину дуги экваториальной параллели в 1 градус) на косинус угла, соответствующего искомой параллели.

Чему равна длина в градусах параллели?

Длина дуг параллелей и меридианов на эллипсоиде Красовского

Широта в градусах	Длина дуги параллели в 1° по долготе, м
1	111305
2	111254
3	111170
4	111052

Сколько 1 градус в КМ?

Тут все просто: длина окружности (меридиана) постоянна — 40 008,55 км, разделим на 360°, получим: 111,134861111 км в одном градусе, делим на 60 минут: 1,85224768519 км в одной минуте, делим на 60 секунд: 0,0308707947531 км (30,8707947531 м) в одной секунде.

Сколько минут в градусе долготы?

Окружность разделяется на 360° или 400 градов. Каждый градус делится на 60 минут, каждая из которых состоит из 60 секунд. Географическая система координат состоит из линий широты и долготы. Каждая линия долготы простирается в направлении «юг-север», определяя число градусов к востоку или западу от нулевого меридиана.

Сколько минут и секунд в градусе?

Минуты и секунды По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″.

Где проходит нулевая параллель?

На глобусе экватор представляет собой окружность. На мировых картах имеет вид прямой линии. Экватор имеет широту 0º. Поэтому её действительно можно назвать нулевой параллелью.

Сколько метров в 1 секунде?

Одна секунда вдоль меридиана соответствует примерно 31 м

Как считается широта и долгота?

Значения широты и долготы, как правило, измеряются либо в десятичных градусах, либо в градусах, минутах, секундах (DMS). Значения широты отсчитываются относительно экватора и могут изменяться от 90° на Южном полюсе до +90° на Северном полюсе.

Как рассчитать длину дуги меридиана?

Длина дуги меридиана и параллели

Если необходимо вычислить длину дуги меридиана ΔХ =Х2-Х1 , заключенную между двумя точками с широтами, соответственно В2 и В1, то ее получают как разность длин дуг меридианов от экватора до этих точек.

Сколько параллелей можно провести на глобусе?

Что касается количества линий, то оно ничем не ограничивается, однако следует помнить, что через любую точку возможно провести лишь один меридиан или одну параллель, за исключением полюсов, где число меридианов не ограничено.

Сколько есть параллелей?

В географии выделяют 5 основных параллелей: Экватор; Северный тропик (тропик Рака); Южный тропик (тропик Козерога);

Источник

Пусть точка А
(рис. 11.1) на меридианном эллипсе имеет
широту В.
Возьмем на бесконечно малом расстоянии
ds
от точки А
точку А₁,
имеющую широту B+dB;
таким образом, разность широт точек А
и А₁
,соответствующая дуге меридиана ds,
будет dB.

Рис.
11.1

Рассматривая
элементарную дугу ds
как дугу окружности с радиусом M,
будем иметь:

ds
= MdB,

или

.

Длина дуги меридиана
между точками, имеющими широты В₁
и В₂,
выразится так:

.
(11.1)

Таким образом,
вычисление длины дуги меридиана сводится
к нахождению эллиптического интеграла
вида

,

который, как
известно, в элементарных функциях не
интегрируется.

Для вычисления
указанного интеграла разложим
подинтегральную функцию

в ряд по биному Ньютона, после чего
почленно произведем интегрирование,
удерживая необходимое число членов.

Разложение дает:

(11.2)

Для простоты
дальнейших выкладок ограничимся членами
с е⁴.
Четные степени синусов, входящих в
разложение функции

,
в ряд, заменим косинусами четных дуг
согласно следующим равенствам:

Теперь формула
(11.2) будет иметь вид:

(11.3)

Обозначая

(11.4),
(11.5)

Подставляя
найденное значение

в (11.1), получим:

.
(11.6)

Интегрируя
почленно, найдем:

.
(11.7)

Полученная формула
является общей для дуги меридиана.
Рассмотрим основные преобразования
формулы (11.7) в зависимости от цели ее
применения.

1.
При вычислении
геодезических таблиц,
например для вычисления таблиц координат
Гаусса, возникает необходимость вычислять
длины дуг меридианов от экватора до
точек дуги, расположенных через
определенные интервалы широты. В этом
случае начальная широта B₁
= 0. Переменной
величиной при вычислении будет широта
B₂
= В, поэтому
формула (11.7) может быть оставлена без
перегруппировки членов. Будем иметь:

(11.8)

Особенностью
этого случая является то, что широта В
может изменяться от 0
до 90°,
длина дуги значительна, и вычисления
следует вести, как правило, с большим
числом членов.

2. При обработке
градусных измерений с целью вывода
размеров земного эллипсоида
формула (11.7) становится неудобной. В
этом случае широты концов измеренных
меридианных дуг, участвующих в обработке
градусных измерений, могут считаться
постоянными; в отличие от предыдущего
случая размеры эллипсоида (или поправки
к некоторым приближенным их значениями
подлежат определению. Поэтому нужно
расположить члены ряда, выражающего
дугу меридиана, так, чтобы около
определяемых величин а,
е²,
е⁴
и т. д. сгруппировать постоянные члены.
Уравнения градусных измерений составляются
обычно по отдельным дугам длиной не
свыше 400 —
600 км, которым
соответствуют разности широт приблизительно
4 — 6°.
Так как эти дуги гораздо короче, чем
дуги, рассматриваемые в первом случае,
то число членов ряда, подлежащих
удержанию, должно быть меньше.

Преобразуем
формулу (11.7), учитывая изложенные
соображения и заменяя разности синусов
через произведения синусов и косинусов
соответствующих углов:

(11.9)

Примем:

(как стоящий при
коэффициенте с е⁴)
и введем среднюю широту дуги В_m
по формуле:

.

Получим:

(11.10)

или

(11.10΄)

Член

,
стоящий в последнем выражении, мал: даже
при s = 2000 км,
что соответствует

,
его значение будет равно

т. е. этим членом
можно пренебречь. Поэтому далее:

,

причем в последнем
выражении отброшены малые члены с е⁶
и е⁴
(B₂
– В₁)².

Делая приведение
подобных членов по возрастающим степеням
е
и выражая разность широт в секундах,
получим окончательно:

(11.11)

3. Для вычислений
в триангуляции,
когда стороны незначительны и редко
превосходят 40-50
км, дадим
более простую и удобную формулу.
Обозначим:

.

Введем вспомогательную
величину:

которая, очевидно,
представляет собою длину дуги окружности
с радиусом, равным радиусу кривизны
меридиана в точке со средней широтой
данной дуги. На основании (11.5) напишем:

Подставляем
значения коэффициентов А,
В, С:

(11.12)

Сравнивая (11.12) с
(11.10′), получим:

Полагая в поправочном
члене последней формулы a(1
— е²)
=M_m,
т. е. пренебрегая членами порядка

s
получим:

.

Окончательная
формула для вычислений в триангуляции
имеет вид:

.
(11.13)

Формула (11.13)
пригодна для расстояний до
400 км (при s
= 400 км допущенная выше погрешность
порядка

даст ошибку в значении s,
равную приблизительно 1 мм).

При s
≤
45 км значение
поправочного члена будет менее
1 мм, поэтому
поправочный член в (11.13) можно отбросить
и вычисления вести по формуле:

(11.14)

Следовательно,
при длине дуги, меньшей 45 км, ее можно
рассматривать как сферическую с
центральным углом, равным разности
широт ее конечных точек, и описанную
радиусом меридианного сечения,
соответствующим средней широте дуги.

На основании
формулы (11.14) можно решить обратную
задачу: зная длину дуги и среднюю широту
ее, определить разность широт конечных
точек
дуги:

.

(11.15)

Практически
нередко приходится решать следующую
задачу. Даны
широта первой точки В₁,
расстояние по дуге меридиана до второй
точки s;
требуется определить широту второй
точки В₂.
Имеем:

B₂=B₁
+
(B₂
–
B₁).

Для определения
(B₂
–
B₁)
воспользуемся
формулой (11.15); однако сразу по этой
формуле искомая разность (B₂
–
B₁)
вычислена
быть не может, так как неизвестна средняя
широта В_m,
по которой должен быть рассчитан радиус
М
или взята из таблиц величина [1]_m
. Рассмотрим решение задачи с применением
метода последовательных приближений.

В первом приближении
вычисляют (B₂
–
B₁),
используя для определения [1]
широту первой точки, и получают
приближенное значение

(B₂
–
B₁)₁
= s[1]₁,

и далее

(B₂)₁
=
B₁
+ (В₂—
В₁)₁.

С этим значением
широты второй точки вычисляют приближенно
среднюю широту

,
используя найденную приближенную
среднюю широту (В_m)₁,
находят разность широт (B₂
— B₁)₂
и среднюю широту (В_m)₂
во втором приближении; далее, аналогично
производят вычисления в третьем
приближении, четвертом и т. д. до тех
пор, пока два смежных приближения не
дадут одинаковые результаты в пределах
заданной точности, которые и будут
окончательными.

При вычислении
длин дуг свыше
45 км формулу
(11.13) употребляют в
логарифмическом виде:

.
(11.16)

Известно, что

,

где х
— малая величина, меньшая единицы, а μ
— переходный модуль от натуральных
логарифмов к десятичным.

Применяя это
разложение к выражению (11.16), получим
формулу для вычисления с помощью
восьмизначных таблиц логарифмов:

.
(11.17)

Используя прежние
обозначения и, кроме того, обозначая

,

получим окончательно:

,
(11.18)

причем последний
член уравнения (11.18) выражен в единицах
8-го десятичного знака логарифма.

Коэффициенты А,
В, С,
которые были, введены ранее при выводе
формул для дуги меридиана, для эллипсоида
Красовского имеют следующие значения:

А =
1,005 051 7739,

В =
0,005 062 37764,

С
= 0,000 010 62451,

D
= 0,000 000 02081.

В табл. 1 приведены
для справок длины дуг меридиана на
эллипсоиде Красовского для некоторых
широт с точностью до 0,1 м.

Таблица 1

B	Длина дуги меридиана (м)
В один градус	В одну минуту	В одну секунду
0°	110 576,3	1842,9	30,7
30°	110 854,4	1847,6	30,8
60°	111 414,1	1856,9	30,9
90°	111 695,8	1861,6	31,0

П р и м е р 1.
Вычислить длину дуги меридиана между
двумя его точками (s
> 45 км),
широты которых равны В₁
= 46°59’10”,315;
В₂
= 48°54’36”,482.

Вычисления
производим по формуле (11.18), т. е.

,

по следующей схеме:

B2	48°54’36”,482 lg(B2 – B1)΄΄	3.8404 9296
B1	46°59’10”,315 lg[1]m	8.5102 3202
B2 – B1	1°55‘26”,167 lgs΄	5.3302 6094
(B2 – B1)΄΄	6926”,167 Δ lgs	-4
Bm	47°56‘53”,4 lgs	5.3302 6090
2Bm	95°53‘47” s	213 924,685 м
lgk	3.932-10 lgμ	9.638-10
lg(B2 – B1)΄΄2	7.681 lg108	8.000-10
lg cos2Bm	9.012-10 lg e2	7.826-10
	доп. lg8	9.097-10
lgΔ lgs	0.624-10 доп. lgρ΄΄2	9.371-20
Δ lgs	– 4.2 lg k	3.932-10

Для контроля длина
той же дуги может быть вычислена по
таблицам для
вычисления
координат Гаусса.
В таблицах приводятся длины дуг меридианов
от экватора -до заданных точек через
одну
минуту.

Искомая длина
дуги меридиана в определится как разность
дуг меридианов
х₂
и х₁
от экватора
до точек с широтами В₂
и В₁.
Указания
о порядке вычислений
дуг
приведены во введении к упомянутым
таблицам.

Если длина дуги
s
≤ 45
км, то, как
следует из формулы (11.14),
вычисление
ведется
по схеме
примера
в его первом и втором столбцах, но без
вычислений поправочного члена.

П
р
и
м
е
р
2.
Вычислить широту В₂
точки 2,
если известна широта В₁
точки 1
и
расстояние s
между
этими точками, лежащими на одном меридиане
(точка 2—севернее
точки 1).

lg
s
= 4.494 2945,
В₁
= 57°24’49”,218.

Задача решается
методом приближений.

1-е приближение

lg s	4.49 429
lg[1]1	8.50 954
lg b”	3.00 383
b	+16‘48”,8
B1	57°24’49”,2
B‘2	57°41‘37”,0

2-е
приближение

B1	57°24’49”,2
½ b	+8.24,4
B΄m	57°33‘13”,6
lg s	4.494 2945
lg[1]m	8.509 5279
lg b”	3.003 8224
b	16‘48”,840
B1	57°24’49”,218
b	+16‘48”,840
B”2	57°41‘38”,058

3-е приближение

B1	57°24’49”,218
½ b	+8.24,420
Bm	57°33‘13”,638

Так как величина
[1]_m,

соответствующая значению широты В_m
полученной для решения задачи в третьем
приближении, будет иметь то же значение,
что и во втором, то в продолжении
вычислений необходимости нет. Искомое
значение широты для точки 2
будет В₂
= 57°41′38”,058.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #

  05.09.2019181.25 Кб3Л1.doc

• #
• #

  05.09.2019249.34 Кб6Л2.doc

• #
• #

  05.09.2019454.66 Кб10Л3.doc

• #
• #

  05.09.2019179.71 Кб11Л4.doc

• #
• #
• #

В первом приближении длина 1 градуса дуги меридиана для всех широт одинакова, что непосредственно следует из факта шарообразности Земли. Собственно, определение метра, как оно было принято Парижской академией наук во время оно, даёт и длину дуги. Коль скоро метр, согласно этому определению, есть одна десятимиллионная четверти дуги Парижского меридиана, а в этой четверти – 90 градусов, то 1 градус – это 111,1(1) км.

Но поскольку Земля – это не точно шар, а немного сплюснута с полюсов (эллипсоид вращения), то длина дуги меридиана несколько меняется при перемещении от полюса к экватору. Таблица длин выглядит так:

0 110579

5 110596

10 110629

15 110676

20 110739

25 110814

30 110898

35 110989

40 111085

45 111182

50 111278

55 111370

60 111455

65 111531

70 111594

75 111643

80 111677

85 111694

Слева широта, справа – длина дуги 1 градуса в метрах.