Как найти угол между плоскостями?
Найти угол между плоскостями можно двумя способами: геометрическим и алгебраическим.
Геометрический способ
При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.
Алгебраический способ
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
Вот такая:
( displaystyle cos gamma =frac{{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}}{sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}})
Здесь ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}) — коэффициенты уравнений плоскостей ( displaystyle alpha ) и ( displaystyle beta ) соответственно.
Подробнее про уравнение плоскости ты можешь прочитать в статье «Расстояние от точки до плоскости»!
( displaystyle alpha ): ( displaystyle {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+D=0)
( displaystyle beta ): ( displaystyle {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+D=0).
Какой же способ лучше? Зависит от задачи.
Если нужно найти, скажем, двугранный угол при основании правильной , то проще использовать геометрический способ.
А если линейный угол двугранного угла никак не хочет проходить ни через какие удобные точки, то можно использовать метод координат как палочку выручалочку.
Но тогда нужно очень твёрдо знать формулы и не делать арифметических ошибок при многочисленных подсчётах – ведь придётся искать ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}), а потом ещё и ( displaystyle cos gamma ).
Давай разберём несложную задачу для примера. Мы применим оба метода к одной и той же задаче.
План урока:
Понятие двугранного угла и угла между плоскостями
Перпендикулярность плоскостей
Прямоугольный параллелепипед
Трехгранный угол
Многогранный угол
Типичные задачи на углы между плоскостями
Понятие двугранного угла и угла между плоскостями
Напомним, что в планиметрии углом называют фигуру, состоящую из точки и двух лучей, выходящих из нее. Сама точка именуется вершиной угла, а лучи – сторонами угла.
По аналогии в стереометрии рассматривается схожая фигура – двугранный угол. Он состоит из двух полуплоскостей, которые исходят из одной прямой. Каждая из этих полуплоскостей именуется гранью двугранного угла, а их общая прямая – это ребро двугранного угла.
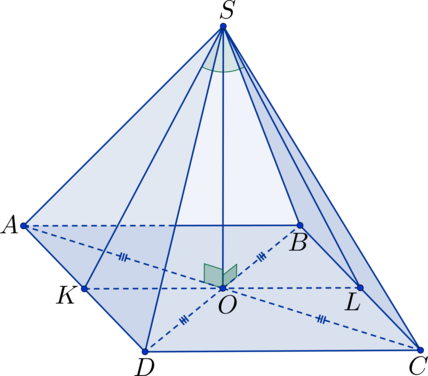
Для обозначения двугранного угла достаточно указать две точки на его ребре, а также ещё по одной точке на каждой грани. Например, на следующем рисунке показан угол САВD:
Двугранные углы часто встречаются в обычной жизни. Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.
Двугранные углы можно измерять. Для этого надо выбрать произвольную точку на ребре угла и на каждой грани построить перпендикуляр, проходящий через эту точку. Через эти два перпендикуляра можно построить единственную плоскость. Угол между двумя перпендикулярами и принимается за величину двугранного угла.
Отдельно отметим, что плоскость, проходящая через перпендикуляры (на рисунке выше это γ) перпендикулярна ребру угла АВ. Это вытекает из признака перпендикулярности прямой и плоскости. Действительно, АВ⊥ВС и АВ⊥BD, поэтому и АВ⊥γ. Построенный угол ∠СBD называют линейным углом двугранного угла.
Понятно, что в каждом двугранном угле можно построить сколько угодно линейных углов:
Здесь помимо ∠ВСD построены линейные углы ∠В’С’D’ и ∠В’’С’’D’’. Однако все эти углы имеют одинаковую градусную меру. Сравним, например, ∠ВСD и ∠В’С’D’. Так как BD⊥AB и B’D’⊥АВ, то BD||B’D’. Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.
Двугранные углы, как и обычные углы, можно разделить на острые (их градусная мера меньше 90°), прямые (они в точности равны 90°) и тупые (которые больше 90°).
Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла. Если среди них есть острый угол, то его величина считается углом между плоскостями. Если же все образуется 4 прямых двугранных угла, то угол между плоскостями принимается равным 90°.
Перпендикулярность плоскостей
В частном случае, когда угол составляет 90°, говорят, что пересекающиеся плоскости перпендикулярны.
Перпендикулярны друг другу пол и стены в доме, смежные грани кубика, стенки коробки. Существует особый признак перпендикулярности плоскостей.
Действительно, пусть плоскости α и β пересекаются по линии n, и в β есть такая прямая m, что m⊥α. Тогда m и n должны пересекаться в какой-нибудь точке К. Проведем в плоскости α через К прямую р, перпендикулярную n. Ясно, что m⊥р, ведь m⊥α. Получается, угол между m и р как раз и является углом между плоскостями α и β, ведь m⊥n и р⊥n. И этот угол равен 90°, ведь m⊥p, ч т. д.
Из доказанного признака вытекает следующее утверждение:
Прямоугольный параллелепипед
Ранее мы уже узнали про параллелепипед. Это фигура с 6 гранями, каждая из которых представляет собой параллелограмм. Особый интерес представляет его частный случай – прямоугольный параллелепипед.
Такую форму имеют многие шкафы, другие предметы мебели, коробки для обуви, небоскребы. Изображают прямоугольный параллелепипед так:
Для обозначения вершин параллелепипеда применяют латинские буквы. Очень часто для вершин одной грани используют 4 буквы без индекса (на рисунке выше это А, В, С, D), а другие 4 вершины обозначают такими же буквами, но с нижним индексом 1: А1, B1, C1 и D1. При этом одноименные вершины (например, А и А1) находятся на одном ребре, которое располагается на рисунке вертикально.
Докажем некоторые свойства прямоугольного параллелепипеда.
Например, ребро АD пересекается с гранями АВВ1А1 и CDD1C1. Значит, оно перпендикулярно этим граням (точнее говоря, оно перпендикулярно плоскостям, проходящим через эти грани). Действительно, AD⊥DC, ведь ∠ADC является углом в прямоугольнике АВСD и потому он прямой. Аналогично и AD⊥DD1, ведь и ADD1A1 – прямоугольник. Получается, что ребро AD перпендикулярно 2 прямым в грани CDD1C1 (которые при этом пересекаются), и потому оно перпендикулярно и всей грани. То же самое можно продемонстрировать для любого ребра прямоугольного параллелепипеда и любой грани, которую она пересекает.
Эти грани пересекаются по ребру А1D1. Этому ребру в свою очередь перпендикулярны ребра АА1 и А1В1, лежащие в гранях ADD1A1 и A1D1C1B1. Значит, ∠АА1В1 и будет углом между этими гранями. Но он составляет 90°, то есть грани перпендикулярны, ч. т. д.
Хотя у прямоугольного параллелепипеда есть 12 граней, многие из них имеют одинаковую длину. Поэтому для описания размеров этой фигуры достаточно указать только три параметра. Обычно их называют длиной, шириной и высотой:
Эти параметры также называют измерениями прямоугольного параллелепипеда. Зная их, можно вычислить длину диагонали прямоугольного параллелепипеда. Для этого используется следующая теорема:
Действительно, пусть есть прямоугольный параллелепипед АВСDA1B1C1D1. Назовем ребро AD его длиной, АВ – шириной, а ВВ1 – высотой. Пусть необходимо найти длину диагонали В1D:
Сначала построим отрезок BD и рассмотрим ∆ABD. Он прямоугольный, и потому для него верна теорема Пифагора:
Теперь перейдем к ∆В1ВD. Так как ребро BB1 перпендикулярно грани ABCD, то ∠В1ВD – прямой. Тогда и ∆В1ВD – прямоугольный, а потому и для него можно записать теорему Пифагора:
Дополнительно отметим уже известный нам факт, что тот прямоугольный параллелепипед, у которого все стороны одинаковы, именуется кубом. Можно дать и такое определение куба:
Трехгранный угол
Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости:
В результате мы получили фигуру, которую именуют трехгранным углом. Она состоит их трех плоских углов: ∠АКС, ∠АКВ и ∠ВКС. Эти углы так и называются – плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС. Обратите внимание, что через каждую пару лучей КА, КВ и КС можно провести плоскость. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани. Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла:
Доказательство. Пусть в пространстве из точки D выходят лучи AD, BD и CD. Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется. Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:
Это возможно сделать, ведь ∠BDC > AD, поэтому внутри ∠BDC можно провести луч DK. Далее «сместим» точку А на луче АD так, чтобы DK = AD. Естественно, что при этом плоские углы трехгранного угла никак не изменятся, также как останется верным равенство
Сравним ∆ADC и ∆DKC. У них есть общая сторона DC, одинаковы стороны DK и AD, а также совпадают углы между ними. Значит, эти треугольники равны, и тогда можно записать, что:
Теперь сравним ∆ABD и ∆DBK. У них BD – общая сторона, а DK = AD. При этом BK < AB. В таком случае против меньшей стороны будет лежать меньший угол (смотри примечание после доказательства), то есть
Именно это неравенство и необходимо было доказать.
Примечание. В ходе доказательства было использовано утверждение, что если у двух треугольников две стороны одинаковы, в третьи стороны отличаются, то против меньшей третьей стороны будет располагаться меньший угол:
Это утверждение часто не рассматривается в курсе планиметрии, поэтому есть смысл доказать его отдельно. Действительно, пусть есть ∆АВС и ∆А’B’C’, АС = А’C’ и АВ = A’B’, а СВ < C’B’. Надо показать, что ∠А <∠A’. Для этого выразим стороны СВ и C’B’ (а точнее говоря, их квадраты) с помощью теоремы косинусов:
Из последнего неравенства на основе определения косинуса для углов из интервала от 0° до 180° вытекает, что и
Многогранный угол
Возможен случай, когда из одной точки в пространстве выходят не три, а большее количество лучей, причем образуемые ими углы не располагаются в единой плоскости. Такая фигура именуется многогранным углом. Трехгранный угол можно считать его частным случаем. Также его частными случаями будут четырехгранный угол, пятигранный угол, шестигранный угол и т. д.
Более наглядна следующая демонстрация многогранного угла. Построим на плоскости α произвольный многоугольник. Далее выберем какую-нибудь точку вне плоскости α и соединим ее с вершинами многоугольника с помощью лучей. При этом у нас как раз получится многогранный угол. Если, например, в качестве многоугольника мы использовали пятиугольник, то и получим мы пятигранный угол:
Важно отметить, что в данном случае состоит многогранный угол именно из лучей КА1, КА2, КА3…, а не из одноименных отрезков. То есть многогранный угол – это ни в коем случае не многогранник КА1А2А3А4А5, у него есть только одна вершина – точка К. Многогранник КА1А2А3А4А5 – это пирамида, такая фигура изучается в курсе стереометрии чуть позже. Многоугольник А1А2А3А4А5 – это сечение многогранного угла. Углы ∠А1КА2, ∠А2КА3, ∠А3КА4… – это плоские углы многогранного угла.
Заметим, что на исходный многоугольник на плоскости может быть как выпуклым, так и невыпуклым. Соответственно и многогранный угол может быть как выпуклым, так и невыпуклым:
Так как любой треугольник – это выпуклый многоугольник, то и любой трехгранный угол является выпуклым. В выпуклом угле все его точки лежат по одну сторону от любой плоскости, проходящей, через какие-нибудь два смежных луча угла. Вообще любое сечение многогранного угла представляет собой выпуклый многоугольник.
Докажем важное утверждение:
Для доказательства возьмем произвольный многогранный угол и проведем в нем сечение А1А2А3…Аn, которое будет являться выпуклым многоугольником:
В последнем равенстве в каждой скобке стоят по два плоских угла в тех трехгранных углах, вершины которых совпадают с вершинами многоугольника А1А2А3…Аn. В предыдущей теореме мы выяснили, что эта сумма меньше третьего плоского угла, то есть
В правой части в скобках стоит сумма углов выпуклого n-угольника А1А2А3…Аn. Она, как мы знаем, составляет 180°•(n – 2), то есть
Последнее неравенство и необходимо было доказать.
Типичные задачи на углы между плоскостями
В школьной практике почти не встречаются задачи с многогранными углами, поэтому достаточно понимания и двугранного угла.
Задание. У тетраэдра ABCD все ребра одинаковы. Найдите величину двугранного угла между плоскостями АВС и АСD.
Решение. Отметим на ребре АС точку М, которая является его серединой:
Заметим, что плоскости АВС и АСD пересекаются по прямой АС. Раз все ребра тетраэдра одинаковы, то ∆АВС и ∆АСD – равносторонние. DM и BM – это медианы в ∆АВС и ∆АСD соответственно, ведь M – середина АС. Но раз треугольники равносторонние, то они одновременно являются и высотами, то есть BM⊥AC и DM⊥АС. Тогда ∠DMB как раз и представляет собой линейный угол двугранного угла BАСD. То есть именно его значение нам и надо вычислить (если, конечно, он окажется не больше 90°).
Пусть ребра тетраэдра имеют длину а. Тогда АМ вдвое короче. Найдем из прямоугольного ∆АМD длину MD:
Задание. Двугранный угол равен φ, меньший 90°. На одной из его граней отмечена точка К, которая находится на расстоянии d от другой грани. Каково расстояние между точкой К и ребром двугранного угла?
Решение. Пусть угол образован плоскостями α и β. Опустим из K два перпендикуляра – один на плоскость β в точку Н, а другой на линию пересечения плоскостей в точку Р:
По условию задачи ∠НРК = φ, а HK = d. Нам же надо найти РК. Это можно сделать, применив определение синуса к ∆РНК:
Задание. Верно ли, что плоскость, пересекающая две параллельные плоскости, образует с ними одинаковые углы?
Решение. Пусть есть параллельные друг другу плоскости α и β, а пересекает их плоскость γ. Линию пересечения α и γ обозначим как n, и такую же линию для β и γ обозначим как m:
Заметим, что m и n располагаются в одной плоскости γ и при этом не пересекаются, в противном случае у α и β нашлась бы общая точка, которой быть не должно. Значит, m||n.
Далее проведем в γ прямую р, перпендикулярную n. Раз m||n и р⊥n, то и р⊥m. То есть р – общий перпендикуляр для m и n.
Далее в α через точку пересечения n и p проведем прямую k, перпендикулярную n. Ясно, что k||β. После уже через точку пересечения m и p построим такую прямую k’, что k||k’:
Так как k||β и k||k’, то прямая k’ будет принадлежать плоскости β (по теореме 6 из этого урока). Так как k||k’, m||n и n⊥k, то по теореме о сонаправленных лучах можно утверждать, что и m⊥k’. Тогда углы, отмеченные на рисунке синим цветом – это и есть линейные углы двугранных углов. Они одинаковы, так как являются соответственными при секущей р и параллельных прямых k и k’. Если же двугранные углы равны, то одинаковы и углы между плоскостями, ч. т. д.
Примечание. Доказанный факт можно сформулировать в виде теоремы:
Она может быть использована при решении некоторых сложных задач.
Задание. В прямоугольном ∆АВС АВ и АС – катеты с длиной 7 и 24 соответственно. Через гипотенузу проведена плоскость β, образующая с плоскостью АВС угол 30°. Каково расстояние между точкой А и плоскостью β?
Решение.
Опустим из А перпендикуляр АН на β. Это и будет искомое нами расстояние. Также в ∆АВС построим высоту AD. Заметим, что раз АН⊥β, то по определению и АН⊥HD. Можно сказать, что HD – это проекция AD на β. Раз прямая ВС перпендикулярна наклонной AD, то она одновременно будет перпендикулярна и наклонной HD по обратной теореме о трех перпендикулярах.
Плоскости АВС и β пересекаются по прямой ВС, АD⊥ВС и HD⊥BC. Получается, что ADH – это как раз угол между АВС и β, и по условию он составляет 30°.
По теореме Пифагора вычислим гипотенузу ВС:
Теперь перейдем к ∆AHD. Он также прямоугольный (∠Н = 90°). Используем для него тригонометрию:
Задание. Известны измерения прямоугольного параллелепипеда. Его длина составляет 90 см, ширина – 20 см, а высота – 60 см. Какова длина диагонали такого параллелепипеда?
Решение. Обозначим измерения буквами а, b, с, а диагональ буквой d. Достаточно просто воспользоваться формулой:
Далее рассмотрим несколько задач, в которых надо найти угол между плоскостями, находящимися в кубе с ребром, чья длина составляет единицу.
Задание. Вычислите угол между гранью ADHЕ и сечением АBGН:
Решение. Заметим, что сечение АВGH содержит прямую АВ. Но АВ – это перпендикуляр к АЕНD. Если АВGH содержит перпендикуляр к ADH, то эти две плоскости перпендикулярны, и угол между ними составляет 90°.
Ответ: 90°.
Задание. Определите угол между гранью ADHE и сечением ADGF:
Решение. Две рассматриваемые плоскости пересекаются по ребру AD. Ребра DH и AD перпендикулярны как стороны квадрата. Так как AD – это перпендикуляр к грани СDHG, то AD⊥DG. Получается, что ∠HDG – это и есть искомый угол. Его величина равна 45°, ведь это угол между диагональю квадрата и его стороной.
Ответ: 45°.
Задание. Вычислите угол между сечениями АВGH и EFCD:
Решение. Пересекаются эти две плоскости по прямой KP, где K и P – точки пересечения диагоналей квадратов BFGH и AEHD. Докажем, что отрезки KG и KC перпендикулярны KP.
Действительно, рассмотрим четырехугольник АВGH. Ребра АВ и GH перпендикулярны граням AEHD и BFGH, поэтому все углы в АВGH – прямые, то есть это прямоугольник и BG||AH. Теперь рассмотрим четырехугольник АВKP. Стороны BK и AP параллельны и равны как половины равных отрезков BG и AH. Значит, BKAP – параллелограмм. Но в нем есть прямые углы ∠В и ∠А, поэтому BKAP – прямоугольник. Аналогично можно показать, что и KGHP – прямоугольник. Это и приводит к выводу о том, что KG⊥KP и PH⊥KP. Поэтому ∠СKG и является искомым углом между сечениями. Он является углом между диагоналями квадрата, то есть равен 90°.
Ответ: 90°.
Задание. Найдите угол между сечением AFH и гранью AEHD:
Решение. Обозначим середину диагонали AH буквой K. Докажем ∠EKF – искомый нами угол:
Действительно, плоскости AHD и AFH пересекаются по прямой AH. EK – медиана в равнобедренном ∆AEH с основанием AH, поэтому она также является и высотой, то есть EK⊥AH. AF и FH – диагонали в равных квадратах ABFE и EFGH, поэтому эти диагонали одинаковы. Значит, ∆AFH – равнобедренный, и поэтому его медиана FK также перпендикулярна основанию AH. Получается, что ∠EKF и является искомым. Вычислить его можно из ∆EKF.
Сначала найдем длину EK. В прямоугольном ∆AEK ∠KAE составляет 45° (угол между диагональю и стороной квадрата), поэтому
Задание. Вычислите угол между гранью BCGF и сечением AFH:
Решение. Вспомним, что в предыдущей задаче мы уже вычислили угол между гранью АЕHD и тем же сечением АFH. Но грани AEHD и BCFG параллельны, поэтому АFH должна пересекаться их под одним и тем же углом. Поэтому ответ этой задачи совпадает с ответом к предыдущей задаче.
Ответ: ≈ 54,74°.
Задание. Чему равен угол между сечениями АСH и AFGH?
Решение. Пусть диагонали СН и DG пересекаются в точке К. Точка K будет принадлежать обоим сечениям, как и точка А. Значит, сечения пересекаются по линии АК. Проведем в сечении AFGH через точку K прямую, перпендикулярны АК и пересекающую FG в какой-то точке Р (позже мы убедимся, что прямая действительно должна пересекать отрезок FG):
Докажем, что ∠CPK и является углом между сечениями. Мы специально провели РК так, что РК⊥АК. Теперь посмотрим на ∆АСН. Он равносторонний, ведь его стороны АС, СН и DH – это диагонали равных квадратов (граней куба). Прямая АК – медиана, ведь K – точка пересечения диагоналей квадрата СDHG, которая делит диагонали пополам. Но раз ∆АСН равносторонний, то его медиана – это ещё и высота, то есть АК⊥РК. Итак, АК⊥СК и АК⊥РК, поэтому ∠CPK – это угол между сечениями. Для его вычисления необходимо найти все стороны в ∆РСК и далее применить теорему косинусов.
Проще всего найти СК. ∆СKD – прямоугольный (∠К = 90°), а ∠СDK составляет 45° (угол между стороной и диагональю в квадрате). Тогда можно записать, что
Отдельно отметим, что отрезки GK и KD имеют такую же длину, ведь диагонали в квадрате (а значит и их половины) одинаковы.
Для нахождения РК покажем отдельно плоскость AFG, то есть красное сечение:
Обозначим ∠KAD как φ. Тогда ∠АКD будет составлять 90 – φ. Углы ∠АКD, ∠АKP и ∠PKG в сумме дают 180°, что позволяет найти ∠PKG:
Получилось, что у ∆АКD и ∆PKG есть по два одинаковых угла (φ и 90°). Значит, они подобны. Составим такую пропорцию:
Теперь можно вернуться ко всему кубу и найти отрезок РС. Здесь снова можно применить теорему Пифагора, но уже к ∆PCG:
Теперь для ∆PCK мы можем записать теорему косинусов
Неожиданно мы доказали, что два построенных сечения перпендикулярны друг другу. Прийти к этому выводу можно было и иначе. Достаточно было бы показать, что прямая CH – это перпендикуляр к сечению AFGD. Попробуйте сделать это самостоятельно.
Ответ: 90°.
Задание. Вычислите угол между сечениями BDHF и ADGF:
Решение. У сечений общими являются точки F и D. Значит, именно по прямой FD они пересекаются.
Опустим в синей сечении BDHF перпендикуляр на FD, который упадет в некоторую точку K:
Докажем, что отрезок GK также перпендикулярен FD. Действительно, BK – это высота в ∆BDF. Но ∆BDF и ∆GDF равны, ведь они одинаковы все три стороны (FD – общая сторона, BF и FG – ребра куба, BD и DG – диагонали на гранях куба). В равных треугольниках высоты должны делить стороны на равные отрезки, поэтому высота, опущенная из G на FD, также разделит FD на отрезки FK и KD. То есть она просто упадет в точку K. Это и значит, что KG – высота. Получается, что нам надо вычислить ∠BKG.
Сначала найдем длину диагоналей BD и BG. Можно применить теорему Пифагора для ∆BFG:
KG имеет ту же длину, ведь KG и BK – одинаковые высоты в равных треугольниках ∆BDF и ∆GDF.
Теперь используем теорему косинусов для ∆BKG:
Мы вычислили двугранный угол, но он оказался больше 90°. Это значит, угол между плоскостями равен не 120°, а 180° – 120°, то есть 60°.
Ответ: 60°.
Сегодня мы познакомились с понятием двугранного угла, научились вычислять углы между плоскостями. В частном случае вместо вычисления угла можно просто доказать перпендикулярность плоскостей.
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между плоскостями (двугранный угол)
(blacktriangleright) Двугранный угол – угол, образованный двумя полуплоскостями и прямой (a), которая является их общей границей.
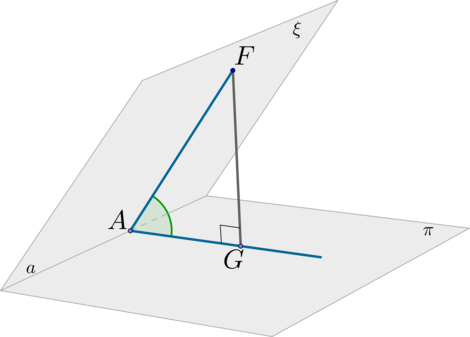
(blacktriangleright) Чтобы найти угол между плоскостями (xi) и (pi), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями (xi) и (pi):
Шаг 1: пусть (xicappi=a) (линия пересечения плоскостей). В плоскости (xi) отметим произвольную точку (F) и проведем (FAperp
a);
Шаг 2: проведем (FGperp pi);
Шаг 3: по ТТП ((FG) – перпендикуляр, (FA) –наклонная, (AG) – проекция) имеем: (AGperp a);
Шаг 4: угол (angle FAG) называется линейным углом двугранного угла, образованного плоскостями (xi) и (pi).
Заметим, что треугольник (AG) – прямоугольный.
Заметим также, что плоскость (AFG), построенная таким образом, перпендикулярна обеим плоскостям (xi) и (pi). Следовательно, можно сказать по-другому: угол между плоскостями (xi) и (pi) — это угол между двумя пересекающимися прямыми (cin xi) и (binpi), образующими плоскость, перпендикулярную и (xi), и (pi).
Задание
1
#2875
Уровень задания: Сложнее ЕГЭ
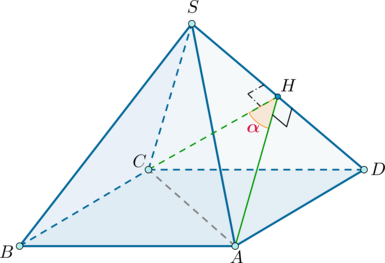
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите (6cos alpha), где (alpha) – угол между ее смежными боковыми гранями.
Пусть (SABCD) – данная пирамида ((S) – вершина), ребра которой равны (a). Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями (SAD) и (SCD).
Проведем (CHperp SD). Так как (triangle SAD=triangle SCD), то (AH) также будет высотой в (triangle SAD). Следовательно, по определению (angle AHC=alpha) – линейный угол двугранного угла между гранями (SAD) и (SCD).
Так как в основании лежит квадрат, то (AC=asqrt2). Заметим также, что (CH=AH) – высота равностороннего треугольника со стороной (a), следовательно, (CH=AH=frac{sqrt3}2a).
Тогда по теореме косинусов из (triangle AHC): [cos alpha=dfrac{CH^2+AH^2-AC^2}{2CHcdot AH}=-dfrac13 quadRightarrowquad
6cosalpha=-2.]
Ответ: -2
Задание
2
#2876
Уровень задания: Сложнее ЕГЭ
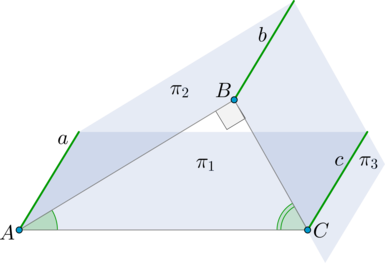
Плоскости (pi_1) и (pi_2) пересекаются под углом, косинус которого равен (0,2). Плоскости (pi_2) и (pi_3) пересекаются под прямым углом, причем линия пересечения плоскостей (pi_1) и (pi_2) параллельна линии пересечения плоскостей (pi_2) и (pi_3). Найдите синус угла между плоскостями (pi_1) и (pi_3).
Пусть линия пересечения (pi_1) и (pi_2) – прямая (a), линия пересечения (pi_2) и (pi_3) – прямая (b), а линия пересечения (pi_3) и (pi_1) – прямая (c). Так как (aparallel b), то (cparallel aparallel b) (по теореме из раздела теоретической справки “Геометрия в пространстве” (rightarrow) “Введение в стереометрию, параллельность”).
Отметим точки (Ain a, Bin b) так, чтобы (ABperp a, ABperp b) (это возможно, так как (aparallel b)). Отметим (Cin c) так, чтобы (BCperp c), следовательно, (BCperp b). Тогда (ACperp c) и (ACperp a).
Действительно, так как (ABperp b, BCperp b), то (b) перпендикулярна плоскости (ABC). Так как (cparallel aparallel b), то прямые (a) и (c) тоже перпендикулярны плоскости (ABC), а значит и любой прямой из этой плоскости, в частности, прямой (AC).
Отсюда следует, что (angle BAC=angle (pi_1, pi_2)), (angle
ABC=angle (pi_2, pi_3)=90^circ), (angle BCA=angle (pi_3,
pi_1)). Получается, что (triangle ABC) прямоугольный, а значит [sin angle BCA=cos angle BAC=0,2.]
Ответ: 0,2
Задание
3
#2877
Уровень задания: Сложнее ЕГЭ
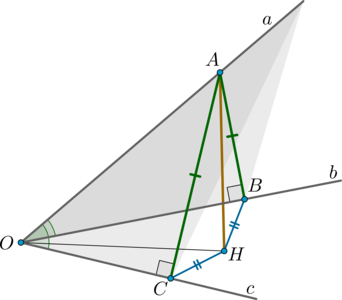
Даны прямые (a, b, c), пересекающиеся в одной точке, причем угол между любыми двумя из них равен (60^circ). Найдите (cos^{-1}alpha), где (alpha) – угол между плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Ответ дайте в градусах.
Пусть прямые пересекаются в точке (O). Так как угол между любыми двумя их них равен (60^circ), то все три прямые не могут лежать в одной плоскости. Отметим на прямой (a) точку (A) и проведем (ABperp
b) и (ACperp c). Тогда (triangle AOB=triangle AOC) как прямоугольные по гипотенузе и острому углу. Следовательно, (OB=OC) и (AB=AC).
Проведем (AHperp (BOC)). Тогда по теореме о трех перпендикулярах (HCperp c), (HBperp b). Так как (AB=AC), то (triangle
AHB=triangle AHC) как прямоугольные по гипотенузе и катету. Следовательно, (HB=HC). Значит, (OH) – биссектриса угла (BOC) (так как точка (H) равноудалена от сторон угла).
Заметим, что таким образом мы к тому же построили линейный угол двугранного угла, образованного плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Это угол (ACH).
Найдем этот угол. Так как точку (A) мы выбирали произвольно, то пусть мы выбрали ее так, что (OA=2). Тогда в прямоугольном (triangle AOC): [sin 60^circ=dfrac{AC}{OA}
quadRightarrowquad AC=sqrt3 quadRightarrowquad
OC=sqrt{OA^2-AC^2}=1.] Так как (OH) – биссектриса, то (angle
HOC=30^circ), следовательно, в прямоугольном (triangle HOC): [mathrm{tg},30^circ=dfrac{HC}{OC}quadRightarrowquad HC=dfrac1{sqrt3}.] Тогда из прямоугольного (triangle ACH): [cosangle alpha=cosangle ACH=dfrac{HC}{AC}=dfrac13 quadRightarrowquad
cos^{-1}alpha=3.]
Ответ: 3
Задание
4
#2910
Уровень задания: Сложнее ЕГЭ
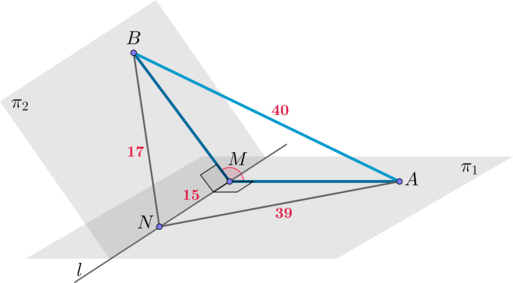
Плоскости (pi_1) и (pi_2) пересекаются по прямой (l), на которой лежат точки (M) и (N). Отрезки (MA) и (MB) перпендикулярны прямой (l) и лежат в плоскостях (pi_1) и (pi_2) соответственно, причем (MN = 15), (AN = 39), (BN = 17), (AB = 40). Найдите (3cosalpha), где (alpha) – угол между плоскостями (pi_1) и (pi_2).
Треугольник (AMN) прямоугольный, (AN^2 = AM^2 + MN^2), откуда [AM^2 = 39^2 – 15^2 = 36^2.] Треугольник (BMN) прямоугольный, (BN^2 = BM^2 + MN^2), откуда [BM^2 = 17^2 – 15^2 = 8^2.] Запишем для треугольника (AMB) теорему косинусов: [AB^2 = AM^2 + MB^2 – 2cdot AMcdot MBcdotcosangle AMB.] Тогда [40^2 = 36^2 + 8^2 – 2cdot 36cdot 8cdotcosangle AMBqquadLeftrightarrowqquad cosangle AMB = -dfrac{5}{12}] Так как угол (alpha) между плоскостями – это острый угол, а (angle AMB) получился тупым, то (cosalpha=dfrac5{12}). Тогда [3cosalpha = dfrac54=1,25.]
Ответ: 1,25
Задание
5
#2911
Уровень задания: Сложнее ЕГЭ
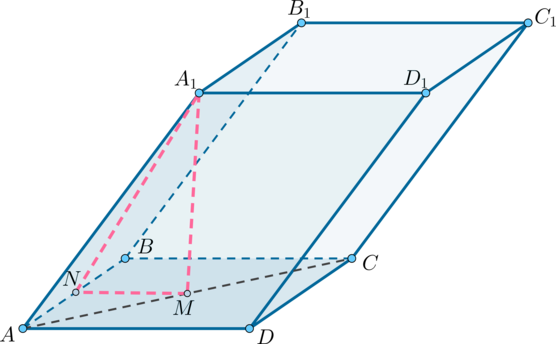
(ABCDA_1B_1C_1D_1) – параллелепипед, (ABCD) – квадрат со стороной (a), точка (M) – основание перпендикуляра, опущенного из точки (A_1) на плоскость ((ABCD)), кроме того (M) – точка пересечения диагоналей квадрата (ABCD). Известно, что (A_1M = dfrac{sqrt{3}}{2}a). Найдите угол между плоскостями ((ABCD)) и ((AA_1B_1B)). Ответ дайте в градусах.
Построим (MN) перпендикулярно (AB) как показано на рисунке.
Так как (ABCD) – квадрат со стороной (a) и (MNperp AB) и (BCperp AB), то (MNparallel BC). Так как (M) – точка пересечения диагоналей квадрата, то (M) – середина (AC), следовательно, (MN) – средняя линия и (MN =frac12BC= frac{1}{2}a).
(MN) – проекция (A_1N) на плоскость ((ABCD)), причем (MN) перпендикулярен (AB), тогда по теореме о трех перпендикулярах (A_1N) перпендикулярен (AB) и угол между плоскостями ((ABCD)) и ((AA_1B_1B)) есть (angle A_1NM).
[mathrm{tg}, angle A_1NM = dfrac{A_1M}{NM} = dfrac{frac{sqrt{3}}{2}a}{frac{1}{2}a} = sqrt{3}qquadRightarrowqquadangle A_1NM = 60^{circ}]
Ответ: 60
Задание
6
#1854
Уровень задания: Сложнее ЕГЭ
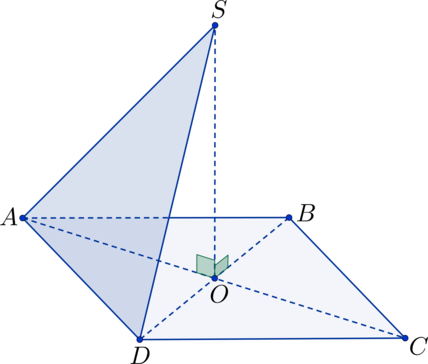
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (ABC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO) и (triangle SDO) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = 90^circ); (AO = DO), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = SD) (Rightarrow) (triangle ASD) – равнобедренный. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскостям (ASD) и (ABC) (Rightarrow) (angle SKO) – линейный угол, равный искомому двугранному углу.
В (triangle SKO): (OK = frac{1}{2}cdot AB = frac{1}{2}cdot 10 = 5 = SO) (Rightarrow) (triangle SOK) – равнобедренный прямоугольный треугольник (Rightarrow) (angle SKO = 45^circ).
Ответ: 45
Задание
7
#1855
Уровень задания: Сложнее ЕГЭ
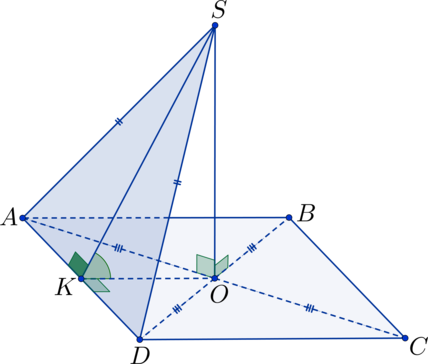
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (BSC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO), (triangle SDO), (triangle SOB) и (triangle SOC) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = angle SOB = angle SOC = 90^circ); (AO = OD = OB = OC), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = DS = BS = CS) (Rightarrow) (triangle ASD) и (triangle BSC) – равнобедренные. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскости (ASD). Точка (L) – середина (BC), тогда (SL) – высота в треугольнике (triangle BSC), а (OL) – высота в треугольнике (BOC) (Rightarrow) плоскость (SOL) (она же плоскость (SOK)) перпендикулярна плоскости (BSC). Таким образом получаем, что (angle KSL) – линейный угол, равный искомому двугранному углу.
(KL = KO + OL = 2cdot OL = AB = 10) (Rightarrow) (OL = 5); (SK = SL) – высоты в равных равнобедренных треугольниках, которые можно найти по теореме Пифагора: (SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50). Можно заметить, что (SK^2 + SL^2 = 50 + 50 = 100 = KL^2) (Rightarrow) для треугольника (triangle KSL) выполняется обратная теорема Пифагора (Rightarrow) (triangle KSL) – прямоугольный треугольник (Rightarrow) (angle KSL = 90^circ).
Ответ: 90
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
-
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.
-
Вначале необходимо определить прямую, по которой пересекаются плоскости.
-
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.
-
Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.
-
Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.

УСТАЛ? Просто отдохни
На этой странице вы узнаете
- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Углы между плоскостями
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
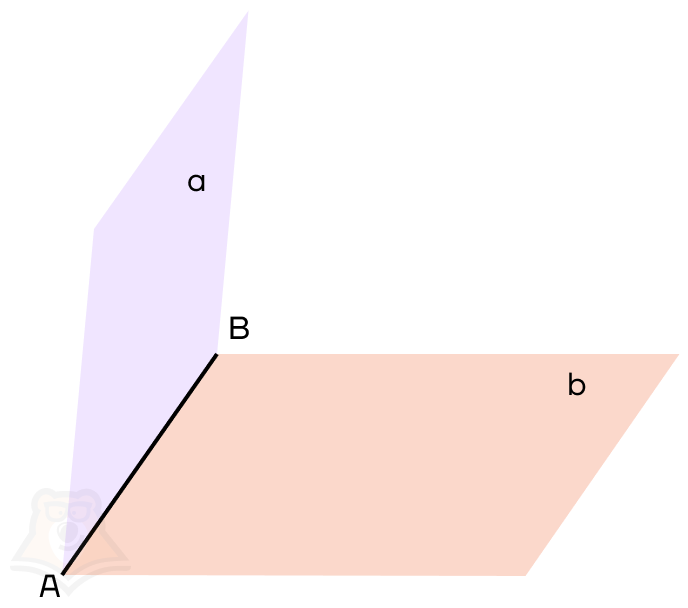
Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
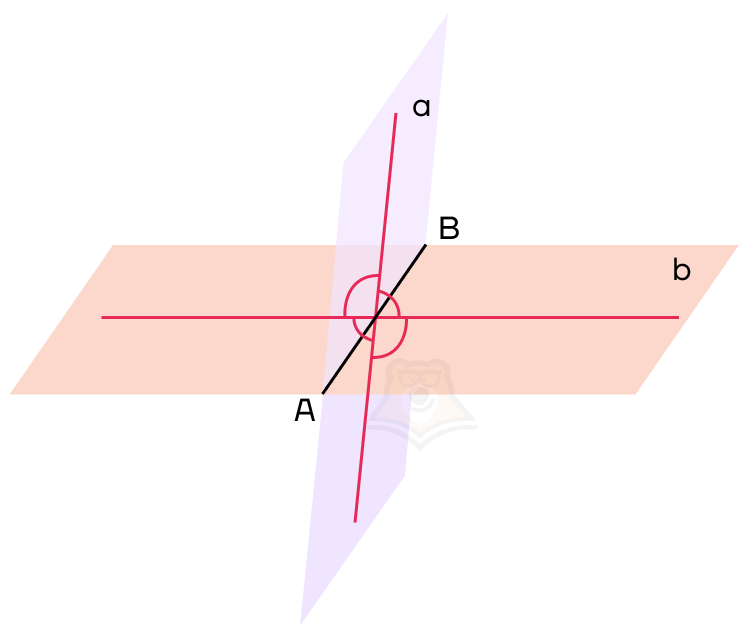
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
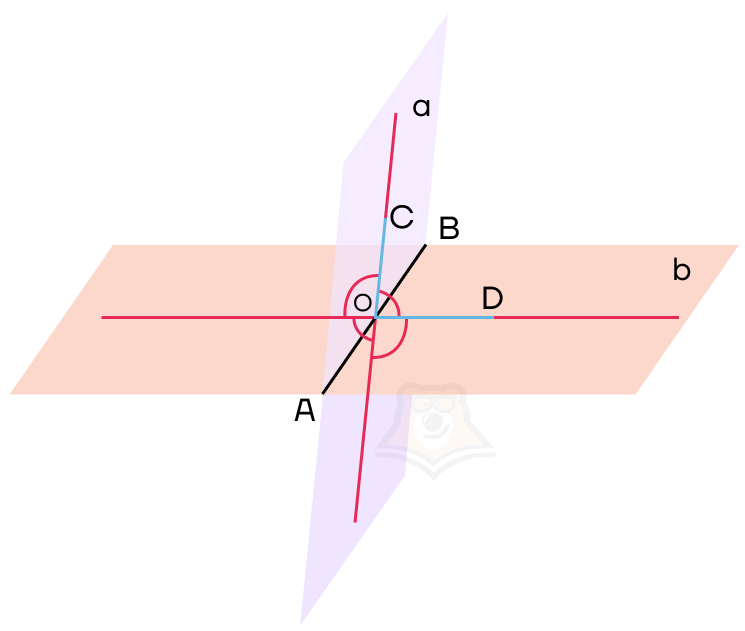
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
Как и обычные углы, углы между плоскостями бывают трех видов:
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
А что будет, если между плоскостями получится прямой угол?
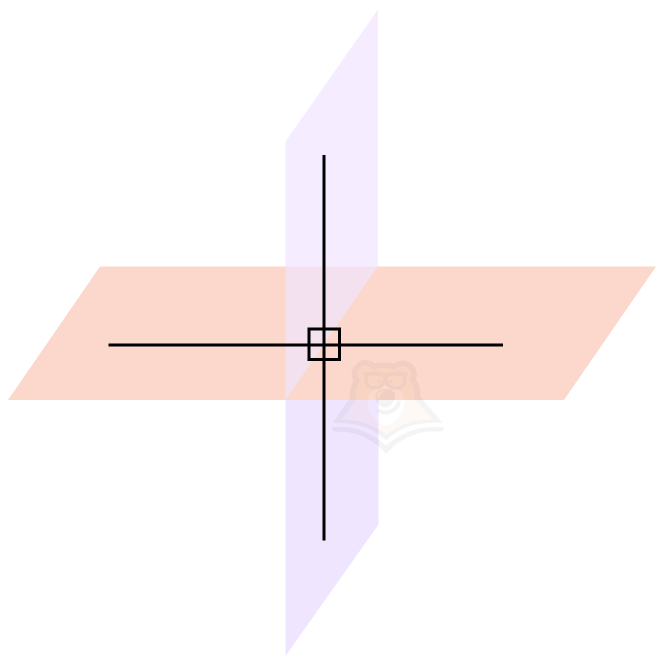
Такие плоскости называются перпендикулярными.
Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.
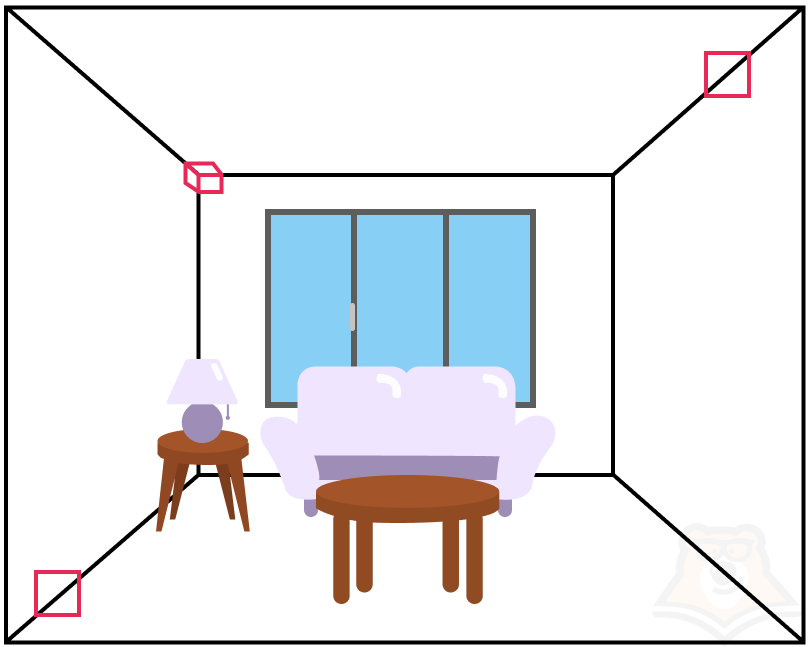
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
1 шаг. Найти линию пересечения плоскостей.
2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости.
3 шаг. Найти острый угол между построенными перпендикулярами.
Углы между прямой и плоскостью
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
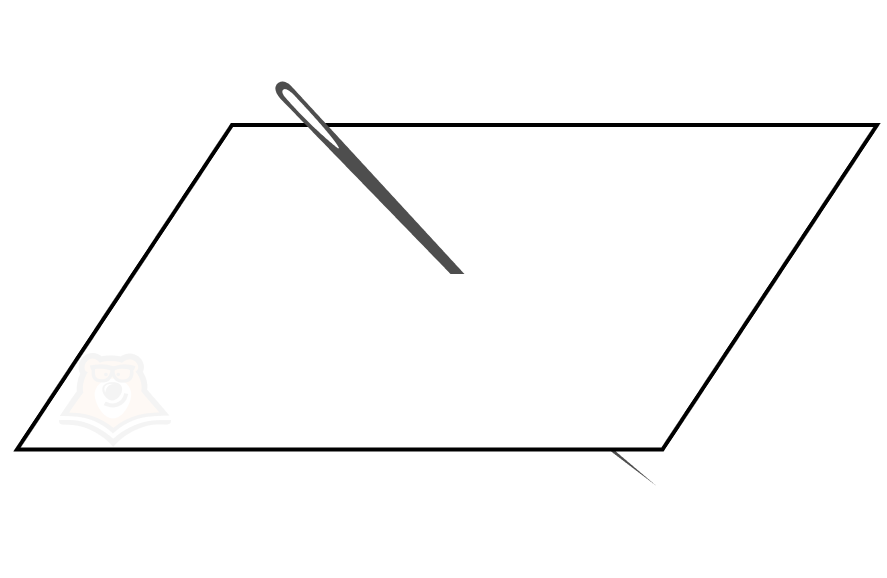
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
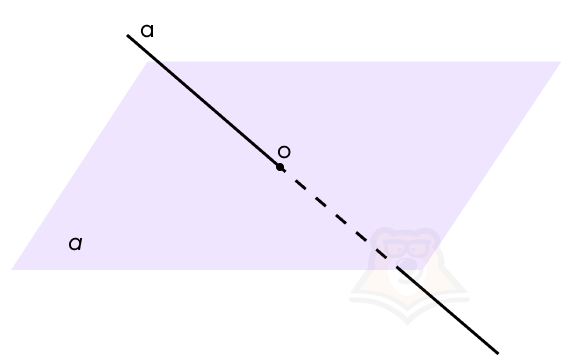
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.
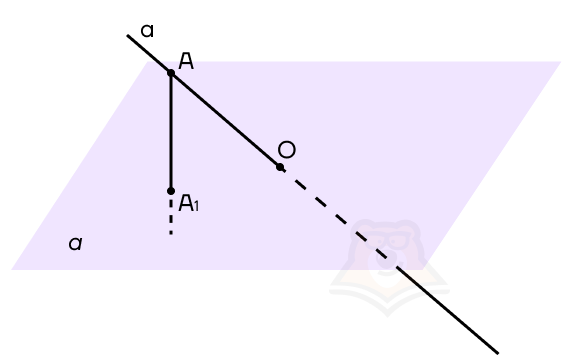
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
Шаг 1. Построить проекцию прямой на плоскость.
Шаг 2. Найти угол между прямой и построенной проекцией.
Если прямая параллельна плоскости угол будет равен 0.
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
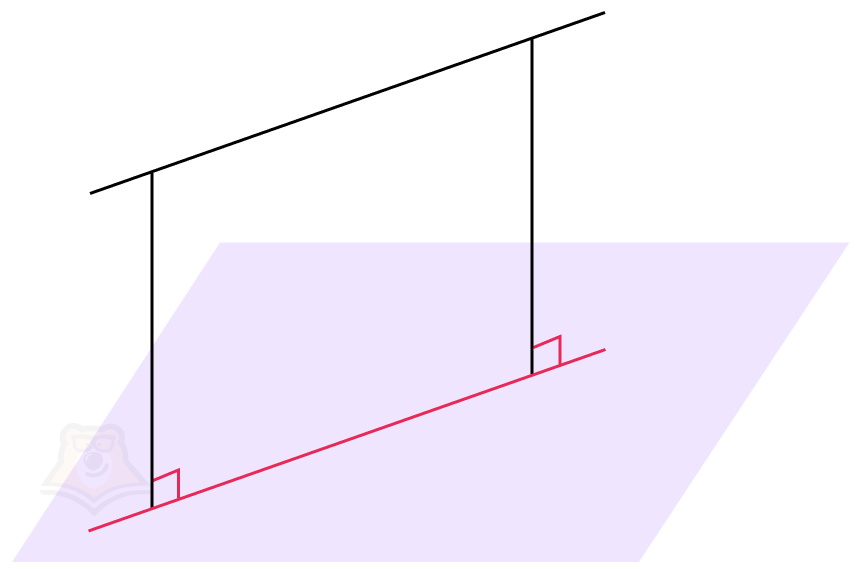
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
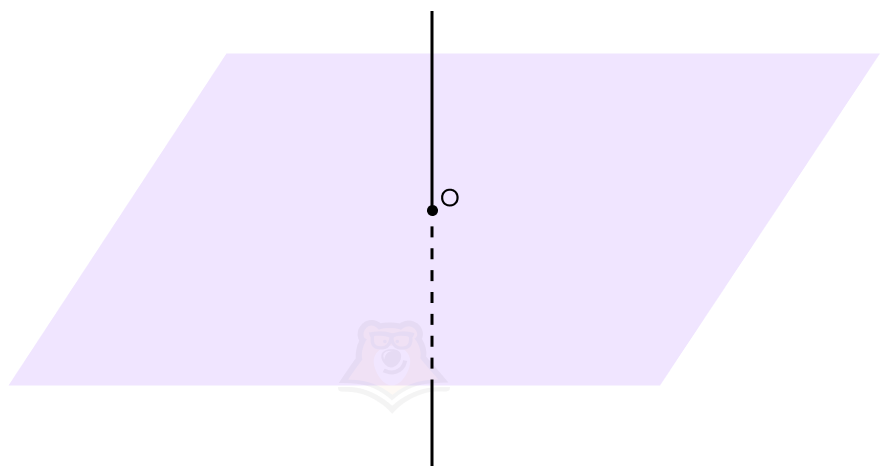
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
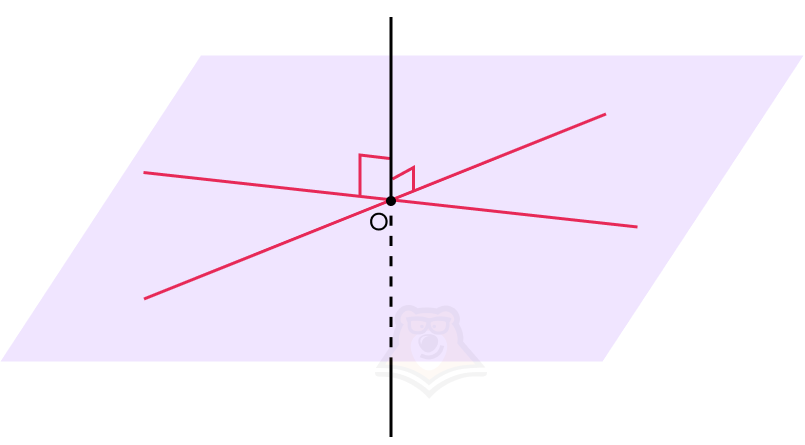
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
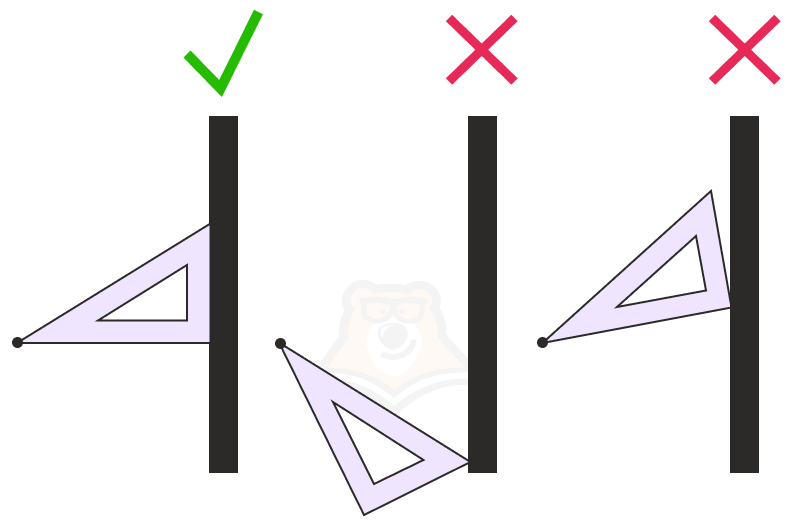
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.

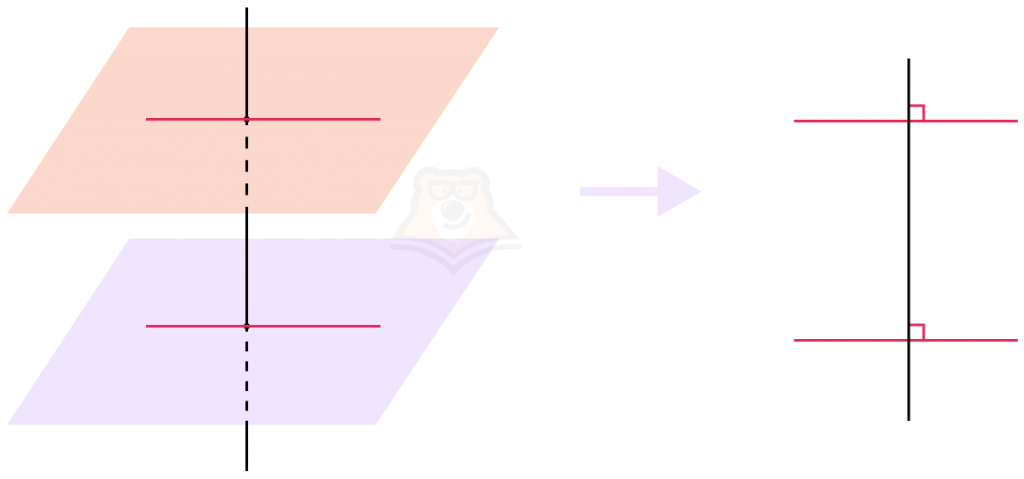
Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
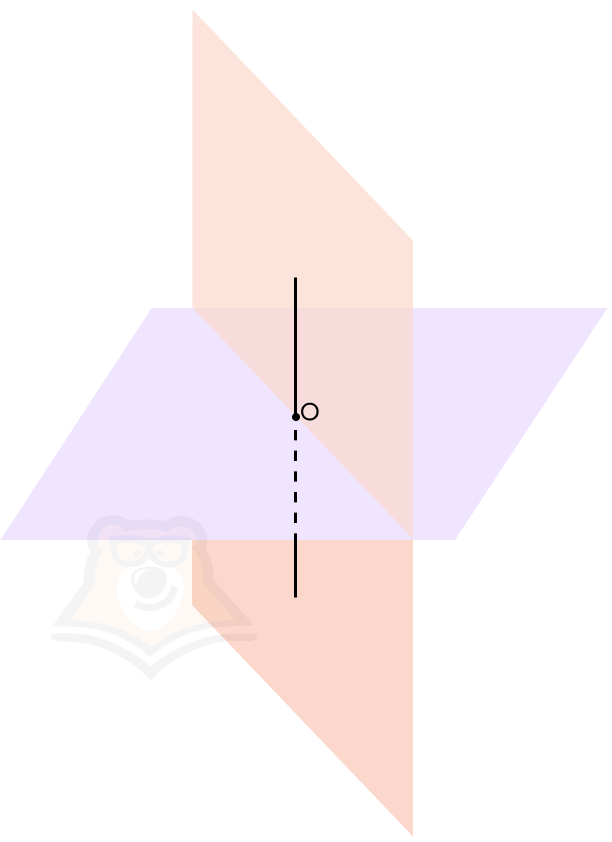
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
Теорема о трех перпендикулярах
Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол.
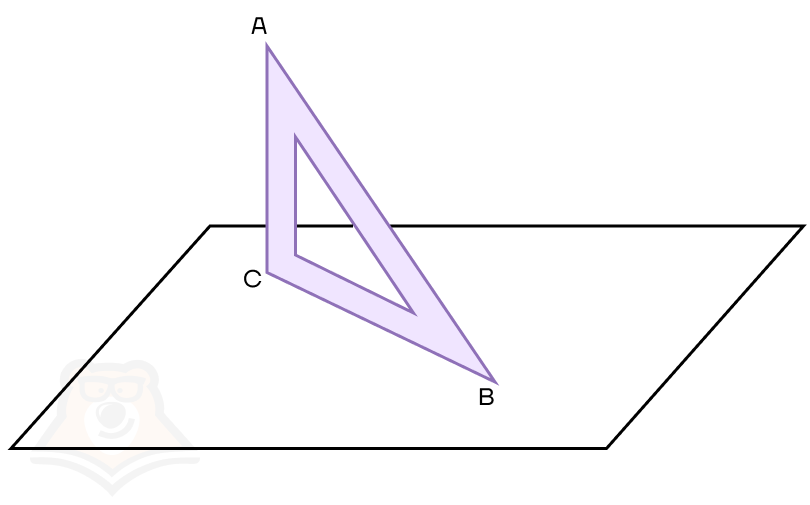
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
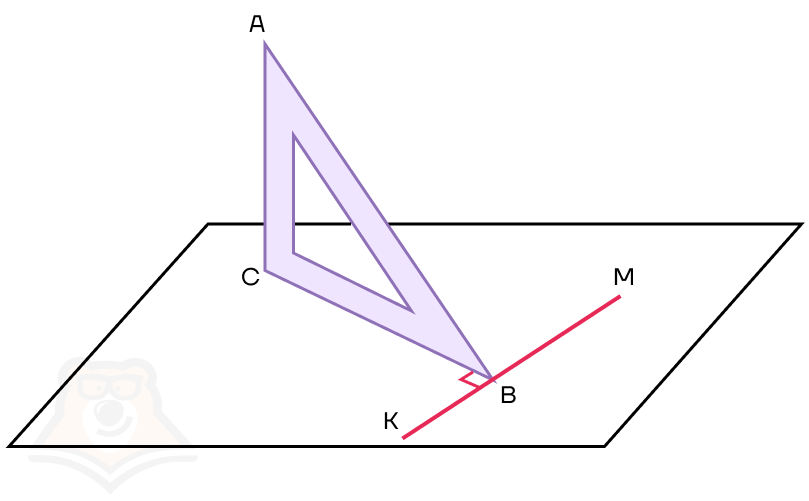
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.
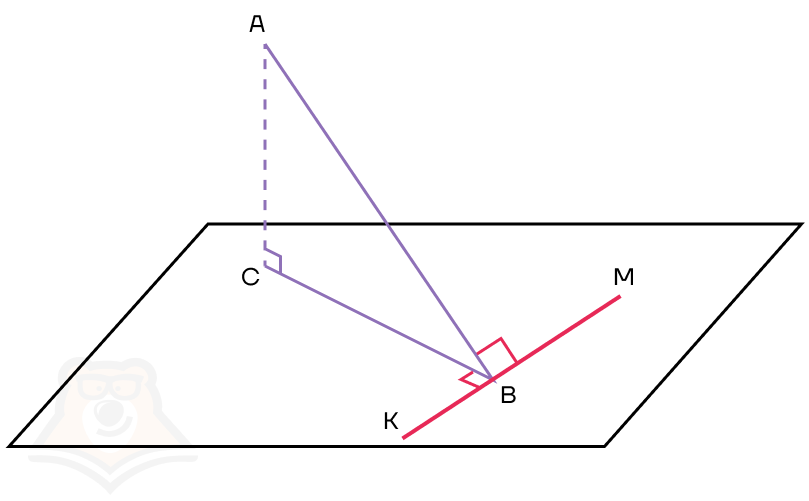
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек
- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
- Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.
- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Проверь себя
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.
Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.
Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4
Инфоурок
›
Алгебра
›Презентации›“Нахождение двугранного угла между плоскостями”
“Нахождение двугранного угла между плоскостями”
Скачать материал

Скачать материал


- Сейчас обучается 26 человек из 17 регионов


- Сейчас обучается 97 человек из 37 регионов


- Сейчас обучается 35 человек из 26 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Методическая разработка Савченко Е.М.
МОУ гимназия №1, г. Полярные Зори, Мурманской обл.
Двугранный угол
Л.С. Атанасян “Геометрия 10-11” -
2 слайд
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки А на прямую.
a
Н
А
Расстояние от точки до плоскости – длина перпендикуляра
Повторение
Н
А -
3 слайд
В
С
M
Из точки В к плоскости проведена наклонная, равная 12 см. Угол между наклонной и ее проекцией на плоскость равен 300. Найти расстояние от точки В до плоскости.
12 см
300
? -
4 слайд
В
С
M
А
Из точки В к плоскости проведены две наклонные, которые образуют со своими проекциями на плоскость углы в 300. Угол между наклонными равен 600. Найдите расстояние между основаниями наклонных, если расстояние от точки В до плоскости равно .
300
300
? -
5 слайд
М
П-я
Через вершину С треугольника АВС проведена прямая СМ, перпендикулярная к его плоскости. Угол С равен 300. Найдите расстояния: 1) от точки А до прямой ВС;
2) от точки М до прямой ВС, если АС = 12 см, а АМ =
А
В
С
П-Р
Н-я
TTП
СВ АF
П-я
СВ MF
Н-я
АF и МF –
искомые расстояния
F
300 -
6 слайд
Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.
Двугранный угол
А
В
С
А
В
С -
7 слайд
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.
Две полуплоскости – грани двугранного угла
Прямая a – ребро двугранного угла
a -
8 слайд
O
Угол РDEK
Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях двугранного угла
А
В
N
Р
M
К
D
E
Угол SFX – линейный угол двугранного угла
S
X
F -
9 слайд
Угол РОК – линейный угол двугранного угла РDEК.
D
E
Р
К
O
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Алгоритм построения линейного угла. -
10 слайд
Все линейные углы двугранного угла равны друг другу.
А
В
O
А1
В1
O
1
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными сторонами -
11 слайд
Двугранный угол может быть прямым, острым, тупым
-
12 слайд
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
N
П-р
Н-я
П-я
TTП
АС ВМ
H-я
АС NМ
П-я
Угол ВMN – линейный угол двугранного угла ВАСК
К
M -
13 слайд
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
N
П-р
Н-я
П-я
TTП
АС ВС
H-я
АС NС
П-я
Угол ВСN – линейный угол двугранного угла ВАСК
К
С -
14 слайд
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
N
П-р
Н-я
П-я
TTП
АС ВS
H-я
АС NS
П-я
Угол ВSN – линейный угол двугранного угла ВАСК
К
С
S -
15 слайд
Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
N
П-р
Н-я
П-я
TTП
DС BС
H-я
DС NС
П-я
Угол ВСN – линейный угол двугранного угла ВDСК
К
С
D -
16 слайд
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
П-р
П-я
TTП
DС ВM
H-я
DС NM
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
N
Н-я
M -
17 слайд
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
П-я
TTП
DС ВM
H-я
DС NM
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
M
N -
18 слайд
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
П-я
TTП
DС ВM
H-я
DС NM
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
M
N -
19 слайд
Неперпендикулярные плоскости и пересекаются по прямой МN. В плоскости из точки А проведен перпендикуляр АВ к прямой МN и из той же точки А проведен перпендикуляр АС к плоскости . Докажите, что угол АВС – линейный угол двугранного угла АМNC.
№ 166.
M
N
А
С
В
П-р
Н-я
П-я
TTП
МN АB
H-я
MN ВС
П-я
Угол АВС – линейный угол двугранного угла АМNC -
20 слайд
С
А
В
D
M
В тетраэдре DАВС все ребра равны, точка М – середина ребра АС. Докажите, что угол DМВ – линейный угол двугранного угла ВАСD.
№ 167. -
21 слайд
Двугранный угол равен . На одной грани этого угла лежит точка, удаленная на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла.
№ 168.
В
d
N
А
? -
22 слайд
Даны два двугранных угла, у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 1800.
№ 169.
F
В
А
О
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 262 555 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 03.01.2016
- 2451
- 1
- 03.01.2016
- 853
- 3
Рейтинг:
3 из 5
- 03.01.2016
- 3842
- 64
- 03.01.2016
- 2215
- 12
- 03.01.2016
- 998
- 16
- 03.01.2016
- 594
- 0
- 03.01.2016
- 823
- 3
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Скачать материал
-
03.01.2016
2394
-
PPTX
582.5 кбайт -
13
скачиваний -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Зарьянцева Виктория Павловна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 10 месяцев
- Подписчики: 0
- Всего просмотров: 27862
-
Всего материалов:
19