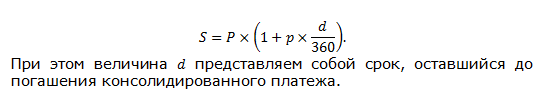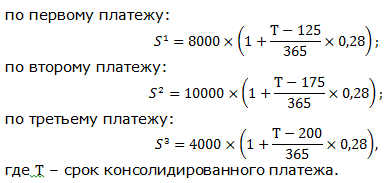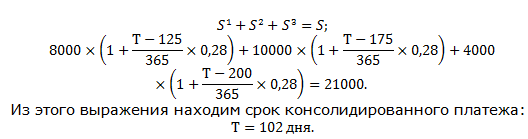На практике часто
возникают ситуации, когда участники
сделки вынуждены изменять условия ранее
заключенного финансового соглашения.
В результате изменений условий контракта
ни один из его участников не должен
терпеть убытков, поэтому в таких ситуациях
также составляется уравнение
эквивалентности.
Согласно уравнению
эквивалентности сумма нового и старого
платежей приводится к одному моменту
времени. Для краткосрочных контрактов
процесс приведения осуществляется, как
правило, на основе простых ставок. При
использовании сложных ставок время
приведения контрактов не имеет значения.
При консолидации
платежей возникают две задачи: 1)
определение величины консолидированного
платежа при известном сроке, когда этот
платеж должен быть сделан; 2) определение
срока известного консолидированного
платежа.
Обе задачи решаются
с использованием уравнения эквивалентности
контрактов.
Два контракта считаются эквивалентными,
если потоки платежей по этим контрактам,
приведенные к одному моменту времени,
одинаковы.
При замене или
объединении платежей используется
принцип эквивалентности: ни одна из
сторон финансовой сделки не должна
казаться в убытке или получить
дополнительную прибыль.
Цель
проведения занятия –
научиться проводить расчеты по замене
ставок и условий финансовых контрактов,
используя формулы финансовых вычислений
и электронные таблицы EXCEL.
Основные
формулы
Рассмотрим ситуацию,
когда платеж Р1
со
сроком уплаты
n
1
заменяется
на платеж Р0
со сроком
уплаты
n
0
Простые
ссудные ставки
Формула
для нахождения величины нового платежа
при использовании простой ссудной
ставки:
Формула
для нахождения срока нового платежа,
если
Формула
для нахождения срока нового платежа,
если
Формула
для определения величины консолидированного
платежа при использовании простой
ссудной ставки
Формула
для определения срока консолидированного
платежа при использовании простых
ссудных ставок
Сложные
ссудные ставки
Формула для
нахождения величины нового платежа при
использовании сложной ссудной ставки:
Формула
для нахождения срока нового платежа
Формула
для определения величины консолидированного
платежа
Формула
для определения срока консолидированного
платежа
Типовые задачи
с решениями
Задача 1. Согласно
новому финансовому соглашению платеж
в 100000 руб. со сроком уплаты через 1 год
заменяется платежом со сроками уплаты
1) через полгода;
2) через два года.
Определить величину нового платежа,
если используется простая ставка 20 %
годовых.
Решение
1) Так как срок
нового платежа меньше года, то его
величина — это
дисконтированная стоимость 100000 руб.,
срок дисконтирования —
0,5 года, поэтому величина нового платежа
равна:
100 000 / (1 + 0,5 ·0,2) =
90 909 руб.
2) Так как срок
нового платежа больше года, то его
величина — это будущая стоимость 100000
руб., наращение происходит один год по
ставке 20 % годовых, поэтому величина
нового платежа равна:
100 000 · (1+1·0,2)= 120 000
руб.
Задача 2. Найти
величину нового срока, если платеж в
100 000 руб. с уплатой через 250 дней
заменяется платежом в 95 000 руб.
Используется простая ставка 10 % годовых.
Решение
Так как сумма
нового платежа меньше 100 000 руб.,
поэтому новый срок должен быть также
меньше 250 дней.
Графически это
можно показать следующим образом:
Будем приводить
потоки платежей по новому и старому
контракту к моменту времени 250 дней.
Тогда
на сумму в 95 000 руб.
должны начисляться простые проценты
по ставке 10 % в течение (250 – х)
дней и наращенная сумма должна равняться
100 000 руб. Составляем уравнение
эквивалентности
95000
(1 +0,1
(250 – х)
/ 360)) = 100000,
х
= 60,5 дней.
Проверим
этот результат. Получив через 60,5 дней
95000 руб. и
вложив их в банк на срок (250 – 60,5) дней,
получим
95000
(1+0,1
(250 – 60,5) /360) = 100000 руб.
Заметим, что платеж
в 100000 руб. нельзя заменить любым меньшим
по величине платежом. Величина нового
платежа не может быть меньше, чем сумма
100000 руб., приведенная к начальному
моменту времени, т. е. меньше, чем 100000 /
(1+ 0,1
250/360) = 93500 руб.
Задача 3. Два
векселя номинальной стоимостью 20000 руб.
и 30000 руб. и сроком погашения 1 июня и 1
сентября заменяются одним с продлением
срока погашения до 1 октября. При
объединении используется простая
учетная ставка 10 % годовых. Определить
номинальную стоимость нового векселя.
Решение
Поскольку срок
погашения нового векселя позже, чем
сроки погашения объединяемых векселей,
то на сумму 20000 руб. в течение 122 дней (с
1 июня по 1 октября) происходит наращение
капитала по простой учетной ставке 10
%; на сумму 30000 руб. в течение 30 дней (с 1
сентября по 1 октября) также происходит
наращение капитала по простой учетной
ставке 10 % годовых. Поэтому номинальная
стоимость нового векселя равна:
Задача 4. Платежи
в 6000, 4000 и 10000 руб. должны быть погашены
соответственно через 90, 165 и 270 дней.
Кредитор идолжник
согласились заменить три платежа одним
через 120 дней. Найти величину
консолидированного платежа, если
используется простая процентная ставка
38% годовых и в расчет принимаются
обыкновенные проценты.
Решение
Приведем
все платежи к моменту погашения
консолидированного платежа, т.е. к 120
дням. Тогда
на платеж в 6000 руб., срок погашения
которого меньше 120 дней, будут начисляться
простые проценты за период в 120-90=30 дней,
платеж в 4000 руб. необходимо дисконтировать
на срок в 165-120=45 руб., платеж в 10000 руб.
необходимо дисконтировать на срок
270-120=150 дней.
Складывая
суммы приведенных платежей, получим
уравнение для определения величины
консолидированного платежа:
поэтому Х=18642 руб.
Если
бы за дату приведения выбрали время
выплаты платежа в 6000 руб., то получили
бы следующее уравнение:

откуда
Х=18683 руб.
Приводя
все платежи к начальному моменту времени,
получим уравнение:

откуда Х=18780 руб.
Поэтому
при выборе финансового соглашения в
случае использования простых процентов
необходимо оговорить дату, на которую
будет осуществляться приведение всех
сумм.
Задача 5. Согласно
контракту предприниматель должен
выплатить кредитору 100 000 руб. через
год, 200 000 руб. через два года и 400 000
руб. через 3 года. Предприниматель
планирует выплатить через 2 года 300 000
руб., оставшуюся сумму долга вернуть
через 4 года. Какую сумму предприниматель
должен будет выплатить через 4 года,
если в расчетах используется сложная
ставка 20% годовых?
Решение.
Изобразим
схему выплат на графике. Под осью отметим
платежи по старому соглашению, над осью
– по новому контракту.
|
300 |
х |
|
1 |
2 |
3 |
4 |
|
100 |
200 |
400 |
Величину
неизвестного платежа находим из условия
эквивалентности контрактов. Приведенные
стоимости платежей по старому контракту
необходимо приравнять к приведенным
стоимостям потоков платежей по новому
контракту и из полученного уравнения
определить неизвестную величину нового
платежа.
Х=
508 800 руб.
В
случае сложных ставок результат не
зависит от момента времени, для которого
составляется уравнение эквивалентности
контрактов. Действительно, если все
платежи приводить к моменту окончания
года 4, уравнение примет вид:
Разделив
это обе части уравнения на
,
получим первоначально составленное
уравнение.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача №480 (расчет срока консолидированного платежа)
Три платежа 8000 руб. со сроком 125 дней, 10000 руб. со сроком 175 дней и 4000 руб. со сроком 200 дней заменяются одним в размере 21000 руб. Стороны договорились об использовании простой процентной ставки 28% годовых. Определить срок консолидированного платежа при базе Тгод=365.
Решение задачи:
Для определения величины консолидированного платежа определяем наращенную стоимость каждого из платежей. Для этого используем формулу простых процентов:
Поскольку в данном случае условие оперирует сроками, выраженными в днях (d), формула приобретает следующий вид:
Записываем выражения для определения наращенной суммы по каждому платежу:
Сумма этих платежей должна составить величину консолидированного платежа:
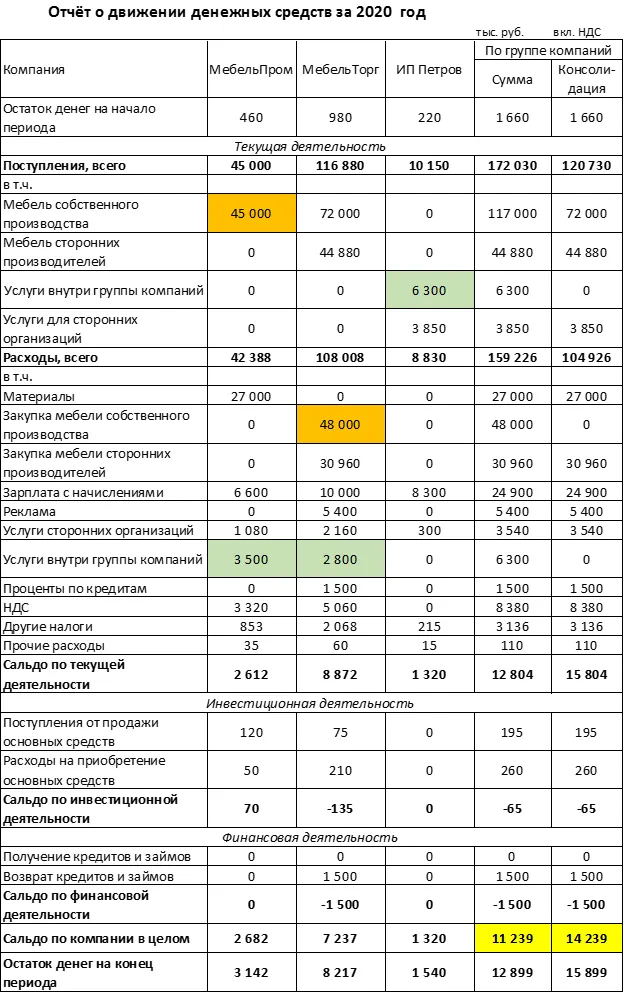
Как правильно посчитать денежный поток группы компаний
Чтобы правильно рассчитать финансовые потоки по группе компаний, нужно составить консолидированный отчёт о движении денежных средств. Звучит сложно, но на самом деле эта работа под силу любому бухгалтеру. Рассказываем, как это сделать. В конце статьи подарок — запись вебинара по основам управленческого учёта.

Как составить консолидированный отчёт о движении денежных средств
Чтобы получить консолидированную информацию о финансовых потоках по группе компаний, нужно:
1. Сформировать отчёты о движении денег для отдельных компаний и ИП группы по одинаковой форме и свести их в таблицу.
2. Выделить поступления и платежи по расчётам внутри группы.
3. Сложить поступления и платежи по всем компаниям, убрав внутренние поступления и выплаты.
Рассмотрим на примере мебельного бизнеса, который организован в виде группы компаний.
1. ООО «МебельПром» занимается производством мебели.
2. ООО «МебельТорг» продаёт эту мебель, но параллельно продаёт и мебель других производителей.
3. ИП Петров оказывает компаниям группы услуги, связанные с управлением. Такие же услуги он оказывает и сторонним организациям.
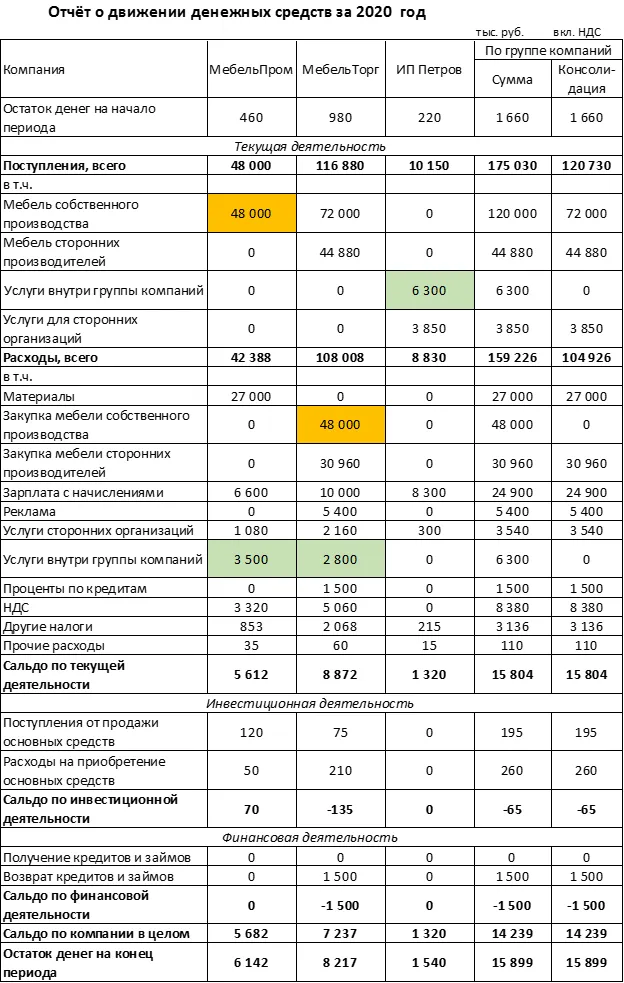
Консолидированный отчёт о движении денежных средств этой группы компаний будет выглядеть так:
При подсчёте из консолидированных оборотов исключены следующие суммы (выделены цветом):
1. Оплата от ООО «МебельТорг» в адрес ООО «МебельПром» за мебель на сумму 48 000 тыс. руб.
2. Расчёты компаний группы с ИП Петровым за управленческие услуги на общую сумму 6 300 тыс. руб.
Моё дело Финансы
Облачный сервис для ведения управленческого учёта, услуги по постановке и ведению управленки
Как проверить правильность составления консолидированного отчёта о движении денежных средств
Консолидированное сальдо по отчёту о движении денежных средств в общем случае должно равняться сумме сальдо по отдельным компаниям группы. Сальдо — это разность между всеми поступлениями и платежами за отчётный период.
При исключении внутренних платежей, у одной компании уменьшаются поступления, а у другой — снижаются выплаты на ту же сумму. Поэтому общее сальдо по группе не должно измениться.
Если суммарное и консолидированное сальдо не совпали, то в первую очередь нужно проверить, нет ли в отчёте сумм, которые «зависли» при перечислении между компаниями группы.
Такая ситуация возникает, если платёж внутри группы проводят в последнюю дату отчётного периода. В этом случае банк может зачислить деньги на счёт получателя на следующий день, т.е. уже в новом периоде.
Предположим, что ООО «МебельТорг» провело завершающий платёж на сумму 3 000 тыс. руб. в последний рабочий день 2020 года. Эта сумма не была зачислена на счёт ООО «МебельПром» в 2020 году. Тогда отчёт по группе компаний за 2020 год будет выглядеть следующим образом:
Разница между суммарным (11 239 тыс. руб.) и консолидированным (14 239 тыс. руб.) сальдо соответствует «переходящему» платежу в 3 000 тыс. руб.
Чтобы избежать разрывов, в этом случае нужно отнести внутренний платёж и поступление к одному из соседних периодов. К какому именно — руководитель может определить самостоятельно, принципиального значения это не имеет.
Например, можно принять решение, что в целях управленческого учёта сумму в 3 000 тыс. руб. следует считать зачисленной на счёт ООО «МебельПром» в 2020 году. Тогда разрыв будет устранён и отчёт примет вид, приведённый в предыдущем разделе.
Если зависших платежей нет, а сальдо всё равно не сходится — значит, при консолидации была допущена ошибка. Тогда нужно ещё раз проверить, что все суммы внутренних расчётов исключены, как из поступлений, так и из расходов. Чтобы было удобнее проверять и не запутаться, выделяйте удаляемые цифры одинаковым цветом, как это показано в примерах.
Подарок для наших читателей — запись вебинара «Зачем бизнесу управленческий учёт и как его внедрить». Два часа подробного разбора, конкретных примеров и ответов на вопросы! Спикер — Ольга Головина — финансовый директор с шестнадцатилетним стажем и опытом работы в «Теле2», «Азия Цементе», «Юниуме» и «Моё дело».
Зачем бизнесу управленческий учёт
и как его внедрить
Получите бесплатное видео с экспертным обзором!
Оставьте заявку в форме ниже, и мы вышлем вам запись.
Объединение платежей и эквивалентные платежи
Краткая теория
Принцип эквивалентности применяется при различных изменениях
условий выплат денежных сумм. Общий метод решения подобного рода задач заключается
в разработке так называемого уравнения эквивалентности, в котором сумма
заменяемых платежей, приведенных к какому-либо моменту времени, приравнивается
к сумме платежей по новому обязательству, приведенных к той же дате. Для
краткосрочных обязательств приведение осуществляется обычно на основе
простых ставок,
для средне- и долгосрочных — с помощью
сложных ставок. Заметим, что в
простых случаях конверсии платежей часто можно обойтись без специальной разработки и решения
уравнения эквивалентности.
Одним из распространенных случаев изменения условия выплат является объединение платежей.
Пусть платежи
со сроками
заменяются одним в сумме
и сроком
.
В этом случае возможны две постановки задачи: если задается срок
,
то находится сумма
и наоборот, если задана сумма
консолидированного платежа
,
то определяется срок
.
При
решении задачи определения суммы консолидированного платежа уравнение
эквивалентности имеет простой вид. В общем случае, когда
,
причем
,
искомую величину находим как сумму наращенных и дисконтированных платежей. При
применении простых процентных ставок, получим:
где
– размеры объединяемых платежей со сроками
– размеры платежей со сроками
В частном случае, когда
При объединении обязательств можно
применить и учетные ставки. В этом случае при условии, что все сроки выплат
пролонгируются, то есть
, находим сумму наращенных по учетной ставке
платежей:
В общем случае имеем:
и
имеют тот же смысл, что и выше.
Объединение платежей можно осуществить и на основе сложных
ставок. Для общего случая получим:
Рассмотрим теперь более общие случаи изменения условий
выплат, предусматриваемых в контрактах, для которых решение нельзя получить
простым суммированием приведенных на некоторую дату платежей. Когда некоторое количество платежей заменяется эквивалентными платежами, с другими сроками и суммами. И в таких случаях
решение основывается на принципе эквивалентности платежей до и после изменения
условий. Метод решения заключается в разработке упоминавшегося выше уравнения
эквивалентности. Если приведение
платежей осуществляется на некоторую начальную дату, то получим следуюшие
уравнения эквивалентности в общем виде.
при использовании простых процентов:
при использовании сложных процентов:
где
и
– параметры заменяемых платежей,
и
– параметры эквивалентных им платежей.
Конкретный вид уравнения определяется
содержанием контрактов.
Примеры решения задач
Задача 1
По
условиям погашения краткосрочного кредита, полученного под 15% годовых 12
февраля, предприятие должно выплатить следующие суммы в три срока: 16 марта -30
тыс.руб., 10 мая – 26 тыс.руб. и 1 сентября – 18 тыс.руб. В связи с возникшими
обстоятельствами предприятие просит банк объединить три платежа и перенести
дату выплаты долга на 1 июля. Определить величину консолидированного платежа.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Величину
суммы консолидированного платежа можно найти по формуле:
– размеры объединяемых платежей со сроками
– размеры платежей со сроками
Подсчитаем
сроки платежей в днях (от 12.02):
Для
1-го платежа 16-го марта:
Для
2-го платежа 10 мая:
Для
3-го платежа 1 сентября:
Срок
консолидированного платеж 1 июля:
Ответ:
Задача 2
Замените
поток платежей – 70000 руб. – через 1 год, 120000 руб. – через 2 года, 90000
руб. – через 3 года – эквивалентным множеством, состоящим из двух выплат,
равных по величине: первая – через 1.5 года, вторая – через 4 года. Проценты
начисляются по ставке 8% годовых каждые 6 месяцев.
Решение
Если
приведение платежей осуществляется на некоторую начальную дату, то при получим
следующее уравнение эквивалентности:
Примем
в качестве базовой даты текущий момент. Уравнение эквивалентности в этом случае
запишется в следующем виде:
Решая
полученное уравнение, получаем:
Размер
платежа через 1.5 и 4 года равен 132337.1 руб.
Ответ: