Физика работы импульсного трансформатора
Расчет трансформатора является одним из наиболее
трудных вопросов при проектировании и разработке импульсных источников питания. Для предварения практических
технических расчетов представим основные соотношения и определения, описывающие физику работы трансформатора,
используемые далее в практических расчетах.
Определение трансформатора как устройства
Трансформатор представляет собой электромагнитное устройство, предназначенное для преобразования
электрической энергии переменного тока с одними параметрами (напряжение, ток) в энергию переменного тока с
другими параметрами (напряжение, ток). Частота при этом не изменяется. Преобразование параметров переменного
напряжения осуществляется с помощью двух и более индуктивно связанных обмоток намотанных на одном
магнитопроводе. Схематично конструкция трансформатора представлена на рисунке T.1.
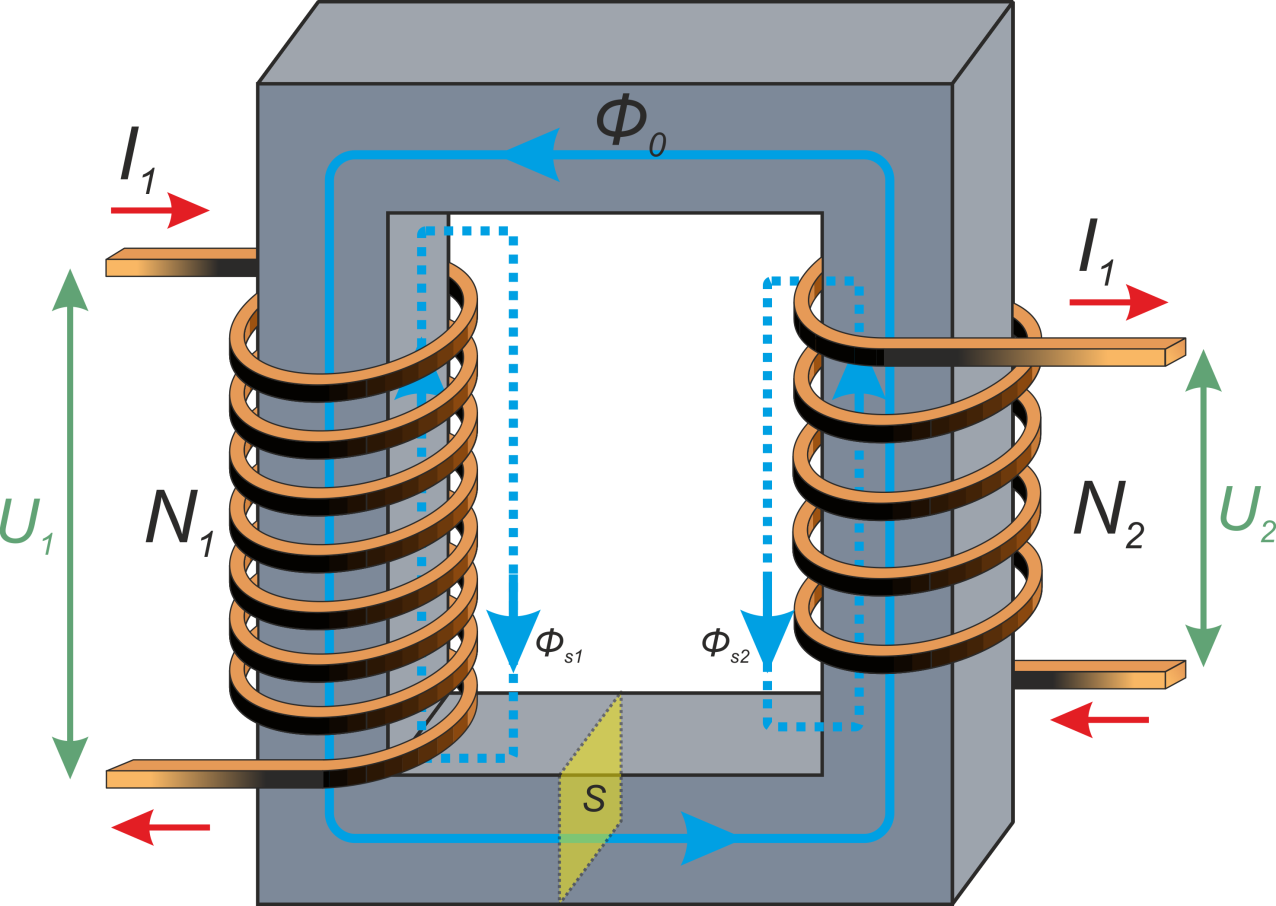
Рисунок T.1 – Устройство трансформатора
Трансформаторы играют двоякую роль – с одной стороны преобразуют параметры электрической энергии – повышают
или понижают напряжение и соответственно понижают или повышают ток, с другой стороны трансформатор
обеспечивает гальваническую развязку между первичной и вторичной обмотками.
Базовые характеристики магнитного поля
Поскольку трансформатор является электромагнитным устройством, то для количественного расчета трансформатора
кроме электрических параметров (напряжение, ток и т.д.) необходимо оперировать магнитными величинами.
Основной характеристикой магнитного поля является напряженность магнитного поляона количественно
описывает степень взаимодействия проводников с током. Обозначение – H. Единица измерения в системе СИ – А/м.
Магнитная индукция – векторная величина характеризующая силу магнитного поля. Обозначение – B.
Единица измерения в системе СИ – Тесла, Тл, (кг·с−2·А−1).
Интегральной характеристикой является поток вектора магнитной индукции. Обозначение – Ф. Единица
измерения в системе СИ – Вебер, Вб (кг·м²·с−2·А−1).
Мера сохранения магнитных свойств тел называется намагниченностью. Обозначение – J. Единица
измерения в системе СИ – А/м.
Намагниченность связана с напряженность внешнего магнитного поля:
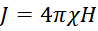
где:
χ – магнитная восприимчивость материала;
H – напряженность магнитного поля.
Простейший трансформатор. Исходные параметры
Для выполнения дальнейших математических выкладок, необходимых для количественного расчета трансформатора
определим основные параметры трансформатора:
– Количество обмоток – 2;
– Количество выводов от каждой обмотки – 2
– Число витков первичной обмотки – N1 ;
– Число витков вторичной обмотки – N2 ;
– Площадь поперечного сечения магнитопровода – S (полагается неизменной по всей длине);
Таким образом, рассматриваемый в дальнейшем трансформатор имеет простейшую конфигурацию без выводов от
средней точки в первичной и вторичной обмотках. Введение дополнительных отводов вносит некоторую коррективу
в расчет, но не влияет на основные выкладки.
Закон электромагнитной индукции и коэффициент трансформации
Как и следует из определения трансформатора первичная и вторичная обмотки трансформатора связаны индуктивно
магнитным потоком магнитопровода Φ0 (единым для всех обмоток трансформатора), точнее его
изменением во времени. Так ЭДС первичной и вторичной обмотки в соответствии с законом электромагнитной
индукции равны:
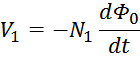
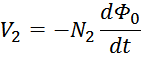
Данные соотношения показывают физические процессы, происходящие при работе трансформатора:
– скорость изменения магнитного потока в магнитопроводе (сердечнике) пропорциональна напряжению на выводах
первичной обмотки и обратно пропорциональна числу витков в ней;
– напряжение на выводах вторичной обмотки пропорционально скорости изменения магнитного потока в
магнитопроводе и числу витков в ней.
В соответствии с принципом причинно-следственной закономерности скорость изменения магнитного потока является
причиной возникновения следствия – ЭДС во вторичной обмотке. Для многообмоточного трансформатора соотношения
для других обмоток, третьей, четвертой и т.д. идентичны.
Отношение напряжений на обмотках пропорционально отношению витков в обмотках:
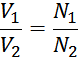
Коэффициент трансформации k равен отношению числа витков первичной обмотки N1 к числу витков во
вторичной обмотке N2:
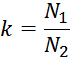
Магнитный поток в сердечнике трансформатора. Влияние нагрузки
При подключении к первичной обмотке источника переменного напряжения V1 по ней в ней возникнет ток
i1 и в магнитопроводе возникнет первичный магнитный поток Ф1(t). В результате действия
магнитного потока во вторичной обмотке возникает ЭДС самоиндукции V2и, при наличии нагрузки,
подключенной ко вторичной обмотке, возникает ток вторичной обмотки i2. Ток i2 в свою
очередь создает вторичный магнитный поток Ф2(t) направленный навстречу первичному потоку. В
результате в магнитопроводе устанавливается суммарный магнитный поток:
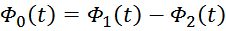
Незначительная часть потока первичной обмотки замыкается через воздух и называется потоком рассеяния
первичной обмотки ФS1(t). Аналогично существует поток рассеяния вторичной обмотки
ФS2(t).
Увеличение нагрузки и соответственно тока вторичной обмотки приводит к увеличению магнитного потока
Ф2(t) и соответственно потока Ф1(t). При этом суммарный магнитный поток Ф0(t)
практически не изменяется. Как и не изменится магнитная индукция в магнитопроводе. Это важно понимать.
Аналогичный процесс происходит при уменьшении нагрузки. Результирующий магнитный поток Ф0(t) и
вызывает перемагничивание сердечника трансформатора [Гейтенко Е.Н. Источники вторичного электропитания.
Схемотехника и расчет.Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с.].
Фазировка обмоток трансформатора. Полярность. Связь геометрии намотки и полярностей входного и
выходного напряжения
При намотке и подключении трансформатора в «несимметричных» преобразователях (обратноходовой, прямоходовый)
важно соблюдать правильную фазировку обмоток трансформатора – то есть соблюдение «полярности» начала и конца
обмотки. На условном обозначении трансформатора начало обмотки отмечается точкой (рисунок T.2).
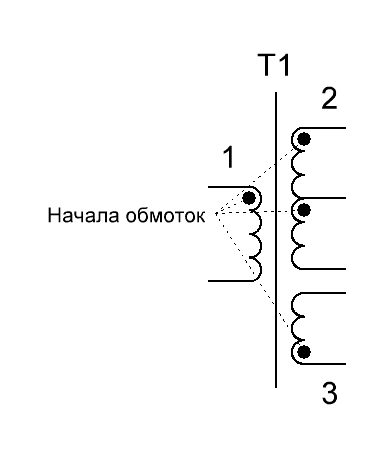
Рисунок T.2 – Начало обмотки отмечается точкой
Физически расположение начала и конца обмотки на магнитопроводе изображено на рисунке T.3.
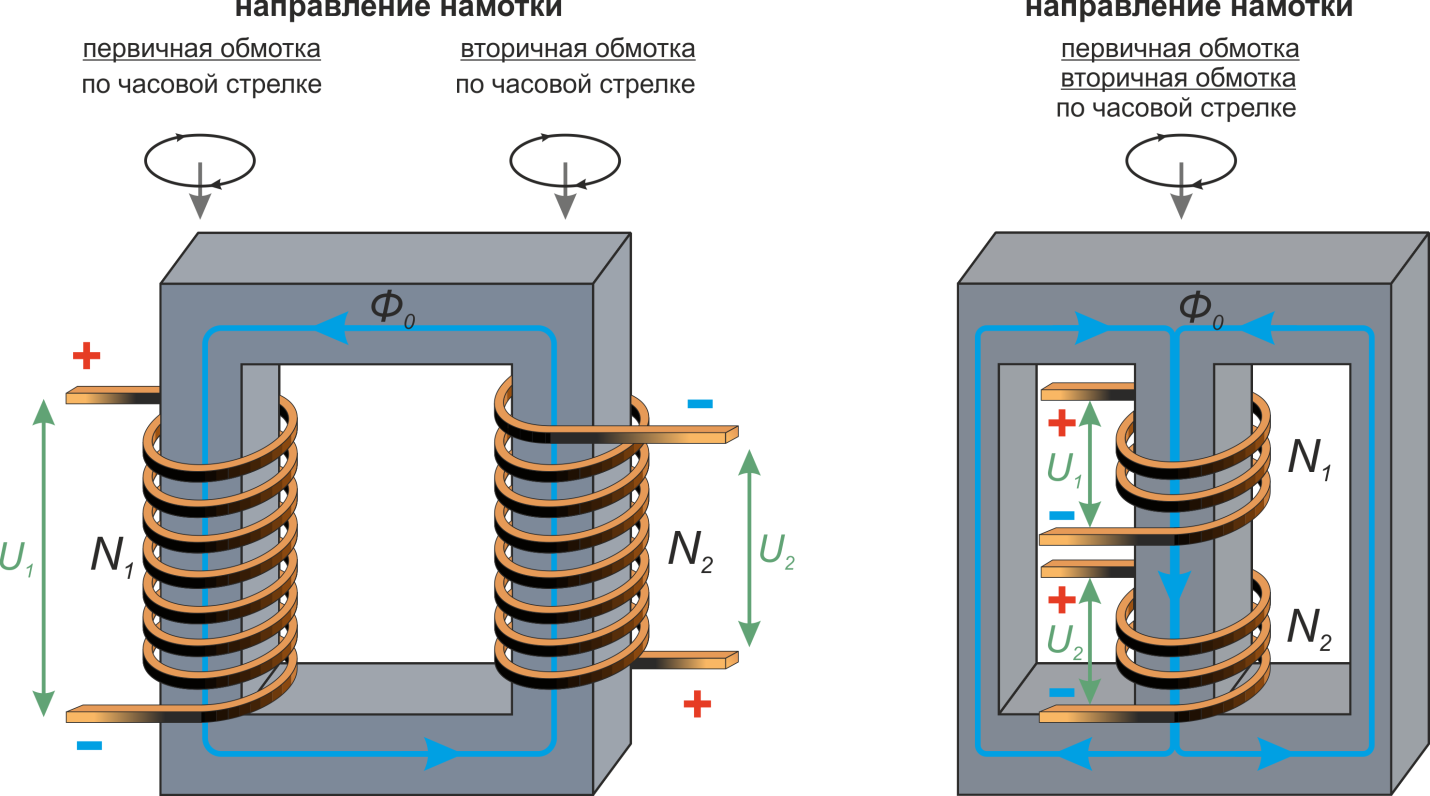
Рисунок T.3 – К определению полярности входного и выходного напряжения трансформатора
Для наглядности можно представить, что:
– ток, проходя по кольцам обмотки, раскручивает находящиеся в ней электроны в некотором направлении создавая
вихрь. Электроны, находящиеся в другой, изолированной обмотке чувствуют этот вихрь и раскручиваются в том же
направлении, создавая ток.
Или:
– если сложить два изолированных провода вместе, затем намотать их на магнитопровод, то начала и концы
обмоток будут вместе.
Конструктивные элементы трансформатора и дросселя
Магнитопровод
Ключевым элементом любого трансформатора или дросселя является магнитопровод. Он обеспечивает сильную
магнитную связь между обмотками трансформатора. Именно благодаря наличию этой связи энергия передается от
первичной обмотки во вторичную. Магнитопровод характеризуется своей формой и ферромагнитным материалом, из
которого он был изготовлен.
Геометрия магнитопровода
Геометрические параметры магнитопровода
Основными геометрическими параметрами магнитопровода, определяемыми его формой являются:
– длина средней линии – lav;
– площадь окна – S0;
– площадь сечения Sc;
– объем – Vm;
– длина немагнитного зазора lg;
– суммарная и рабочая площадь охлаждения магнитопровода ST.
Геометрические параметры магнитопровода – длина средней линии и площади окна входят в формулу расчета
габаритной мощности.
Объем магнитопровода используется при расчете потерь в магнитопроводе и соответственно его температурного
режима.
Площадь сечения и длина немагнитного зазора входит в формулы расчета индуктивности намагничивания
трансформатора и ряда других параметров. Существуют магнитопроводы с уже выставленным немагнитным
зазором.
Все геометрические параметры магнитопровода определяются типом формы или другими словами типом геометрии
магнитопровода. Об этом – в следующем разделе.
Типы геометрии магнитопроводов
Существует большое число типов геометрий магнитопроводов. Многообразие форм продиктовано многообразием
применений, для которых важны те или иные параметры геометрии или конструктивные факторы. Так в соответствии
с принятой международной классификацией магнитопроводы разделяются на следующие типы, представленные в
таблице T.1 [Swithing Power Supply Design. Second Edition. Abraham I. Pressman. The McGraw-Hill Companies.
1998. 669 p. ; http://ferrite.rct.ru/uu-ferrite-cores.html].
Таблица T.1 – Типы и сравнительная характеристика магнитопроводов различных типов.
| Тип магнитопровода | Описание | Изображение | Особенности применения |
| EE | Ш-образный магнитопровод cпрямоугольным центральным стрежнем | 
|
– стандартные силовые трансформаторы, дроссели |
| ETD | Ш-образный магнитопровод c круглым центральным стрежнем |

|
– стандартные силовые трансформаторы, дроссели |
| EC | Ш-образный магнитопровод c круглым центральным стрежнем и пазом вблизи него |

|
– стандартные силовые трансформаторы, дроссели |
| EER | Ш-образный широкий магнитопровод c круглым центральным стрежнем |

|
– силовые трансформаторы низкопрофильных конструкций источников питания |
| PEE | Ш-образный плоский магнитопровод c прямоугольным стрежнем |

|
– планарные трансформаторы на основе печатных плат |
| PEI | Магнитопровод состоящий из Ш-образного плоского сегмента и сегмента в виде бруска |

|
– планарные трансформаторы на основе печатных плат |
| EFD | Ш-образный магнитопровод c узким прямоугольным центральным стрежнем |

|
– силовые трансформаторы низкопрофильных конструкций источников питания |
| UU | П-образный с прямоугольным стержнем |

|
– высоковольтные трансформаторы |
| CUT | Чашкообразный магнитопровод |

|
– низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| POT | Чашкообразный магнитопровод |

|
– низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| PM | Чашкообразный магнитопровод открытого типа круглой формы |

|
– низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| PQ | Чашкообразный магнитопровод открытого типа прямоугольной формы |

|
– низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| RM | Чашкообразный магнитопровод открытого типа ромбовидной формы |

|
– низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| LP | Чашкообразный ассиметричный магнитопровод открытого типа прямоугольной формы |

|
– низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| R | Кольцевой магнитопровод |

|
– силовые трансформаторы низкопрофильных конструкций источников питания, дроссели, дроссели фильтров |
Подробное описание типоразмеров магнитопроводов и параметров существующих стандартных рядов представлены
datasheet-ах производителей магнитопроводов.
Выбор типа магнитопровода осуществляется в зависимости от ряда факторов, включая назначение устройства,
планируемую стоимость, особенности корпуса конечного устройства и т.д. В таблице T.2 представлено
сравнительное описание преимуществ и недостатков различных типов геометрии магнитопроводов [Magnetic Cores
for Switching Power Supplies.Magnetics. Technical documents. General information.
https://www.mag-inc.com/Design/Technical-Documents/General-Information.aspx ps-01.pdf]:
Таблица T.2 – Применимость магнитопроводов различных геометрий
| Характеристика | Тип магнитопровода | ||||
| POT | RM | EE | EER | ETD | |

|

|

|

|

|
|
| Стоимость магнитопровода | высокая | высокая | Низкая | средняя | средняя |
| Стоимость каркаса | низкая | низкая | Низкая | средняя | средняя |
| Стоимость намотки | низкая | низкая | Низкая | низкая | низкая |
| Гибкость (технологическая простота) намотки | хорошая | хорошая | Отличная | отличная | отличная |
| Сборка | простая | простая | Простая | средняя | средняя |
| Технологичность монтажа | хорошая | хорошая | Хорошая | приемлемая | приемлемая |
| Теплорассеяние | плохое | хорошее | Отличное | хорошее | хорошее |
| Экранирование, электромагнитная совместимость | отличное | хорошее | хорошее | хорошее | хорошее |
Таблица T.2 – Применимость магнитопроводов различных геометрий. Продолжение.
| Характеристика | Тип магнитопровода | ||||
| EС | PQ | EP, LP | R | UU | |

|

|

|

|

|
|
| Стоимость магнитопровода | средняя | высокая | Средняя | очень низкая | низкая |
| Стоимость каркаса | средняя | высокая | Высокая | – | низкая |
| Стоимость намотки | низкая | низкая | Низкая | высокая | низкая |
| Гибкость (технологическая простота) намотки | отличная | хорошая | Хорошая | приемлемая | отличная |
| Сборка | средняя | простая | Простая | – | простая |
| Технологичность монтажа | приемлемая | приемлемая | Хорошая | плохая | хорошая |
| Теплорассеяние | хорошее | хорошее | Плохое | хорошее | Отличное |
| Экранирование, электромагнитная совместимость | хорошее | приемлемая | Отличное | хорошее | Хорошее |
Как правило, в справочных листках (по английскому – datasheet) компанией-производителем представлены
исчерпывающие данные о геометрических параметрах конкретного магнитопровода.
Универсальными типами магнитопроводов являются те, которые позволяют установку немагнитного зазора между
частями сердечника, что бывает необходимо при проектировании однотактных типов преобразователей. При
разработке двухтактных преобразователей (в которых наличие зазора не так важно) возможно использование
кольцевых тороидальных магнитопроводов. Преимуществами кольцевых магнитопроводов являются относительно малая
стоимость, отсутствие каркаса. Ш-образные магнитопроводы (E, EI, ER, ETD и т.д.) и особенно П-образные
магнитопроводы (UU) хорошо подходят для построения мощных и высоковольтных трансформаторов, поскольку имеют
большую ширину окна для размещения межслоевой и межобмоточной изоляции значительной толщины. С целью
увеличения эффективной площади сечения магнитопроводы можно складывать параллельно. Для этой цели особенно
шорошо подходят Ш-образные магнитопроводы типа EE, П-образные типа UU и кольцевые магнитопроводы.
Факторы, определяющие выбор типа магнитопровода
Преимущество использования того или иного типа магнитопровода (и феррита из которого он изготовлен, но об
этом – далее), зависит от ряда факторов:
– Топология преобразователя
– Рабочая частота
– Необходимость регуляции
– Стоимость
– КПД источника питания
– Выходное напряжение
– Допустимый температурный режим
– Массогабаритные требования
Для каждой топологии преобразователей существуют наиболее подходящие типы магнитопроводов, что обусловлено
физикой работы преобразователей и особенностями конструкции. Сравнительные данные о целесообразности
использования того или иного типа магнитопровода для построения различных типов преобразователей
представлены в таблице T.3 [Transformers, Inductors, and Coils. Design Guide. OEM Group. ACTOWN ELECTROCOIL,
INC]:
Таблица T.3 – Использование того или иного типа магнитопровода для построения различных типов
преобразователей
| Тип магнитопровода | Обратноходовый, дроссель импульсных стабилизаторов | Прямоходовый | Полумост, мост, пуш-пул |
| EE, EС | Хорошо | Хорошо | Приемлемо |
| ETD | Приемлемо | Хорошо | Хорошо |
| EFD | Нежелательно | Хорошо | Хорошо |
| EP | Нежелательно | Хорошо | Приемлемо |
| RM | Приемлемо | Хорошо | Приемлемо |
| POT | Приемлемо | Хорошо | Приемлемо |
| R | Нежелательно | Хорошо | Приемлемо |
Материал магнитопровода
Геометрия магнитопровода это форма, теперь перейдем к содержанию – ферромагнитному материалу из которого
изготавливаются магнитопроводы. Подавляющее большинство магнитопроводов импульсных источников питания
изготавливается из ферритов. Другие типы ферримагнитных материалов – сталь, альсиферы и т.д. используются
крайне редко. Поэтому в данной работе будут рассмотрены только ферриты.
Ферриты – основной материал магнитопроводов импульсных источников питания
Феррит – это класс материалов, из которых сделан магнитопровод практически всех импульсных источников
питания. Другие типы ферромагнитных материалов – электротехнические стали (частотный диапазон – до 3000 Гц),
альсиферы, пермаллои (чувствительность к механическим воздействиям, сложность технологии изготовления),
пресспермы, карбонильное железо используются в инверторной технике существенно реже. Ферриты представляют
собой керамические материалы, состоящие из смеси оксидов магнитных металлов с оксидом железа. Оксиды
металлов в той или иной степени являются изоляторами, что и обуславливает высокое сопротивление
ферритов.
По своему составу ферриты делятся на никель-цинковые (NiZn), марганец-цинковые (MnZn), и ферритовые
полимерные композиционные материалы (FPC) с распределенным магнитным зазором. [Ферритовые изделия фирмы
EPCOS. В. Мелёшин. Компоненты и технологии, №4, 2002]. Каждый из выпускаемых типов феррита имеет свою
область применения. NiZn-ферриты используются преимущественно для радиотехнических задач (рабочих частотах
выше 2 МГц) [Трансформаторы и дроссели для импульсных источников питания. А. Кузнецов. Схемотехника, 2000,
№1, с. 30—33, №2, с. 48, 49, 2001, №1, с. 32—34.]. Для магнитопроводов изделий силовой электроники
традиционно используются MnZn-ферриты. Марки ферритов, предназначенные для использования в импульсных
источниках питания с указанием их характеристик представлены в таблице Т.4. [Трансформаторы и дроссели для
импульсных источников питания. А. Кузнецов. Схемотехника, 2000, №1, с. 30—33, №2, с. 48, 49, 2001, №1, с.
32—34.].
Характеристики ферритов
Основными количественными параметрами ферритов являются:
– магнитная проницаемость;
– максимальное значение магнитной индукции;
– частотный диапазон (верхняя граничная частота);
– величина удельных потерь;
– коэрцитивная сила;
– точка Кюри (критическая температура, при которой ферромагнетики теряют свои магнитные свойства).
Четыре параметра одной петли: индукция насыщения, коэрцитивная сила, остаточная индукция,
напряженность магнитного поля при насыщении
Изменение напряженности магнитного поля H, создаваемой внешним током, приводит к увеличению магнитной
индукции в нем [Transformer and inductor design Handbook. Third Edition, Revised and Expanded. Colonel Wm.
T. McLyman. Marcel Dekker, Inc., 2004]. Однако это зависимость нелинейна – во первых, с ростом напряженности
H замедляется рост индукции B, во вторых при некотором значении H наступает насыщение магнитной индукции и
она более не увеличивается, в третьих зависимость B от H имеет гистерезис, то есть эффект памяти предыдущего
состояния.
Петля гистерезиса зависимости B(H) определяет ряд базовых параметров феррита (рисунок T.4):
– Bs – индукция насыщения, не изменяющаяся при дальнейшем увеличении Н магнитного поля;
– Hs – максимальная напряженность поля, при которой достигается индукция насыщения;
– Hc – коэрцитивная сила или напряжённость магнитного поля, в котором происходит размагничивание
(B=0) феррита намагниченного до насыщения;
– Br – остаточная индукция, – величина магнитной индукции после снятия магнитного поля.
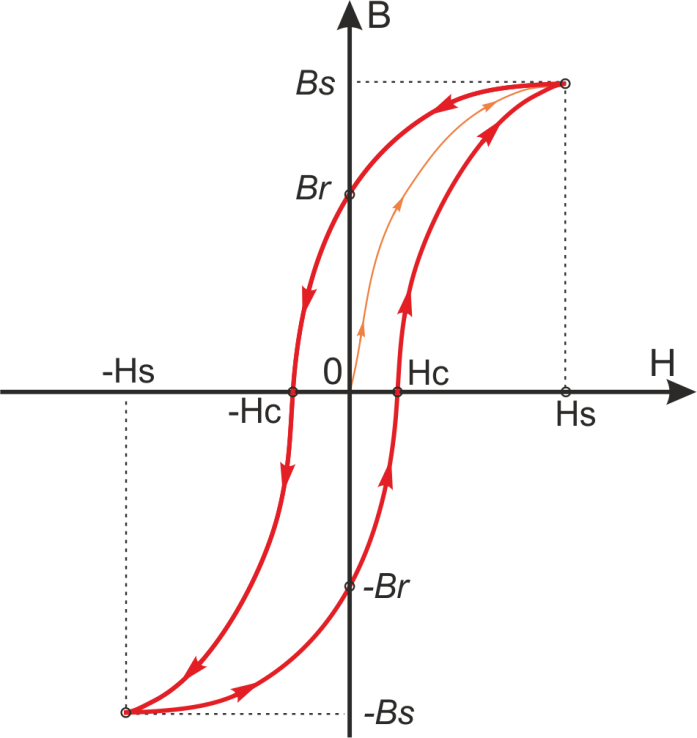
Рисунок T.4 – Общий вид петли гистерезиса для феррита
Максимальное значение индукции в магнитопроводе. Насыщение магнитопровода
Если через обмотку трансформатора или силового дросселя протекает слишком большой ток, создающий в сердечнике
величину индукции магнитного поля большую чем величина предельного значения индукции Bmax, то
материал магнитопровода входит в насыщение. При насыщении сердечника его магнитная проницаемость резко
уменьшается, что приводит к соответствующему уменьшению индуктивности и резкому росту тока. Визуально
симметричный рабочий цикл магнитной индукции с заходом в область насыщения представлен на рисунке T.5
[Импульсные источники питания. Теоретические основы проектирования и руководство по практическому
применению. Раймонд Мэк. Додэка XXI. 2008. 274 с.]
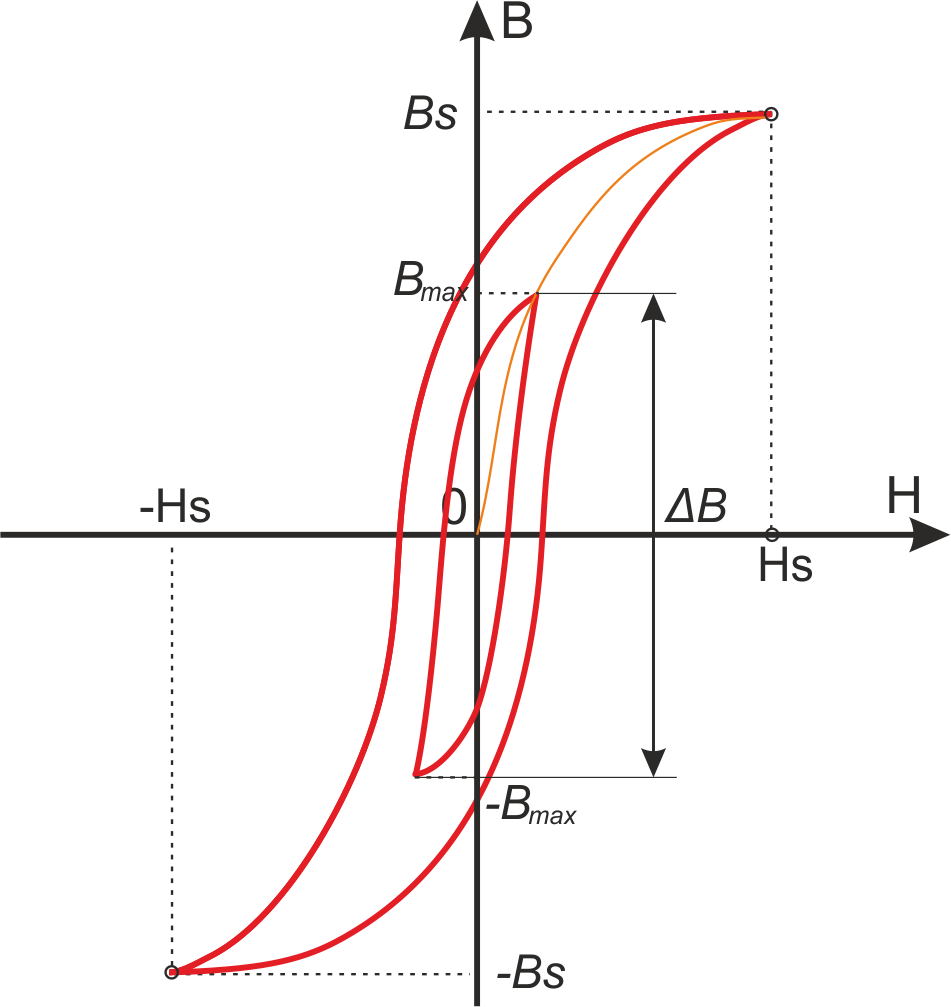
Рисунок T.5 Петли гистерезиса для феррита: a – с заходом в область насыщения (основная кривая
намагничивания), б – кривая рабочего цикла перемагничивания магнитопровода без насыщения
Негативными последствиями насыщения трансформаторов и дросселей являются:
– резкий рост тока через первичную обмотку вызывает токовые перегрузки ключей, их перегрев, что может стать
причиной выхода их из строя;
– увеличение потерь в магнитопроводе;
– большие импульсные токи через обмотки могут стать причиной перегрева электролитических конденсаторов;
– рост омических потерь в обмотках (пропорциональны квадрату тока).
Двухтактные преобразователи критичны к несимметричному перемагничиванию магнитопровода в результате которого
возникает подмагничивающий ток и возможно насыщение магнитопровода. Для предотвращения этого вводят
воздушный зазор и включают конденсатор последовательно с первичной обмоткой трансформатора.
Временная диаграмма тока (треугольной составляющей) первичной обмотки трансформатора (и силового дросселя)
при вхождении в режим насыщения представлена на рисунке T.6.
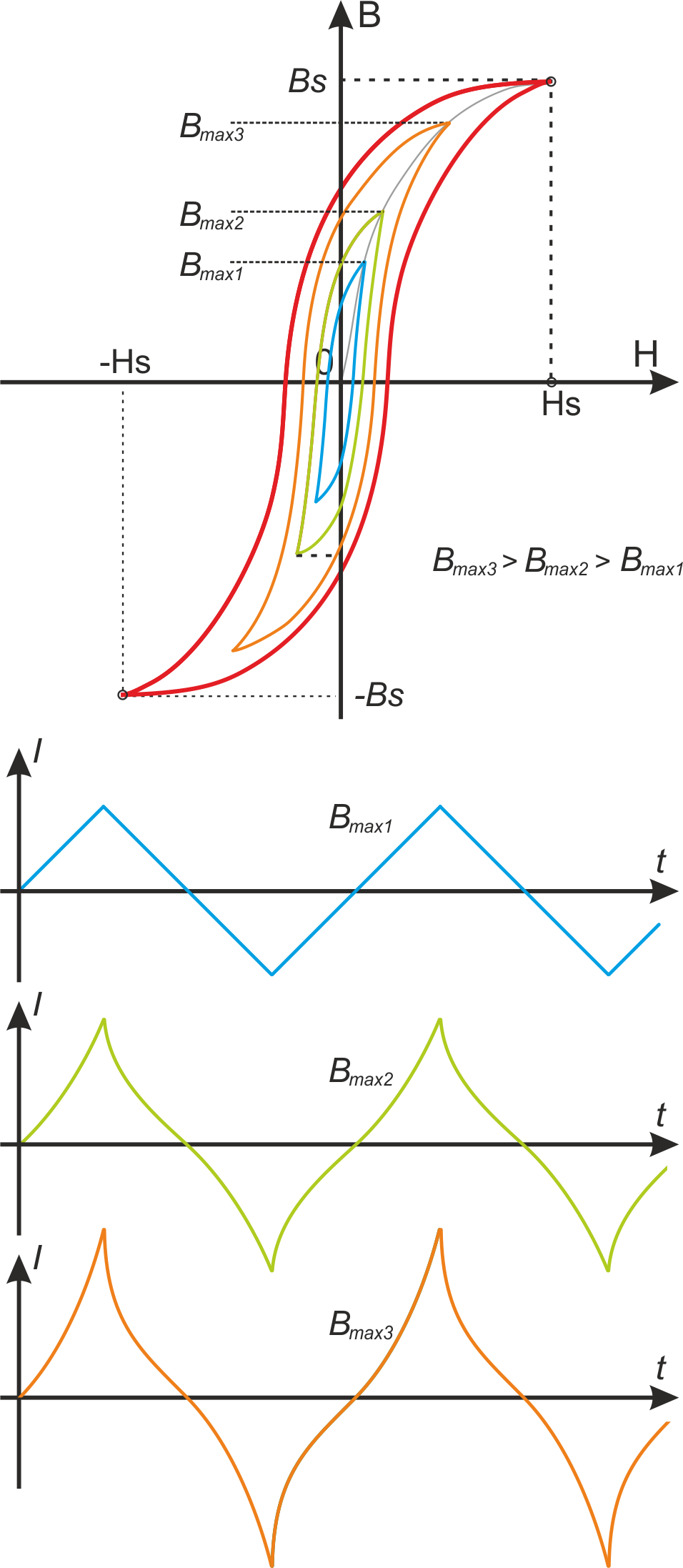
Рисунок T.6 – Петли гистерезиса и соответствующая им форма тока
Магнитная проницаемость
Одной из основных характеристик ферритов является магнитная проницаемость μ. Чем выше магнитная
проницаемость, тем выше значение индуктивности первичной обмотки при прочих равных условиях. Обратной
стороной является то, что с ростом μ возрастают потери на высоких частотах. Поэтому высокочастотные марки
ферритов обладают меньшими значениями магнитной проницаемости.
Величина магнитной проницаемости не является однозначной константой. Для определения магнитной проницаемости
в каждой точки цикла гистерезиса используют понятие дифференциальной магнитной проницаемости [Вдовин С. С.
Проектирование импульсных трансформаторов. – 2-е изд., перераб. и доп. — Л.: Энергоатомиздат. Ленингр.
отд-ние, 1991. — 208 с: ил.]:
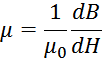
Для оценки магнитной проницаемости на конкретной кривой гистерезисного цикла:
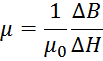
то есть магнитная проницаемость является фактически касательной к кривой петли гистерезиса.
График зависимости индукции магнитного поля в ферромагнетике от напряженности магнитного поля имеет вид петли
гистерезиса. Типичный вид петли гистерезиса феррита представлен на рисунке T.7.
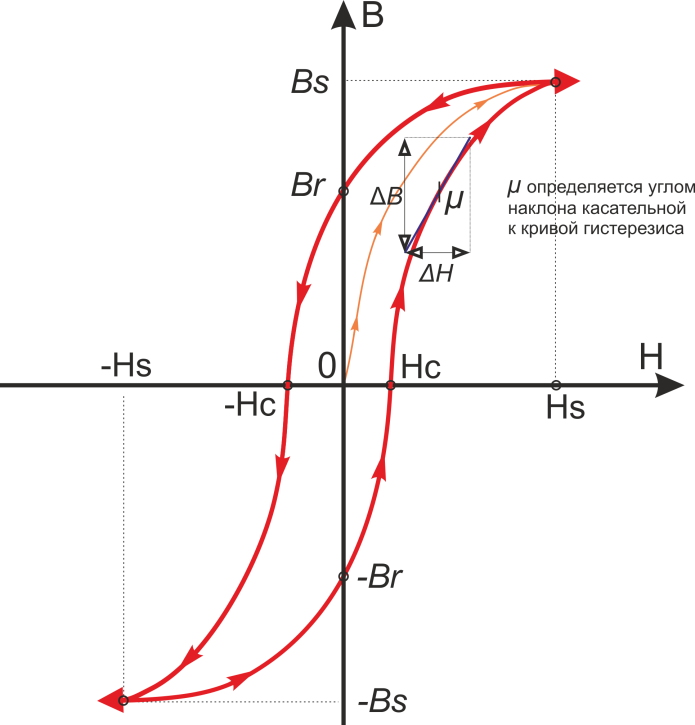
Рисунок T.7 – К пояснению понятия магнитной проницаемости. Магнитная проницаемость μ определяется
касательной к кривой петли гистерезиса.
Обычно в datasheet представлена так называемая начальная магнитная проницаемость μi(Initial
permeability) измеряемая в начале петли гистерезиса при малых магнитных полях – рисунок T.7.
Зависимость магнитной проницаемости феррита от температуры
Зависимость магнитной проницаемости ферритов от температуры имеет сложный характер. В целом увеличение
температуры примерно от 25 °С до 200 °С приводит к росту μ, а далее достигая максимума при некоторой
температуре (температуре Ж. Кюри) ≈200 °С резко спадает (рисунок T.8).
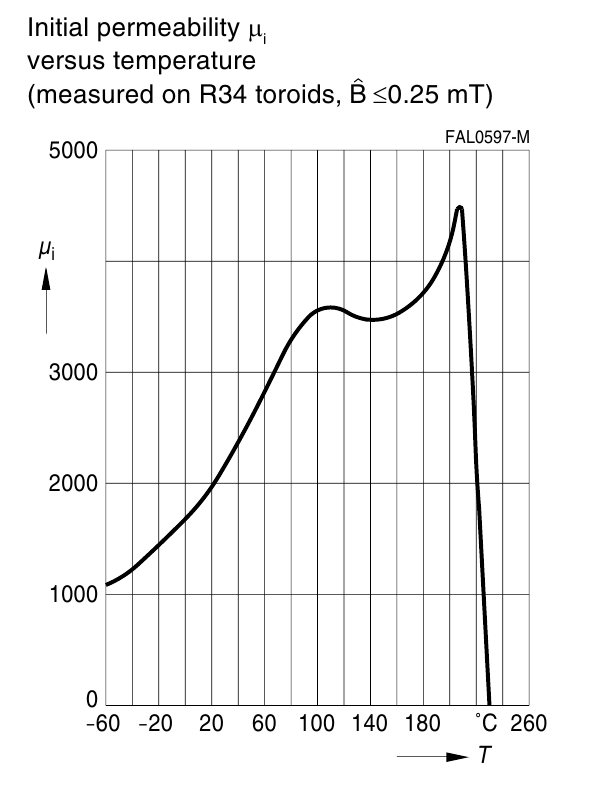
Рисунок T.8 – Зависимость начальной магнитной проницаемости от температуры для феррита N87 [Ferrites and
accessories. SIFERRIT material N87, EPCOS AG 2006]
Зависимость магнитной проницаемости феррита от частоты
Прежде чем рассмотреть зависимость магнитной проницаемости феррита от частоты сделаем небольшое отступление,
чтобы понять глубину вопроса.
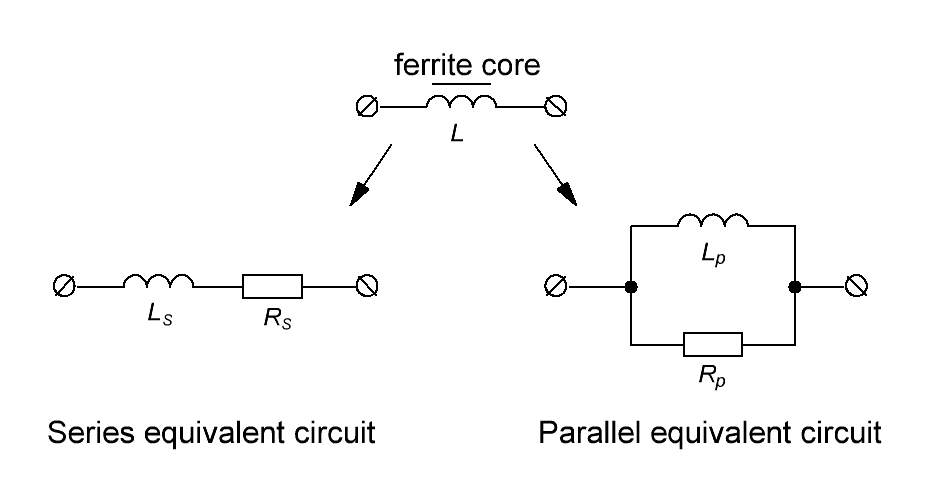
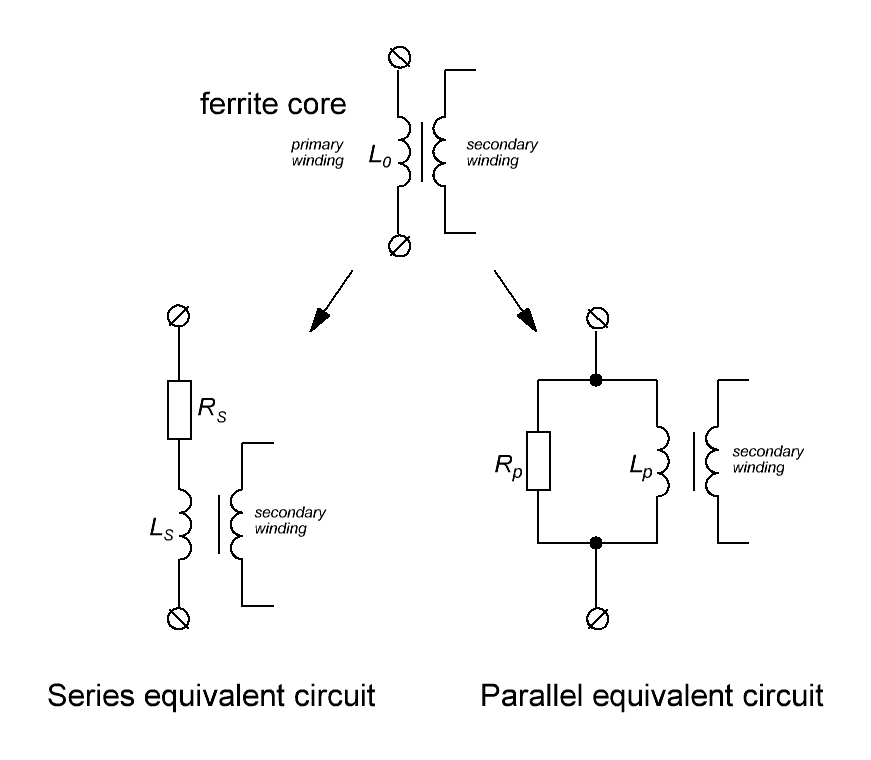
Индуктивность намагничивания L0 первичной обмотки трансформатора с сердечником из магнитомягкого
материала, например феррита (провода без сопротивления) можно представить как последовательное соединение
идеальной индуктивности Ls и некоторого сопротивления потерь Rs (последовательная
схема замещения) или как параллельное соединение идеальной индуктивности LP и некоторого
сопротивления потерь RP (параллельная схема замещения). Оба типа схемы замещения
представлены на рисунке T.9.
а
б
Рисунок T.9 – Последовательная и параллельная схемы замещения дросселя (а), и первичной обмотки
трансформатора (б) с ферритовым сердечником. Схема учитывает особенности поведения конкретного типа
феррита
с измерением частоты
Вводимые в схему замещения эквивалентные сопротивления учитывают (обобщают) потери на гистерезис, вихревые
токи и остаточную намагниченность.
Для последовательной схемы замещения суммарное активно-реактивное сопротивление Z будет определяться
выражением [Electronic components and materials textbook volume ii. Thanassis G. Giokas. ATH. STAMOULIS
PUBLICATIONS. 2004. 332 p. (CHAPTER 6 – 6.2 Attributes of ferrites)]:
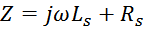
Соответственно реактивная и активная составляющая этой формулы определяют действительную и мнимую
составляющую:
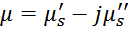
где:
μS’ – действительная составляющая μ, которая отвечает за собственно индуктивность LS;
μS’’ – мнимая составляющая μ, которая определяет потери – эквивалентное последовательное
сопротивление RS.
При этом отношение мнимой части к действительной равно отношению активного сопротивления к реактивному и
определяет угол сдвига фаз (тангенс угла потерь):
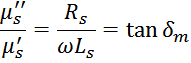
Отсюда можно вычислить величину активного сопротивления потерь:
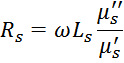
Для схемы замещения с параллельным сопротивлением Rp суммарное активно-реактивное сопротивление
будет определяться выражением:
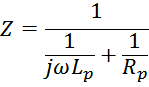
Соответственно:
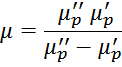
Тангенс угла будет иметь значение:
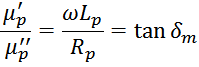
В datasheet на ферриты как правило приводится только данные по схеме с последовательным сопротивлением.
Однако зная μS’ и μS’’ можно получить μP’ и μP’’. Всоотсветствии
с [Electronic components and materials textbook volume ii. Thanassis G. Giokas. ATH. STAMOULIS PUBLICATIONS.
2004. 332 p. (CHAPTER 6 – 6.2 Attributes of ferrites)] получаем:
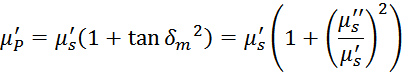
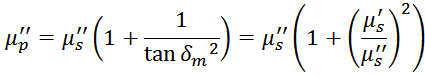
В эквивалентной схеме трансформатора удобнее использовать параллельное сопротивление Rp, напротив
при расчете дросселей удобнее использование последовательного сопротивления потерь RS.
Пример частотной зависимости различных составляющих магнитной проницаемости ферритов представлен на рисунке
T.10. Видно, что μ при малых частотах «индуктивная» часть μS’ практически не изменяется, далее
немного возрастает и резко спадает, начиная с некоторой граничной частоты. А «омическая» часть μS’’
определяющая потери с ростом частоты существенно возрастает приближаясь в максимуме к μS’ . Спад
μS’’ начинается после спада μS’.
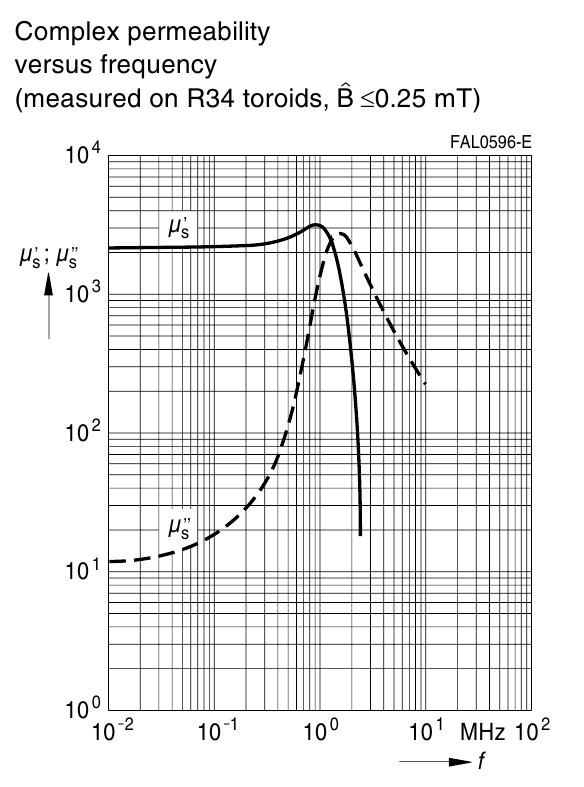
Рисунок T.10 – Зависимость различных составляющих комплексной проницаемости от частоты для феррита N87
[Ferrites and accessories. SIFERRIT material N87, EPCOS AG 2006]
Потери в магнитопроводе обусловленные свойствами феррита
Тепловая энергия, выделяемая в магнитопроводе выполненном из любого магнитного материала определяется
траекторией полета по петле гистерезиса и сколько кругов по этой петле будет намотано за единицу времени.
Выражаясь научными терминами, – размахом магнитной индукции B и рабочей частотой f. Для расчета потерь в
магнитопроводе Pferrit можно использовать следующее аппроксимирующее выражение [Optimum design of
a high-power, high-frequency transformer. R. Petkov. IEEE Transactions on Power Electronics (Volume: 11,
Issue: 1, Jan 1996)]:
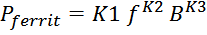
где:
f – частота;
B – размах индукции;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
В большинстве случаев справочные листки на ферриты не содержат информации об аппроксимационных коэффициентах,
и для определения потерь в магнитопроводе можно использовать соотношение:
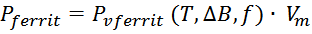
где:
Pvferrit – мощность потерь на единицу объема, являющаяся функцией температуры, магнитной индукции
и частоты;
Vm – объем магнитопровода.
Мощность потерь на единицу объема Pvferrit определяется типом феррита и приводится в
справочных данных на конкретный тип магнитного материала. Использование удельной мощности потерь на единицу
объема является удобным способом расчета потерь в магнитопроводе.
На рисунке T.11 представлена зависимость мощности потерь от частоты при различных значениях индукции
магнитного поля и температуре для феррита N87.
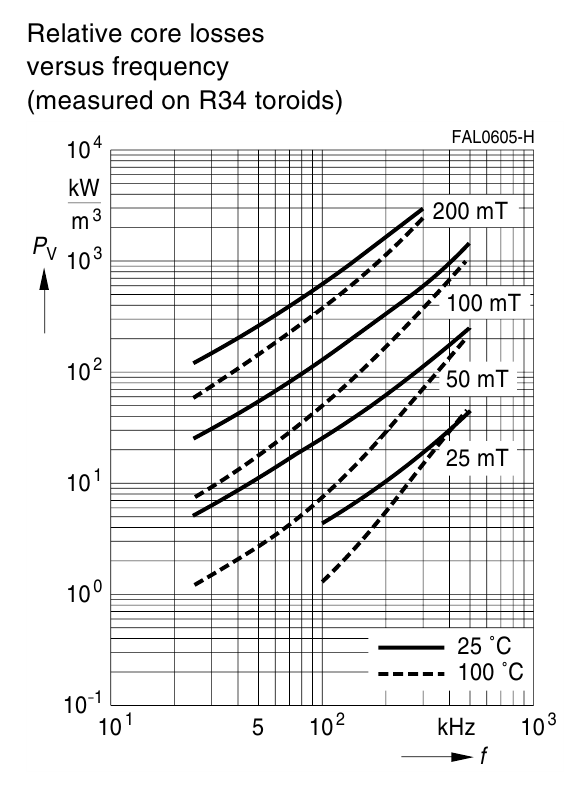
Рисунок T.11 – Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87[Ferrites and accessories. SIFERRITmaterial N87, EPCOS AG 2006]
Распространенные типы ферритов для импульсных источников питания и их характеристики
Таблица T.4 содержит данные о наиболее используемых типах силовых ферритов. Более подробно параметры всех
основных типов ферритов используемых в элементах силовой электроники представлены в соответствующих
datasheet-ах производителей магнитопроводов.
Таблица T.4 – Наиболее распространенные типы ферритов, предназначенные для использования в импульсных
источниках питания
|
Тип феррита |
Область применения, особенности |
Материал |
Оптимальный частотный диапазон, кГц |
Магнитная проницаемость μ |
Максимальная индукция Bmax, Тл |
Коэрцитивная сила, Hс, |
Производитель, ссылка |
||
| 25 ºС | 100 ºС | 25 ºС | 100 ºС | ||||||
| N27 | Трансформаторы обратноходовых преобразователей. Низкая стоимость, используется. для мощных источников |
MnZn | 25 – 150 | 2000 | 500 | 410 | 23 | 19 | EPCOS [Ferrites and accessories SIFERRIT material N27. EPCOS AG 2006] [Siemens Matsushita Components. Ferrites and Accessories] |
| N41 | Трансформаторы тока, дроссели | MnZn | 25 – 150 | 2800 | 490 | 390 | 22 | 20 | EPCOS [Ferrites and accessories SIFERRIT material N41. EPCOS AG 2006] [Siemens Matsushita Components. Ferrites and Accessories] |
| N87 | Стандартные источники питания | MnZn | 25 – 500 | 2200 | 490 | 390 | 21 | 13 | EPCOS [Ferrites and accessories SIFERRIT material N87. EPCOS AG 2006] |
| 3C90 | Трансформаторы импульсных источников питания | MnZn | До 200 кГц | 2300 | 470 | 380 | 16 | 12 | Philips – Ferroxcube [Soft Ferrites and Accessories, 2000 Apr 20] [3C90 Material specification, Ferroxcube, 2008 Sep 01] |
| 3C95 | Трансформаторы импульсных источников питания | MnZn | До 500 кГц | 3000 | 530 | 410 | 13 | 7 | Philips – Ferroxcube [3C95Material specification, Ferroxcube, 2008 Sep 01] |
| 3F3 | Трансформаторы импульсных источников питания | MnZn | 200-500 | 2000 | 440 | 370 | 15 | 11 | Philips – Ferroxcube [Soft Ferrites and Accessories, 2000 Apr 20] [3F3Material specification, Ferroxcube, 2008 Sep 01] |
| PC47 | Для силовых трансформаторов и дросселей | MnZn | До 300 кГц* | 2500 | 530 | 420 | 13 | 6 | TDK [Ferrite for Switching Power Supplies Summary. June 2012. TDK] |
| PC90 | Для силовых трансформаторов и дросселей | MnZn | До 300 кГц* | 2200 | 540 | 450 | 13 | 6.5 | TDK [Ferrite for Switching Power Supplies Summary. June 2012. TDK] |
| PC95 | Для силовых трансформаторов и дросселей | MnZn | До 300 кГц* | 3300 | 530 | 410 | 9.5 | 6.5 | TDK [Ferrite for Switching Power Supplies Summary. June 2012. TDK] |
| 2500НМС1 | Для силовых трансформаторов и дросселей | MnZn | До 100 кГц | 2500 | 290 | ОАО “Ферроприбор” [http://www.rusgates.ru] | |||
| 2500НМС2 | Для силовых трансформаторов и дросселей | MnZn | До 100 кГц | 2200 | 330 | ОАО “Ферроприбор” [http://www.rusgates.ru] | |||
| 2500НМС5 | Для силовых трансформаторов и дросселей | MnZn | До 200 кГц | 3300 | 310 | ОАО “Ферроприбор” [http://www.rusgates.ru] | |||
| 3000НМС | Для силовых трансформаторов и дросселей | MnZn | 30-50 кГц | ОАО “Ферроприбор” [http://www.rusgates.ru] |
Среди ферритов российского производства наилучшими характеристиками для целей силовой электроники обладают
ферриты марки 2500НМС [Силовая электроника. Профессиональны решения. Борис Семенов. Солон-Пресс, ДМК Пресс,
2011, 416 c.].
Необходимо отметить, что ферриты подвержены старению. В связи с этим необходимо проектирование устройств с
некоторым запасом.
Обмотки
Обмотка трансформатора или дросселя – это базовый элемент обеспечивающий формирование магнитного поля и
возбуждение ЭДС индукции (см. пункт «Физика работы импульсного трансформатора» настоящего раздела). Она
играет роль «концентрированного» проводника с током.
Как правило, обмотка выполняется из медного провода в эмалевой изоляции и выполняется на каркасе,
конструктивно комплементарном с магнитопроводом. Ниже представлены конструктивные особенности данных
элементов.
Конструктивные особенности обмоток
Обмотки трансформатора и силового дросселя должны быть хорошо изолированы как от магнитопровода, так и между
собой [Расчет трансформаторов и дросселей малой мощности. Белопольский И.И. М.: Госэнергоиздат, 1963. – 207
с.: ил.].
Для изоляции обмоток от магнитопровода используется каркас (или изоляционный слой в случае кольцевых
трансформаторов), изоляция обмоток между собой осуществляется за счет межобмоточной изоляции и наконец, для
обеспечения взаимной изоляции слоев при высоких напряжениях на обмотке используют межслоевую изоляцию.
Межслоевая изоляция
Межслоевая изоляция используется при достаточно высоких напряжениях в обмотках трансформаторов для
предотвращения межвиткового пробоя. При малых напряжениях на обмотке межслоевая изоляция может не
использоваться и её функцию выполняет изоляция провода обмотки. При выполнении одной из обмоток хорошо
изолированным проводом необходимость в межобмоточной изоляции так-же отсутствует.
Межслоевая изоляция напрямую влияет на паразитные параметры трансформатора – увеличение межслоевой изоляции
приводит с одной стороны к росту индуктивности рассеяния обмотки, а с другой стороны – к уменьшению её
паразитной емкости.
Межобмоточная изоляция
Межобмоточная изоляция необходима для изоляции обмоток друг от друга. В ряде случаев функцию межобмоточной
изоляции выполняет секционированный каркас. Толщина изоляции влияет на межобмоточную емкость.
Материалы для изоляции обмоток
Тип используемых изоляционных материалов зависит от условий эксплуатации трансформатора. Срок службы изоляции
определяется, прежде всего, температурой её эксплуатации. Используются две величины температур:
– среднее значение увеличения температуры;
– увеличение температуры в горячих пятнах, образующихся в результате неравномерности охлаждения
трансформатора;
Таблица T.5 – Взаимосвязь между допускаемым температурным режимом, способом охлаждения и рекомендуемым типом
диэлектрика для выполнения межобмоточной и межслоевой изоляции [Силовая электроника. Руководство
разработчика. Кит Сукер. Додэка XXI. 2008. 256 c. ; Источники питания. Расчет и конструирование. Мартин
Браун. МК-Пресс. 2005, 288 c.]
| Способ охлаждения | Среднее увеличение температуры, °С | Увеличение температуры в горячих пятнах, °С | Рекомендуемый диэлектрик |
| Масло или принудительная воздушное охлаждение | 55 | 10 | Крафт-бумага, ХБ-лента, ПВХ-лента и т.д. |
| Воздушное охлаждение | 80 | 30 | Майларовая пленка, эпоксидные композиции |
| Воздушное охлаждение | 115 | 30 | Изоамидная изоляция |
| Воздушное охлаждение | 150 | 30 | Изоамидная изоляция, Номекс |
Способы намотки
Существует несколько способов намотки – рядовая обмотка («виток к витку») имеющая две разновидности: –
N-образная намотка и U- образная намотка [Импульсные источники питания. Теоретические основы проектирования
и руководство по практическому применению. Раймонд Мэк. “Додэка-XXI”, 2008. 274 с.]. Рядовой способ намотки
позволяет обеспечить максимальную равномерность и плотность обмотки.
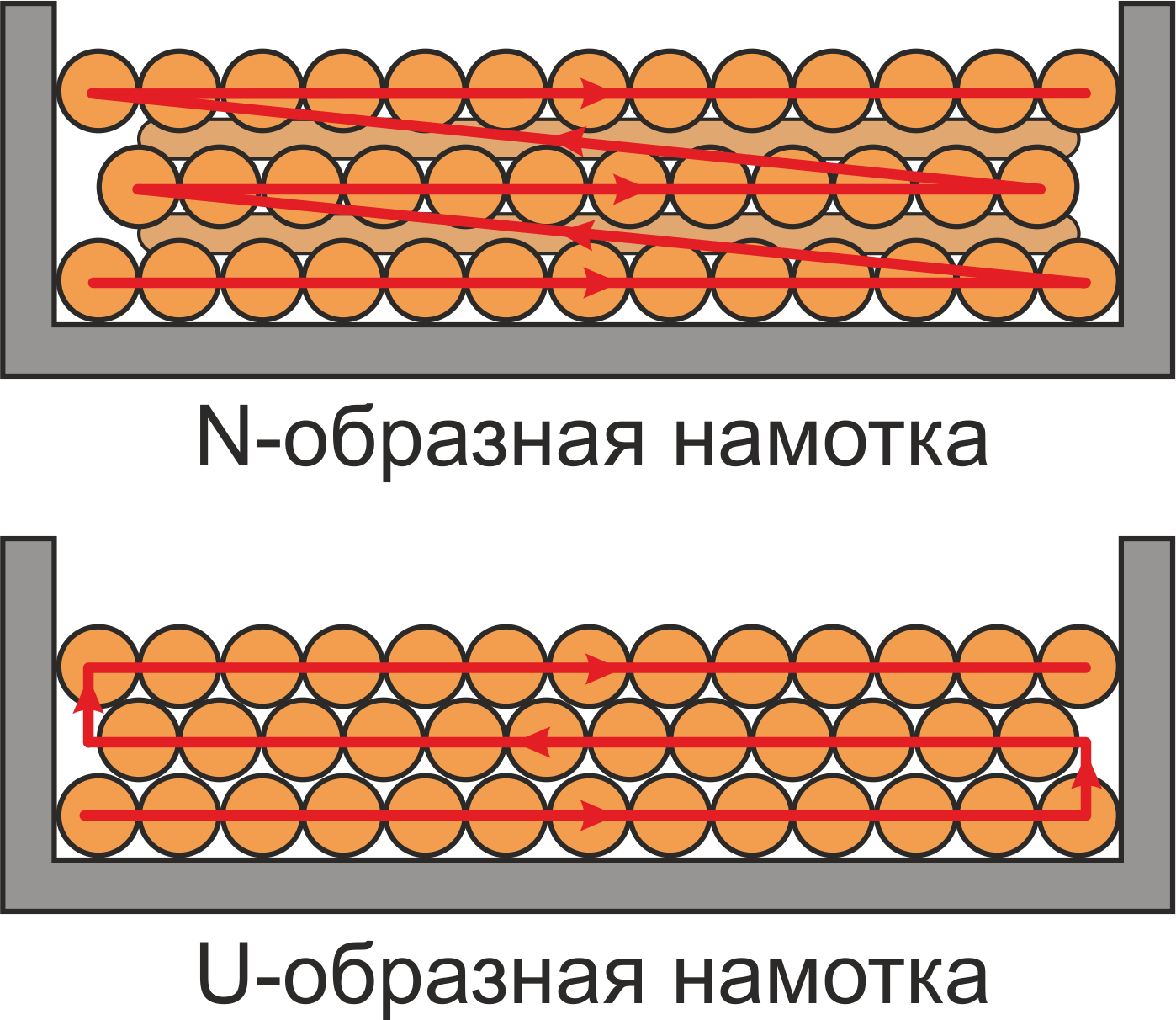
Рисунок T.12 – Способы намотки: N-образная намотка и U-образная намотка
Другой способ выполнения обмотки – обмотка «внавал», с беспорядочным расположением витков в окне
магнитопровода. Такой способ намотки допустим при небольших напряжениях.
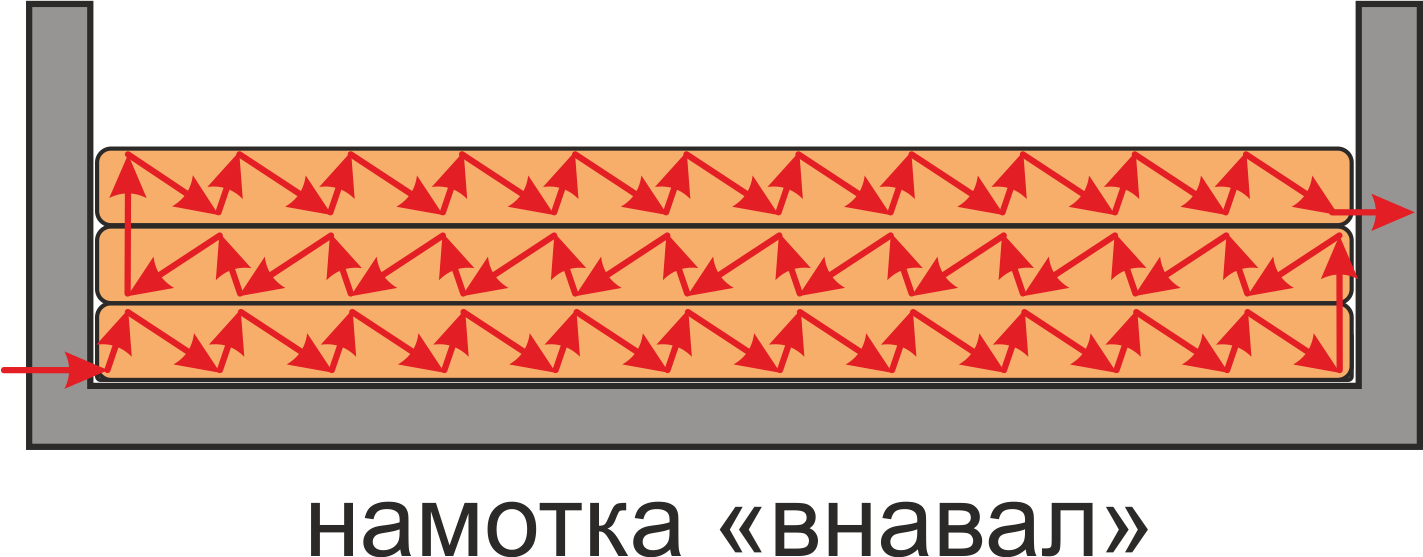
Рисунок T.13 Способ намотки «внавал»
При рядовом способе выполнения обмотки («виток к витку») чаще всего используется U-образная намотка (рисунок
T.12) в которой между концами слоев существует большая разность потенциалов и следовательно запасаемая
энергия и эквивалентная паразитная емкость обмотки. С целью уменьшения паразитной емкости обмотки используют
N-образный способ намотки, при котором каждый слой наматывается в одном и том-же направлении, а соединение
слоев осуществляется стежками прокладываемыми вдоль обмотки. При этом разность потенциалов между обмотками
будет одинакова по всей длине обмотки.
С целью снижения паразитной емкости между слоями используют прокладку слоев изолирующей ленты.
Для уменьшения паразитной емкости используют поступательную намотку (при сравнительно толстом проводе и в
случае если число слоев равно 2-м) или секционную обмотку (рисунок T.14). Кроме уменьшения емкости
использование секционной обмотки существенно увеличивает рабочее напряжение обмотки и поэтому конструктивный
прием секционирования обмоток часто используется в высоковольтных трансформаторах.
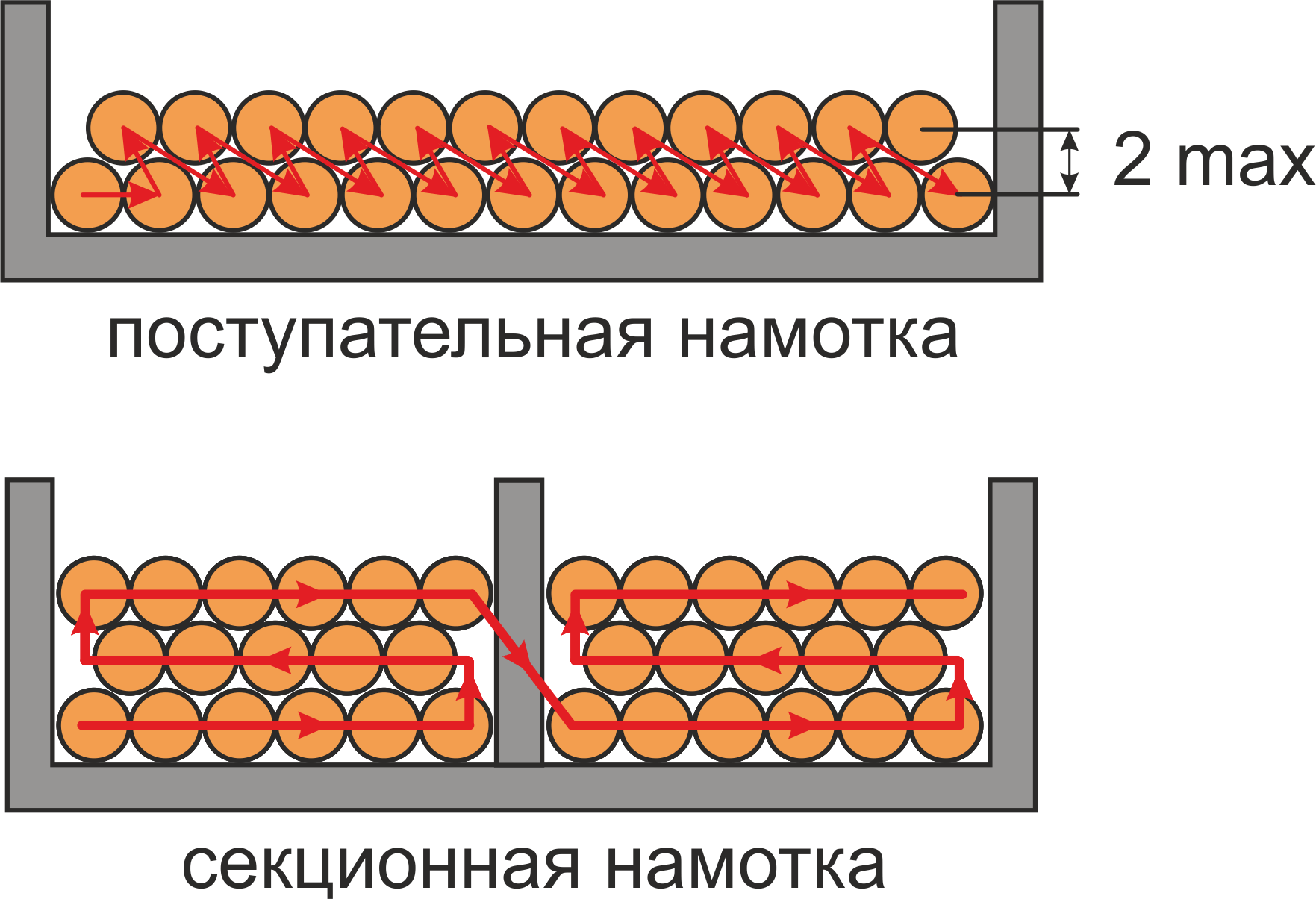
Рисунок T.14 – Способы намотки: поступательная намотка, секционная обмотка
Каркас
Для Ш- П- образных (и т.д.) магнитопроводов обмотка выполняется на каркасе, изготавливаемом из пластмассы и
играющем роль изолятора обмоток от магнитопровода. Кроме этого каркас содержит выводы для крепления выводов
обмоток. Особо следует отметить, что каркас, изготавливаемый из термопластичных пластмасс – ПВХ,
полипропилена может размягчаться под действием чрезмерного нагрева магнитопровода и обмоток.
Расположение обмоток внутри магнитопровода
С целью уменьшения длины провода обмоток ближе к сердечнику целесообразно располагать обмотку имеющую большее
число витков. С целью увеличения магнитной связи между обмотками и уменьшения индуктивности рассеяния
используют чередование обмоток внутри магнитопровода: сначала на каркас наматывается половина
первичной обмотки, затем половина вторичной, затем вторая половина первичной затем вторая половина
вторичной. Таким образом, получается слоеный бутерброд, межобмоточная емкость возрастает, а индуктивность
рассеяния снижается. Для трансформаторов с малым числом витков и низким межобмоточным напряжением
используется намотка соединёнными вместе проводами первичной и вторичной обмоток. Этот способ часто
используется при создании трансформаторов пуш-пул преобразователей.
Электростатическая защита (экран Фарадея) между обмотками
Электростатическая защита между первичной и вторичной обмотками используется для устранения синфазных помех
из цепи первичной обмотки возникающих за счет емкостной связи между обмотками [Силовая электроника.
Руководство разработчика. Кит Сукер. Додэка XXI. 2008. 256 c.]. Электростатическая защита представляет собой
заземленный экран из медной фольги, размещаемый между первичной и вторичной обмотками. Введение экрана
Фарадея в конструкцию трансформатора снижает его технологичность и может стать причиной электрического
пробоя межу экраном и проводниками обмоток в местах их выхода для соединения с выводами каркаса
трансформатора. По этим причинам использование экрана Фарадея в трансформаторах допускается в случае крайней
необходимости. Виток экрана должен быть обязательно разомкнутым.
Технологические особенности намотки кольцевых и тороидальных трансформаторов
Особенностью намотки трансформаторов на кольцевых и тороидальных магнитопроводах является необходимость
равномерности распределения обмотки по всей длине магнитопровода. Несоблюдение этого условия может стать
причиной насыщения отдельных участков магнитопровода, что приведет к увеличению потерь в магнитопроводе и
возрастанию тока в цепи.
Выполнение обмоток для тороидальных трансформаторов имеет ряд конструктивных особенностей [Расчет
трансформаторов и дросселей малой мощности. Белопольский И.И. М.: Госэнергоиздат, 1963. – 207 с.: ил.].
Во-первых, для у тороидальных трансформаторов отсутствует каркас и изоляция осуществляется путем обматывания
магнитопровода изоляционным материалом. Необходимо отметить, что существуют кольцевые магнитопроводы с уже
нанесенным однородным слоем полимерной изоляции. Во-вторых, обмотка располагается по всей длине
магнитопровода трансформатора (закрывает его). Третьей конструктивно особенностью является различие внешнего
и внутреннего диаметров. Следствием этого является высокая плотность обмотки по внутренней части окна и
расстояния между витками по наружной части магнитопровода (рисунок T.15). Это ограничивает возможности
применения межслоевой изоляции, и для изготовления обмоток тороидальных трансформаторов используют провода с
повышенной электрической прочностью.
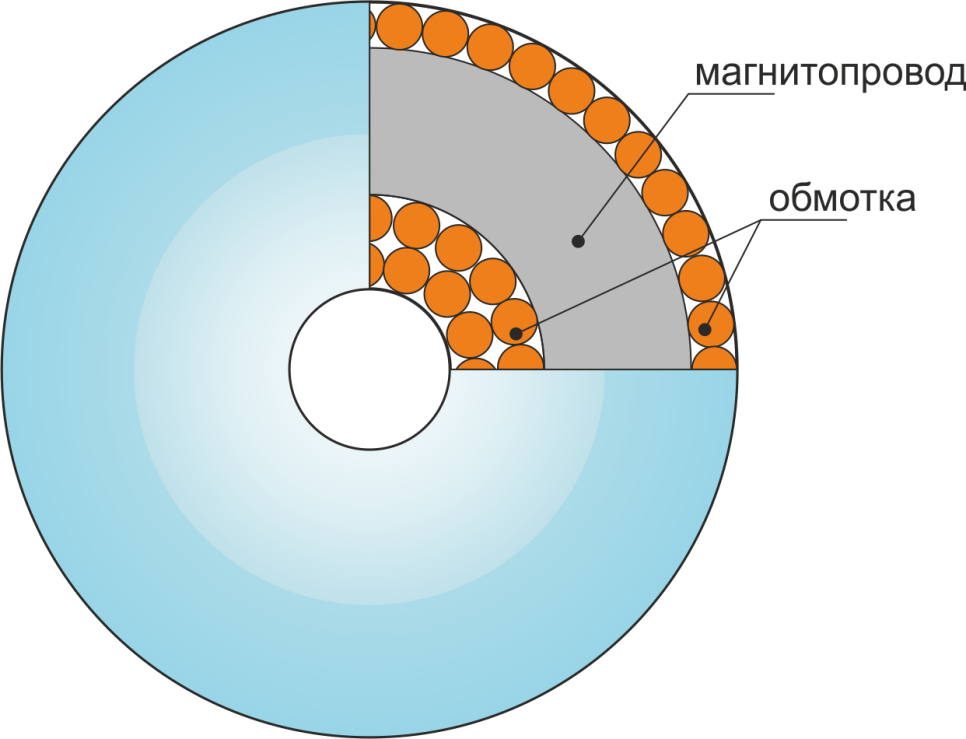
Рисунок T.15 – Обмотка тороидальных трансформаторов. Видно утолщение обмотки обмотки во внутреннем кольце
тора
Эквивалентная схема трансформатора
Для расчета работы трансформатора в том или ином режиме используют эквивалентную схему замещения
трансформатора, учитывающую его реальные характеристики и паразитные параметры. В настоящее время существует
несколько типов эквивалентных схем замещения, учитывающих или не учитывающих те или иные паразитные
параметры трансформатора.
Наиболее полная эквивалентная схема двухобмоточного трансформатора, приведенная к первичной обмотке
представлена на рисунке T.16 [Силовая электроника: от простого к сложному. Борис Семенов. Солон-Пресс. 2006.
416 с. ; Теория и расчет трансформаторов малой мощности. Ю.Н. Стародубцев. РадиоСофт. 2011. 320 с.] [Вдовин
С. С. Проектирование импульсных трансформаторов. – 2-е изд., перераб. и доп. — Л.: Энергоатомиздат. Ленингр.
отд-ние, 1991. — 208 с: ил.]. В данной эквивалентной схеме в качестве внешних элементов присутствует
электрическое сопротивление, емкость нагрузки и внутреннее сопротивление источника.
При расчете паразитных элементов необходимо помнить, что трансформатор – это достаточно сложный
электромагнитный прибор с распределенными паразитными параметрами, и приведение их к дискретным параметрам
весьма условно, но, тем не менее, позволяет оценить порядки величин искажений, обусловленных паразитными
элементами.
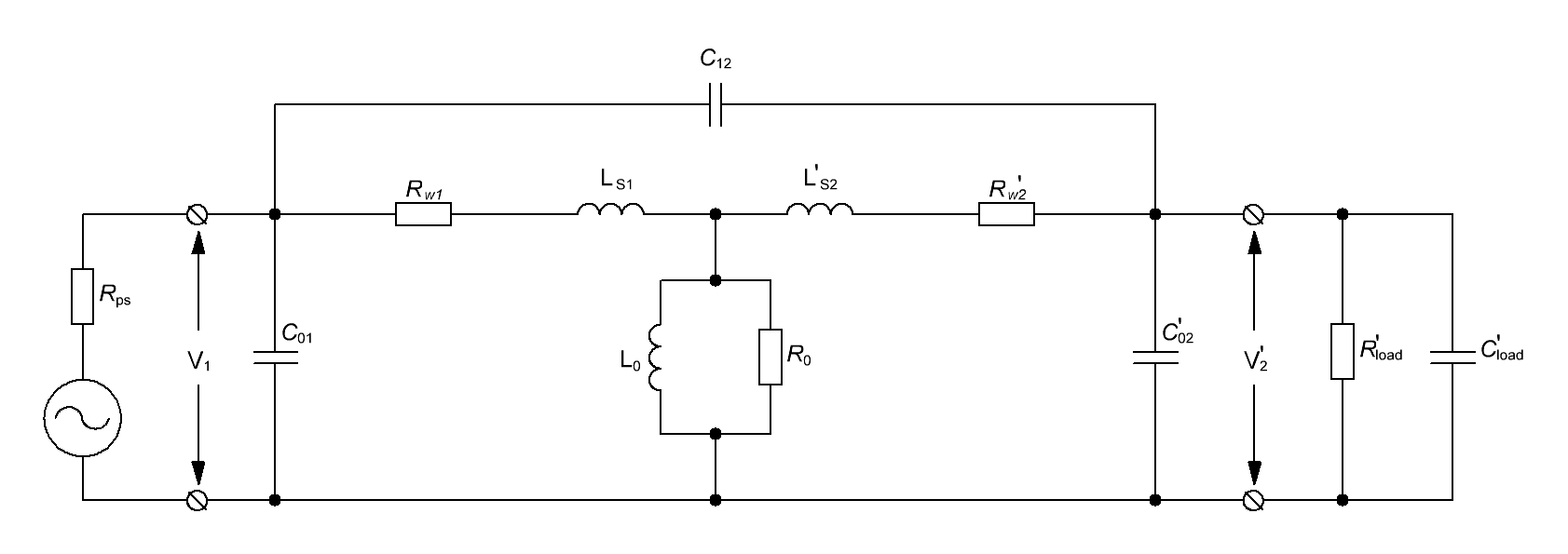
Рисунок T.16 – Эквивалентная схема трансформатора
Эквивалентная схема трансформатора содержит следующие параметры:
– индуктивность намагничивания L0 ;
– индуктивность рассеивания первичной обмотки LS1 ;
– приведенная индуктивность рассеивания вторичной обмотки LS2’ ;
– сопротивление первичной обмотки Rw1 ;
– приведенное сопротивление вторичной обмотки Rw2’ ;
– сопротивление активных потерь в магнитопроводе R0 ;
– межвитковая емкость первичной обмотки С01 ;
– приведенная межвитковая емкость вторичной обмотки С02’;
– межобмоточная емкость С12 .
Индуктивность намагничивания L
0
Индуктивность намагничивания фактически представляет собой собственную индуктивность первичной обмотки
трансформатора. Она определяется геометрическими параметрами магнитопровода и материала, из которого он
изготовлен. Расчет индуктивности намагничивания для магнитопроводов с зазором и без него осуществляется по
формулам:
– для трансформаторов с замкнутыми магнитопроводами (например ферритовые кольца) индуктивность определяется
по формуле:
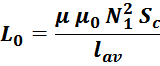
μ0 – магнитная постоянная, 1,25663 – 10-6 Гн/м;
μ – магнитная проницаемость материала сердечника;
N1 – число витков первичной обмотки;
Sc – эффективная площадь сечения магнитопровода;
lav – эффективная длина средней линии магнитопровода.
– для трансформаторов с зазором в магнитопроводе индуктивность намагничивания определяется по формуле [Теория
и расчет трансформаторов источников вторичного электропитания. А. В. Хныков. СОЛОН-Пресс. 2010. 127 с.]:
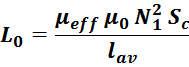
где:
μeff – магнитная проницаемость материала сердечника с зазором:
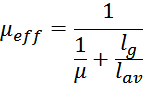
где:
μ – магнитная проницаемость материала сердечника;
lg – длина магнитного зазора.
Как правило, в справочных листках (datasheet) на конкретный магнитопровод приводится справочный параметр
сердечника AL , (nH). Этот параметр учитывает параметры и геометрию магнитопровода более точно,
по сравнению с соотношением L0 (особенно для магнитопроводов с интегрированным зазором). В этом
случае индуктивность намагничивания вычисляется по соотношению:
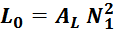
Индуктивность рассеивания первичной обмотки LS1
Индуктивность рассеяния рассчитывают исходя из площади охватываемой током и не являющейся частью площади
магнитопровода. Индуктивность рассеяния первичной обмотки является та часть её индуктивности, которая не
связанна с магнитопроводом и вторичной обмоткой. То есть фактически это площадь «воздушного зазора» между
обмоткой и магнитопроводом, поскольку в данном случае часть магнитного потока замыкается не через
магнитопровод, а замыкается «через воздух».
Для Ш- и П- образных сердечников индуктивность рассеяния рассчитывается по формуле для индуктивности
соленоида без магнитопровода:
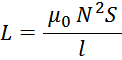
в которой в качестве площади S входит эффективная площадь Sis охватываемая током, и не являющаяся
площадью магнитопровода, в качестве длины соленоида входит hw1 – высота обмотки.
Эффективная площадь Sis может быть определена по соотношению (рисунок T.17):
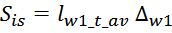
где:
– lw1_t_av – средняя длина витка первичной обмотки;
– Δw1 – расстояние от «среднего витка» первичной обмотки, расположенного посередине
толщины намотки, до магнитопровода. Или Δw1 – толщина намотки в случае соленоида.
В итоге получаем, формулу для приближенного расчета индуктивность рассеяния:
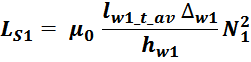
lw1_t_av – средняя длина витка первичной обмотки;
Δw1 – расстояние от «среднего витка» первичной обмотки (расположенного посередине
обмотки), до магнитопровода;
hw1 – высота первичной обмотки. В случае кольцевых магнитопроводов – длина средней
линии магнитопровода, в случае если обмотка равномерно распределена по магнитопроводу или длина сектора, в
случае частичного охвата обмоткой длины кольца магнитопровода.
Представленной формулы так же будет достаточно для получения оценочного значения индуктивности рассеяния.
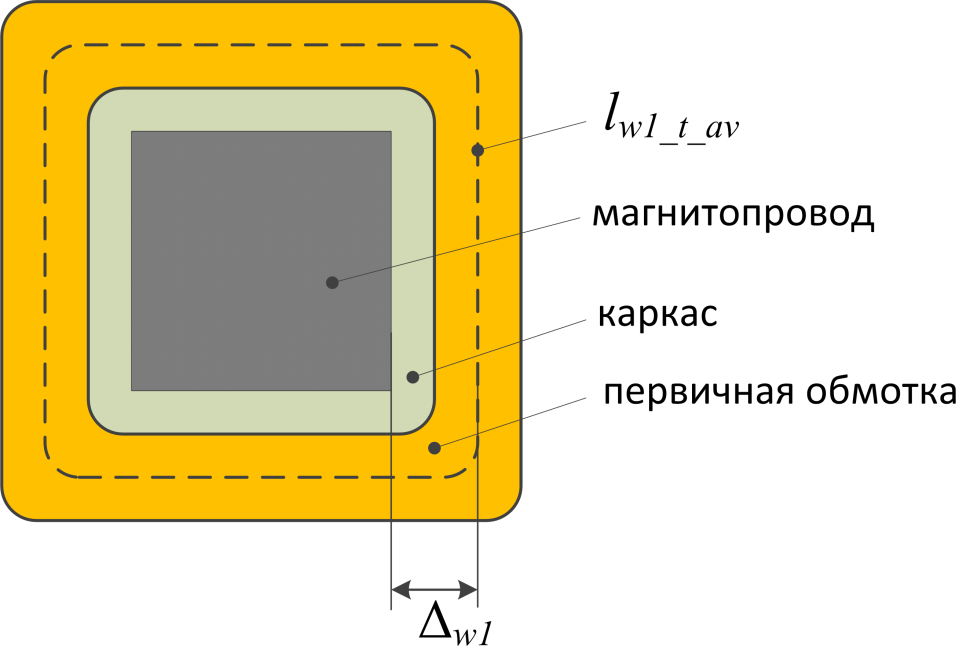
Рисунок T.17 – К оценке индуктивности рассеяния. Поперечное сечение трансформатора – сердечника, каркас,
первичная обмотка. Показана ширина обмотки и средняя линия
Для вычисления индуктивности рассеяния обмоток на магнитопроводах различных конфигураций, отличающихся от Ш-
и П- образной геометрии можно воспользоваться соотношениями приведенными ниже.
Соотношения для вычисления индуктивность рассеивания первичной обмотки LS1
для различных геометрий магнитопроводов
Коаксиальные цилиндрические обмотки
Для более точного вычисления индуктивности рассеяния коаксиальных цилиндрических обмоток можно
воспользоваться следующим соотношением [Электромагнитные элементы радиоэлектронной аппаратуры. Русин Ю.С.,
Гликман И.Я., Горский А.Н. Радио и связь. 1991. 224 с.]:
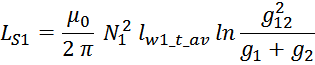
где:
lw1_t_av– средняя длина витка первичной обмотки;
μ0 – магнитная постоянная, 1,25663 – 10-6 Гн/м;
N1 – число витков первичной обмотки;
g1, g2, g12 – параметры геометрии.
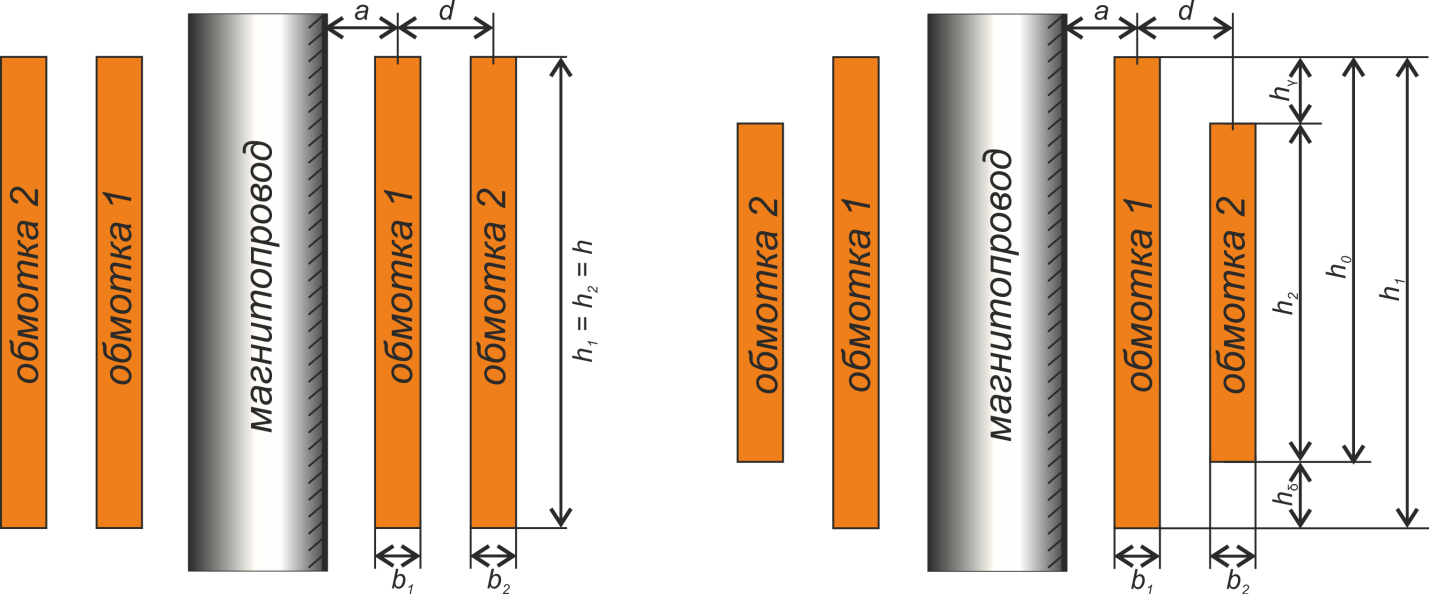
Рисунок T.18 – К расчету индуктивности рассеяния коаксиальных цилиндрических обмоток
Характерные параметры геометрии g1, g2, g12 – находятся из соотношений
(рисунок T.18):
g1 – характерный параметр для первичной обмотки вычисляется по формуле:
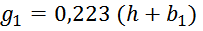
g2 – характерный параметр для вторичной обмотки вычисляется по формуле:
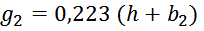
g12 – характерный параметр для межобмоточного пространства вычисляется по формуле:
– для обмоток, имеющих одинаковую высоту:
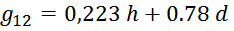
– для обмоток, имеющих разную высоту при условии, что
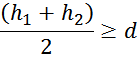
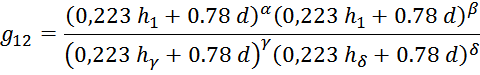
где:
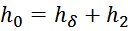
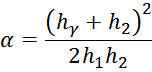
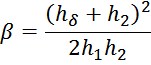
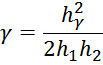
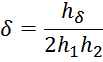
здесь:
h1 – высота первичной обмотки;
h2 – высота вторичной обмотки;
hδ – смещение вторичной обмотки относительно первичной снизу;
hγ – смещение вторичной обмотки относительно первичной сверху;
h0 – сумма высоты вторичной обмотки и смещения вторичной обмотки относительно первичной сверху;
b1 – толщина первичной обмотки;
b2 – толщина вторичной обмотки;
a – расстояние от магнитопровода до центральной части первичной обмотки;
d – расстояние от центральной части первичной обмотки до центральной части вторичной обмотки.
В первом приближении при значительной толщине обмоток данные расчетные соотношения можно использовать для
расчета трансформаторов с квадратным сечением магнитопровода.
Обмотки на кольцевом сердечнике
Для обмоток на кольцевом сердечнике можно воспользоваться следующим соотношением
[Электромагнитные элементы радиоэлектронной аппаратуры. Русин Ю.С., Гликман И.Я., Горский А.Н. Радио и
связь. 1991. 224 с.]:
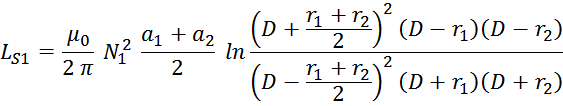
μ0 – магнитная постоянная, 1,25663 – 10-6 Гн/м;
N1 – число витков первичной обмотки;
D – средний диаметр кольцевого сердечника (среднее между внешним и внутренним диаметром);
a1 – высота среднего витка первичной обмотки (см. рисунок T.19);
a2 – высота среднего витка вторичной обмотки (см. рисунок T.19);
r1 – ширина среднего витка первичной обмотки (см. рисунок T.19);
r2 – ширина среднего витка вторичной обмотки (см. рисунок T.19).
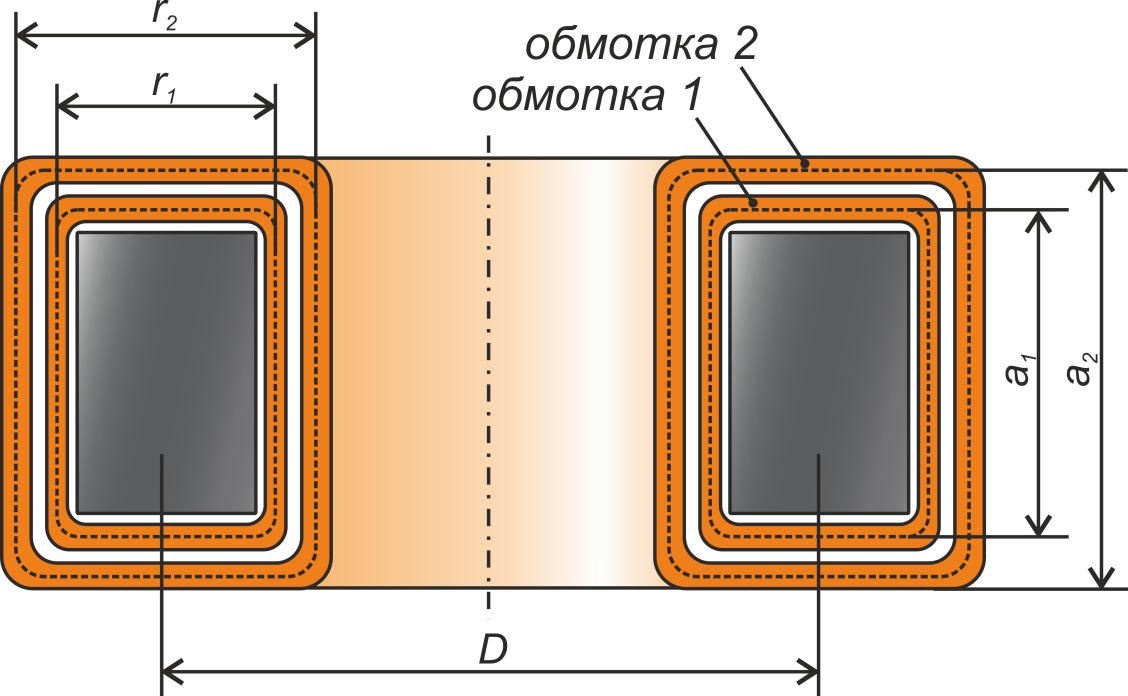
Рисунок T.19 – К расчету индуктивности рассеяния коаксиальных цилиндрических обмоток
При частичном заполнении обмотками поверхности кольцевого магнитопровода индуктивность рассеяния рассчитывают
как индуктивность рассеяния цилиндрических обмоток, принимая за высоту обмотки её радиальную длину.
Способы уменьшения индуктивности рассеяния
Индуктивность рассеяния, как правило, оказывает негативное влияние на работу трансформатора (индуктивность
рассеяния влияет на динамические характеристики, снижая скорость роста тока в обмотках). Кроме этого
трансформатор с высокой индуктивностью рассеяния является источником электромагнитных помех повышенного
уровня.
Из представленных формул для нахождения индуктивностей рассеяния обмоток трансформатора следуют несколько
важных выводов:
– чем ближе обмотка к сердечнику, тем меньше индуктивность рассеяния;
– чем меньше толщина обмотки, тем меньше индуктивность рассеяния;
– в случае кольцевых магнитопроводов необходимо равномерно распределять обмотку по всему кольцу
магнитопровода с целью уменьшения индуктивность рассеяния;
– в зависимости от того, какая обмотка первичная или вторичная будет ближе к магнитопроводу у той и
индуктивность рассеяния будет меньше;
– использование магнитопровода с длинным центральным стержнем приводит к снижению индуктивности рассеяния
(так как высота первичной обмотки стоит в знаменателе выражения для расчета индуктивности рассеяния). Чем
длиннее обмотка, тем меньше индуктивность рассеяния [Источники питания. Расчет и конструирование. Мартин
Браун. МК-Пресс. 2005, 288 c.];
– значительного уменьшения индуктивности рассеяния можно добиться путем секционирования обмоток;
– уменьшение числа витков приводит к уменьшению индуктивности рассеяния и эта зависимость квадратична (так,
для случая трансформатора обратноходового преобразователя уменьшение числа витков приводит к существенному
снижению требований к демпферу и соответственно к его массогабаритным характеристикам).
Существует несколько способов снижения индуктивности рассеяния [Транзисторная преобразовательная техника.
Мелешин В.И. Техносфера. 2005. 626 с.]:
– для трансформаторов на кольцевых сердечниках целесообразно совместная намотка проводников первичной и
вторичной обмоток;
– для П- и Ш- образных сердечников необходимо располагать одну обмотку под другой, размещение обмотки в один
ряд, чередование обмоток. Или размещение вторичной обмотки между двух слоев первичной приводит к снижению
индуктивности рассеяния [Источники питания. Расчет и конструирование. Мартин Браун. МК-Пресс. 2005, 288
c.].
Индуктивность рассеяния увеличивается при:
– разнесении обмоток на магнитопроводе;
– увеличение толщин изоляции между магнитопроводом и обмотками, изоляции между обмотками;
– увеличение толщины обмотки;
– увеличение числа витков;
– уменьшение длины обмотки.
Индуктивность рассеяния трансформатора кроме этого зависит от посторонних факторов – близко расположенных к
трансформатору предметов из магнитных материалов, других магнитопроводов и т.д.
Приведенная индуктивность рассеивания вторичной обмотки LS2’
Индуктивность рассеивания вторичной обмотки LS2’, приведенная к первичной обмотке
вычисляется по соотношению:
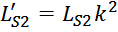
где k – коэффициент трансформации.
Индуктивность рассеивания вторичной обмотки LS2: рассчитывается аналогично
индуктивности рассеивания первичной обмотки:
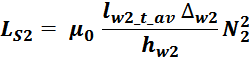
lw2_t_av – средняя длина витка вторичной обмотки;
Δw2 – расстояние от «среднего витка» вторичной обмотки (расположенного посередине
обмотки), до магнитопровода;
hw2 – высота вторичной обмотки.
Сопротивление первичной обмотки Rw1
Электрическое сопротивление первичной обмотки R1 рассчитывается по соотношению для расчета омического
сопротивления проводника:
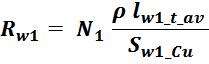
где:
N1 – число витков первичной обмотки;
ρ – удельное сопротивление материала провода (для меди – 0,0175 Ом·мм2 м-1);
lw1_t_av – средняя длина витка первичной обмотки;
Sw1_Cu – площадь поперечного сечения провода первичной обмотки.
При высоких рабочих температурах трансформатора необходимо учитывать влияние температуры на удельное
сопротивление проводников обмоток. При высоких частотах необходимо оценить увеличение эффективного
сопротивления обмоток в результате действия скин-эффекта (см. пункт «Влияние скин-эффекта на сопротивление
обмоток при высоких частотах» настоящего раздела).
Приведенное сопротивление вторичной обмотки Rw2’
Приведенное электрическое сопротивление вторичной обмотки R2’ (значение, приведенное к первичной обмотке)
определяется по соотношению:
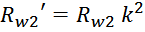
где омическое сопротивление вторичной обмотки:
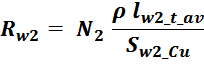
где:
N2 – число витков вторичной обмотки;
ρ – удельное сопротивление материала провода (для меди – 0,0175 Ом·мм2 м-1 );
lw2_t_av – средняя длина витка вторичной обмотки;
Sw1_Cu – площадь поперечного сечения провода вторичной обмотки.
Рекомендации по учету влияния температуры и высокой частоты на эффективное сопротивление аналогичны
рекомендациям для первичной обмотки (см. следующий раздел).
Особенности и тонкости расчета омического сопротивления обмоток
Влияние температуры на удельное сопротивление обмоток
Рост температуры приводит к увеличению удельного сопротивления проводников. Так для меди это изменение
описывается уравнением [Вдовин С. С. Проектирование импульсных трансформаторов. – 2-е изд., перераб. и доп.
— Л.: Энергоатомиздат. Ленингр. отд-ние, 1991. — 208 с: ил.]:
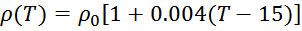
здесь:
ρ0 – удельное сопротивление меди – 0,0175 Ом·мм2 м-1 при T=15 °C );
T – температура в градусах Цельсия.
Так, при повышении температуры с 15 °C до 70 °C удельное сопротивление меди возрастает на 22% и составляет
0,02135 Ом·мм2 м-1. Этот простой расчет показывает важность учета влияния температуры
при расчете трансформатора.
Увеличение сопротивления с ростом температуры приводит к положительной обратной связи – с ростом температуры
увеличивается сопротивление, рост сопротивления приводит к увеличению выделяемой мощности, а рост выделяемой
мощность приводит к увеличению температуры. Таким образом, при проектировании трансформатора или силового
дросселя следует уделять особое внимание режиму охлаждения.
Влияние скин-эффекта на сопротивление обмоток при высоких частотах
Для уменьшения омических потерь в обмотках необходимо использовать провод большего сечения. При этом
омическое сопротивление постоянному току снижается пропорционально увеличению площади сечения. Однако на
высокой частоте (более 50-100 кГц) и особенно при толстых проводах обмоток и более начинает проявляться
скин-эффект.
Физика скин-эффекта заключается в следующем – при высоких частотах изменение тока протекающего через
проводник, приводит к изменению магнитного поля внутри этого проводника, а изменение магнитного поля, в свою
очередь приводит к образованию вихревого электрического поля (см. рисунок T.20). Это вихревое электрическое
поле Erot накладывается на линейное поле постоянного тока Elin однородное по всему
сечению проводника. В результате близи поверхности проводника поля складываются, а внутри – вычитаются и
взаимно компенсируются. Таким образом, ток вытесняется к поверхности.
Сущность скин-эффекта заключается в вытеснении на высоких частотах тока к поверхности проводника. При этом
распределение плотности тока изменяется (рисунок T.20). Видно, что ток внутренняя часть проводника
практически не переносит тока и весь ток протекает вблизи поверхности.
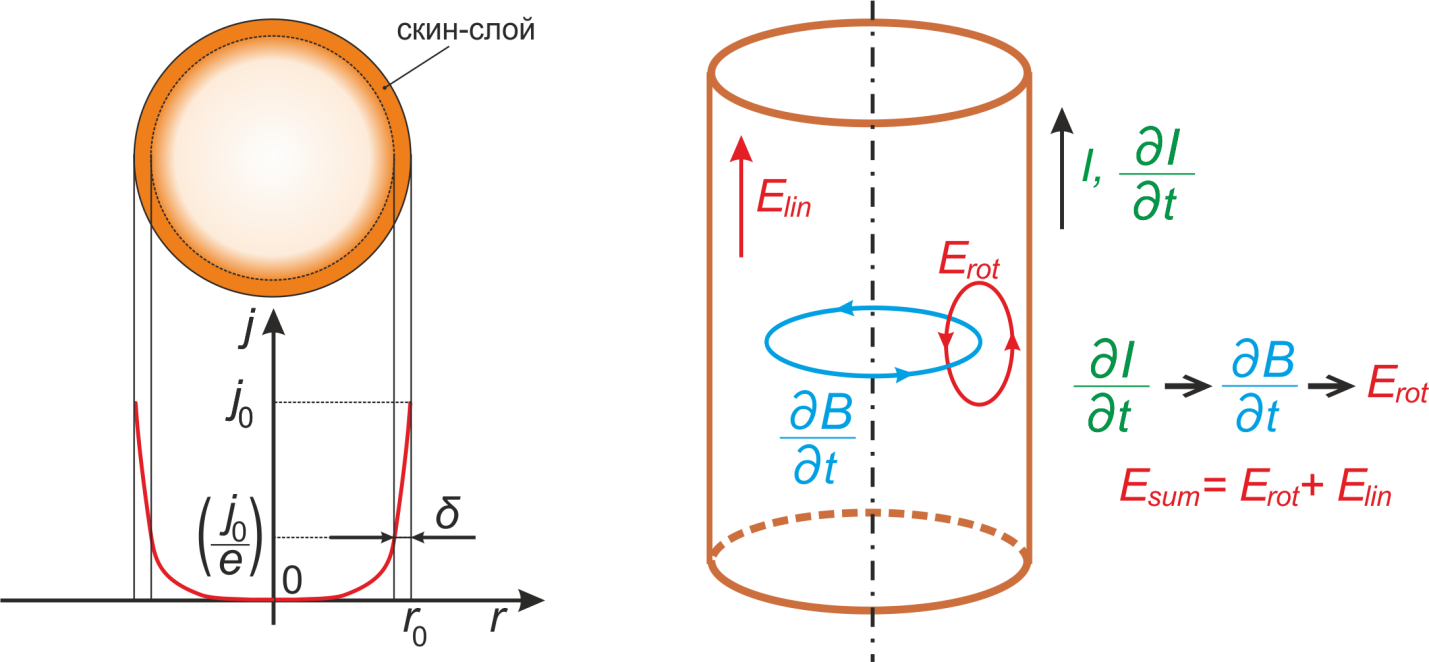
Рисунок T.20 – Распределение плотности тока в цилиндрическом проводнике вдоль радиуса при высоких
частотах
(глубина скин-слоя, на которой плотность тока j уменьшается в eраз обозначена символом δ) и иллюстрация
причинно-следственной связи возникновения скин-эффекта: рост тока (∂I/∂t) приводит к изменяющемуся
магнитному полю (∂B/∂t) которое порождает вихревое электрическое поле Erot уменьшающее
напряженность поля внутри проводника и увеличивающее вблизи поверхности и соответственно
перераспределяющее
плотность тока по сечению.
Таким образом, сопротивление проводника на высоких частотах Reff определяется по формуле [Силовая
электроника: от простого к сложному. Борис Семенов. Солон-Пресс. 2006. 416 с.]:
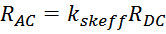
kskeff – коэффициент добавочных потерь в результате скин-эффекта;
RDC – сопротивление проводника на постоянном токе.
RAC – сопротивление проводника на переменном токе.
kskeff – коэффициент добавочных потерь является функцией частоты, толщины провода, его геометрии и
определяется как отношение сопротивления проводника на переменном токе к его сопротивлению постоянному току:
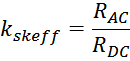
Для определения влияния скин-эффекта на сопротивление проводника в первом приближении можно использовать
таблицу T.6 [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян. Энергоатомиздат.
Ленингр. отд-ние, 1991, 176 с.]:
Таблица T.6 – Значения коэффициента добавочных потерь kskeff для одиночных проводов
|
Частота, кГц |
Диаметр провода (мм) и соответствующий коэффициент добавочных |
||||||
| 0,8 мм | 0,7 мм | 0,6 мм | 0,5 мм | 0,4 мм | 0,3 мм | 0,2 мм | |
| 500 кГц | 2,37 | 2,12 | 1,85 | 1,59 | 1,32 | 1,13 | 1,026 |
| 400 кГц | 2,16 | 1,93 | 1,67 | 1,46 | 1,21 | 1,083 | 1,0 |
| 300 кГц | 1,9 | 1,7 | 1,48 | 1,3 | 1,14 | 1,06 | 1,0 |
| 250 кГц | 1,76 | 1,57 | 1,38 | 1,23 | 1,1 | 1,034 | 1,0 |
| 200 кГц | 1,6 | 1,43 | 1,27 | 1,2 | 1,083 | 1,03 | 1,0 |
| 150 кГц | 1,4 | 1,28 | 1,11 | 1,072 | 1,0 | 1,0 | 1,0 |
| 100 кГц | 1,3 | 1,24 | 1,08 | 1,025 | 1,0 | 1,0 | 1,0 |
| 75 кГц | 1,24 | 1,097 | 1,06 | 1,0 | 1,0 | 1,0 | 1,0 |
| 50 кГц | 1,065 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 |
| 20 кГц | 1,014 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 |
Для цилиндрического проводника (рисунок T.20) плотность тока на расстоянии х от поверхности проводника
определяется из выражения:
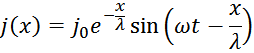
где
j0 – плотность тока у поверхности проводника;
ω – круговая частота тока (2 π f);
λ – глубина проникновения тока внутрь проводника:
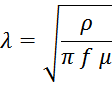
где
ρ – удельное сопротивление проводника;
f – частота переменного тока;
μ – абсолютная магнитная проницаемость материала проводника.
Для практических расчетов граничной частоты, при которой проявляется скин-эффект в медном проводе круглого
сечения используют формулу [Импульсные источники питания. Теоретические основы проектирования и руководство
по практическому применению. Раймонд Мэк. “Додэка-XXI”, 2008. 274 с.]:
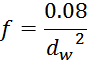
где:
f – граничная частота в МГц;
dw – диаметр провода в мм.
Если проводники обмоток трансформатора и частота их режима работы удовлетворяют данным критериям, то влиянием
скин-эффекта можно пренебречь, если нет, то изменение сопротивление провода можно рассчитать.
Однако таблица T.6 не учитывает «эффект близости» (proximity effect), проявляющийся во взаимном влиянии
близкорасположенных проводников в обмотке друг на друга. Влияние эффекта близости особенно сильно
проявляется при значительном (большем 2-3) числе слоев в обмотке.
Рекомендации по снижению потерь в трансформаторе обусловленных скин-эффектом
При проектировании трансформатора существует баланс между сечением проводов и потерями. Для минимизации
потерь целесообразно увеличение сечения проводов до достижения условия заполнения обмоткой всей площади окна
магнитопровода.
С целью снижения потерь, возникающих вследствие скин-эффекта используют:
– обмотки, выполненные из нескольких параллельных проводов меньшего диаметра; вместо одного толстого провода
использую несколько изолированных друг от друга жил
– обмотки, выполненные из литцендрата;
– обмотки, выполненные из плоских проводников.
Сопротивление активных потерь в магнитопроводе R0
Сопротивление активных потерь в магнитопроводе – параметр, характеризующий потери в магнитопроводе. При этом
мощность потерь в магнитопроводе можно выразить через произведение напряжения прикладываемого к первичной
обмотке V1 и некоторого приведенного к первичной обмотке эквивалентного тока протекающего в
феррите Ieqv_ferrit :
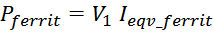
Сопротивление потерь в магнитопроводе R0 определяется как:
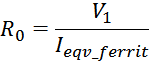
Выражая ток Ieqv_ferrit как:
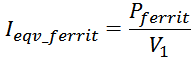
И подставляя в выражение для сопротивления получаем:
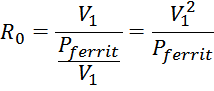
Поскольку мощность потерь в феррите можно представить как произведение мощности удельных потерь на объем
магнитопровода, то итоговое выражение для сопротивления эквивалентных потерь:
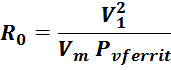
где:
Vm – объем магнитопровода (м3);
PVferrit – мощность удельных объемных потерь (Вт/м3) – индивидуальная для каждого типа
материала магнитопровода характеристика, зависящая от частоты, величины магнитной индукции и температуры
(фактически также являющаяся функцией напряжения V1);
V1 – напряжение, приложенное к первичной обмотке (В).
При этом важно понимать, что мощность удельных потерь увеличивается с ростом напряжения.
Другой способ расчета сопротивления активных потерь в магнитопроводе состоит в использовании данных о мнимой
составляющей магнитной проницаемости μ, представленной в справочных данных для ферритов. Подробно об этом –
пункт «Зависимость магнитной проницаемости феррита от частоты» настоящего раздела.
Межвитковая емкость первичной обмотки С01
Межвитковая емкость первичной обмотки представляет собой распределенную емкость первичной обмотки. В
межвитковой емкости, особенно при больших напряжениях может запасаться значительная энергия, что может
вносить существенные искажения в работу схемы.
По причине распределенного характера емкости её приведение к некому эквиваленту C01 представляет
собой достаточно сложную задачу, решение которой целесообразно с позиций расчета суммарной энергии,
запасаемой в емкостной структуре обмотке.
Емкость Clines между двумя параллельными проводниками в вакууме определяется по соотношению
[Classical Electrodynamics. Jackson, J. D. 1975. Wiley. (p. 80). ; Transmission Lines, Matching, and
Crosstalk. Kenneth L. Kaiser. CRC Press. 2005. (2-28). 448 p.]:
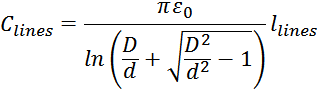
где:
D – расстояние между проводниками;
d – диаметр проводников;
llines – длина проводников.
Это соотношение учитывает неоднородное распределение поверхностной плотности заряда по поверхности
проводников и позволяет рассчитывать емкость при малых значениях расстояния, меньших диаметра
проводников.
Реальное значение емкости между соседними витками будет несколько больше по причине того, что изоляция
провода выполнена из материала с некоторой диэлектрической проницаемостью, например полиэфирных и
полиуретановых лаков с ε = 3 – 5.
Для приближенного учета заместим провод с диэлектрическим покрытием на провод без изоляции, но большего
диаметра, с тем, чтобы их единичные емкости в вакууме были одинаковы.
Соотношение для определения емкости между двумя соседними витками в
изоляции Ct
(turn-виток)
Конфигурация двухпроводной системы с цилиндрическими проводниками диаметром «по меди» dCu и
диаметром по изоляции dins и диэлектрической проницаемости изоляции εinsпредставлена
на рисунке T.21.
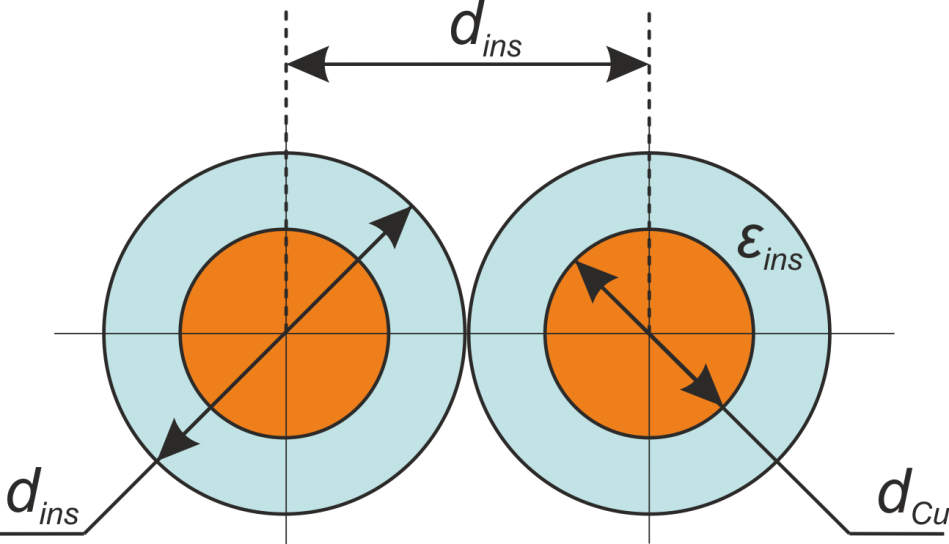
Рисунок T.21 – Конфигурация двухпроводной системы с цилиндрическими проводниками диаметрами «по меди»
dCu
и диаметрами по изоляции dins и диэлектрической проницаемости изоляции εins
В работе [Смородинов Д. А. Оценивание рабочей ёмкости и эквивалентной диэлектрической проницаемости изоляции
витой пары кабеля связи. Молодой ученый. — 2013. — №4. — С. 27-33.] с использованием конформных
преобразований получено соотношение для данной сложной системы, которое после
преобразованийдля случая емкости между двумя соседними витками проводников
обмотокимеет вид:

где:
dins – диаметр проводников в изоляции (равен расстоянию между проводниками);
dCu – диаметр проводников «по меди»;
lt – длина витка проводника обмотки;
εeff – эффективная диэлектрическая проницаемость системы:
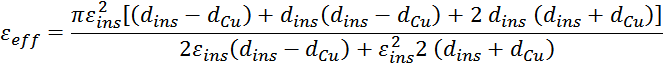
где:
εins – диэлектрическая проницаемость изоляции.
Это соотношение справедливо для случая, когда цилиндрические проводники соприкасаются друг с другом (диаметр
проводников в изоляции равен расстоянию между проводниками.
Элементарная емкость между двумя соседними витками Ct в первом приближении может быть определена
по вышеприведенному соотношению в котором длина проводника равна средней длине витка.
Суммарная емкость намотки рассчитывается в зависимости от типа намотки. Об этом далее.
Расчет емкостей обмотки при различных типах намотки
Тип намотки – «виток к витку», послойно
На рисунке изображена внутренняя структура межвитковой емкости обмотки, и распределение потенциала в случае
отсутствия межслойной изоляции и обмотки уложенной «виток к витку».
Для расчета данной энергии введем условные обозначения:
– емкость между двумя соседними витками равна Ct (turn-виток);
– число витков в слое обмотки – m;
– число слоев обмотки – n;
– напряжение, прикладываемое к обмотке – Vw.
Энергия запасается внутри структуры обмотки как между витками одного слоя (turn-turn) так и между витками
различных слоев (layer-layer);
Рассчитаем энергию, запасаемую в межвитковых емкостях (turn-turn) одного слоя:
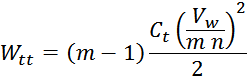
здесь :
число элементарных межвитковых емкостей:
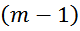
напряжение между двумя соседними витками:
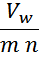
Отсюда следует, что общая энергия Wtt_summ, запасаемая в межвитковых
емкостях внутри слоев равна:
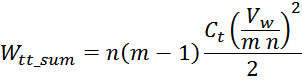
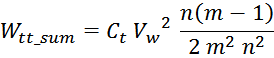
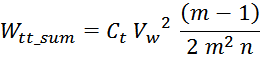
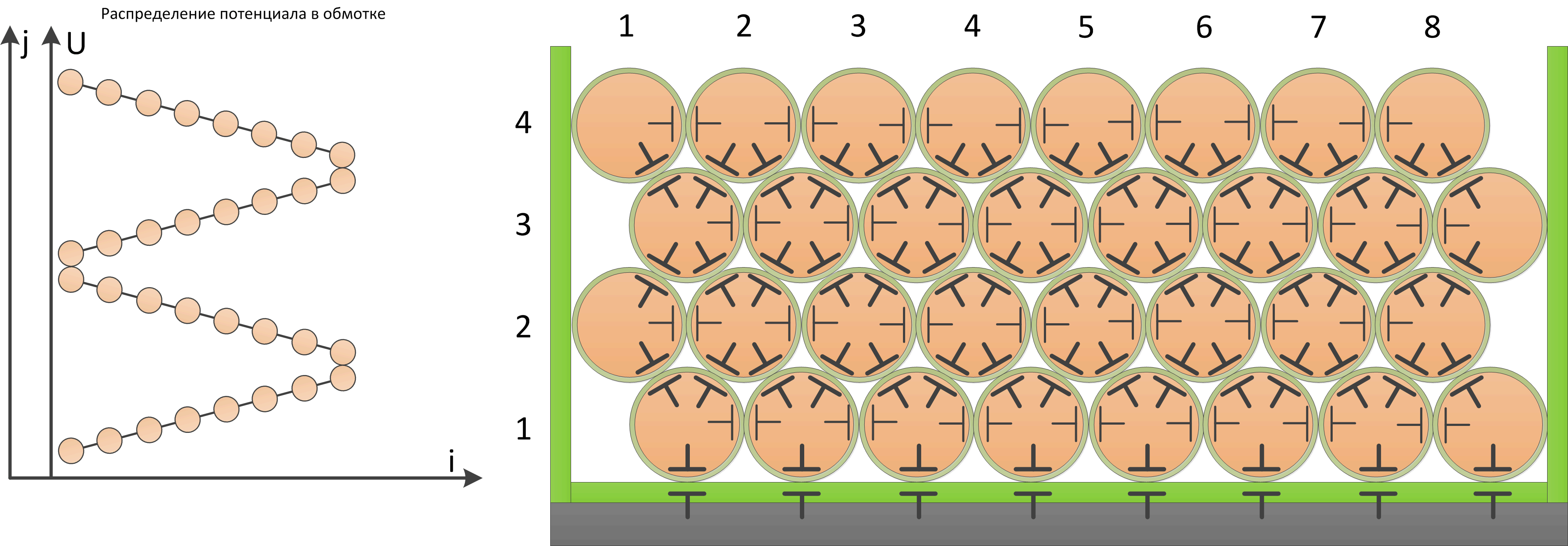
Рисунок T.22 – Межвитковые емкости и распределение потенциала по обмотке для обмотки уложенной «виток к
витку»
Рассчитаем энергию, запасаемую в межслоевых емкостях (между двумя слоями) при условии, что число слоев – n ≥
2. При способе намотки виток к витку каждый виток имеет емкость по отношению к двум соседним виткам другого
слоя (рисунок T.22). Энергия, запасаемая в этих емкостях равна:
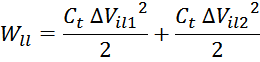
здесь:
∆Vil1, ∆Vil2 – напряжения между витком и двумя соседними виткам
другого слоя;
С учетом того, что разница напряжения между соседними витками составляет величину:
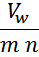
то выражение для энергии, запасаемой в межслоевых емкостях можно переписать в виде:
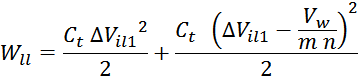
или:
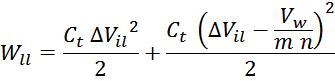
где:
∆Vil – напряжение между соседними витками разных слоев (для упрощения ∆Vil1
было заменено на ∆Vil);
Wll – энергия, запасаемая в межвитковой емкости «виток – два соседних витка другого слоя».
При этом энергия запасается в межслоевой границе. Число межслоевых границ равно:
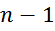
Максимальное падение напряжения между крайними витками соседних слоев равно (максимальное напряжение между
витками слоев у краев):
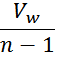
Таким образом, с учетом линейного распределения напряжения между витками в слое получим выражение для
суммарной энергии в межслоевых емкостях Wll_summ:
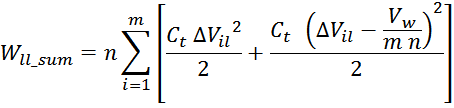
где:
∆Vil – напряжение между соседними витками разных слоев:
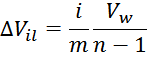
Подставляя, получаем:
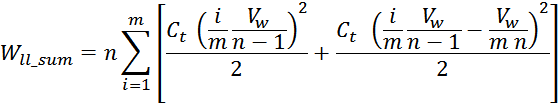
В этом выражении член:
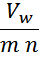
показывает разность потенциалов между соседними витками одного слоя. При достаточно большом числе витков
обмотки (а именно в этом случае и рассчитывают паразитную емкость обмотки) этой разностью можно пренебречь и
выражение упростить:
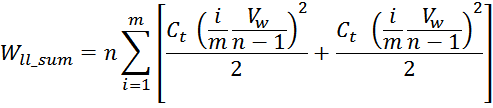
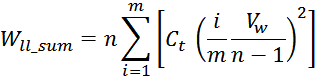
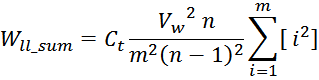
В соответствии с выражением для суммы квадратов первых натуральных чисел получаем:
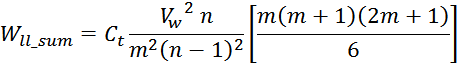
Сокращая, получаем:
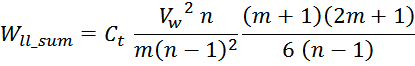
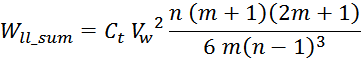
Таким образом, суммарная энергия, запасаемая в паразитной емкостной структуре равна сумме энергии межвитковых
емкостей внутри слоев Wtt_summ и энергии межслоевых емкостей Wll_summ:

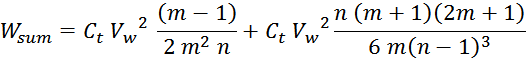
Или, упрощая:
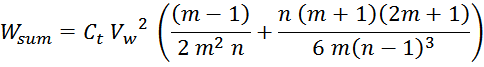
Эквивалентная ёмкость первичной обмотки может быть определена из выражения:
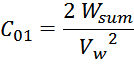
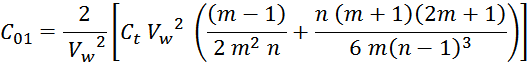
Упрощая которое (Vw сокращается) получаем итоговое выражение для емкости многослойной обмотки
трансформатора с укладкой виток к витку:
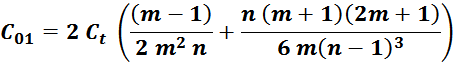
где:
Ct – емкость между двумя соседними витками равна (turn-виток);
m – число витков в слое;
n – число слоев.
Тип намотки – «один слой поверх магнитопровода»
На рисунке T.23 изображена внутренняя структура межвитковой емкости обмотки, и распределение потенциала в
обмотке, когда обмотка представляет собой один слой, уложенный поверх изоляции на магнитопроводе.

Рисунок T.23 – Межвитковые емкости и распределение потенциала в однослойной обмотке уложенной «виток к
витку»
поверх магнитопровода
Для расчета данной энергии введем условные обозначения:
– емкость между двумя соседними витками равна Ct (turn-виток);
– емкость между витком и магнитопроводом равна Ctm (core-магнитопровод);
– число витков в слое – m;
– напряжение, прикладываемое к обмотке – Vw;
Энергия, запасаемая в межвитковых емкостях слоя обмотки (layer):
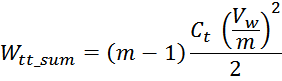
здесь напряжение между двумя соседними витками равно:
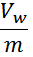
Энергия, запасаемая в емкости между витками и магнитопроводом:
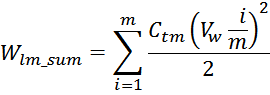
здесь:
Vw – максимальное напряжение между витками и магнитопроводом (у края);

– множитель, показывающий постепенное увеличение напряжения между витками и магнитопроводом (справа налево
или слева направо);
Сtm – элементарная емкость «виток-магнитопровод» (эквивалентная). Может быть упрощенно определена
по выражению:
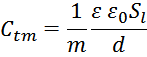
ε – диэлектрическая проницаемость материала каркаса обмотки;
Sl – площадь внутреннего слоя обмотки;
d – расстояние между обмоткой и магнитопроводом.
Упрощая выражение под знаком суммы (с учетом выражения для суммы квадратов первых натуральных чисел)
получаем:
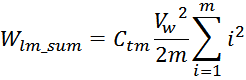
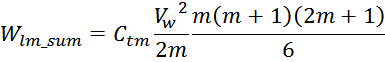
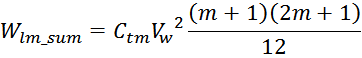
Таким образом, суммарная энергия, запасаемая в паразитной емкостной структуре в данном случае равна сумме
энергии межвитковых емкостей внутри слоев Wtt_summ и энергии в емкости
между витками и магнитопроводом Wlm_summ:
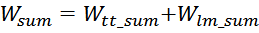
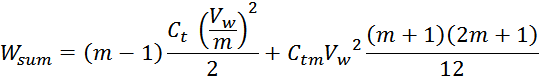
Эквивалентная ёмкость первичной обмотки:
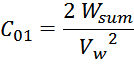
Подставляя в которое выражение для энергии получаем:
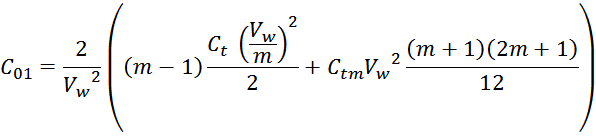
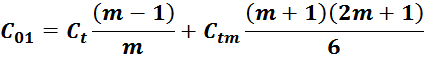
Это итоговое выражение для емкости однослойной обмотки трансформатора с укладкой виток к витку:
где:
Ct – емкость между двумя соседними витками равна (turn-виток);
Сtm – элементарная емкость «виток-магнитопровод»;
m – число витков в слое обмотки.
Тип намотки – «виток к витку N-образная»
Данный тип намотки отличается от обычного W-образного типа намотки «виток к витку» тем, что выполняется
перехлест провода обмотки для уменьшения межслоевой емкости.
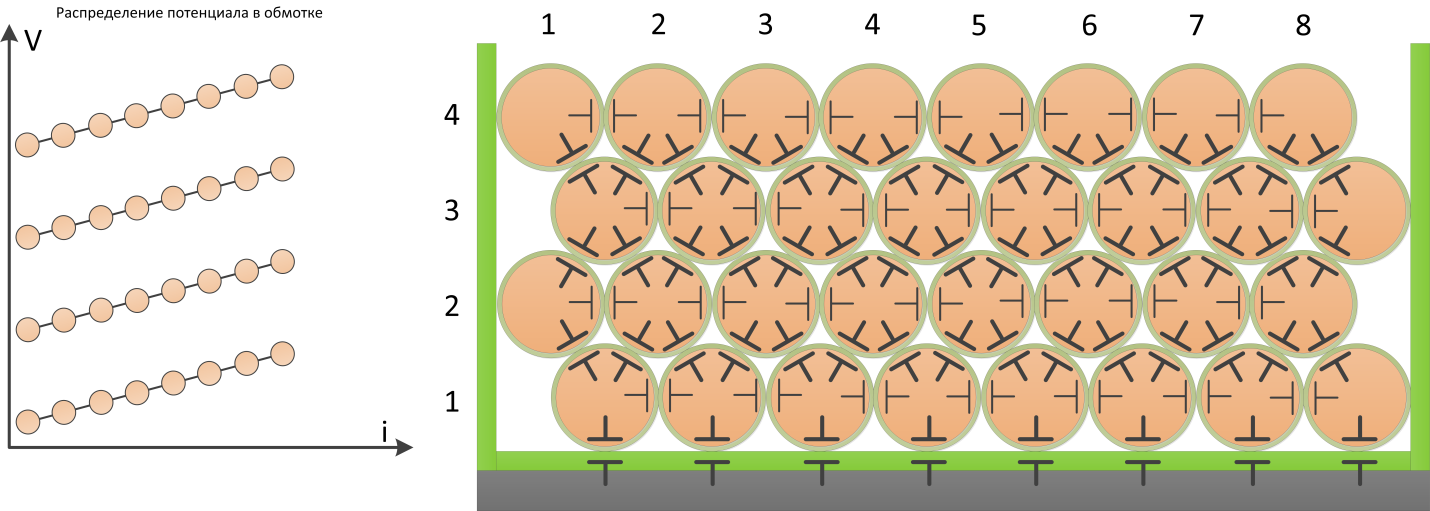
Рисунок T.24 – Межвитковые емкости и распределение потенциала в N-образной обмотке
На рисунке T.24 изображена внутренняя структура межвитковой емкости N-образной обмотки, и распределение
потенциала в случае отсутствия межслойной изоляции.
Расчет емкости обмотки аналогичен расчету емкости обычной W-образной обмотки. Энергия запасается внутри
структуры обмотки как между витками одного слоя (turn-turn) так и между витками различных слоев
(layer-layer).
Энергия, запасаемая в межвитковых емкостях (turn-turn) одного слоя равна:
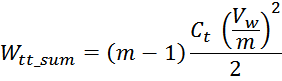
здесь напряжение между двумя соседними витками равно:
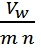
Общая энергия, запасаемая в межвитковых емкостях внутри слоев равна (выражение выведено ранее в разделе «Тип
намотки – «виток к витку»):
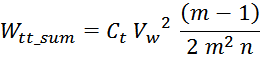
Рассчитаем энергию, запасаемую в межслоевых емкостях (между двумя слоями) при условии, что число слоев – n ≥
2. При способе намотки виток к витку каждый виток имеет емкость по отношению к двум соседним виткам другого
слоя (рисунок T.24). Энергия, запасаемая в этих емкостях равна:
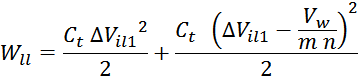
Здесь:
∆Vil – напряжение между соседними витками разных слоев;
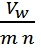
При этом энергия запасается в межслоевой границе. Число межслоевых границ равно:
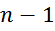
Напряжение между витками соседних слоев при N-образном способе намотки одинаково по всей длине обмотки и
равно:
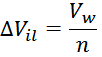
Таким образом, с учетом линейного распределения напряжения между витками в слое получим выражение для
суммарной энергии в межслоевых емкостях:
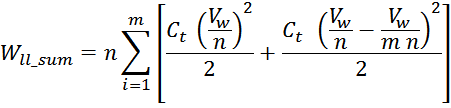
В этом выражении член:
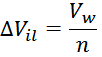
показывает разность потенциалов между соседними витками одного слоя. При достаточно большом числе витков
обмотки (а именно в этом случае и рассчитывают паразитную емкость обмотки) этой разностью можно пренебречь и
выражение упростить:
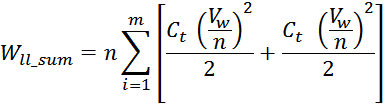
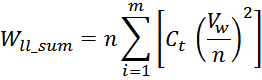
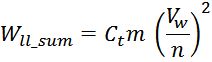
Таким образом, суммарная энергия, запасаемая в паразитной емкостной структуре равна сумме энергии межвитковых
емкостей внутри слоев Wtt_summ и энергии межслоевых емкостей Wll_summ:
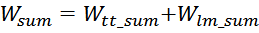
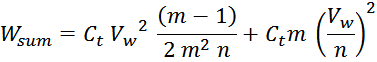
или, упрощая:
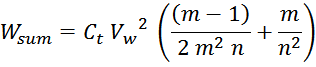
Эквивалентная ёмкость первичной обмотки может быть определена из выражения:
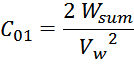
Подставляя в которое выражение для энергии получаем:
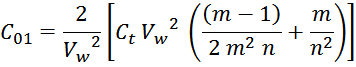
Упрощая которое (Vw сокращается) получаем итоговое выражение для емкости многослойной обмотки
трансформатора с укладкой виток к витку:
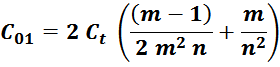
где:
Ct – емкость между двумя соседними витками равна (turn-виток);
m – число витков в слое;
n – число слоев.
Межвитковая емкость вторичной обмотки С02’
Межвитковая емкость вторичной обмотки С02’(значение, приведенное к первичной обмотке)
рассчитывается в соответствии с соотношением:
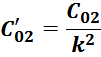
где:
C02 – емкость вторничной обмотки трансформатора (рассчитывается, в зависимости от типа обмотки, по
соотношениям, представленным ранее для емкости первичной обмотки C01);
k – коэффициент трансформации.
Межобмоточная емкость С12
Межобмоточная емкость определяется конструкцией взаимного расположения обмоток. В случае наиболее
распространенной геометрии расположения одной обмотки поверх другой емкость рассчитывается по соотношению
емкости плоского конденсатора:
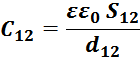
где:
ε – диэлектрическая проницаемость;
ε0 – диэлектрическая постоянная;
S12 – эффективная площадь между обмотками;
d12 – толщина межобмоточной изоляции.
Эффективную площадь между обмотками можно оценить по соотношению:
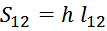
где:
h – высота обмотки;
l12 – длина витка межобмоточной изоляции.
Через межобмоточную емкость осуществляется передача синфазной помехи.
В случае введения электростатической защиты (экрана Фарадея) между обмотками с целью устранения синфазной
помехи, эквивалентная схема трансформатора изменяется и появляются дополнительные емкости – между обмотками
и общим проводом (землей), расчет которых осуществляется аналогично расчету межобмоточной емкости.
Особенности влияния паразитных параметров на работу импульсных трансформаторов
Особенностью повышающего высоковольтного трансформатора является то, что на режим работы большое влияние
суммарная индуктивность рассеяния LS = LS1 + LS2’,
паразитная емкость вторичной обмотки C02 , межобмоточная емкость С12. [Динамические
характеристики умножителей напряжения высоковольтных электротехнических систем. Диссертация. Хречков Николай
Григорьевич. 2006 г.].
Потери в трансформаторе
Омические потери в проводниках обмоток
Суммарные потери на омическом сопротивлении обмоток трансформатора определяются по формуле:
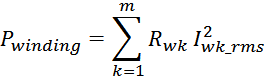
Rwk – сопротивление k-й обмотки;
Iwk_rms – ток в k-й обмотки (действующее или среднеквадратичное значение);
m – число обмоток.
Среднеквадратичное или действующее значение для тока (периодическая несинусоидальная функция с периодом T)
определяется по формуле:
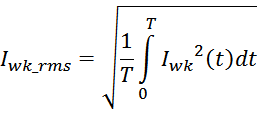
Таким образом, выделяемая мощность рассчитывается с учетом значения относительной длительность импульса q и
формы тока (включающих прямоугольную и треугольную составляющие) [Трансформаторы и дроссели для импульсных
источников питания. А. Кузнецов. Схемотехника, 2000, №1, с. 30—33, №2, с. 48, 49, 2001, №1, с. 32—34.].
Сопротивление обмотки не является величиной постоянной и зависит от температуры и частоты протекающего
тока.
Выбор допустимой плотности тока в обмотках
Допустимая величина плотности тока определяется типом и геометрией трансформатора и как правило выбирается в
пределах 2-5 А/мм2 в зависимости от условий охлаждения и типа магнитопровода. Так при
использовании чашеобразных магнитопроводов (POT) целесообразно использовать меньшую плотность тока (2-3 А/мм2),
поскольку условия охлаждения обмоток затруднены. При использовании стандартных, не низкопрофильных Ш- или
П-образных магнитопроводов допустимую плотность тока можно взять вблизи верхней границы этого диапазона (3-5
А/мм2). При использовании обмоток малой толщины (1-2 слоя) возможно повышение допустимой
плотности тока вплоть до 7-10 А/мм2. Оценка максимальной величины плотности тока в зависимости от
мощности преобразователя представлена в таблице Т.8 настоящего раздела.
Потери в магнитопроводе
Тепловая энергия, выделяемая в магнитопроводе определяется режимом работы, – частотой работы f и уровнем
магнитной индукции B. Для расчета потерь в магнитопроводеPferrit используют следующее
аппроксимирующее выражение [Optimum design of a high-power, high-frequency transformer. R. Petkov. IEEE
Transactions on Power Electronics (Volume: 11, Issue: 1, Jan 1996)]:
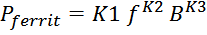
где:
f – частота;
B – индукция;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
В случае, если справочные листы на магнитомягкие материалы не содержат информации об аппроксимационных
коэффициентах, то для определения потерь в магнитопроводе можно использовать соотношение:
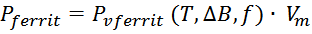
где:
Pvferrit – мощность потерь на единицу объема, являющейся функцией температуры, магнитной индукции
и частоты;
Vm – объем магнитопровода.
Мощность потерь на единицу объема определяется типом феррита и приводится в справочных данных на конкретный
тип магнитного материала (пример – на рисунке T.25).

Рисунок T.25 – Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87
Диэлектрические потери
Примечание – в ряде случаев, особенно при высокой частоте и в высоковольтных трансформаторах возможны потери
в изоляционных слоях, выполненных из диэлектриков с высоким коэффициентом потерь. Для большинства
практических случаев эти потери пренебрежимо малы по сравнению с остальными видами потерь.
Потери в трансформаторе определяют нагрев его элементов – обмоток, магнитопровода.
Тепловой режим трансформатора
Тепловой режим трансформатора фактически является лимитирующим фактором для габаритной мощности
трансформатора, поскольку в формулу её расчета входит плотность тока, максимальная индукция и частота.
Основными источниками тепла, выделяемого трансформатором в процессе работы являются обмотки и магнитопровод.
В процессе работы трансформатора тепло передается в окружающую среду и при некоторой температуре
устанавливается тепловое равновесие. При этом мощность суммарных потерь выделяемая трансформатором Ptotal_loss
будет равна мощности рассеиваемой в окружающую среду Pdissipation. Рассеиваемая
мощностьпропорциональна площади поверхности трансформатора ST, и разности температур
трансформатора и окружающей среды ΔT:
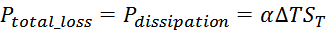
где α – коэффициент теплоотдачи, равный мощности рассеиваемой единицей поверхности при изменении температуры
трансформатора на 1º. Коэффициент теплоотдачи определяется множеством факторов, но для практических расчетов
[Теория и расчет трансформаторов малой мощности. Ю.Н. Стародубцев. РадиоСофт. 2011. 320 с. стр. 67] можно
использовать значение α равное 12 Вт/(м2 град) представляющее среднее значение коэффициента
теплоотдачи при условии естественной конвекции и интервале температур ΔT = 20 – 50 °С.
Установившаяся температура перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева) может
быть приблизительно оценена по соотношению [McLymanC. Transformer and inductor design handbook.2004]:
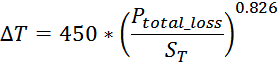
где:
Ptotal_loss – мощность суммарных потерь в трансформаторе;
ST – суммарная эффективная площадь охлаждения трансформатора (в см2).
Для трансформаторов больших габаритов (с рассеваемой площадью более 1000 см2) установившаяся
температуру перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева) целесообразно
оценивать по соотношению [В.Е. Китаев, А.А. Бокуняев. Проектирование источников электропитания устройств
связи. Учеб. пособие.- М.: Связь,1972.- 200 с.]:
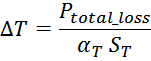
где:
Ptotal_loss – мощность суммарных потерь в трансформаторе;
αT – коэффициент теплоотдачи, зависящий от множества факторов (материал трансформатора,
конструктивное исполнение, температуры окружающей среды и т.д.) и для практических расчетов принимается
равным 11-13 Вт/м2 °С.
ST – суммарная площадь охлаждения трансформатора.
Трансформаторы импульсных источников питания
Режимы работы импульсного трансформатора
Форма переменного напряжения, прикладываемого к первичной обмотке, теоретически может быть любой. В случае,
если форма напряжения является или близка к форме прямоугольных импульсов, то трансформатор называется
импульсным. Исключение составляют лишь резонансные трансформаторы, питание которых осуществляется от
ключевых преобразователей.
Трансформатор в преобразовательной технике может работать в двух принципиально различных режимах
[Транзисторная преобразовательная техника. Мелешин В.И. Техносфера. 2005. 626 с.]:
– прямая передача энергии «из обмотки в обмотку». Энергия передается из первичной обмотки во вторичную,
синхронно во времени в соответствии с законом электромагнитной индукции (пункт «Физика работы импульсного
трансформатора» настоящего раздела). В данном случае энергия, накапливаемая в сердечнике не передается в
выходные обмотки. Это режим работы обычного трансформатора, он еще называется прямоходовым режимом;
– трансформатор является промежуточным накопителем энергии: в один интервал времени он накапливает энергию в
сердечнике, подводимую через первичную обмотку, в другой интервал времени эта энергия передается в нагрузку
через вторичную обмотку. Это трансформатор обратноходового преобразователя. По сути это уже не
трансформатор, а дроссель с двумя изолированными обмотками.
Первый, классический «трансформаторный» режим используется в двухтактных преобразователях с топологией мост,
полумост, пуш-пул, и однотактных прямоходовых преобразователях, второй «накопительный» – в
обратноходовых.
В подходах к расчету трансформаторов можно четко выделить три типа:
– прямоходовый двухтактный трансформатор;
– прямоходовый однотактный трансформатор;
– обратноходовый трансформатор.
Порядок расчета трансформаторов для различных топологий отличается, но имеет ряд общих моментов.
Понятие габаритной мощности трансформатора
Величина габаритной мощности трансформатора является одним из базовых понятий. По габаритной мощности
определяется тип и размеры сердечника трансформатора.
Согласно определению, габаритная мощность трансформатора равна сумме мощностей первичных и вторичных обмоток
[Transformer and inductor design Handbook. Third Edition, Revised and Expanded. Colonel Wm. T. McLyman.
Marcel Dekker, Inc., 2004]. Это обусловлено тем, что все обмотки и первичная и вторичная размещаются в одном
окне трансформатора. Кроме этого если обмотка имеет отвод от середины, то это два сегмента обмотки – две
полуобмотки, мощность каждой из них считается отдельно. Если имеется несколько вторичных обмоток, то также
мощность каждой из них считается отдельно. Таким образом, суммарная мощность обмотки трансформатора
складывается из мощностей всех его сегментов – обмоток или полуобмоток.
В простейшем случае для двухобмоточного трансформатора его габаритная мощность PTравна:
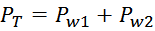
где:
Pw1 – мощность первичной обмотки;
Pw2 – мощность вторичной обмотки.
В общем случае, если первичная обмотка трансформатора состоит из n сегментов (обмоток или полуобмоток), а
вторичная обмотка трансформатора состоит из m сегментов, то соотношение для габаритной мощности будет иметь
вид:
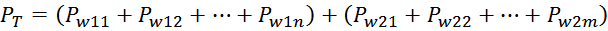
где:
Pw11 , Pw12 , Pw1n – мощности
сегментов первичной обмотки;
Pw21 , Pw22 , Pw2m – мощности
сегментов вторичной обмотки.
Поскольку мощность в трансформаторе передается из первичной обмотки во вторичную обмотку то мощности
первичной и вторичной обмотки связаны между собой через КПД-трансформатора:
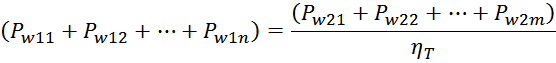
где:
ηT – КПД трансформатора.
Обобщенно габаритную мощность трансформатора можно записать как сумму всех сегментов обмоток трансформатора –
всех первичных и вторичных обмоток или полуобмоок:
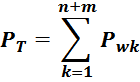
где:
n+m – суммарное число всех обмоток трансформатора (первичных и вторичных обмоток или полуобмоок);
Pwk – мощность k-й обмотки.
Представляя мощность как произведение среднеквадратичных значений напряжения и тока получим:
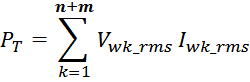
где:
Vwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
Iwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
n+m – суммарное число всех обмоток или полуобмоток.
Данное соотношение является базовым для расчета габаритной мощности трансформатора преобразователя прямого
хода.
Соотношения для габаритной мощности, представленного выше, недостаточно для взаимосвязи мощности с
габаритными (геометрическими) параметрами магнитопровода. Получим еще несколько опорных формул.
Действующее значение тока в k-й обмотке равно произведению плотности тока в проводе обмотки j на площадь
поперечного сечения провода этой обмотки Sk :
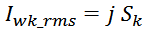
Подставляя это соотношение в выражение для габаритной мощности получаем новое соотношение:
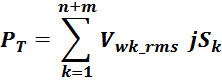
где:
j – плотность тока в проводах обмотки (среднеквадратичная);
Sk – площадь поперечного сечения провода k-й обмотки;
Vwk_rms – действующее значение тока в k-й обмотке;
n+m – суммарное число всех обмоток или полуобмоток.
В реальности не все окно магнитопровода может быть заполнено «медью обмоток», есть еще изоляция, воздушные
промежутки – зазоры, каркас, много чего. В связи с этим вводят понятие коэффициента заполнения окна.
Габаритная мощность представляет собой практически важный параметр, физически обозначающий максимальную
мощность, которую можно прокачать в данных габаритах и конструкции трансформатора.
Коэффициент заполнения окна сердечника k0 определяется
отношением:
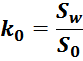
где:
S0 – общая площадь окна сердечника;
Sw – часть площади окна сердечника заполненную проводниками обмоток (площадь, заполненная медью).
Площадь окна сердечника определяется конкретным типом магнитопровода и его значение представлено в
datasheet-ах на магнитопровод. Коэффициент заполнения окна сердечника k0 зависит от различных
факторов – плотности намотки, изоляции проводников обмоток, межслоевой изоляции, толщины каркаса и т.д.
Из определения коэффициента заполнения окна сердечника k0 следует выражение, определяющее полезную
площадь по меди Sw:
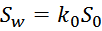
Суммарная площадь проводников обмоток Sw внутри окна магнитопровода равна сумме площадей,
занимаемых каждой из обмоток в отдельности.
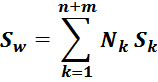
где:
Nk – число витков в k-й обмотке (полуобмотке);
Sk – площадь поперечного сечения провода k-й обмотки.
Таким образом, полученная система опорных уравнений:
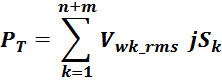
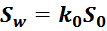
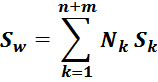
будет использоваться для вывода выражений габаритной мощности трансформаторов различных типов
преобразователей прямого хода.
Влияние и взаимовлияние различных параметров на габаритную мощность трансформаторов прямого
хода
Рабочая индукция В
Рабочая индукция уменьшается при увеличении числа витков, при увеличении площади поперечного сечения
магнитопровода. Уменьшение индукции приводит к снижению потерь. Но если это уменьшение было достигнуто
увеличением числа витков, то потери в меди возрастают.
Число витков N
Уменьшение числа витков приводит к уменьшению потерь в проводниках, с другой стороны это приводит к
увеличению потерь в магнитопроводе. Увеличение потерь в проводниках, приводит к росту температуры, что
увеличивает сопротивление обмоток и соответственно потери.
Площадь сечения магнитопровода S
С ростом площади сечения уменьшаются потери в магнитопроводе. С другой стороны с ростом S увеличивается длина
провода и возрастают потери в обмотках.
Частота f
С ростом частоты увеличиваются потери в магнитопроводе, но при этом, если напряжение постоянно снижается
уровень рабочей индукции. При высоких частотах начинает проявляться скин-эффект в проводниках. Повышение
частоты приводит к уменьшению габаритов трансформатора.
Трансформатор двухтактного прямоходового преобразователя
Режим работы. Основные соотношения
Прямоходовый двухтактный трансформатор – это трансформатор преобразователей с симметричным перемагничиванием
магнитопровода. Такими преобразователями являются – полумостовой, мостовой преобразователи и пуш-пул.
В качестве примера, для более наглядного рассмотрения процессов используем простой двухобмоточный
трансформатор с одной первичной и одной вторичной обмотками без выводов. В любой топологии прямоходового
двухтактного трансформатора (полумост, мост, в случае пуш-пул – то же самое, только первичная обмотка
разбивается на две полуобмотки) к первичной обмотке прикладываются импульсы напряжения различной полярности,
следующие через некоторую паузу.
Установим взаимосвязь между параметрами импульсов напряжения (амплитуда, длительность), прикладываемого к
первичной обмотке трансформатора, числом витков в ней, параметрами магнитопровода и достигаемой величины
индукции магнитного поля.
Начальные условия и соотношения:
Основные количественные параметры прямоугольных импульсов прикладываемых к первичной обмотке:
– длительность импульса напряжения, прикладываемого к первичной обмотке трансформатора – ti ;
– период импульсов напряжения, прикладываемого к первичной обмотке трансформатора T ;
– время задержки между импульсами верхнего и нижнего ключей (мертвое время) – tdeadtime ;
– амплитуда напряжения, прикладываемого к первичной обмотке трансформатора – VIN .
Форма импульсов напряжения, прикладываемых к первичной обмотке трансформатора представлена на рисунке T.26.
Форма импульсов напряжения соответствует реальной работе двухтактных преобразователей прямого хода.
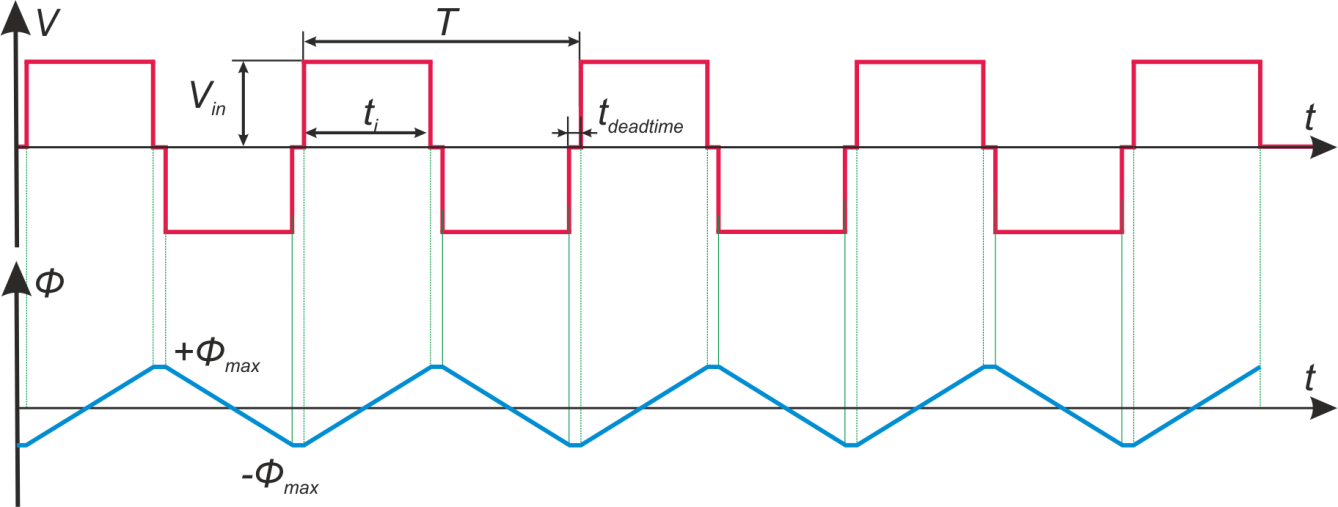
Рисунок T.26 – Напряжение на первичной обмотке и магнитный поток (индукция) в сердечнике.
Как видно из рисунка T.26 период между импульсами складывается из длительностей импульсов напряжения и
длительностей времен задержки:
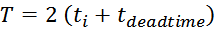
При отсутствии нагрузки на вторичной обмотке после приложения к первичной обмотке трансформатора импульса
напряжения в ней возникнет ток, поскольку первичная обмотка ведет себя как дроссель с индуктивностью,
называемой индуктивностью намагничивания. При этом в магнитопроводе возникает магнитный поток Ф0(t).
То есть, если вторичная обмотка ни к чему не подключена, то трансформатор ведет себя как дроссель.
Рассмотрим случай, когда к выходу вторичной обмотки трансформатора подключается нагрузка (омическая для
простоты выводов). В результате действия закона электромагнитной индукции на выводах вторичной обмотке
возникает ЭДС самоиндукции V2, которое прикладывается к нагрузке, подключенной к вторичной
обмотке. Таким образом, во вторичной обмотке возникает ток I2 который в свою очередь индуцирует в
магнитопроводе вторичный магнитный поток Ф2(t). Реакцией на это является одновременное увеличение
тока первичной обмотки I1 который создаёт дополнительный первичный магнитный поток Ф1(t)
направленный противоположно Ф2(t). Поскольку увеличение магнитного потока Ф1(t) от
тока первичной обмотки практически равно увеличению магнитного потока Ф2(t) от тока вторичной
обмотки, то результирующее изменение магнитного потока в магнитопроводе практически равно нулю:
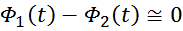
Увеличение нагрузки и соответственно тока вторичной обмотки приводит к увеличению магнитного потока вторичной
обмотки Ф2(t) и соответственно потока Ф1(t). При этом протекающий в магнитопроводе
магнитный поток Ф0(t) практически не изменяется и определяется только индуктивностью первичной
обмотки. Аналогичный процесс происходит при уменьшении нагрузки. Магнитный поток Ф0(t) вызывает
перемагничивание сердечника трансформатора [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника
и расчет.Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с.]. Таким образом, магнитные потоки обмоток,
обусловленные током нагрузки в магнитопроводе взаимно компенсируют друг друга. Магнитопровод «не чувствует»
нагрузки.
Таким образом, после приложения к первичной обмотке импульса напряжения начинает возрастать ток
намагничивания через неё. При этом магнитный поток Φ(t) за время импульса tiтакже увеличивается,
что описывается соотношением:
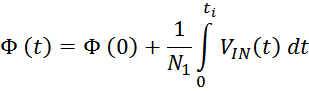
где:
Φ(0) – начальное значение магнитного потока в магнитопроводе до приложения импульса.
Полагая, что амплитуда напряжение VIN прикладываемого к первичной обмотке трансформатора в течение
импульса не изменяется (VIN = const) – получим выражение для магнитного потока:
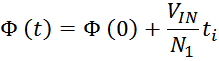
В процессе работы преобразователя происходит симметричное перемагничивание сердечника трансформатора по
линейному закону. Полагая, что во время задержи между импульсами tdeadtime магнитный поток
изменяется незначительно, то к моменту времени соответствующему началу импульса поток в сердечнике был равен
максимальному значению, достигнутому в ходе предыдущего импульса отрицательной полярности:
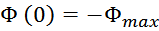
А значение магнитного потока в конце импульса равно:
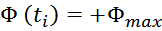
Таким образом, подставляя это значение в формулу для временной зависимости магнитного потока получаем:
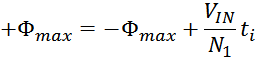
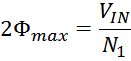
Откуда:
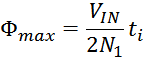
Из этого соотношения выразим амплитуду импульсов напряжения через достигаемое значение магнитного потока и
длительность импульса и число витков первичной обмотки:
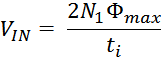
Магнитный поток равен произведению индукции магнитного поля на площадь, в которой она есть:
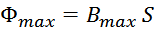
С учетом этого предыдущее выражение для амплитуды напряжения VIN приобретает вид:
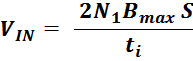
Это выражение определяетвзаимосвязь между амплитудой VIN и длительностью
импульсов напряжения ti, прикладываемого к первичной обмотке трансформатора, числом витков в ней
N1, площадью поперечного сечения магнитопровода S и достигаемой величины индукции магнитного поля
Bmax. Это практически важное выражение, часто используемое в расчетах двухтактных
преобразователей. Продолжим эволюцию данного соотношения.
При расчете элементов импульсной преобразовательной техники часто пользуются понятием относительной
длительности импульса q равным отношению длительности ti к периоду T:
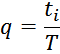
С учетом этого можно получить выражение, содержащее относительную длительность импульса q :
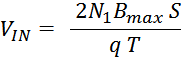
И вспоминая, что частота, есть величина, обратная периоду получаем:
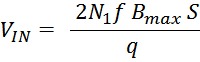
Поскольку в реальности не вся площадь контура охватываемого витками обмотки занята магнитопроводом, то
использую понятие коэффициента заполнения сердечника.
Коэффициент заполнения сердечника (ferrimagnetic core) kc находится из соотношения
площади контура, охватываемого током (витком) S и площади занимаемой собственно магнитопроводом
Sc:
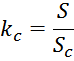
Выражая отсюда площадь:
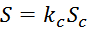
И подставляя это выражение в формулу для VIN, получаем соотношение для величины напряжения,
прикладываемого к первичной обмотке трансформатора:
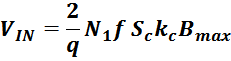
где:
q – относительная длительность импульса по отношению к периоду;
N1 – чисто витков первичной обмотки;
f – частота импульсов;
kc – коэффициент заполнения сердечника магнитопроводом;
Sc – площадь магнитопровода;
Bmax – максимальное значение индукции магнитного поля.
Данное соотношение устанавливает взаимосвязь между амплитудой, длительностью импульсов напряжения
прикладываемого к первичной обмотке трансформатора, характеристиками магнитопровода, числом витков и
максимальным значением индукции магнитного поля, достигаемым в сердечнике. В соотношении подразумевается,
что размах магнитной индукции ΔB равен удвоенному значению максимальной индукции в магнитопроводе:
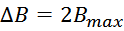
Для величины напряжения появляющегося на вторичной обмотке соотношение аналогично. Покажем это. В
соответствии с соотношением для ЭДС индукции вторичной обмотки напряжение V2 на ней
пропорционально числу витков и скорости изменения магнитного потока через неё:
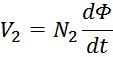
Скорость изменения магнитного потока с учетом всех преобразований равна:
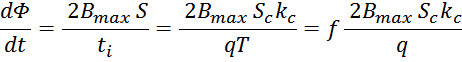
Подставляя это соотношение в предыдущее получаем выражение для напряжения на вторичной обмотке:
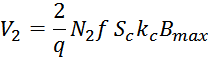
Если выходных обмоток много, то выражения аналогичны:
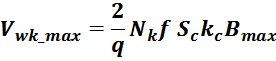
где:
Vwk_max – максимальное (амплитудное) напряжение на k-й обмотке (для любой
k-й обмотки).
Расчет числа витков первичной обмотки
Из полученного выше выражения для VIN можно определить число витков первичной обмотки. Число
витков первичной обмотки трансформатора двухтактного преобразователя определяется по соотношению:
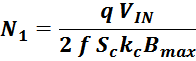
Оно позволяет определить минимальное число витков в первичной обмотке трансформатора при заданных q,
VIN, f, Sc, kc, Bmax. Полученные выше соотношения для
VIN и N1 справедливы для двухтактных преобразователей c топологией «мост» и
«полумост», а также «пуш-пул».
При расчете числа витков здесь используется максимальное значение относительной длительности импульса по
отношению к периоду (в большинстве случаев – 0,5, если нет дополнительных мер по ограничению верхнего
значения q за счет управления временем задержки «deadtime»). Несоблюдение этого может привести к насыщению
сердечника и выходу источника из строя [Сетевые блоки питания с высокочастотными преобразователями. О.А.
Эраносян. Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]. В случае если входное напряжение изменяется в
широком диапазоне, то в формулу расчета числа витков подставляется минимальное значение напряжения и
максимальное значение относительной длительности импульса. При этом в процессе работы преобразователя
обратная связь ШИМ контроллера обеспечивает произведение qVIN неизменным:
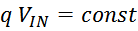
Важно понимать, что при практических расчетах используется произведение максимальных значений q и
VIN с целью обеспечения безопасного режима работы преобразователя во всем диапазоне входных
напряжений при инерционности обратной связи, отрабатывающей изменение коэффициента q с некоторой задержкой.
Расчет максимального значения индукции в магнитопроводе трансформатора двухтактного прямоходового
преобразователя
При прямоугольной форме импульсов в двухтактном преобразователе выражение для магнитного потока Φ имеет
вид:
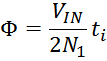
где:
VIN – амплитуда импульсов напряжения прикладываемых к обмотке;
ti – длительность импульсов напряжения прикладываемых к обмотке;
N1 – число витков в первичной обмотке трансформатора.
NB. Важно понимать, что «2» в знаменателе стоит только потому, что
магнитный поток в двухтактных преобразователях в установившемся режиме изменяется от «минус Φmax»
до «плюс Φmax» , то есть с размахом 2 Φmax. В начальный момент запуска
преобразователя, если к обмотке с нулевым значением магнитного потока приложить напряжение VIN то
сердечник впадет в глубокое насыщение, что станет причиной неконтролируемого роста тока и, как правило,
выход из строя силовых ключей. В связи с этим двухтактные трансформаторы «раскачивают» плавно либо
постепенно повышая рабочее напряжение, либо постепенно увеличивая длительность импульсов ti но
номинальной. Последнее встречается чаще и называется схемой плавного пуска (soft start).
Учитывая, что магнитный поток равен произведению индукции магнитного поля на площадь, то :
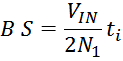
Отсюда следует выражение для значения индукции в магнитопроводе:
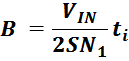
Это соотношение связывает величину индукции B достигаемой в магнитпроводе двухтактного преобразователя c
амплитудой импульсов VIN их длительностью ti площадью S и числом витков обмотки N1.
Важно понимать, что величина индукции B ограничена «сверху» индукцией насыщения Bsat:
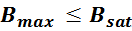
Необходимо отметить, что в начальный момент времени после подачи импульса напряжения, когда B(0) = 0 возможен
импульс тока. Для предотвращения этого необходимо при включении источника обеспечивать постепенное
увеличение длительности импульса до номинального ti – так называемый «мягкий старт». Большинство
специализированных силовых контроллеров имеют функцию «мягкий старт» с возможностью управления времени
перехода в квазистационарный режим. [Теория и расчет трансформаторов малой мощности. Ю.Н. Стародубцев.
РадиоСофт. 2011. 320 с.].
Как видно из формулы для индукции в магнитопроводе магнитный поток в магнитопроводе зависит только от
амплитуды импульсов напряжения VIN прикладываемых к первичной обмотке, длительности импульса
ti и числа витков N1. При подключении нагрузки ко вторичной обмотке возникающий в ней
ток создает магнитный поток, направленный навстречу основному магнитному потоку. Это ведет к увеличению тока
в первичной обмотке, которое в свою очередь компенсирует ожидаемое снижение магнитного потока. Таким
образом, величина магнитного потока и соответственно магнитной индукции не изменяются при подключении
нагрузки. Это следует и из эквивалентной схемы трансформатора.
Габаритная мощность прямоходового двухтактного трансформатора
Базовое соотношение для расчета габаритной мощности прямоходового трансформатора имеет вид:
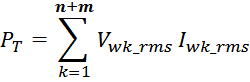
где:
Vwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
Iwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
n+m – суммарное число всех обмоток или полуобмоток.
Формулу как было показано ранее можно преобразовать к виду
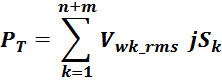
где:
j – плотность тока в проводах обмотки;
Sk – площадь поперечного сечения провода k-й обмотки;
Среднеквадратичное значение напряжения и его амплитудное значение для формы импульсов характерных для
двухтактного преобразователя (рисунок T.26) связано выражением (см. раздел «Резисторы»):
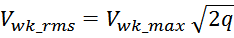
где q – коэффициент заполнения.
С учетом этого соотношение для габаритной мощности будет иметь вид:
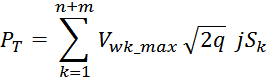
Физически выражение наглядно показывает, что при постоянных максимальных значениях напряжения и тока через
обмотки мощность «прокачиваемая» через трансформатор пропорциональна коэффициенту заполнения q и максимальна
при полном заполнении периода импульсами. В этом случае, при q=0.5 выражение для PT можно
упростить:
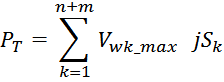
Выражение для амплитудного значения напряжения Vwk_max любой k-q обмотки
двухтактного прямоходового преобразователя (полученное ранее) имеет вид:
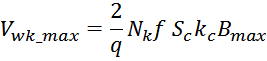
А с учетом максимального q=0.5 :
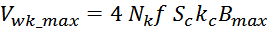
Подставляя в формулу для габаритной мощности получаем:
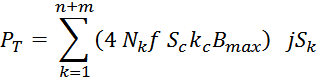
Выносим все постоянные из под знака суммы:
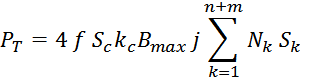
Поскольку суммарная площадь проводников обмоток внутри равна сумме площадей, занимаемых каждой из обмоток в
отдельности (соотношение в пункте «Понятие габаритной мощности трансформатора» настоящего радела):
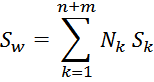
получаем:
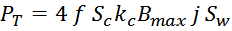
Подставляя выражение, связывающее общую площадь окна Sw и коэффициент его заполнения «медью»:
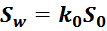
Получаем почти финишное выражение:
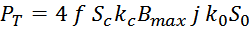
Перегруппируя множители, получаем выражение для габаритной мощности двухтактного прямоходового
преобразователя:
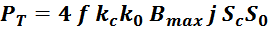
где:
f – рабочая частота;
kс – коэффициент заполнения сердечника;
k0 – коэффициент заполнения окна сердечника медью;
Bmax – максимальное значение индукции в магнитопроводе;
j – максимальная плотность тока в проводах обмотки (среднеквадратичное значение);
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника.
Из выражения для габаритной мощности определяют соотношение габаритного типоразмера, необходимое для выбора
параметров магнитопровода трансформатора:
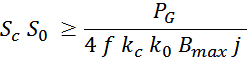
Данное соотношение выведено при допущении, что КПД трансформатора равен 1. При практических расчетах,
значение КПД трансформатора ηT вносится и конечная формула будет иметь вид:
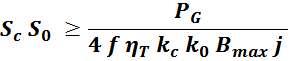
где:
ηT – КПД трансформатора;
f – рабочая частота;
k0 – коэффициент заполнения окна сердечника медью;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
j – максимальная плотность тока в проводах обмотки (среднеквадратичное значение).
Эта формула для габаритной мощности одно из базовых соотношений, используемых при расчете трансформатора.
Из соотношения следует, что массогабаритные показатели трансформатора, характеризуемые
ScS0 снижаются с ростом частоты, увеличением максимальной индукции насыщения
материала, плотности тока в обмотке.
Важно понимать, что соотношение для расчета габаритной мощности во многом носит формальный характер. В
реальности максимальная мощность трансформатора определяется, прежде всего, конструктивными особенностями и
условиями охлаждения. Один и тот-же трансформатор может иметь различную максимальную выходную мощность в
зависимости от условий отвода тепла от него. Интересно, что при резком уменьшении сопротивления нагрузки и
последующем увеличения тока нагрузки возрастет плотность тока в обмотках j, входящая в формулу габаритной
мощности. При этом габаритная мощность формально увеличивается, но при этом возрастают тепловые потери в
обмотке, что приводит к увеличению температуры трансформатора и следовательно снижению допустимого уровня
магнитной индукции Bmax.
Взаимосвязь габаритной мощности с выходной мощностью трансформатора для различных топологий
Установим взаимосвязь между мощностью выходной (вторичной) обмотки и габаритной мощностью трансформатора.
Мощность обмотки определяется формой тока в ней. А форма тока определяется в свою очередь топологией
трансформатора и схемы преобразователя. Рассмотрим основные распространенные случаи. Полученные соотношению
имеют практическую важность при расчете трансформаторов преобразователей различных конфигураций.
Двухобмоточный трансформатор двухтактного преобразователя
Область использования: топологии полумостовой и мостовой двухтактные преобразователи. Энергетически выгодна
при сравнительно небольших выходных токах и больших значениях выходного напряжения. Вторичная обмотка
трансформатора подключена к мостовому выпрямителю.
Рисунок T.27 – Двухобмоточный трансформатор двухтактного преобразователя
Для двухобмоточного трансформатора двухтактного преобразователя (рисунок T.27) габаритная мощность
трансформатора определяется по формуле:
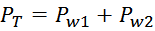
Поскольку мощность в трансформаторе передается из первичной обмотки во вторичную обмотку, то мощности обмоток
связаны между собой через КПД-трансформатора:
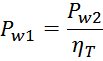
Отсюда соотношение габаритной мощность трансформатора можно представить в виде:
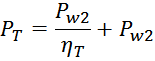
или:
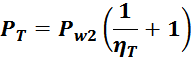
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Трансформатор двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней точки
Область использования: топологии полумостовой и мостовой двухтактные преобразователи. Энергетически выгодна
при больших выходных токах и небольших значениях выходного напряжения. Вторичная обмотка трансформатора
подключена к двухполупериодному выпрямителю со средней точкой.
Рисунок T.28 – Трансформатор двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней
точки
Для трансформатора двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней точки (рисунок
T.28) габаритная мощность определяется по формуле:
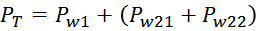
Ток через каждую полуобмотку имеет форму прямоугольных импульсов, максимальное значение коэффициента
заполнения в двухтактных преобразователях равно 0,5. Таким образом, среднеквадратичное значение тока в
полуобмотках определяется по соотношению:
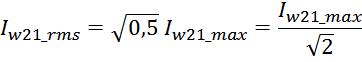
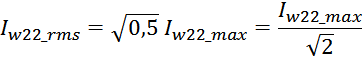
Здесь амплитудные значения токов в полуобмотках равны между собой и равны суммарному выходному току вторичной
обмотки трансформатора:
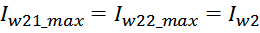
Напряжение на выходе вторичных полуобмоток равно выходному напряжению вторичной обмотки
Vw2 .
С учетом этого соотношение для габаритной мощности можно переписать в виде:
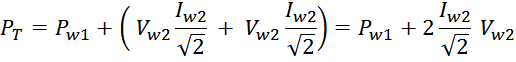
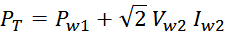
Здесь произведение выходного напряжения обмотки на выходной ток равно суммарной мощности вторичной обмотки
Pw2:
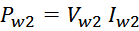
С учетом того, что мощности первичной и вторичной обмоток связаны через КПД-трансформатора, получаем:
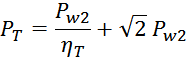
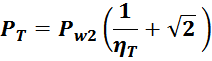
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Трансформатор двухтактного преобразователя с первичной обмоткой, имеющей отвод средней точки
Область использования: топология пуш-пулл. Энергетически выгодна при сравнительно небольших выходных токах и
больших значениях выходного напряжения. Вторичная обмотка трансформатора подключена к мостовому
выпрямителю.
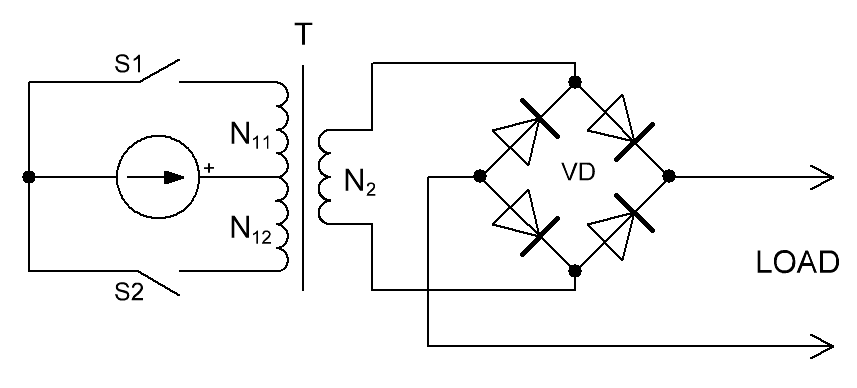
Рисунок T.29 – Трансформатор двухтактного преобразователя с первичной обмоткой, имеющей отвод средней точки
Для трансформатора двухтактного преобразователя с первичной обмоткой, имеющей отвод средней точки (рисунок
T.29) габаритная мощность определяется по формуле:
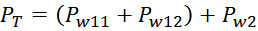
Ток через каждую полуобмотку имеет форму прямоугольных импульсов, максимальное значение коэффициента
заполнения в двухтактных преобразователях равно 0,5. Таким образом, среднеквадратичное значение тока в
полуобмотках определяется по соотношению:
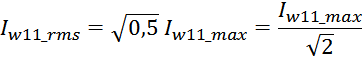
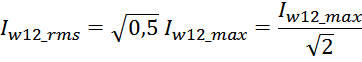
Здесь амплитудные значения токов в полуобмотках равны между собой и равны суммарному входному току первичной
обмотки трансформатора:
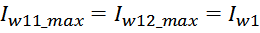
Напряжение на входе первичных полуобмоток фактически равно входному напряжению Vw1 .
С учетом этого соотношение для габаритной мощности можно переписать в виде:
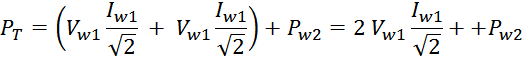
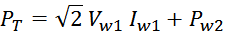
Здесь произведение входного напряжения первичной обмотки на входной ток равно суммарной мощности первичной
обмотки Pw1:
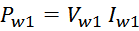
С учетом того, что мощности первичной и вторичной обмоток связаны через КПД-трансформатора, получаем:
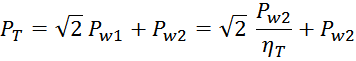
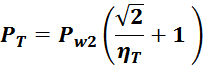
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Трансформатор двухтактного преобразователя с первичной и вторичной обмотками, имеющими отвод средней
точки
Область использования: топология пуш-пулл. Энергетически выгодна при больших выходных токах и небольших
значениях выходного напряжения. Вторичная обмотка трансформатора подключена к двухполупериодному выпрямителю
со средней точкой.
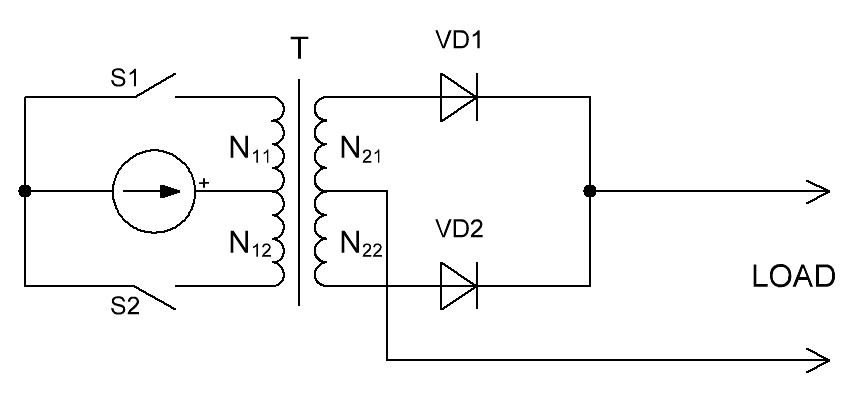
Рисунок T.30 – Трансформатор двухтактного преобразователя с первичной и вторичной обмотками, имеющими
отвод
средней точки
Для трансформатора двухтактного преобразователя с первичной и вторичной обмотками, имеющими отвод средней
точки (рисунок T.30) габаритная мощность определяется по формуле:
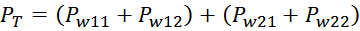
Ток через каждую полуобмотку имеет форму прямоугольных импульсов, максимальное значение коэффициента
заполнения в двухтактных преобразователях равно 0,5. Таким образом, среднеквадратичное значение тока в
полуобмотках определяется по соотношению:
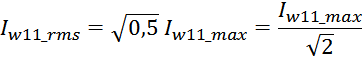
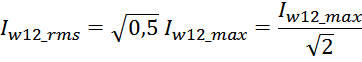
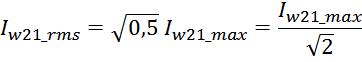
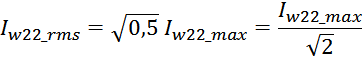
Для каждой обмотки амплитудные значения токов в полуобмотках равны между собой и равны суммарному току
соответствующей обмотки трансформатора:
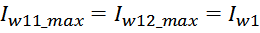
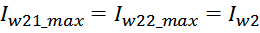
С учетом этого соотношение для габаритной мощности можно переписать в виде:
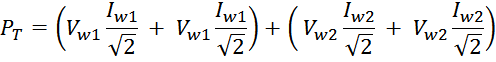
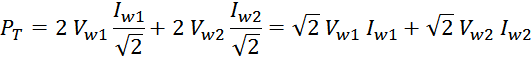
Здесь произведение напряжения обмотки на ток равно суммарной мощности соответствующей обмотки:
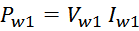
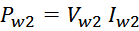
С учетом того, что мощности первичной и вторичной обмоток связаны через КПД-трансформатора, получаем:
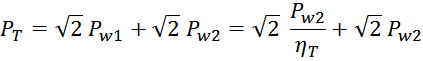
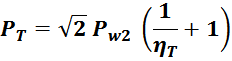
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Пояснение уменьшения габаритной мощности трансформатора при использовании обмоток с отводом от
средней точки
На первый взгляд может показаться, что разбивка обмотки на две полуобмотки никак не влияет на габаритную
мощность трансформатора. Такое впечатление может сложиться из-за того, что ток распределяется поровну меду
обмотками.
В реальности габаритная мощность трансформатора ограничена шириной окна магнитопровода, в котором размещаются
обмотки. Площадь окна распределяется между первичной и вторичной обмотками. Для случая простой двухвыводной
обмотки в каждый момент времени через обмотку протекает ток, в прямом или в обратном направлении,
следовательно, выделенная под обмотку часть окна магнитопровода используется полностью. Если мы разбиваем
обмотку на две полуобмотки, то в каждый момент времени для прохождения тока используется только одна
половина выделенной под обмотку части окна. Это служит причиной снижения габаритной мощности
трансформатора.
На рисунке T.31 схематично изображены два случая расположения обмоток в окне магнтопровода. В первом случае
вторичная обмотка состоит из одной обмотки, во втором – из двух полуобмоток.
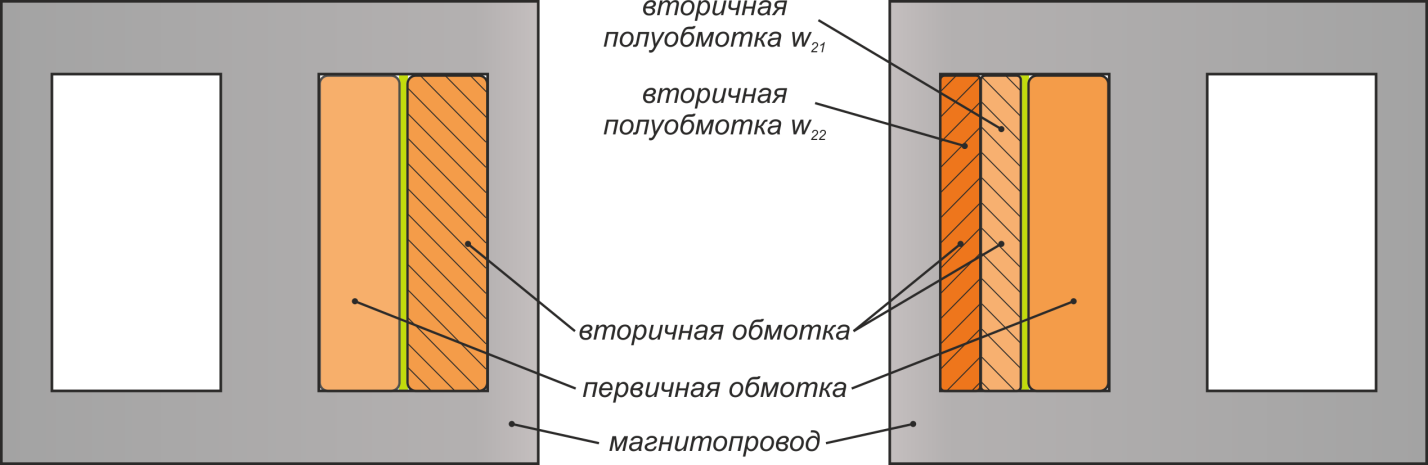
Рисунок T.31 – Схематичное изображение трансформатора с единой вторичной обмоткой и с разделенной
вторичной
обмоткой имеющей отвод от средней точки
Мощность, которую можно отвести из площади окна, отведенной под вторичную обмотку определятся конструктивом
трансформатора и не зависит от того разбита ли обмотка на полуобмотки или нет. Максимальная мощность
определяет максимальный ток, который можно пропустить через обмотку:
Для простой двухвыводной вторичной обмотки соотношение, связывающее максимальный ток и максимальная мощность
имеет вид:
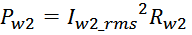
Для вторичной обмотки, состоящей из двух полуобмоток:
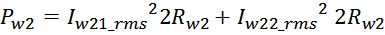
Здесь сопротивление полуобмоток в два раза больше, поскольку площадь сечения проводников полуобмоток
уменьшена в два раза пропорционально уменьшению площади сечения полуобмотки по отношению к обмотке. Вынесем
общий множитель за скобки.
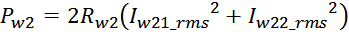
С учетом формы тока в полуобмотках:
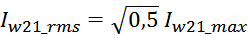
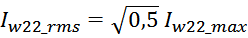
Получаем:
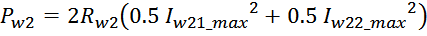
Амплитудные значения токов в полуобмотках равны между собой и равны суммарному выходному току вторичной
обмотки трансформатора с выводом от средней точки (при прямоугольной форме импульсов для суммарного
выходного тока при q=0.5 максимальное и среднеквадратичное значения равны):
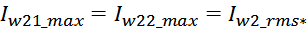
Таким образом, можно записать мощности вторичной обмотки для двух случаев:
– для простой двухвыводной обмотки:
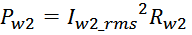
– для вторичной обмотки состоящей из двух полуобмоток:
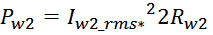
Приравнивая мощности:
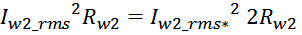
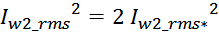
Получаем соотношение выходных токов обычной обмотки и обмотки с отводом от средней точки при условии
одинаковой рассеваемой мощности :
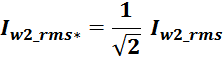
где:
Iw2_rms – среднеквадратичное значение тока простой двухвыводной обмотки;
Iw2_rms* – максимальное среднеквадратичное значение тока обмотки
с отводом от средней точки.
Таким образом, можно сделать практически важный вывод о том, что ток, который можно пропустить через обмотку
разбитую на две полуобмотки уменьшиться в 1/√2 раза (≈0,707). То есть габаритная мощность трансформатора при
использовании обмоток с отводами от средней точки должна быть больше.
Зазор в магнитопроводе трансформатора двухтактного преобразователя
Введение магнитного зазора позволяет существенно увеличить ток через индуктивный элемент (обмотку
трансформатора), при этом чем больше зазор тем больший ток насыщения будет достигнут. Обратной стороной
этого является снижение индуктивности. Чтобы сохранить величину индуктивности на прежнем уровне необходимо
увеличивать число витков. Это ведет к омическими потерям… И ограничено сверху шириной окна [Трансформаторы и
дроссели для импульсных источников питания. А. Кузнецов. Схемотехника, 2000, №1, с. 30—33, №2, с. 48, 49,
2001, №1, с. 32—34.]. Так что, как правило, зазор в магнитопровод трансформатора двухтактного
преобразователя как правил не вводят. Однако, в ряде случаев, для повышения устойчивости режима работы
трансформатора по отношению к несимметричному подмагничиванию магнитопровода зазор используют.
Основные соотношения расчета конструкции трансформатора
Конструктивный расчет является важной составляющей расчета трансформатора, так как только после выполнения
расчета конструкции можно корректно рассчитать все паразитные параметры трансформатора, определить его
тепловой режим и в конечном итоге спроектировать надежный источник питания.
Расчет конструктивных особенностей трансформатора во многом определяется типом магнитопровода. Порядок
расчета значительным образом отличается для магнитопровода с цилиндрической обмоткой (Ш-, П-образный,
чашкообразный) и обмоткой тороидальной (тор, кольцо).
Параметры обмоточного провода
Площадь поперечного сечения провода первичной и вторичной обмоток Sw1_Cu , Sw2_Cuрассчитывается
по соотношению, связывающему заданную максимальную плотность тока в обмотке jmax и максимальное
значение тока Iw1_max, Iw2_max :
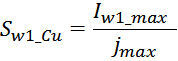
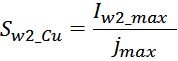
Более корректно было бы учитывать не максимальное, а среднеквадратичное значение, но на практике в
большинстве случаев такое упрощение не существенно влияет на результат, поскольку для двухтактных
преобразователей при максимальной выходной мощности обеспечивается максимальное значение коэффициента
заполнения и среднеквадратичное значение приближается к максимальному. Кроме этого, плотность тока в начале
расчета выбирается ориентировочно. В дальнейшем выполняется точное вычисление рассеиваемой мощности и по
необходимости вносятся коррективы в конструкцию.
В случае если первичная обмотка состоит из двух полуобмоток (пуш-пул преобразователь) то полученное значение
площади сечения Sw1_Cu делится на два. Аналогично в случае если вторичная
обмотка состоит из двух полуобмоток (вторичная обмотка трансформатора имеет вывод от средней точки) то
полученное значение площади сечения Sw2_Cu делится на два.
Исходя из вычисленных значений площади Sw1_Cu ,
Sw2_Cu рассчитывают диаметр проводов обмоток (по меди)
dw1_Cu , dw2_Cu исходя из соотношения,
связывающего площадь с диаметром:
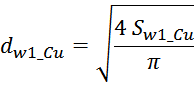
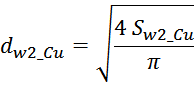
Однако полученные значения диаметров dw1_Cu ,
dw2_Cu почти наверняка точно не совпадет с характеристиками выпускаемых
обмоточных проводов. Поэтому на основании вычисленного диаметра провода (по меди) выбирается ближайший
диаметр провода (по меди) из номенклатуры диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление
производится в большую сторону:
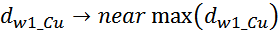
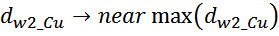
В соответствии со справочным листком определяется диаметр с изоляцией выбранного типа обмоточного провода
dw1_ins , dw2_ins :
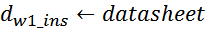
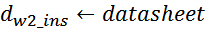
Диаметр провода в изоляции, является одним из базовых параметров и учитывается при расчете числа витков в
одном слое, проверки условия размещения обмоток в окне магнитопровода и т.д.
Средняя длина витка обмоток трансформатора
Средняя длина витка для первичной lw1_t_av, и
вторичной обмоток lw2_t_avопределяется исходя из
геометрических соображений как среднее арифметическое между длинами первых lw1_first,
lw2_first и последних витков lw1_last ,
lw1_last обмоток:
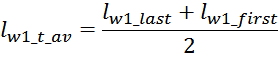
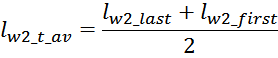
Ниже представлены соотношения для расчета средней длины витка для различных типов магнитопроводов.
Ш- и П- образные и чашеобразные магнитопроводы
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредняя длина
витка оценивается исходя из конфигурации магнитопровода (рисунок T.32).
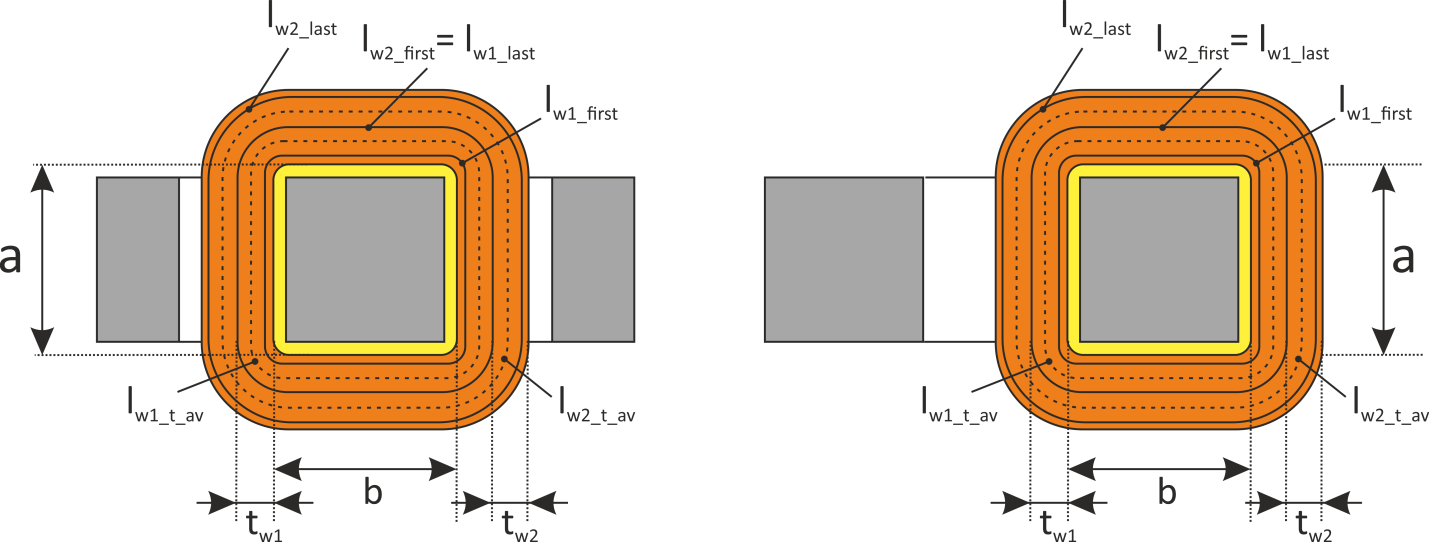
Рисунок T.32 – К определению средней длины витка для Ш- и П- образных магнитопроводов
Как правило, первичная обмотка наматывается первой (располагается ближе к магнитопроводу). Длина внешнего
витка первичной обмотки lw1_last (без учета закруглений) равна:
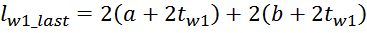
Или, упрощая:
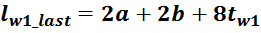
Длина внутреннего витка lw1_first равна:
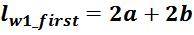
Здесь:
a, b – геометрические параметры характеризующие сечение каркаса магнитопровода;
tw1 – толщина первичной обмотки.
В первом приближении толщину первичной обмотки tw1 можно посчитать исходя из
соотношения, учитывающего число слоев и толщину провода (здесь не учитывается межслоевая изоляция и
плотность намотки):
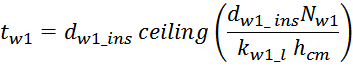
где:
dw1_ins – диаметр провода первичной обмотки с изоляцией;
функция (ceiling) – округление до большего целого;
hcm – высота каркаса магнитопровода определяющая высоту обмотки;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины
провода (таблица T.7).
Таблица T.7 – Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
| Диаметр провода с изоляцией, мм | 0,08 – 0,31 | 0,31-0,5 | 0,5-2,1 |
| Коэффициент укладки | 0,8-0,75 | 0,75-0,7 | 0,65-0,6 |
Итого, объединяя, получаем для первичной обмотки:
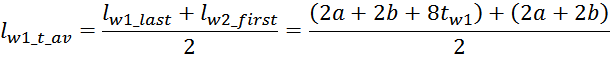
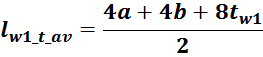
где:
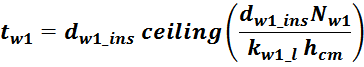
Длина внутреннего витка вторичной обмотки lw2_first принимается равной длине
внешнего витка первичной обмотки (при условии, что вторичная обмотка укладывается поверх вторичной):
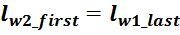
Длина внешнего витка вторичной обмотки (без учета закруглений) равна:
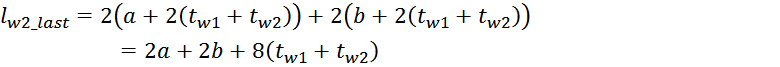
Или, упрощая:
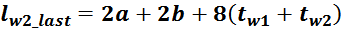
Здесь:
tw2 – толщина вторичной обмотки.
Толщина вторичной обмотки tw2 оценивается по соотношению:
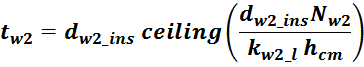
где:
dw1=2_ins – диаметр провода вторичной обмотки с изоляцией;
функция (ceiling) – округление до большего целого;
hcm – высота каркаса магнитопровода определяющая высоту обмотки;
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Итого, объединяя, получаем для вторичной обмотки:
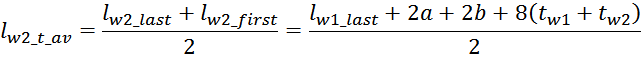
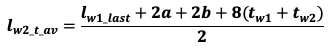
где:
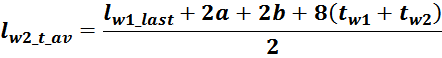
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка оценивается следующим образом:
Длина внутреннего витка первичной обмотки lw1_first равна:
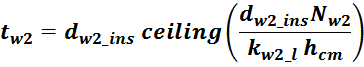
где:
R – радиус каркаса магнитопровода.
Длина внешнего витка первичной lw1_last равна:
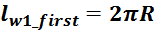
где:
tw1 – толщина первичной обмотки.
В первом приближении толщину первичной обмотки tw1 можно посчитать исходя из
соотношения учитывающее число слоев и толщину провода (здесь не учитывается межслоевая изоляция и плотность
намотки):
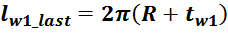
Итого, объединяя, получаем для первичной обмотки:
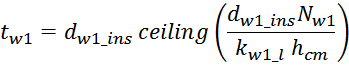
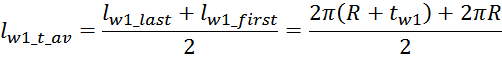
где:
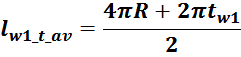
Длина внутреннего витка вторичной обмотки lw2_first принимается равной длине
внешнего витка первичной обмотки (при условии, что вторичная обмотка укладывается поверх вторичной):
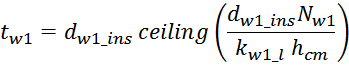
Длина внешнего витка вторичной обмотки (без учета закруглений) равна:
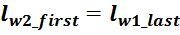
где:
tw1 – толщина первичной обмотки;
tw2 – толщина вторичной обмотки.
Толщину вторичной обмотки tw2 можно оценить исходя из соотношения, учитывающего число
слоев и толщину провода (здесь не учитывается межслоевая изоляция и плотность намотки):
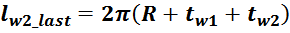
Итого, объединяя, получаем для вторичной обмотки:
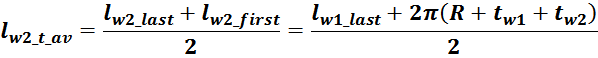
где:
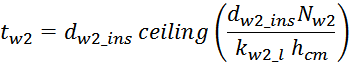
Тороидальные магнитопроводы
Для тороидальных магнитопроводов расчет среднего витка несколько сложнее. Это обусловлено тем, что толщина
внутреннего слоя обмотки будет выше плотности намотки внешнего слоя вследствие того, что длина внутреннего
кольца тора меньше длины внешнего кольца.
Внешний виток обмотки на тороидальных магнитопроводах представляет собой трапецию со скругленными углами
(рисунок T.33). Разобьём внешний виток первичной обмотки на 8 частей: четыре сектора по четверти окружности,
два из которых имеют радиус равный толщине внешнего tw1_ext, а два –
внутреннего tw1_int слоев обмотки, две высоты магнитопровода hm
и два сегмента (боковые стороны трапеции) длина которых определяется из теоремы Пифагора для прямоугольного
треугольника (из ширины магнитопровода wm, и разницы высот внутреннего tw1_ext
и внешнего tw1_int витков).
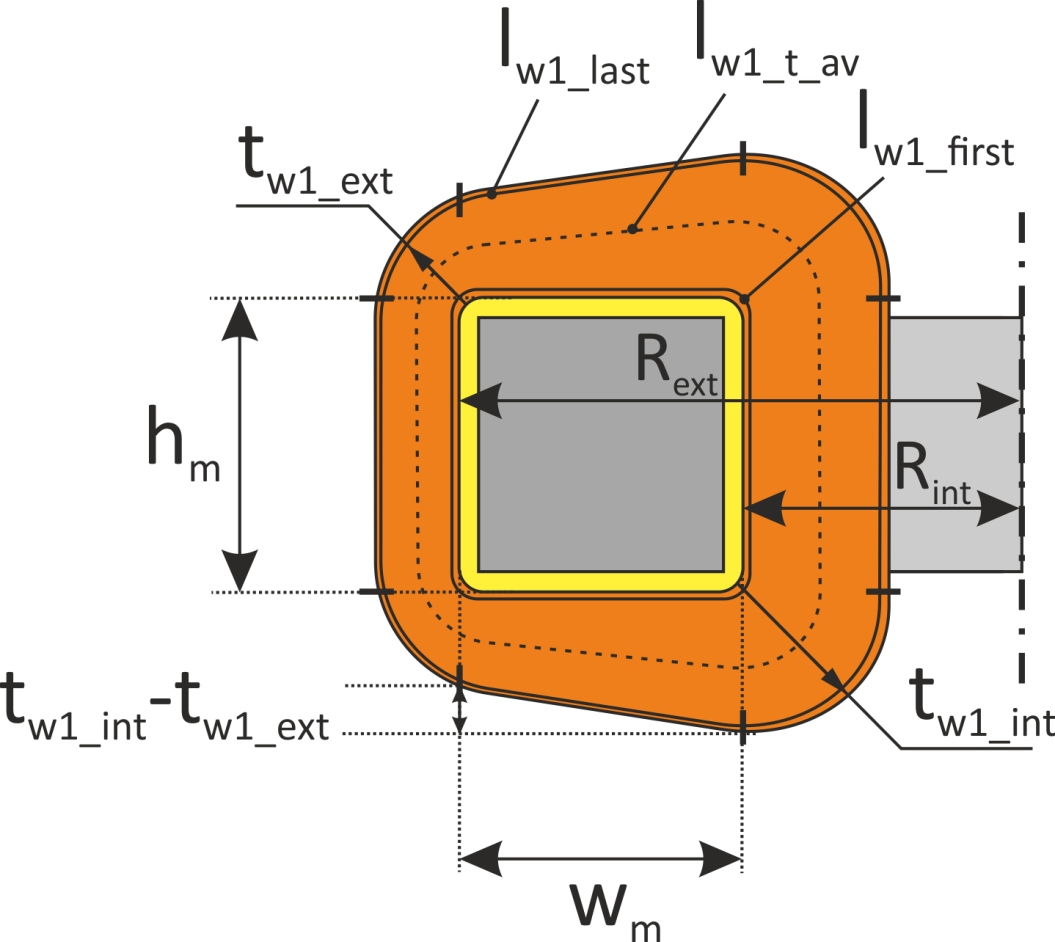
Рисунок T.33 – К определению средней длины витка тороидальных магнитопроводов (показаны обозначения
только
первичной обмотки)
Общая длина внешнего витка первичной обмотки с учетом закруглений равна:
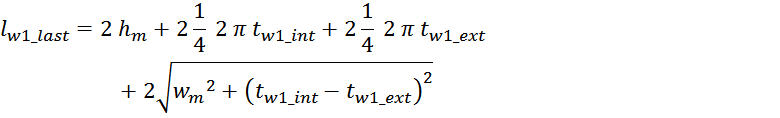
Или:
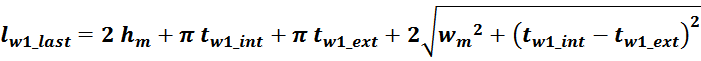
Общая длина внутреннего витка первичной обмотки при условии прямоугольного сечения магнитопровода равна:
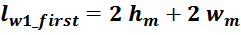
Плотность намотки и соответственно толщина внутреннего слоя обмотки будет выше плотности намотки внешнего
слоя. В первом приближении коэффициент пропорциональности равен отношению длин окружностей внешнего и
внутреннего радиусов тора. Можно считать, что толщины внешнего tw1_ext и
внутреннего tw1_int слоев обмотки связаны этим коэффициентом
пропорциональности. Таким образом:
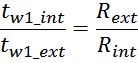
Rext – внешний радиус тора (с учетом изоляции);
Rint – внутренний радиус тора (с учетом изоляции).
Аналогично случаю с Ш- и П- образными магнитопроводами можно в первом приближении найти толщину
tw1_int
внутреннего слоя первичной обмотки исходя их соотношения учитывающее число слоев и толщину провода (здесь не
учитывается межслоевая изоляция и плотность намотки). Только в качестве высоты обмотки используем длину
внутренней окружности тора:
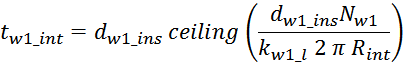
где:
функция (ceiling) – округление до большего целого;
dw1_ins – диаметр обмоточного провода первичной обмотки с изоляцией;
Rint – внутренний радиус тора;
Nw1 – число витков в обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины
провода (таблица T.7).
На основании оценочного значения толщины внутреннего слоя tw1_int можно
воспользовавшись пропорцией определить толщину внешнего слоя первичной обмотки:
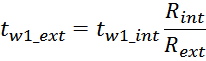
Итого, объединяя, получаем для первичной обмотки:
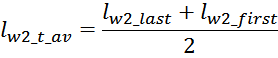
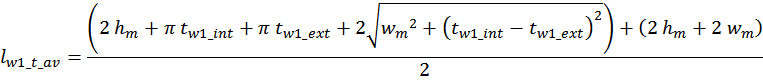
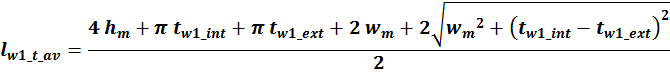
где:
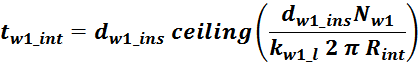
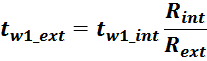
Длина внутреннего витка вторичной обмотки lw2_first принимается равной длине
внешнего витка первичной обмотки (при условии, что вторичная обмотка укладывается поверх вторичной):
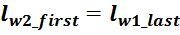
Толщина внутреннего слоя вторичной обмотки рассчитывается аналогично:
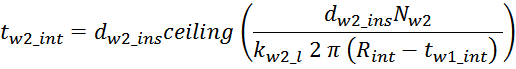
Формула учитывает уменьшение внутреннего радиуса тора за счет размещения первичной обмотки. На основании
оценочного значения толщины внутреннего слоя tw2_intможно воспользовавшись
пропорцией определить толщину внешнего слоя:
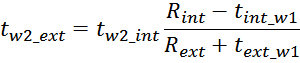
Общая длина внешнего витка вторичной обмотки с учетом закруглений равна:
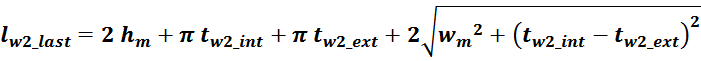
Итого, объединяя, получаем для вторичной обмотки:
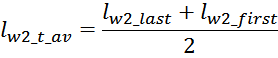
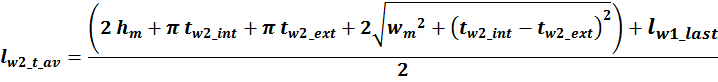
где:
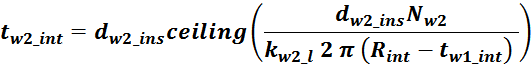
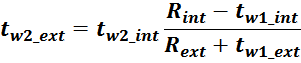
Определение длины обмотки
Длина обмоток определяется как произведение средней длины витка на число витков:
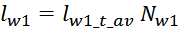
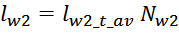
Полученная величина определяет, сколько провода нужно отмерить на обмотки трансформатора и используется при
расчете омического сопротивления обмоток.
Фактическая проверка возможности размещения обмоток трансформатора
Несмотря на то, что в начале проектирования дросселя задается коэффициент заполнения окна магнитопровода
k0, исходя из типа магнитопровода, по окончании расчета необходимо выполнить окончательную
проверку возможности размещения обмотки. Дело в том, что коэффициент заполнения окна магнитопровода
k0 является оценочным параметром, на основе которого определяется габаритный параметр
трансформатора. В зависимости от выбранного типа магнитопровода, типа и толщины обмоточного провода, толщины
межслоевой изоляции реальный коэффициент k0 может существенно изменяться. Поэтому после всех
расчетов необходимо проверить факт реального размещения обмотки в окне магнитопровода. Кроме этого, может
быть неоптимальное использование окна магнитопровода, если останется слишком много свободного места в окне
обмотки.
Расчет структуры трансформатора существенным образом различается для различных типов магнитопровода. Ниже
приведен расчет для наиболее распространенных геометрий магнитопровода:
Ш- и П- образные и чашеобразные магнитопроводы
Для конструктивного расчета структуры цилиндрической обмотки трансформатора определяется средняя ширина
намоточного слоя hlav. Она равна высоте каркаса магнитопровода hcm (рисунок
T.34):
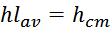
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.
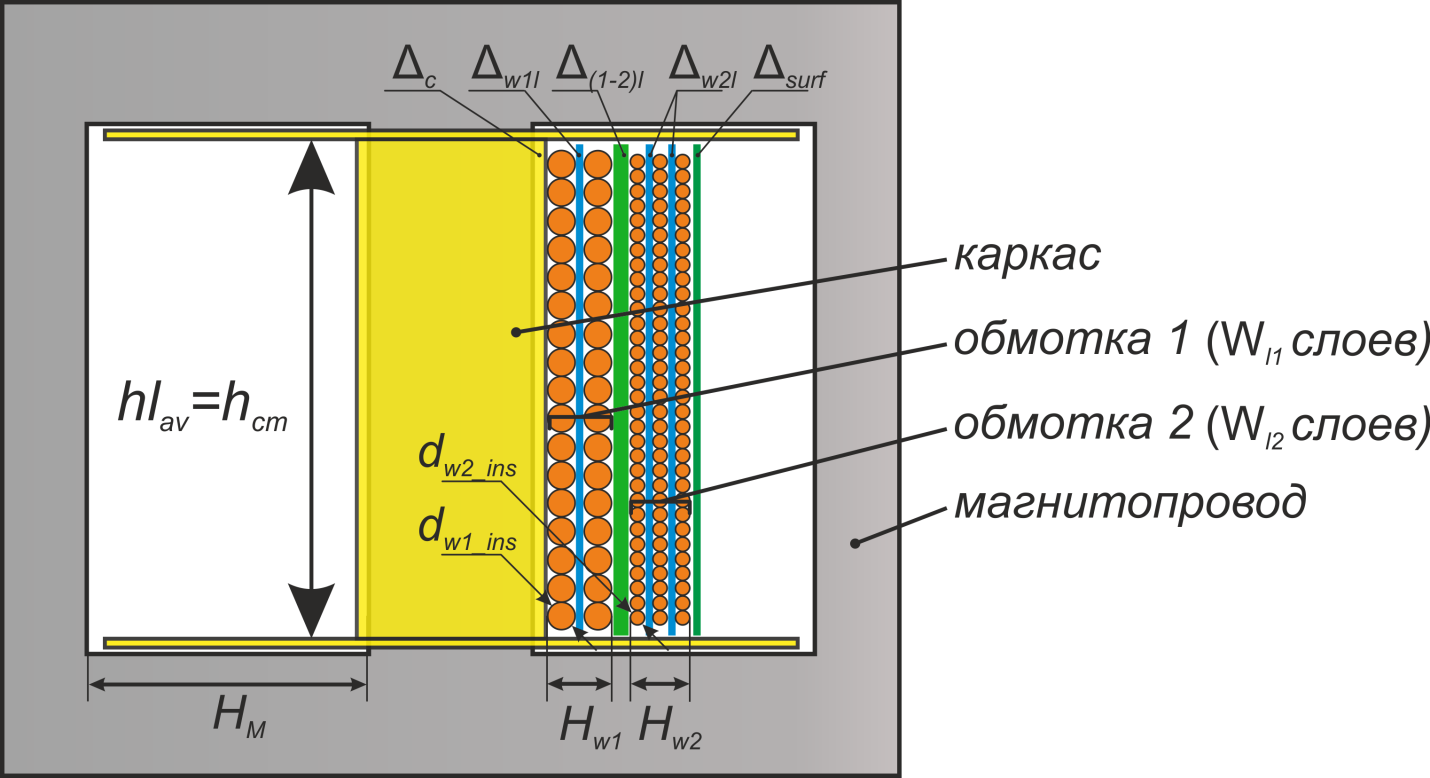
Рисунок T.34 – К расчету конструкции обмотки трансформатора преобразователя
Исходя из полученной величины hlav и известной величины диаметра проводников обмоток с изоляцией dw1_ins
и dw2_ins определяются числа витков в одном слое обмоток Nw1_l
и Nw2_l. Число витков в одном слое рассчитывается как меньшее целое (floor)
от произведения коэффициента укладки kw1_l ,
kw2_l и отношения hcm (определяет hlav) к диаметру
проводника обмотки с изоляцией:
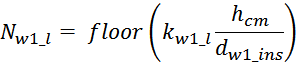
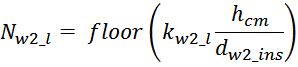
где:
hcm – высота каркаса магнитопровода;
dw1_ins , dw2_ins – диаметры проводников
обмоток с изоляцией;
kw1_l , kw2_l – коэффициенты укладки
(laying), зависящие от толщины провода (таблица T.7).
Таблица T.7 Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.].
| Диаметр провода с изоляцией, мм | 0,08 – 0,31 | 0,31-0,5 | 0,5-2,1 |
| Коэффициент укладки | 0,8-0,75 | 0,75-0,7 | 0,65-0,6 |
На основе числа витков в одном слое обмоток Nw1_l и
Nw2_l рассчитывается общее число слоев обмоток. Число слоев в первичной
Wl1 и вторичной Wl2 обмотках трансформатора определяется как
отношение числа витков в обмотке к числу витков в единичном слое с округлением до большего целого (ceiling):
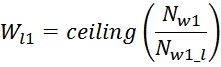
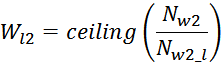
где:
Nw1, Nw2 – число витков в первичной и вторичной обмотках,
соответственно;
Nw1_l , Nw2_l – число витков в одном слое
первичной и вторичной обмоток, соответственно.
Теперь, когда известно число слоев можно рассчитать толщины обмоток. Толщины обмоток трансформатора
Hw1 , Hw2 рассчитываются по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
для первичной обмотки:
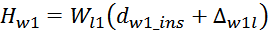
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 – число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
для вторичной обмотки:
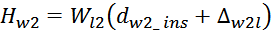
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 – число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величины Δw1l и
Δw2lпринимаются равными нулю (в реальности, при плотной намотке за счет
укладывания витков следующего слоя в пазы слоя предыдущего толщина обмотки может быть несколько меньше).
Далее рассчитывается общая толщина обмоток. В случае намотки обмоток трансформатора одна поверх другой
(типично для импульсных преобразователей) общая толщина обмоток складывается из толщин каждой из обмоток,
толщины межобмоточной изоляции Δ(1-2)l и толщины каркаса Δc (расстояния
между поверхностью каркаса и магнитопроводом) и толщины слоя внешней изоляции обмотки Δsurf:
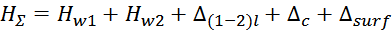
Складывая все составляющие, проверяется условие фактического размещения обмотки в окне магнитопровода:
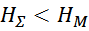
где:
HΣ – суммарная толщина «пирога» намотки;
HM – ширина окна магнитопровода.
Тороидальные магнитопроводы
Особенностью использования тороидальных (кольцевых) магнитопроводов является то, что по мере выполнения
обмотки ширина намоточного слоя hl (высота обмотки) которая определяется внутренней окружностью уменьшается.
То есть число витков в последующем слое обмотке будет меньше, чем в предыдущем. Эта нелинейность вносит
существенные коррективы в расчет конструкции трансформаторов и дросселей, выполненных на тороидальных
магнитопроводах (рисунок T.35). Полученные ниже соотношения в целом аналогичны соотношениям, представленным
в разделе «Индуктивность», но вместе с тем имеется ряд особенностей.
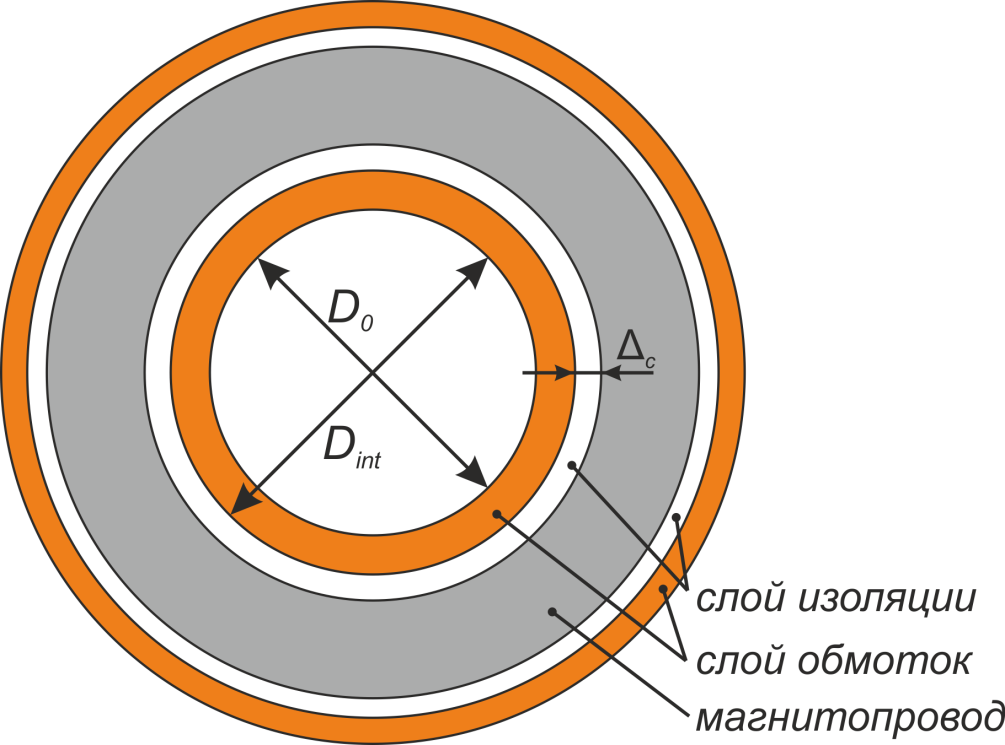
Рисунок T.35 – К расчету конструкции обмоток тороидального трансформатора: Dint – внутренний
диаметр тора магнитопровода с учетом слоя изоляции, D0 – остаточный технологический диаметр.
В разделе «Индуктивность» были получены соотношения для расчета конструкции дросселей на тороидальном
магнитопроводе. Эти соотношения применимы и для трансформаторов.
Число слоев первичной обмотки Wl1 определяется выражением:
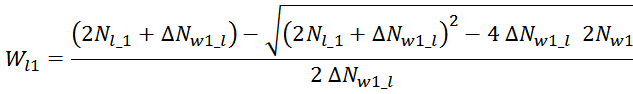
где:
Nw1 – число витков первичной обмотки;
Nl_1 – число витков первого слоя первичной обмотки, определяемое из выражения:
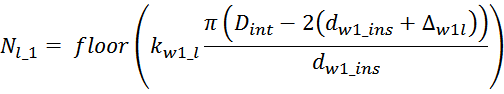
здесь:
операция (floor) – округление до меньшего целого;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw1l – толщина межслоевой изоляции первичной обмотки;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
kw1_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7).
ΔNw1_l – уменьшение числа витков от слоя к слою определяется выражением:
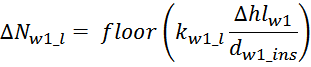
где:
операция (floor) – округление до меньшего целого;
Δhlw1 – уменьшение ширины намоточного слоя от слоя к слою для первичной обмотки:
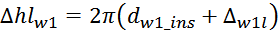
Полученное значение Wl1, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
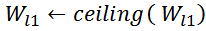
Толщина первичной обмотки Hw1 рассчитывается по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
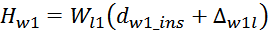
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 – число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
Далее выполняют аналогичные расчеты для вторичной обмотки:
Число слоев вторичной обмотки Wl2 определяется выражением:
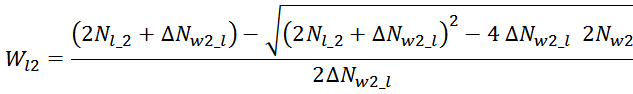
где:
Nw2 – число витков вторичной обмотки;
Nl_2 – число витков первого слоя вторичной обмотки, определяемое из выражения:
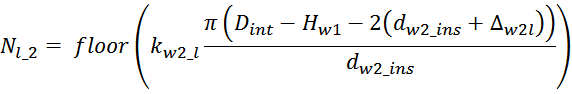
здесь:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw2l – толщина межслоевой изоляции вторичной обмотки;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
kw2_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7);
Hw1 – толщина первичной обмотки.
ΔNw2_l – уменьшение числа витков от слоя к слою для вторичной обмотки
определяется выражением:
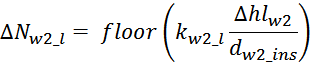
где:
операция (floor) – округление до меньшего целого;
Δhlw2 – уменьшение ширины намоточного слоя от слоя к слою для вторичной обмотки:
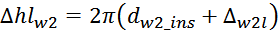
Полученное значение Wl2, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
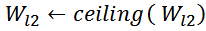
Толщина вторичной обмотки Hw2 рассчитывается по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
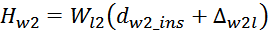
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 – число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
Далее необходима проверка условия фактического размещения обмотки в окне тороидального магнитопровода.
Суммарная толщина «пирога» намотки составляет:
Общая толщина обмоток складывается из толщин каждой из обмоток, толщины межобмоточной изоляции
Δ(1-2)l и толщины слоя внешней изоляции обмотки Δsurf:
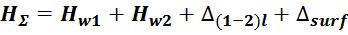
Складывая все составляющие, проверяется условие фактического размещения обмотки в окне магнитопровода:
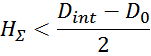
где:
HΣ – суммарная толщина «пирога» намотки;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции) который фактически определяет
ширину окна магнитопровода;
D0 – остаточный диаметр внутри тороидального трансформатора (технологический).
Последовательность расчета трансформатора двухтактного преобразователя
Данный алгоритм расчета относится к расчету трансформаторов двухтактных преобразователей прямого хода:
полумостового преобразователя, мостового преобразователя, преобразователя «пуш-пул».
1. Начальное определение типа магнитопровода и феррита
Определяем типы магнитопровода и феррита на основе исходных данных проектирования. Рекомендации по выбору
типа магнитопровода и феррита представлены в пункте «Конструктивные элементы трансформатора и дросселя.
Магнитопровод» настоящего раздела. Этот шаг необходим для предварительного определения коэффициента
заполнения окна сердечника медью k0 имаксимального значения индукции в магнитопроводе
Bmax, входящих в формулу габаритной мощности.
2. Расчет габаритного параметра
трансформатора SCS0
Определяем габаритный параметр трансформатора SCS0:
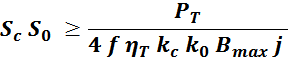
где:
PT – габаритная мощность трансформатора;
ηT – КПД трансформатора;
f – рабочая частота;
k0 – коэффициент заполнения окна сердечника медью;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
j – плотность тока в проводах обмотки.
Габаритная мощность трансформатора PT является исходным параметром
расчета. Габаритная мощность трансформатора определяется максимальной мощностью вторичной обмотки
Pw2, КПД трансформатора ηT и типом топологии трансформатора, которая в свою
очередь зависит от выбранного типа выходного выпрямителя – с отводом от средней точки или мостовой:
– для простого двухобмоточного трансформатора двухтактного преобразователя с мостовым выпрямителем:

Рисунок T.36 – Двухобмоточный трансформатор двухтактного преобразователя
габаритная мощность равна:
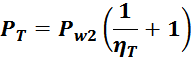
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
– для трансформатора двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней точки:

Рисунок T.37 – Трансформатор двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней
точки
габаритная мощность равна:
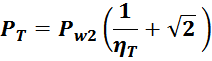
– для трансформатора двухтактного преобразователя с первичной обмоткой, имеющей отвод средней точки
(топология преобразователя – пуш-пул):

Рисунок T.38 – Трансформатор двухтактного преобразователя с первичной обмоткой, имеющей отвод средней
точки
габаритная мощность равна:
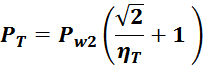
– для трансформатора двухтактного преобразователя с первичной и вторичной обмотками, имеющими отвод средней
точки (топология преобразователя – пуш-пул):

Рисунок T.39 – Трансформатор двухтактного преобразователя с первичной и вторичной обмотками, имеющими
отвод
средней точки
габаритная мощность равна:
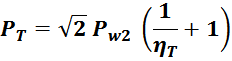
Коэффициент полезного действия трансформатора ηT принимается в
соответствии с мощностью трансформатора. В соответствии с [Эраносян О.А. Сетевые блоки питания с
высокочастотными преобразователями.— Л.: Энергоатомиздат. Лени игр. отд-ние, 1991,— 176 с: ил. 109 стр.],
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.] на начальной стадии расчета КПД трансформатора ηT принимается в
соответствии с мощностью трансформатора (у Эраносяна – мощностью нагрузки):
– при POUT_max ≤ 10 Вт принимается ηT = 0,93;
– при 10 Вт < POUT_max ≤ 50 Вт принимается ηT = 0,95;
– при POUT_max > 50 Вт принимается ηT = 0,97.
Необходимо отметить, что не более чем начальное приближение, необходимое для выполнения предварительного
этапа расчета.
Коэффициент заполнения окна сердечника медью k0 выбирается
в зависимости от типа используемого магнитопровода:
– для Ш-образного магнитопровода [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
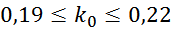
в ряде случаев, в особенности, когда S0 представляет собой площадь окна сердечника дросселя уже с
учетом каркаса магнитопровода, то может быть выбран k0 вплоть до 0,28-0,4 – [McLyman C.
Transformer and inductor design handbook.2004].
– для кольцевого магнитопровода [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет.
Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с. – 57 стр.]:
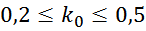
В любом случае это является первым приближением и факт размещения обмотки проверяется последующим
конструктивным расчетом.
Коэффициент заполнения сердечника kС принимается равным 1 в
случае использования магнитопровода из феррита.
Максимальное значение индукции в магнитопроводе Bmax определяется
исходя из параметров выбранного феррита и рабочей частоты. В первом приближении и в типовом случае
принимается в пределах 0,15-0,2 Тл.
Максимальное значение плотность тока в проводах обмотки j выбирается в зависимости
от выходной мощности источника в соответствии с таблицей [Эраносян О.А. Сетевые блоки питания с
высокочастотными преобразователями.— Л.: Энергоатомиздат. Лени игр. отд-ние, 1991,— 176 с: ил. 109 стр.].
Таблица T.8 – Максимально допустимая плотность тока в проводах обмотки при различной выходной мощности
источника
| POUT_max , Вт | 1 – 7 | 8 – 15 | 16 – 40 | 41 – 100 | 101 – 200 |
| j, А/мм2 | 7 – 12 | 6 – 8 | 5 – 6 | 4 – 5 | 4 – 4,5 |
Обычно плотность тока в проводнике выбирается в пределах 4-8 А/мм2. Чем больше «прокачиваемая»
мощность, тем меньше выбирается значение плотности тока. При
POUT_maxбольшей 200 Вт
плотность тока может быть выбрана в пределах 3-4 А/мм2.
Необходимо понимать, что это тоже первое приближение, необходимое для начального расчета и корректируемое
впоследствии.
Абсолютной гарантией того, что потери в обмотках не приведут к их перегреву является выбор плотности тока
равной 2 А/мм2. Однако это «советское» решение приведет к значительному увеличению габаритов и
повышению стоимости данного решения.
3. Выбор типа магнитопровода и феррита
Выбор марки магнитопровода осуществляется в соответствии с рассчитанным параметром ScS0
и конструктивными особенностями (формфактор, технологичность намотки, электромагнитная совместимость,
экономика и т.д.). Феррит выбирается исходя из компромисса «стоимость-технические характеристики».
При этом в качестве площади поперечного сечения сердечника SС должна быть использована минимально
обеспечиваемая величина площади поперечного сечения (Minimum core cross section) – Amin, а не
Ae эффективная площадь сечения магнитопровода (Effective magnetic cross section). Все эти
параметры указаны в datasheet-ах.
Определившись с конкретной маркой магнитопровода и феррита мы будем знать следующие параметры:
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
Bmax – максимальное значение индукции в магнитопроводе при выбранной частоте;
4. Расчет числа витков первичной обмотки
Число витков первичной обмотки рассчитывается по формуле:
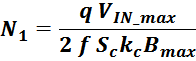
где:
q – относительная длительность импульса (максимальное значение);
VIN_max – напряжение на первичной обмотке трансформатора (максимальное
значение);
f – рабочая частота;
SС – площадь поперечного сечения сердечника;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе (если габаритный параметр выбранного
типоразмера магнитопровода трансформатора более чем в 1,5 раза превышает рассчитанное значение то имеет
смысл уменьшить максимальную индукцию в магнитопроводе за счет увеличения числа витков в обмотках. При этом
потери в магнитопроводе могут быть значительно уменьшены);
Относительная длительность импульса q рассчитывается как отношение максимальной
длительности импульса ti_max к периоду и для двухтактных преобразователей
может быть принята равной 0,5:
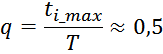
Здесь напряжение на первичной обмотке трансформатора в первом приближении принимается равным входному
напряжению преобразователя VIN_max (по максимальному значению). При расчете
преобразователей с широким диапазоном входного напряжения используется максимальное значение относительной
длительности импульса qmax и максимальное значение напряжения
Vin_max. Это обеспечит область безопасной работы трансформатора во всем
диапазоне входных напряжений и коэффициентов заполнения, что особенно важно при большой иннерции обратной
связи. В установившемся рабочем режиме преобразователя при увеличении напряжения коэффициент q будет
пропорционально уменьшаться и произведение qV останется неизменным.
5. Расчет выходного напряжения вторичной обмотки трансформатора
Выходное напряжение вторичной обмотки трансформатора V2 рассчитывается как сумма выходного
напряжения преобразователя и суммы падений напряжений на выходном выпрямителе и силовом дросселе:
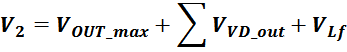
где:
VOUT_max – выходное напряжение преобразователя;
ΣVVD_out – суммарное падение напряжения на диодах выходного выпрямителя;
VLf – падение напряжения на выходном силовом дросселе.
На первой итерации расчета можно использовать оценочные значения величин падений напряжения. Так в случае
использования выпрямителя с выводом от средней точки суммарное падение напряжения на выходном выпрямителе
равно падению напряжения на диоде (для Siдиодов – 1,5 В, для диодов Шоттки – 0,5 В). При использовании
мостового выпрямителя суммарное падение напряжения на выпрямителе равно удвоенному падению напряжения на
диоде. В первом приближении падение напряжения на выходном дросселе VLf можно в первом
приближении принять равным 2-5 % от выходного напряжения преобразователя.
6. Расчет коэффициента трансформации
Коэффициент трансформации k рассчитывается как отношение входного напряжения VIN_min,
прикладываемого к первичной обмотке трансформатора и выходного напряжения на вторичной обмотке V2
:
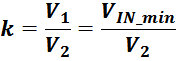
где:
V2 – напряжение на выходе вторичной обмотки;
VIN_min – минимальное значение напряжения, прикладываемого к первичной обмотке.
7. Расчет числа витков вторичной обмотки
Число витков вторичной обмотки N2 рассчитываются по соотношению:
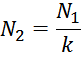
где:
N1 – число витков первичной обмотки;
k – коэффициент трансформации.
8. Расчет индуктивности намагничивания первичной обмотки трансформатора
Индуктивность намагничивания первичной обмотки трансформатора L0 рассчитывается по соотношению:
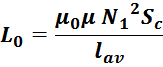
где:
µ0 – магнитная постоянная;
µ – магнитная проницаемость материала магнитопровода;
SС – площадь сечения магнитопровода;
lav – эффективная длина средней линии магнитопровода;
N1 – число витков первичной обмотки.
9. Расчет токов первичной обмотки трансформатора
Подробный вывод выражений для расчета токов обмоток трансформатора двухтактного преобразователя прямого хода
представлен в разделах «Полумостовой преобразователь», «Мостовой преобразователь» и «Двухтактный
преобразователь push-pull».
Амплитудное значение тока первичной обмотки
Амплитудное значение тока первичной обмотки Iw1_max определяется выражением:
для мостовой схемы и пуш-пул:
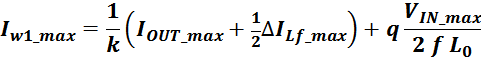
для полумостовой схемы:
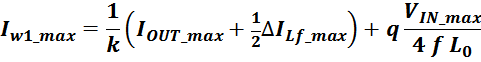
где:
k – коэффициент трансформации;
IOUT_max – выходной ток преобразователя (максимальное значение);
∆ILf_max – максимальная величина пульсаций тока дросселя, размах пульсаций
(входное значение для расчета трансформатора);
q – относительная длительность импульса (максимальное значение);
VIN_max – напряжение, прикладываемое к первичной обмотке (максимальное
значение);
f – рабочая частота;
L0 – индуктивность намагничивания первичной обмотки трансформатора.
Среднее значение тока первичной обмотки
Среднее значение тока первичной обмотки Iw1_avg определяется выражением:
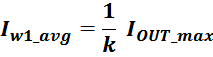
где:
k – коэффициент трансформации;
IOUT_max – выходной ток преобразователя (используется максимальное значение
тока).
Среднеквадратичное значение тока первичной обмотки
Среднеквадратичное значение тока первичной обмотки Iw1_rms вычисляется по
формуле (см. раздел «Резисторы»):
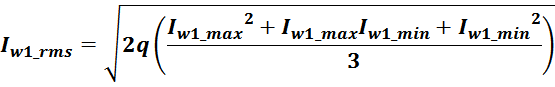
где:
q – относительная длительность импульса (максимальное значение);
Iw1_max, Iw1_min – максимальное и
минимальное значения тока первичной обмотки вычисляются по соотношениям:
для мостовой схемы и пуш-пул:
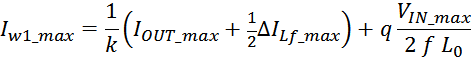
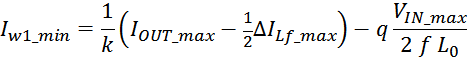
для полумостовой схемы:
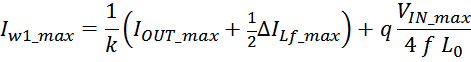
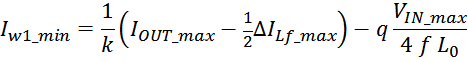
10. Расчет токов вторичной обмотки трансформатора
Амплитудное значение тока вторичной обмотки
Амплитудное значение тока вторичной обмотки Iw2_max определяется выражением:
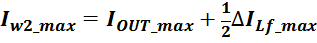
где:
IOUT_max – выходной ток преобразователя (максимальное значение);
∆ILf_max – максимальная величина пульсаций тока дросселя (входное значение
для расчета трансформатора).
Среднее значение тока вторичной обмотки
Среднее значение тока вторичной обмотки Iw2_avg определяется выражением:
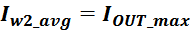
В случае наличия двух полуобмоток, итоговое выражение имеет вид:
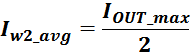
Среднеквадратичное значение тока вторичной обмотки
В достаточно точном приближении среднеквадратичное значение тока вторичной обмотки Iw2_rms
(пусть даже состоящей из двух полуобмоток) равно среднеквадратичному значению тока выходного дросселя. Ток
выходного дросселя имеет форму треугольных импульсов с постоянной составляющей и вычисляется по выражению
(см. раздел «Резисторы»):
вычисляется по выражению:
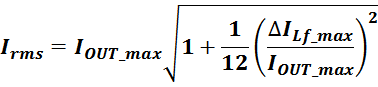
где:
IOUT_max – выходной ток (максимальное значение);
ΔILf_max – пульсация тока дросселя (размах между максимальным и
минимальным значениями).
11. Расчет конструкции трансформатора
В результате выполненного последовательного расчета по шагам 1-10 мы получаем следующие параметры:
– конкретный тип магнитопровода c конкретными геометрическими параметрами;
– число витков первичной и вторичной обмоток N1 и N2.
Далее после получения этих базовых параметров выполняется детальный конструктивный расчет. Последовательность
расчета представлена ниже.
11.1 Расчёт параметров проводов обмоток
Минимальная площадь поперечного сечения обмоток (по меди) рассчитывается по соотношениям:
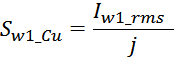
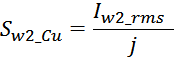
Sw1_Cu – площадь поперечного сечения проводника первичной обмотки;
Sw2_Cu – площадь поперечного сечения проводника вторичной обмотки;
Iw1_rms , Iw2_rms – среднеквадратичные
значения токов первичной и вторичной обмоток соответственно;
j – выбранное значение максимальной плотности тока в обмотках.
В случае если первичная обмотка состоит из двух полуобмоток (пуш-пул преобразователь) то полученное значение
площади сечения Sw1_Cu делится на два. Аналогично в случае если вторичная
обмотка состоит из двух полуобмоток (вторичная обмотка трансформатора имеет вывод от средней точки) то
полученное значение площади сечения Sw2_Cu делится на два.
Далее вычисляется диаметр проводов (по меди) для выполнения обмоток:
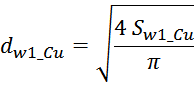
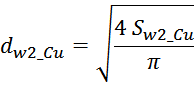
11.2 Выбор типа провода обмоток и определение диаметра и площади поперечного сечения проводников с
изоляцией
На основании вычисленного диаметра провода (по меди) выбирается ближайший диаметр провода из номенклатуры
диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление производится в большую сторону:
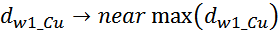
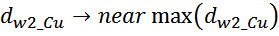
В соответствии с выбранным типом провода пересчитывается площадь поперечного сечения выбранного типа провода
по меди по формулам:
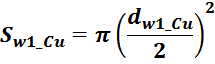
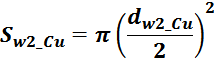
Далее в соответствии со справочным листком на выбранный тип обмоточного провода определяется его диаметр с
изоляцией для первичной и вторичной обмоток dw1_ins и
dw2_ins :
11.3 Расчёт средней длины витка обмоток трансформатора
Ш- и П- образные, чашеобразные магнитопроводы
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредние длины
витков рассчитываются по соотношениям:
для первичной обмотки:
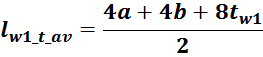
где:
a, b – геометрические параметры характеризующие сечение каркаса магнитопровода (см. рисунок T.40);
tw1 – толщина обмотки, вычисляемая по соотношению:
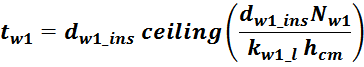
здесь:
функция (ceiling) – округление до большего целого;
hcm – высота каркаса магнитопровода определяющая высоту обмотки;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины
провода (таблица T.7).
Таблица T.7 – Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
| Диаметр провода с изоляцией, мм | 0,08 – 0,31 | 0,31-0,5 | 0,5-2,1 |
| Коэффициент укладки | 0,8-0,75 | 0,75-0,7 | 0,65-0,6 |

Рисунок T.40 – К определению средней длины витка для Ш- и П- образных магнитопроводов
для вторичной обмотки:
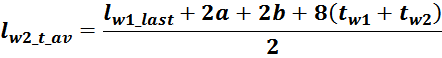
где:
lw1_last – длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
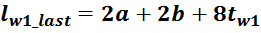
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
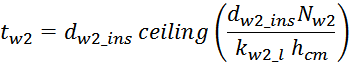
здесь:
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка рассчитывается по следующим соотношениям:
для первичной обмотки:
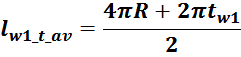
где:
R – радиус каркаса магнитопровода;
tw1 – толщина первичной обмотки, вычисляемая по соотношению:
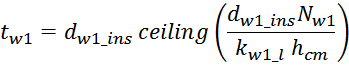
где:
функция (ceiling) – округление до большего целого;
hcm – высота каркаса магнитопровода определяющая высоту обмотки;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
для вторичной обмотки:
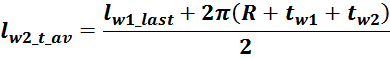
где:
lw1_last – длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
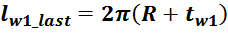
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
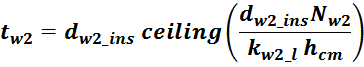
здесь:
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Тороидальные магнитопроводы
Для тороидальных магнитопроводов расчет среднего витка осуществляется по соотношениям:
для первичной обмотки:
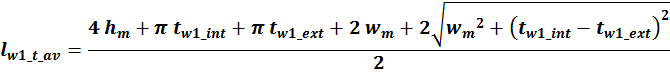
где:
wm – ширина магнитопровода;
hm – высота магнитопровода;
tw1_int – толщина внутреннего слоя первичной обмотки;
tw1_ext – толщина внешнего слоя первичной обмотки.
Толщины tw1_int и tw1_ext определяются по
соотношениям:
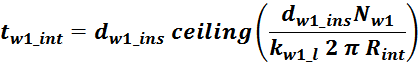
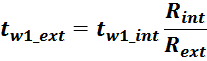
здесь:
функция (ceiling) – округление до большего целого;
Rint – внутренний радиус тора;
Rext – внешний радиус тора;
dw1_ins – диаметр обмоточного провод первичной обмотки с изоляцией;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).

Рисунок T.41 – К определению средней длины витка тороидальных магнитопроводов. (показаны обозначения
только первичной обмотки)
для вторичной обмотки:
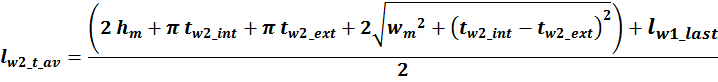
где:
lw1_last – длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
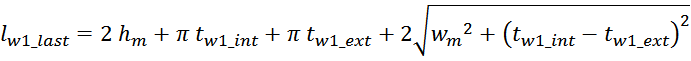
tw1_int и tw1_ext определяются по
соотношениям:
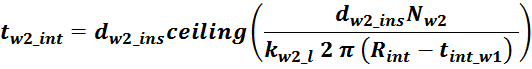
здесь:
dw2_ins – диаметр обмоточного провод первичной обмотки с изоляцией;
Nw2 – число витков в первичной обмотке;
kw2_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
11.4 Определение длин проводников первичной и вторичной обмоток
Длина проводников обмоток определяется как произведение средней длины витка на число витков:
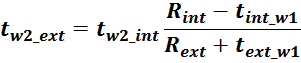
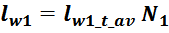
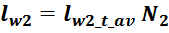
Полученная величина определяет, сколько провода нужно отмерить на обмотки трансформатора.
11.5 Конструктивный расчет структуры обмотки трансформатора, фактическая проверка возможности
размещения обмотки
Использование некоторой предопределенной величины коэффициента заполнения окна не дает однозначной гарантии
размещения обмотки в окне магнитопровода. Поэтому необходима проверка конструктивного условия размещения
обмотки в окне магнитопровода. Кроме этого, может быть неоптимальное использование окна магнитопровода, если
останется слишком много свободного места в окне обмотки.
Для конструктивного расчета структуры обмотки трансформатора выполняется следующая последовательность
действий:
Ш- и П- образные, чашеобразные магнитопроводы
– определяется средняя ширина намоточного слоя hlav. Она равна высоте каркаса магнитопровода
hcm (рисунок T.42):
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.

Рисунок T.42 – К расчету конструкции обмотки трансформатора преобразователя
– определяется число витков в одном слое для первичной и вторичной обмоток
Nw1_l и Nw2_l :
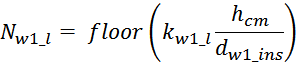
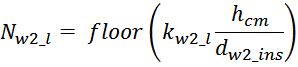
где:
операция (floor) – округление до меньшего целого;
hcm – высота каркаса магнитопровода;
dw1_ins , dw2_ins – диаметры проводников
обмоток с изоляцией;
kw1_l , kw2_l – коэффициенты укладки
(laying), зависящие от толщины провода (таблица T.7).
– рассчитывается общее число слоев для первичной и вторичной обмоток Wl1 ,
Wl2:
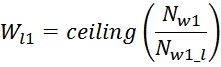
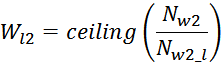
где:
(ceiling) – округление до большего целого;
Nw1, Nw2 – число витков в первичной и вторично обмотках,
соответственно;
Nw1_l , Nw2_l – число витков в одном слое
первичной и вторичной обмоток, соответственно.
– рассчитываются толщины обмоток трансформатора Hw1 , Hw2 :
для первичной обмотки:
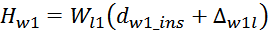
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 – число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
для вторичной обмотки:
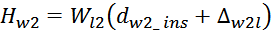
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 – число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величины Δ1l и
Δ2lпринимаются равными нулю (в реальности, при плотной намотке за счет укладывания
витков следующего слоя в пазы слоя предыдущего толщина обмотки может быть несколько меньше).
– рассчитывается общая толщина «пирога» обмотки HΣ:
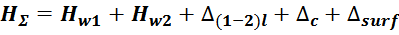
где:
Δ(1-2)l – толщина слоя межобмоточной изоляции;
Δc – толщина каркаса (расстояние между поверхностью каркаса и магнитопроводом);
Δsurf – толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 – толщины обмоток трансформатора.
– проверяется условие фактического размещения всех конструктивных элементов «пирога» обмоток в окне
магнитопровода:
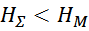
где:
HΣ – суммарная толщина «пирога» обмоток;
HM – ширина окна магнитопровода.
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 3 – 11).
Тороидальные магнитопроводы
В случае тороидальных магнитопроводов ширина намоточного слоя уменьшается по мере намотки. Поэтому все
сложнее.
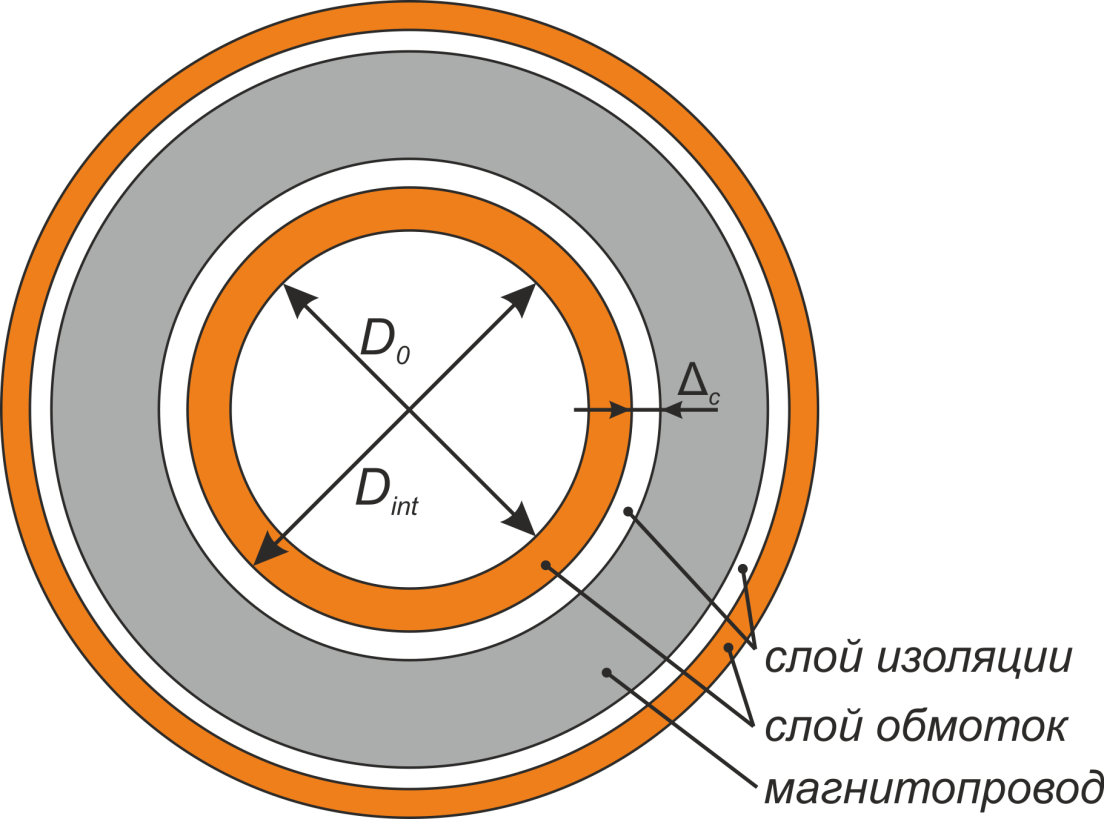
Рисунок T.43 – К расчету конструкции обмоток тороидального трансформатора: Dint – внутренний
диаметр тора магнитопровода с учетом слоя изоляции, D0 – остаточный технологический диаметр.
– рассчитывается число слоев первичной обмотки Wl1 по выражению:
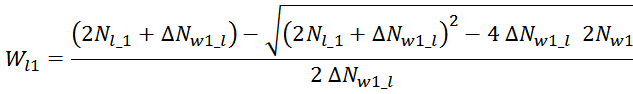
где:
Nw1 – число витков первичной обмотки;
Nl_1 – число витков первого слоя первичной обмотки, определяемое из выражения:
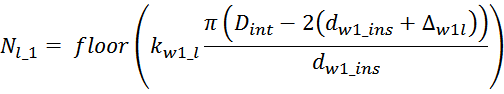
здесь:
операция (floor) – округление до меньшего целого;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw1l – толщина межслоевой изоляции первичной обмотки;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
kw1_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7).
ΔNw1_l – уменьшение числа витков от слоя к слою определяется выражением:
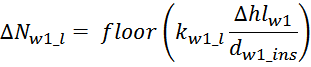
где:
операция (floor) – округление до меньшего целого;
Δhlw1 – уменьшение ширины намоточного слоя от слоя к слою:
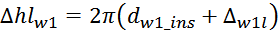
Полученное значение Wl1, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
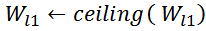
– рассчитывается толщина первичной обмотки Hw1 по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
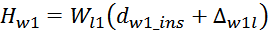
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 – число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
– рассчитывается число слоев вторичной обмотки Wl2 по выражению:
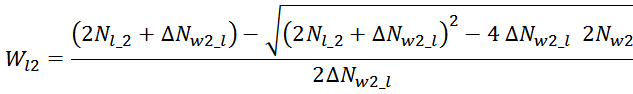
где:
Nw2 – число витков вторичной обмотки;
Nl_2 – число витков первого слоя вторичной обмотки, определяемое из выражения:
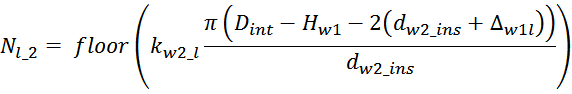
здесь:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw2l – толщина межслоевой изоляции вторичной обмотки;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
kw2_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7);
Hw1 – толщина первичной обмотки.
ΔNw2_l – уменьшение числа витков от слоя к слою для вторичной обмотки
определяется выражением:
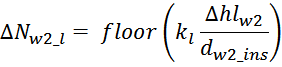
где:
операция (floor) – округление до меньшего целого;
Δhlw2 – уменьшение ширины намоточного слоя от слоя к слою:
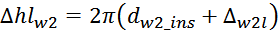
Полученное значение Wl2, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
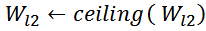
– рассчитывается толщина вторичной обмотки Hw2 по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
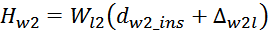
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 – число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
– рассчитывается суммарная толщина «пирога» намотки HΣ:
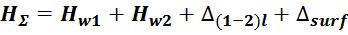
где:
Δ(1-2)l – толщины межобмоточной изоляции
Δsurf – толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 – толщины обмоток трансформатора.
– проверяется условие фактического размещения обмотки в окне магнитопровода:
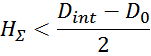
где:
HΣ – суммарная толщина «пирога» намотки;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции) который фактически определяет
ширину окна магнитопровода;
D0 – остаточный диаметр внутри тороидального трансформатора (технологический).
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 3-11).
12. Расчет сопротивления обмоток трансформатора
Электрическое сопротивление обмоток трансформатора Rw1 и Rw2
рассчитывается по формуле для расчета омического сопротивления протяженного проводника:
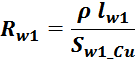
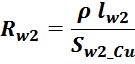
где:
ρ – удельное сопротивление материала провода (для меди – 0,0175 Ом·мм2 м-1 );
lw1 , lw2 – длины проводов первичной и вторичной обмоток
соответственно;
Sw1_Cu , Sw2_Cu – площади поперечного
сечения выбранного типа провода (по меди).
13. Расчет омических потерь в обмотках
Суммарные потери на омическом сопротивлении обмоток определяются по формулам:
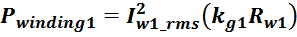
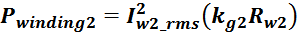
где:
Rw1 , Rw2 – сопротивление первичной и вторичной обмоток на
постоянном токе;
kg1 , kg2 – коэффициент добавочных потерь за счет скин-эффекта и
эффекта близости в первичной и вторичной обмотках соответственно;
Iw1_rms , Iw2_rms –
среднеквадратичное значение тока в первичной и вторичной обмотках соответственно.
NB: При высоких рабочих температурах трансформатора необходимо учитывать влияние температуры на удельное
сопротивление проводников обмоток. При высоких частотах необходимо оценить увеличение эффективного
сопротивления обмоток в результате действия скин-эффекта (см. пункт «Влияние скин-эффекта на сопротивление
обмоток при высоких частотах»).
14. Оценка уровня потерь в магнитопроводе
Существуют три способа определения потерь в магнитопроводе:
– рассчитать по формуле (при наличии аппроксимацонных коэффициентов);
– определить по графику из datasheet;
– определить экспериментально.
Расчёт по аппроксимацонным коэффициентам
Тепловая энергия, выделяемая в магнитопроводе определяется режимом работы дросселя – частотой работы f и
уровнем магнитной индукции Bmax. Для расчета потерь в магнитопроводе Pferrit
используют следующее аппроксимирующее выражение [Optimum designof a high-power, high-frequency transformer.
R. Petkov. IEEE Transactions on Power Electronics (Volume: 11, Issue: 1, Jan 1996)]:
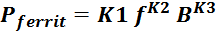
где:
f – частота;
B – индукция;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
Определение по графику относительных потерь из datasheet
Для определения потерь в магнитопроводе можно использовать соотношение:
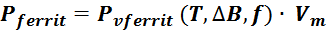
где:
Pvferrit – мощность потерь на единицу объема, являющейся функцией температуры, магнитной индукции
и частоты. Графики данной зависимости представлены в справочных листах (datasheet) на каждый ферромагнитный
материал магнитопровода;
V – объем магнитопровода (приводится в справочных листах (datasheet).
Мощность потерь на единицу объема определяется типом феррита и приводится в справочных данных на конкретный
тип магнитного материала.
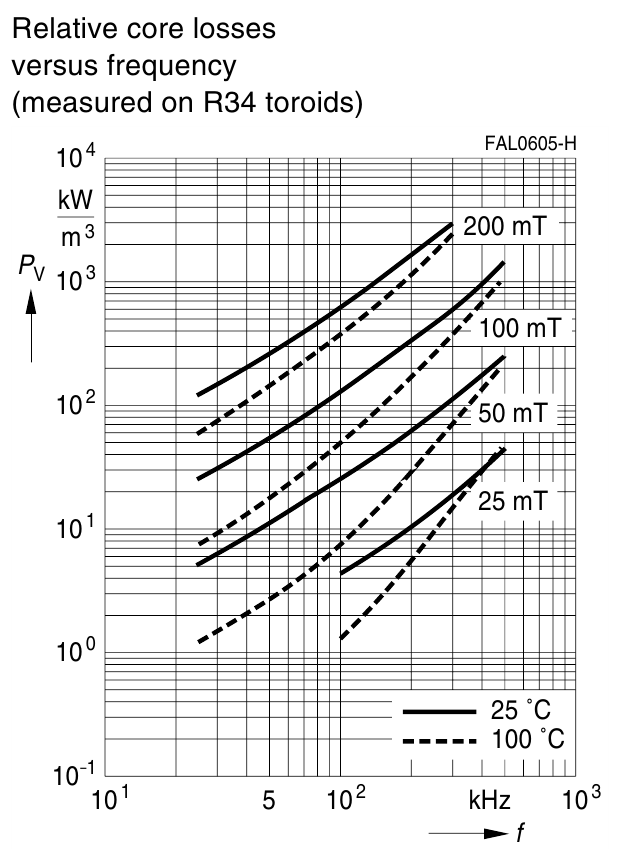
Рисунок T.44 – Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87 [Ferrites and accessories. SIFERRITmaterial N87, EPCOS AG 2006]
Определение по уровню максимальных потерь из datasheet на магнитопровод
Максимальный уровень потерь в магнитопроводе соответствует крайним режимам эксплуатации магнитопровода.
Уровень максимальных потерь часто приводится в datasheet на конкретный тип магнитопровода при различных
условиях (индукция магнитного поля, частота, температура). Уровень максимальных потерь обозначается как
PV (W/set).
В этом случае мощности потерь в магнитопроводе Pferrit приравнивается к уровню максимальных потерь
PV представленном в datasheet для наиболее близких условий эксплуатации:
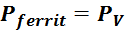
Экспериментальное определение
В случае отсутствия данных для расчета остается путь экспериментального определения потерь.
15. Расчет суммарных потерь
Суммарные потери трансформатора Ptotal_loss складываются из омических потерь
обмотки и потерь магнитопровода:
где:
Pwinding1 , Pwinding2 – омические потери в первичной и вторичной
обмотке соответственно;
Pferrit – потери в магнитопроводе.
16. Расчет температурного режима трансформатора и оптимизация
Установившаяся температура перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева)
приблизительно оценивается по соотношению [McLyman C. Transformer and inductor design handbook.2004]:
где:
Ptotal loss – мощность суммарных потерь в трансформаторе;
ST – суммарная эффективная площадь охлаждения трансформатора (в см2).
Если полученное с учетом рассчитанной «дельты перегрева» значение температуры нагрева трансформатора лежит в
пределах 50-80°С, то расчет трансформатора можно считать законченным. Если полученное значение превышает
80°С, то имеет смысл использовать магнитопровод большего размера.
Если в результате расчета уровень перегрева трансформатора ΔT будет значительно меньше максимально
допустимого:
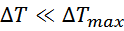
то имеет смысл использовать оптимизировать конструкцию трансформатора с целью уменьшения стоимости и
массогабаритных показателей – уменьшить формфактор магнитопровода и варьировать плотность тока, размах
индукции (можно делать одновременно с повышением частоты).
Кроме того, если при допустимом уровне нагрева трансформатора получится, что мощность, выделяемая на активном
сопротивлении обмотки существенно меньше, чем в феррите магнитопровода:
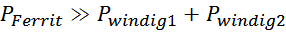
то имеет смысл использовать большую плотность тока, протекающего через обмотки и повторить расчет по пунктам
1-12.
Для трансформаторов больших габаритов (с рассеваемой площадью более 1000 см2) установившаяся
температура нагрева трансформатора относительно окружающей среды ∆T (дельта перегрева) оценивается по
соотношению [В.Е. Китаев, А.А. Бокуняев. Проектирование источников электропитания устройств связи. Учеб.
пособие.- М.: Связь,1972.- 200 с.]:
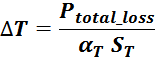
где:
Ptotal_loss – мощность суммарных потерь в трансформаторе;
αT – коэффициент теплоотдачи, зависящий от множества факторов (материал трансформатора,
конструктивное исполнение, температуры окружающей среды и т.д.). Для практических расчетов принимается
равным: 11-13 Вт/м2 °С.
ST – суммарная площадь охлаждения трансформатора.
Необходимо понимать, что оптимизация расчета трансформатора проводится с учетом целевых приоритетов:
Приоритет 1 – Малые массогабаритные параметры трансформатора и, соответственно, стоимость. В этом случае
необходимо провести расчет всех параметров трансформатора с целью обеспечения (но не превышения) заданного
уровня перегрева и минимальной стоимости/массогабаритных параметров. В этом случае плотность тока, размах
индукции итерационно увеличиваются;
Приоритет 2 – Высокий КПД. В этом случае необходимо задаться максимальными массогабаритными параметрами и с
учетом этого варьируя параметры трансформатора (индукция, плотность тока и т.д.) провести расчет всех
параметров трансформатора с целью минимизации мощности потерь. В этом случае плотность тока, размах индукции
итерационно уменьшаются;
Трансформатор однотактного прямоходового преобразователя
Режим работы. Основные соотношения
Прямоходовый однотактный трансформатор – это трансформатор преобразователей с несимметричным
перемагничиванием магнитопровода, когда используется только работа в одном квадранте петли гистерезиса.
Такими преобразователями являются – прямоходовый одноключевой однотактный преобразователь, и прямоходовый
двухключевой однотактный преобразователь (он же – «косой полумост»).
В качестве примера, для более наглядного рассмотрения процессов, используем простой двухобмоточный
трансформатор с одной первичной и одной вторичной обмотками без дополнительных отводов, что типично для
преобразователя «косой полумост», где размагничивающая обмотка отсутствует. В другой топологии прямоходового
однотактного одноключевого преобразователя трансформатора присутствует размагничивающая обмотка, но в целом
режим работы трансформатора остается все тот же.
К первичной обмотке трансформатора однотактного прямоходового преобразователя прикладываются однополярные
импульсы напряжения следующие друг за другом через некоторую паузу.
Установим взаимосвязь между параметрами импульсов напряжения (амплитуда, длительность), прикладываемого к
первичной обмотке трансформатора, числом витков в ней, параметрами магнитопровода и достигаемой величины
индукции магнитного поля.
Начальные условия и соотношения :
Основные количественные параметры прямоугольных импульсов прикладываемых к первичной обмотке:
– длительность импульсов напряжения, прикладываемого к первичной обмотке трансформатора – ti ;
– период импульсов напряжения, прикладываемого к первичной обмотке трансформатора T ;
– амплитуда напряжения, прикладываемого к первичной обмотке трансформатора – VIN .
Форма импульсов напряжения, прикладываемых к первичной обмотке трансформатора представлена на рисунке T.45.
Форма импульсов напряжения соответствует реальной работе однотактных преобразователей прямого хода.
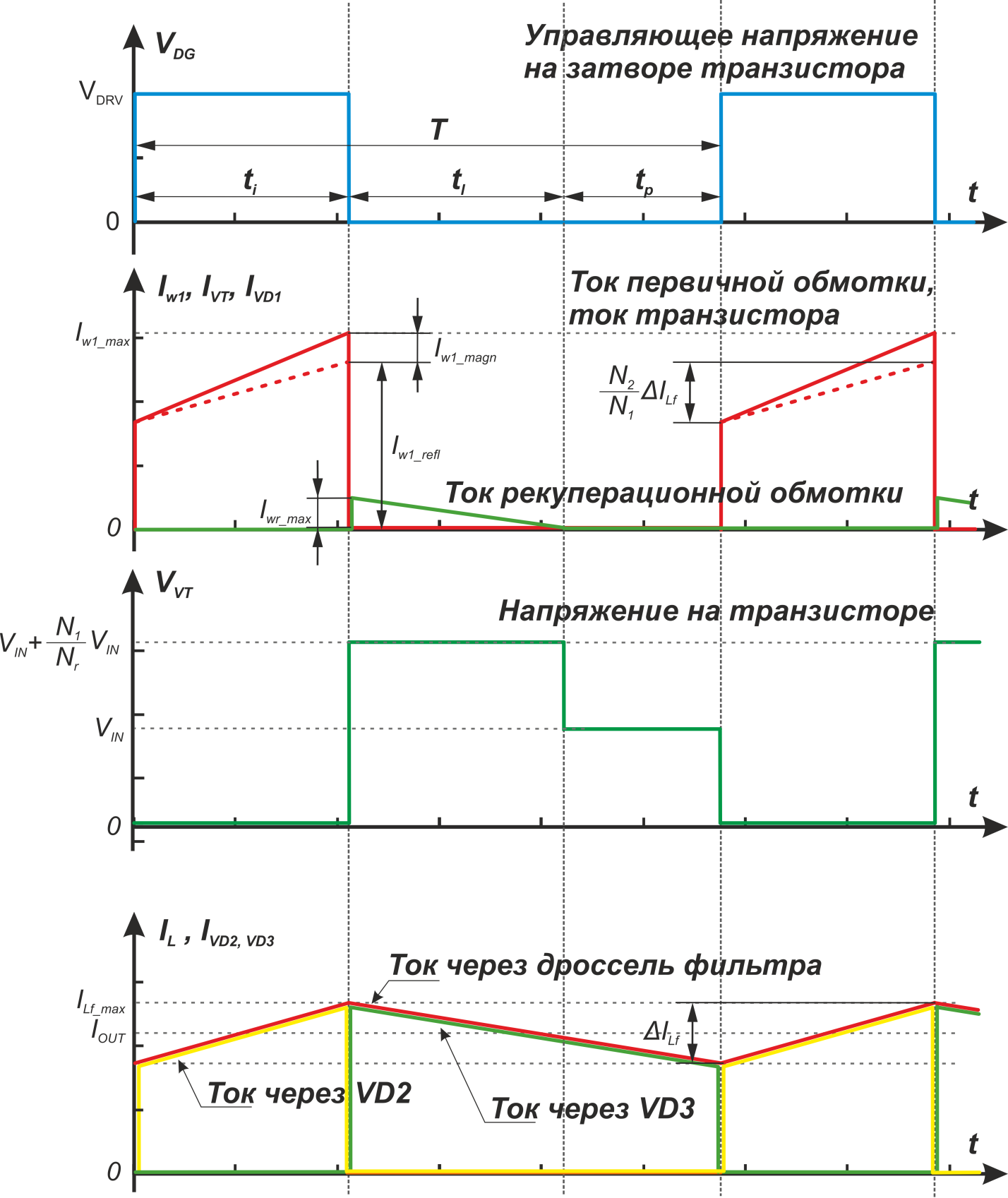
Рисунок T.45 – Временные диаграммы импульсов управления, токов через первичную и рекуперирующую обмотки,
напряжения на силовом ключе, тока через силовой дроссель фильтра и диоды. [Dokic B.L., Blanusa B. Power
Electronics: Converters and Regulators. Springer Cham Heidelberg New York Dordrecht London, 2015. XVIII,
598
p. – стр. 241]
После приложения к первичной обмотке трансформатора импульса напряжения в ней возникнет ток, и при отсутствии
нагрузки первичная обмотка ведет себя как дроссель с индуктивностью, называемой индуктивностью
намагничивания. При этом в магнитопроводе возникает магнитный поток Ф0(t).
Если к вторичной обмотке трансформатора подключается нагрузка (омическая для простоты выводов), то в во
вторичной обмотке возникает ток I2 который в свою очередь индуцирует в магнитопроводе вторичный
магнитный поток Ф2(t). Реакцией на это является одновременное увеличение тока первичной обмотки I1
который создаёт дополнительный первичный магнитный поток Ф1(t) направленный противоположно Ф2(t).
Поскольку увеличение магнитного потока Ф1(t) от тока первичной обмотки практически равно
увеличению магнитного потока Ф2(t) от тока вторичной обмотки, то результирующее изменение
магнитного потока в магнитопроводе практически равно нулю:
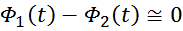
Увеличение нагрузки и соответственно тока вторичной обмотки приводит к увеличению магнитного потока вторичной
обмотки Ф2(t) и соответственно потока Ф1(t). При этом протекающий в магнитопроводе
магнитный поток Ф0(t) практически не изменяется и определяется только индуктивностью первичной
обмотки. Аналогичный процесс происходит при уменьшении нагрузки. Магнитный поток Ф0(t) вызывает
перемагничивание сердечника трансформатора [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника
и расчет.Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с.]. Таким образом, магнитные потоки обмоток,
обусловленные током нагрузки в магнитопроводе взаимно компенсируют друг друга. Магнитопровод «не чувствует»
нагрузки.
Тем не менее, магнитный поток в магнитопроводе все равно изменяется, поскольку он (магнитопровод)
намагничивается током первичной обмотки, которая ведет себя как дроссель. Первичная обмотка-дроссель имеет
индуктивность называемую индуктивностью намагничивания.
После приложения к первичной обмотке импульса напряжения начинает возрастать ток намагничивания через неё.
При этом магнитный поток Φ(t) в магнитопроводе за время импульса ti также увеличивается, что
описывается соотношением [Теория и расчет трансформаторов источников вторичного электропитания. А. В.
Хныков. СОЛОН-Пресс. 2010. 127 с.]:
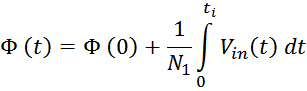
где:
Φ(0) – начальное значение магнитного потока в магнитопроводе до приложения импульса.
Полагая, что амплитуда напряжение VIN прикладываемого к первичной обмотке трансформатора в течение
импульса не изменяется (VIN = const) – получим выражение для магнитного потока:
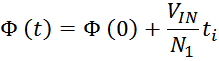
В процессе работы преобразователя происходит перемагничивание сердечника трансформатора по линейному закону.
При этом схемотехника работы такова, что за время паузы ток намагничивания в первичной обмотке спадает до
нуля, то есть к моменту времени соответствующему началу следующего импульса поток в сердечнике определяется
остаточным значением индукции магнитопровода Br (величина магнитной индукции после снятия
магнитного поля):
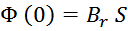
А значение магнитного потока в конце импульса равно:
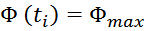
Таким образом, подставляя это значение в формулу для временной зависимости магнитного потока получаем:
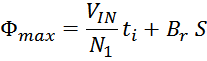
Магнитный поток равен произведению индукции магнитного поля на площадь, в которой она есть:
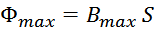
С учетом этого предыдущее выражение приобретает вид:
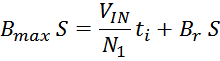
Из этого соотношения выразим амплитуду импульсов напряжения через достигаемое значение магнитного потока,
длительность импульса и число витков первичной обмотки:
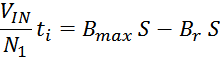
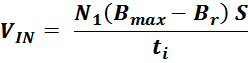
Это выражение определяетвзаимосвязь между амплитудой VIN и длительностью
импульсов напряжения, прикладываемого к первичной обмотке трансформатора, числом витков в ней N1,
площадью поперечного сечения магнитопровода S и достигаемой величины индукции магнитного поля. Это
практически важное выражение, часто используемое в расчетах однотактных прямоходовых преобразователей.
Продолжим эволюцию данного соотношения.
При расчете элементов импульсной преобразовательной техники часто пользуются понятием относительной
длительности импульса q равным отношению длительности ti к периоду T:
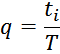
С учетом этого можно получить выражение, содержащее относительную длительность импульса q :
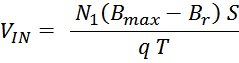
И вспоминая, что частота, есть величина, обратная периоду получаем:
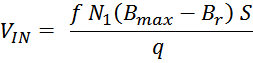
Поскольку в реальности не вся площадь контура охватываемого витками обмотки занята магнитопроводом, то
используют понятие коэффициента заполнения сердечника.
Коэффициент заполнения сердечника (ferrimagnetic core) kc находится из соотношения
площади контура, охватываемого током (витком) S и площади занимаемой собственно магнитопроводом
Sc:
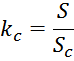
Выражаем отсюда площадь S:
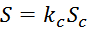
И подставляя эту формулу в выражение для VIN, получаем соотношение для величины напряжения
прикладываемого к первичной обмотке однотактного прямоходового трансформатора:
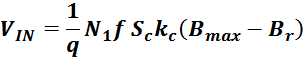
где:
q – относительная длительность импульса по отношению к периоду;
N1 – чисто витков первичной обмотки;
f – частота импульсов;
kc – коэффициент заполнения сердечника магнитопроводом;
Sc – площадь магнитопровода;
Bmax – максимальное значение индукции магнитного поля;
Br – остаточное значение индукции магнитопровода (величина магнитной индукции после снятия
магнитного поля индукцией Bmax).
Данное соотношение устанавливает взаимосвязь между амплитудой, длительностью импульсов напряжения
прикладываемого к первичной обмотке трансформатора, характеристиками магнитопровода, числом витков и
максимальным значением индукции магнитного поля, достигаемым в сердечнике. В соотношении подразумевается,
что размах магнитной индукции ΔB равен разнице между максимальной индукцией в магнитопроводе и остаточным
значением индукции для данного магнитопровода :
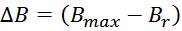
Таким образом, отсюда видно, что максимальный размах индукции магнитного поля определяется разницей между
максимальным значением магнитной индукции, которая ограничивается «сверху» индукцией насыщения
Bsat и «снизу» остаточной индукцией Br.
Основным способом снижения остаточной индукции Br является введение немагнитного зазора в
магнитопровод (см. раздел «Индуктивность»). При введении зазора эта величина уменьшается пропорционально
уменьшению эффективной магнитной проницаемости:
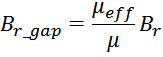
где:
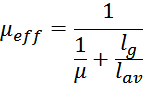
где:
μ – магнитная проницаемость материала сердечника;
lg – длина магнитного зазора;
lav – эффективная длина средней линии магнитопровода.
Для напряжения на вторичной обмотке соотношение аналогично. Покажем это. В соответствии с соотношением для
ЭДС индукции вторичной обмотки напряжение на ней V2пропорционально числу витков и скорости
изменения магнитного потока через неё:
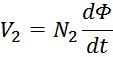
Скорость изменения магнитного потока с учетом всех преобразований равна:
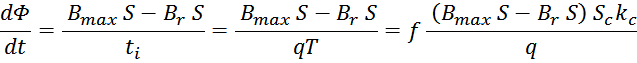
Подставляя это соотношение в предыдущее получаем выражение для напряжения на вторичной обмотке:
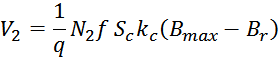
Если выходная обмотка не одна, то это выражение можно обобщить на все обмотки:
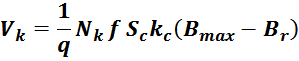
(для любой k-й обмотки).
Расчет числа витков первичной обмотки
Из выражения для VIN полученного в предыдущем разделе можно определить число витков первичной
обмотки. Число витков первичной обмотки трансформатора однотактного прямоходового преобразователя
определяется по соотношению:
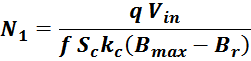
Эта формула позволяет определить минимальное число витков в первичной обмотке трансформатора при заданных q,
VIN, f, Sc, kc, Bmax, Br. Полученные выше соотношения
для VINи N1 для справедливы для однотактного одноключевого прямоходового
преобразователя с размагничивающей обмоткой и двухключевого прямоходового преобразователя (косой полумост).
При расчете числа витков здесь используется максимальное значение относительной длительности импульса q по
отношению к периоду (в большинстве случаев – 0,5, если нет дополнительных мер по увеличению q путем
интенсивного размагничивания магнитопровода. В случае если входное напряжение изменяется в широком
диапазоне, то в формулу расчета числа витков подставляется минимальное значение напряжения и максимальное
значение относительной длительности импульса. При этом в процессе работы преобразователя обратная связь ШИМ
контроллера обеспечивает произведение qVIN неизменным:
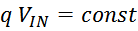
При практических расчетах используется произведение максимальных значений q и VIN с целью
обеспечения безопасного режима работы преобразователя во всем диапазоне входных напряжений, и учете
инерционности обратной связи, отрабатывающей изменение коэффициента q с некоторой задержкой.
Расчет максимального значения индукции в магнитопроводе трансформатора однотактного
прямоходового
преобразователя
При прямоугольной форме импульсов в однотактном преобразователе выражение для максимального значения
магнитного потока Φmax имеет вид:
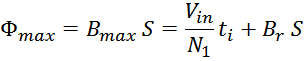
где:
VIN – амплитуда импульсов напряжения прикладываемых к обмотке;
ti – длительность импульсов напряжения прикладываемых к обмотке;
N1 – число витков в первичной обмотке трансформатора;
S – площадь магнитопровода;
Bmax – максимальное значение индукции магнитного поля;
Br – остаточное значение индукции магнитопровода (величина магнитной индукции после снятия
магнитного поля).
Отсюда следует выражение для максимального достигаемого значения индукции в магнитопроводе:
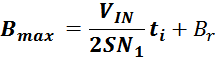
Это соотношение связывает величину индукции B достигаемой в магнитпроводе однотактного прямоходового
преобразователя c амплитудой импульсов VIN их длительностью tiплощадью S и числом
витков обмотки N1. Важно понимать, что максимальная величина индукции B ограничена «сверху»
индукцией насыщения Bsat.
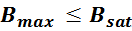
Как видно из формулы для максимального значения индукции магнитный поток в магнитопроводе зависит только от
амплитуды импульсов напряжения VIN прикладываемых к первичной обмотке, длительности импульса
ti, числа витков N1 и – остаточного значения индукции Br. При подключении
нагрузки ко вторичной обмотке возникающий в ней ток создает магнитный поток, направленный навстречу
основному магнитному потоку. Это ведет к увеличению тока в первичной обмотке, которое в свою очередь
компенсирует ожидаемое снижение магнитного потока. Таким образом, величина магнитного потока и
соответственно магнитной индукции не изменяются при подключении нагрузки. Это следует и из эквивалентной
схемы трансформатора.
Габаритная мощность прямоходового однотактного трансформатора
Базовое соотношение для расчета габаритной мощности прямоходового трансформатора имеет вид:
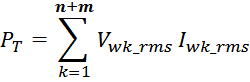
где:
Vwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
Iwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
n+m – суммарное число всех обмоток или полуобмоток.
Формулу, как было показано ранее, можно преобразовать к виду
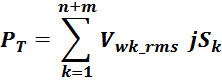
где:
j – плотность тока в проводах обмотки;
Sk – площадь поперечного сечения провода k-й обмотки;
Среднеквадратичное значение напряжения и его амплитудное значение для формы импульсов характерных для
однотактного преобразователя (рисунок T.45) связаны выражениями:
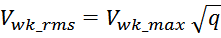
где q – коэффициент заполнения.
С учетом этого соотношение для габаритной мощности будет иметь вид:
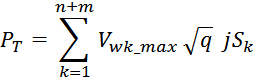
Физически выражение наглядно показывает, что при постоянных максимальных значениях напряжения и тока через
обмотки мощность «прокачиваемая» через трансформатор пропорциональна коэффициенту заполнения q и максимальна
при полном заполнении периода импульсами. Типовой случай максимального значения коэффициента заполнения qдля
однотактного прямоходового преобразователя: q=0.5. В этом случае, при q=0.5 выражение для PT
можно упростить:
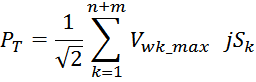
Выражение для напряжения любой k-q обмотки однотактного прямоходового преобразователя (полученное ранее)
имеет вид:
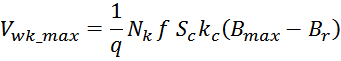
здесь Vwk_max – амплитудное значение напряжения.
С учетом максимального значения коэффициента q=0.5 получаем:
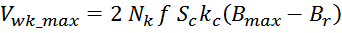
Подставляя в формулу для габаритной мощности получаем:
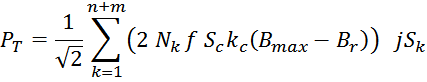
Выносим все постоянные из под знака суммы:
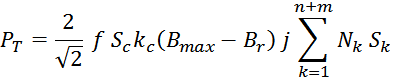
Поскольку суммарная площадь проводников обмоток внутри равна сумме площадей, занимаемых каждой из обмоток в
отдельности (соотношение в пункте «Понятие габаритной мощности трансформатора» настоящего радела):
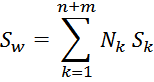
получаем:
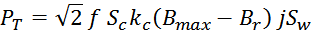
Подставляя выражение, связывающее общую площадь окна и коэффициент его заполнения «медью»:
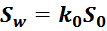
Получаем выражение:
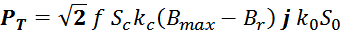
Перегруппируя множители, получаем выражение для габаритной мощности однотактного прямоходового
преобразователя:
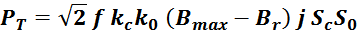
где:
f – рабочая частота;
kс – коэффициент заполнения сердечника;
k0 – коэффициент заполнения окна сердечника медью;
Bmax – максимальное значение индукции в магнитопроводе;
Br – остаточное значение индукции магнитопровода;
j – максимальная плотность тока в проводах обмотки (среднеквадратичное значение);
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника.
Из выражения для габаритной мощности определяют соотношение габаритного типоразмера, необходимое для выбора
параметров магнитопровода трансформатора:
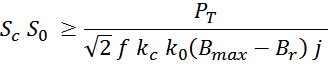
Данное соотношение выведено при допущении, что КПД трансформатора равен 1. При практических расчетах,
значение КПД трансформатора ηT вносится и конечная формула будет иметь вид:
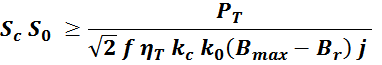
где:
ηT – КПД трансформатора;
f – рабочая частота;
k0 – коэффициент заполнения окна сердечника медью;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
Br – остаточная индукция магнитопровода;
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
j – максимальная плотность тока в обмотках (среднеквадратичное значение).
Это соотношение для габаритной мощности одно из базовых соотношение используемых при расчете
трансформатора.
Из соотношения следует, что массогабаритные показатели трансформатора, характеризуемые
ScS0 снижаются с ростом частоты, увеличением максимальной индукции насыщения
материала, плотности тока в обмотке.
Важно понимать, что соотношение для расчета габаритной мощности во многом носит формальный характер. В
реальности максимальная мощность трансформатора определяется, прежде всего, конструктивными особенностями и
условиями охлаждения. Один и тот-же трансформатор может иметь различную максимальную выходную мощность в
зависимости от условий отвода тепла от него. Интересно, что при резком уменьшении сопротивления нагрузки и
последующем увеличения тока нагрузки возрастет плотность тока в обмотках j входящая в формулу габаритной
мощности. При этом габаритная мощность формально увеличивается, но при этом возрастают тепловые потери в
обмотке, что приводит к увеличению температуры трансформатора и следовательно снижению допустимого уровня
магнитной индукции Bmax.
NB: Сопоставляя полученное соотношение габаритной мощности трансформатора однотактного прямоходового
преобразователя с формулой для габаритной мощности трансформатора двухтактного преобразователя видно, что
при одинаковой мощности габаритный параметр однотактного трансформатора должен быть в 2√2 больше
двухтактного трансформатора. Это обусловлено двумя факторами. Во-первых, максимальный размах индукции в
магнитопроводе однотактного трансформатора в 2-а раза меньше. Это дает двукратное увеличение необходимого
габаритного параметра (по площади сечения магнитопровода). Во-вторых, за счет прямоугольной формы импульсов
тока в обмотке необходимый габаритный параметр должен быть в √2-раза больше (по площади окна
магнитопровода).
Способы уменьшения остаточной индукции, зазор в трансформаторе однотактного прямоходового
преобразователя
В соотношение габаритной мощности трансформатора однотактного прямоходового преобразователя входит
Br – остаточное значение индукции магнитопровода. Чем больше Brтем меньше габаритная
мощность. С целью снижения остаточной индукции используют немагнитный зазор.
Введение зазора увеличит габаритную мощность трансформатора за счет увеличения размаха индукции магнитного
поля. С другой стороны это приведет к снижению индуктивности намагничивания первичной обмотки трансформатора
L0, что приведет к некоторому росту амплитуды тока первичной обмотки и увеличению потерь в
обмотке. Для обоснованного ответа на этот вопрос нужен технико-экономический расчет в каждом конкретном
случае.
Поскольку параметр остаточной индукции феррита Br_max, соответствующий
предельной петле гистерезиса проходящей через точки Bsat и Hc в подавляющем
большинстве случаев практических расчетов не используется, то в datasheet-ах его численное значение
приводится редко (обозначается в datasheet просто как Br). Поэтому распространенным приближением
является расчет габаритной мощности, в котором Br принимается равным нулю и выбирается
магнитопровод обеспечивающий 30-40% запас по габаритной мощности. Однако в ряде случаев, особенно для мощных
преобразователей с топологией «косой полумост» необходим более точный расчет. Дело в том, что Br
для различных типов ферритов может оставлять 20-50% от величины Bmax. Ниже приведена методика
оценки значения остаточной индукции феррита Br и соответствующего расчета габаритной мощности
трансформатора.
Величина максимального значения остаточной индукции феррита Br_max может
быть определена следующими способами:
– поиск численного значения Br_max в datasheet-ах на выбранный тип
ферромагнитного материала (обозначается в datasheet просто как Br);
– определение Br_max из приведенных в datasheet-ах кривых гистерезиса.
Необходимо отметить, что это определение не всегда получается точным по причине большого масштаба по оси
магнитной напряженности H в результате размер петли становится сопоставим с шириной линии графика;
Полученное значение остаточной индукции Br_max сравнивается с максимальным
значением индукции насыщения Bsat и принимается решение о целесообразности или нецелесообразности
введения немагнитного зазора. В случае если остаточная индукция Br_maxсоставляет
более 25-35% от значения максимальной индукции Bsat то рекомендуется вводить в магнитопровод
немагнитный зазор. Если же значение Br составляет меньше 25-35% от Bsat то решение о
зазоре принимается исходя из технико-экономических соображений конкретного случая.
Величина остаточной индукции Br зависит от величины максимально достигаемой индукции. Отношение
остаточной индукции Br к индукции насыщения называется коэффициентом прямоугольности α [В. П.
Миловзоров. Электромагнитная техника. М., Высшая школа. 1966г., стр. 19-20]:
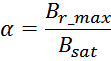
Исходя из приближения подобия петель гистерезиса (рисунок T.46) можно считать, что коэффициент α остается
постоянным для различных петель гистерезиса, соответствующих различным токам:
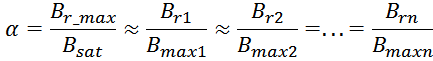
где:
Br_max , Br1 , Br2 ,
Brn – значения остаточной индукции соответствующие петлям гистерезиса с максимальным значением
индукции Bsat , Bmax1 , Bmax2 и
Bmaxn соответственно.
Отсюда следует, что для выбранного максимального значения индукции Bmax можно определить
Br :
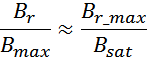
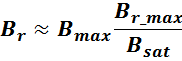
где:
Br – величина остаточной индукции соответствующая максимальному значению индукции Bmax;
Br_max – величина остаточной индукции соответствующая индукции насыщения
Bsat.
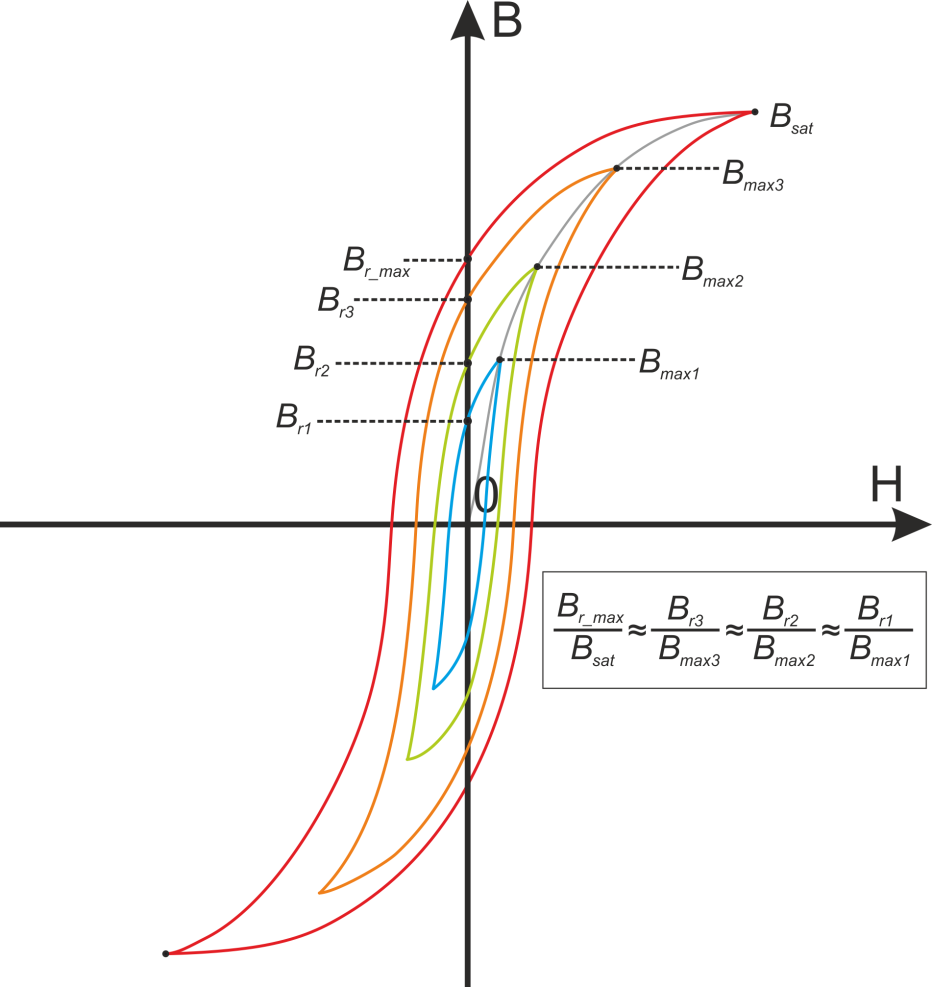
Рисунок T.46 – Петли гистерезиса при различных значениях достигаемой индукции.
Введение в магнитопровод немагнитного зазора изменяет ход петли гистерезиса (рисунок T.47) – петля
вытягивается вдоль оси H. Участок кривой гистерезиса соединяющий точки Br и Hcхорошо
аппроксимируется линейной функцией. Угол наклона линейной функции для магнитопровода без зазора
пропорционален эффективной магнитной проницаемости µ магнитопровода, а для магнитопровода с зазором угол
наклона пропорционален эффективному значению магнитной проницаемости µeff.
Поскольку обе линейных функции имеют пересечение на оси H в точке советующей коэрцитивной силе Hc
, то можно вывести пропорцию:
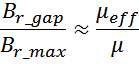
Отсюда следует выражение для оценки величины остаточной индукции Br_gap в
случае введения зазора в магнитопровод:
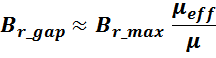
где:
Br_max – величина остаточной индукции соответствующая индукции насыщения
Bsat;
µ – магнитная проницаемость магнитнопровода без зазора (эффективное значение относительной магнитной
проницаемости магнитопровода без зазора – Relative effective permeability, часто обозначается в datasheet
как µe);
µeff – эффективное значение магнитной проницаемости магнитнопровода с зазором.
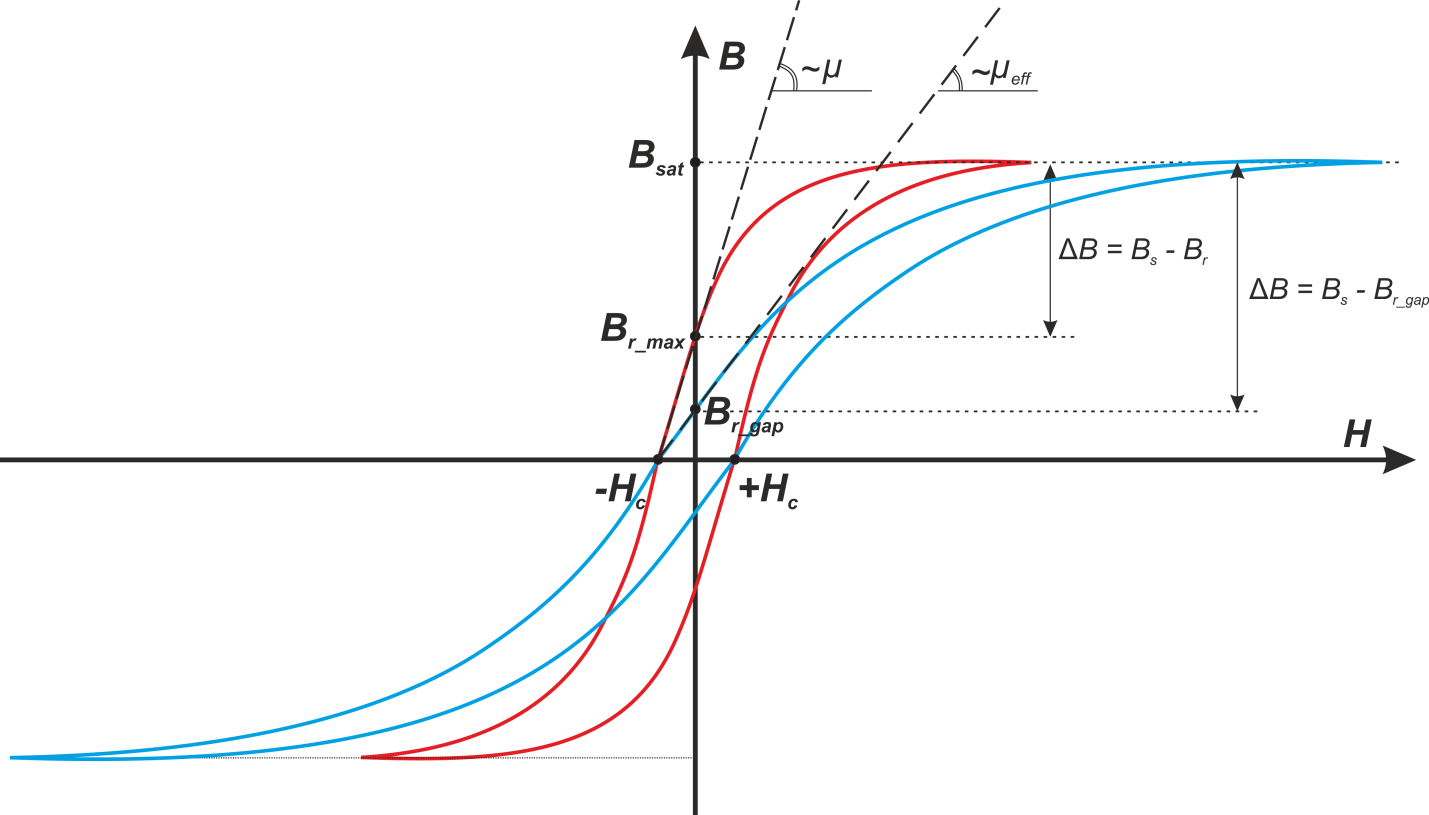
Рисунок T.47 – Изменение хода петли гистерезиса при введении в магнитопровод немагнитного зазора.
Эффективная магнитная проницаемость сердечника с зазором μeff вычисляется по соотношению:
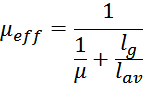
где:
μ – магнитная проницаемость материала сердечника;
lg – длина немагнитного зазора;
lav – длина магнитной линии магнитопровода.
Как правило, если принимается решение вводить зазор, то целевое значение эффективной проницаемости
μeff принимается в 2-10 раз меньше магнитной проницаемость материала сердечника μ :
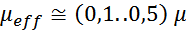
При таком уровне уменьшения μ до μeff величина вводимого зазора незначительна и явлением
«выпучивания поля» можно пренебречь.
Длина зазора в этом случае вычисляется согласно выражению:
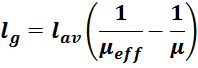
где:
lav – длина магнитной линии магнитопровода;
μeff – эффективная магнитная проницаемость сердечника с зазором;
μ – магнитная проницаемость материала сердечника.
Взаимосвязь габаритной мощности однотактного прямоходового трансформатора с его выходной
мощностью
Установим взаимосвязь между мощностью выходной (вторичной) обмотки и габаритной мощностью трансформатора.
Мощность обмотки определяется формой тока в ней. Форма тока в обмотках однотактного прямоходового
преобразователя в первом приближении имеет форму однополярных прямоугольных импульсов. В дальнейших расчетах
мы не будем учитывать рекуперационную обмотку, поскольку её мощность существенно меньше мощности силовых
обмоток.
Для двухобмоточного трансформатора однотактного прямоходового трансформатора габаритная мощность
трансформатора определяется по формуле:
Поскольку мощность в трансформаторе передается из первичной обмотки во вторичную обмотку то мощности обмоток
связаны между собой через КПД-трансформатора:
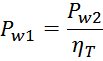
Отсюда соотношение габаритной мощность трансформатора можно представить в виде:
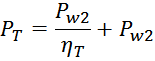
или:
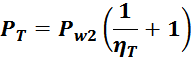
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Последовательность расчета трансформатора однотактного прямоходового преобразователя
Данный алгоритм расчета относится к расчету трансформаторов однотактных преобразователей прямого хода:
прямоходового одноключевого преобразователя, преобразователя «косой полумост».
1. Начальное определение типа магнитопровода и феррита
Определяем типы магнитопровода и феррита на основе исходных данных проектирования.
Рекомендации по выбору типа магнитопровода и феррита представлены в разделе «Конструктивные элементы
трансформатора и дросселя. Магнитопровод». Предварительный выбор магнитопровода и феррита необходим для
определения коэффициента заполнения окна сердечника медью k0 ,максимального значения индукции в
магнитопроводе Bmax и величины остаточной индукции Br входящих в формулу габаритной
мощности. Феррит выбирается исходя из компромисса «стоимость-технические характеристики». При этом выбранный
тип феррита менять нежелательно, поскольку это приведет к необходимости пересчета значения габаритной
мощности.
2. Расчет габаритного параметра трансформатора SCS0, оценка
целесообразности
введения немагнитного зазора и расчет его параметров
Определяем габаритный параметр трансформатора однотактного преобразователя SCS0:
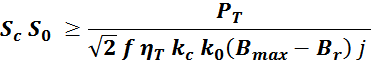
где:
η – КПД трансформатора;
f – рабочая частота;
k0 – коэффициент заполнения окна сердечника медью;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
Br – остаточная индукция магнитопровода;
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника.
j – максимальная плотность тока в обмотках (среднеквадратичное значение).
Габаритная мощность трансформатора PT является исходным параметром
расчета. В данном соотношении габаритная мощность трансформатора принимается равной максимальной входной
мощности PIN_max:
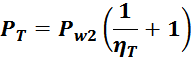
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Коэффициент полезного действия трансформатора ηT принимается в
соответствии с мощностью трансформатора. В соответствии с [Эраносян О.А. Сетевые блоки питания с
высокочастотными преобразователями.— Л.: Энергоатомиздат. Лени игр. отд-ние, 1991,— 176 с: ил. 109 стр.],
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.] на начальной стадии расчета трансформатора ηT принимается в
соответствии с мощностью трансформатора (у Эраносяна – мощностью нагрузки):
– при PIN_max ≤ 10 Вт принимается ηT = 0,93;
– при 10 Вт < PIN_max ≤ 50 Вт принимается ηT = 0,95;
– при PIN_max > 50 Вт принимается ηT = 0,97.
Необходимо отметить, что это начальное приближение, необходимое для выполнения предварительного этапа
расчета.
Коэффициент заполнения окна сердечника медью k0 выбирается
в зависимости от типа используемого магнитопровода:
– для Ш-образного магнитопровода [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
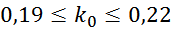
в ряде случаев, в особенности, когда S0 представляет собой площадь окна сердечника дросселя уже с
учетом каркаса магнитопровода, то может быть выбран k0 вплоть до 0,28-0,4 – [McLyman C.
Transformer and inductor design handbook.2004].
– для кольцевого магнитопровода [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет.
Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с. – 57 стр.]:
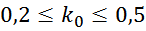
В любом случае это является первым приближением и факт размещения обмотки проверяется последующим
конструктивным расчетом.
Коэффициент заполнения сердечника kС принимается равным 1 в
случае использования магнитопровода из феррита.
Максимальное значение индукции в магнитопроводе Bmax определяется
исходя из параметров используемого феррита и рабочей частоты. В первом приближении и в типовом случае
принимается в пределах 0,15-0,2 Тл.
Плотность тока в проводах обмотки j выбирается в зависимости от выходной мощности
источника в соответствии с таблицей T.8 [Эраносян О.А. Сетевые блоки питания с высокочастотными
преобразователями.— Л.: Энергоатомиздат. Лени игр. отд-ние, 1991,— 176 с: ил. 109 стр.].
Таблица T.8 – Максимально допустимая плотность тока в проводах обмотки при различной выходной мощности
источника
|
POUT_max , Вт |
1 – 7 | 8 – 15 | 16 – 40 | 41 – 100 | 101 – 200 |
| j, А/мм2 | 7 – 12 | 6 – 8 | 5 – 6 | 4 – 5 | 4 – 4,5 |
При POUT_max большей 200 Вт плотность тока может быть выбрана в пределах 3-4
А/мм2.
Остаточная индукция Br магнитопровода определяется исходя из
соотношения:
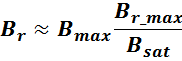
где:
Bmax – выбранное максимальное значение индукции в магнитопроводе;
Bsat – индукция насыщения материала магнитопровода;
Br_max – величина остаточной индукции соответствующая индукции насыщения
Bsat.
Величина максимального значения остаточной индукции феррита Br_max может
быть определена следующими способами:
– поиск численного значения Br_max в datasheet-ах на выбранный тип
ферромагнитного материала (обозначается в datasheet просто как Br);
– определение Br_max из приведенных в datasheet-ах кривых гистерезиса.
Необходимо отметить, что это определение не всегда получается точным по причине большого масштаба по оси
магнитной напряженности H в результате размер петли становится сопоставим с шириной линии графика. В
качестве примера на рисунке T.48 представлена петля гистерезиса популярного феррита N87 (согласно
datasheet). Оценочное значение Br_max для феррита N87 составляет примерно
160 мТл.
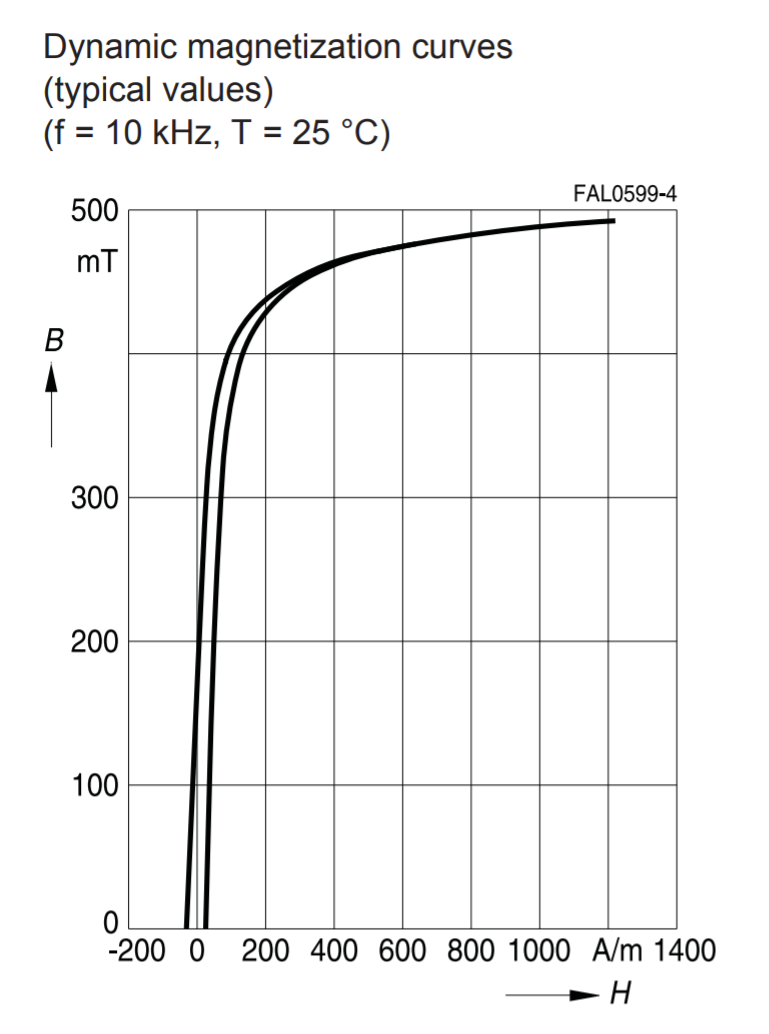
Рисунок T.48 – Петля гистерезиса феррита N87 согласно данным [datasheet EPCOS AG – Ferritesand
accessories
SIFERRIT material N87. September 2017]
Оценка целесообразности введения немагнитного зазора и расчет его параметров
Полученное значение остаточной индукции Br_max сравнивается с максимальным
значением индукции насыщения Bsat и принимается решение о целесообразности или нецелесообразности
введения немагнитного зазора. В случае если остаточная индукция Br_maxсоставляет
более 25-35% от значения максимальной индукции Bsat то для трансформаторов прямоходовых
преобразователей рекомендуется вводить в магнитопровод немагнитный зазор.В особенности это касается мощных
преобразователей с топологией «косой полумост». Если же значение Br_max
составляет меньше 25-35% от Bsat то решение о зазоре принимается исходя из технико-экономических
соображений конкретного случая.
В случае введения зазора в магнитопровод целевое значение эффективной проницаемости μeff
принимается в 2-10 раз меньше начальной магнитной проницаемости материала сердечника μ (при таком уровне
уменьшения μ до μeff величина вводимого зазора незначительна и явлением «выпучивания поля» можно
пренебречь):
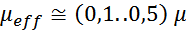
где:
µ – магнитная проницаемость магнитнопровода без зазора (эффективное значение относительной магнитной
проницаемости магнитопровода без зазора – Relative effective permeability, часто обозначается в datasheet
как µe).
При введении зазора новая величина остаточной индукции Br_gap
пересчитывается по формуле:
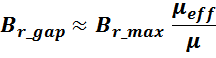
где:
Br_max – величина остаточной индукции соответствующая индукции насыщения
Bsat;
µ – магнитная проницаемость магнитнопровода без зазора (эффективное значение относительной магнитной
проницаемости магнитопровода без зазора – Relative effective permeability, часто обозначается в datasheet
как µe);
µeff – эффективное значение магнитной проницаемости магнитнопровода с зазором.
При расчете габаритной мощности трансформатора с зазором используется новое скорректированное значение
остаточной индукции Br_gap. Далее при расчетах необходимо использовать это
значение остаточной индукции Br_gap , а также значение эффективной
магнитной проницаемости μeff .
3. Выбор конкретного типа магнитопровода и феррита
Выбор конкретной марки магнитопровода осуществляется в соответствии с рассчитанным параметром
ScS0 и конструктивными особенностями (формфактор, технологичность намотки,
электромагнитная совместимость, экономика и т.д.).
При этом в качестве площади поперечного сечения сердечника SС должна быть использована минимально
обеспечиваемая величина площани поперечного сечения (Minimum core cross section) – Amin, а не
Ae (Effective magnetic cross section). Все эти параметры указаны в datasheet-ах.
Определившись окончательно с конкретной маркой магнитопровода и феррита мы будем знать следующие
параметры:
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
Bmax – максимальное значение индукции в магнитопроводе при выбранной частоте.
В случае введения немагнитного зазора его длина lg вычисляется согласно выражению:
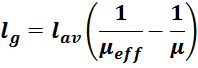
где:
lav – длина магнитной линии выбранного типа магнитопровода;
μeff – эффективная магнитная проницаемость сердечника с зазором;
μ – магнитная проницаемость материала сердечника (определяется из datasheet на выбранный магнитопровод).
В случае если магнитопровод состоит из двух половинок, то мы имеем два зазора, длина каждого из них
составляет половину вычисленного значения немагнитного зазора lg.
4. Расчет числа витков первичной обмотки
Число витков первичной обмотки рассчитывается по формуле:
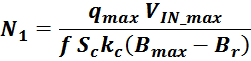
где:
qmax – относительная длительность импульса (максимальное значение);
VIN_max – напряжение на первичной обмотке трансформатора (максимальное
значение);
f – рабочая частота;
SС – площадь поперечного сечения сердечника;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
Br – остаточная индукция магнитопровода (при введении в магнитопровод немагнитного зазора
используется величина Br_gap).
Относительная длительность импульса qmax рассчитывается как отношение
максимальной длительности импульса к периоду и может быть принята равной 0,5:
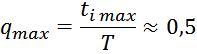
Напряжение на первичной обмотке трансформатора VIN принимается равным
максимальному входному напряжению преобразователя. При расчете преобразователей с широким диапазоном
входного напряжения используется максимальное значение относительной длительности импульса qmax и
максимальное значение напряжения VIN_max. Это условие обеспечивает
безопасную работу трансформатора преобразователя без выхода в область насыщения при переходных процессах или
при резком изменении напряжения. В установившемся режиме при увеличении напряжения коэффициент q будет
пропорционально уменьшаться и произведение qV останется неизменным.
5. Расчет выходного напряжения вторичной обмотки трансформатора
Выходное напряжение вторичной обмотки трансформатора V2 рассчитывается как сумма выходного
напряжения преобразователя и суммы падений напряжений на выходном выпрямителе и силовом дросселе:
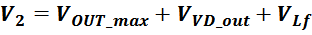
где:
VOUT_max – выходное напряжение преобразователя (максимальное значение);
VVD_out – падение напряжения на диодах выходного выпрямителя;
VLf – падение напряжения на выходном силовом дросселе.
На первой итерации расчета можно использовать оценочные значения величин падений напряжения. Так в случае
использования кремниевого диода падение напряжение составляет 1,2 В, для диодов Шоттки – 0,5 В. При
использовании мостовой схемы выпрямления падение напряжения на диодах выходного выпрямителя равно удвоенному
падению напряжения на единичном диоде. В случае использования выпрямителя с отводом от средней точки падение
напряжения на диодах выходного выпрямителя равно падению напряжения на единичном диоде.
Падение напряжения на выходном силовом дросселе зависит от выходного тока и мощности преобразователя. В
качестве первого приближения может быть принята равной в пределах 2-5 % от выходного напряжения
преобразователя VOUT_max.
6. Расчет коэффициента трансформации
Коэффициент трансформации k рассчитывается как отношение выходного напряжения на вторичной обмотке
трансформатора V2 и напряжения прикладываемого к первичной обмотке, практически равному входному
напряжению VIN_min :
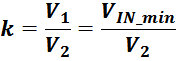
где:
V2 – напряжение на выходе вторичной обмотки;
VIN_min – напряжение, прикладываемое к первичной обмотке (минимальное
значение).
7. Расчет числа витков вторичной обмотки
Число витков во вторичной обмотке N2 рассчитываются по соотношению:
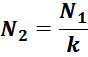
где:
N1 – число витков первичной обмотки;
k – коэффициент трансформации.
8. Расчет числа витков рекуперационной обмотки
Рассчитываем число витков рекуперационной обмотки Nr при её наличии в конструкции трансформатора.
Число витков рекуперационной обмотки Nr принимается равным числу витков первичной обмотки:
Рекуперационная обмотка используется в трансформаторе одноключевого однотактного преобразователя. В
однотактом двухключевом преобразователе типа «косой полумост» рекуперационная обмотка не нужна.
9. Расчет индуктивности намагничивания первичной обмотки трансформатора
Индуктивность намагничивания первичной обмотки трансформатора L0 рассчитывается по соотношению:
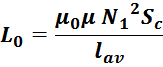
где:
µ0 – магнитная постоянная;
µ – магнитная проницаемость материала магнитопровода (при введении зазора используется μeff –
эффективная магнитная проницаемость сердечника с зазором);
SС – площадь сечения магнитопровода;
lav – эффективная длина средней линии магнитопровода;
N1 – число витков первичной обмотки.
10. Расчет токов первичной обмотки трансформатора
Амплитудное значение тока первичной обмотки
Амплитудное значение тока первичной обмотки определяется выражением:
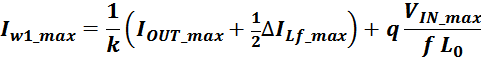
где:
k – коэффициент трансформации;
IOUT_max – выходной ток преобразователя (используется максимальное значение тока);
∆ILf_max – максимальная величина пульсаций тока дросселя (входное значение
для расчета трансформатора);
q – относительная длительность импульса (максимальное значение);
VIN_max – напряжение, прикладываемое к первичной обмотке (максимальное
значение);
f – рабочая частота;
L0 – индуктивность намагничивания первичной обмотки трансформатора.
Среднее значение тока первичной обмотки
Среднее значение тока первичной обмотки определяется выражением:
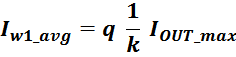
где:
q – относительная длительность импульса (максимальное значение);
k – коэффициент трансформации;
IOUT_max – выходной ток преобразователя.
Для случая преобразователя типа «косой полумост» через обмотку еще дополнительно протекает рекуперационный
ток и выражение для среднего значения тока имеет вид:
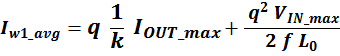
Среднеквадратичное значение тока первичной обмотки
Среднеквадратичное значение тока первичной обмотки вычисляется по формуле (см. раздел «Резисторы»):
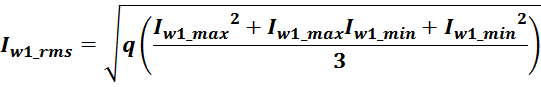
где:
q – относительная длительность импульса (максимальное значение);
Iw1_max, Iw1_min – максимальное и
минимальное значения вычисляются по соотношениям:
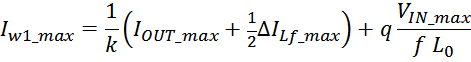
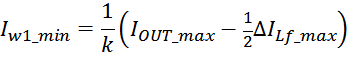
Подробный вывод выражений для расчета токов обмоток трансформатора двухтактного преобразователя прямого хода
представлен в разделе «Однотактный прямоходовый преобразователь».
11. Расчет токов вторичной обмотки трансформатора
Амплитудное значение тока вторичной обмотки
Амплитудное значение тока вторичной обмотки определяется выражением:
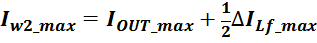
где:
IOUT_max – выходной ток преобразователя (максимальное значение);
∆ILf_max – максимальная величина пульсаций тока дросселя (входное значение
для расчета трансформатора).
Среднее значение тока вторичной обмотки
Среднее значение тока вторичной обмотки определяется выражением:
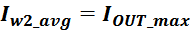
В случае наличия двух полуобмоток, итоговое выражение имеет вид:
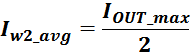
Среднеквадратичное значение тока вторичной обмотки
sСреднеквадратичное значение тока вторичной обмотки имеющего форму прямоугольной трапеции
вычисляется аналогично первичной обмотке и определяется выражением (см. раздел «Резисторы»):
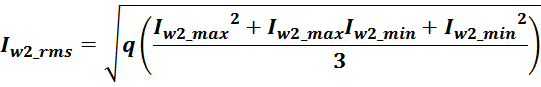
где:
q – относительная длительность импульса (максимальное значение);
Iw2_max, Iw2_min – максимальное и
минимальное значения вычисляются по соотношениям:
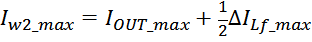
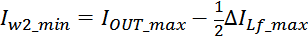
где:
IOUT_max – выходной ток преобразователя (максимальное значение);
ΔILf_max – пульсация тока дросселя.
12. Расчет токов рекуперационной обмотки трансформатора
Амплитудное значение тока рекуперационной обмотки
Амплитудное значение тока рекуперационной обмотки рассчитывается по выражению:
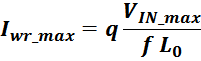
где:
L0 – индуктивность намагничивания (фактически индуктивность первичной обмотки);
VIN_max – напряжение, приложенное к первичной обмотке (максимальное
значение);
q – коэффициент заполнения.
Среднеквадратичное значение тока рекуперационной обмотки
Среднеквадратичное значение тока рекуперационной обмотки Iwr_rms
рассчитывается по выражению:
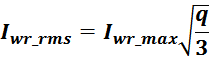
где:
Iwr_max – амплитудное значение тока рекуперационной обмотки;
q – коэффициент заполнения.
13. Расчет конструкции трансформатора
В результате выполненного последовательного расчета по шагам 1-10 мы получаем следующие параметры:
– конкретный тип магнитопровода c конкретными геометрическими параметрами;
– число витков первичной, вторичной обмоток N1 , N2. и при использовании –
рекуперационной обмотки Nr .
Далее после получения этих базовых параметров выполняется детальный конструктивный расчет. Последовательность
расчета представлена ниже.
13.1 Расчёт параметров проводов обмоток
Минимальная площадь поперечного сечения обмоток (по меди) рассчитывается по соотношениям:
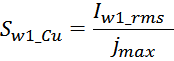
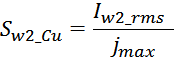
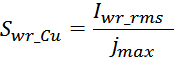
Sw1_Cu – площадь поперечного сечения проводника первичной обмотки;
Sw2_Cu – площадь поперечного сечения проводника вторичной обмотки;
Swr_Cu – площадь поперечного сечения проводника рекуперационной обмотки;
jmax – выбранное максимальное значение среднеквадратичной плотности тока в обмотках.
Для однотактных трансформаторов, в отличие от двухтактных, при расчете сечения провода необходимо
использовать именно среднеквадратичное (в крайнем случае – среднее) значение тока. Упрощенный расчет с
использованием максимального значения приведет к значительной ошибке.
Далее вычисляется диаметр проводов (по меди) для выполнения обмоток:
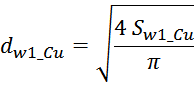
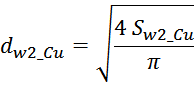
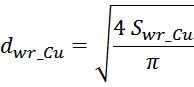
13.2 Выбор типа провода обмотки и определение диаметра и площади поперечного сечения проводника с
изоляцией
На основании вычисленного диаметра провода (по меди) выбирается ближайший диаметр провода из номенклатуры
диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление производится в большую сторону.
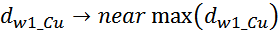
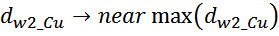
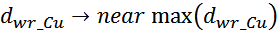
В соответствии с выбранным типом провода пересчитывается площади поперечного сечения выбранного типа провода
по меди по формулам:
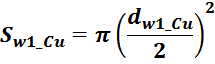
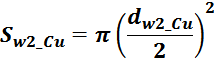
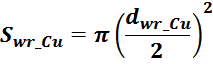
Далее в соответствии со справочным листком на выбранный тип обмоточного провода определяется его диаметр с
изоляцией для первичной и вторичной обмоток dw1_ins ,
dw2_insи, при использовании рекуперационной обмотки,
dwr_ins:
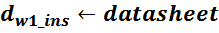
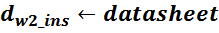
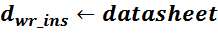
13.3 Расчёт средней длины витка обмоток трансформатора
Ш- и П- образные, чашеобразные магнитопроводы
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредние длины
витков рассчитываются по соотношениям:
для первичной обмотки:
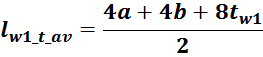
где:
a, b – геометрические параметры характеризующие сечение каркаса магнитопровода (см. рисунок T.49);
tw1 – толщина обмотки, вычисляемая по соотношению:
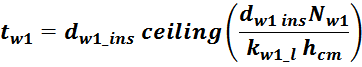
здесь:
функция (ceiling) – округление до большего целого;
hcm – высота обмотки, определяется высотой каркаса магнитопровода;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины
провода (таблица T.7).
Таблица T.7 – Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
| Диаметр провода с изоляцией, мм | 0,08 – 0,31 | 0,31-0,5 | 0,5-2,1 |
| Коэффициент укладки | 0,8-0,75 | 0,75-0,7 | 0,65-0,6 |

Рисунок T.49 – К определению средней длины витка для Ш- и П- образных магнитопроводов
для вторичной обмотки:
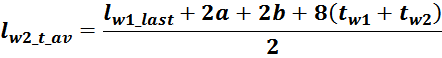
где:
lw1_last – длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
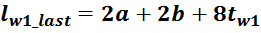
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
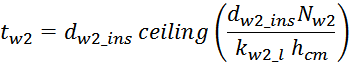
здесь:
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка рассчитывается по следующим соотношениям:
для первичной обмотки:
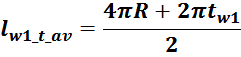
где:
R – радиус каркаса магнитопровода;
tw1 – толщина первичной обмотки, вычисляемая по соотношению:
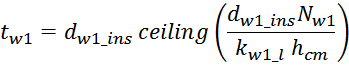
где:
функция (ceiling) – округление до большего целого;
hcm – высота обмотки, определяется высотой каркаса магнитопровода;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
для вторичной обмотки:
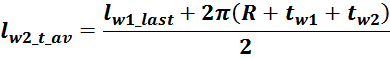
где:
lw1_last – длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
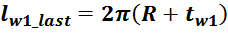
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
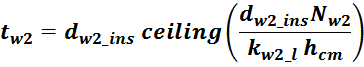
здесь:
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Тороидальные магнитопроводы
Для тороидальных магнитопроводов расчет среднего витка осуществляется по соотношениям:
для первичной обмотки:
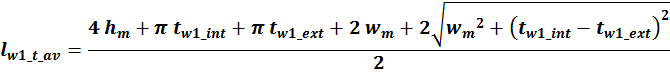
где:
wm – ширина магнитопровода;
hm – высота магнитопровода;
tw1_int – толщина внутреннего слоя первичной обмотки;
tw1_ext – толщина внешнего слоя первичной обмотки.
tw1_int и tw1_ext определяются по
соотношениям:
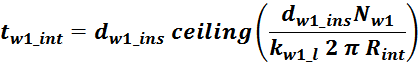
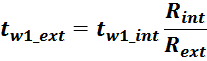
здесь:
функция (ceiling) – округление до большего целого;
Rint – внутренний радиус тора;
Rext – внешний радиус тора;
dw1_ins – диаметр обмоточного провод первичной обмотки с изоляцией;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).

Рисунок T.50 – К определению средней длины витка тороидальных магнитопроводов. (показаны обозначения
только первичной обмотки)
для вторичной обмотки:
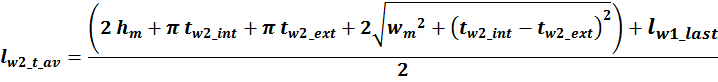
где:
lw1_last – длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
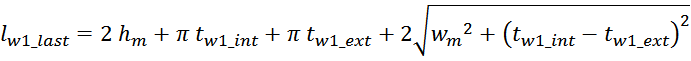
tw1_int и tw1_ext определяются по
соотношениям:
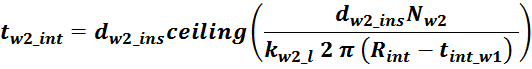
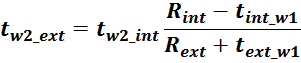
здесь:
dw2_ins – диаметр обмоточного провод первичной обмотки с изоляцией;
Nw2 – число витков в первичной обмотке;
kw2_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
Средняя длина витка рекуперционной обмотки
Поскольку рекуперционная обмотка имеет малую толщину, располагается между первичной и вторичной обмотками и,
как правило, укладывается в один слой и, то можно считать, что средняя длина витка рекуперционной обмотки
lwr_t_av равна длине внешнего витка первичной обмотки
lw1_last:
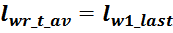
Это применимо для трансформаторов, выполняемых на всех типах магнитопроводов.
13.4 Определение длин проводников первичной, вторичной и рекуперационной обмоток
Длина обмоток определяется как произведение средней длины витка на число витков:
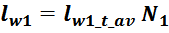
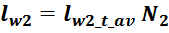
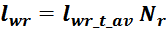
Полученная величина определяет, сколько провода нужно отмерить на обмотки трансформатора.
13.5 Конструктивный расчет структуры обмотки трансформатора, фактическая проверка возможности
размещения обмотки
Использование некоторой предопределенной величины коэффициента заполнения окна не дает однозначной гарантии
размещения обмотки в окне магнитопровода. Поэтому необходима проверка конструктивного условия размещения
обмотки в окне магнитопровода. Кроме этого, может быть неоптимальное использование окна магнитопровода, если
останется слишком много свободного места в окне обмотки.
Для конструктивного расчета структуры обмотки трансформатора выполняется следующая последовательность
действий:
Ш- и П- образные и чашеобразные магнитопроводы
– определяется средняя ширина намоточного слоя hlav. Она равна высоте каркаса магнитопровода
hcm (рисунок T.51):
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.
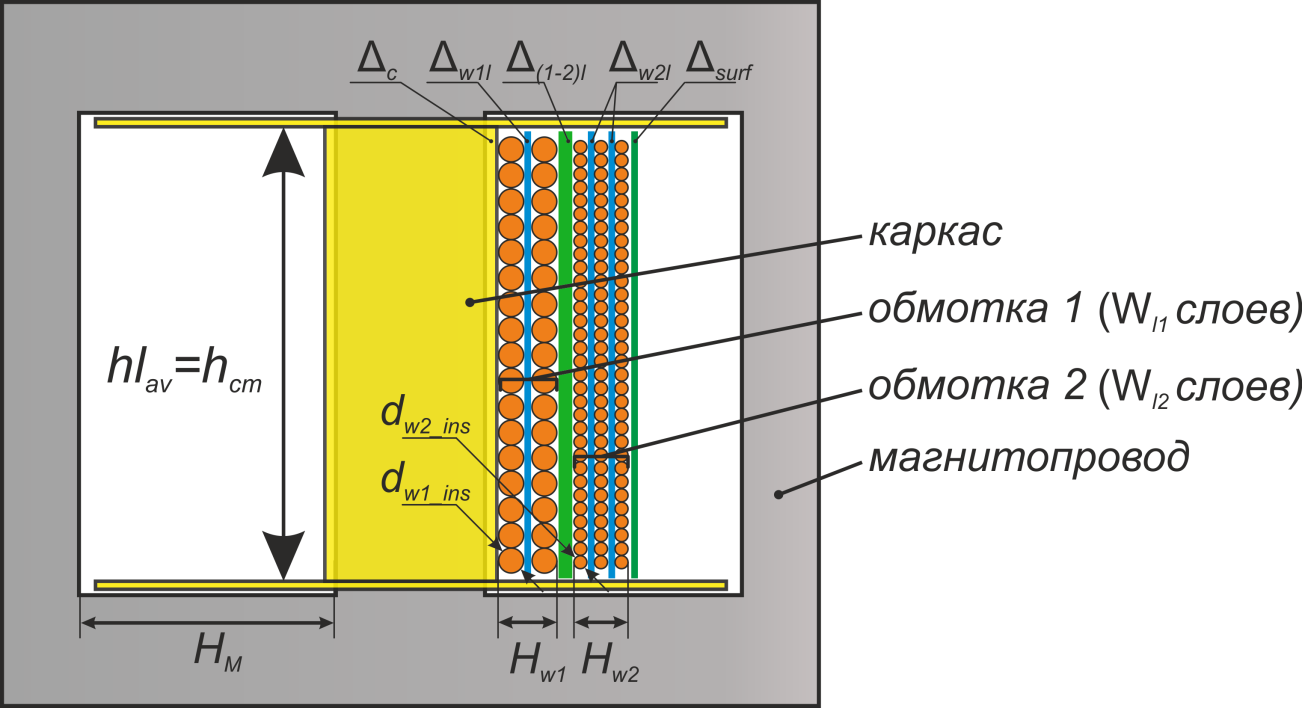
Рисунок T.51 – К расчету конструкции обмотки трансформатора преобразователя
– определяется число витков в одном слое для первичной и вторичной обмоток
Nw1_l и Nw2_l :
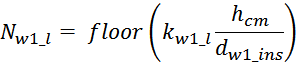
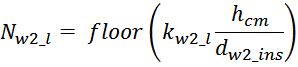
где:
операция (floor) – округление до меньшего целого;
hcm – высота каркаса магнитопровода;
dw1_ins , dw2_ins – диаметры проводников
обмоток с изоляцией;
kw1_l , kw2_l – коэффициенты укладки
(laying), зависящие от толщины провода (таблица T.7).
– рассчитывается общее число слоев для первичной и вторичной обмоток Wl1 ,
Wl2:
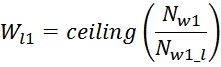
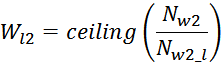
где:
(ceiling) – округление до большего целого;
Nw1, Nw2 – число витков в первичной и вторично обмотках,
соответственно;
Nw1_l , Nw2_l – число витков в одном слое
первичной и вторичной обмоток, соответственно.
– рассчитываются толщины обмоток трансформатора Hw1 , Hw2 ,
Hwr:
для первичной обмотки:
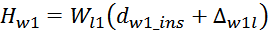
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 – число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
для вторичной обмотки:
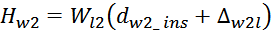
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 – число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
для рекуперационной обмотки:
Hwr – толщина слоя рекуперационной обмотки трансформатора, определется по соотношению:
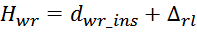
здесь:
Δrl – толщина изоляции рекуперационной обмотки;
dwr_ins – диаметр провода рекуперационной обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величины Δ1l и
Δ2lпринимаются равными нулю (в реальности, при плотно намотке за счет укладывания
витков следующего слоя в пазы слоя предыдущего толщина обмотки может быть несколько меньше).
– рассчитывается общая толщина «пирога» обмотки HΣ:
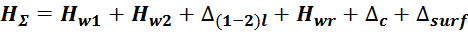
где:
Δ(1-2)l – толщины межобмоточной изоляции;
Δc – толщина каркаса (расстояние между поверхностью каркаса и магнитопроводом);
Δsurf – толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 , Hwr – толщины обмоток трансформатора.
– проверяется условие фактического размещения всех конструктивных элементов «пирога» обмоток в окне
магнитопровода:
где:
HΣ – суммарная толщина «пирога» обмоток;
HM – ширина окна магнитопровода.
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 3 – 13).
Тороидальные магнитопроводы
В случае тороидальных магнитопроводов ширина намоточного слоя hl уменьшается по мере намотки. Поэтому все
сложнее.
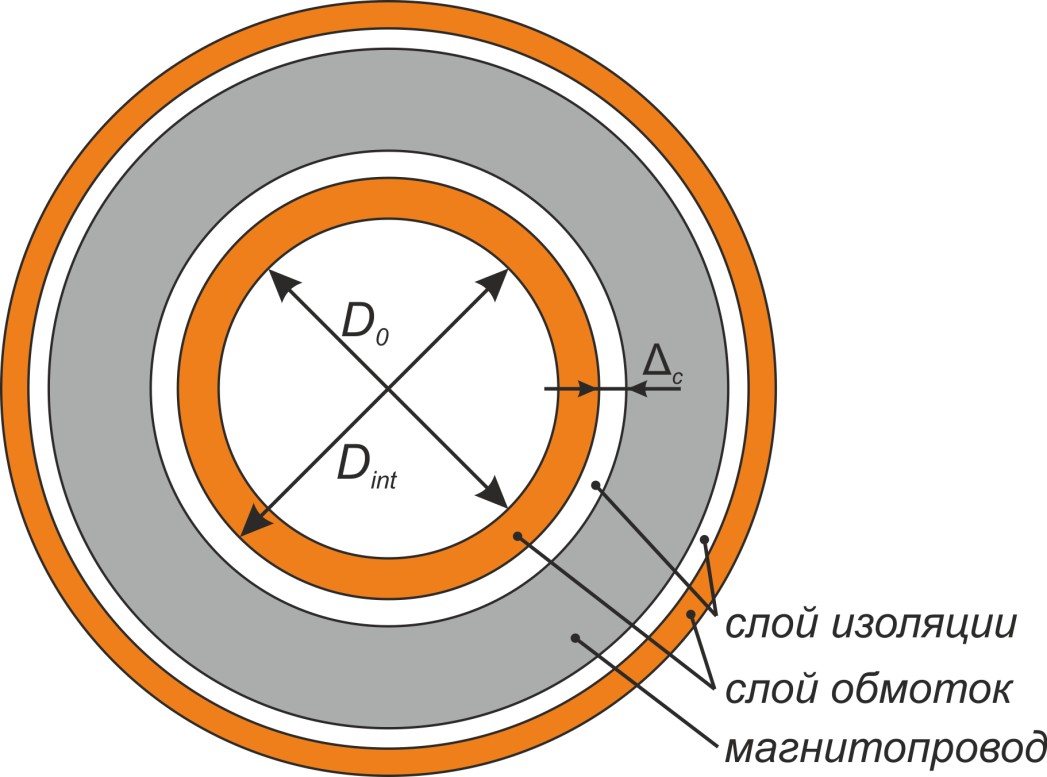
Рисунок T.52 – К расчету конструкции обмоток тороидального трансформатора: Dint – внутренний
диаметр тора магнитопровода с учетом слоя изоляции, D0 – остаточный технологический диаметр.
– рассчитывается число слоев первичной обмотки Wl1 по выражению:
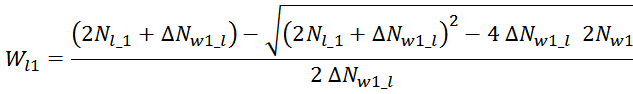
где:
Nw1 – число витков первичной обмотки;
Nl_1 – число витков первого слоя первичной обмотки, определяемое из выражения:
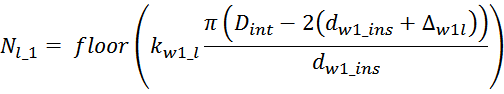
здесь:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw1l – толщина межслоевой изоляции первичной обмотки;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
kw1_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7).
ΔNw1_l – уменьшение числа витков от слоя к слою определяется выражением:
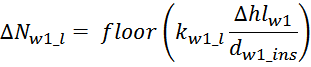
где:
операция (floor) – округление до меньшего целого;
Δhlw1 – уменьшение ширины намоточного слоя от слоя к слою:
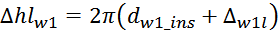
Полученное значение Wl1, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
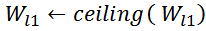
– рассчитывается толщина первичной обмотки Hw1 по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
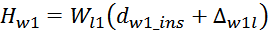
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 – число слоев в первичной обмотке;
dw1 ins – диаметр провода первичной обмотки с изоляцией.
– рассчитывается число слоев вторичной обмотки Wl2 по выражению:
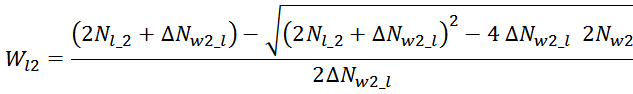
где:
Nw2 – число витков вторичной обмотки;
Nl_2 – число витков первого слоя вторичной обмотки, определяемое из выражения:
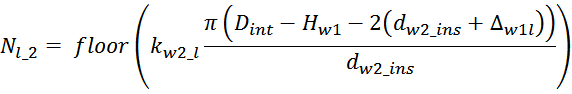
здесь:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw2l – толщина межслоевой изоляции вторичной обмотки;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
kw2_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7);
Hw1 – толщина первичной обмотки.
ΔNw2_l – уменьшение числа витков от слоя к слою для вторичной обмотки
определяется выражением:
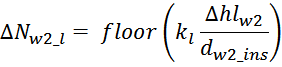
где:
операция (floor) – округление до меньшего целого;
Δhlw2 – уменьшение ширины намоточного слоя от слоя к слою:
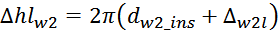
Полученное значение Wl2, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
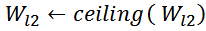
– рассчитывается толщина вторичной обмотки Hw2 по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
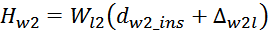
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 – число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
Расчитывается толщина слоя рекуперационной обмотки трансформатора Hwr, определяемая по
соотношению:
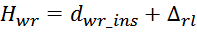
здесь:
Δrl – толщина изоляции рекуперационной обмотки;
dwr_ins – диаметр провода рекуперационной обмотки с изоляцией.
– рассчитывается суммарная толщина «пирога» намотки HΣ:
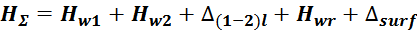
где:
Δ(1-2)l – толщины межобмоточной изоляции
Δsurf – толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 , Hwr – толщины обмоток трансформатора.
– проверяется условие фактического размещения обмотки в окне магнитопровода:
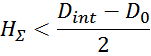
где:
HΣ – суммарная толщина «пирога» намотки;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции) который фактически определяет
ширину окна магнитопровода;
D0 – остаточный диаметр внутри тороидального трансформатора (технологический).
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 3-13).
14. Расчет сопротивления обмоток трансформатора
Электрическое сопротивление обмоток трансформатора Rw1 и Rw2
рассчитывается по формуле для расчета омического сопротивления протяженного проводника:
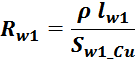
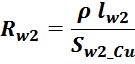
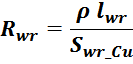
где:
ρ – удельное сопротивление материала провода (для меди – 0,0175 Ом·мм2 м-1 );
lw1 , lw2 , lwr – длины проводов первичной, вторичной
и рекуперационной обмоток соответственно;
Sw1_Cu , Sw2_Cu ,
Swr_Cu – площади поперечного сечения выбранного типа провода (по
меди).
15. Расчет омических потерь в обмотках
Суммарные потери на омическом сопротивлении обмоток определяются по формулам:
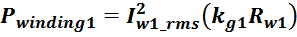
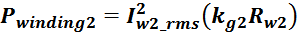
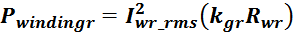
где:
Rw1 , Rw2 , Rwr – сопротивление первичной, вторичной и
рекуперационной обмоток на постоянном токе;
kg1 , kg2 , kgr – коэффициенты добавочных потерь за
счет скин-эффекта и эффекта близости в обмотках;
Iw1_rms ,
Iw2_rms ,Iwr_rms –
среднеквадратичные значение тока в первичной, вторичной и рекуперационной обмотках соответственно.
NB: При высоких рабочих температурах трансформатора необходимо учитывать влияние температуры на удельное
сопротивление проводников обмоток. При высоких частотах необходимо оценить увеличение эффективного
сопротивления обмоток в результате действия скин-эффекта (см. пункт «Влияние скин-эффекта на сопротивление
обмоток при высоких частотах» настоящего раздела).
16. Оценка уровня потерь в магнитопроводе
Существуют три способа определения потерь в магнитопроводе:
– рассчитать по формуле (при наличии аппроксимацонных коэффициентов);
– определить по графику из datasheet;
– определить экспериментально.
Расчёт по аппроксимацонным коэффициентам
Тепловая энергия, выделяемая в магнитопроводе определяется режимом работы дросселя – частотой работы f и
уровнем магнитной индукции Bmax. Для расчета потерь в магнитопроводе Pferrit
используют следующее аппроксимирующее выражение [Optimum designof a high-power, high-frequency transformer.
R. Petkov. IEEE Transactions on Power Electronics (Volume: 11, Issue: 1, Jan 1996)]:
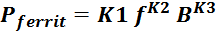
где:
f – частота;
B – индукция;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
Определение по графику относительных потерь из datasheet
Для определения потерь в магнитопроводе можно использовать соотношение:
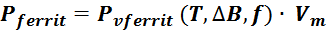
где:
Pvferrit – мощность потерь на единицу объема, являющейся функцией температуры, магнитной индукции
и частоты. Графики данной зависимости представлены в справочных листах (datasheet) на каждый ферромагнитный
материал магнитопровода;
Vm – объем магнитопровода (приводится в справочных листах (datasheet).
Мощность потерь на единицу объема определяется типом феррита и приводится в справочных данных на конкретный
тип магнитного материала.

Рисунок T.53 – Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87 [Ferrites and accessories. SIFERRITmaterial N87, EPCOS AG 2006]
Экспериментальное определение
В случае отсутствия данных для расчета остается путь экспериментального определения потерь.
17. Расчет суммарных потерь
Суммарные потери трансформатора Ptotal_loss складываются из омических потерь
обмотки и потерь магнитопровода:
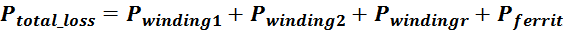
где:
Pwinding1 , Pwinding1 , Pwindingr – омические потери в
первичной, вторичной и рекуперационной обмотках соответственно;
Pferrit – потери в магнитопроводе.
18. Расчет температурного режима трансформатора и оптимизация
Установившаяся температура перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева)
приблизительно оценивается по соотношению [McLyman C. Transformer and inductor design handbook.2004]:
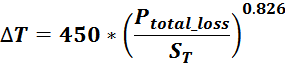
где:
Ptotal loss – мощность суммарных потерь в трансформаторе;
ST – суммарная эффективная площадь охлаждения трансформатора (в см2).
Если полученное значение температуры нагрева трансформатора лежит в пределах 50-80°С, то расчет
трансформатора можно считать законченным. Если полученное значение превышает 80°С, то имеет смысл
использовать магнитопровод большего размера.
Если в результате расчета уровень перегрева трансформатора ΔT будет значительно меньше максимально
допустимого:
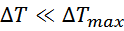
то имеет смысл использовать оптимизировать конструкцию трансформатора с целью уменьшения стоимости и
массогабаритных показателей – уменьшить формфактор магнитопровода и варьировать плотность тока, размах
индукции (можно делать одновременно с повышением частоты).
Кроме того, если при допустимом уровне нагрева трансформатора получится, что мощность, выделяемая на активном
сопротивлении обмоток существенной меньше, чем в феррите магнитопровода:
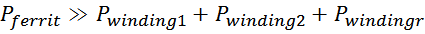
то имеет смысл использовать большую плотность тока, протекающего через обмотки и повторить расчет по пунктам
2-18.
Для трансформаторов больших габаритов (с рассеваемой площадью более 1000 см2) установившаяся
температура нагрева трансформатора относительно окружающей среды ∆T (дельта перегрева) оценивается по
соотношению [В.Е. Китаев, А.А. Бокуняев. Проектирование источников электропитания устройств связи. Учеб.
пособие.- М.: Связь,1972.- 200 с.]:
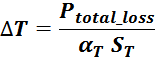
где:
Ptotal_loss – мощность суммарных потерь в трансформаторе;
αT – коэффициент теплоотдачи, зависящий от множества факторов (материал трансформатора,
конструктивное исполнение, температуры окружающей среды и т.д.). Для практических расчетов принимается
равным: 11-13 Вт/м2 °С.
ST – суммарная площадь охлаждения трансформатора.
Необходимо понимать, что оптимизация расчета трансформатора проводится с учетом целевых приоритетов:
Приоритет 1 – Малые массогабаритные параметры трансформатора и, соответственно, стоимость. В этом случае
необходимо провести расчет всех параметров трансформатора с целью обеспечения (но не превышения) заданного
уровня перегрева и минимальной стоимости/массогабаритных параметров. В этом случае плотность тока, размах
индукции итерационно увеличиваются;
Приоритет 2 – Высокий КПД. В этом случае необходимо задаться максимальными массогабаритными параметрами и с
учетом этого варьируя параметры трансформатора (индукция, плотность тока и т.д.) провести расчет всех
параметров трансформатора с целью минимизации мощности потерь. В этом случае плотность тока, размах индукции
итерационно уменьшаются;
Трансформатор обратноходового преобразователя
Трансформатор обратноходового преобразователя, по сути, представляет собой многообмоточный дроссель.
Индуктивность первичной обмотки играет роль накопителя энергии, которая «складируется» в магнитопрововоде
(и, забегая вперед, в немагнитном зазоре). Передача накопленной энергии осуществляется через вторичные
обмотки, которые расположены на этом же магнитопроводе. Таким образом, Flyback-трансформатор представляет
собой несколько магнитно-связанных индуктивностей, что и отличает его от обычного трансформатора. Хотя
конструктивно он выглядит практически аналогично.
Поскольку накопление энергии осуществляется через первичную обмотку, то это формулирует основное исходное
требование методики проектирования: первичная обмотка должна иметь заданную величину индуктивности
L1, которая должна работать без насыщения при заданном максимальном токе
Iw1_max. При этом должны быть обеспечены минимальные габариты и стоимость и
потери.
Трансформатор обратноходового преобразователя может работать в двух режимах:
– режим прерывистых токов;
– режим непрерывных токов.
Подробно особенности работы и сопоставление обоих режимов дано в специализированном разделе «Обратноходовый
преобразователь». Резюмируя можно сказать, что режим прерывистых токов имеет ряд преимуществ, прежде всего –
позволяет использовать меньшие размеры трансформатора.
При выборе материала трансформатора обратноходового преобразователя целесообразно учитывать ряд факторов
[Magnetics Design Handbook from TI by Lloyd H. Dixon. Section 5. Inductor and Flyback. Transformer Design.
Texas Instruments. 2001. http://www.ti.com/lit/ml/slup127/slup127.pdf]:
– при работе преобразователя в непрерывном режиме необходимо чтобы присутствовал некоторый запас по индукции
насыщения, поскольку к началу нового цикла заряда магнитопровод остается подмагниченным. Целесообразно
использовать материалы с большей индуктивностью насыщения – аморфное железо, Kool-mu, пермаллой.
При выборе формы магнитопровода трансформатора обратноходового преобразователя целесообразно использовать
магнитопровод обеспечивающий хорошее охлаждение обмоток. И в конструкции использовать минимальное число
слоев.
EC, ETD, LP, EE – типы магнитопровода являются подходящими для трансформатора flyback-преобразователя. Так же
могут быть использованы кольцевые магнитопроводы с распределенным зазором. PQ и чашкообразные сердечники не
рекомендуется использовать по причине того, что соотношение размера магнитопровода и окна магнитопровода не
является оптимальным для обратноходовых преобразователей [Magnetics Design Handbook from TI byLloyd H.
Dixon. Section 5. Inductor and Flyback. Transformer Design. Texas Instruments. 2001.
http://www.ti.com/lit/ml/slup127/slup127.pdf].
Методика проектирования трансформатора обратноходового преобразователя и соотношение для расчета габаритного
параметра даны в разделе «Индуктивность» – пункт «Трансформатор обратноходового преобразователя».
Магнитной цепью или магнитопроводом называется путь, по которому замыкается магнитный поток. Этот путь может проходить целиком по воздуху.
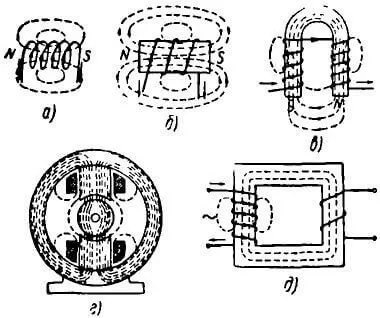 |
| Рисунок 1. Примеры магнитных цепей |
На рисунке 1, а показан соленоид. Магнитная цепь здесь проходит через воздух. Магнитное сопротивление воздуха очень велико, поэтому даже при большой намагничивающей силе магнитный поток мал.
Для увеличения магнитного потока в состав магнитной цепи вводят ферромагнитные материалы (обычно литая или электротехническая сталь), имеющие меньшее магнитное сопротивление.
На рисунке 1, б представлен прямой электромагнит с разомкнутым сердечником. Магнитные линии только небольшую часть своего пути проходят по стальному сердечнику, большую же часть своего пути они проходят по воздуху. Полюсы электромагнита определяются при помощи “правила буравчика”.
Подковообразный электромагнит, изображенный на рисунке 1, в, представляет магнитную цепь с лучшими условиями для прохождения магнитного потока. При такой конструкции поток большую часть пути проходит по стали и меньшую часть от полюса N до полюса S по воздуху.
На рисунке 1, г представлена конструкция магнитной цепи, применяемая в электромашиностроении и приборостроении. Между полюсами электромагнита помещается стальной якорь. Большую часть своего пути магнитные линии проходят по стали и только очень малую часть (от нескольких долей миллиметра до 2–3 мм) проходят по двум воздушным промежуткам.
Трансформаторы имеют замкнутый стальной сердечник (рисунок 1, д). Сердечники трансформаторов собираются из нескольких частей, но во время сборки принимают меры к тому, чтобы воздушные зазоры между отдельными частями практически были равны нулю.
До сих пор мы не говорили о том, что магнитный поток, созданный намагничивающей силой, не весь замыкается по тому пути, который ему предназначен. Помимо рабочего магнитного потока, существует магнитный поток рассеяния, который замыкается вне того места, где используется рабочий поток. На рисунке 1, б, в, г, д показаны потоки рассеяния.
Таким образом, общий магнитный поток, который должна создать обмотка возбуждения электромагнита, равен сумме рабочего потока и потока рассеяния.
Расчет магнитной цепи, казалось бы, можно производить по формуле:
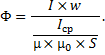
Но если вспомнить, что относительная магнитная проницаемость µ для ферромагнитных тел непостоянна и зависит от многих причин, то становится ясно, что этой формулой можно пользоваться лишь в том случае, когда в состав магнитной цепи входят только немагнитные тела (в том числе и воздух), для которых µ есть заранее заданная величина.
На практике для расчета магнитных цепей предпочитают пользоваться графическими методами решения.
Расчет магнитной цепи производят в следующем порядке. Задаются необходимой величиной магнитного потока. Разбивают магнитную цепь на участки, имеющие одинаковые поперечные сечения и однородный материал, и для каждого участка определяют величину магнитной индукции по формуле:
![]()
Затем по кривым намагничивания для данного материала находят для каждого значения магнитной индукции величину напряженности H. Если в магнитной цепи встречаются воздушные зазоры, то зависимость B0 и H0 определяется по формуле:
![]()
Здесь B0 выражено в Вб/м², µ0 – в Гн/м, H0 – в А/см .
Если индукция выражена в гауссах, а напряженность в А/см, то зависимость между B0 и H0 будет:
H0 = 0,8 × B0 .
Определив величину H для каждого участка, находим по закону полного тока величину намагничивающей силы по формуле:
![]()
Пример. Найти намагничивающую силу обмотки электромагнита, изображенного на рисунке 2. Размеры даны в миллиметрах. Материал сердечника – электротехническая сталь. В сердечнике необходимо создать магнитный поток 60 000 Мкс. Магнитным рассеянием пренебрегаем.
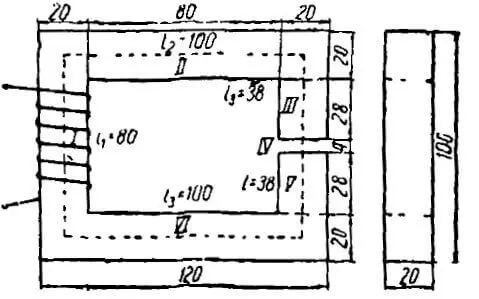
Рисунок 2. К примеру расчета магнитной цепи
Проводим среднюю линию по все длине магнитной цепи. Разбиваем цепь на пять участков и определяем длину каждого участка.
Так как магнитный поток во всех участках одинаков и площадь поперечного сечения всех участков магнитной цепи (2 × 2 см), то магнитная индукция везде также будет одинакова.
![]()
По кривой намагничивания (рисунок 3) для электротехнической стали по индукции 15000 Гс находим напряженность магнитного поля H = 30 А/см. Для воздушного зазора имеем:
H0 = 0,8 × 15000 = 12000 А/см .
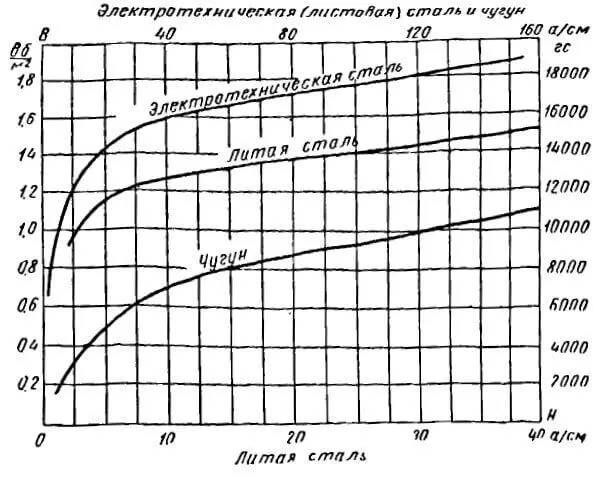
Рисунок 3. Кривые намагничивания электротехнической стали, литой стали и чугуна
Умножая величины напряженности на длины соответствующих участков, получаем произведения H × l для этих участков.
Результаты вычислений записываем в таблицу (таблица 1).
Таблица 1
| Номера участков | Материал | B | l | H | H × l |
| Гс | см | А/см | А | ||
| I II и VI III и V IV |
Электротехническая сталь То же То же Воздух |
15000 15000 15000 15000 |
8 10 × 2 3,8 × 2 0,4 |
30 30 30 12000 |
240 600 228 4800 |
I × w = ∑ (H × l) = 5868 А .
Интересно отметить, что если на участках из электротехнической стали I, II, III, V и VI общей протяженностью 35,6 см (8 + 20 + 7,6 см) для проведения магнитного потока необходима намагничивающая сила 1068 А (240 + 600 + 228 А), то на воздушный зазор длиной всего 4 мм (в 89 раз меньше длины пути стали) нужна намагничивающая сила 4800 А. Отсюда становится понятной необходимость создания магнитных цепей с минимальными воздушными зазорами.
Источник: Кузнецов М. И., “Основы электротехники” – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
→
2.1 Методы расчета магнитных цепей постоянного тока
2.1 Методы расчета магнитных цепей постоянного тока
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
Расчет магнитных цепей при постоянных токах
Основанием к расчету магнитных цепей служат: первый закон Кирхгофа для магнитных цепей и закон полного тока — второй закон Кирхгофа для магнитных цепей.
Первый закон Кирхгофа для магнитных цепей гласит: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.
Закон полного тока применяется к замкнутому контуру, образованному средними магнитными линиями магнитной цепи и имеет вид:
∫ H → ⋅ dl → = ∑ I⋅w ,
где
∫ H → ⋅ dl → = ∑ H⋅l — падение магнитного напряжения UM = H·l в контуре;
F= ∑ I⋅w — магнитодвижущая сила контура (м. д. с.).
Второй закон Кирхгофа для магнитных цепей сформулируем следующим образом: алгебраическая сумма магнитных напряжений UM = H·l в замкнутом контуре магнитной цепи ( ∑ U M = ∑ H⋅l ) равна алгебраической сумме магнитодвижущих сил F = I·w в том же контуре ( ∑ F = ∑ I⋅w ) :
∑ U M = ∑ F
или
∑ H⋅l = ∑ I⋅w .
Задачи на расчет магнитной цепи могут быть двух видов: прямая задача на расчет магнитной цепи — когда задан поток и требуется рассчитать магнитодвижущую силу (м. д. с.) и обратная задача на расчет магнитной цепи — когда по заданной м. д. с. требуется рассчитать магнитный поток.
В обоих случаях должны быть известны геометрические размеры магнитной цепи и заданы кривые намагничивания ее материалов.
Алгоритм прямой задачи расчета неразветвленной магнитной цепи
Дана конфигурация и геометрические размеры неразветвленной магнитной цепи, кривая (или кривые) намагничивания магнитного материала и магнитный поток или индукция магнитного поля в каком-либо сечении. Требуется найти магнитодвижущую силу, ток или число витков намагничивающей обмотки.
Расчет проводим в соответствии с алгоритмом:
1. Разбиваем магнитную цепь на однородные (из одного магнитного материала) участки постоянного сечения и определяем длины lk и площади поперечного сечения Sk участков. Длины участков (в метрах) берем по средней силовой линии.
2. Исходя из постоянства потока вдоль всей неразветвленной магнитной цепи, по заданному магнитному потоку Ф и сечениям Sk участков находим магнитные индукции на каждом участке:
B k = Ф S k .
Если задана магнитная индукция на каком-либо участке магнитной цепи, то магнитный поток вдоль всей неразветвленной цепи
Ф = Bk·Sk.
3. По найденным магнитным индукциям Bk участков цепи и кривой намагничивания материала k-го участка цепи (например, рис. 2.1, табл. 2.1) определяем напряженности поля Hk на каждом участке магнитной цепи.
Напряженность поля в воздушном зазоре находим по формуле
H возд = B возд μ 0 = B возд 4π⋅ 10 −7 .
4. Подсчитаем сумму падений магнитных напряжений UMk = Hk·lk вдоль всей магнитной цепи ∑ U Mk = ∑ H k ⋅ l k и на основании второго закона Кирхгофа для магнитной цепи приравниваем сумме магнитодвижущих сил Fk = Ik·wk вдоль всей магнитной цепи:
∑ H k ⋅ l k = ∑ I k ⋅ w k .
Основным допущением при расчете является то, что магнитный поток вдоль всей неразветвленной магнитной цепи полагаем неизменным. В действительности не большая часть потока всегда замыкается, минуя основной путь. Этот поток называют потоком рассеяния.
Единицы измерения магнитных величин
B — индукция магнитного поля, Тл (Тесла);
H — напряженность магнитного поля, А/м (Ампер/метр);
Ф — поток индукции магнитного поля, Вб (Вебер);
F = I·w — магнитодвижущая сила (м. д. с.), А (Ампер);
UM = H·l — магнитное напряжение, А (Ампер!).
Константы
μ 0 =4π⋅ 10 −7 Гн/м — магнитная постоянная.
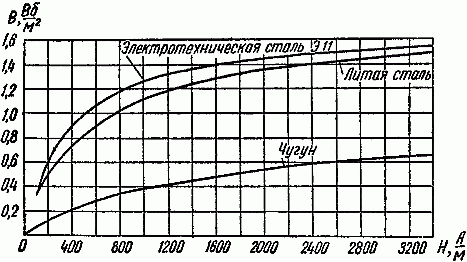
Рис. 2.1 Кривые намагничивания стали и чугуна
Таблица 2.1 — Данные основной кривой намагничивания листовой электротехнической стали Э11
|
B, Вб/м2 |
H, А/м |
|||||||||
|
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
|
0,4 |
140 |
143 |
146 |
149 |
152 |
155 |
158 |
161 |
164 |
167 |
|
0,5 |
171 |
175 |
179 |
183 |
187 |
191 |
195 |
199 |
203 |
207 |
|
0,6 |
211 |
216 |
221 |
226 |
231 |
236 |
241 |
246 |
251 |
256 |
|
0,7 |
261 |
266 |
271 |
276 |
281 |
287 |
293 |
299 |
306 |
312 |
|
0,8 |
318 |
324 |
330 |
337 |
344 |
352 |
360 |
369 |
378 |
387 |
|
0,9 |
397 |
407 |
417 |
427 |
437 |
447 |
458 |
469 |
480 |
491 |
|
1,0 |
502 |
514 |
527 |
541 |
555 |
570 |
585 |
600 |
615 |
631 |
|
1,1 |
647 |
664 |
682 |
701 |
720 |
739 |
759 |
779 |
800 |
821 |
|
1,2 |
843 |
866 |
891 |
918 |
946 |
976 |
1010 |
1040 |
1070 |
1100 |
|
1,3 |
1140 |
1180 |
1220 |
1260 |
1300 |
1340 |
1380 |
1430 |
1480 |
1530 |
|
1,4 |
1580 |
1640 |
1710 |
1780 |
1860 |
1950 |
2050 |
2150 |
2260 |
2380 |
|
1,5 |
2500 |
2640 |
2790 |
2950 |
3110 |
3280 |
3460 |
3660 |
3880 |
4120 |
|
1,6 |
4370 |
4630 |
4910 |
5220 |
5530 |
5880 |
6230 |
6600 |
6980 |
7370 |
|
1,7 |
7780 |
8200 |
8630 |
9070 |
9630 |
10100 |
10600 |
11100 |
11600 |
12200 |
|
1,8 |
12800 |
13400 |
14000 |
14600 |
15200 |
15900 |
16600 |
17300 |
18000 |
18800 |
|
1,9 |
19700 |
20600 |
21600 |
22 600 |
23600 |
24600 |
25600 |
26800 |
28200 |
29600 |
|
2,0 |
31000 |
32500 |
34300 |
36500 |
39000 |
42000 |
45500 |
49500 |
54500 |
59500 |
Примеры пользования таблицей:
1) При B = 0,80 Вб/м2: H = 318 А/м; при B = 0,85 Вб/м2: H = 352 А/м.
2) При B = 1,13 Вб/м2: H = 701 А/м.
Решение задач на расчет магнитных цепей при постоянных токах
Задача 2.1. На рис. 2.2 изображен разрез трех катушек, по которым проходят токи I1 = 8 А, I2=10 А и I3 = 5 А.
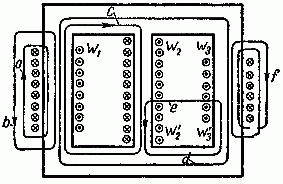
Рис. 2.2
Катушки размещены на стальном сердечнике. Первая катушка (левая) w1 имеет 8 витков, вторая (средняя) w2 — 10 витков и третья (правая) w3 — 6 витков. Определить полную магнитодвижущую силу (м. д. с.) по замкнутым контурам а, b, с, d, е, f, показанным на рис. 2.2. Контур е охватывает катушки w’2 с 4 витками и w’3 с 2 витками.
Изменится ли результат решения задачи, если при тех же данных катушки разместить на сердечнике из другого магнитного материала?
Решение
Воспользуемся законом полного тока. Линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, проходящих сквозь поверхность, ограничиваемую контуром интегрирования,
∫ H → ⋅ dl → = ∑ I⋅w .
Пользуясь законом полного тока, найдем:
∫ a H → ⋅ dl → = w 1 ⋅ I 1 =8⋅8=64 А; ∫ b H → ⋅ dl → =− w 1 ⋅ I 1 =−8⋅8=−64 А; ∫ c H → ⋅ dl → = w 2 ⋅ I 2 − w 1 ⋅ I 1 =10⋅10−8⋅8=36 А; ∫ d H → ⋅ dl → = w 1 ⋅ I 1 − w 2 ⋅ I 2 + w 2 ⋅ I 2 + w 3 ⋅ I 3 =8⋅8+6⋅5=94 А; ∫ e H → ⋅ dl → = w ′ 2 ⋅ I 2 − w ′ 3 ⋅ I 3 =4⋅10+2⋅5=50 А; ∫ f H → ⋅ dl → =2 w 3 ⋅ I 3 =2⋅6⋅5=60 А.
В правой части последнего выражения коэффициент 2 учитывает то обстоятельство, что витки w3 охватываются контуром интегрирования (циркуляции) дважды.
Следует заметить, что при пользовании правилом винта необходимо всегда сопоставлять направление обхода по контуру циркуляции с направлениями токов, пронизывающих поверхность, ограниченную контуром циркуляции.
Результаты решения задачи не изменятся, если катушки разместить на сердечнике из другого магнитного материала, так как м. д. с. определяется только величиной полного тока и не зависит от магнитных свойств вещества.
Задача 2.2. Определить магнитодвижущую силу (прямая задача расчета одноконтурной магнитной цепи), необходимую для получения магнитного потока в 5,9·10–4 Вб в кольцеобразном сердечнике, сечением S = 5 см2. Длина средней линии магнитной индукции l = 25 см.
Определить Н (напряженность магнитного поля в сердечнике) и μ r (относительная магнитная проницаемость материала сердечника). Материал сердечника — слаболегированная электротехническая листовая сталь Э11.
Решение
Найдем магнитную индукцию
B= Ф S = 5,9⋅ 10 −4 5⋅ 10 −4 =1,18 Вб м 2 .
По кривой намагничивания для стали Э11 найдем, что индукции B = 1,18 Вб/м2 соответствует H = 800 А/м.
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F = H·l = 800·0,25 = 200 А.
Определим абсолютную магнитную проницаемость:
μ a = B H = 1,18 800 =1475⋅ 10 −6 Гн м .
Магнитная проницаемость (относительная магнитная проницаемость)
μ r = μ a μ 0 = 1475⋅ 10 −6 4π⋅ 10 −7 =1175.
Задача 2.3. На рис. 2.3 изображен электромагнит, сердечник которого изготовлен из слаболегированной листовой электротехнической стали Э11, а якорь — из литой стали.
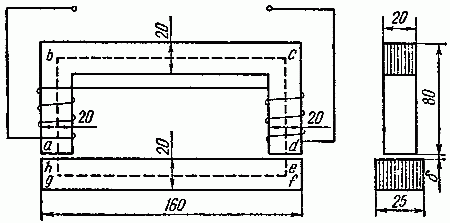
Рис. 2.3
Какой ток должен быть пропущен через обмотку электромагнита (прямая задача расчета одноконтурной магнитной цепи), состоящую из w = 500 витков, для того, чтобы в якоре была создана магнитная индукция в 0,84 Вб/м2. Размеры на рис. 2.3 даны в миллиметрах. Длина воздушного зазора δ = 1 мм. Площадь сечения воздушного зазора считать равной площади сечения сердечника (пренебрегаем потоком рассеяния). Чему равна статическая индуктивность электромагнита?
Решение
Это пример прямой задачи на расчет магнитной цепи. На рис. 2.3 пунктиром проведена средняя линия магнитной индукции (приближенно). Длина проходящей вдоль сердечника части средней линии магнитной индукции abсd = l1 = 0,28 м. Сечение сердечника S1 = 2·2 = 4 см2 = 4·10–4 м2.
Сечение якоря S2 = 2·2,5 = 5 см2 = 5·10–4 м2, длина проходящей через него части средней линии магнитной индукции efgh = l2 = 0,16 м. Магнитная индукция в якоре B2 = 0,84 Вб/м2 (по условию задачи).
Из условия равенства магнитных потоков в якоре и в сердечнике (одноконтурная магнитная цепь, потоком рассеяния пренебрегаем)
Ф1 = B1·S1 = B2·S2
найдем магнитную индукцию в сердечнике:
B 1 = B 2 ⋅ S 2 S 1 = 0,84⋅5⋅ 10 −4 4⋅ 10 −4 =1,05 Вб м 2 .
Сечение воздушного зазора, длина проходящей в нем части линии магнитной индукции и магнитная индукция равны:
S 3 =4⋅ 10 −4 м 2 ; l 3 =2δ=2⋅ 10 −3 м; B 3 =1,05 Вб м 2 ,
напряженность магнитного поля в воздухе:
H 3 = B 3 μ 0 = 1,05 4π⋅ 10 −7 =84⋅ 10 4 А м .
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F = H1·l1 + H2·l2 + H3·l3.
В целях большей наглядности расчеты удобно свести в таблицу, в которой данные для напряженности магнитного поля в отдельных элементах магнитопровода взяты по соответствующим кривым намагничивания. Так, для сердечника, изготовленного из стали Э11, находим, что индукции B1 = 1,05 Вб/м2 соответствует значение напряженности магнитного поля H1 = 570 А/м, а для якоря, изготовленного из литой стали, имеем, что величине B2 = 0,84 Вб/м2 соответствует значение H2 = 540 А/м.
|
Название участка |
Материал |
S, м2 |
l, м |
B, Вб/м2 |
H, А/м |
H·l, А |
|
Сердечник |
Сталь Э11 |
4·10–4 |
0,28 |
1,05 |
570 |
160 |
|
Якорь |
Литая сталь |
5·10–4 |
0,16 |
0,84 |
540 |
85 |
|
Воздушный зазор |
Воздух |
4·10–4 |
0,002 |
1,05 |
84·104 |
1680 |
F= ∑ H k ⋅ l k =160+85+1680=1925 А.
Искомый ток найдем, пользуясь формулой F = I·w:
I= F w = 1925 500 =3,85 А.
Статическая индуктивность электромагнита равна отношению потокосцепления (полного магнитного потока) к току:
L ст = Ψ I = w⋅Ф I = 500⋅4,2⋅ 10 −4 3,85 =0,053 Гн=053 мГн.
Задача 2.4. Найти магнитную индукцию в якоре электромагнита (обратная задача расчета одноконтурной магнитной цепи), изображенном на рис. 2.3, если на электромагнит намотано w = 250 витков, по которым проходит ток I = 4,4 А. Сердечник изготовлен из листовой электротехнической стали Э11, а якорь — из литой стали. Размеры сердечника и якоря те же, что и в предыдущей задаче. Длина воздушного зазора 0,5 мм. Площадь сечения воздушного зазора считать равной площади сердечника.
Решение
Это пример обратной задачи на расчет магнитной цепи. Для ее решения надо построить кривую зависимости магнитного потока Ф в функции магнитодвижущей силы F и на кривой найти рабочую точку.
Чтобы построить кривую Ф = f (F) будем задаваться различными величинами магнитных потоков Ф, по которым вычисляем соответствующие им значения магнитной индукции B в каждом из участков магнитной цепи. Затем по кривым намагничивания находим напряженность поля H, соответствующую каждому значению индукции B, и, наконец, вычисляем магнитодвижущую силу по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F= ∑ H k ⋅ l k .
Так, например, примем Ф = 3,2·10–4 Вб. Тогда
B серд = Ф S серд = 3,2⋅ 10 −4 4⋅ 10 −4 =0,8 Вб м 2 ; B як = Ф S як = 3,2⋅ 10 −4 5⋅ 10 −4 =0,64 Вб м 2 ; B заз = B серд =0,8 Вб м 2 .
По кривым намагничивания находим напряженности магнитного поля:
H серд =318 А м ; H як =330 А м ; H заз = B заз μ 0 = 0,8 4π⋅ 10 −7 =64⋅ 10 4 А м .
Магнитодвижущая сила
F= H серд ⋅ l серд + H як ⋅ l як + H заз ⋅ l заз = =318⋅0,28+330⋅0,16+64⋅ 10 4 ⋅ 10 −3 =780 А.
Эта магнитодвижущая сила меньше заданной, которая равна
I·w = 4,4·250 = 1100 А.
Аналогично проводим расчеты для больших значений Ф, которые сведены в следующую таблицу:
|
Ф, Вб |
Bсерд, Вб/м2 |
Нсерд, А/м |
lсерд, м |
Bяк, Вб/м2 |
Hяк, А/м |
lяк, м |
Bзаз, Вб/м2 |
Hзаз, А/м |
lзаз, м |
F, А |
|
3,2·10–4 |
0,8 |
318 |
0,28 |
0,64 |
330 |
0,16 |
0,8 |
64·104 |
1·10–3 |
780 |
|
3,6·10–4 |
0,9 |
397 |
0,28 |
0,72 |
400 |
0,16 |
0,9 |
72·104 |
1·10–3 |
895 |
|
4,0·10–4 |
1,0 |
502 |
0,28 На http://www.online-invest.org проекты хайп. |
0,80 |
490 |
0,16 |
1,0 |
80·104 |
1·10–3 |
1020 |
|
4,4·10–4 |
1,1 |
647 |
0,28 |
0,88 |
600 |
0,16 |
1,1 |
88·104 |
1·10–3 |
1160 |
Мы остановились на величине Ф = 4,4·10–4 Вб потому, что для этого значения магнитного потока суммарная магнитодвижущая сила равна 1160 А, что больше заданных 1100 А. По данным расчетов построена кривая Ф = f (F) и на ней определена рабочая точка, которая при F = 1100 А соответствует значению магнитного потока в 4,24·10–4 (рис. 2.4).
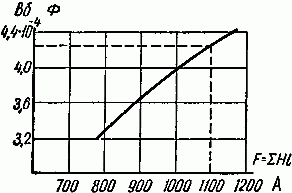
Рис. 2.4
Следовательно, искомая индукция в якоре электромагнита
B як = Ф S як = 4,24⋅ 10 −4 5⋅ 10 −4 =0,848 Вб м 2 .
Обычно в технических расчетах значения магнитной индукции округляют до сотых долей Вб/м2 (целые сотни гауссов); поэтому считаем Bяк = 0,85 Вб/м2.
Укажем, что задача могла бы быть решена и другим путем — методом проб: суть его состоит в том, что так же, как и выше, задаются некоторым значением магнитного потока Ф, для которого подсчитывают магнитодвижущую силу F. Если она окажется меньше заданной, то берут большие значения Ф до тех пор, пока не получат F больше заданной величины. После этого значения Ф, соответствующие большим и меньшим против заданного значениям F сужают до тех пор, пока для одного из сечений магнитной цепи полученные значения магнитной индукции будут различаться друг от друга не более чем на 0,1 Вб/м2 (1000 Гс). Искомое значение Ф можно затем найти путем интерполирования.
Так, например, задаемся величиной Ф = 3,2·10–4 Вб, которой соответствует магнитодвижущая сила F = 780 А, что меньше заданного значения Fзад = 1100 А. Теперь зададимся Ф’ = 4,4·10–4 Вб, для которого найдем F’ = 1160 А; это больше заданной величины Fзад. Уменьшаем значение Ф, принимая его, например, равным 4·10–4 Вб; ему соответствует значение F” = 1020 А, что вновь меньше заданной величины магнитодвижущей силы. Итак, при Ф” = 4·10–4 Вб: B”як = 0,8 Вб/м2, а при Ф’ = 4,4·10–4 Вб: B’як = 0,88 Вб/м2.
Таким образом, значения магнитной индукции B в одном из сечений (в данном случае в якоре) отличаются одно от другого менее, чем на 0,1 Вб/м2 (0,88 — 0,8 = 0.08 Вб/м2).
Окончательное значение магнитного потока найдем линейным интерполированием.
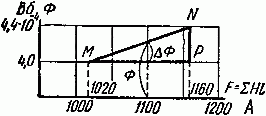
Рис. 2.5
Из треугольника MNP (рис. 2.5) имеем:
ΔФ 4,4⋅ 10 −4 −4⋅ 10 −4 = 1100−1020 1160−1020 ,
отсюда
ΔФ=0,23⋅ 10 −4 Вб, а Ф=4⋅ 10 −4 +0,23⋅ 10 −4 =4,23⋅ 10 −4 Вб.
Искомая индукция в якоре
B як = Ф S як = 4,23⋅ 10 −4 5⋅ 10 −4 ≈0,85 Вб м 2 .
Задача 2.5. Найти магнитную индукцию в воздушном зазоре тороида (обратная задача расчета одноконтурной магнитной цепи), изготовленного из литой стали (рис. 2.6), если на тороид намотано w = 400 витков, по которым проходит ток I = 4 А. Воздушный зазор = 2 мм. Размеры тороида на рисунке даны в мм.
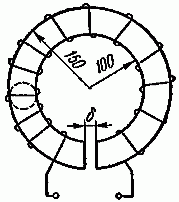
Рис. 2.6
Решение
Задача может быть решена аналогично предыдущей. Мы здесь укажем, как быстрее всего найти первое приближенное значение магнитного потока. Для этого предполагаем, что вся заданная магнитодвижущая сила F = I·w расходуется на ту часть магнитопровода, которая предполагается имеющей наибольшее магнитное сопротивление. Получаемое при этом значение магнитного потока будет завышено по сравнению с фактическим, ибо в расчете не были учтены магнитные сопротивления других участков цепи.
Полагая в нашем случае, что вся магнитодвижущая сила падает на магнитном сопротивлении воздушного зазора, запишем по второму закону Кирхгофа для магнитной цепи (закону полного тока):
F=I⋅w= H возд ⋅δ= B μ 0 ⋅δ,
откуда
B= I⋅w⋅ μ 0 δ = 4⋅400⋅4π⋅ 10 −7 2⋅ 10 −3 =1,0 Вб м 2 .
Так как это значение индукции, как указано выше, явно завышено, проведем новый расчет для меньшего значения магнитной индукции, например, для 0,8 Вб/м2. По кривой намагничивания для литой стали этой индукции соответствует величина напряженности магнитного поля Hст = 490 А/м.
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока) при этом будет равна
F= H ст ⋅ l ст + H возд ⋅δ=490⋅0,785+ 0,8 4π⋅ 10 −7 ⋅2⋅ 10 −3 =1650 А,
что превышает заданную величину 1600 А.
Теперь проведем расчет для еще меньшей индукции B = 0,7 Вб/м2. Для нее по кривой намагничивания напряженность Hст = 380 А/м. Общая магнитодвижущая сила в этом случае будет
F= H ст ⋅ l ст + H возд ⋅δ=490⋅0,785+ 0,7 4π⋅ 10 −7 ⋅2⋅ 10 −3 =1410 А,
что меньше заданной величины 1600 А.
Таким образом, истинная величина индукции находится в пределах от 0,7 до 0,8 Вб/м2. Ее мы найдем интерполированием (рис. 2.7).
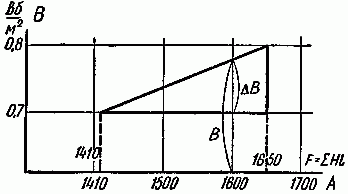
Рис. 2.7
Искомая индукция B=0,7+ΔB, где ΔB находится из соотношения
ΔB 0,1 = 1600−1410 1650−1410 = 190 240 ,
откуда
ΔB= 190 240 ⋅0,1≈0,08 Вб м 2 .
Итак, искомая индукция равна 0,78 Вб/м2 (7800 Гс).
Задача 2.6. Определить все магнитные потоки и ток, проходящий через катушку, расположенную на среднем стержне сердечника, если в левом стержне имеется магнитная индукция в 0,95 Вб/м2. Размеры магнитопровода на рис. 2.8 даны в миллиметрах. Материал сердечника — листовая сталь Э11. Число витков катушки w = 500.
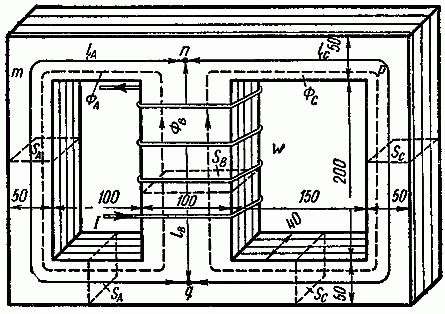
Рис. 2.8
Решение
Покажем на рисунке средние линии магнитной индукции. По данным задачи найдем их длины:
lA = 60 см; lB = 25 см; lC = 70 см.
Задачи на сложную разветвленную несимметричную магнитную цепь решаются на основании первого и второго законов Кирхгофа для магнитной цепи:
для узла n
ФB = ФA + ФC; (1)
для контура npqn
HB·lB + HC·lC = I·w; (2)
для контура npqmn
HC·lC — HA·lA = 0. (3)
В уравнениях (2) и (3) HA, HB и HC соответственно напряженности магнитного поля в стержнях A, B и C.
Для магнитной индукции в левом стержне BA = 0,95 Вб/м2 по кривой намагничивания для листовой стали найдем HA = 447 А/м.
Из уравнения (3) получим
H C = H A ⋅ l A l C = 447⋅60 70 =384 А м .
По кривой намагничивания находим, что H = 384 А/м соответствует индукция BC = 0,89 Вб/м2.
По уравнению (1) получим
Ф B = Ф A + Ф C = B A ⋅ S A + B C ⋅ S C = =0,95⋅20⋅ 10 −4 +0,89⋅20⋅ 10 −4 =36,8⋅ 10 −4 Вб.
Следовательно,
B B = Ф B S B = 36,8⋅ 10 −4 40⋅ 10 −4 =0,92 Вб м 2 .
Этой индукции по кривой намагничивания соответствует HB = 417 А/м. По уравнению (2) найдем
I·w = HB·lB + HC·lC = 417·0,25 + 384·0,7 = 373 А.
Искомый ток
I= F w = 373 500 ≈0,75 А.
Задача 2.7. Магнитная цепь изготовлена из листовой электротехнической стали Э11. На средний стержень сердечника намотана катушка, содержащая w = 930 витков, по которым проходит ток I = 1 А (рис. 2.8). На всем участке A сечение магнитной цепи считать SA = 20 см2, на участке B — SB = 40 см2, на участке С — SC = 20 см2. Длины средних линий магнитной индукции каждого из участков считать равными: lA = 55 см, lB = 25 см, lC = 80 см.
Найти значения магнитной индукции во всех стержнях.
Решение
Выберем на рис. 2.8 пути средних линий магнитной индукции и запишем уравнения:
для узла n
ФB = ФA + ФC; (1)
для контура npqn
HB·lB + HC·lC = I·w; (2)
для контура npqmn
HC·lC — HA·lA = 0. (3)
Построим кривые зависимостей
ФA = f1 (HA·lA) = f1 (UMnq);
ФB = f2 (I·w — HB·lB) = f2 (UMnq);
ФC = f3 (HC·lC) = f3 (UMnq).
Здесь UMnq — разность скалярных магнитных потенциалов точек n и q, или магнитодвижущая сила между теми же точками.
Для построения кривой f1 задаемся различными величинами магнитных потоков ФA, по которым находим соответствующие им значения магнитной индукции BA, для которых по кривой намагничивания определяем напряженность магнитного поля HA. Беря произведение HA·lA, находим для различных потоков значения магнитных напряжений на участке A. Результаты вычислений сводим в таблицу. Таким же путем производим расчет для построения кривой на участке C. Наконец, для построения кривой f2 (участок B) задаемся значениями ФB и по ним находим BB, HB, HB·lB и разность I·w — HB·lB. Указанные вычисления сведены в таблицу.
|
ФА, 10–4 Вб |
BA, Вб/м2 |
HA, А/м |
HAlA, А |
ФC, 10–4 Вб |
BC, Вб/м2 |
HC, А/м |
HClC, А |
ФB, 10–4 Вб |
BB, Вб/м2 |
HB, А/м |
HBlB, А |
Iw–HBlB, Смотрите на сайте tłumacz Warszawa. Утепление деревянного дома снаружи. А |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
930 |
|
10 |
0,5 |
171 |
94 |
10 |
0,5 |
171 |
137 |
20 |
0,5 |
171 |
43 |
887 |
|
12 |
0,6 |
211 |
116 |
12 |
0,6 |
211 |
169 |
24 |
0,6 |
211 |
53 |
877 |
|
14 |
0,7 |
261 |
143 |
14 |
0,7 |
261 |
209 |
28 |
0,7 |
261 |
65 |
865 |
|
16 |
0,8 |
318 |
175 |
16 |
0,8 |
318 |
254 |
32 |
0,8 |
318 |
80 |
850 |
|
18 |
0,9 |
397 |
218 |
18 |
0,9 |
397 |
318 |
36 |
0,9 |
397 |
99 |
831 |
|
20 |
1,0 |
502 |
276 |
20 |
1,0 |
502 |
402 |
40 |
1,0 |
502 |
126 |
804 |
|
22 |
1,1 |
647 |
356 |
22 |
1,1 |
647 |
518 |
44 |
1,1 |
647 |
162 |
768 |
|
24 |
1,2 |
843 |
463 |
24 |
1,2 |
843 |
675 |
48 |
1,2 |
843 |
210 |
720 |
|
26 |
1,3 |
1140 |
626 |
26 |
1,3 |
1140 |
913 |
52 |
1,3 |
1140 |
285 |
645 |
|
28 |
1,4 |
1580 |
870 |
28 |
1,4 |
1580 |
1265 |
56 |
1,4 |
1580 |
395 |
535 |
|
30 |
1,5 |
2500 |
1375 |
30 |
1,5 |
2500 |
2000 |
60 |
1,5 |
2500 |
625 |
305 |
По этим данным построены кривые ФA, ФB, ФC (рис. 2.9).
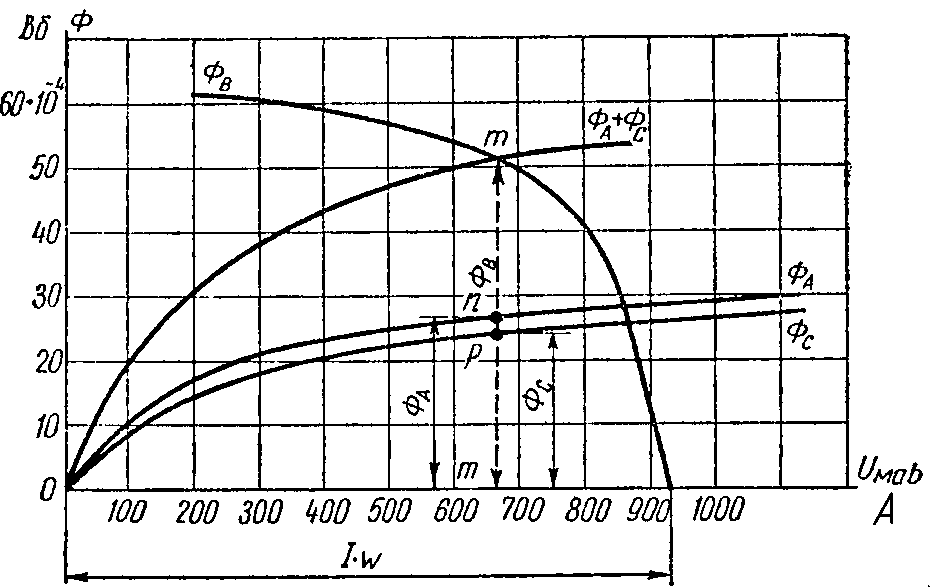
Рис. 2.9
Так как величины магнитных потоков должны удовлетворять уравнению (1), то проводим еще одну вспомогательную кривую ФB = ФA + ФC; она строится путем суммирования ординат кривых ФA и ФC для одних и тех же значений абсцисс. Точка m ее пересечения с кривой ФB = f2 (I·w — HB·lB) определяет величину искомого потока
ФB = 50,4·10–4 Вб.
Перпендикуляр mm’, опущенный из m на ось абсцисс, пересечет кривую ФA в точке n, а кривую ФC — в точке p, отрезок nm’ выражает искомый магнитный поток в стержне A:
ФA = 26,4·10–4 Вб, а отрезок pm’ — поток ФC = 24·10–4 Вб.
По найденным потокам находим магнитные индукции в каждом из стержней:
B A = Ф A S A = 26,4⋅ 10 −4 20⋅ 10 −4 =1,32 Вб м 2 ; B B = Ф B S B = 50,4⋅ 10 −4 40⋅ 10 −4 =1,26 Вб м 2 ; B C = Ф C S C = 24,0⋅ 10 −4 20⋅ 10 −4 =1,20 Вб м 2 .
Проверка. Можно убедиться, что при найденных значениях магнитных индукций удовлетворяются уравнения (1) — (3). Для этого по кривой намагничивания надо найти для каждого значения B соответствующее значение H и подставить в указанные уравнения.
Задача 2.8. Сердечник собран из листов электротехнической стали марки Э11. Форма и размеры сердечника (в мм) указаны на рис. 2.10.
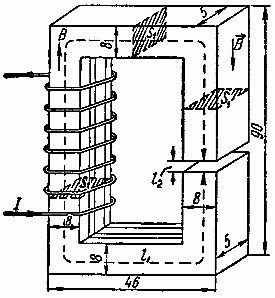
Рис. 2.10
Обмотка имеет w = 400 витков, по которым проходит ток I = 3,5 А. Длина воздушного зазора составляет 1 мм. Определить магнитный поток в сердечнике. При расчете следует считать, что сечение воздушного зазора равно сечению сердечника.
Задачу решить следующими аналитическими методами: а) линейной аппроксимации, б) кусочно-линейной аппроксимации, в) дробно-линейной аппроксимации.
Результаты, полученные для каждого из случаев, сравнить с теми, какие получаются при решении задачи обычным способом.
Решение
Найдем длину средней линии магнитной индукции и сечение стального сердечника (рис. 2.10):
l1 = 2· (90 — 8) + 2· (46 — 8) = 240 мм = 0,24 м;
S1 = 8·5 = 40 мм2 = 0,4·10–4 м2.
Длина средней линии магнитной индукции в воздушном зазоре и его сечение равны:
l2 = 1 мм = 1·10–3 м;
S2 = 8·5 = 40 мм2 = 0,4·10–4 м2.
Решая задачу способом, указанным в решении задачи 2.4, найдем магнитную индукцию B = 1,35 Вб/м2 и соответствующий магнитный поток
Ф = B·S = 1,35·0,4·10–4 = 0,54·10–4 Вб.
а) Расчет магнитной цепи методом линейной аппроксимации кривой намагничивания
Здесь расчет магнитной цепи основан на замене рабочей части кривой намагничивания прямой линией в некоторой области изменения магнитной индукции. Примем, например, что магнитная индукция изменяется в пределах от нуля до 1,5 Вб/м2. Заменим кривую намагничивания (рис. 2.11) прямой линией 0b.
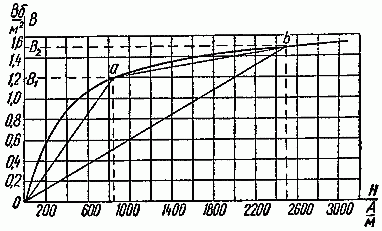
Рис. 2.11
Ее уравнение B = k1·H, здесь коэффициент k1 равен тангенсу угла наклона прямой 0b к оси абсцисс и выражает приближенное значение абсолютной магнитной проницаемости стали в рассматриваемом интервале
μ a1 = μ r1 ⋅ μ 0 = k 1 = B H = 1,5 2500 =6⋅ 10 −4 Гн м .
Искомый магнитный поток определяем по уравнению:
Ф= I⋅w R M1 + R M2 ,
где
R M1 = l 1 μ a1 ⋅ S 1 = l 1 μ r1 μ 0 ⋅ S 1 ; R M2 = l 2 μ 0 ⋅ S 2 — магнитные сопротивления, соответственно стальной части и воздушного зазора.
Производим вычисления:
R M1 = l 1 μ a1 ⋅ S 1 = 0,24 6⋅ 10 −4 ⋅0,4⋅ 10 −4 =1,0⋅ 10 7 1 Гн ; R M2 = l 2 μ 0 ⋅ S 2 = 1⋅ 10 −3 4π⋅ 10 −7 ⋅0,4⋅ 10 −4 =1,98⋅ 10 7 1 Гн ; Ф= I⋅w R M1 + R M2 = 3,5⋅400 1,0⋅ 10 7 +1,98⋅ 10 7 =0,47⋅ 10 −7 Вб.
Ошибка в сравнении с результатами, полученными обычным способом, составляет
0,54⋅ 10 −4 −0,47⋅ 10 −4 0,54⋅ 10 −4 ⋅100%≈13%.
б) Расчет магнитной цепи методом кусочно-линейной аппроксимации кривой намагничивания
Здесь расчет магнитной цепи основан на замене рабочей части кривой намагничивания отрезками прямых линий, например, из двух прямых отрезков 0a и ab (рис. 2.11).
Предполагается, что рабочий режим лежит в области индукций между B1 и B2, соответствующих точкам a и b.
Уравнение прямой ab, выражающей зависимость магнитной индукции от напряженности магнитного поля в стали, имеет вид:
B ст = B 1 + k 2 ⋅ ( H ст − H 1 ), (1)
где k2 — тангенс угла наклона прямой ab с осью абсцисс:
k 2 = B 2 − B 1 H 2 − H 1 . (2)
Напряженность магнитного поля в воздухе может быть выражена следующим образом:
H в = B в μ 0 = Ф μ 0 ⋅ S 2 = B ст ⋅ S 1 μ 0 ⋅ S 2 = B ст μ ′ 0 , (3)
где ради краткости обозначено
μ ′ 0 = μ 0 ⋅ S 2 S 1 . (4)
Подставляя в уравнение (3) вместо Bст его значение из уравнения (1), получим:
H в =[ B 1 + k 2 ⋅ ( H ст − H 1 ) ]⋅ 1 μ ′ 0 . (5)
Для определения Hст воспользуемся уравнением второго закона Кирхгофа для магнитной цепи (законом полного тока)
Hст·l1 + Hв·l2 = I·w. (6)
Подставляя в уравнение (6) значение Нв из уравнения (5), будем иметь:
H ст ⋅ l 1 + B 1 ⋅ l 2 μ ′ 0 + k 2 ⋅ l 2 μ ′ 0 ⋅ ( H ст − H 1 )=I⋅w.
Решая это алгебраическое уравнение относительно Hст, найдем:
H ст = I⋅w⋅ μ ′ 0 − B ′ ⋅ l 2 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 , (7)
где
B ′ = B 1 − k 2 ⋅ H 1 . (8)
Величина магнитной индукции в стали находится путем подстановки найденного значения Hс в уравнение (1):
B ст = μ ′ 0 ⋅ I⋅w⋅ k 2 + B ′ ⋅ l 1 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 , (9)
Для нашей задачи выберем ломаную так, что:
в точке a
B1 = 1,2 Вб/м2, соответствующее H1 = 843 А/м,
в точке b
B2 = 1,5 Вб/м2, соответствующее H2 = 2500 А/м.
По формулам (2), (4), (8), (7) и (1) находим:
k 2 = B 2 − B 1 H 2 − H 1 = 1,5−1,2 2500−843 =18,15⋅ 10 −5 Гн м ; μ ′ 0 = μ 0 ⋅ S 2 S 1 = μ 0 ⋅ 0,4⋅ 10 −4 0,4⋅ 10 −4 = μ 0 =4π⋅ 10 −7 Гн м ; B ′ = B 1 − k 2 ⋅ H 1 =1,2−18,15⋅ 10 −5 ⋅843=1,05 Вб м 2 ; H ст = I⋅w⋅ μ ′ 0 − B ′ ⋅ l 2 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 = 3,5⋅400⋅4π⋅ 10 −7 −1,05⋅1⋅ 10 −3 4π⋅ 10 −7 ⋅0,24+18,15⋅ 10 −5 ⋅1⋅ 10 −3 =1470 А м ; B ст = B 1 + k 2 ⋅ ( H ст − H 1 )=1,2+18,15⋅ 10 −5 ⋅ ( 1470−843 )=1,314 Вб м 2 .
И, наконец, искомый поток
Ф = Bст·S1 = 1,314·0,4·10–4 = 0,525·10–4 Вб.
Ошибка по сравнению с обычным способом расчета составляет
0,54⋅ 10 −4 −0,525⋅ 10 −4 0,54⋅ 10 −4 ⋅100%≈3%.
в) Расчет магнитной цепи методом дробно-линейной аппроксимации кривой намагничивания
Дробно-линейная аппроксимация делается посредством уравнения:
B ст = H ст α+β⋅ H ст . (10)
Входящие сюда коэффициенты α и β находятся из известных значений магнитной индукции и напряженности магнитного поля в двух выбранных точках кривой намагничивания, между которыми ожидается действительный режим работы стального участка магнитной цепи.
Для определения Нст поступим следующим образом: из уравнения (10) значение Вст подставим в уравнение (3), тогда получим:
H в = B ст μ ′ 0 = H ст μ ′ 0 ⋅ ( α+β⋅ H ст ) .
Это значение Нв подставим в уравнение (6) второго закона Кирхгофа для магнитной цепи (закона полного тока):
H ст ⋅ l 1 + H ст ⋅ l 2 μ ′ 0 ⋅ ( α+β⋅ H ст ) =I⋅w.
Решая относительно Нст это квадратное уравнение, найдем:
H ст = 1 2 ( I⋅w l 1 − 1+p q )+ 1 4 ( I⋅w l 1 − 1+p q ) 2 + I⋅w q⋅ l 1 . (11)
Второй корень квадратного уравнения, как не имеющий физического смысла, ввиду того что Нст должна выражаться положительным числом, опущен.
В уравнении (11) введены ради краткости обозначения:
p= l 2 ⋅ S 1 l 1 ⋅ S 2 ⋅ μ 0 ⋅α ; q= β α . (12)
Проведем числовые расчеты для нашей задачи, принимая для B и H те числовые значения, какие они имеют на границах рассматриваемого интервала в указанных выше точках a и b. По уравнению (10) имеем:
1,2= 843 α+β⋅843 ; 1,5= 2500 α+β⋅2500 .
Решая эти два уравнения, найдем:
α=213 м Гн ; β=0,581 м 2 Вб .
Далее по формулам (12), (13), (11) и (10) получим:
p= l 2 ⋅ S 1 l 1 ⋅ S 2 ⋅ μ 0 ⋅α = 1⋅ 10 −3 ⋅0,4⋅ 10 −4 0,24⋅0,4⋅ 10 −4 ⋅4π⋅ 10 −7 ⋅α 213=15,6; q= β α = 0,581 213 =2,73⋅ 10 −3 м А ; I⋅w q⋅ l 1 = 3,5⋅400 2,73⋅ 10 −3 ⋅0,24 =2,14⋅ 10 6 А 2 м 2 ; 1 2 ( I⋅w l 1 − 1+p q )= 1 2 ( 3,5⋅400 0,24 − 16,6 2,73⋅ 10 −3 )=−125; H ст = 1 2 ( I⋅w l 1 − 1+p q )+ [ 1 2 ( I⋅w l 1 − 1+p q ) ] 2 + I⋅w q⋅ l 1 = =−125+ 125 2 +2,14⋅ 10 6 =−125+1515=1390 А м ; B ст = H ст α+β⋅ H ст = 1390 213+0,581⋅1390 =1,363 Вб м 2 .
Искомый магнитный поток равен:
Ф = Bст·S1 = 1,363·0,4·10–4 = 0,545·10–4 Вб.
Ошибка в сравнении с обычным методом расчета магнитных цепей составляет:
0,545⋅ 10 −4 −0,54⋅ 10 −4 0,545⋅ 10 −4 ⋅100%≈0,9%.
Отметим, что расчет при помощи дробно-линейной аппроксимации приводит к удовлетворительным результатам даже в тех случаях, когда велико расстояние между граничными точками.
 закон полного тока,
закон полного тока,
магнитная цепь,
расчет магнитной цепи,
методы расчета магнитных цепей,
решение задач магнитные цепи
Содержание:
Магнитные цепи:
В конструкцию многих электротехнических устройств (электрических машин, трансформаторов, электрических аппаратов, измерительных приборов и т. д.) входят магнитные цепи.
Магнитной цепью называется часть электротехнического устройства, содержащая ферромагнитные тела, в которой при наличии намагничивающей силы возникает магнитный поток и вдоль которой замыкаются линии магнитной индукции. Источниками намагничивающей силы могут быть катушки с токами, постоянные магниты.
В конструктивном отношении магнитные цепи выполняют неразветвленными и разветвленными; применение того или иного вида цепи определяется в основном назначением электромагнитного устройства.
Расчет неразветвленной однородной магнитной цепи
В неразветвленной магнитной цепи (рис. 9.1, 9.2) магнитный поток во всех участках один и тот же.
При расчете и конструировании магнитной цепи электромагнитного устройства решаются вопросы, связанные с выбором размеров, формы, материалов. Эти вопросы изучают в специальных курсах.
Здесь рассмотрим расчет для существующей или сконструированной магнитной цепи, размеры и материалы которой, а также расположение обмоток с токами известны. При этом решают задачи двух типов.
Прямая задача:
По заданному магнитному потоку в цепи требуется определить намагничивающую силу, необходимую для создания этого потока.
Рассмотрим решение этой задачи для неразветвленной однородной магнитной цепи (см. рис. 9.1) без учета потоков рассеяния.
1. По заданному магнитному потоку и известной площади S поперечного сечения сердечника находят магнитную индукцию:
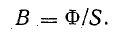
2. Определяют напряженность магнитного поля Н в сердечнике. Зависимость В(Н) — характеристика намагничивания — для стали нелинейная, а магнитная проницаемость 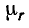
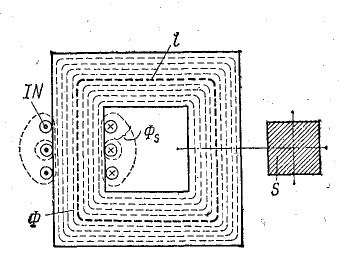
Рис. 9.1. Неразветвленная однородная магнитная цепь
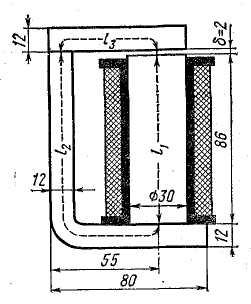
Рис. 9.2. Неразветвленная неоднородная магнитная цепь
Обычно напряженность магнитного поля определяют по кривой намагничивания данного сорта стали (см. рис. 8.30 и приложение 4).
3. Находят намагничивающую силу по закону полного тока [см. формулу (8.41)]:
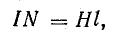
где l — длина магнитопровода, подсчитанная по средней линии без учета закруглений, причем условно принимается, что эта средняя линия во всех точках совпадает с линией магнитной индукции.
Обратная задача:
По заданной намагничивающей силе требуется найти магнитный поток в магнитопроводе.
1. Определяют напряженность магнитного поля в сердечнике:
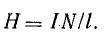
2. По кривой намагничивания данного сорта стали находят магнитную индукцию В.
3. Определяют магнитный поток:
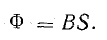
Для конкретных величин В и Н, определенных в ходе решения задачи, можно подсчитать статическую магнитную проницаемость данного сорта стали по формуле (8.37):
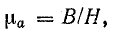
тогда магнитная индукция
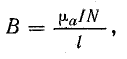
магнитный поток
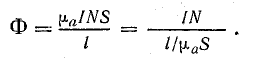
Обозначив знаменатель этого выражения через Rм:
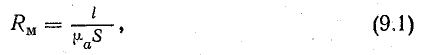
получим
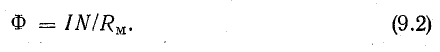
Магнитное сопротивление
Выражение (9.2) по форме напоминает закон Ома для электрической цепи: на месте тока стоит магнитный поток, на месте э. д. с. — намагничивающая сила (ее называют еще магнитодвижущей силой — м. д. с.). Величину Rм называют магнитным сопротивлением. Выражение магнитного сопротивления сердечника по форме аналогично выражению для определения сопротивления проводника электрическому току. Нужно отметить, что формулы для электрической и магнитной цепей похожи только написанием. Никакого физического подобия явлений в электрической и магнитной цепях не существует.
Расчет магнитных цепей обычно проводят без определения магнитного сопротивления. Это понятие используют в некоторых случаях при качественном рассмотрении явлений в магнитных цепях. Пользуясь им, найдем, как должна измениться намагничивающая сила катушки, если в стальном сердечнике (см. рис. 9.1) сделать хотя бы незначительный воздушный зазор, а магнитный поток при этом должен остаться таким же.
Предположим, что в стальном сердечнике длиной l = 100 мм имеется воздушный зазор δ = 1 мм.
Магнитное сопротивление сердечника
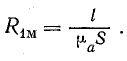
Магнитное сопротивление сердечника с воздушным зазором равно сумме сопротивлений двух участков.
Сопротивление стальной части магнитной цепи при той же магнитной индукции останется практически без изменения, так как уменьшение длины ее очень незначительно (≈ 1 %).
Сопротивление воздушного зазора
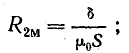
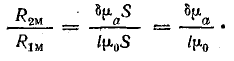
Предположим, что относительная магнитная проницаемость стали  = 1000, тогда
= 1000, тогда
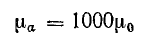
и
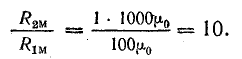
Магнитное сопротивление воздушного зазора оказывается в 10 раз больше сопротивления стального сердечника.
Отсюда следует, что для обеспечения того же магнитного потока при наличии воздушного зазора в 1 мм нужно иметь намагничивающую силу примерно в 10 раз большую, чем при его отсутствии. Эта разница оказывается во много раз большей для сердечников из специальных сплавов, для которых величина 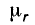 достигает сотен тысяч.
достигает сотен тысяч.
Поэтому во всех случаях, когда по условиям работы электромагнитного устройства без воздушного зазора обойтись нельзя, следует по возможности его сокращать.
Задача 9.1.
В сердечнике кольцевой формы из электротехнической стали нужно получить магнитный поток Ф = 2 • 10-3 Вб. Определить: 1) ток в обмотке, имеющей N = 100 витков; 2) магнитную проницаемость стали при заданном потоке в сердечнике; 3) индуктивность катушки.
Размеры сердечника заданы в миллиметрах на рис. 9.3.
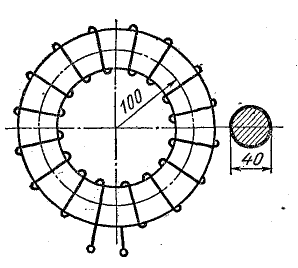
Рис. 9.3. К задаче 9.1
Решение. Площадь сечения сердечника
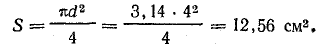
Считая магнитную индукцию по сечению сердечника постоянной, найдем ее величину по заданному потоку:
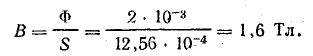
По кривой намагничивания (см.рис. 8.30) определим напряженность магнитного поля: H = 50 А/см = 5000 А/м.
Намагничивающая сила, необходимая для создания заданного потока,
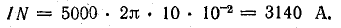
Ток в обмотке
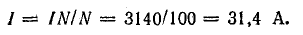
Магнитная проницаемость стали при найденных величинах В и H
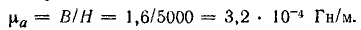
Относительная магнитная проницаемость
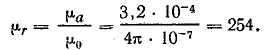
Индуктивность катушки
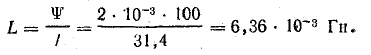
Задача 9.3.
Определить магнитный поток и магнитное сопротивление сердечника (рис. 9.4), размеры которого заданы в миллиметрах, если в катушке с числом витков N = 200 ток I = 6 А. Сердечник изготовлен из электротехнической стали 1511, причем 10% его сечения занимает изоляция между листами.
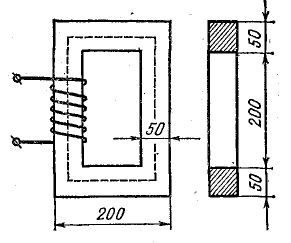
Рис. 9.4. К задаче 9.3
Решение. Намагничивающая сила и напряженность поля
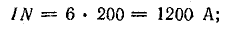
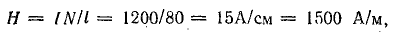
где I — длина замкнутого сердечника по средней линии; согласно размерам, указанным на чертеже, l = 80 см = 0,8 м.
Магнитная индукция по характеристике намагничивания электротехнической стали 1511 В = 1,42 Тл.
Полная площадь сечения сердечника
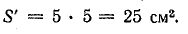
Активная площадь
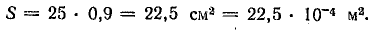
Магнитный поток
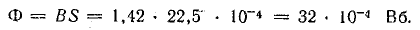
Магнитная проницаемость при заданной величине намагничивающей силы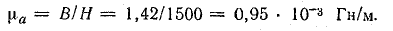
Магнитное сопротивление
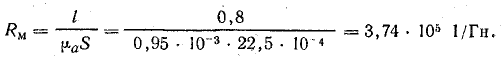
Расчет неразветвленной неоднородной магнитной цепи
Неоднородная магнитная цепь состоит из нескольких участков, отличающихся в общем случае длиной, поперечным сечением и материалом. Чаще всего встречаются магнитные цепи, у которых кроме участков из ферромагнитных материалов имеются воздушные зазоры.
Прямая задача:
При решении прямой задачи размеры и материалы каждого участка цепи известны, а магнитный поток задан; определяют намагничивающую силу. Порядок решения прямой задачи такой же, как и для однородной цепи, но магнитную индукцию и напряженность поля определяют для каждого участка; при этом потоки рассеяния в расчет не принимают.
Магнитная индукция k-го участка
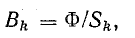
где Sk — площадь поперечного сечения k-го участка.
По магнитной индукции определяют напряженность поля: для участков из ферромагнитных материалов — по кривым намагничивания; для воздушных зазоров и других участков из неферромагнитных материалов — по формуле 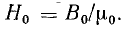
Далее составляют уравнение согласно закону полного тока:

где Нk — напряженность магнитного поля k-го участка (принимают ее одинаковой во всех точках этого участка); lk — длина k-то участка, взятая по средней линии; Нklk — магнитное напряжение к-то участка (далее магнитное напряжение будем обозначать Um); 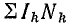 — алгебраическая сумма намагничивающих сил всех обмоток, входящих в рассматриваемую цепь.
— алгебраическая сумма намагничивающих сил всех обмоток, входящих в рассматриваемую цепь.
Намагничивающую силу считают положительной в левой части уравнения (9.3), если ее направление, определенное по правилу буравчика, совпадает с направлением обхода магнитного контура. Магнитное напряжение в правой части уравнения считают положительным, если направление магнитного потока совпадает с направлением обхода контура.
Для магнитной цепи (см. рис. 9.2) развернутое уравнение (9.3) имеет вид
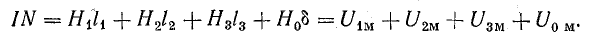
Обратная задача:
Обратную задачу — определение магнитного потока по заданным намагничивающим силам — нельзя решить так же просто, как для однородной цепи, так как нельзя сразу установить распределение магнитного напряжения между участками.
Нельзя воспользоваться формулой (9.2), так как магнитное сопротивление участка из ферромагнитного материала зависит от величины  , которая определяется не известной еще магнитной индукцией.
, которая определяется не известной еще магнитной индукцией.
Задачу можно решить методом последовательных приближений.
При наличии в цепи воздушного зазора первое значение магнитного потока можно взять, считая магнитное сопротивление воздушного зазора равным сопротивлению всей магнитной цепи.
Основанием для такого выбора является то, что даже малый воздушный зазор имеет магнитное сопротивление, значительно большее, чем вся остальная часть цепи, выполненная из ферромагнитных материалов.
Пренебрегая в первом приближении магнитным сопротивлением ферромагнитной части цепи, получим поток
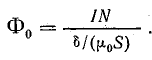
Определить магнитный поток можно, построив кривую намагничивания цепи в целом. Для этого нужно задаться произвольно несколькими величинами магнитного потока и определить соответствующие им величины намагничивающей силы.
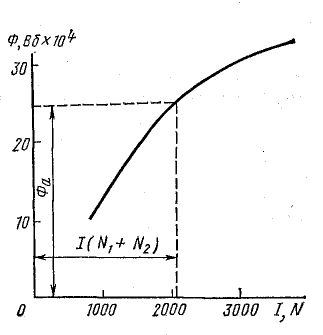
Рис. 9.5. Кривая намагничивания магнитной цепи
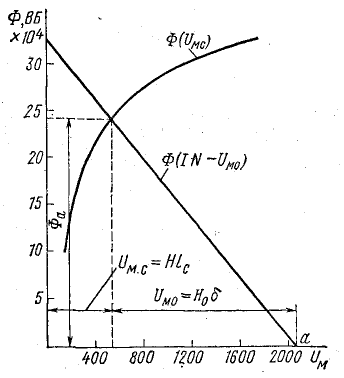
Рис. 9.6. К расчету неразветвленной неоднородной магнитной цепи (обратная задача)
По результатам расчета строится кривая намагничивания цепи (рис. 9.5). По кривой находят магнитный поток, соответствующий заданной намагничивающей силе.
Возможен и другой путь графо-аналитического решения обратной задачи (рис. 9.6). По взятым произвольно нескольким величинам магнитного потока находят величины 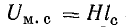 (для стальной части цепи) и
(для стальной части цепи) и 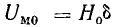 (для воздушного зазора). Затем из начала координат строят кривую
(для воздушного зазора). Затем из начала координат строят кривую 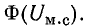
На оси абсцисс находят точку a, соответствующую заданной намагничивающей силе IN, из которой влево проводят прямую Ф(IN — Uм0).
В точке пересечения этих графиков по оси ординат находят искомый поток, а по оси абсцисс — величины Uм.с = Нlс и Uм0 = Н0δ.
Задача 9.5.
Магнитная цепь электромагнитного реле клапанного типа, изготовленная из стали, имеет поток Ф = 1,2 • 10-3 Вб. Определить число витков катушки реле, необходимое для возбуждения созданного магнитного потока при токе в катушке 0,2 А. Ярмо и якорь реле прямоугольного сечения 7,5 x 1,2 см, сердечник круглого сечения диаметром 3 см. Другие размеры показаны на рис. 9.2.
Решение. Магнитная цепь реле делится на однородные участки:
а) сердечник круглого сечения
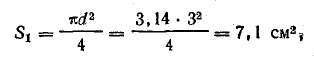
длина l1 = 8,6 см;
б) ярмо прямоугольного сечения
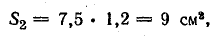
длина l2 = 14,9 см (см. рис. 9.2);
в) якорь прямоугольного сечения
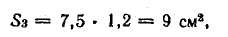
длина l3 = 6,1 см;
г) воздушный зазор, сечение которого принимаем равным сечению сердечника, пренебрегая некоторым увеличением его за счет выпучивания линий магнитной индукции:
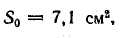
длина δ = 0,2 см.
Магнитная индукция в участках цепи:
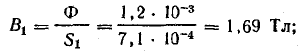
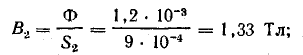
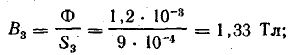
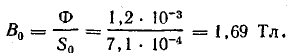
Напряженность магнитного поля в стальных участках определена по кривой намагничивания литой стали, которая принята такой же и для кованой стали: Н1 = 57 А/см; Н2 = 18 А/см; Нз = 18 А /см.
В воздушном зазоре
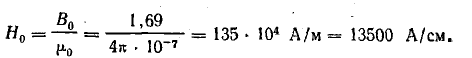
Составляем уравнение по закону полного тока:
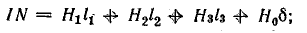
Число витков обмотки
Задача 9.7.
Две катушки N1 = 2000 и N2 = 600 витков насажены на стержни сердечника из электротехнической стали 1211. Размеры магнитной цепи показаны на рис. 9.7. Определить магнитный поток при токе в катушках I = 0,8 А и при соединении концов катушек по схеме: К1 соединен с К2 напряжение приложено к зажимам Н1 и Н2.
Решение. Магнитная цепь рис. 9.7 имеет шесть участков, размеры которых найдены из чертежа:
а) воздушный зазор — δ01 = 0,09 см, S01 = 5 • 4,5 = 22,5 см2;
б) стержень А — l1 = 20 см, S1 = 22,5 см2;
в) ярмо Б — l2 = 25 см, S2 = 22,5 см2;
г) стержень В — lз = 20 см, S3 = 22,5 см2;
д) воздушный зазор — δ02 = 0,09 см, S02 = 22,5 см2;
е) якорь Д — l0 = 25 см, S6 = 22,5 см2.
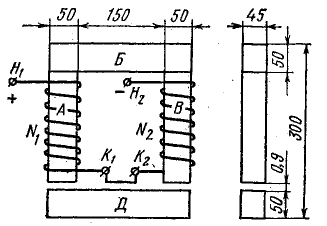
Рис. 9.7. К задаче 9.7
Задаемся несколькими величинами магнитного потока, причем наибольший возможный поток найдем в предположении, что магнитное сопротивление создают только воздушные зазоры [см. формулы (9.1), (9.2)]:
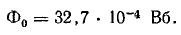
При определении потока учтено, что катушки включены согласно, поэтому их намагничивающие силы сложены.
Для полученного потока найдем намагничивающую силу с учетом стальной части магнитной цепи. Последовательность решения та же, что и при решении задачи 9.5. Результаты расчета для Ф0 и других величин потока сведены в табл. 9.1.
Таблица 9.1
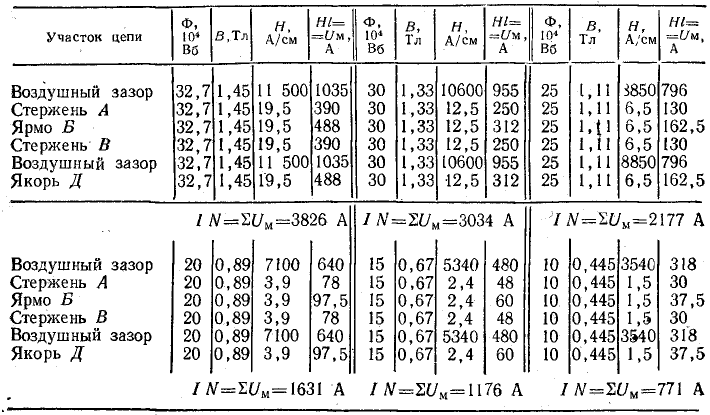
Зависимость Ф(IN) построена на рис. 9.5.
По этой кривой определяем искомый поток, соответствующий намагничивающей силе:
Для графо-аналитического способа определения потока по типу рис. 9.6 из табл. 9.1 выпишем величины Ф и Нlc в табл. 9.2.
Таблица 9.2

Зависимости Ф(Um.c) и Ф(IN — Um0) показаны на рис. 9.6, причем прямая Ф(IN — Um0) построена по двум точкам. При IN — Um0 = 0
при Ф = 0
В точке пересечения графиков определяем искомый магнитный поток, а также величины Hlc = Um.c и H0δ = Um0, соответствующие этому потоку:
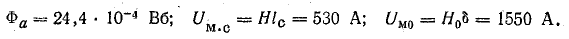
Расчет разветвленной магнитной цепи
В разветвленной магнитной цепи магнитные потоки в общем случае различны в разных ветвях (рис. 9.8).
Разветвленные магнитные цепи делятся на симметричные и несимметричные.
Рис. 9.8. Разветвленная симметричная магнитная цепь
Рис. 9.9. Магнитная цепь четырехполюсной электрической машины
Симметричную магнитную цепь мысленно можно разделить на неразветвленные цепи таким образом, что во всех участках выделенной цепи магнитный поток будет один и тот же. Кроме того, предполагается симметричное расположение намагничивающих сил (рис. 9.8, 9.9).
Если указанные условия симметрии не соблюдаются, то магнитная цепь относится к несимметричным (рис. 9.10).
Узловые и контурные уравнения магнитной цепи
Симметричная магнитная цепь (см. рис. 9.8) состоит из двух одинаковых контуров. Средний стержень вместе с катушкой (источником намагничивающей силы) входит в оба контура.
Место соединения среднего стержня с ярмом является узлом магнитной цепи, в котором магнитный поток Ф1, делится на два равных потока, если магнитное сопротивление обоих контуров одинаково:
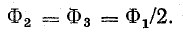
Расчет разветвленной симметричной цепи из-за равенств потоков симметричных контуров сводится к расчету одного контура, который выполняют в том же порядке, что и расчет неразветвленной цепи.
В аналогичной несимметричной магнитной цепи поток в узле делится на неравные части, но для любого узла пригодно уравнение
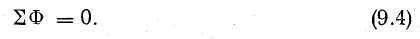
Для схемы рис. 9.8 это уравнение в развернутом виде записывают так:
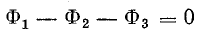 или
или 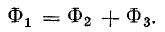
При составлении такого уравнения учитывают направления потоков: направленные к узлу и направленные от узла потоки берутся с разными знаками.
Для каждого контура магнитной цепи можно также составить уравнение по закону полного тока.
Предположим, что все участки магнитной цепи выполнены из материалов с постоянными значениями магнитной проницаемости. Каждый участок и вся цепь имеют линейную зависимость магнитного потока от магнитного напряжения Ф(Uм).
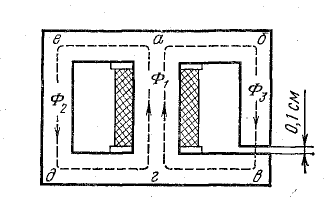
Рис. 9.10. Разветвленная несимметричная магнитная цепь
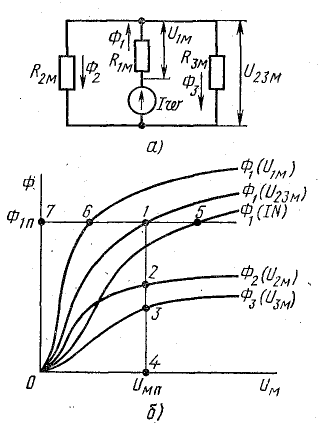
Рис. 9.11. К расчету разветвленной магнитной цепи графическим методом
Определив для каждого участка магнитное сопротивление Rм, магнитную цепь можно представить соответствующей схемой замещения, в которую войдут постоянные магнитные сопротивления участков и намагничивающие силы.
На рис. 9.11, а показана схема замещения магнитной цепи (см. рис. 9.8). Пренебрегая потоками рассеяния, расчет магнитной цепи можно выполнить аналогично расчету электрической цепи, решая систему линейных уравнений, составленных для узлов (см. формулу (9.4)] и контуров [см. формулу (9.3)].
Графический расчет разветвленной цепи
Элементы схем замещения магнитных цепей, осуществляемых на практике (кроме элементов, соответствующих воздушным зазорам), имеют нелинейные характеристики Ф(Uм), так как магнитная проницаемость ферромагнитных материалов зависит от напряженности поля. Нелинейными являются и магнитные цепи в целом.
Аналогия с электрической цепью указывает на возможность графического расчета нелинейной магнитной цепи в порядке. Первый этап расчета состоит в построении характеристик Ф(Uм) для каждого участка цепи в общей системе координат. Для этого используются характеристики намагничивания материалов, из которых изготовлена магнитная цепь. Например, чтобы построить характеристику Ф3(U3м), нужно ряд величин напряженности поля Н3, взятых из характеристики намагничивания материала третьего участка магнитной цепи, умножить на длину этого участка (H3l3 = U3м), а соответствующие им величины магнитной индукции умножить на площадь S3 этого участка (В3S3 = Ф3).
По полученным значениям U3м и Ф3 строят график Ф3(U3м) (рис. 9.11, б). Магнитные сопротивления R2м и R3м соединены параллельно. Поэтому магнитные напряжения второго и третьего участков одинаковы: U2м = U3м = U2.3м.
Сумма магнитных потоков этих участков равна магнитному потоку первого участка (сопротивление R1м): Ф1 = Ф2 + Ф3.
Складывая магнитные потоки Ф2 и Ф3 для ряда значений магнитного напряжения, получим кривую Ф1 (U2.3м).
На рис. 9.11, б это показано для одного значения Uм.п.Отрезки 4-3 и 4-2 в масштабе магнитных потоков выражают потоки Ф3 и Ф2. Сумма этих отрезков, равная отрезку 4-1, выражает магнитный поток Ф1П. Магнитное сопротивление R1м и сопротивление, эквивалентное R2м и R3м, соединены последовательно. Поэтому намагничивающая сила всей цепи IN равна сумме магнитных напряжений U1м и U2.3м: IN = U1м + U2.3м. Магнитные же потоки участков цепи с сопротивлениями R1м и R2.3м одинаковы.
Складывая магнитные напряжения U1м и U2.3м для ряда значений магнитного потока, получим кривую Ф1(IN). На рис. 9.11, б это показано для одного значения Ф1п. Отрезки 7-6 и 7-1 в масштабе магнитных напряжений выражают магнитные напряжения U1м и U2.3м. Сумма этих отрезков дает отрезок 7-5, выражающий намагничивающую силу IN.
Выполнив указанные построения, нетрудно решить различные задачи расчета магнитной цепи.
Задача 6.9.
Катушка, имеющая 500 витков, расположена на среднем стержне магнитопровода, изготовленного из стали 1511 (см. рис. 9.8). Определить ток в катушке, если в крайнем стержне поток Ф2 = Ф3 = 2 • 10-3Вб. Рассеяние потока не учитывается.
Решение. В данной симметричной цепи можно наметить два одинаковых в магнитном отношении контура: а-б-в-г-а и а-е-д-г-а. В каждом из них по два участка:
Рассматривая один из контуров, решим задачу в порядке, принятом для неразветвленной цепи:
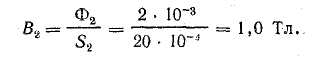
Магнитный поток в среднем стержне в два раза больше, чем в крайних:
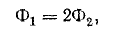
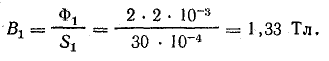
По кривым намагничивания стали 1511 находим:
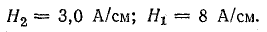
По закону полного тока,
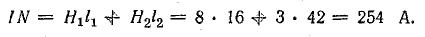
Ток в катушке
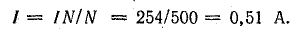
Задача 9.10.
В крайнем стержне магнитопровода, взятого по условию задачи 9.9, имеется воздушный зазор δ = 0,1 см. Определить, как нужно изменить ток в катушке, чтобы сохранить прежнюю величину потока в этом стержне (см. рис. 9.10).
Решение. При наличии воздушного зазора в одном крайнем стержне магнитная цепь становится несимметричной.
В контуре а-е-д-г-а сохранились те же участки; в контуре а-б-в-г-а: l1 = 16 см; l3 = 41,9 см; δ = 0,1 см; S1 = 30 см2;
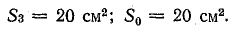
Магнитная индукция в воздушном зазоре и крайнем стержне 6-в
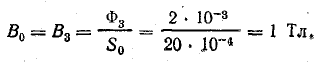
Напряженность поля
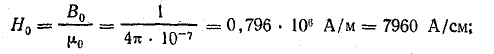
по кривой намагничивания стали 1511 Н3 = 3 А/см.
В магнитной цепи можно наметить третий контур (а-б-в-г-д-е-а). Для этого контура, по закону полного тока,
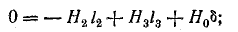
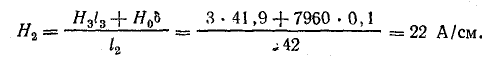
Магнитная индукция на участке l2 по кривой намагничивания В2 = 1,48 Тл. Магнитный поток на участке l2
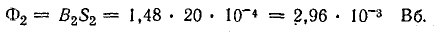
Магнитный поток в среднем стержне (участок l1) определим на основании первого закона Кирхгофа для узла а:
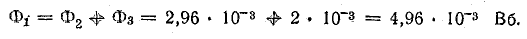
Магнитная индукция на этом участке
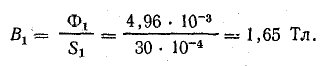
Напряженность поля Н1 = 69,5 А/см.
Для одного из контуров, включающего средний стержень, например а-б-в-г-а, по закону полного тока,
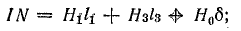
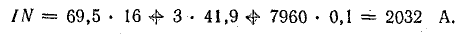
Ток в катушке
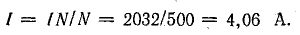
Вывод. Для того чтобы сохранить в крайнем стержне такой же магнитный поток при наличии воздушного зазора δ = 0,1 см, требуется увеличить ток в катушке почти в восемь раз по сравнению с тем случаем, когда зазор отсутствует.
Постоянные магниты
В измерительных приборах, электрической аппаратуре и других устройствах в качестве источников намагничивающей силы широко применяют постоянные магниты.
На рис. 9.12 схематично изображены магнитные системы магнито-электрического измерительного прибора (а) и поляризованного реле (б).
Эти системы, как и большинство им подобных, имеют несколько участков: 1) из магнитно-твердого материала— постоянного магнита 1; 2) из магнитно-мягкого материала 2, служащего магнитопроводом, и воздушного зазора 3, форма и размеры которого определяются конструкцией и назначением устройства.
При расчете магнитной цепи с постоянным магнитом требуется определить магнитный поток и индукцию в воздушном зазоре или по заданному потоку найти оптимальные размеры постоянного магнита (наименьшие объем и габариты).
Характеристики размагничивания постоянных магнитов
Величины остаточной магнитной индукции Вг и коэрцитивной силы Hс характеризуют материал постоянного магнита: чем они больше, тем выше его качество. Как известно, на петле гистерезиса Вг соответствует Н = 0, а при В = 0 Н = Нс.
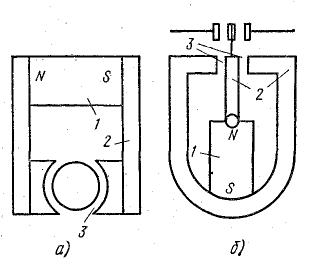
Рис. 9.12. Магнитные цепи с постоянными магнитами
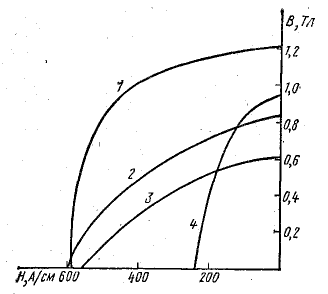
Рис. 9.13. Характеристики размагничивания постоянных магнитов:
1 — АНКО-4; 2 — АНКО-2; З-АН-2; 4 — сталь с 30% СО
Промежуточные магнитные состояния определяются частью петли магнитного гистерезиса, лежащей во второй четверти, — характеристикой размагничивания (рис. 9.12). Эта характеристика используется при расчете постоянных магнитов.
Согласно закону полного тока, сумма магнитных напряжений участков магнитной цепи (рис. 9.12) равна нулю, так как внешняя намагничивающая сила (ампер-витки) отсутствует:
где Uм.т — магнитное напряжение постоянного магнита;  — сумма магнитных напряжений всех участков магнитной цепи, включая воздушные зазоры, но без постоянного магнита.
— сумма магнитных напряжений всех участков магнитной цепи, включая воздушные зазоры, но без постоянного магнита.
Левая и правая части равенства (9.5) связаны с магнитной индукцией и потоком определенными зависимостями: Фт(Uм.т) — кривая размагничивания постоянного магнита (по форме повторяет кривую размагничивания материала, из которого выполнен постоянный магнит); Фм(Uм.с) — кривая намагничивания части конструкции устройства, изготовленной из магнитно-мягкого материала; Ф0(Uм0) — прямая, проходящая через начало координат и повторяющая в других масштабах зависимость 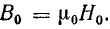
Определение магнитного потока в магнитной цепи с постоянным магнитом
Пренебрегая потоком рассеяния 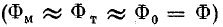 и магнитным напряжением в участках из магнитно-мягкого материала (
и магнитным напряжением в участках из магнитно-мягкого материала (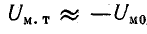 ), можно построить в общей системе координат зависимости
), можно построить в общей системе координат зависимости 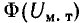 и
и 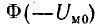 .
.
В этом случае искомый магнитный поток Ф0 определяется точкой их пересечения (рис. 9.14).
Магнитная индукция в воздушном зазоре
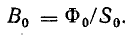
Из равенства (9.5) следует, что напряженности поля в воздушном зазоре и магните направлены в противоположные стороны.
При отсутствии воздушного зазора (постоянный магнит замкнут) остаточная индукция имеет величину Вг, а при наличии зазора будет меньше Вг (рис. 9.14). Воздушный зазор создает эффект размагничивания магнита.
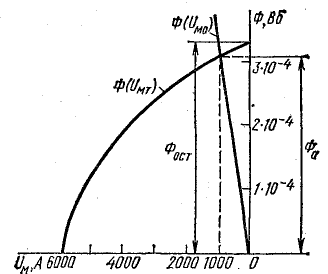
Рис. 9.14. К расчету магнитной цепи с постоянным магнитом
Задача 9.12.
Определить магнитный поток и индукцию в воздушном зазоре постоянного магнита (см. рис. 9.12, а), если магнит, изготовленный из сплава АНКО-2, имеет длину lт = 10 см; SТ = 4 см2. Полюса и цилиндрический сердечник изготовлены из магнитно-мягкой стали, имеют общую длину lм = 15 см; воздушный зазор между полюсом и сердечником δ = 0,2 см с каждой стороны и площадь S = 10 см2. Характеристика размагничивания сплава АНКО-2 представлена на рис. 9.13.
Решение. Построим зависимость магнитного потока в магните от магнитного напряжения Ф(Uм.т).
Для этого, согласно кривой 2 на рис. 9.13, берем величины В и Н, подсчитываем Ф и Uм.т и результаты подсчета сводим в табл. 9.3.
Для тех же величин магнитного потока определим Uм0 = Н0δ для воздушного зазора. Величинами Hсlс для участков из стали пренебрегаем из-за их незначительной величины.
Т а б л и ц а 9.3

Для потока Ф = 3,28 • 10-4 Вб
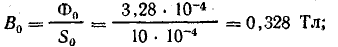
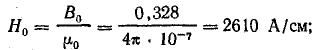
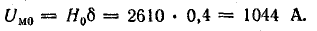
Результаты подсчетов сводим в табл. 9.4.
Таблица 9.4
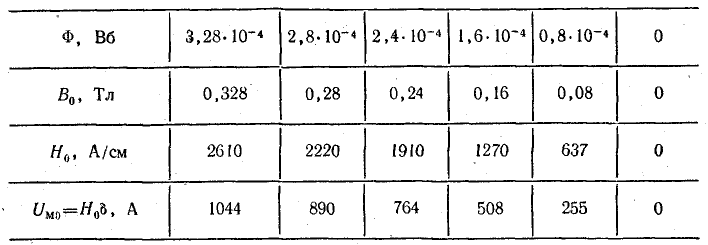
Зависимости Ф(Uм.т) и Ф(Uм0) построены на рис. 9.14. В точке пересечения этих графиков находим магнитный поток:
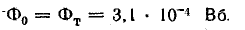
Магнитная индукция в воздушном зазоре
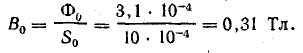
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
- Резонанс в электрических цепях
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Электрическое поле и его расчёт
Ток или поток? Магнитные цепи и их основные характеристики
Время на прочтение
6 мин
Количество просмотров 13K
Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это… а что это такое?
Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.
Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим.
Что нужно вспомнить?
Для более четкого представления сей статьи, неплохо бы вспомнить основные характеристики самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции – а также нужно вспомнить немного про магнитные вещества, а именно про ферромагнетики.

Полагается, что вам известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то крайне советую обратиться к сторонним ресурсам, чтобы иметь хотя бы общее представление о том, что последует далее. Крайне советую учебник И.Е. Иродова «Электромагнетизм».
Применение магнитных цепей
Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.

Конечно, можно продолжительное время говорить об устройствах, разных типах магнитопроводов (про которые речь пойдет далее), но наша первичная цель – рассмотреть выводы основных характеристик магнитных цепей. Продолжаем!
Как устроены магнитные цепи?
Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:

Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».
Начнем с тороидального сердечника. Такой тороидальный сердечник может служить формой для катушки, как бы странно это не звучало. Но что за катушка? Ну, первое что приходит в голову – провод, образующий витки. Хорошо, но какого его предназначение? Вернемся к электрическим цепям и вспомним, что существуют источники тока / напряжения, так называемые активные элементы. Так вот, в магнитных цепях роль источника выполняют катушки с током, накрученные на основной элемент магнитной цепи – ферромагнитный магнитопровод.
Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:

Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.
Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.
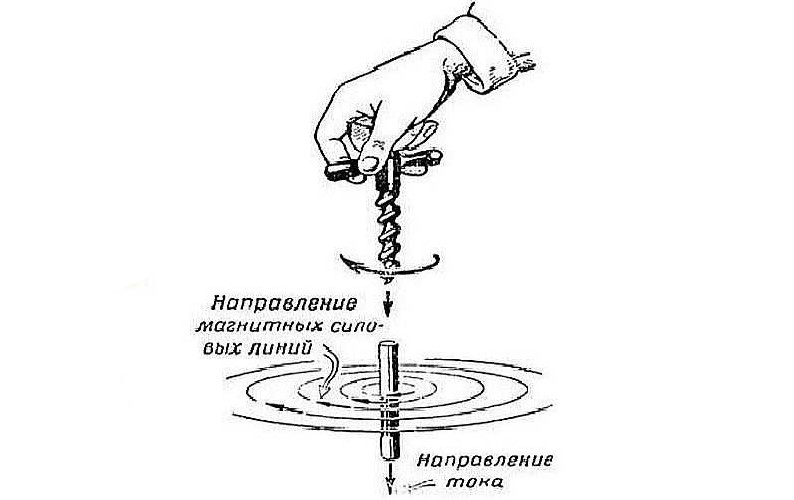
Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения.*

Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.
Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.
1] Магнитные потоки Ф1 и Ф2 через произвольные сечения будут равны между собой.
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю… Мне одному это что-то напоминает?
То есть мы окончательно сформулировали, что замкнутая (или почти замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае – магнитная.
Расчет магнитных цепей
Теперь внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи – силу тока. Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.

Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:
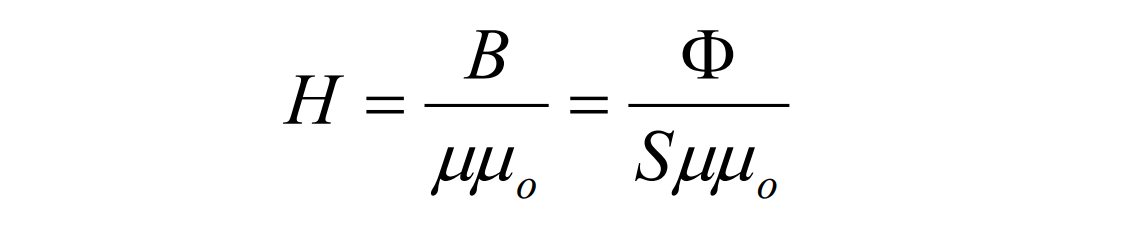
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.

Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.
Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:
В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.
Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.

Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:
-
Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;
-
Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;
-
После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;
-
Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).
Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.
А примеры расчетов будут?
Здесь – нет. А по ссылке – да! В данном документе Самарского государственного технического университета рассмотрены базовые примеры, которые позволят лучше разобраться в теме, если она вас заинтересовала. Помимо всего прочего, там же приведены теоретические справки. Советую прочитать в надежде, что вы сможете для себя что-то новое подчерпнуть.
Заключение
Во-первых, спасибо, что дочитали статью! Один из способов поддержать меня как автора – подписаться на мой паблик Вконтакте, где иногда выходят «локальные статьи».
Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны…
