Как найти величину меньшей дуги стягиваемой хордой

Как найти величину меньшей дуги стягиваемой хордой

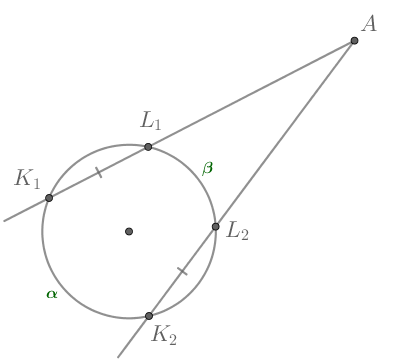
Угол между касательной и хордой

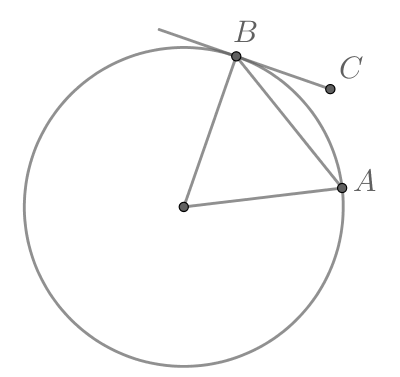
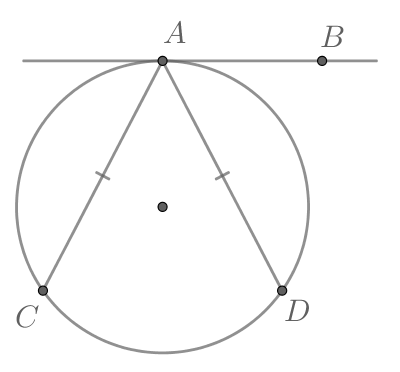
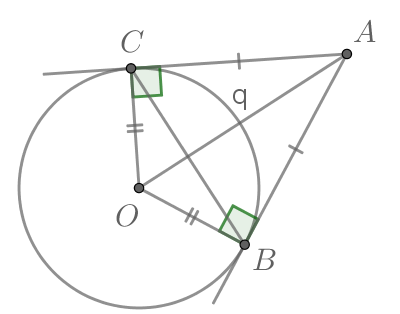
Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

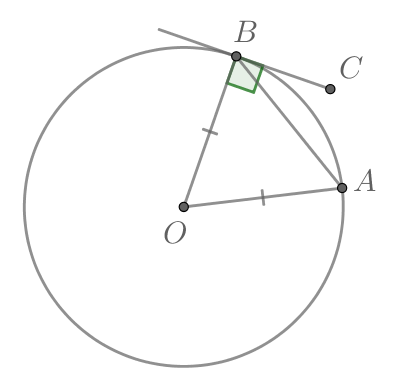
Касательная перпендикулярна радиусу, проведенному в точку касания.

Пусть angle MCA=varphi. Тогда angle OCA = 90 ^{circ}-varphi. Треугольник ОСА – равнобедренный, ОА = ОС (как радиусы окружности). Значит, angle AOC= 180 ^{circ}-2left ( 90 ^{circ} - varphi right )=2varphi, что и требовалось доказать.

Заметим, что angle ABC = varphi – как вписанный, опирающийся на ту же дугу.

Задача ЕГЭ по теме «Угол между касательной и хордой»

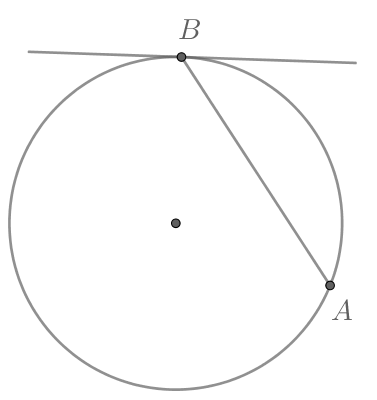
Угол между хордой AB и касательной BC к окружности равен 32 ^{circ}. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная ВС перпендикулярна радиусу ОВ, проведенному в точку касания. Значит, угол ОВС равен 90°, и тогда угол ОВА равен 90 ^{circ} - 32 ^{circ} = 58 ^{circ}. Угол ОАВ также равен 58°, так как треугольник ОАВ – равнобедренный, его стороны ОА и ОВ равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол АОВ, равен 180 ^{circ} - 58 ^{circ} cdot 2 = 64 ^{circ}.

Центральный угол равен угловой величине дуги, на которую он опирается, и тогда дуга АВ равна 64 ^{circ}.

Эту задачу можно решить быстрее, зная теорему об угле между касательной и хордой.
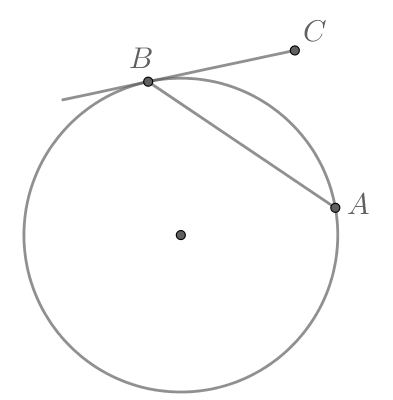
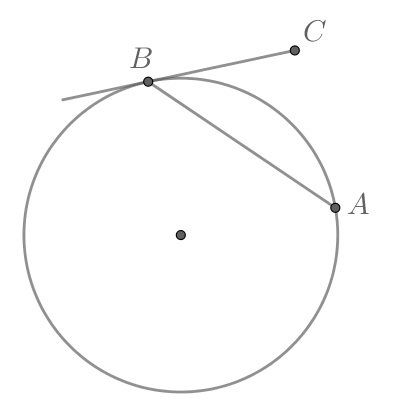
Угол между касательной и хордой, проведенной через точку касания, – это угол АВС. Он равен половине угловой величины дуги, заключенной между касательной ВС и хордой АВ, то есть дуги АВ. Значит, дуга АВ равна 64 ^{circ}.

Ответ: 64.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Угол между касательной и хордой» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник


СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика базового уровня

Математика базового уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Справочник

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

1 мая

Новый сервис: можно исправить ошибки!

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Задания

Версия для печати и копирования в MS Word

Задания Д15 № 52003

Угол между хордой AB и касательной BC к окружности равен 17 градусов. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Спрятать решение

Решение.

Угол между касательной и хордой равен половине дуги, заключённой между ними. Значит, искомая величина дуги равна 34°.

Ответ: 34.

Аналоги к заданию № 27878: 52003 51947 51949 … Все

Спрятать решение

·

Прототип задания

·

Помощь

О проекте · Редакция · Правовая информация · О рекламе

© Гущин Д. Д., 2011—2023

Источник

Дата: 2015-12-15

3339

Категория: Вписанный угол

Метка: ЕГЭ-№1ОкружностьУглы

27878. Угол между хордой AB и касательной BC к окружности равен 320. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

1

Градусная мера искомой дуги соответствует углу АОВ. Угол между радиусом окружности и касательной проходящей через общую точку равен 900, значит мы можем найти:

2

Треугольник ОВА равнобедренный, следовательно

3

Ответ: 64

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Ok

Источник

Тема 1.

Геометрия на плоскости (планиметрия)

1

.

14

Окружность: углы, образованные хордами, секущими, касательными

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами – ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

Решаем задачи

Показать ответ и решение

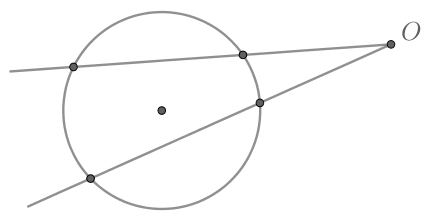
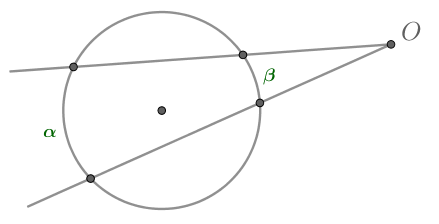
Так как угол между двумя секущими, проведенными из точки вне окружности, равен полуразности дуг, заключенных между ними,
то

∘ ∘ ∘ ∠ACB = 0,5(118 − 38 )= 40

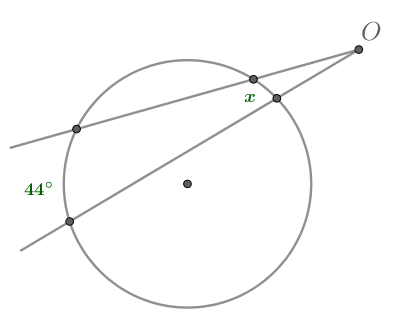
Показать ответ и решение

Найдем градусную меру меньшей дуги, стягиваемой хордой AB. Она равна центральному углу AOB, на нее опирающемуся. Так
как радиус, проведенный в точку касания, перпендикулярен касательной, то ∠OAC = 90∘. Следовательно, из треугольника
OAC :

∘ ∘ ∘ ∠AOC = 90 − 24 = 66

Тогда имеем:

∘ ∘ ∠AOD =180 − ∠AOC = 114

Дуга AD, заключенная внутри угла ACD, равна центральному углу AOD и равна 114∘.

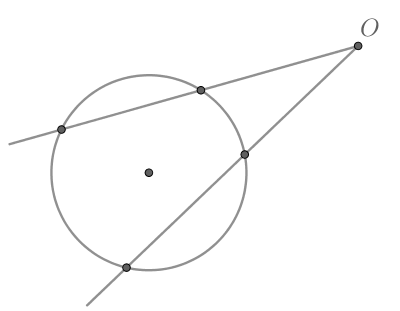
Показать ответ и решение

Так как угол между касательной и хордой, проведенными из одной точки окружности, равен половине дуги, заключенной между
ними, то

∘ ∘ ∠ABC = ∠BAC = 0,5⋅62 = 31

Следовательно, из △ABC имеем:

∘ ∘ ∘ ∠ACB = 180 − 2 ⋅31 = 118

Угол между хордой AB и касательной BC к окружности равен 32∘. Найдите величину меньшей дуги, стягиваемой хордой AB.
Ответ дайте в градусах.

PIC

Показать ответ и решение

1 способ.

Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между
ними, то меньшая дуга A⌣B равна 2⋅32∘ = 64∘.

2 способ.

PIC

Так как радиус, проведенный в точку касания, перпендикулярен касательной, то ∠OBC = 90∘. Следовательно,

∠OBA = 90∘ − 32∘ = 58∘

Так как OB = OA — радиусы, то треугольник OBA равнобедренный, следовательно,

∠AOB = 180∘− 2⋅58∘ = 64∘

Так как дуга равна центральному углу, опирающемуся на нее, то меньшая дуга ⌣ AB равна ∠AOB и равна
64∘.

Хорда AB стягивает дугу окружности в 92∘. Найдите угол ABC между этой хордой и касательной к окружности, проведенной
через точку B. Ответ дайте в градусах.

PIC

Показать ответ и решение

Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между
ними, то

∘ ∘ ∠ABC = 0,5⋅92 = 46

Касательные CA и CB к окружности образуют угол ACB, равный 112∘. Найдите величину меньшей дуги AB, стягиваемой
точками касания. Ответ дайте в градусах.

PIC

Показать ответ и решение

Рассмотрим картинку:

PIC

Т.к. дуги, стягиваемые равными хордами, равны, то ⌣ ⌣ AC= AD= x. Т.к. вся окружность равна 360∘ , то

∘ ∘ ∘ x+ x+ 110 = 360 ⇒ x = 125

Угол BAD, образованный касательной AB и хордой AD, равен половине дуги, заключенной между ними, то
есть

∠BAD = 0,5 A⌣D= 62,5∘

Показать ответ и решение

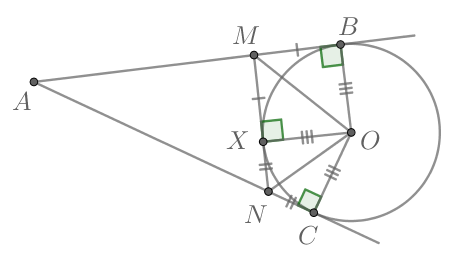
Рассмотрим картинку (пусть B, C — точки касания):

PIC

Т.к. отрезки касательных, проведенные из одной точки, равны, то MB = MX и NC = NX. Т.к. радиусы, проведенные в точку
касания, перпендикулярны касательной, то

∠OCN = ∠OXN = ∠OXM = ∠OBM = 90∘

Таким образом, по двум катетам равны треугольники: △OBM = △OXM и △OXN = △OCN.

Значит, ∠BOM = ∠XOM и ∠XON =∠CON. Следовательно, 1 ∠MON = 2∠BOC.

Т.к. в четырехугольнике сумма углов равна 360∘, то в четырехугольнике ABOC :

∘ ∘ ∘ ∘ ∠BOC =360 − 90 − 90 − ∠A =180 − ∠A.

Следовательно,

1 ∘ ∘ 1 ∘ 1 ∘ ∘ ∠MON = 2 (180 − ∠A )= 90 − 2∠A = 90 − 2 ⋅32 = 74

Показать ответ и решение

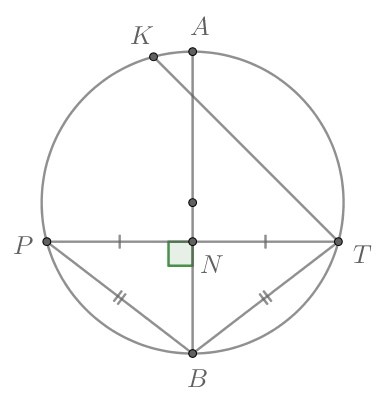
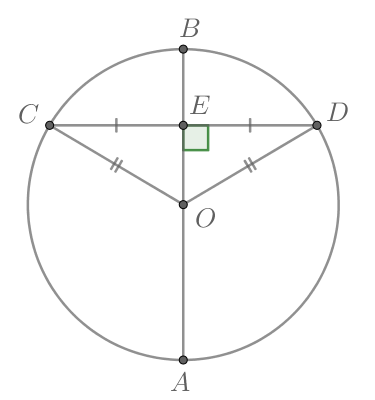
Рассмотрим картинку:

PIC

Т.к. диаметр, делящий хорду пополам, перпендикулярен ей, то AB ⊥ P T. Следовательно, △P NB =△T NB как
прямоугольные по двум катетам (PN = T N, NB — общий). Следовательно, P B = T B.

Т.к. равные хорды стягивают равные дуги, то

T⌣B= P⌣B= 75∘

Тогда угол между хордами AB и KT равен полусумме дуг, заключенных между ними, то есть

0,5(15∘+ 75∘) = 45∘

Т.к. нам необходимо найти угол между прямыми (а это обязательно острый угол), то в данном случае он равен углу между
данными хордами.

Угол между двумя секущими, проведенными к окружности из точки O вне окружности, равен 20∘. Найдите большую дугу,
заключенную между секущими, если сумма градусных мер обеих дуг, заключенных между секущими, равна 100∘. Ответ дайте в
градусах.

PIC

Показать ответ и решение

PIC

Так как угол, образованный двумя секущими, равен полуразности дуг, заключенных между ними, то

∘ ∠O = 0,5(α − β) = 20

С другой стороны, по условию задачи α + β = 100∘.

Решая систему из этих двух уравнений, находим α = 70∘.

Из точки O вне окружности проведены две прямые, пересекающие окружность. Большая дуга, образованная этими прямыми,
равна 44∘, а угол между прямыми равен 15∘. Найдите другую дугу, образованную этими прямыми. Ответ дайте в градусах.

PIC

Показать ответ и решение

Рассмотрим картинку:

PIC

Т.к. угол, образованный двумя такими прямыми-секущими, равен полуразности дуг, заключенных между ними,
то

∠O =15∘ = 1(44∘ − x) ⇒ x = 14∘ 2

Найдите угол между двумя секущими, проведенными к окружности из точки O вне окружности, если дуги, заключенные между
этими секущими, равны 103∘ и 47∘. Ответ дайте в градусах.

PIC

Показать ответ и решение

Т.к. угол, образованный двумя такими секущими, равен полуразности дуг, заключенных между ними, то

1 ∠O = 2 (103∘− 47∘)= 28∘

Показать ответ и решение

Рассмотрим картинку:

PIC

Т.к. BC ∥AD, то

∠CBT = ∠DAT = 30∘

∠DCK, как вписанный и опирающийся на дугу KD, равен ее половине, то есть 20∘. ∠CKD опирается на диаметр CD,
следовательно, равен половине от половины окружности, то есть ∘ 90. Значит,

∠CDK = 180∘− 90∘ − 20∘ = 70∘

∠BT D — внешний угол для треугольника ATD, следовательно, он равен сумме двух углов треугольника, не смежных с
ним:

∠BT D = ∠TDA + ∠T AD = 30∘+ 70∘ =100∘

Показать ответ и решение

Отрезки касательных, проведённых из одной точки, равны: AB = AC. Покажем это: Построим радиусы OB и OC и соединим
OA.

PIC

Так как радиус, проведённый в точку касания, перпендикулярен касательной, то ∠ACO =90∘ =∠ABO. OC = OB, как
радиусы, тогда в прямоугольных треугольниках AOC и AOB катеты OC и OB равны, а гипотенуза AO — общая,
следовательно, треугольники AOC и AOB равны по катету и гипотенузе, откуда получаем AB = AC.

Таким образом, треугольник ABC — равнобедренный и

∠ACB = ∠ABC = 0,5(180∘− ∠CAB )= 61∘

Показать ответ и решение

Хорда, делящаяся диаметром пополам, перпендикулярна ему. Покажем это . Построим радиусы OC и OD.

PIC

Треугольники COE и DOE равны по трём сторонам, тогда ∠CEO = ∠DEO, но ∠CEO + ∠DEO = 180∘, откуда
∠CEO = 90∘.

∠CEB = 180∘ − ∠CEO = 90∘

Прямая b касается окружности в точке B и образует с хордой AB угол, равный 55∘. Найдите градусную меру дуги AB,
которая меньше полуокружности. Ответ дайте в градусах.

PIC

Показать ответ и решение

Угол между касательной и хордой равен половине градусной меры дуги окружности, заключённой внутри него, следовательно
градусная мера искомой дуги равна 2⋅55∘ = 110∘.

Показать ответ и решение

PIC

Так как угол между двумя секущими, проведенными из одной точки вне окружности, равен полуразности дуг, заключенных между
ними, то

⌣ ⌣ ∘ ∠ACB = 0,5(AKB − DNE )= 42

Так как ⌣ ∘ AKB= 124, то

⌣ DNE= 124∘− 2⋅42∘ = 40∘

Тогда ∠DAE, как вписанный и опирающийся на дугу ⌣ DNE, равен ее половине, то есть ∘ 20.

Показать ответ и решение

Рассмотрим картинку:

PIC

Т.к. угол, образованный двумя такими секущими, равен полуразности дуг, заключенных между ними, то

∠A = 0,5 (α − β )= 11∘ (1)

Т.к. равные хорды стягивают равные дуги, то (меньшая полуокружности) дуга ⌣ K2L2= 95∘. Вся окружность равна 360∘,
следовательно,

α + β+ 2⋅95∘ = 360∘ ⇒ α+ β = 170∘ (2)

Решая систему из уравнений (1) и (2), получим, что β = 74∘.

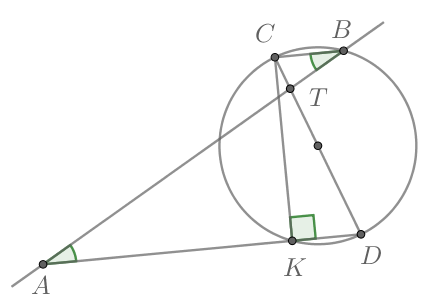
Показать ответ и решение

Треугольник ABC — прямоугольный, причем, т.к. CB = √3-⋅AB, то

√- tg∠BAC = CB-= 3 ⇒ ∠BAC = 60∘ AB

Т.к. угол между касательной AB и хордой AC равен половине дуги ⌣ AC, заключенной между ними, то ⌣ AC= 120∘. Тогда
центральный угол

⌣ ∘ ∠AOC =AC= 120

Источник

Угол между хордой AB и касательной BC равен 32 градуса.

Найдите величину меньшей дуги, стягиваемой хордой AB.

На этой странице сайта вы найдете ответы на вопрос Угол между хордой AB и касательной BC равен 32 градуса?,
относящийся к категории Геометрия. Сложность вопроса соответствует базовым
знаниям учеников 10 – 11 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.

Источник

Добавить комментарий