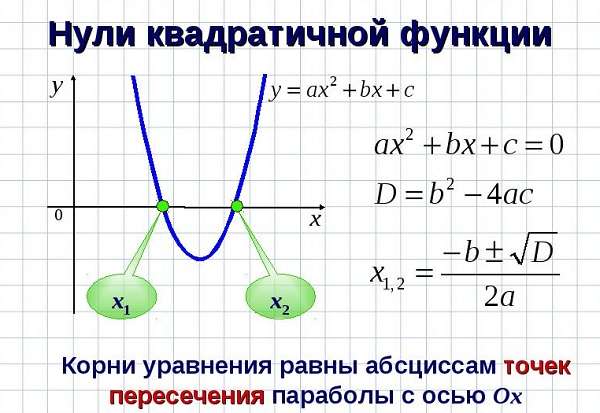
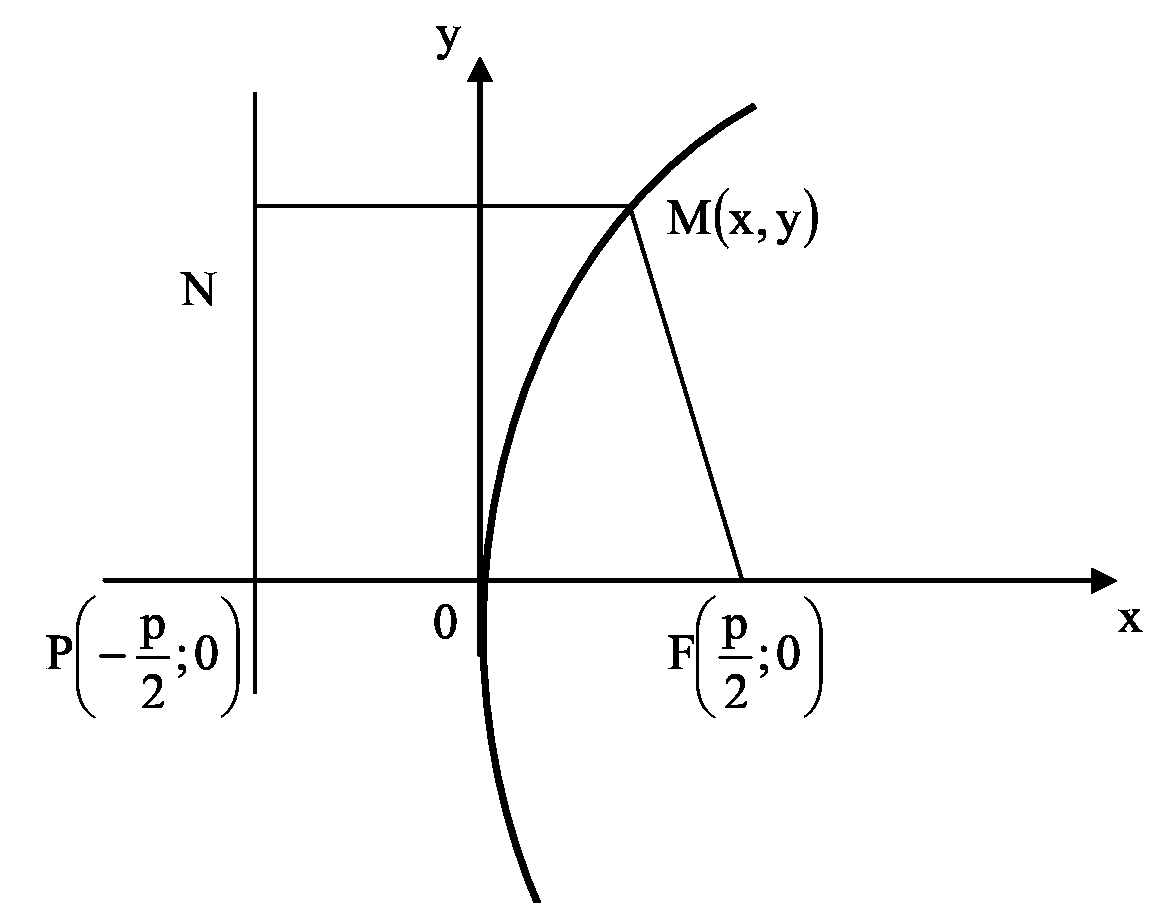оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
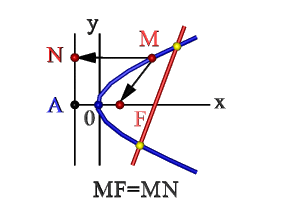
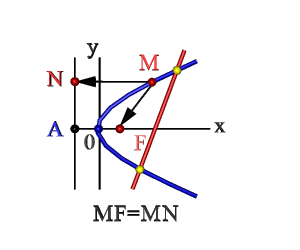
Парабола — это кривая, образованная геометрическим множеством точек, равноудалённых от точки $F$, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.
Рисунок 1. Парабола в прямоугольной системе координат
Парабола наряду с окружностью, эллипсом и гиперболой является одним из сечений конуса.
Парабола симметрична относительно своей оси, и поэтому можно построить сначала одну половину параболы, а затем, отложив симметричные этой половине точки, уже другую.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Определение 2
Классическая парабола описывается уравнением, оно имеет следующий вид:
$y^2 = 2px$, где число $p$ должно быть больше нуля.
Это уравнение является каноническим уравнением параболы и описывает вид параболы в прямоугольной системе координат.
Чаще всего приходится иметь дело с уравнениями параболы с вершиной, располагающейся не на пересечении осей координат, их общий вид представлен формулой:
$y = ax^2 + bx + c$.
Кто придумал параболу
Парабола известна математикам уже очень давно, а название этой функции дал древнегреческий математик Аполлоний Пергский в III в. до н.э., изучавший свойства сечений конуса.
Также изучением параболы занимались Архимед и Папп Александрийский.
В дальнейшем разные учёные показали, что многие явления можно описать параболой, так, например, была открыта траектория движения снаряда.
Основные определения и строение параболы
Вершина параболы — это точка, находящаяся на минимальном расстоянии от директрисы параболы $d$.
«Парабола» 👇
Фокус $F$ параболы — это точка, через которую проходит ось симметрии параболы, перпендикулярная прямой, находящаяся на расстоянии $d$. Фокус расположен на расстоянии $frac{p}{2}$ от вершины.
Координаты фокуса классической параболы можно определить из её уравнения.
Фокус и вершина являются основными точками, характеризующими параболу.
Параметр $p$ параболы иначе называется фокальным параметром и является расстоянием между фокусом и директрисой.
Чтобы найти фокальный параметр параболы, нужно выразить $p$ из формулы канонического уравнения параболы:
$p = frac{y^2}{2x}$, где $x$ и $y$ — координаты точки, лежащей на параболе.
Координаты фокуса параболы определяются через значение фокального параметра и равны ($frac{p}{2};0)$.
Анализ уравнения и описание параболы
-
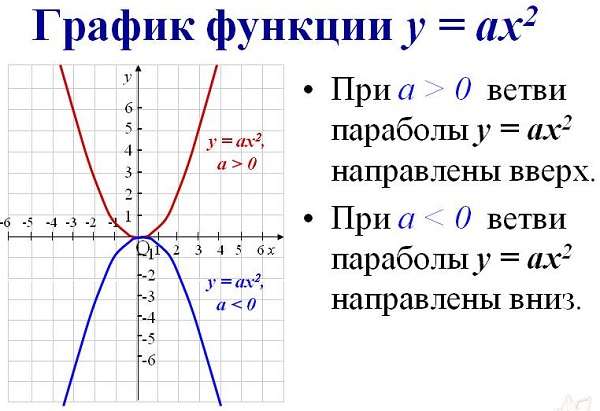
Сначала необходимо обратить внимание на коэффициент $a$ при $x^2$. Если он отрицательный, то парабола перевёрнутая по отношению к обычной и её ветви смотрят вниз, а если положительный – то её ветви смотрят вверх.
Также модуль коэффициента $a$ влияет на степень пологости (ширину) параболы, чем меньше модуль $a$, тем парабола более широкая (пологая), и чем больше модуль $a$, тем она более узкая (крутая). -
Далее необходимо посмотреть на коэффициент $c$. Коэффициент $c$ обозначает смещение по оси $OY$ относительно пересечения осей координат.
Это легко проверить, если приравнять $x$ к нулю в имеющемся уравнении.
Если коэффициент $c$ – положительный, то парабола смещена вверх относительно точки $(0;0)$, а если отрицательный – то вниз.
В случае если $c=0$ — парабола проходит через точку начала координат. -
Теперь можно найти вершину параболы, её координаты вычисляются по формуле:
-
$x = – frac{b}{2a}$ (1).
Чтобы найти $y$, нужно подставить полученный по формуле $x$ в уравнение.
Пример 1
Рассмотрим уравнение параболы $y = x^2 + 2x + 3$
Рисунок 2. Анализ уравнения параболы, график и примеры решения
- Коэффициент при $a$ положительный, значит, ветви параболы смотрят вверх.
- Теперь смотрим на коэффициент $c$, он равен 3, значит, парабола пересекается с осью ординат в точке $(0; 3)$.
- Найдём координату $x$ вершины параболы по формуле (1), она равна $x = – frac{2}{2} = -1$. Теперь найдём значение $y$, подставив значение $x$ в уравнение:
$y = 1^2 +(-1) cdot 2 + 3 = 2$. Координаты вершины равны $(-1; 2)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
- Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
- Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.
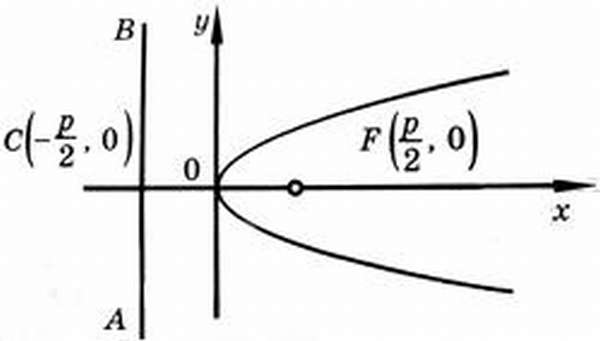
Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
y2 = 2 * p * x,
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.
Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
- x0 = -b / (2 * a),
- y0 = y (x0).
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Для такой линии:
- х = -16 / (2 * 4) = -2,
- y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.
Получаем координаты вершины (-2, -41).
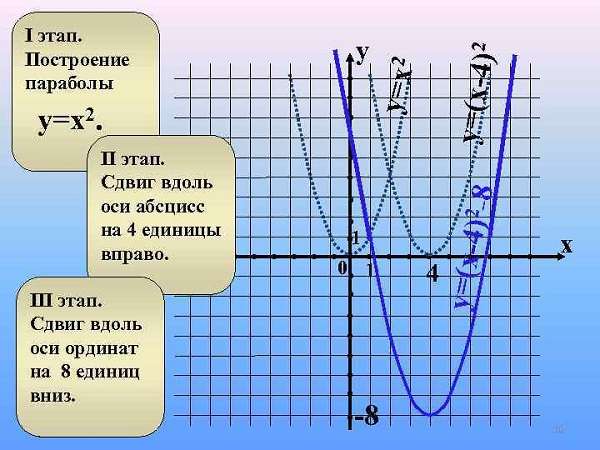
Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Имеем: b = 2, c = 3.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
- Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
- Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
D = (b2 4 * a * c).
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
- D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
- D = 0, то х1, 2 = -b / (2 * a),
- D ˂ 0, то нет точек пересечения с вектором ОХ.
Получаем алгоритм построения параболы:
- определить направление ветвей,
- найти координаты вершины,
- найти пересечение с осью ординат,
- найти пересечение с осью абсцисс.
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
- а = 1, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
- с осью ординат пересекается в значении у = 4,
- найдем дискриминант: D = 25 — 16 = 9,
- ищем корни:
- Х1 = (5 + 3) / 2 = 4, (4, 0),
- Х2 = (5 — 3) / 2 = 1, (1, 0).
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
- а = 3, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
- с осью у будет пересекаться в значении у = -1,
- найдем дискриминант: D = 4 + 12 = 16. Значит корни:
- Х1 = (2 + 4) / 6 = 1, (1,0),
- Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).
По полученным точкам можно построить параболу.
Директриса, эксцентриситет, фокус параболы
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.
Эксцентриситет (константа) = 1.
Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.
Парабола: определение, свойства, построение
Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки и заданной прямой
, не проходящей через заданную точку. Это геометрическое определение выражает директориальное свойство параболы.
Директориальное свойство параболы
Точка называется фокусом параболы, прямая
— директрисой параболы, середина
перпендикуляра, опущенного из фокуса на директрису, — вершиной параболы, расстояние
от фокуса до директрисы — параметром параболы, а расстояние
от вершины параболы до её фокуса — фокусным расстоянием (рис.3.45,а). Прямая, перпендикулярная директрисе и проходящая через фокус, называется осью параболы (фокальной осью параболы). Отрезок
, соединяющий произвольную точку
параболы с её фокусом, называется фокальным радиусом точки
. Отрезок, соединяющий две точки параболы, называется хордой параболы.
Для произвольной точки параболы отношение расстояния до фокуса к расстоянию до директрисы равно единице. Сравнивая директориальные свойства эллипса, гиперболы и параболы, заключаем, что эксцентриситет параболы по определению равен единице .
Геометрическое определение параболы, выражающее её директориальное свойство, эквивалентно её аналитическому определению — линии, задаваемой каноническим уравнением параболы:
(3.51)
Действительно, введем прямоугольную систему координат (рис.3.45,б). Вершину параболы примем за начало системы координат; прямую, проходящую через фокус перпендикулярно директрисе, примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через вершину параболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение параболы, используя её геометрическое определение, выражающее директориальное свойство параболы. В выбранной системе координат определяем координаты фокуса и уравнение директрисы
. Для произвольной точки
, принадлежащей параболе, имеем:
где — ортогональная проекция точки
на директрису. Записываем это уравнение в координатной форме:
Возводим обе части уравнения в квадрат: . Приводя подобные члены, получаем каноническое уравнение параболы
т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.51), и только они, принадлежат геометрическому месту точек, называемому параболой. Таким образом, аналитическое определение параболы эквивалентно его геометрическому определению, выражающему директориальное свойство параболы.
Уравнение параболы в полярной системе координат
Уравнение параболы в полярной системе координат (рис.3.45,в) имеет вид
где
— параметр параболы, а
— её эксцентриситет.
В самом деле, в качестве полюса полярной системы координат выберем фокус параболы, а в качестве полярной оси — луч с началом в точке
, перпендикулярный директрисе и не пересекающий её (рис.3.45,в). Тогда для произвольной точки
, принадлежащей параболе, согласно геометрическому определению (директориальному свойству) параболы, имеем
. Поскольку
, получаем уравнение параболы в координатной форме:
что и требовалось доказать. Заметим, что в полярных координатах уравнения эллипса, гиперболы и параболы совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для эллипса,
для параболы,
для гиперболы).
Геометрический смысл параметра в уравнении параболы
Поясним геометрический смысл параметра в каноническом уравнении параболы. Подставляя в уравнение (3.51)
, получаем
, т.е.
. Следовательно, параметр
— это половина длины хорды параболы, проходящей через её фокус перпендикулярно оси параболы.
Фокальным параметром параболы, так же как для эллипса и для гиперболы, называется половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси (см. рис.3.45,в). Из уравнения параболы в полярных координатах при получаем
, т.е. параметр параболы совпадает с её фокальным параметром.
Замечания 3.11.
1. Параметр параболы характеризует её форму. Чем больше
, тем шире ветви параболы, чем ближе
к нулю, тем ветви параболы уже (рис.3.46).
2. Уравнение (при
) определяет параболу, которая расположена слева от оси ординат (рис. 3.47,a). Это уравнение сводится к каноническому при помощи изменения направления оси абсцисс (3.37). На рис. 3.47,a изображены заданная система координат
и каноническая
.
3. Уравнение определяет параболу с вершиной
, ось которой параллельна оси абсцисс (рис.3.47,6). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).
Уравнение , также определяет параболу с вершиной
, ось которой параллельна оси ординат (рис.3.47,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36) и переименования координатных осей (3.38). На рис. 3.47,б,в изображены заданные системы координат
и канонические системы координат
.
4. График квадратного трехчлена является параболой с вершиной в точке
, ось которой параллельна оси ординат, ветви параболы направлены вверх (при
) или вниз (при
). Действительно, выделяя полный квадрат, получаем уравнение
которое приводится к каноническому виду , где
, при помощи замены
и
.
Знак выбирается совпадающим со знаком старшего коэффициента . Эта замена соответствует композиции: параллельного переноса (3.36) с
и
, переименования координатных осей (3.38), а в случае
еще и изменения направления координатной оси (3.37). На рис.3.48,а,б изображены заданные системы координат
и канонические системы координат
для случаев
и
соответственно.
5. Ось абсцисс канонической системы координат является осью симметрии параболы, поскольку замена переменной на
не изменяет уравнения (3.51). Другими словами, координаты точки
, принадлежащей параболе, и координаты точки
, симметричной точке
относительно оси абсцисс, удовлетворяют уравнению (3.S1). Оси канонической системы координат называются главными осями параболы.
Пример 3.22. Изобразить параболу в канонической системе координат
. Найти фокальный параметр, координаты фокуса и уравнение директрисы.
Решение. Строим параболу, учитывая её симметрию относительно оси абсцисс (рис.3.49). При необходимости определяем координаты некоторых точек параболы. Например, подставляя в уравнение параболы, получаем
. Следовательно, точки с координатами
принадлежат параболе.
Сравнивая заданное уравнение с каноническим (3.S1), определяем фокальный параметр: . Координаты фокуса
, т.е.
. Составляем уравнение директрисы
, т.е.
.
Общие свойства эллипса, гиперболы, параболы
1. Директориальное свойство может быть использовано как единое определение эллипса, гиперболы, параболы (см. рис.3.50): геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
, называется:
а) эллипсом, если ;
б) гиперболой, если ;
в) параболой, если .
2. Эллипс, гипербола, парабола получаются в сечениях кругового конуса плоскостями и поэтому называются коническими сечениями. Это свойство также может служить геометрическим определением эллипса, гиперболы, параболы.
3. К числу общих свойств эллипса, гиперболы и параболы можно отнести биссекториальное свойство их касательных. Под касательной к линии в некоторой её точке понимается предельное положение секущей
, когда точка
, оставаясь на рассматриваемой линии, стремится к точке
. Прямая, перпендикулярная касательной к линии и проходящая через точку касания, называется нормалью к этой линии.
Биссекториальное свойство касательных (и нормалей) к эллипсу, гиперболе и параболе формулируется следующим образом: касательная (нормаль) к эллипсу или к гиперболе образует равные углы с фокальными радиусами точки касания (рис.3.51,а,б); касательная (нормаль) к параболе образует равные углы с фокальным радиусом точки касания и перпендикуляром, опущенным из нее на директрису (рис.3.51,в). Другими словами, касательная к эллипсу в точке является биссектрисой внешнего угла треугольника
(а нормаль — биссектрисой внутреннего угла
треугольника); касательная к гиперболе является биссектрисой внутреннего угла треугольника
(а нормаль — биссектрисой внешнего угла); касательная к параболе является биссектрисой внутреннего угла треугольника
(а нормаль — биссектрисой внешнего угла). Биссекториальное свойство касательной к параболе можно сформулировать так же, как для эллипса и гиперболы, если считать, что у параболы имеется второй фокус в бесконечно удаленной точке.
4. Из биссекториальных свойств следуют оптические свойства эллипса, гиперболы и параболы, поясняющие физический смысл термина “фокус”. Представим себе поверхности, образованные вращением эллипса, гиперболы или параболы вокруг фокальной оси. Если на эти поверхности нанести отражающее покрытие, то получаются эллиптическое, гиперболическое и параболическое зеркала. Согласно закону оптики, угол падения луча света на зеркало равен углу отражения, т.е. падающий и отраженный лучи образуют равные углы с нормалью к поверхности, причем оба луча и ось вращения находятся в одной плоскости. Отсюда получаем следующие свойства:
– если источник света находится в одном из фокусов эллиптического зеркала, то лучи света, отразившись от зеркала, собираются в другом фокусе (рис.3.52,а);
– если источник света находится в одном из фокусов гиперболического зеркала, то лучи света, отразившись от зеркала, расходятся так, как если бы они исходили из другого фокуса (рис.3.52,б);
– если источник света находится в фокусе параболического зеркала, то лучи света, отразившись от зеркала, идут параллельно фокальной оси (рис.3.52,в).
5. Диаметральное свойство эллипса, гиперболы и параболы можно сформулировать следующим образом:
– середины параллельных хорд эллипса (гиперболы) лежат на одной прямой, проходящей через центр эллипса (гиперболы);
– середины параллельных хорд параболы лежат на прямой, коллинеарной оси симметрии параболы.
Геометрическое место середин всех параллельных хорд эллипса (гиперболы, параболы) называют диаметром эллипса (гиперболы, параболы), сопряженным к этим хордам.
Это определение диаметра в узком смысле (см. пример 2.8). Ранее было дано определение диаметра в широком смысле, где диаметром эллипса, гиперболы, параболы, а также других линий второго порядка называется прямая, содержащая середины всех параллельных хорд. В узком смысле диаметром эллипса является любая хорда, проходящая через его центр (рис.3.53,а); диаметром гиперболы является любая прямая, проходящая через центр гиперболы (за исключением асимптот), либо часть такой прямой (рис.3.53,6); диаметром параболы является любой луч, исходящий из некоторой точки параболы и коллинеарный оси симметрии (рис.3.53,в).
Два диаметра, каждый их которых делит пополам все хорды, параллельные другому диаметру, называются сопряженными. На рис.3.53 полужирными линиями изображены сопряженные диаметры эллипса, гиперболы, параболы.
Касательную к эллипсу (гиперболе, параболе) в точке можно определить как предельное положение параллельных секущих
, когда точки
и
, оставаясь на рассматриваемой линии, стремятся к точке
. Из этого определения следует, что касательная, параллельная хордам, проходит через конец диаметра, сопряженного к этим хордам.
6. Эллипс, гипербола и парабола имеют, кроме приведенных выше, многочисленные геометрические свойства и физические приложения. Например, рис.3.50 может служить иллюстрацией траекторий движения космических объектов, находящихся в окрестности центра притяжения.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
-
Парабола
Параболой
называется множество всех точек на
плоскости, каждая из которых одинаково
удалена от заданной точки этой же
плоскости, называемой фокусом, и от
заданной прямой, называемой директрисой.
Число
p>0
называется параметром
параболы и
равно расстоянию от фокуса F
до директрисы l.
Если
фокус параболы
находится в точке
,
а директриса
N
имеет уравнение
,
то такая парабола имеет каноническое
уравнение:
,
(18)
Точка
называется вершиной параболы.
Ось
–
ось симметрии параболы.
Расстояние
от точки
параболы до фокуса F
(фокальный
радиус)
вычисляется по формуле
.
(19)
Рис.6
Парабола,
симметричная относительно оси
,
с вершиной в начале координат, имеет
уравнение
,
(20)
Фокус
параболы находится в точке
.
Уравнение
директрисы этой параболы
.
(21)
Фокальный
радиус точки
параболы
.
(22)
Графики
парабол
и
строятся в полуплоскостях, соответствующих
отрицательным значениям переменных
и
.
Пример
4.1.
Найти
уравнение параболы, симметричной
относительно оси
,
фокус которой
находится в точке пересечения прямой
с осью
Решение.
Найдем
точку пересечения прямой
с осью
.
Т.к.
расстояние от фокуса параболы до начала
координат равно
,
то
Используя
формулу (18), запишем уравнение параболы:
.
Задачи для
самостоятельного решения:
-
Составить
уравнение параболы, вершина которой
находится в начале координат, зная,
что:-
парабола
расположена в правой полуплоскости
симметрично относительно осии ее параметр
; -
парабола
расположена в левой полуплоскости
симметрично относительно осии ее параметр
; -
парабола
расположена в верхней полуплоскости
симметрично относительно осии ее параметр
; -
парабола
расположена в нижней полуплоскости
симметрично относительно осии ее параметр
.
-
-
Определить
величину параметра и расположение
относительно координатных осей
следующих парабол: 1)
;
2)
;
3)
;
4)
. -
Составить
уравнение параболы, вершина которой
находится в начале координат, зная,
что:-
парабола
расположена симметрично относительно
осии проходит через точку
; -
парабола
расположена симметрично относительно
осии проходит через точку
; -
парабола
расположена симметрично относительно
осии проходит через точку
; -
парабола
расположена симметрично относительно
осии проходит через точку
.
-
4.
Установить, какие линии определяются
следующими уравнениями:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
.
Изобразить эти линии на чертеже.
5.
Найти фокус
и уравнение директрисы параболы
.
6.
Вычислить фокальный радиус точки
параболы
,
если абсцисса точки
равна 7.
7.
Вычислить фокальный радиус точки
параболы
,
если ордината точки
равна 6.
8.
На параболе
найти точки, фокальный радиус которых
равен 13.
9.
Составить уравнение параболы, если дан
фокус
и уравнение директрисы
.
10.
На параболе
найти точку, расстояние которой от
директрисы параболы равно 4.
11.
Составить уравнение параболы с вершиной
в начале координат, симметричной
относительно оси
и отсекающей на прямой
хорду длиной
.
12.
На параболе
найти точку, расстояние которой от
прямой
равно 2.
-
Уравнения
кривых второго порядка с осями симметрии,
параллельными осям координат. Приведение
общего уравнения кривой второго
порядка, не содержащего члена с
произведением текущих координат,к
каноническому
виду
Даны
две прямоугольные системы координат
и
со свойствами: оси
и
,
а также
и
параллельны и одинаково направлены, а
начало
системы
имеет известные координаты
относительно системы
.
Тогда
координаты
и
произвольной точки
плоскости связаны соотношениями:
(23)
Формулы
(18) называются формулами преобразования
координат при параллельном переносе
осей координат.
Уравнение
эллипса с полуосями
и
,
центром в точке
и осями симметрии, параллельными
координатным осям, имеет вид:
,
(24)

Рис.7
Уравнение
гиперболы с осями, параллельными
координатным, имеет вид:
,
(25)
где
–
координаты центра гиперболы.
Уравнение
параболы с осью симметрии, параллельной
оси абсцисс, имеет вид:
,
(26)
,
(27)
Если
ось параболы параллельна оси ординат,
то
,
(28)
,
(29)
Пример
5.1.
Уравнение
линии
привести к каноническому виду и построить
ее.
Решение.
Выделим в правой
части уравнения полные квадраты:

Уравнение
определяет гиперболу с центром в точке
,
действительной полуосью
и мнимой полуосью
.
Прямые
и
являются осями симметрии гиперболы,
параллельными координатным осям
и
соответственно.
Построим
основной прямоугольник гиперболы со
сторонами
и
с центром в точке
(рис. 8). Диагонали этого прямоугольника
являются асимптотами гиперболы.
Рис.8
Найдем
уравнения асимптот. Так как асимптоты
проходят через точку
и имеют угловые коэффициенты
(см. уравнение (12)), то уравнения прямых
запишутся следующим образом:
;
;
;
.
Получим
уравнения асимптот:
и
.
Найдем
вершины гиперболы. В системе координат
:
,
,
т.е.
,
;
,
;
.
Из формул (23) получим:
Точка
:
Точка
:
Итак,
в системе координат
вершины гиперболы выглядят следующим
образом:
,
.
Найдем
фокусы гиперболы. Из формулы (10) имеем:
;
.
Координаты фокусов в системе координат
:
и
.
Точка
:
Точка
:
В
системе координат
координаты фокусов:
,
По
формуле (11) вычислим эксцентриситет:
Задачи для
самостоятельного решения:
Каждое
из следующих уравнений путем параллельного
переноса привести к каноническому виду;
определить тип; изобразить на чертеже
расположение геометрических образов
относительно старых и новых координат.
Определить основные характеристики.
1.
9.
2.
10.
3.
11.
4.
12.
5.
13.
6.
14.
7.
15.
8.
16.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
вершина которой находится в начале координат,
зная, что:
расположена в правой полуплоскости, симметрично
относительно оси Ох и ее параметр р=3;
расположена в левой полуплоскости симетрично
относительно оси Ох и ее параметр р=0,5.
расположена в верхней полуплоскости симметрично
относительно оси Оу и ее параметр р=1/4.
расположена в нижней полуплоскости симметрично
оси Оу и ее параметр р=3.
величину параметра и расположение относительно
координатных осей следующих парабол:
уравнение параболы, вершина которой находится в
начале координат, зная, что:
расположена симметрично относительно оси Ох и
проходит через точку А(9; 6);
расположена симметрично относительно оси Ох и
проходит через точку В(-1; 3);
расположена симметрично относительно оси Оу и
проходит через точку С(1; 1);
расположена симметрично относительно оси Оу и
проходит через точку D(4; -8).
подвешен за два конца; точки крепления
расположены на одинаковой высоте; расстояние
между ними равно 20 см. Величина его прогиба на
расстоянии 2 м от точки крепления, считая по
горизонтали, равна 14,4 см. Определить величину
прогиба этого троса в середине между точками
крепления, приближенно считая, что трос имеет
форму дуги параболы.
уравнение параболы, которая имеет фокус Е(0; -3) и
проходит через начало координат, зная, что ее
осью служит ось Оу.
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
уравнение директрисы параболы
фокальный радиус точки М параболы
абсцисса точки М равна 7.
фокальный радиус точки М параболы
ордината точки М равна 6.
которых равен 13.
уравнение параболы, если дан фокус F(-7; 0) и
уравнение директрисы
уравнение параболы, зная, что ее вершина
совпадает с точкой (
Ох и парабола простирается в бесконечность:
направлении оси Ох;
направлении оси Ох.
уравнение параболы, зная, что ее вершина
совпадает с точкой (
Оу и парабола простирается в бесконечность:
направлении оси Оу (т.е. парабола является
восходящей);
направлении оси Оу (т.е. парабола являетя
нисходящей).
каждое из следующих уравнений определяет
параболу, и найти ее вершины А, величину
параметра р и уравнение директрисы:
каждое из следующих уравнений определяет
параболу, и найти координаты ее вершины А и
величину параметра р:
каждое из следующих уравнений определяет
параболу, и найти ее вершины А и величину
параметра р:
линии определяются следующими уравнениями:
уравнение параболы, если даны ее фокус F(4; 3) и
директриса
уравнение параболы, если даны ее фокус F(4; 3) и
директриса
уравнение параболы, если даны ее фокус F(2; -1) и
директриса
параболы А(6; -3) и уравнение ее директрисы
параболы А(-2; -1) и уравнение е директрисы
пересечения прямой
пересечения прямой
пересечения прямой
определить, как расположена данная прямая
относительно данной параболы – пересекает ли,
касается или проходит вне ее:
каких значениях углового коэффициента k прямая
параболу
параболы.
при котором прямая
параболе
только одну касательную с угловым коэффициентом
уравнение касательной к параболе
точке М1(x1; y1).
уравнение прямой, которая касается параболы
уравнение прямой, которая касается параболы
касательную к параболе
прямой
касательной и данной прямой.
вычислить расстояние d от точки М1 до этой прямой.
уравнения касательных к параболе
из точки А(2; 9).
вершина этой параболы лежит посередине между
точкой пересечения касательной с осью Ох и
проекцией точки касания на ось Ох.
проведены касательные к параболе
уравнение хорды, соединяющей точки касания.
проведены касательные к параболе
расстояние d от точки Р до хорды параболы,
соединяющей точки касания.
пересечения эллипса
параболы
пересечения гиперболы
параболы
пересечения парабол
прямая, касающаяся параболы в некоторой точке М,
составляет равные углы с фокальным радиусом
точки М и с лучом, который, исходя из М, идет
параллельно оси параболы в ту сторону, куда
парабола бесконечно простирается.
Ох направлен луч света. Известно, что
до параболы, луч от нее отразился. Составить
уравнение прямой, на которой лежит отраженный
луч.
параболы, имеющую общую ось и общий фокус,
расположенный между ее вершинами, пересекаются
под прямым углом.
две параболы со взаимно перпендикулярными осями
пересекаются в четырех точках, то эти точки лежат
на одной окружности.