Величина плоского угла
Величина плоского угла определяется на основе его свойства ортогонально проецироваться без искажения если обе его стороны параллельны этой плоскости проекций. Это свойство принято за основу при составлении алгоритма решения
задачи по определению действительной величины угла по его искаженным ортогональным проекциям.
Решение задачи будет сводится к перемещению плоскости общего положения, которой принадлежит угол,
в положение, параллельное какой-либо плоскости проекции. Что достигается путем вращения плоскости
угла вокруг линии уровня.
В этом случае, достаточно произвести поворот только одной точки вокруг горизонтали или фронтали
плоскости угла.
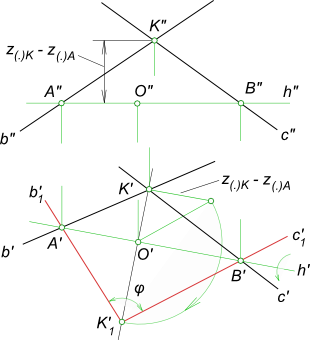
Действительная величина плоского угла, определенная по его ортогональным проекциям
Величина плоского угла
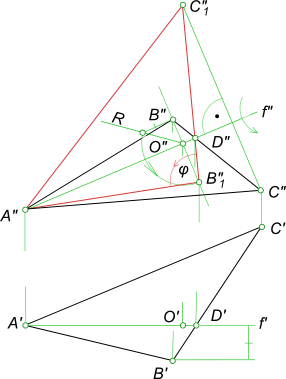
Определение величины углов ΔABC
Величина плоского угла
После поворота треугольника вокруг фронтали f его плоскость переведена в положение ║V. Следовательно, углы при вершинах A”,B”1C”1 проецируются в натуральную величину.
+
4. Решение можно дополнить построением проекций перпендикуляра KL на плоскостях 1 и 2. Построения проекций точки L — основания перпендикуляра — выполняются обратным ходом:
точка L
лежит в пересечении линии проекционной связи, проведенной из LIV перпендикулярно х1, и горизонтальной проекции перпендикуляра, опущенной из K
перпендикулярно С 1 ;
точка L
лежит на линии связи, проведенной из L , на расстоянии zL от
оси z (это расстояние берется с проекций на плоскости 4).
8.4.1. Произвольный плоский угол
О проецировании плоского угла мы рассказывали в разд. 6.3. Как уже отмечалось, в общем случае плоский угол проецируется с искажением. Теперь рассмотрим нахождение натуральной величины плоского угла.
Несколько приемов определения истинной величины плоской фигуры рассматривалось ранее (см. рис. 8.18 и 8.27). Этими же методами можно определить и величину плоского угла. Предлагаем теперь определить угол методом вращения вокруг горизонтали.
Пусть дан угол АВС (рис. 8.34). Вращением вокруг горизонтали повернем угол в положение, параллельное плоскости 1. Тогда угол в своей горизонтальной проекции изобразится без искажения.
1.В плоскости угла проведем горизонталь 12. Поворот треугольника 1В2 вокруг горизонтали 12 сводится к повороту одной вершины — точки В.
Из В
проведем перпендикулярно 1 2
след плоскости вращения этой точки, и в пересечении следа и оси вращения 1 2
получаем проекцию центра вращения OВ .
2.Натуральную величину радиуса вращения RB получаем при построении прямоугольного треугольника В OВВ0 , в котором катет В OВ представляет
собой горизонтальную проекцию радиуса вращения, а катет В В0 — разницу координат между точками В и ОВ по оси z ( zВОВ).
3.Точку В
соединяем с 1
и 2
— горизонтальными проекциями точек, расположенных на оси вращения и принадлежащих сторонам угла. Новая горизонтальная проекция 1 В 2
равна заданному углу АВС.
|
Способы преобразования проекций |
213 |
Рис. 8.34. Определение истинной величины плоского угла АВС
8.4.2. Угол между прямой и плоскостью
Угол между прямой и плоскостью определяется углом между прямой и ее проекцией на эту плоскость, т. е. углом 1 (рис. 8.35). В случаях, когда требуется определить лишь величину этого угла, построение его проекций не является необходимым. Угол между прямой TL и плоскостью можно определить, построив на чертеже угол 2, составленный заданной прямой и перпендикуляром к плоскости, а искомый угол 1 определить как дополнительный до 90 :
1 = 90 – 2.
Рис. 8.35. Угол между прямой и плоскостью
1. Вершины
Рис. 8.36. Определение угла между прямой LT и плоскостью 
Найдем угол между прямой LT и плоскостью , заданной следами (рис. 8.36).
1.Проведем из любой точки прямой LТ, например, точки T перпендикуляр к плоскости :
фронтальная проекция перпендикуляра перпендикулярна f0
;
горизонтальная проекция перпендикуляра перпендикулярна h0
.
2.В плоскости, заданной прямой LТ и перпендикуляром, через любую точку этой плоскости, например, через точку L проводим горизонталь L1.
3.Определяем истинную величину треугольника 1TL и, следовательно, истинную величину угла 1TL. Вращением вокруг горизонтали L1 поворачи-
ваем треугольник TL1 в положение, параллельное плоскости 
L и 1, лежащие на оси вращения, остаются неподвижными. Необходимо повернуть только точку T. Проводим плоскость вращения точки Т — плоскость :
Т
h0
; h0
1 L .
4. Определяем центр вращения ОТ ( OT , OT
) точки Т:
OT = h0
1 L ; OT
1 L .
|
Способы преобразования проекций |
215 |
Радиус вращения точки Т на горизонтальную ( OT Т ) и фронтальную ( OT
Т ) плоскости проекций спроецирован с искажением. Истинную величину радиуса вращения определим как гипотенузу прямоугольного треугольника OT T T0, катетами которого являются горизонтальная проекция
|
радиуса вращения |
OT T |
и разность координат |
zT0 . Новое положение |
||
|
Т |
|||||
|
точки T находится в пересечении дуги радиуса OT T0 с центром в OT со |
|||||
|
следом плоскости вращения точки T — h0 . |
|||||
|
5. Треугольник T L 1 |
является натуральной величиной треугольника TL1, |
||||
|
а угол 2 — натуральной величиной угла между прямой LТ и перпендику- |
|||||
|
ляром к плоскости |
. Дополняем угол |
2 до 90 . |
Искомый угол между |
||
|
прямой LТ и плоскостью |
равен углу 1: |
1 = 90 |
– |
2. |
8.4.3. Угол между двумя пересекающимися плоскостями
Угол между двумя пересекающимися плоскостями измеряется линейным углом, который образуется прямыми, получающимися в результате пересечения данных плоскостей третьей плоскостью, перпендикулярной к линии их пересечения (рис. 8.37). Этот угол равен углу между перпендикулярами, проведенными из произвольной точки пространства (например, точки K) к данным двум плоскостям.
Считается, что линейный угол двугранного угла должен быть не больше 90 . Следовательно, искомый угол между двумя плоскостями будет равен найденному углу 1, если 1 90 , или углу 2 = 180 – 1, если 1 90 .
Рис. 8.37. Угол между двумя пересекающимися плоскостями
Рис. 8.38. Определение линейного угла между двумя пересекающимися плоскостями и 
Определим истинную величину угла между двумя пересекающимися плоско-
|
стями, одна из которых задана следами ( h0 |
и f0 |
), а другая — треугольни- |
|
|
ком АВС (рис. 8.38). |
|||
|
1. Строим проекции перпендикуляров из произвольно выбранной точки K. |
|||
|
Для плоскости проекции перпендикуляров (a , a ) |
будут перпендику- |
||
|
лярны одноименным следам плоскости (a |
h0 |
и a |
f0 ). |
2.Для плоскости, заданной треугольником АВС, предварительно строим проекции горизонтали С1 (C 1 , C 1 ) и фронтали С2 (C 2 , C 2 ). Гори-
зонтальную проекцию перпендикуляра b
проводим перпендикулярно горизонтальной проекции горизонтали (b
C 1 ); фронтальную проекцию перпендикуляра b — перпендикулярно фронтальной проекции фронтали
(b
C 2 ).
3.Угол между перпендикулярами спроецирован на горизонтальную и фронтальную плоскости проекций с искажением. Для определения истинной величины угла поворачиваем его вокруг фронтали 34 до положения, па-
раллельного плоскости 2. Через точку K проводим плоскость вращения : f0
3 4 .
|
4. Определяем центр вращения точки K (ОK): OK = f0 |
3 4 . |
|
Способы преобразования проекций |
217 |
5.Методом прямоугольного треугольника определяем истинную величину радиуса вращения точки K (K0 OK ) и откладываем эту величину на следе плоскости вращения f0
. Угол , равный углу 3
K 
4
, является истинной величиной искомого угла, поскольку он меньше 90 .
Пример 32. Определить двугранный угол, образованный треугольными гранями АВС и АВD (рис. 8.39).
1.Ребром двугранного угла служит отрезок АВ. Если АВ окажется перпендикулярным плоскости проекций, то обе грани спроецируются на эту плоскость в виде отрезков, угол между которыми будет равен линейному углу двугранного угла.
2.Вводим первую дополнительную плоскость проекций 4 таким образом, чтобы она была параллельна ребру двугранного угла АВ (рис. 8.40):
4 
1; 4 
АВ.
На эпюре новая ось х1 будет параллельна горизонтальной проекции ребра:
|
х1 |
А В . |
|
Строим проекции треугольных |
граней на плоскости π4 — АIVВIVСIV |
|
и АIVВIVDIV. |
|
Рис. 8.39. Исходные проекции |
Рис. 8.40. Определение истинной величины |
|
двугранного угла |
двугранного угла |
218 Глава 8
|
3. |
Далее вводим вторую дополнительную плоскость проекций — плоскость |
|
|
5 таким образом, чтобы ребро АВ оказалось перпендикулярным вновь |
||
|
вводимой плоскости: |
||
|
5 |
4; 5 АВ. |
|
|
На эпюре cтроим ось х2: |
||
|
х2 |
АIVВIV. |
|
|
4. |
Строим проекцию ребра двугранного угла АВ на плоскости 5 (АV ВV) и |
|
|
проекции вершин С и D (СV и DV). В результате проведенных построений |
грани двугранного угла стали перпендикулярны плоскости проекций 5, и угол между их “вырожденными” проекциями и есть искомый угол между плоскостями.
В предыдущем параграфе было отмечено, что плоский угол проецируется на плоскость проекции без искажения в том случае, когда его стороны параллельны этой плоскости. Это свойство может быть принято за основу при составлении алгоритма решения задачи на определение величины угла по его искаженным ортогональным проекциям.
Решение задачи будет сводиться к перемещению плоскости общего положения, которой принадлежит угол, в положение, параллельное какой-либо плоскости проекции. Такое перемещение можно осуществить с помощью способов преобразования ортогональных проекций.
Наиболее рациональное решение задачи по переводу плоскости угла в положение, параллельное плоскости проекции, достигается путем вращения плоскости угла вокруг линии уровня. В этом случае для получения ответа на поставленную задачу достаточно произвести поворот только одной точки вокруг горизонтали или фронтали плоскости угла – построить только одну вспомогательную проекцию.
При использовании других способов преобразования нам пришлось бы дважды менять плоскости проекции, либо дважды осуществлять перемещение (или вращение), параллельное плоскости проекции, т. е. в обоих случаях потребовалось бы построение двух вспомогательных проекций.
Приведенные ниже примеры иллюстрируют использование способа вращения вокруг линии уровня для решения задачи по определению величины плоского угла.
ПРИМЕР 1. Определить угол между пересекающимися прямыми а и b (рис. 279).
РЕШЕНИЕ. Вращаем плоскость α, определяемую прямыми а и b, вокруг ее горизонтали h до нового положения, параллельного плоскости π1. Точки А и В принадлежат оси вращения h , поэтому
при вращении плоскости α вокруг оси h они не меняют своего положения. Следо-
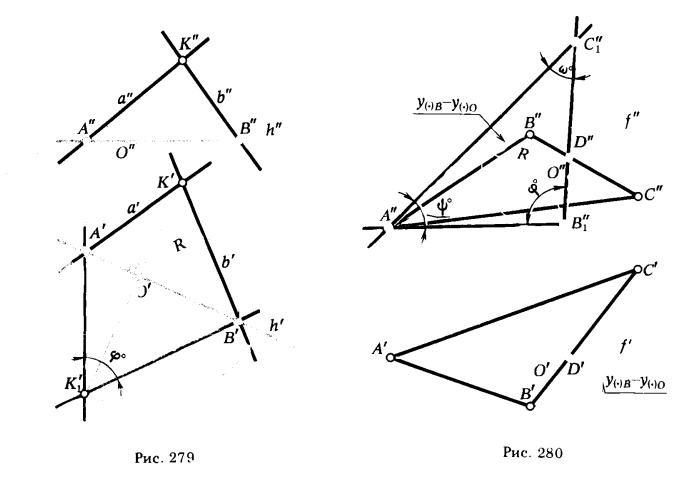
вательно, для определения нового положения плоскости α1 достаточно осуществить поворот только одной точки К. Для этого проводим через К’ прямую, перпендикулярную h’ (с этой прямой будет совпадать горизонтальная проекция окружности, по которой перемещается точка при ее вращении вокруг h ). Далее определяем положение центра вращения О и величину радиуса вращения R для точки К (построения выполнены аналогично тому, как это было сделано на рис. 71, § 11). Положение точки К’1 совместно с А’ и В’ определяет новые проекции прямых a’1 и b’1, задающих плоскость α1.Поэтому А’К’1В’ равен искомому углу φ°.
ПРИМЕР 2. Определить величину углов ΔАВС (рис. 280) .
РЕШЕНИЕ. Вращаем плоскость ΔАВС вокруг фронтали f этого треугольника до положения, параллельного плоскости π2. Через вершину А ΔАВС проводим фронталь f(f’, f”). Точки А и D как принадлежащие оси вращения не изменят своего положения в процессе преобразования. Поэтому, как и в предыдущем примере, достаточно повернуть только одну точку. На рис. 280 в качестве такой точки взята вершина В ΔАВС.
Вершина треугольника С при вращении вокруг фронтали будет перемещаться по дуге окружности, плоскость которой перпендикулярна оси вращения f; поэтому фронтальная проекция этой окружности перпендикулярна f” и новое положение С”1 определится в точке пересечения этого перпендикуляра с новым положением прямой B”1D”. После такого поворота плоскость треугольника переводится в положение, параллельное плоскости π2. Следовательно, на основании инвариантного свойства 2д (см. § 6) углы при вершинах А”, В”1 и С”1 проецируются без искажения.
Как найти величину угла треугольника
Плоский треугольник в евклидовой геометрии составляют три угла, образованные его сторонами. Величины этих углов можно рассчитать несколькими способами. В силу того, что треугольник – одна из простейших фигур, существуют несложные формулы расчета, которые еще более упрощаются, если их применять к правильным и симметричным многоугольникам этого рода.
Инструкция
Если известны величины двух углов произвольного треугольника (β и γ), то величину третьего (α) можно определить исходя из теоремы о сумме углов в треугольнике. Она гласит, что эта сумма в евклидовой геометрии всегда равна 180°. То есть для нахождения единственного неизвестного угла в вершинах треугольника отнимайте от 180° величины двух известных углов: α=180°-β-γ.
Если речь идет о прямоугольном треугольнике, то для нахождения величины неизвестного острого угла (α) достаточно знать величину другого острого угла (β). Так как в таком треугольнике угол, лежащий напротив гипотенузы, всегда равен 90°, то для нахождения величины неизвестного угла отнимайте от 90° величину известного угла: α=90°-β.
В равнобедренном треугольнике тоже достаточно знать величину одного из углов, чтобы вычислить два других. Если известен угол (γ) между сторонами равной длины, то для вычисления обоих остальных углов найдите половину от разницы между 180° и величиной известного угла – эти углы в равнобедренном треугольнике будут равны: α=β=(180°-γ)/2. Из этого вытекает, что если известна величина одного из равных углов, то угол между равными сторонами можно определить как разницу между 180° и удвоенной величиной известного угла: γ=180°-2*α.
Если известны длины трех сторон (A, B, C) в произвольном треугольнике, то величину угла можно найти по теореме косинусов. Например, косинус угла (β), лежащего напротив стороны B, можно выразить как сумму возведенных в квадрат длин сторон A и C, уменьшенную на возведенную в квадрат длину стороны B и поделенную на удвоенное произведение длин сторон A и C: cos(β)=(A²+C²-B²)/(2*A*C). А чтобы найти величину угла, зная чему равен его косинус, надо найти его арк-функцию, то есть арккосинус. Значит β=arccos((A²+C²-B²)/(2*A*C)). Аналогичным способом можно найти величины углов, лежащих напротив остальных сторон в этом треугольнике.
Источники:
- величины углов
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Естественно имеет. Всё, что можно измерить и сравнить по величине, имеет размерность. Если какая-то величина не имеет размерности. а ее нужно измерять, то размерность просто назначают. Для углов было так:
1) Взяли полный угол, разделили его на 360 частей, одну часть назвали градусом, так появилась единица измерения – градус.
2) Взяли полный угол, разделили его на 4 части, каждую часть назвали “прямым углом”. Затем прямой угол разделили на 100 частей, 1 часть назвали градом (“град”, не путать с градусом, градус – 1/360 часть полного угла, град – 1/400 часть полного угла.
3) Если в окружности провести два радиуса, то они разделят окружность на две дуги, а полный угол на 2 угла. Для дуг и углов приняты одинаковые размерности. Но у дуги можно измерить и длину. Так вот, если за ЕДИНИЦУ измерения принять РАДИУС окружности, то длина дуги выразится каким-то числом. Так вот, величину, получающуюся когда длина дуги равна радиусу окружности, то такую величину называют радианом. Соответственно, и углы можно измерять тоже в радианах.
Отметим, что полный угол равен 2*Пи радианам, развернутый угол Пи радианам, прямой угол Пи/2 радианам.
Отсюда соотношения между различными единицами измерения: (Пи радиан)=(180 градусов)=(200 градов).
