Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

3.1. Определение продольной силы
При
осевом растяжении и сжатии возникает
единственный внутренний силовой фактор
продольная сила
![]() .
.
Для определения величины продольной
силы применяется метод сечений. Рассекая
стержень сечением (Рис.3.1,а) и рассматривая
равновесие отсеченной части (Рис.3.1,б),
приходим к следующему правилу:величина
продольной силы численно равняется
алгебраической сумме проекций на
продольную ось стержня всех внешних
сил, действующих по одну сторону от
рассматриваемого сечения.
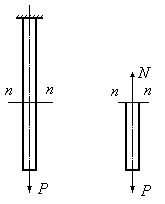
а)
б)
Рис.3.1
Знак
продольной силы будет положительным,
если продольная сила действует от
сечения (Рис.3.2,а), и отрицательным, если
продольная сила действует к сечению.

а)
б)
Рис.3.2
Проиллюстрируем
это правило на примере.
Пример
3.1.
Определить величину продольной силы
на каждом из участков стержня, изображенного
на Рис.3.3,а стержня. Построить диаграмму
распределения продольных усилий по
длине стержня. Влиянием собственного
веса стержня пренебречь.
Решение:
1.
Следуя изложенному выше правилу,
продольную силу на участке №1
найдем, просуммировав проекции на
продольную ось стержня
![]() всех внешних сил, действующих по одну
всех внешних сил, действующих по одну
сторону от сеченияI-I:
![]() 40кН.
40кН.

Рис.3.3
2. На
втором участке величина продольной
силы равняется:
![]() 40+20=20кН.
40+20=20кН.
3. На
третьем участке стержня продольная
сила будет равна:
![]() 40+20+30=10кН.
40+20+30=10кН.
В
каждом из рассматриваемых случаев знак
продольного усилия определяется
направлением внешней силы: от сечения
“+”,
к сечению
“”.
На
рис.3.3,б приведена диаграмма распределения
продольной силы
![]() по длине стержня.
по длине стержня.
3.2. Нормальные напряжения при осевом растяжении и сжатии
При
осевом растяжении и сжатии продольная
сила и нормальные напряжения связаны
следующей интегральной зависимостью:
![]() (3.1)
(3.1)
Чтобы
определить с помощью этой формулы
нормальные напряжения
![]() ,
,
необходимо знать закон распределения
нормальных напряжений по площади
поперечного сечения при осевом растяжении
и сжатии. Такой закон устанавливается
гипотезой плоских сечений (гипотезой
Бернулли):сечения
плоские до деформации остаются плоскими
в процессе деформации.
Из
этой гипотезы следует, что нормальные
напряжения, действующие в поперечных
сечениях стержня при осевом растяжении
и сжатии, являются величиной постоянной
(![]() ).
).
Решая интеграл (3.1) при постоянном
значении нормальных напряжений, получаем
следующее выражение для продольной
силы:
![]() .
.
(3.2)
Откуда:
![]() .
.
(3.3)
Напряжения
определяются в системе единиц SI
в
![]() (Па).
(Па).
Рассмотрим
пример определения напряжений в
поперечнях сечениях стержня, представленного
на рис.3.3.
Пример
3.2.
Найти величину нормальных напряжений
на каждом участке стержня, приведенного
на рис.3.3,а, если площадь поперечного
сечения по всей длине стержня постоянна
и равняется
![]() см2.
см2.
Построить диаграмму распределения
нормальных напряжений по длине стержня.
Влиянием собственного веса стержня
пренебречь.
Решение:
1.
Воспользуемся выражением (3.3) и определим
напряжение на первом участке стержня:
![]() 100
100
МПа.
2.
На втором участке нормальные напряжения
найдем из выражения:
![]() 50
50
МПа.
3.
На третьем участке:
![]() 25МПа.
25МПа.
4.
На рис.3.3,в приведена диаграмма
распределения нормальных напряжений
по длине стержня.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Внутренние силы при растяжении-сжатии
Центральное растяжение-сжатие возникает в случае, когда на концах стержня вдоль его оси действуют две равные противоположно направленные силы. При этом в каждом сечении по длине стержня возникает внутреннее усилие (продольная сила $N$ кН), которая численно равна сумме всех сил, которые действуют вдоль оси стержня и расположены с одной стороны от сечения.

Из условий равновесия отсеченной части стержня $N = F$.
Продольная сила при растяжении считается положительной, при сжатии – отрицательной.
Пример определения внутренних сил.
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.
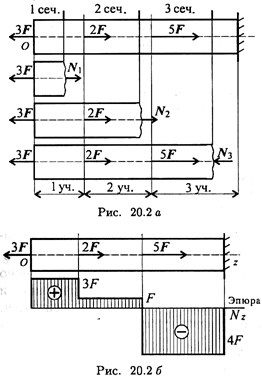
Участком нагружения считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
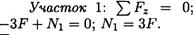
Продольная сила положительна, участок 1 растянут.
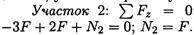
Продольная сила положительна, участок 2 растянут.
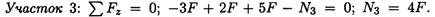
Продольная сила отрицательна, участок 3 сжат.
Полученное значение N3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Напряжения. Действующие и допускаемые напряжения
Величина внутренней силы дает представление о сопротивлении поперечного сечения в целом (интегрально), но не дает представления об интенсивности работы материала в отдельных точках сечения. Так, при равной продольной силе материал в стержне с большим сечением будет работать менее интенсивно, менее напряженно чем меньший.
Напряжения – внутренние силы, приходящиеся на единицу площади сечения. Напряжения, направленные перпендикулярно (по нормали) к сечению называются нормальными.
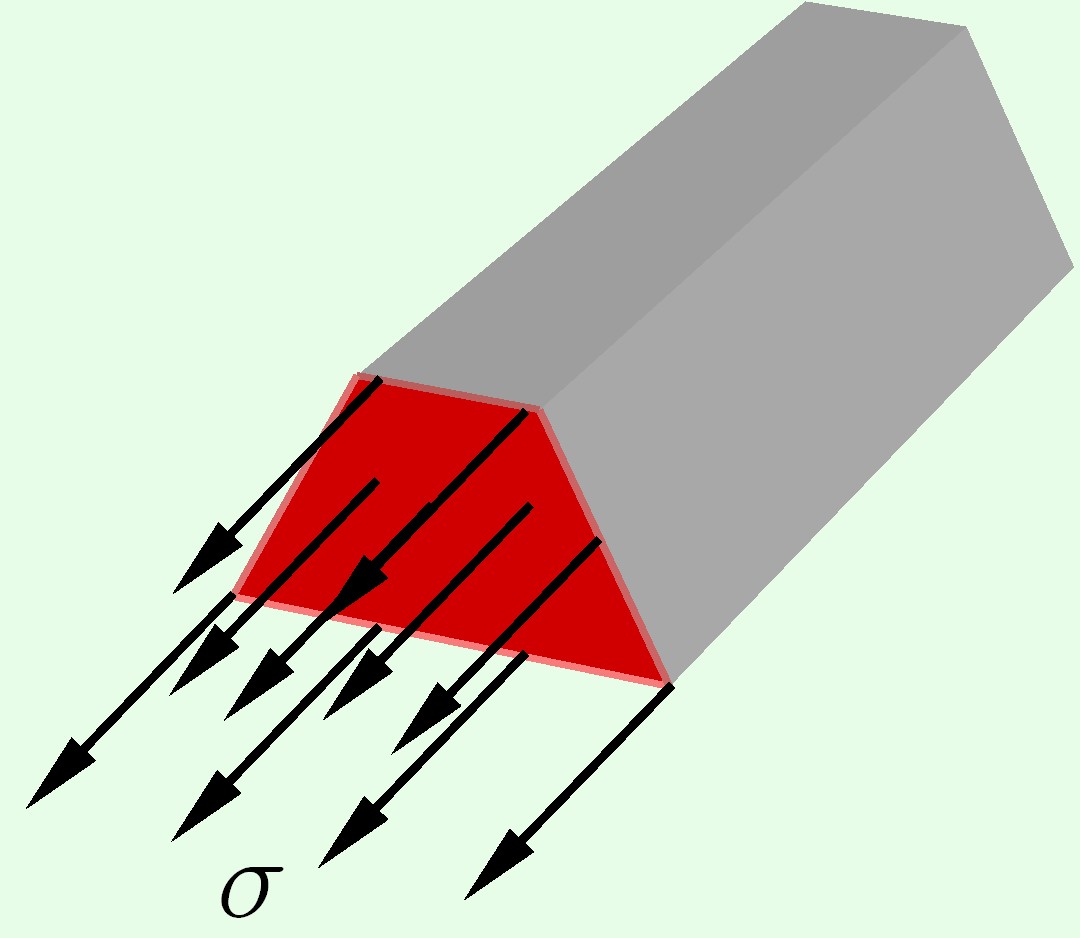
$sigma = frac{N}{A}$
Единицы измерения напряжений – Па, кПа, МПа.
Знаки напряжений принимают так, как и для продольной силы.
Действующие напряжения – напряжения, которые возникают в рассматриваемом сечении.
Любой стержень в момент разрушения имеет определенные напряжения, которые зависят только от материала стержня и не зависят от площади сечения.
Допускаемые напряжения $left[ sigma right]$ – такие напряжения, которые не должны быть превышены в запроектированных конструкциях. Допустимые напряжения зависят от прочности материала, характера его разрушения, степени ответственности конструкции.
Принцип Сен-Венана: в сечениях, достаточно удаленных от места приложения нагрузки, распределение напряжений не зависит от способа приложения нагрузки, а зависит только от его равнодействующей.
то есть, распределение напряжений в сечении I-I для трех различных случаев, показанных на рисунке, принимается одинаковым.
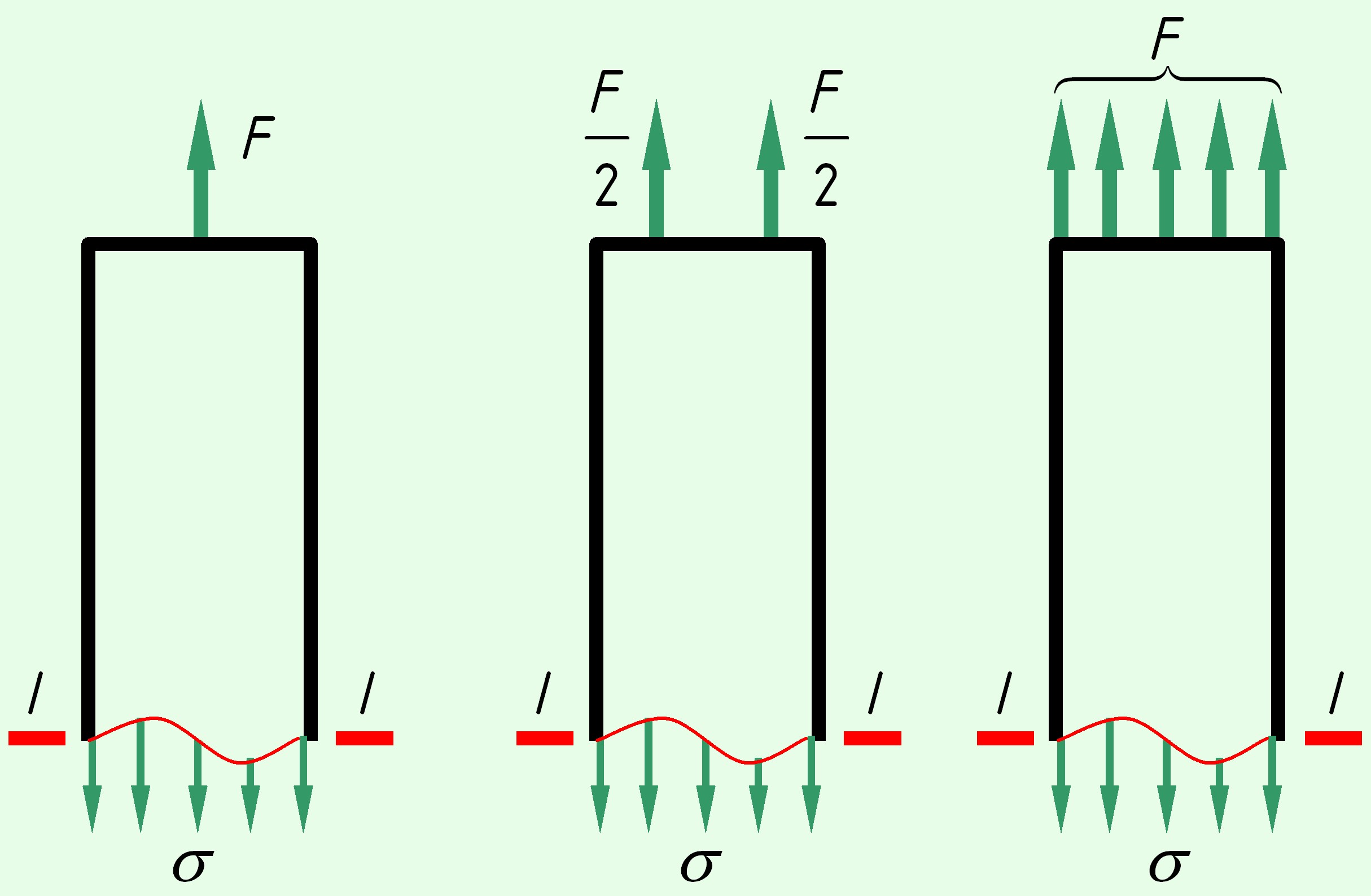
Рисунок – иллюстрация принципа Сен-Венана
Абсолютная и относительная деформация
При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина называется абсолютной деформацией.
$Delta l = {l_1} – l$
Относительная деформация – отношение абсолютной деформации к первоначальной длине.
$varepsilon = frac{{Delta l}}{l}$
$sigma = E cdot varepsilon $
Таблица – физико-механические характеристики материалов
|
Материал |
Модуль упругости, х1010 Па |
Коэффициент Пуассона |
|
Сталь |
19 – 21 |
0,25 – 0,33 |
|
Чугун |
11,5 – 16 |
0,23 – 0,27 |
|
Медь, латунь, бронза |
10 |
0,31 – 0,42 |
|
Алюминий |
7 |
0,32 – 0,36 |
|
Кирпичная кладка |
0,3 |
0,2 |
|
Бетон |
1 – 3 |
0,1 – 0,17 |
|
Каучук |
0,0008 |
0,47 |
Продольная сила
Предмет
Механика
Разместил
🤓 hamssovemo1980
👍 Проверено Автор24
внутреннее усилие N в поперечном сечении стержня, равное сумме проекций элементарных внутренних сил на продольную ось стержня Z.; продольная сила вычисляется как сумма проекций всех внешних сил, расположенных по одну сторону от сечения, на ось Z; продольная сила считается положительной при растяжении и отрицательной при сжатии стержня.
Научные статьи на тему «Продольная сила»
Компоновка сечений сплошностенчатых внецентренно-сжатых колонн
определения требуемой площади сечения используют формулу устойчивости, в которую входят:
расчетная продольная…
сила;
коэффициент устойчивости, учитывающий внецентренное сжатие;
расчетное сопротивление стали….
задача конструктора значительно упрощается, двутавр подбирается из эмпирической зависимости, учитывающей продольную…
силу, максимальный момент, эксцентриситет продольной силы, расчетное сопротивление стали….
внецентренного сжатия выполняется для самых опасных сечений, в которых действия изгибающего момента и продольной

Статья от экспертов
К УЧёТУ ПРОДОЛЬНО-СЖИМАЮЩЕЙ СИЛЫ
Закон Гука
Это означает, что если к телу приложено несколько сил, то можно определить силы реакции (внутренние силы…
силы….
Поскольку $large sigma =F/S$ (2), где:
$F$ – продольная сил,
$S$ – площадь поперечного сечения стержня…
Таким образом получим:
$large frac{1}{rho }=frac{M}{E_{Jx}}$ , (6) где:
$ ρ$ – радиус кривизны продольной…
Потому что деформации в поперечных направлениях тоже влияют на изменение продольных размеров.

Статья от экспертов
Об определении продольной силы в трубопроводе при образовании арки
Исследуется возможность определения продольной силы в трубопроводе при образовании арки по ее геометрической форме. Определяющее значение имеет точность измерений при определении формы. Получена оценка допустимой погрешности измерений, необходимой для определения осевой силы с заданной точностью.
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
Обновлено: 14.05.2023
Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).
Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
Приложим теперь к стержню растягивающую силу (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение , а частица L – в положение . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений .
Этапы метода сечений
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить .
Разрежем стержень, находящийся в равновесии под действием некоторой системы сил (рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.
Отбросим одну из частей стержня и рассмотрим оставленную часть.
Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).
Внутренние силы в методе сечений
Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).
Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.
Получим 6 внутренних силовых факторов , возникающих в поперечном сечении стержня при его деформировании: три силы (рис. 1.3, г) и три момента (рис. 1.3, д).
Сила N – продольная сила
момент относительно оси z () – крутящий момент
моменты относительно осей x, y () – изгибающие моменты.
Запишем для оставленной части тела уравнения равновесия ( уравновесим ):
Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.
Вычисление продольной и поперечных сил, крутящего и изгибающих моментов
продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z;
поперечные силы равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y, соответственно;
крутящий момент равен сумме моментов всех сил, действующих на любую из частей стержня, относительно продольной оси z;
изгибающие моменты равны сумме моментов всех сил, действующих на любую из частей стержня, относительно осей x и y, соответственно.
В этой статье поговорим о таком внутреннем силовом факторе как продольная сила. Также дам ссылки на смежные статьи, которые каким-то образом связаны с продольной силой.
Что такое продольная сила?
Продольная сила – это внутренний силовой фактор, который возникает в поперечных сечениях элементов конструкций, работающих на растяжение (сжатие).
Конечно, продольная сила может появляться не только в элементах конструкций, которые работают только на чистое растяжение или сжатие. Она может возникать в сечениях, как ОДИН ИЗ силовых факторов, совместно с поперечной силой или изгибающим моментом при сложном сопротивлении.
Зачем нужна?
Этот силовой фактор используется в расчётах на прочность и жёсткость элементов конструкций, работающих на растяжение (сжатие).
Зная значение продольной силы в поперечном сечении элемента конструкции, можно определить нормальное напряжение в этом сечении. А зная значение максимального нормального напряжния, которое, как правило, устанавливается из эпюры продольных усилий, осуществляются прочностные расчёты.
Как определяется?
Как и другие внутренние силовые факторы, продольная сила определяется методом сечений.
Для того чтобы определить продольную силу в произвольном сечении элемента, его мысленно рассекают в этом сечении на две части, рассматриваются равновесие одной из частей, заменив действие отброшенной части продольной силой. Из уравнения статики, в частности, суммы проекций на одну из осей, выражается продольное усилие. Для построения эпюр эту процедуру проводят несколько раз, для каждого участка стержня (бруса).
Как обозначается?
Продольная сила обозначается буквой N с индексом, который совпадает с названием продольной оси, направленной в сторону растяжения или сжатия нагруженного элемента и перпендикулярной поперечным сечениям.
Чаще всего, эта ось обозначается буквой – x. Например, таким образом: Nx
В чём измеряется?
Продольная сила, как и обычные внешние сосредоточенные силы, измеряется в ньютонах.
На практике, в расчётах используются килоньютоны (кН). Также иногда в литературе можно встретить размерность – кгс и тс.
Центральное растяжение-сжатие возникает в случае, когда на концах стержня вдоль его оси действуют две равные противоположно направленные силы. При этом в каждом сечении по длине стержня возникает внутреннее усилие ( продольная сила $N$ кН), которая численно равна сумме всех сил, которые действуют вдоль оси стержня и расположены с одной стороны от сечения.

Из условий равновесия отсеченной части стержня $N = F$.
Продольная сила при растяжении считается положительной, при сжатии – отрицательной .
Пример определения внутренних сил.

Участком нагружения считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
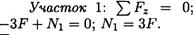
Продольная сила положительна, участок 1 растянут.
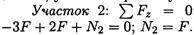
Продольная сила положительна, участок 2 растянут.
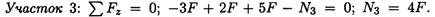
Продольная сила отрицательна, участок 3 сжат.
Полученное значение N3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Напряжения. Действующие и допускаемые напряжения
Величина внутренней силы дает представление о сопротивлении поперечного сечения в целом (интегрально), но не дает представления об интенсивности работы материала в отдельных точках сечения. Так, при равной продольной силе материал в стержне с большим сечением будет работать менее интенсивно, менее напряженно чем меньший.
Напряжения – внутренние силы, приходящиеся на единицу площади сечения. Напряжения, направленные перпендикулярно (по нормали) к сечению называются нормальными .

$sigma = frac$
Единицы измерения напряжений – Па, кПа, МПа.
Знаки напряжений принимают так, как и для продольной силы.
Действующие напряжения – напряжения, которые возникают в рассматриваемом сечении.
Любой стержень в момент разрушения имеет определенные напряжения, которые зависят только от материала стержня и не зависят от площади сечения.
Допускаемые напряжения $left[ sigma right]$ – такие напряжения, которые не должны быть превышены в запроектированных конструкциях. Допустимые напряжения зависят от прочности материала, характера его разрушения, степени ответственности конструкции.
Принцип Сен-Венана : в сечениях, достаточно удаленных от места приложения нагрузки, распределение напряжений не зависит от способа приложения нагрузки, а зависит только от его равнодействующей.
то есть, распределение напряжений в сечении I-I для трех различных случаев, показанных на рисунке, принимается одинаковым.

Рисунок – иллюстрация принципа Сен-Венана
Абсолютная и относительная деформация
При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина называется абсолютной деформацией .
Относительная деформация – отношение абсолютной деформации к первоначальной длине.
Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия (поперечные силы, изгибающие моменты и крутящий момент) равны нулю. Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием).
На рис. 1.2, а изображен прямой брус, закрепленный одним концом и нагруженный на другом конце силой направленной вдоль его оси.
Во всех поперечных сечениях этого бруса возникают только продольные растягивающие силы и, следовательно, такой брус по всей длине является центрально растянутым. При противоположно направленной силе Р (рис. 1.2, б) брус по всей длине испытывает сжатие.
Брус, изображенный на рис. 1.2, в, испытывает центральное растяжение только на участках на участке брус не является центрально растянутым, так как, например, в сечении кроме продольной силы, действуют также поперечная сила и изгибающий момент.
Растягивающие продольные силы принято считать положительными, а сжимающие — отрицательными.
На рис. 2.2, а изображен брус, нагруженный силами направленными вдоль его оси, двумя силами параллельными оси и приложенными на равных расстояниях от нее в поперечном сечении с, а также двумя силами направленными под углом а к оси бруса и приложенными в поперечном сечении d на равных расстояниях от оси.
На рис. 2.2, б изображена расчетная схема, полученная путем замены бруса его осью и переноса внешних нагрузок к этой оси.
Силы на расчетной схеме действуют вдоль оси бруса; силы и силы показанные на рис. 2.2, а, приводятся соответственно к силам также направленным вдоль оси.
Таким образом, на расчетной схеме (рис. 2.2, б) все внешние силы действуют вдоль оси бруса. Следовательно, в поперечных [сечениях рассматриваемого бруса возникают только продольные силы.
Для определения силы N, воспользуемся методом сечений. Составим уравнение равновесия в виде суммы проекций на ось бруса всех сил, действующих на левую его часть (рис. 2.2, в):
Этот же результат можно получить и не составляя уравнения равновесия, а используя то положение, что на основании метода сечений проекция внутренних сил на ось бруса (т. е. продольная сила), действующих со стороны левой его части на правую, равна сумме проекций на эту же ось всех внешних сил, приложенных к левой части.
Аналогично найдем продольные силы в сечениях II—II, III — III, IV—IV (рис. 2.2, б), проектируя силы, приложенные слева от этих сечений, на ось бруса:
Очевидно, что на всем участке (между точками приложения сил ) продольная сила постоянна и равна аналогично и на других участках (между точками приложения внешних сил) продольные силы имеют постоянные значения.
Построим график, показывающий изменение продольных сил по длине оси бруса, называемый эпюрой продольных сил (эпюрой N). Для этого проведем ось эпюры параллельную оси бруса (рис. 2.2, д), и перпендикулярно к ней отложим ординаты, изображающие в некотором масштабе величины продольных сил в поперечных сечениях бруса. Полученную таким путем эпюру принято штриховать (так же как и эпюры других внутренних усилий, рассматриваемые в последующих главах курса) прямыми линиями, перпендикулярными к ее оси. Каждая такая линия в принятом масштабе дает величину продольной силы в соответствующем поперечном сечении бруса.
В поперечном сечении, в котором к брусу приложена сосредоточенная сила, не перпендикулярная к его оси, значение продольной силы изменяется скачкообразно: слева от этого сечения, продольная сила имеет одно, а справа — другое значение, отличающееся на величину проекции (на ось бруса) указанной сосредоточенной силы. В соответствии с этим эпюра, изображенная на рис. 2.2, д, имеет скачки (уступы) в точках а, b, с, d, е, равные соответственно величинам и значению реакции опорного закрепления бруса.
Для построения эпюр внутренних усилий, возникающих в поперечных сечениях бруса, нет необходимости изображать и брус с действующими на него нагрузками и расчетную схему, а достаточно привести один из этих чертежей. Точно так же нет необходимости изображать отдельные части бруса, на которые он расчленяется поперечными сечениями.
Например, для решения рассмотренной задачи можно изобразить лишь брус (рис. 2.2, с) или его расчетную схему (рис. 2.2, б), а также эпюру продольных сил N (рис. 2.2, д) и мысленно представить остальные схемы, приведенные на рис. 2.2.
При действии на брус внешней распределенной осевой (т. е. направленной вдоль оси бруса) нагрузки продольные силы на участке, на котором такая нагрузка приложена, изменяются непрерывно. Для примера на рис. 3.2, б показана эпюра продольных сил для бруса, изображенного на рис. 3.2, а.
На этот брус, кроме двух сосредоточенных сил действует распределенная нагрузка (собственный вес бруса) интенсивностью Эпюра N (рис. 3.2,б) построена на основе уравнений продольных сил, составленных для сечений, отстоящих от верхнего конца бруса на расстоянии
Читайте также:
- Повышение квалификации учителей начальной школы и аттестация педагогических работников
- Как давление влияет на растения кратко
- Кто проводит в школах и доо энергетическое обследование
- Фотоотчет по проекту в детском саду
- Тать что это кратко
